Abstract
In the fields of fluid dynamics and mechanical engineering, most nanofluids are generally not linear in character, and the fractional order model is the most suitable model for representing such phenomena rather than other traditional approaches. The forced convection fractional order boundary layer flow comprising single-wall carbon nanotubes (SWCNTs) and multiple-wall carbon nanotubes (MWCNTs) with variable wall temperatures passing over a needle was examined. The numerical solutions for the similarity equations were obtained for the integer and fractional values by applying the Adams-type predictor corrector method. A comparison of the SWCNTs and MWCNTs for the classical and fractional schemes was investigated. The classical and fractional order impact of the physical parameters such as skin fraction and Nusselt number are presented physically and numerically. It was observed that the impact of the physical parameters over the momentum and thermal boundary layers in the classical model were limited; however, while utilizing the fractional model, the impact of the parameters varied at different intervals.
1. Introduction
This study is concerned with the enhancement of heat transfer through nanofluid, which will play a dynamic role in the field of chemical sciences and the energy sector. The enhancement of heat transfer through nanofluid was studied by many scientists in the field of geometry under diverse conditions. Sparrow and Gregg [1] scrutinized the removal of humidity, using centrifugal force procedures on a cooled rotary disk. The energy obtaining and cooling behavior of the devices mainly depend on the heat transfer liquid used, and the lower thermal efficiency of these fluids can create harsh restrictions for device performance. The limitations and low thermal efficiency of these liquids delay the device performance and compression of heat exchangers. Choi [2] explored the idea of nanofluids by utilizing small nanosized (10–50 nm) particles in base fluids. The anticipated factors influencing the performance of nanofluids during heat transfer were: (i) thermal properties; (ii) chemical stability; (iii) compatibility with the base fluid; (iv) toxicity; (v) accessibility; and (vi) cost. Possible nanomaterials include metals, metal oxides, and carbon materials. Carbon materials play a significant role in enhancing the thermal efficiency of base fluids, and carbon nanotubes (CNTs) are the renowned family of carbons that have been used for thermal and cooling applications in recent studies. Carbon nanotubes are further divided into two classes: single-walled carbon nanotubes (SWCNTs) and multiple-walled carbon nanotubes (MWCNTs). Single-walled carbon nanotubes are created by packaging a layer of carbon one-atom thick, while MWCNTs contain multiple rolled layers of carbon. Carbon nanotubes nanofluids have many important applications in industries such as aerospace, electronics, optics, and energy conservation, as reported by Volder et al. [3] and Terrones [4]. The higher thermal conductivity (2000–6000 W/mK) of carbon nanotubes make them more valuable for the augmentation of heat transfer devices. Ellahi et al. [5] investigated CNTs’ nanofluid flow along a vertical cone under the influence of a variable wall temperature, and a comparison between SWCNTs and MWCNTs was made in their study. Gohar et al. [6] have studied SWCNTs/MWCNTs’ nanofluid flow over a non-linear stretching disc. The high thermal efficiency of CNTs increased the heat flux and thermal efficiency of the base liquids as the heat fluxed, compared to other nanofluids as reported by Murshed et al. [7,8]. Various thermal conductivity models have been proposed by researchers for nanofluid flow problems. The appropriate and frequently-used thermal conductivity models for CNTs were reported by Xue [9]. The flow problem which passes over a thin needle under the effect of convection has been considered by many scholars Narain and Uberoi [10,11] and Chen [12]. Wang [13] and Grosan and Pop [14] have deliberated the mixed convection boundary layer flows over an upright thin needle including an intense heat source at the tip of the needle.
This study was carried out considering water-based CNT nanofluid flow over a thin needle. Further, the variable surface temperature with forced convection comprising single walled carbon nanotubes (SWCNT) and multi walled carbon nanotube (MWCNT) water-based nanofluid past over a thin needle was investigated in classical and fractional models, respectively.
The integer order derivatives or the classical model of fluid dynamics investigate the flow behavior at the integer steps, while the fractional order derivatives of the same fluid flow explore the natural phenomena to expose the internal behavior of the fluid flow by taking the fractional values among the integers. However, the idea of fractional calculus has been conventional for approximately three hundred years [15,16,17].
In fluid mechanics, most fluids are not generally linear in characteristic and the fractional order model is more appropriate for the illustration of such a kind of spectacle, rather than traditional methods. Caputo [18] introduced the idea of fractional derivatives from the modified Darcy’s law using the concept of unsteadiness. This idea was further modified by other researchers [19,20,21] through the introduction of a variety of new fractional derivatives and their applications. Agarwal et al. [22] studied neural network models using ynchronization and impulsive Caputo fractional differential equations. Khan et al. [23] examined the fractional order solution of the Phi-4 equations using the GO/G expansion technique. Hameed et al. [24] examined the fractional order second grade fluid peristaltic transport in a vertical cylinder. A variety of numerical techniques have been used to find solutions to the classical models [25,26,27,28,29,30], and these techniques have been further combined to find solutions for fractional order problems.
The aim of this study is to analyze the force convectional CNT nanofluid flow passing over a thin needle including the elastic heat flux. The FDE-12 method was used for the solution for the fractional order non-linear differential equations. It is the execution of the predictor corrector method of the Adams–Bash Forth–Moulton technique derived by Diethelm and Freed [31]. Diethelm et al. [32] found the convergence and validity of this method for the solution of fractional order differential equations. The solution for classical and fractional order mathematical models containing (SWCNT/MWCNT) water-based nanofluids was obtained through the solution for fractional order systems, which was solved by the Adams-type predictor corrector method as used in References [33,34]. The range of the parameters in this study were selected as per the investigation by Gul et al. [35] using the BVP 2.0 package and the Optimal Homotopy Analysis Method OHAM technique. They used the 20th order approximation for the selected range of the parameters and obtained the minimum square residual error. The important outcomes were presented physically and numerically.
2. Mathematical Formulation
The axisymmetric boundary layer comprising SWCNT and MWCNT nanofluids’ flow over the surface of a thin needle, including position-dependent wall temperature at the ambient temperature was considered. The radius of the thin needle is defined as. The surface temperature, , of the thin needle is considered heavier than Ambient temperature . The external flow velocity of the nanofluid is considered to be . The momentum and thermal boundary layer equations were derived in the axial and radial coordinates and all the assumption are imposed as [14]:
The physical conditions satisfy [14] and are defined as:
The velocity components are represented by towards the axial and radial directions, respectively.
is the density of the nanofluids, is the dynamic viscosity of the nanofluids such that is the kinematic viscosity of the nanofluid, is the solid particle volume fraction, is the thermal conductivity, and is the specific heat capacity of the nanofluids such that . The thermophysical properties for the CNT nanofluids were presented and satisfy Xue [9]:
To bring the basic Equations (1)–(3) into a dimensionless form, under boundary limitations, as per Equation (4), we adopted the scaling transformations as [14]:
Here, is the Reynolds number, is the characteristic length of the needle, is the dimensionless radial coordinate, is the dimensionless radius of the needle, is the characteristic velocity, is the characteristic temperature, and is the dimensionless axial coordinate. Bringing Equation (6) into the basic Equations (1)–(4) cuts into the following non-linear differential form as:
The suitable boundary conditions are:
Next, the similarity variables are:
Here, is the dimensionless velocity of the external flow, is used to demonstrate the stream function and satisfy the continuity Equation (7). The velocity components derived from the stream function are defined as: . Putting into Equation (11) describes the size of the needle: , along the surface. Using Equation (11) in the basic Equations (7)–(10), the continuity equation is satisfied characteristically, and the rest of the equations are transformed as:
The suitable boundary conditions are:
The skin friction coefficient and the local Nusselt number satisfy [14]:
Here, is the local Reynolds number.
3. Preliminaries on the Caputo Fractional Derivatives
The useful definition of Caputo fractional order derivatives and their properties are presented below.
Definition 1.
Let. The Caputo fractional derivative of orderof the functionis given by:
Property 1.
Letbe such thatandexist almost everywhere, and letThenexists almost everywhere and
Property 2.
The functionis constant and therefore, the fractional derivative is zero:The general description of the fractional differential equation was assumed including the Caputo concept:
With the initial conditions
4. Solution Methodology
The following variables were selected for the momentum and thermal boundary layer (12, 13) to reduce the system into the first order differential equations as:
The Caputo fractional order derivative applied to the first order ODE system was obtained from (12, 13) with the efforts of the proposed variables given in Equation (19).
The fractional order system was obtained from Reference [32]:
Equation (20) represents a matrix system of fractional order equations of an initial value problem. Considering (), we have an integer order model or a classical model.
5. Results and Discussion
The two-dimensional forced conventional boundary layer SWCNT/MWCNT nanofluid flow for the enhancement of heat transmission over a thin needle was examined. A comparison of the influence of the physical constraints was studied for the integer and fractional order values
The fractional order system was solved numerically through the Adams-type predictor corrector method.
The geometry of the problem is displayed in Figure 1. The influence of the constant m versus velocity field is shown in Figure 2 and Figure 3, for the classical and fractional order values, respectively. The larger values of the parameter m cause lower velocity. Physically, the rising values of m enhance the non-linearity to generate a friction force to decline the radial velocity. This decline is comparatively fast in the fractional order scheme. Due to the high thermophysical properties, the decline effect is comparatively rapid using the SWCNTs. The impact of over the for the integer and fractional order values is displayed in Figure 4 and Figure 5, respectively. The larger value of causes a decrease in the velocity, and this effect is clearly larger when using the SWCNTs when compared to the MWCNTs. In fact, the larger amount of enhances the efficiency of the frictional force, and as a result, the viscous forces become strong enough to stop the fluid motion. Again, the decline effect is stronger using the fractional values. Figure 6 and Figure 7 indicate the influence of the various values of the nanoparticle volume fraction versus the temperature field. The larger value of raises the temperature profile, and this effect is comparatively strong by means of the SWCNTs. In fact, the thermal conductivity of SWCNTs is high and provides rapid thermal efficiency to enhance the temperature field.
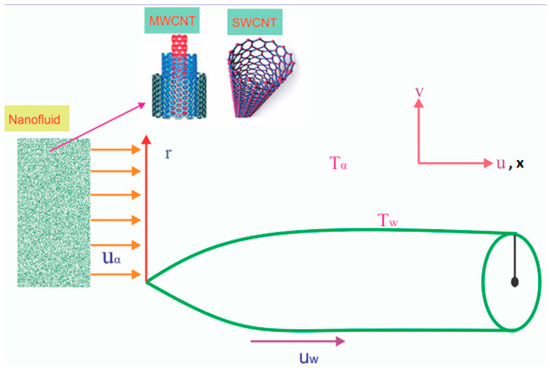
Figure 1.
The geometry of the problem.
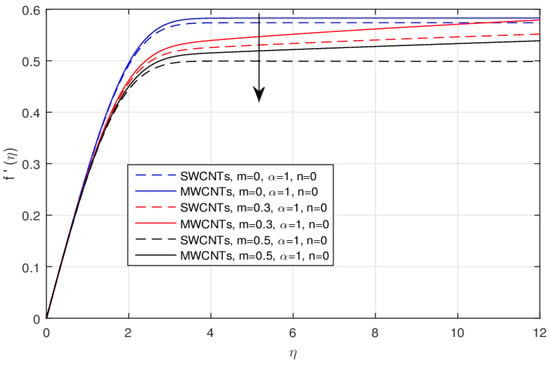
Figure 2.
The impact of over the for the integer values.
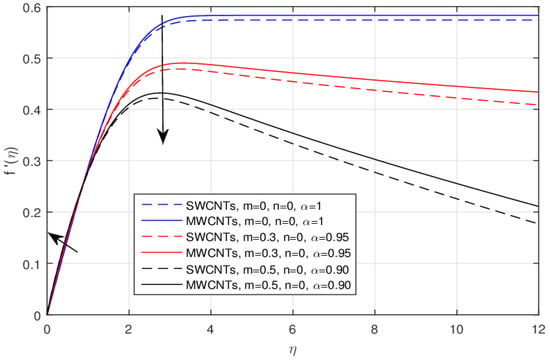
Figure 3.
The impact of over the for the fractional values.
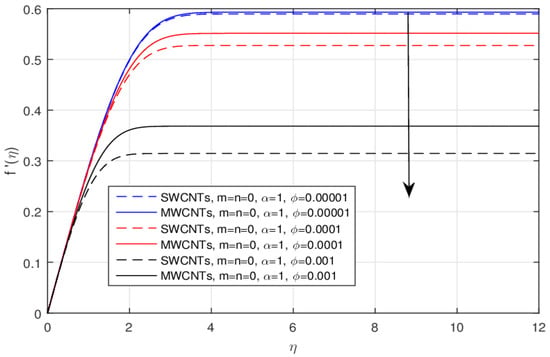
Figure 4.
The impact of over the for the integer values.
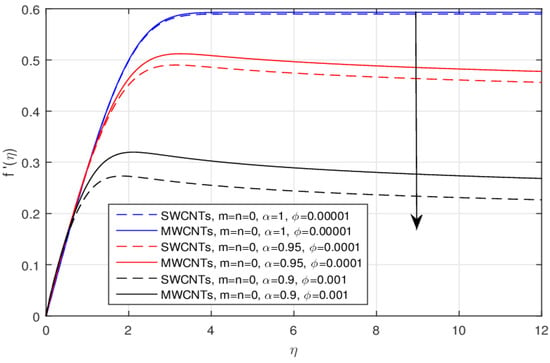
Figure 5.
The impact of over the for the fractional values.
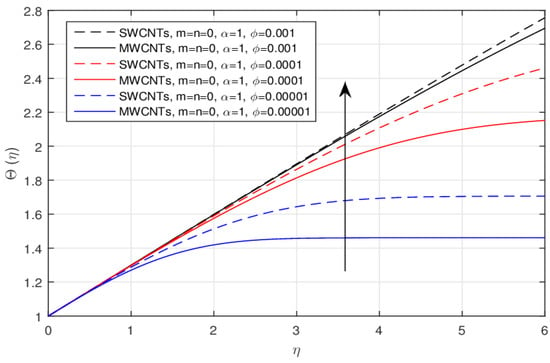
Figure 6.
The impact of over the for the integer values.
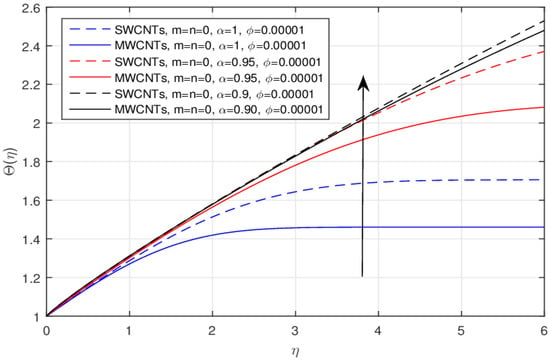
Figure 7.
The impact of over the for the fractional values.
The impact of the wall temperature profile parameter n over the for the integer and fractional values are shown in Figure 8 and Figure 9, respectively. The smaller values of n are enhancing the cooling effect, and as a result, the temperature field declines for the integer values and this effect is reversed for the fractional order values. The performance of the parameter n decreases the temperature field near the surface of the needle for the fractional values and this effect changes to increase the temperature profile after the critical point, as shown in Figure 9. The impact of the Prandtl number over the temperature profile for the integer and fractional values is displayed in Figure 10 and Figure 11, respectively. The rising values of causes lower values compared to the classical model, as usually shown in the literature, but using the fractional model for the same values as the Prandtl number, the temperature profile near the needle surface increases and declines after the point of inflection.
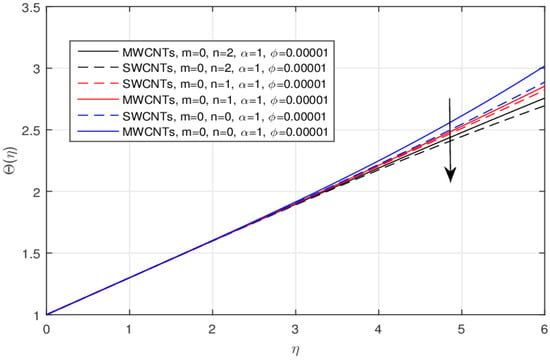
Figure 8.
The impact of n over the for the integer values.
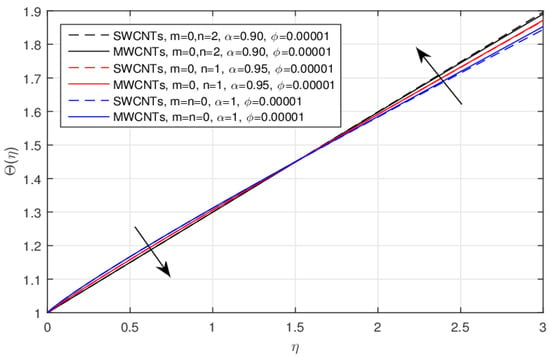
Figure 9.
The impact of n over the for the fractional values.
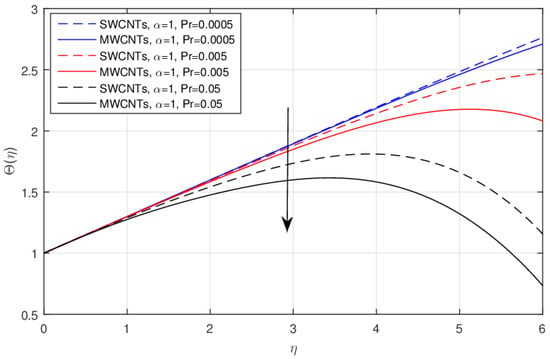
Figure 10.
The impact of over the for the integer values.
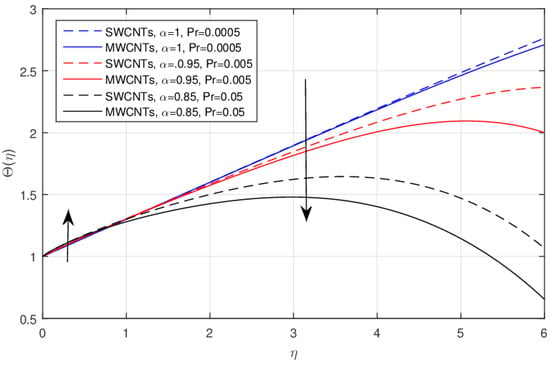
Figure 11.
The impact of over the for the fractional values.
The thermophysical properties of the base fluid and SWCNTs/MWCNTs are shown in Table 1. Skin friction and the Nusselt number are the physical parameters of interest under the influence of classical and fractional values. The classical and fractional model outputs for the skin friction and Nusselt number are displayed in Table 2 and Table 3, respectively. Both tables specify the decline in the numerical values using the fractional order model. The two types of CNTs were compared in these tables for the fractional order values, and it was observed that the impact of the SWCNTs and MWCNTs varies using the fractional model, which is completely different from the classical model, where identical outputs occur in all cases.

Table 1.
The thermo physical properties of carbon nanotubes (CNTs) and the base fluid water.

Table 2.
The classical and fractional order comparison for the skin fraction comprising (SWCNTs/MWCNTs). When

Table 3.
The classical and fractional order comparison for the Nusselt number (SWCNTs/MWCNTs). When
6. Conclusions
The SWCNT and MWCNT water-based nanofluids’ flow over a thin needle was analyzed for the enhancement of temperature. Classical and fractional models were used to investigate the impact of the physical parameters and for similar values for the boundary conditions. The non-linear system was solved through the FDE-12 method. The classical and fractional results were obtained for and , respectively. The impact of the physical parameters over the velocity and temperature profiles in the classical model were limited, but utilizing the fractional model, the impact of the parameters varied for different intervals. It was observed that the fractional order model specifies the accuracy of the physical parameters more precisely considering the small interval of the derivative between 0 and 1, which have important applications, such as for a fractional order PID controller which may provide a more effective way to improve the system control routine; similarly, non-Fickian transport and anomalous diffusion in porous media, polymer flows, or very high gradients of concentration or heat are important application areas of the fractional order derivative in the field of engineering.
The main findings of this study are:
- Greater values of cause decreases in the thickness of the thermal boundary layer when using the classical model, but by means of the fractional model for the same values of the Prandtl number, the thermal boundary layer near the needle surface increases and decreases after the critical point.
- Lower values of n lead to a decrease in the temperature profile using the classical model values, and this effect is upturned for the fractional order values near the wall and change to an upsurge in the thermal boundary layer after the point of inflection.
Author Contributions
T.G.; conceptualization, M.A.K. and W.N.; methodology, I.K.; software, T.A.A.; and I.T.; validation, T.G., M.A.K. and W.N.; formal analysis, I.K.; investigation, T.A.A.; I.K.; and I.T.; writing—original draft preparation, T.G.; M.A.K. and W.N.; writing—review and editing.
Funding
This research received no external funding.
Acknowledgments
Authors acknowledge anonymous referees for their valuable suggestions.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Sparrow, E.M.; Gregg, J.L. A theory of rotating condensation. J. Heat Transf. 1959, 81, 113–120. [Google Scholar]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. FED-231lMD 1995, 66, 99–105. [Google Scholar]
- Volder, M.D.; Tawfick, S.; Baughman, R.; Hart, A. Carbon nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Terrones, M. Science and technology of the twenty-first century: Synthesis, properties, and applications of carbon nanotubes. Annu. Rev. Mater. Res. 2003, 33, 491–501. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of Natural Convection MHD Nanofluid by Means of Single and Multi-Walled Carbon Nanotubes Suspended in a Salt-Water Solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Taza, G.; Waris, K.; Muhammad, S.; Muhammad, A.K.; Ebenezer, B. MWCNTs/SWCNTs Nanofluid Thin Film Flow over a Nonlinear Extending Disc: OHAM Solution. J. Therm. Sci. 2018. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Nieto de Castro, C.A.; Loureno, M.J.V.; Lopes, M.L.M.; Santos, F.J.V. A review of boiling and convective heat transfer with nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 2342–2354. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Leong, K.C.; Yang, C. Thermophysical and electro kinetic properties of nanofluids a critical review. Appl. Therm. Eng. 2008, 28, 2109–2125. [Google Scholar] [CrossRef]
- Xue, Q. Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter. 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Narain, J.P.; Uberoi, M.S. Combined Forced and Free-Convection Heat Transfer From Vertical Thin Needles in a Uniform Stream. Phys. Fluids 1972, 15, 1879–1882. [Google Scholar] [CrossRef]
- Narain, J.P.; Uberoi, M.S. Combined Forced and Free- Convection Over Thin Needles. Int. J. Heat Mass Transf. 1973, 16, 1505–1512. [Google Scholar] [CrossRef]
- Chen, J.L.S. Mixed Convection Flow About Slender Bodies of Revolution. ASME J. Heat Transf. 1987, 109, 1033–1036. [Google Scholar] [CrossRef]
- Wang, C.Y. Mixed convection on a vertical needle with heated tip. Phys. Fluids A 1990, 2, 622–625. [Google Scholar] [CrossRef]
- Grosan, T.; Pop, I. Forced convection boundary layer flow past nonisothermal thin needles in nanofluids. J. Heat Transf. 2011, 133, 1–4. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Benson, D.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Benson, D.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection–dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Caputo, M. Models of flux in porous media with memory. Water Resour. Res. 2000, 36, 693–705. [Google Scholar] [CrossRef]
- El Amin, M.F.; Radwan, A.G.; Sun, S. Analytical solution for fractional derivative gas-flow equation in porous media. Results Phys. 2017, 7, 2432–2438. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 156, 1–13. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Koca, I.; Atangan, A. A novel approach of variable order derivative: Theory and Methods. J. Nonlinear Sci. Appl. 2016, 9, 4867–4876. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Global Mittag-Leffler Synchronization for Neural Networks Modeled by Impulsive Caputo Fractional Differential Equations with Distributed Delays. Symmetry 2018, 10, 473. [Google Scholar] [CrossRef]
- Khan, U.; Ellahi, R.; Khan, R.; Mohyud-Din, S.T. extracting new solitary wave solutions of Benny–Luke equation and Phi-4 equation of fractional order by using (G0/G)-expansion method. Opt. Quant. Electron. 2017, 49, 362–376. [Google Scholar] [CrossRef]
- Hameed, M.; Ambreen, A.K.; Ellahi, R.; Raza, M. Study of magnetic and heat transfer on the peristaltic transport of a fractional second grade fluid in a vertical tube. Eng. Sci. Technol. Int. J. 2015, 18, 496–502. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Ellahi, R.; Sheikholeslami, T.F.; Behzadmehr, A. Numerical investigation of heat and mass transfer flow under the influence of silicon carbide by means of plasmaenhanced chemical vapor deposition vertical reactor. Neural Comput. Appl. 2018, 30, 3721–3731. [Google Scholar] [CrossRef]
- Barikbin, Z.; Ellahi, R.; Abbasbandy, S. The Ritz-Galerkin method for MHD Couette ow of non-Newtonian fluid. Int. J. Ind. Math. 2014, 6, 235–243. [Google Scholar]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study of boundary-layer flow due to a nonlinear curved stretching sheet with convective heat and mass conditions. Results Phys. 2017, 7, 2601–2606. [Google Scholar] [CrossRef]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study for Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov heat flux and homogeneous heterogeneous reactions. Results Phys. 2017, 7, 2886–2892. [Google Scholar] [CrossRef]
- Javeed, S.; Baleanu, D.; Waheed, A.; Khan, M.S.; Affan, H. Analysis of Homotopy Perturbation Method for Solving Fractional Order Differential Equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Sayed, A.M.A.; Gaafar, F.M. A Class of Nonlinear Boundary Value Problems for an Arbitrary Fractional-Order Differential Equation with the Riemann-Stieltjes Functional Integral and Infinite-Point Boundary Conditions. Symmetry 2018, 10, 508. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The Frac PECE subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen; Heinzel, S., Plesser, T., Eds.; Gessellschaft fur Wissenschaftliche Datenverarbeitung: Gottingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Saifullah Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar]
- Gul, T.; Khan, M.A.; Khan, A.; Shuaib, M. Fractional-order three-dimensional thin-film nanofluid flow on an inclined rotating disk. Eur. Phys. J. Plus 2018, 133, 500–5011. [Google Scholar] [CrossRef]
- Gul, T.; Haleem, I.; Ullah, I.; Khan, M.A.; Bonyah, E.; Khan, I.; Shuaib, M. The study of the entropy generation in a thin film flow with variable fluid properties past over a stretching sheet. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).