Soliton and Breather Splitting on Star Graphs from Tricrystal Josephson Junctions
Abstract
:1. Introduction
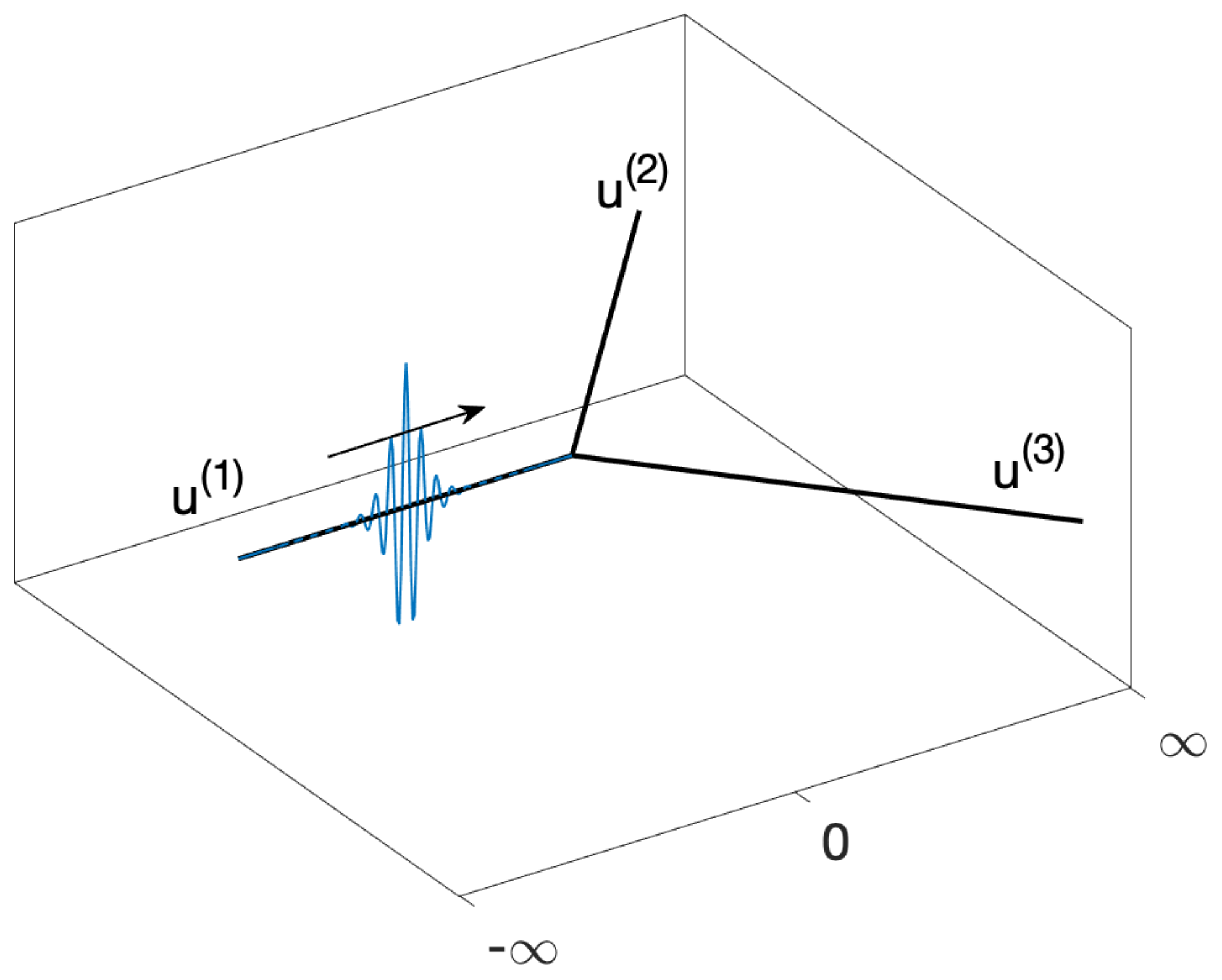
2. Governing Equations
3. Scattering of NLS Solitons
3.1. Scattering in the Linear Problems
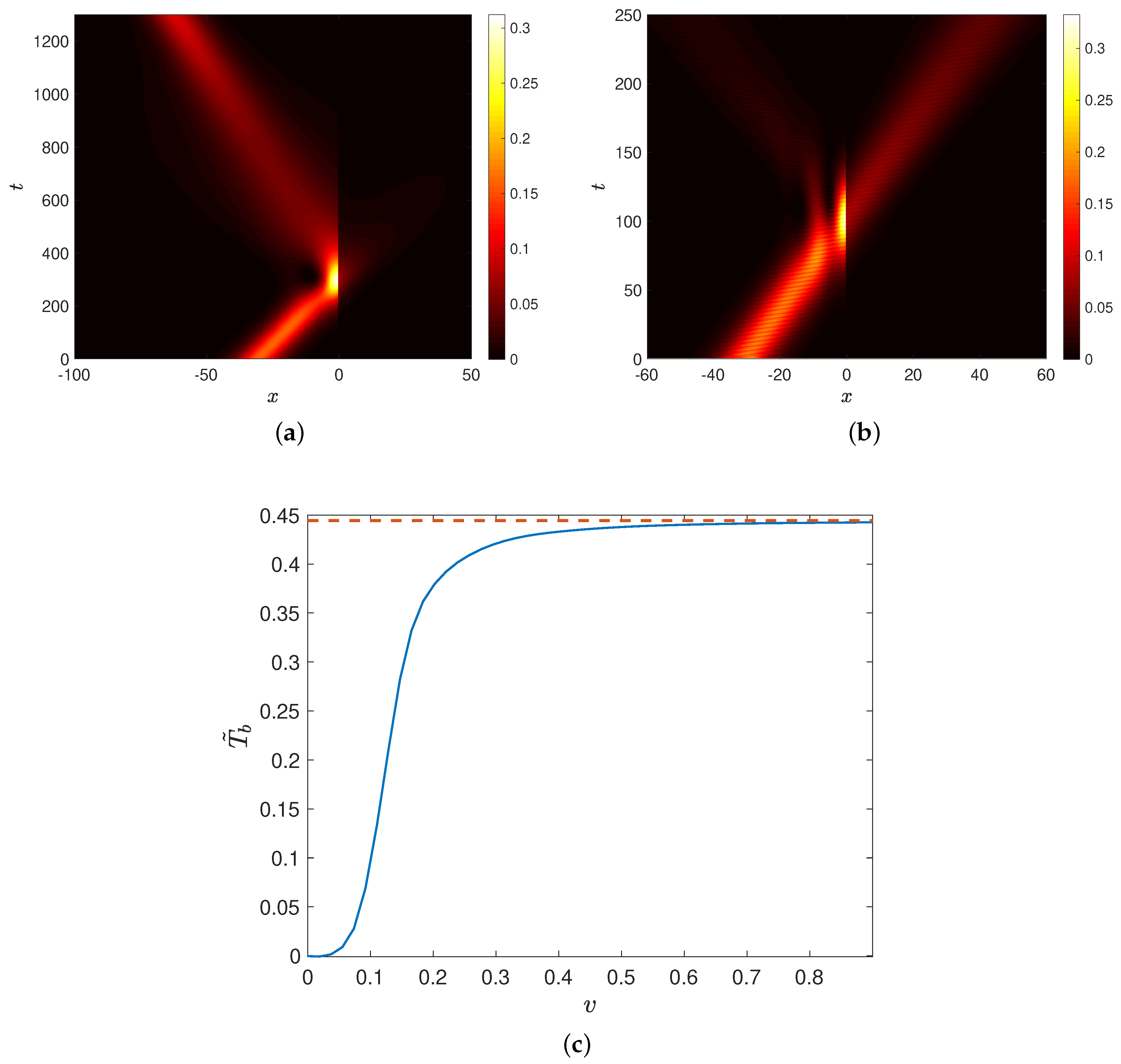
3.2. NLS Soliton Scattering
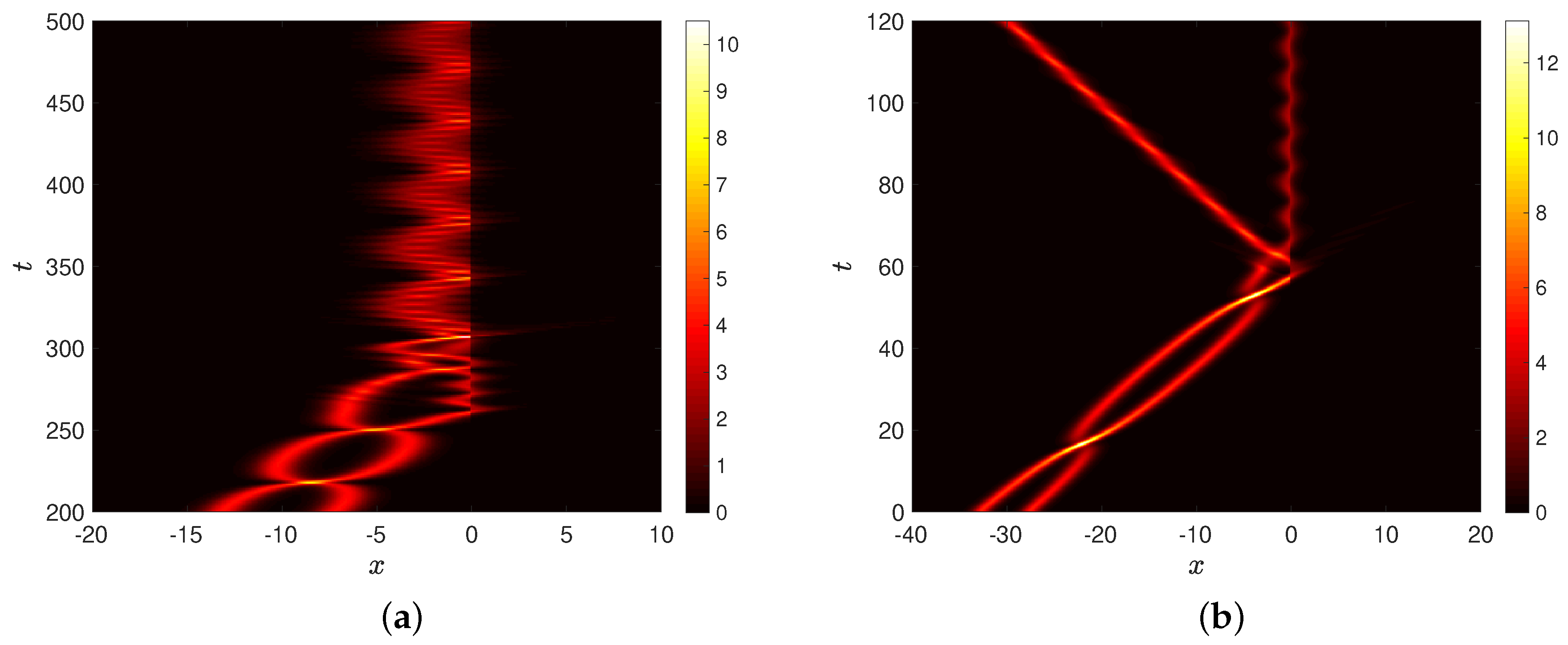
4. Scattering of sG Breathers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NLS | nonlinear Schrödinger |
| sG | sine-Gordon |
References
- Pauling, L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals; Cornell University Press: Ithaca, NY, USA, 1939. [Google Scholar]
- Kottos, T.; Smilansky, U. Quantum chaos on graphs. Phys. Rev. Lett. 1997, 79, 4794–4797. [Google Scholar] [CrossRef]
- Berkolaiko, G. An Elementary Introduction to Quantum Graphs. Geom. Comput. Spectr. Theory 2017, 700, 41–72. [Google Scholar]
- Gnutzmann, S.; Smilansky, U. Quantum graphs: Applications to quantum chaos and universal spectral statistics. Adv. Phys. 2006, 55, 527–625. [Google Scholar] [CrossRef]
- Berkolaiko, G.; Kuchment, P. Introduction to Quantum Graphs, Volume 186 of Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2013. [Google Scholar]
- Kuchment, P. Quantum graphs: An introduction and a brief survey. In Analysis on Graphs and its Applications, Proceedings of Symposia in Pure Mathematics; American Mathematical Society: Providence, RI, USA, 2008; pp. 291–314. Available online: https://arxiv.org/abs/0802.3442 (accessed on 8 January 2019).
- Noja, D. Nonlinear Schrödinger equation on graphs: Recent results and open problems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130002. [Google Scholar] [CrossRef] [PubMed]
- Adami, R.; Cacciapuoti, C.; Finco, D.; Noja, D. On the structure of critical energy levels for the cubic focusing NLS on star graphs. J. Phys. A. Math. Theor. 2012, 45, 192001. [Google Scholar] [CrossRef]
- Adami, R.; Cacciapuoti, C.; Finco, D.; Noja, D. Stationary states of NLS on star graphs. EPL Europhys. Lett. 2012, 100, 10003. [Google Scholar] [CrossRef]
- Adami, R.; Cacciapuoti, C.; Finco, D.; Noja, D. Constrained energy minimization and orbital stability for the NLS equation on a star graph. Ann. Inst. H. Poincaré C Anal. Non Linéare 2014, 31, 1289–1310. [Google Scholar] [CrossRef]
- Adami, R.; Cacciapuoti, C.; Finco, D.; Noja, D. Stable standing waves for a NLS on star graphs as local minimizers of the constrained energy. J. Differ. Eqn. 2015, 260, 7397–7415. [Google Scholar] [CrossRef]
- Kairzhan, A. Orbital instability of standing waves for NLS equation on star graphs. arXiv, 2017; arXiv:1712.02773. [Google Scholar]
- Li, Y.; Li, F.; Shi, J. Ground states of nonlinear Schrödinger equation on star metric graphs. J. Math. Anal. Appl. 2018, 459, 661–685. [Google Scholar] [CrossRef]
- Noja, D.; Pelinovsky, D.E.; Shaikhova, G. Bifurcations and stability of standing waves in the nonlinear Schrödinger equation on the tadpole graph. Nonlinearity 2015, 28, 2343–2378. [Google Scholar] [CrossRef]
- Marzuola, J.L.; Pelinovsky, D.E. Ground state on the dumbbell graph. Appl. Math. Res. eXpress 2016, 2016, 98–145. [Google Scholar] [CrossRef]
- Goodman, R. NLS Bifurcations on the bowtie combinatorial graph and the dumbbell metric graph. arXiv, 2017; arXiv:1710.00030. [Google Scholar]
- Noja, D.; Rolando, S.; Secchi, S. Standing waves for the NLS on the double-bridge graph and a rational–irrational dichotomy. J. Differ. Eqn. 2019, 266, 147–178. [Google Scholar] [CrossRef]
- Adami, R.; Cacciapuoti, C.; Finco, D.; Noja, D. Fast solitons on star graphs. Rev. Math. Phys. 2011, 23, 409–451. [Google Scholar] [CrossRef]
- Holmer, J.; Marzuola, J.; Zworski, M. Fast soliton scattering by delta impurities. Commun. Math. Phys. 2007, 274, 187–216. [Google Scholar] [CrossRef]
- Sobirov, Z.; Matrasulov, D.; Sabirov, K.; Sawada, S.; Nakamura, K. Integrable nonlinear Schrödinger equation on simple networks: connection formula at vertices. Phys. Rev. E 2010, 81, 066602. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, K.; Onodera, Y.; Ogawa, Y. Logic design of Josephson network. J. Appl. Phys. 1976, 47, 1620–1627. [Google Scholar] [CrossRef]
- Nakajima, K.; Onodera, Y. Logic design of Josephson network. II. J. Appl. Phys. 1978, 49, 2958–2963. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R.; Chi, C.C.; Yu-Jahnes, L.S.; Gupta, A.; Shaw, T.; Sun, J.Z.; Ketchen, M.B. Pairing symmetry and flux quantization in a tricrystal superconducting ring of YBa2Cu3O7-δ. Phys. Rev. Lett. 1994, 73, 593–596. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.H., Jr.; Ying, Q.Y.; Zou, Z.G.; Fan, N.Q.; Xu, J.H.; Davis, M.F.; Wolfe, J.C. Use of tricrystal junctions to probe the pairing state symmetry of YBa2Cu3O7-δ. Phys. Rev. Lett. 1995, 74, 2347–2350. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, C.C.; Kirtley, J.R. Phase-sensitive evidence for d-wave pairing symmetry in electron-doped cuprate superconductors. Phys. Rev. Lett. 2000, 85, 182–185. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Tomaschko, J.; Scharinger, S.; Leca, V.; Nagel, J.; Kemmler, M.; Selistrovski, T.; Koelle, D.; Kleiner, R. Phase-sensitive evidence for dx2-y2-pairing symmetry in the parent-structure high-Tc cuprate superconductor Sr1-xLaxCuO2. Phys. Rev. B 2012, 86, 094509. [Google Scholar] [CrossRef]
- Kogan, V.G.; Clem, J.R.; Kirtley, J.R. Josephson vortices at tricrystal boundaries. Phys. Rev. B 2000, 61, 9122–9129. [Google Scholar] [CrossRef]
- Susanto, H.; van Gils, S.A. Existence and stability analysis of solitary waves in a tricrystal junction. Phys. Lett. A 2005, 338, 239–246. [Google Scholar] [CrossRef]
- Susanto, H.; van Gils, S.A.; Doelman, A.; Derks, G. Analysis on the stability of Josephson vortices at tricrystal boundaries: A 3ϕ0/2-flux case. Phys. Rev. B 2004, 69, 212503. [Google Scholar] [CrossRef]
- Grunnet-Jepsen, A.; Fahrendorf, F.N.; Hattel, S.A.; Grønbech-Jensen, N.; Samuelsen, M.R. Fluxons in three long coupled Josephson junctions. Phys. Lett. A 1993, 175, 116–120. [Google Scholar] [CrossRef]
- Hattel, S.A.; Grunnet-Jepsen, A.; Samuelsen, M.R. Dynamics of three coupled long Josephson junctions. Phys. Lett. A 1996, 221, 115–123. [Google Scholar] [CrossRef]
- Krämer, P. The Method of Multiple Scales for nonlinear Klein-Gordon and Schrödinger Equations. Diploma Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2013. [Google Scholar]
- Ali, A.; Susanto, H.; Wattis, J.A. Breathing modes of long Josephson junctions with phase-shifts. SIAM J. Appl. Math. 2011, 71, 242–269. [Google Scholar] [CrossRef]
- Forinash, K.; Peyrard, M.; Malomed, B. Interaction of discrete breathers with impurity modes. Phys. Rev. E 1994, 49, 3400–3411. [Google Scholar] [CrossRef]
- Goodman, R.H.; Holmes, P.J.; Weinstein, M.I. Strong NLS soliton–defect interactions. Phys. D 2004, 192, 215–248. [Google Scholar] [CrossRef]
- Holmer, J.; Zworski, M. Slow soliton interaction with delta impurities. J. Mod. Dyn. 2007, 1, 689–718. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Susanto, H.; Karjanto, N.; Zulkarnain; Nusantara, T.; Widjanarko, T. Soliton and Breather Splitting on Star Graphs from Tricrystal Josephson Junctions. Symmetry 2019, 11, 271. https://doi.org/10.3390/sym11020271
Susanto H, Karjanto N, Zulkarnain, Nusantara T, Widjanarko T. Soliton and Breather Splitting on Star Graphs from Tricrystal Josephson Junctions. Symmetry. 2019; 11(2):271. https://doi.org/10.3390/sym11020271
Chicago/Turabian StyleSusanto, Hadi, Natanael Karjanto, Zulkarnain, Toto Nusantara, and Taufiq Widjanarko. 2019. "Soliton and Breather Splitting on Star Graphs from Tricrystal Josephson Junctions" Symmetry 11, no. 2: 271. https://doi.org/10.3390/sym11020271
APA StyleSusanto, H., Karjanto, N., Zulkarnain, Nusantara, T., & Widjanarko, T. (2019). Soliton and Breather Splitting on Star Graphs from Tricrystal Josephson Junctions. Symmetry, 11(2), 271. https://doi.org/10.3390/sym11020271





