1. Introduction
The nonlinear dynamics of discrete chaotic systems are not new for research, but they have not lost their relevance, due to a number of unresolved issues. As it is known [
1], the implementation of chaotic systems on digital computers with finite-precision arithmetic (i.e., on real computers) has significant difficulties. It results in the fact that we get pseudochaotic systems [
2]. This problem has led to the need for further development of analytical methods in the theory of nonlinear dynamics of discrete chaotic systems. New effective approaches to the synthesis and analysis of chaotic systems have appeared. Thus, Reference [
3] shows the increasing importance that the fractional calculus of meromorphic functions has in chaotic systems. References [
4,
5] show the prospect of solving a number of problems using wavelet analysis.
There are a limited number of papers devoted to the study of nonlinear dynamics of discrete discrete chaotic systems (DCS) of the third order, in which fairly complete and accurate results are represented. This mainly concerns studies in which periodic motions and the acquisition band of synchronization systems [
1,
2] and numerical studies [
3,
4] are examined numerically. The purpose of this paper is to summarize theoretically the results of investigating the nonlinear dynamics of a third order phase synchronization systems (SPS), both in terms of the development of qualitatively-numerical methods of analysis, and in part of the study of specific systems described by the generalized model, Equation (1):
where
,
,
are the generalized coordinates of the system,
,
,
, d, h, g are generalized parameters,
is a variable component of the input frequency.
The expression in Equation (1) reduces to a general expression, as written:
where
is the state vector of the system at the n-th time moment, the dimension of the vector is determined by the order of the system;
is the phase difference of the impulse or code sequences at the inputs of the detector;
is a nonlinear transition matrix whose properties depend on the kind of characteristics of the phase detector
;
is the exposure vector; and
B is the exposure matrix.
2. Phase Portraits of the Onset of Instability of Fixed Points of Piecewise Linear Expressions of the Third Order
The study of steady motions of piecewise linear 3D DCS of the third order is based on the study of typical bifurcations of phase portraits of the mapping (Equation (1)). These include [
5,
6,
7,
8,
9,
10]:
(1) The loss of stability by k-fold fixed points associated with the transition of local stability boundaries , , ;
(2) The loss of stability by k-fold fixed points associated with the transition of limiting points of nonlinearity ( for and for );
(3) The bifurcations of phase portraits caused by the intersection of separatrix invariant manifolds of k-fold saddle points.
At the qualitative level, the basic regularities of the appearance of fixed k-fold points for mappings of the second and third orders are repeated [
5]. The transition of the boundaries of the areas of local stability
,
,
leads to the loss of stability of the fixed points and to qualitatively similar motions. The boundaries of the existence of fixed points of piecewise linear mappings of both orders in the general case for non-zero frequency detunings do not coincide with the boundaries of local stability. In the phase space, the boundaries of existence correspond to the boundaries of linear sections. This allows the condition for the
k-fold fixed point to hit the linearity boundary as one of the necessary conditions for the appearance of periodic motions of the period k [
6].
The cross sections of the local stability body of the mapping (Equation (1)) for various values of the generalized parameter
n have a shape close to a triangular one. They are bounded by the curves
,
,
corresponding to the transition of one of the eigenvalues of the linearized matrix of the map (Equation (1)) through the values
± 1 or
. The line
R on the sections bounds the region of existence of a simple fixed point. Its equation is obtained from Equation (1) and it is written as follows:
The singularity of the transition of stability boundaries, in the case of a third order mapping, consists of a large variety of possible combinations of the eigenvalues of the linearized matrix A corresponding to the boundary.
In accordance with
Table 1, when the boundary
is crossed, there are also three types of nodes and with the transition of the vibrational boundary
, there are four types of foci. The transition through the boundaries
,
occurs in the linear sections of the functions
and
. It is accompanied respectively by such bifurcations as a stable focus-complex saddle and a stable node, i.e. a real saddle. As in the case of second order mappings, the bifurcation data leads to the appearance of invariant closed curves, which are quasiperiodic motions. By virtue of the existence of a boundary
R (for ) that does not coincide with
for piecewise linear mappings, in the general case the bifurcations of the appearance of both simple and k-fold fixed points occur on this boundary. In this case, a fixed point (one of the types of a stable node or focus) is generated simultaneously with one of the types of a saddle fixed point. The disappearance of a fixed stable point also occurs at the boundary
R because of the fusion of a stable node or focus with a saddle point, followed by the formation of a stream of densified trajectories. The condition for the appearance of a pair of fixed points on the boundaries of piecewise linear mappings will be laid down below as the basis for the method of calculating bifurcation parameters.
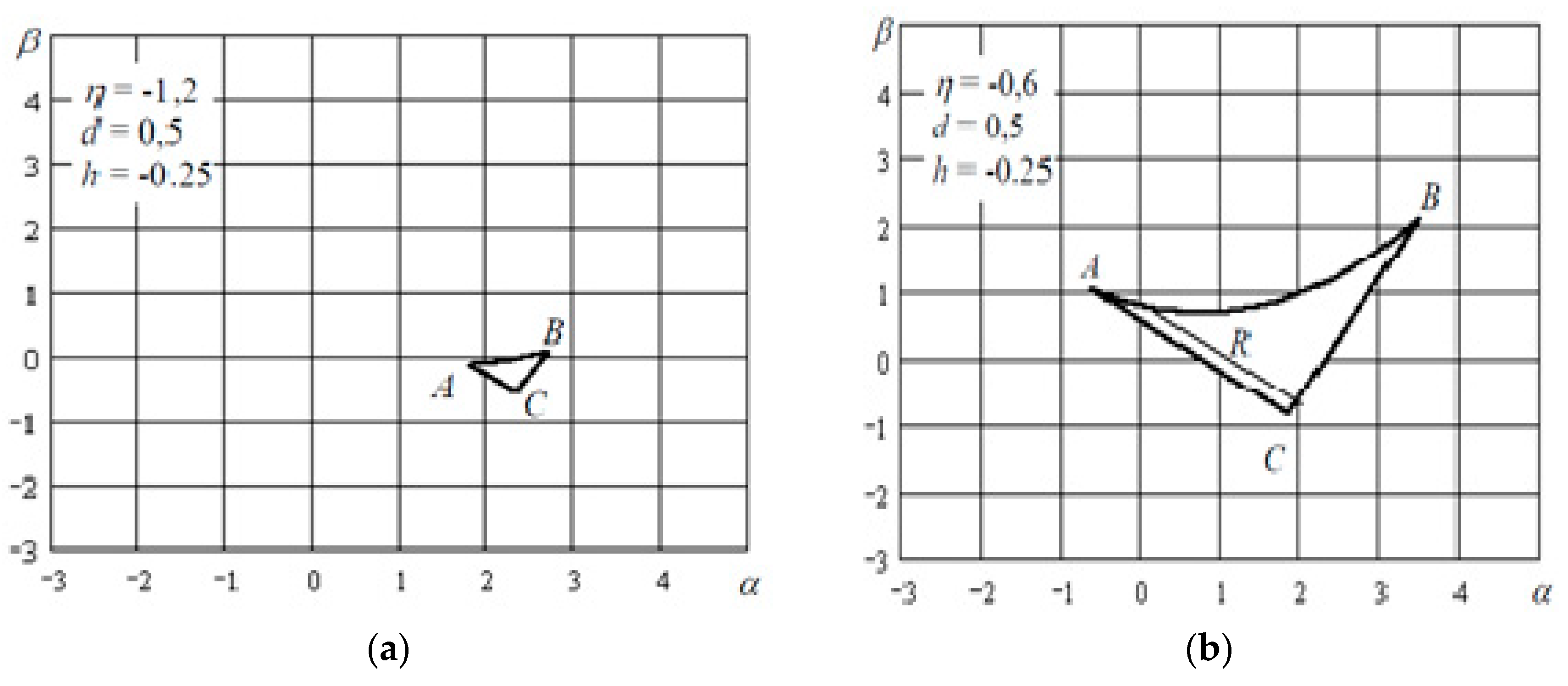
In
Figure 1, sections of the local stability body of the mapping (Equation (1)) for various values of the generalized parameter
n are given on the plane of generalized parameters
a, b.
The formation of quasiperiodic motions under the conditions of the existence of fixed points is determined by the mutual arrangement of invariant separatrix manifolds of a simple or k-fold saddle fixed point. The difference from the second order mapping consists of a greater number of typical phase portraits near the saddle point, determined by the variety of the point itself.
3. SPS Model with Saw-Tooth Nonlinearity
The proposed method for calculating the bifurcation parameters of piecewise linear mappings of the third order is based on the assertions that fixed points on the boundaries of the linear sections of the functions and can arise. For the occurrence of simple fixed points of data, the assertions are sufficient. For the appearance of k-fold fixed points, the formulated assertions appear as necessary ones.
Let
. Since
is periodic, the phase space of the mapping (Equation (1)) is a three-dimensional cylinder, whose scan cross-sections are shown in
Figure 2.
Figure 2 shows the section of the phase space by the plane
. The lines
,
and
are sections of the surfaces of the map preserving the coordinates
,
x and
y, respectively. The equations of these surfaces can be obtained from (Equation (1)) respectively with
,
,
:
The mapping (display) surface with the preserved coordinate y is defined under the condition . It should be noted that the coordinate y is not included in the equation for , so the surface under consideration is perpendicular to the plane . Moreover, the surface b passes through the origin of coordinates, and like in the second order system, it does not depend on the normalized initial detuning g. The point of intersection of these surfaces is the equilibrium state of the system (at the same time, the conditions , and are satisfied, and has the coordinates .
By analogy with a system of the second order, domains of space can be found starting from which the solution (Equation (1)) falls on the boundary of the nonlinearity period
and
. The required domains are a set of planes
(the index
m is the number of the period
) on whose boundary the solution falls) whose equations are written as follows [
11,
12,
13,
14,
15,
16,
17]:
And
In Equations (5) and (6), like in the expression for , the coordinate y is not included, and consequently these planes are perpendicular to the plane .
The arrows show the directions of the motion of the state vector
along the directions
and
under the mapping, in each of the four zones formed by the segments
AB and
CD. For some saddle points shown in
Figure 2, quasiperiodic motions do not take place.
In
Figure 2, the domains of the nonlinear mapping are shaded with output correspondingly to the boundaries
and
of the phase cylinder scan
and
. On both sides, the domains
and
are bounded by the planes
, with the third one, by the plane
for
(mapping in the direction of increasing
) and the plane
for
(the mapping in the direction of decreasing
). In the directions
and one of the directions
, the domains
and
are unbounded. Between the domains
and
there is a domain
, the map from which occurs linearly.
For a nonlinear mapping, the domain passes to the domain . Moreover, the point is mapped to the point ; to the point , and so on.
Changing the coordinate of the state vector in the , a domain leads to a change in the coordinate of the vector in : With increasing (decreasing) increases (decreases) . Thus, the entire domain is mapped into an infinite strip along the -axis bounded along the axis by the planes and, in addition, by two parallel planes that are mappings of the planes . Analogous arguments lead to the construction of the domain , which is a mapping of . It should be noted that there is an intersection of the domains and , as well as and , which fundamentally distinguishes the considered system from the second order system.
Let us consider iterations with initial conditions from an arbitrary state vector
. According to (Equation (1)) vector
may be expressed by means of
as follows:
where
A is linearized matrix corresponding to (Equation (1)) under the linear mapping
, in the case of a nonlinear mapping
, with this, the sign "+" corresponds to going abroad
, the sign "-" corresponds to going abroad
. The vector
returns the state vector of the system to the
-step in the interval [−1; 1] for the coordinate
x. We rewrite (Equation (7)) as:
For a cycle of period
k existing, it is necessary that the closure condition
be satisfied. Taking this condition into account, the expression for the initial point of the cycle follows from (Equation (8)):
The expression (Equation (9)) may be considered as the first necessary condition for the existence of a cycle, or the closure condition. The second condition is to find all the state vectors of a cycle of a required structure within the interval (i.e., the structural condition). Implementation of this condition means that all state vectors of the cycle are in the corresponding domains , , . Otherwise, Equation (9) can formally lead to some state that is not a point of the cycle. The formulated conditions are necessary and sufficient for the existence of a cycle with a certain structure.
Similar to a discrete SPS of the second order, it can be shown that an arbitrary cycle existing in a system with nonlinearity is stable under the conditions of local stability of the mapping (Equation (1)).
Consider the structure cycle
, where
u is the number of nonlinear mappings on the cycle period,
k is the cycle period. For the limit cycle of the first kind
, for the limit cycle of the second kind in the case of rotation along the coordinate
p in the direction of increasing
, in the case of rotation in the direction of decreasing the coordinate
. In accordance with (9), the vector of an arbitrary point of the cycle can be represented as follows:
where
is a vector, depending on the structure of the cycle and the choice of the starting point,
is a vector depending neither on the structure of the cycle nor its initial state.
When is changed, all points of the cycle in the phase domain are displaced along the vector . This can lead to both the occurrence and destruction of the cycle due to the transition of cycle points between the domains , , , and also when the points of the plane cycle intersect the vectors.
Let us find conditions for the generalized detuning
for which there exists a cycle of a certain structure
. To do this, we use the above conditions for the existence of a cycle. From (7–9) we assess the values of the generalized detuning
and
for which the state vector
intersects the boundaries
and
, respectively:
All points of the cycle intersect the plane
if the condition
is satisfied, at least one cycle point intersects the plane
for
. A cycle can exist when:
in the detuning range
.
5. SPS Model with a Triangular Nonlinearity
Let
. The basic laws of the appearance of periodic motions of the second kind and quasiperiodic motions in a third order system with a triangular nonlinearity repeat at a qualitative level in the results obtained for a second order system [
12,
19,
21,
22,
23,
24,
25]. In this case, both the final dependencies and the mechanisms explaining them are qualitatively repeated. In this regard, we will not dwell on them in detail below. The quantitative differences will be demonstrated on a number of graphs devoted to the analysis of the acquisition band.
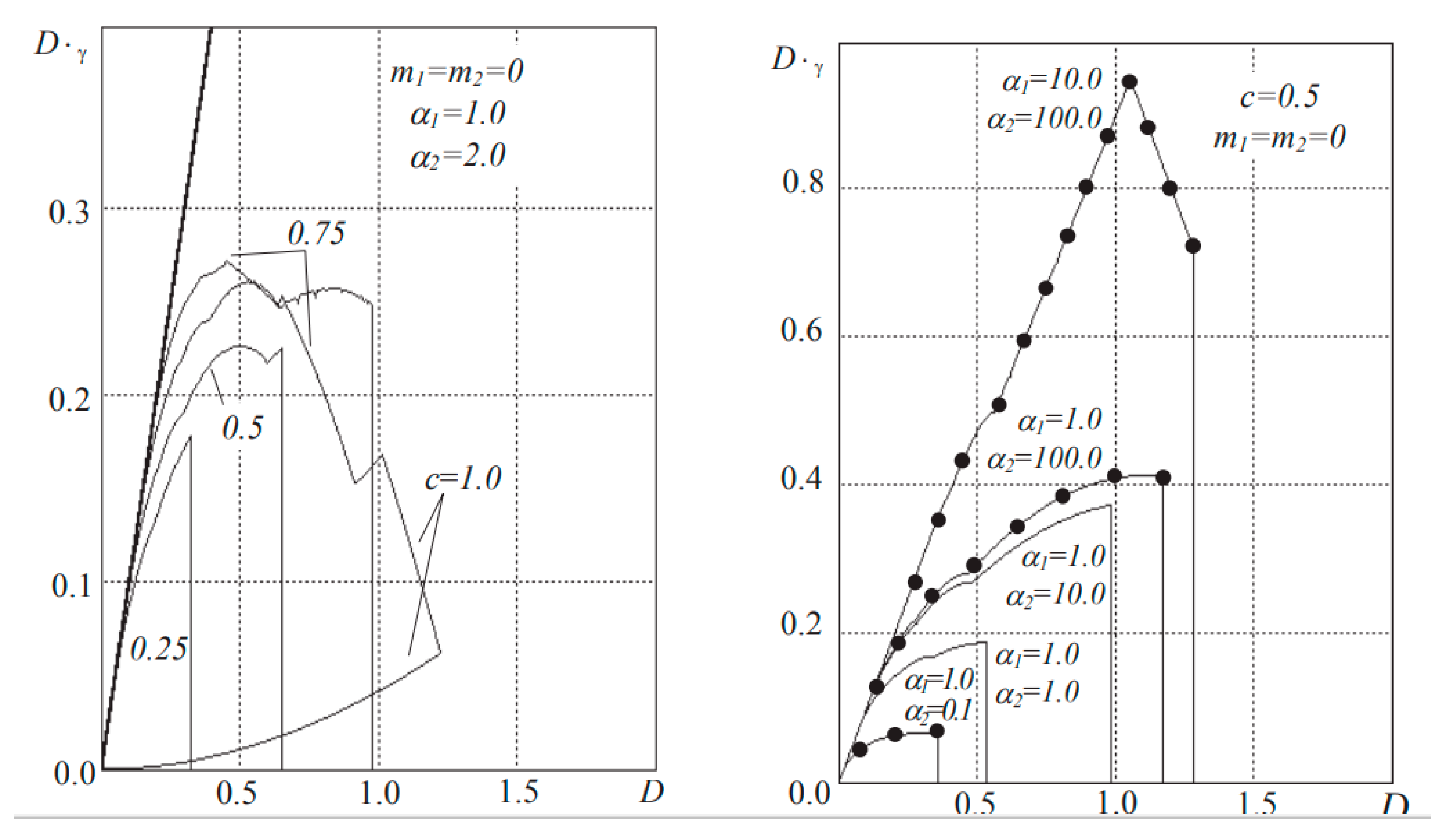
The situation with cycles of the first kind, whose existence has been established in a system with a saw-tooth nonlinearity, is completely different. Their analysis is important because they have occurred with small initial detuning and limit the acquisition domain in frequency from below.
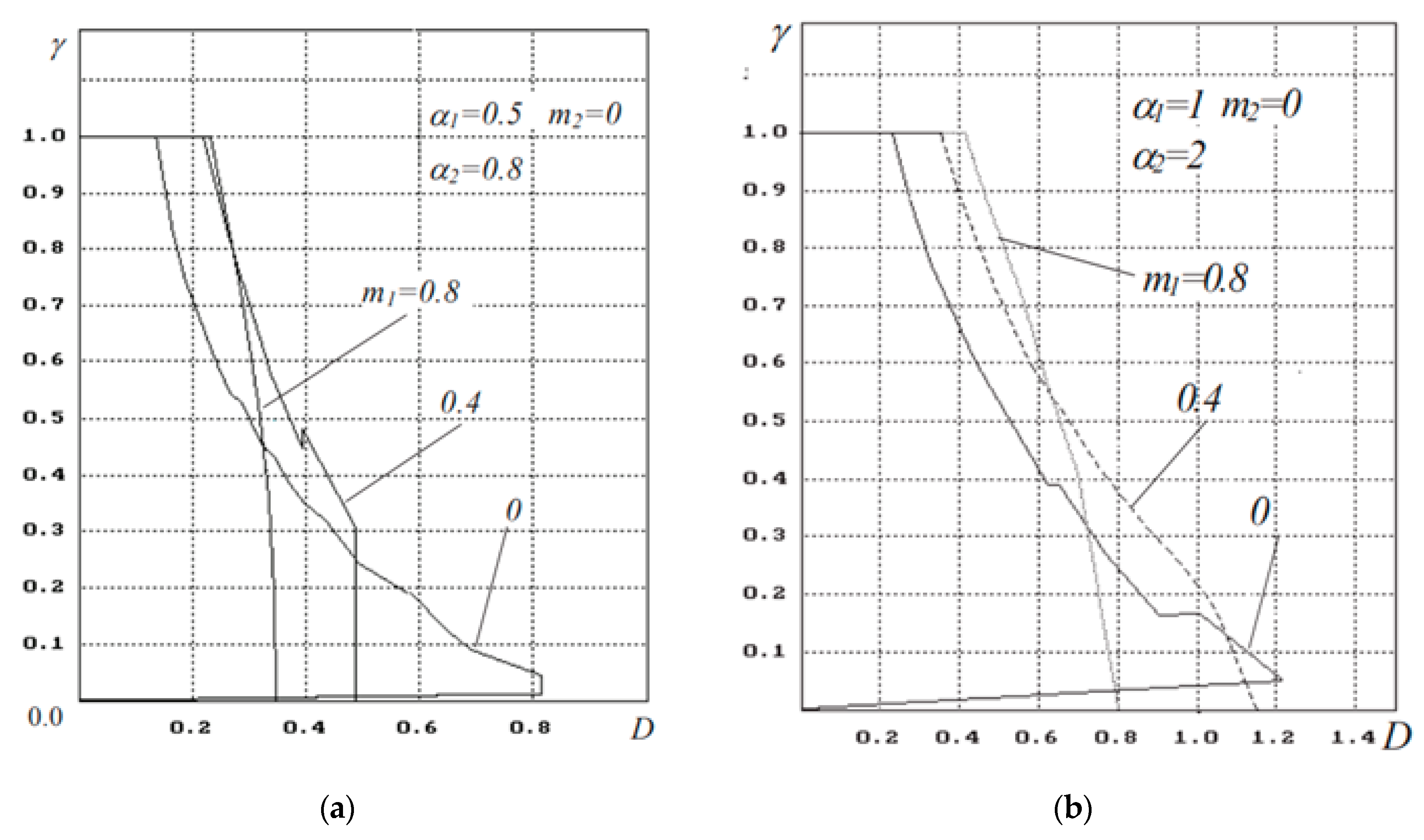
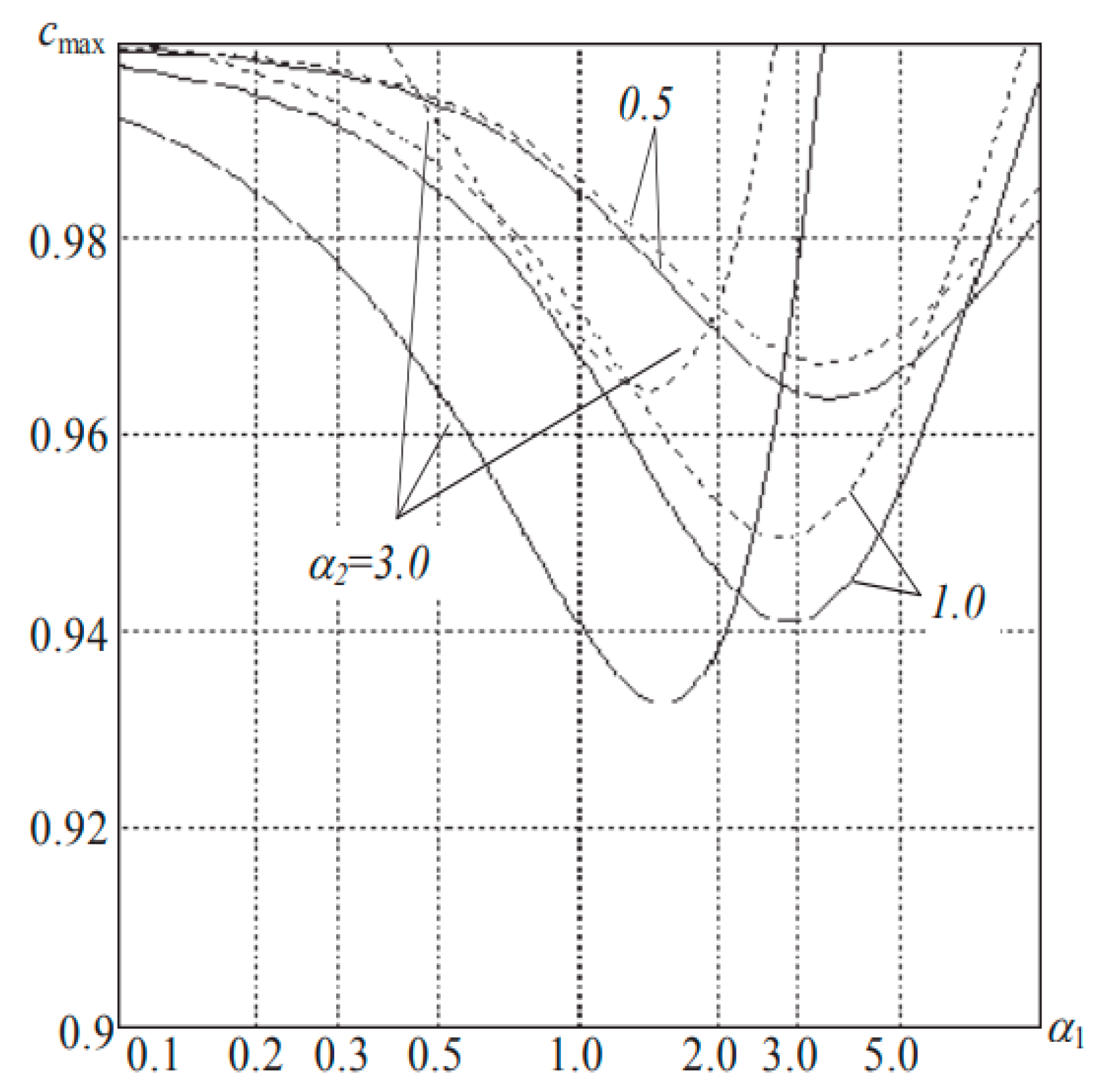
A quantitative estimate of the boundary of first kind cycles can be obtained by considering the change in the area of their existence in the parameter space with a change in the shape of the characteristic. Figure 5 shows the region of existence of PC1 on the plane
,
for different values of
. The boundaries of the areas are almost straight lines, the slope of which depends only on the filter parameters (
). Changing
does not change the shape of these curves, but shifts them along the abscissa. PC1 cycles disappear in two cases: Firstly, at a certain maximum value of the parameter
; and secondly, with a saw-tooth characteristic of the detector and certain filter parameters (
Figure 4).
The authors can note the strong influence of parameters on these dependencies.
From a practical point of view, the filter parameters are of a certain interest. Limit cycles of the first kind (quasi-synchronism mode) are impossible for them.
Figure 5 shows the regions of existence of PC1 on the plane
with equal forcing coefficients
. For
, there is a boundary close to a straight line, above which there are no cycles. With increasing
, the area of existence of cycles is symmetrically limited by
, and disappears when
.
Analysis of the above results shows that the existence of cycles of the first kind with a saw-tooth-like, or close to it, detector characteristic is determined only by the filter parameters and is not related to the gain of the system.
The dependencies in
Figure 5 allow us to analyze the acquisition band when changing the duration of the stable branch of the detector characteristics and to answer the question about its optimal value. As in the case of pulsed DSC of the second order, for small
, a weak dependence of the acquisition band on the shape of the characteristics is observed. There is some loss for
, increasing with the steepness of the stable branch.
With increasing
(to the boundary of local stability) due to a shift in the boundary of the onset of quasiperiodic motions towards large
, the maximum of the acquisition band is provided in the case of
. With different ratios of filter parameters, the gain in the acquisition band can reach up to 50% as compared with
.
Figure 5 also shows the limitations of the acquisition area from below due to PC1. It is possible to get rid of such restrictions by increasing the steepness (decreasing the duration) of a stable part of the characteristics.