Determining Crossing Number of Join of the Discrete Graph with Two Symmetric Graphs of Order Five

Abstract

The main aim of the paper is to give the crossing number of the join product $G+D_n$ for the disconnected graph G of order five consisting of one isolated vertex and of one vertex incident with some vertex of the three-cycle, and $D_n$ consists of n isolated vertices. In the proofs, the idea of the new representation of the minimum numbers of crossings between two different subgraphs that do not cross the edges of the graph G by the graph of configurations ${\mathcal{G}}_D$ in the considered drawing D of $G+D_n$ will be used. Finally, by adding some edges to the graph G, we are able to obtain the crossing numbers of the join product with the discrete graph $D_n$ and with the path $P_n$ on n vertices for three other graphs.

1. Introduction

The investigation of the crossing number of graphs is a classical and very difficult problem provided that computing of the crossing number of a given graph in general is an NP-complete problem. It is well known that the problem of reducing the number of crossings in the graph has been studied in many areas, and the most prominent area is very large-scale integration technology.

In the paper, we will use notations and definitions of the crossing numbers of graphs like in [1]. We will often use Kleitman’s result [2] on crossing numbers of the complete bipartite graphs. More precisely, he proved that:

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{if}m\le 6.$$

Using Kleitman’s result [2], the crossing numbers for join of two paths, join of two cycles, and for join of path and cycle were studied in [1]. Moreover, the exact values for crossing numbers of $G+D_n$ and $G+P_n$ for all graphs G of order at most four are given in [3]. Furthermore, the crossing numbers of the graphs $G+D_n$ are known for a few graphs G of order five and six in [4,5,6,7,8,9,10]. In all of these cases, the graph G is connected and contains at least one cycle. Further, the exact values for the crossing numbers $G+P_n$ and $G+C_n$ have been also investigated for some graphs G of order five and six in [5,7,11,12].

The methods presented in the paper are new, and they are based on multiple combinatorial properties of the cyclic permutations. It turns out that if the graph of configurations is used like a graphical representation of the minimum numbers of crossings between two different subgraphs, then the proof of the main theorem will be simpler to understand. Similar methods were partially used for the first time in the papers [8,13]. In [4,9,10,14], the properties of cyclic permutations were also verified with the help of software in [15]. In our opinion, the methods used in [3,5,7] do not allow establishing the crossing number of the join product $G+D_n$.

2. Cyclic Permutations and Configurations

Let G be the disconnected graph of order five consisting of one isolated vertex and of one vertex incident with some vertex of the three-cycle. We will consider the join product of the graph G with the discrete graph on n vertices denoted by $D_n$. The graph $G+D_n$ consists of one copy of the graph G and of n vertices $t_1,\dots ,t_n$, where any vertex $t_i$, $i=1,\dots ,n$, is adjacent to every vertex of G. Let $T^i$, $1\le i\le n$, denote the subgraph induced by the five edges incident with the vertex $t_i$. Thus, the graph $T^1\cup \dots \cup T^n$ is isomorphic with the complete bipartite graph $K_{5,n}$ and:

$$G+D_n=G\cup K_{5,n}=G\cup \left(\bigcup _{i=1}^n{T}^i\right).$$

(1)

In the paper, we will use the same notation and definitions for cyclic permutations and the corresponding configurations for a good drawing D of the graph $G+D_n$ like in [9,14]. Let D be a drawing of the graph $G+D_n$. The rotation ${\mathrm{rot}}_D\left(t_i\right)$ of a vertex $t_i$ in the drawing D like the cyclic permutation that records the (cyclic) counter-clockwise order in which the edges leave $t_i$ has been defined by Hernández-Vélez, Medina, and Salazar [13]. We use the notation $\left(12345\right)$ if the counter-clockwise order the edges incident with the vertex $t_i$ is $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$, and $t_i{v}_5$. We have to emphasize that a rotation is a cyclic permutation. In the paper, each cyclic permutation will be represented by the permutation with one in the first position. Let ${\overline{\mathrm{rot}}}_D\left(t_i\right)$ denote the inverse permutation of ${\mathrm{rot}}_D\left(t_i\right)$. We will deal with the minimal necessary number of crossings between the edges of $T^i$ and the edges of $T^j$ in a subgraph $T^i\cup T^j$ depending on the rotations ${\mathrm{rot}}_D\left(t_i\right)$ and ${\overline{\mathrm{rot}}}_D\left(t_j\right)$.

We will separate all subgraphs $T^i$, $i=1,\dots ,n$, of the graph $G+D_n$ into three mutually-disjoint subsets depending on how many of the considered $T^i$ cross the edges of G in D. For $i=1,\dots ,n$, let $R_D=\{T^i:{\mathrm{cr}}_D(G,T^i)=0\}$ and $S_D=\{T^i:{\mathrm{cr}}_D(G,T^i)=1\}$. Every other subgraph $T^i$ crosses the edges of G at least twice in D. Moreover, let $F^i$ denote the subgraph $G\cup T^i$ for $T^i\in R_D$, where $i\in \{1,\dots ,n\}$. Thus, for a given subdrawing of G, any subgraph $F^i$ is exactly represented by ${\mathrm{rot}}_D\left(t_i\right)$.

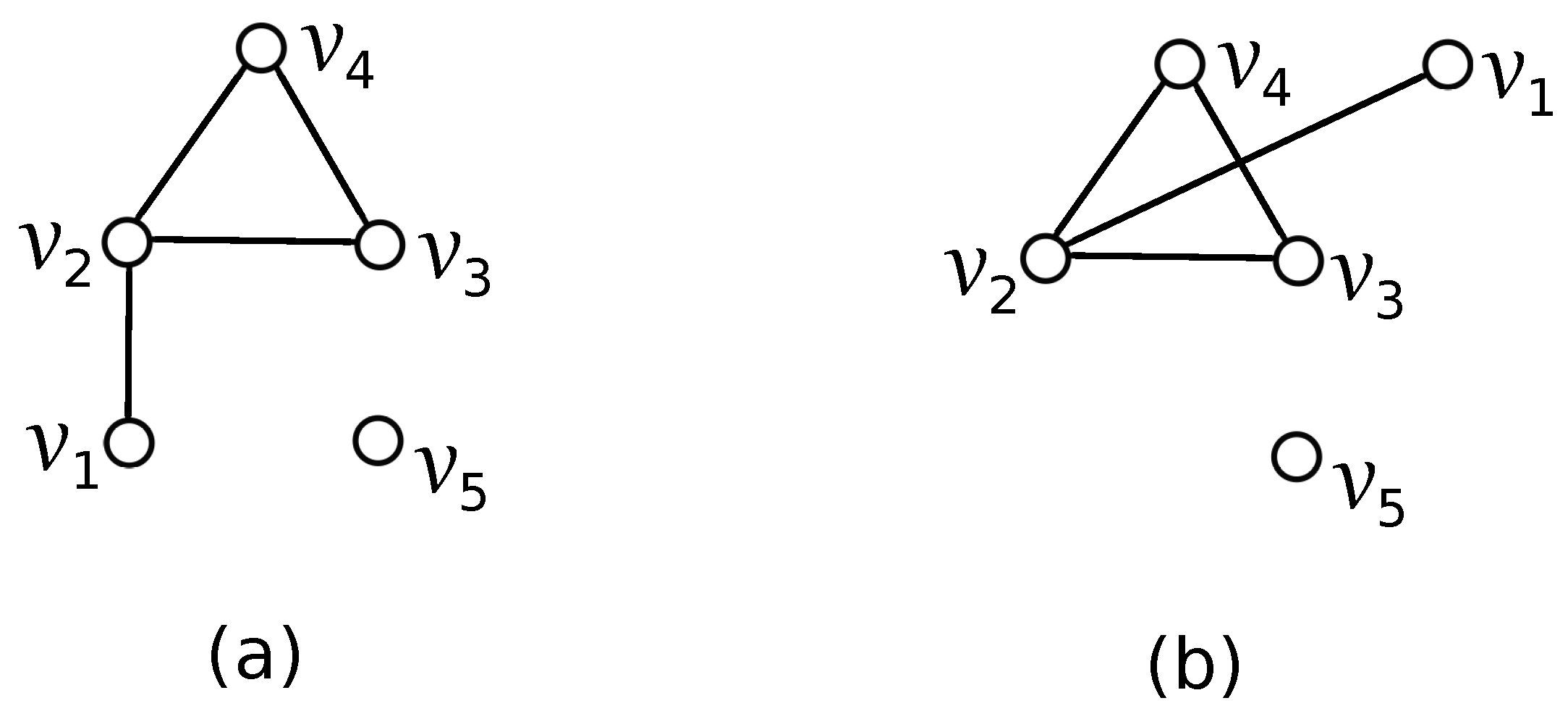
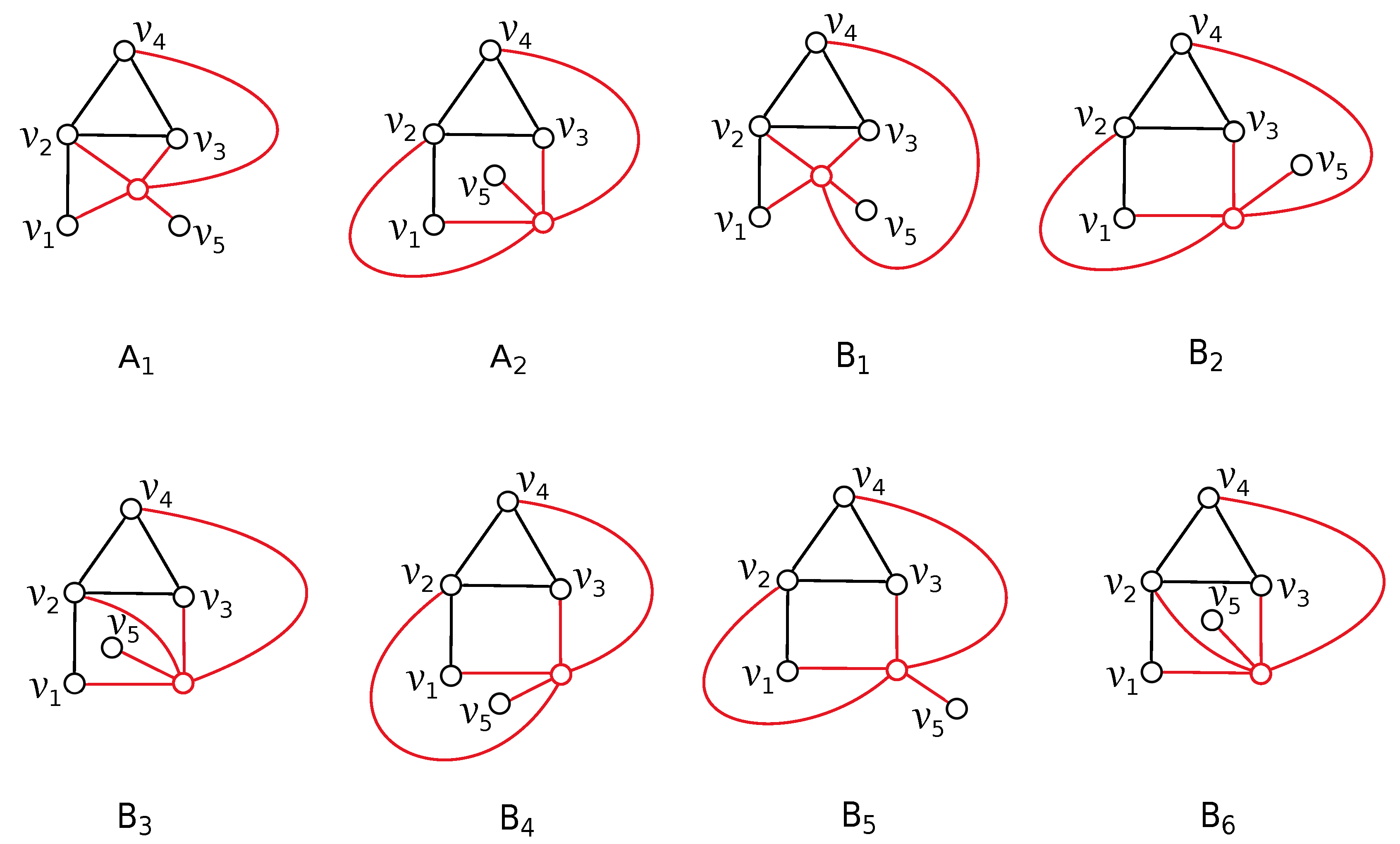
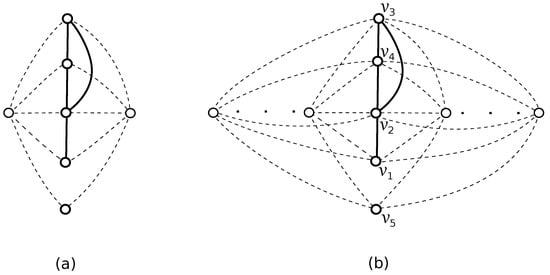
Let us suppose first a good drawing D of the graph $G+D_n$ in which the edges of G do not cross each other. In this case, without loss of generality, we can choose the vertex notation of the graph in such a way as shown in Figure 1a. Our aim is to list all possible rotations ${\mathrm{rot}}_D\left(t_i\right)$ that can appear in D if the edges of $T^i$ do not cross the edges of G. Since there is only one subdrawing of $F^i\backslash \{v_2,v_5\}$ represented by the rotation $\left(143\right)$, there are two possibilities for how to obtain the subdrawing of $F^i\backslash v_5$ depending on in which region the edge $t_i{v}_2$ is placed. Of course, the vertex $v_5$ can be placed in one of four regions of the subdrawing $F^i\backslash v_5$ with the vertex $t_i$ on their boundaries. These $2\times 4=8$ possibilities under our consideration will be denoted by $A_k$ and $B_l$, for $k=1,2$ and $l=1,\dots ,6$. The configuration is of type A or B in the considered drawing D, if the vertex $v_5$ is placed in the quadrangular or in the triangular region in the subdrawing $D(F^i\backslash v_5)$, respectively. As for our considerations, it does not play a role in which of the regions is unbounded; assume the drawings shown in Figure 2. Thus, the configurations $A_1$, $A_2$, $B_1$, $B_2$, $B_3$, $B_4$, $B_5$, and $B_6$ are represented by the cyclic permutations $\left(15432\right)$, $\left(12435\right)$, $\left(14532\right)$, $\left(12453\right)$, $\left(14325\right)$, $\left(15243\right)$, $\left(12543\right)$, and $\left(14352\right)$, respectively. In a fixed drawing of the graph $G+D_n$, some configurations from $\mathcal{M}$ need not appear. We denote by ${\mathcal{M}}_D$ the subset of $\mathcal{M}=\{A_1,A_2,B_1,B_2,B_3,B_4,B_5,B_6\}$ consisting of all configurations that exist in the drawing D.

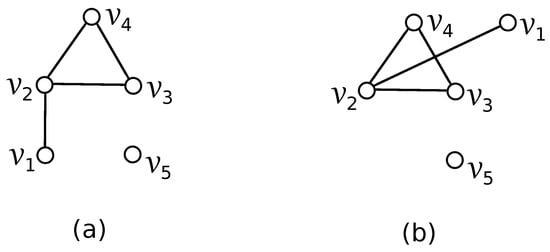
Figure 1. Two good drawings of the graph G. (a): the planar drawing of G; (b): the drawing of G with cr_D(G) = 1.

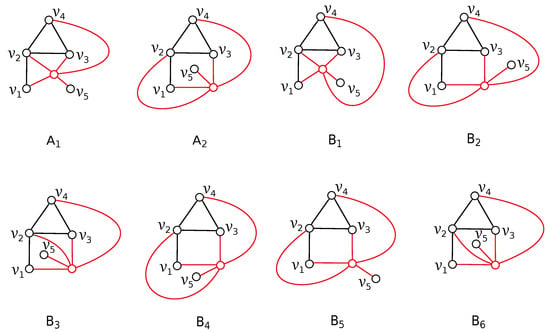
Figure 2. Drawings of eight possible configurations from $\mathcal{M}$ of the subgraph $F^i$.

We remark that if two different subgraphs $F^i$ and $F^j$ with their configurations from ${\mathcal{M}}_D$ cross in a considered drawing D of the graph $G+D_n$, then the edges of $T^i$ are crossed only by the edges of $T^j$. Let X, Y be the configurations from ${\mathcal{M}}_D$. We briefly denote by ${\mathrm{cr}}_D(X,Y)$ the number of crossings in D between $T^i$ and $T^j$ for two different $T^i,T^j\in R_D$ such that $F^i$, $F^j$ have configurations X, Y, respectively. Finally, let $\mathrm{cr}(X,Y)=min\left\{{\mathrm{cr}}_D(X,Y)\right\}$ over all good drawings of the graph $G+D_n$ with $X,Y\in {\mathcal{M}}_D$. Our aim shall be to establish $\mathrm{cr}(X,Y)$ for all pairs $X,Y\in \mathcal{M}$.

The configurations $A_1$ and $A_2$ are represented by the cyclic permutations $\left(15432\right)$ and $\left(12435\right)$, respectively. Since the minimum number of interchanges of adjacent elements of $\left(15432\right)$ required to produce cyclic permutation $\overline{\left(12435\right)}=\left(15342\right)$ is one, any subgraph $T^j$ with the configuration $A_2$ of $F^j$ crosses the edges of $T^i$ at least once, i.e., $\mathrm{cr}(A_1,A_2)\ge 1$. Details have been worked out by Woodall [16]. The same reason gives $\mathrm{cr}(A_1,B_2)\ge 2$, $\mathrm{cr}(A_1,B_4)\ge 2$, $\mathrm{cr}(A_1,B_6)\ge 2$, $\mathrm{cr}(A_2,B_1)\ge 2$, $\mathrm{cr}(A_2,B_3)\ge 2$, $\mathrm{cr}(A_2,B_5)\ge 2$, $\mathrm{cr}(B_i,B_j)\ge 2$, and $\mathrm{cr}(A_i,B_j)\ge 3$ for $i\equiv j(mod2)$. Moreover, by a discussion of possible subdrawings, we can verify that $\mathrm{cr}(B_1,B_5)\ge 4$, $\mathrm{cr}(B_3,B_5)\ge 4$, $\mathrm{cr}(B_2,B_6)\ge 4$, and $\mathrm{cr}(B_4,B_6)\ge 4$. Let $F^i$ be the subgraph having the configuration $B_5$, and let $T^j$ be a subgraph from $R_D$ with $j\ne i$. Using Woodall’s result ${\mathrm{cr}}_D(T^i,T^j)=Q({\mathrm{rot}}_D\left(t_i\right),{\mathrm{rot}}_D\left(t_j\right))+2k$ for some nonnegative integer k, let us also suppose that $Q({\mathrm{rot}}_D\left(t_i\right),{\mathrm{rot}}_D\left(t_j\right))=2$. Of course, any subgraph $F^j$ having the configuration $B_1$ or $B_3$ satisfies the mentioned condition. One can easily see that if $t_j\in {\omega }_{1,2}\cup {\omega }_{3,4}\cup {\omega }_{1,2,3}$, then $\mathrm{cr}(T^i,T^j)>2$. If $t_j\in {\omega }_{2,4,5}$ and $\mathrm{cr}(T^i,T^j)=2$, then the subdrawing $D\left(F^j\right)$ induced by the edges incident with the vertices $v_1$ and $v_3$ crosses the edges of $T^i$ exactly once, and once, respectively. Thus, ${\mathrm{rot}}_D\left(t_j\right)=\left(12435\right)$, i.e., the subgraph $F^j$ has the configuration $A_2$. This forces $\mathrm{cr}(B_5,B_1)\ge 4$ and $\mathrm{cr}(B_5,B_3)\ge 4$. Similar arguments are applied for $\mathrm{cr}(B_6,B_2)\ge 4$ and $\mathrm{cr}(B_6,B_4)\ge 4$. Clearly, also $\mathrm{cr}(A_k,A_k)\ge 4$ and $\mathrm{cr}(B_l,B_l)\ge 4$ for any $k=1,2$ and $l=1,\dots ,6$. Thus, all lower bounds of the number of crossing of configurations from $\mathcal{M}$ are summarized in the symmetric Table 1 (here, $X_k$ and $Y_l$ are configurations of the subgraphs $F^i$ and $F^j$, where $k,l$ are integers from $\{1,2\}$ or $\{1,\dots ,6\}$, and $X,Y\in \{A,B\}$).

Table 1. The necessary number of crossings between $T^i$ and $T^j$ for the configurations $X_k$, $Y_l$.

−	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{B}}_1$	${\mathit{B}}_2$	${\mathit{B}}_3$	${\mathit{B}}_4$	${\mathit{B}}_5$	${\mathit{B}}_6$
$A_1$	4	1	3	2	3	2	3	2
$A_2$	1	4	2	3	2	3	2	3
$B_1$	3	2	4	3	2	3	4	3
$B_2$	2	3	3	4	3	2	3	4
$B_3$	3	2	2	3	4	3	4	3
$B_4$	2	3	3	2	3	4	3	4
$B_5$	3	2	4	3	4	3	4	3
$B_6$	2	3	3	4	3	4	3	4

Assume a good drawing D of the graph $G+D_n$ with one crossing among edges of the graph G (in which there is a subgraph $T^i\in R_D$). In this case, without loss of generality, we can choose also the vertex notations of the graph in such a way as shown in Figure 1b. Since there is only one subdrawing of $F^i\backslash \left\{v_5\right\}$ represented by the rotation $\left(1324\right)$, we have four possibilities for how to obtain the subdrawing of $F^i$ depending on in which region the vertex $v_5$ is placed. Thus, there are four different possible configurations of the subgraph $F^i$ denoted as $A_1$, $A_2$, $A_3$, and $A_4$, with the corresponding rotations $\left(13245\right)$, $\left(13524\right)$, $\left(13254\right)$, and $\left(15324\right)$, respectively. We denote by ${\mathcal{N}}_D$ the subset of $\mathcal{N}=\{A_1,A_2,A_3,A_4\}$ consisting of all configurations that exist in the drawing D. The same way as above can be applied for the verification of the lower bounds of the number of crossings of two different configurations from $\mathcal{N}$. Thus, all lower bounds of the numbers of crossings of two configurations from $\mathcal{N}$ are summarized in the symmetric Table 2 (here, $A_k$ and $A_l$ are configurations of the subgraphs $F^i$ and $F^j$, where $k,l\in \{1,2,3,4\}$).

Table 2. The necessary number of crossings between $T^i$ and $T^j$ for the configurations $A_k$, $A_l$.

−	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$
$A_1$	4	2	3	3
$A_2$	2	4	3	3
$A_3$	3	3	4	2
$A_4$	3	3	2	4

3. The Graph of Configurations ${\mathcal{G}}_{\mathit{D}}$

In general, the low possible number of crossings between two different subgraphs in a good subdrawing of $G+D_n$ is one of the main problems in the proofs on the crossing number of the join of the graph G with the discrete graphs $D_n$. The lower bounds of the numbers of crossings between two subgraphs, which do not cross the edges of G, were summarized in the symmetric Table 1. Since some configurations from the set $\mathcal{M}$ need not appear in the fixed drawing of $G+D_n$, we will first deal with the smallest possible values in Table 1 as with the worst possible case in the mentioned proofs. Thus, a new graphical representation of Table 1 by the graph of configurations will be useful.

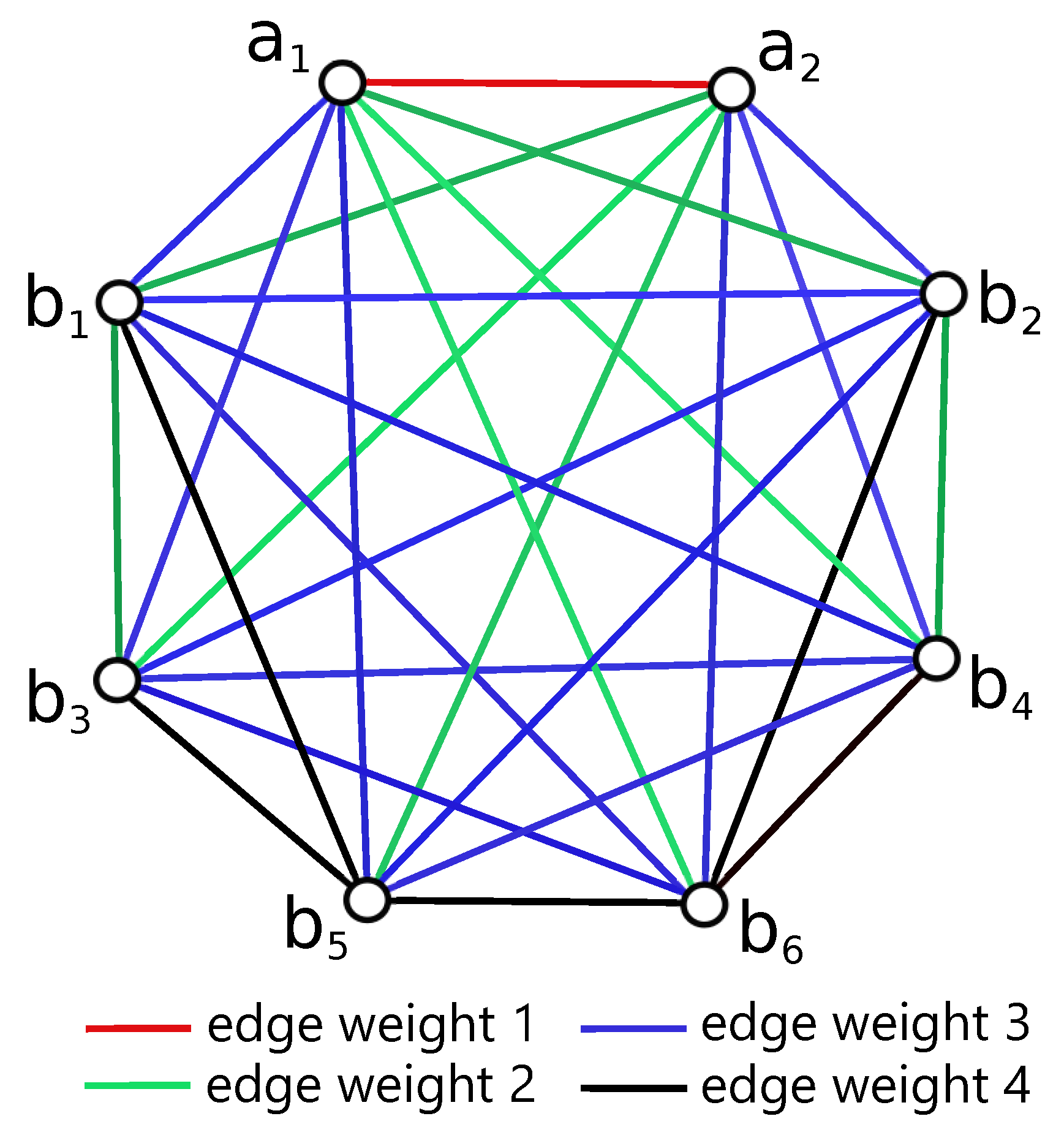
Let us suppose that D is a good drawing of the graph $G+D_n$ with ${\mathrm{cr}}_D\left(G\right)=0$, and let ${\mathcal{M}}_D$ be the nonempty set of all configurations that exist in the drawing D belonging to the set $\mathcal{M}=\{A_1,A_2,B_1,B_2,B_3,B_4,B_5,B_6\}$. A graph of configurations ${\mathcal{G}}_D$ is an ordered triple $(V_D,E_D,w_D)$, where $V_D$ is the set of vertices, $E_D$ is the set of edges, which is formed by all unordered pairs of distinct vertices, and a weight function $w:E_D\to \mathbb{N}$ that associates with each edge of $E_D$ an unordered pair of two vertices of $V_D$. The vertex $x_k\in V_D$ for some $x\in \{a,b\}$ if the corresponding configuration $X_k\in {\mathcal{M}}_D$ for some $X\in \{A,B\}$, where $k\in \{1,2\}$ or $k\in \{1,\dots ,6\}$. The edge $e=x_k{y}_l\in E_D$ if $x_k$ and $y_l$ are two different vertices of the graph ${\mathcal{G}}_D$. Finally, $w_D\left(e\right)=m\in \mathbb{N}$ for the edge $e=x_k{y}_l$, if m is the associated lower bound between two different configurations $X_k$, and $Y_l$ in Table 1. Of course, ${\mathcal{G}}_D$ is the simple undirected edge-weighted graph uniquely determined by the drawing D. Moreover, if we define the graph $\mathcal{G}=(V,E,w)$ in the same way over the set $\mathcal{M}$, then ${\mathcal{G}}_D$ is the subgraph of $\mathcal{G}$ induced by $V_D$ for the considered drawing D. Since the graph $\mathcal{G}=(V,E,w)$ can be represented like the edge-weighted complete graph $K_8$, it will be more transparent to follow the subcases in the proof of the main theorem; see Figure 3.

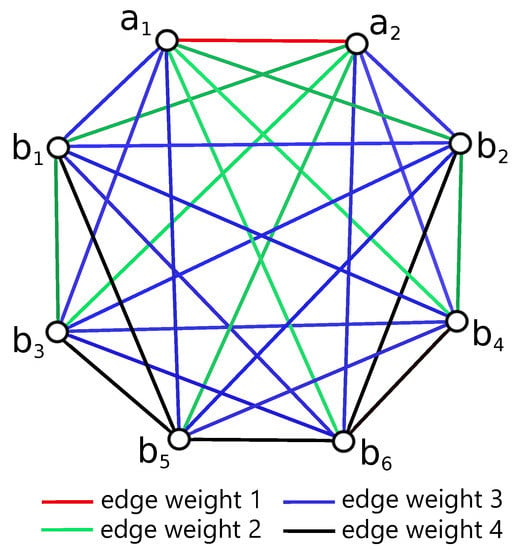
Figure 3. Representation of the lower bounds of Table 1 by the graph $\mathcal{G}=(V,E,w)$.

4. The Crossing Number of $\mathit{G}+{\mathit{D}}_{\mathit{n}}$

Two vertices $t_i$ and $t_j$ of $G+D_n$ are antipodal in a drawing of $G+D_n$ if the subgraphs $T^i$ and $T^j$ do not cross. A drawing is antipodal-free if it has no antipodal vertices. In the rest of the paper, each considered drawing of the graph $G+D_n$ will be assumed antipodal-free. In the proof of the main theorem, the following lemma related to some restricted subdrawings of the graph $G+D_n$ is helpful.

Lemma 1.

Let D be a good and antipodal-free drawing of $G+D_n$, $n>2$. If $T^i,T^j\in R_D$ are different subgraphs such that $F^i$, $F^j$ have different configurations from any of the sets $\{A_1,B_2\}$, $\{A_1,B_6\}$, $\{A_2,B_1\}$, and $\{A_2,B_5\}$, then:

$${\mathrm{cr}}_D(G\cup T^i\cup T^j,T^k)\ge 4forany{T}^k\in S_D.$$

Proof of Lemma 1.

Let us suppose the configuration $A_1$ of the subgraph $F^i$, and note that it is exactly represented by ${\mathrm{rot}}_D\left(t_i\right)=\left(15432\right)$. The unique drawing of the subgraph $F^i$ contains four regions with the vertex $t_i$ on their boundaries (Figure 2). If there is a $T^k\in S_D$ with ${\mathrm{cr}}_D(T^i,T^k)=1$, then one can easily see that $t_k\in {\omega }_{1,2,4,5}$. Of course, the edge $t_k{v}_3$ must cross one edge of the graph G. If $t_k{v}_3$ crosses the edge $v_1{v}_2$, then the subgraph $F^k$ is represented by ${\mathrm{rot}}_D\left(t_k\right)=\left(13245\right)$. If the edge $t_k{v}_3$ crosses the edge $v_2{v}_4$, then there are only three possibilities for the considered subdrawing of $F^k$, i.e., the subgraph $F^k$ can be represented by three possible cyclic permutations $\left(13452\right)$, $\left(15234\right)$, or $\left(12354\right)$.

For the remaining configurations $A_2$, $B_1$, $B_2$, $B_5$, and $B_6$ of $F^i$, using the same arguments, one can easily verify that the rotations of the vertex $t_k$ are from the sets $\left\{\right(15324),(12534),(13425),(13542\left)\right\}$, $\left\{\right(12345),(14235\left)\right\}$, $\left\{\right(15342),(15423\left)\right\}$, $\left\{\right(12345\left)\right\}$, and $\left\{\right(15342\left)\right\}$, respectively. This forces that there is no subgraph $T^k\in S_D$ with ${\mathrm{cr}}_D(T^i\cup T^j,T^k)=2$, where the subgraph $F^j$ has the configuration $B_2$ or $B_6$. The same reason is given for the case of $A_2$ with the configurations $B_1$ and $B_5$. Finally, ${\mathrm{cr}}_D(G\cup T^i\cup T^j,T^k)\ge 1+3=4$ for any $T^k\in S_D$. This completes the proof. □

We have to emphasize that we cannot generalize Lemma 1 for all pairs of different configurations from $\mathcal{M}$. Let us assume the configurations $A_1$ of $F^i$ and $B_4$ of $F^j$. For $T^k\in S_D$, the reader can easily find a subdrawing of $G\cup T^i\cup T^j\cup T^k$ in which ${\mathrm{cr}}_D(T^i,T^k)={\mathrm{cr}}_D(T^j,T^k)=1$. The same remark holds for pairs $A_2$ with $B_3$, $B_1$ with $B_3$, and $B_2$ with $B_4$.

Theorem 1.

$\mathrm{cr}(G+D_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ for $n\ge 1$.

Proof of Theorem 1.

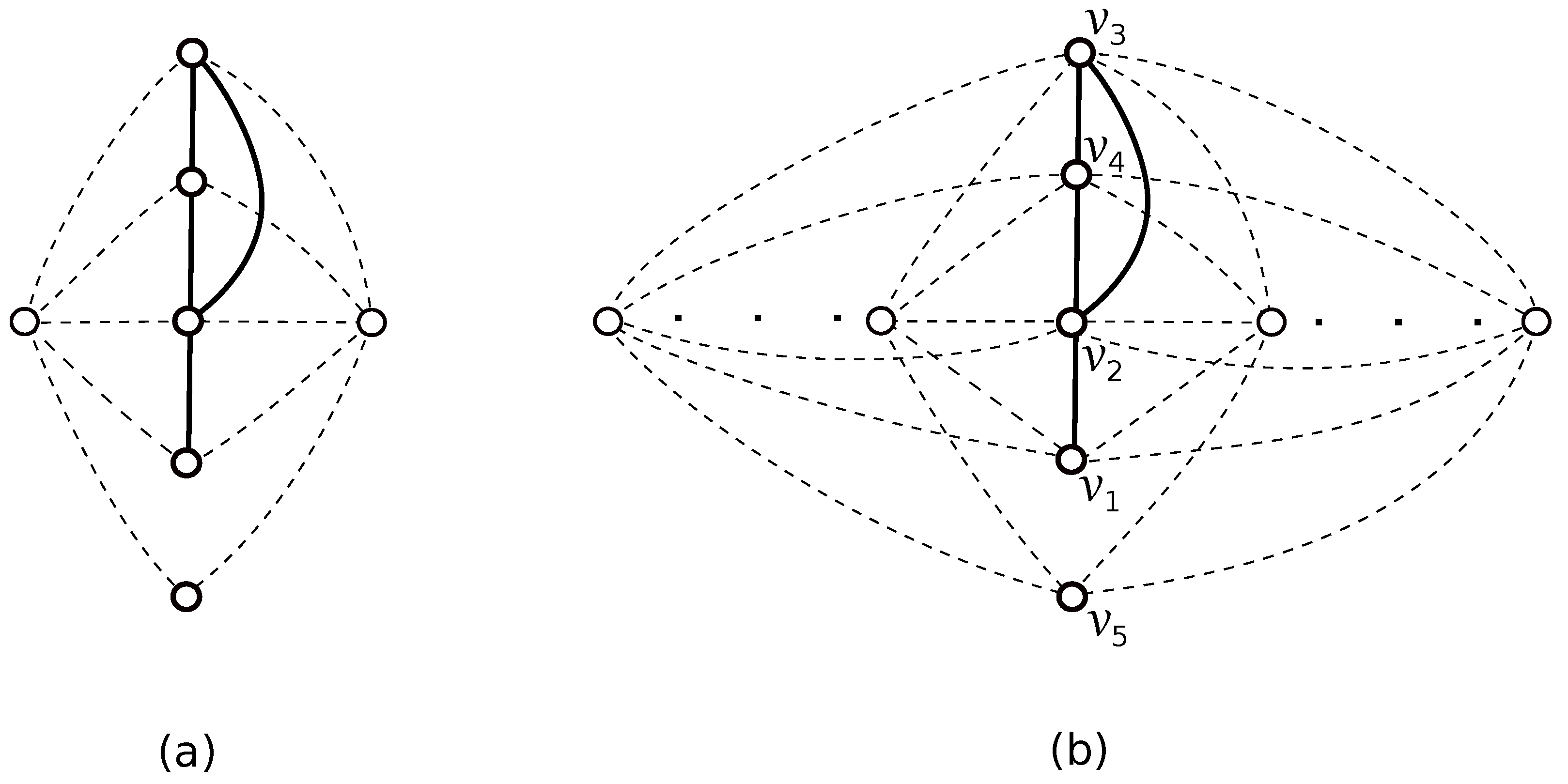
The drawing in Figure 4b shows that $\mathrm{cr}(G+D_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$. We prove the reverse inequality by contradiction. The graph $G+D_1$ is planar; hence, $\mathrm{cr}(G+D_1)=0$. Since the graph $G+D_2$ contains a subdivision of the complete bipartite graph $K_{3,3}$, we have $\mathrm{cr}(G+D_2)\ge 1$. Thus, $\mathrm{cr}(G+D_2)=1$ by the good drawing of $G+D_2$ in Figure 4a. Suppose now that for $n\ge 3$, there is a drawing D with:

$${\mathrm{cr}}_D(G+D_n)<4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋,$$

(2)

and let

$$\mathrm{cr}(G+D_m)\ge 4⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+⌊\frac{m}{2}⌋\mathrm{for}\mathrm{any}\mathrm{integer}m<n.$$

(3)

Figure 4. The good drawings of $G+D_2$ and of $G+D_n$. (a): the drawing of G + D₂ with one crossing; (b): the drawing of G + D_n with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ crossings.

Let us first show that the considered drawing D must be antipodal-free. As a contradiction, suppose that, without loss of generality, ${\mathrm{cr}}_D(T^n,T^{n-1})=0$. Using positive values in Table 1 and Table 2, one can easily verify that both subgraphs $T^n$ and $T^{n-1}$ are not from the set $R_D$, i.e., ${\mathrm{cr}}_D(G,T^n\cup T^{n-1})\ge 1$. The known fact that $\mathrm{cr}\left(K_{5,3}\right)=4$ implies that any $T^k$, $k=1,\dots ,n-2$, crosses the edges of the subgraph $T^n\cup T^{n-1}$ at least four times. Therefore, for the number of crossings in the considered drawing D, we have:

$${\mathrm{cr}}_D(G+D_n)={\mathrm{cr}}_D\left(G+D_{n-2}\right)+{\mathrm{cr}}_D(G,T^n\cup T^{n-1})+{\mathrm{cr}}_D(T^n\cup T^{n-1})+{\mathrm{cr}}_D(K_{5,n-2},T^n\cup T^{n-1})$$

$$\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+⌊\frac{n-2}{2}⌋+1+0+4(n-2)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

This contradiction with the assumption (2) confirms that D must be an antipodal-free drawing. Moreover, if $r=|R_D|$ and $s=|S_D|$, the assumption (3) together with the well-known fact $\mathrm{cr}\left(K_{5,n}\right)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ imply that in D, there are at least $⌈\frac{n}{2}⌉+1$ subgraphs $T^i$, which do not cross the edges of G. More precisely:

$${\mathrm{cr}}_D\left(G\right)+{\mathrm{cr}}_D(G,K_{5,n})\le {\mathrm{cr}}_D\left(G\right)+0r+1s+2(n-r-s)<⌊\frac{n}{2}⌋,$$

i.e.,

$$s+2(n-r-s)<⌊\frac{n}{2}⌋.$$

(4)

This forces that $r\ge 2$, and $r\ge ⌈\frac{n}{2}⌉+1$. Now, for $T^i\in R_D$, we will discuss the existence of possible configurations of subgraphs $F^i=G\cup T^i$ in the drawing D.

Case 1. ${\mathrm{cr}}_D\left(G\right)=0$. Without loss of generality, we can choose the vertex notation of the graph G in such a way as shown in Figure 1a. Thus, we will deal with the configurations belonging to the nonempty set ${\mathcal{M}}_D$. According to the minimum value of the weights of edges in the graph ${\mathcal{G}}_D=(V_D,E_D,w_D)$, we will fix one, or two, or three subgraphs with a contradiction with the condition (2) in the following subcases:

i.

$\{A_1,A_2\}\subseteq {\mathcal{M}}_D$, i.e., $w_D\left(a_1{a}_2\right)=1$. Without loss of generality, let us consider two different subgraphs $T^n,T^{n-1}\in R_D$ such that $F^n$ and $F^{n-1}$ have configurations $A_1$ and $A_2$, respectively. Then, ${\mathrm{cr}}_D(G\cup T^n\cup T^{n-1},T^i)\ge 5$ for any $T^i\in R_D$ with $i\ne n-1,n$ by summing the values in all columns in the considered two rows of Table 1. Moreover, ${\mathrm{cr}}_D(T^n\cup T^{n-1},T^i)\ge 3$ for any subgraph $T^i$ with $i\ne n-1,n$ due to the properties of the cyclic permutations. Hence, by fixing the graph $G\cup T^n\cup T^{n-1}$,

$${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+5(r-2)+4(n-r)+1=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+r-9$$

$$\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+\left(⌈\frac{n}{2}⌉+1\right)-9\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

ii.

$\{A_1,A_2\}⊈{\mathcal{M}}_D$, i.e., $w_D\left(e\right)\ge 2$ for any $e\in E_D$.

Let us assume that $\{A_1,B_2,B_4\}\subseteq {\mathcal{M}}_D$ or $\{A_2,B_1,B_3\}\subseteq {\mathcal{M}}_D$, i.e., there is a three-cycle in the graph ${\mathcal{G}}_D$ with weights of two of all its edges. Without loss of generality, let us consider three different subgraphs $T^n,T^{n-1}{T}^{n-2}\in R_D$ such that $F^n$, $F^{n-1}$m and $F^{n-2}$ have different configurations from $\{A_1,B_2,B_4\}$. Then, ${\mathrm{cr}}_D(G\cup T^n\cup T^{n-1}\cup T^{n-2},T^i)\ge 8$ for any $T^i\in R_D$ with $i\ne n-1,n$ by Table 1, and ${\mathrm{cr}}_D(G\cup T^n\cup T^{n-1}\cup T^{n-2},T^i)\ge 5$ for any subgraph $T^i\in S_D$ by Lemma 1. Thus, by fixing the graph $G\cup T^n\cup T^{n-1}\cup T^{n-2}$,

$${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+8(r-3)+5(n-r)+6\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+5n+3r-18$$

$$\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+5n+3\left(⌈\frac{n}{2}⌉+1\right)-18\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

In the next part, let us suppose that $\{A_1,B_2,B_4\}\subseteq {\mathcal{M}}_D$ and $\{A_2,B_1,B_3\}\subseteq {\mathcal{M}}_D$,

(1)

$\{A_j,B_k\}\subseteq {\mathcal{M}}_D$ for some $k\equiv j+1(mod2)$ or $\{B_j,B_{j+2}\}\subseteq {\mathcal{M}}_D$, where $j\in \{1,2\}$. Without loss of generality, let us consider two different subgraphs $T^n,T^{n-1}\in R_D$ such that $F^n$ and $F^{n-1}$ have configurations $A_1$ and $B_2$, respectively. Then, ${\mathrm{cr}}_D(G\cup T^n\cup T^{n-1},T^i)\ge 6$ for any $T^i\in R_D$ with $i\ne n-1,n$ by Table 1. Moreover, ${\mathrm{cr}}_D(T^n\cup T^{n-1},T^i)\ge 2$ for any subgraph $T^i$ with $i\ne n-1,n$ due to properties of the cyclic permutations. Hence, if we fix the graph $G\cup T^n\cup T^{n-1}$,

$${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+6(r-2)+3s+4(n-r-s)+2=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋$$

$$+4n+r+r-s-10\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+⌈\frac{n}{2}⌉+1+1-10\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

(2)

$\{A_j,B_k\}⊈{\mathcal{M}}_D$ for any $k\equiv j+1(mod2)$ and $\{B_j,B_{j+2}\}⊈{\mathcal{M}}_D$, where $j=1,2$, i.e., $w_D\left(e\right)\ge 3$ for any $e\in E_D$. Without loss of generality, we can assume that $T^n\in R_D$. Then, ${\mathrm{cr}}_D(T^n,T^i)\ge 3$ for any $T^i\in R_D$ with $i\ne n$. Thus, by fixing the graph $G\cup T^n$,

$${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3(r-1)+2(n-r)+0=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+r-3$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+\left(⌈\frac{n}{2}⌉+1\right)-3\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

Case 2. ${\mathrm{cr}}_D\left(G\right)=1$. Without loss of generality, we can choose the vertex notation of the graph G in such a way as shown in Figure 1b. Thus, we will deal with the configurations belonging to the nonempty set ${\mathcal{N}}_D$ in the following two cases:

i.

$\{A_i,A_{i+1}\}\subseteq {\mathcal{N}}_D$ for some $i\in \{1,2\}$. Without loss of generality, let us consider two different subgraphs $T^n,T^{n-1}\in R_D$ such that $F^n$ and $F^{n-1}$ have different configurations from the set $\{A_1,A_2\}$. Then, ${\mathrm{cr}}_D(G\cup T^n\cup T^{n-1},T^i)\ge 6$ for any $T^i\in R_D$ with $i\ne n-1,n$ by Table 2. Moreover, ${\mathrm{cr}}_D(T^n\cup T^{n-1},T^i)\ge 2$ for any subgraph $T^i$ with $i\ne n-1,n$ due to the properties of the cyclic permutations. Hence, by fixing the graph $G\cup T^n\cup T^{n-1}$,

$${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+6(r-2)+3s+4(n-r-s)+2+1=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋$$

$$+4n+r+r-s-9\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+⌈\frac{n}{2}⌉+1+1-9\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

If $F^n$ and $F^{n-1}$ have different configurations from the set $\{A_3,A_4\}$, then the same argument can be applied.

ii.

$\{A_i,A_{i+1}\}⊈{\mathcal{N}}_D$ for any $i=1,2$. Without loss of generality, we can assume that $T^n\in R_D$. Then, ${\mathrm{cr}}_D(T^n,T^i)\ge 3$ for any $T^i\in R_D$ with $i\ne n$. Thus, by fixing the graph $G\cup T^n$,

$${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3(r-1)+2(n-r)+1=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+r-2$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+\left(⌈\frac{n}{2}⌉+1\right)-2\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋.$$

Thus, it was shown that there is no good drawing D of the graph $G+D_n$ with less than $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ crossings. This completes the proof of Theorem 1. □

5. Three Other Graphs

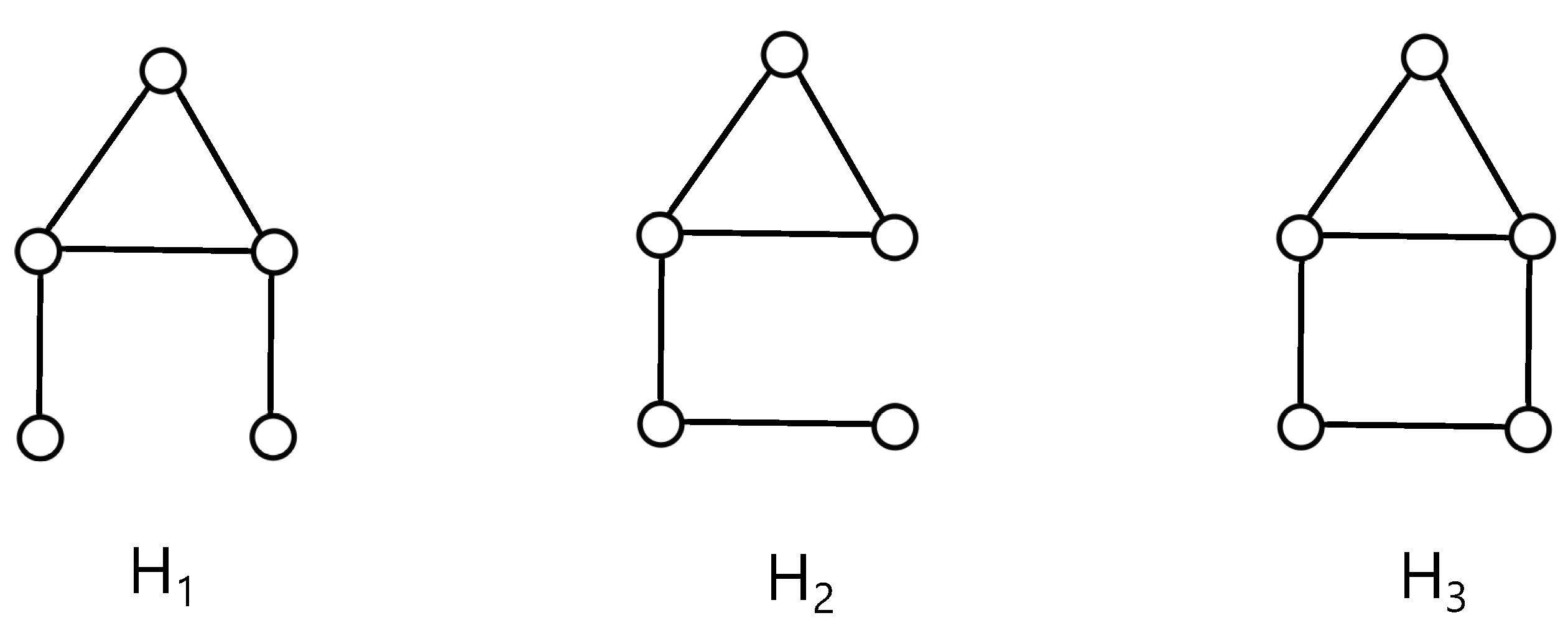
Finally, in Figure 4b, we are able to add the edges $v_3{v}_5$ and $v_1{v}_5$ to the graph G without additional crossings, and we obtain three new graphs $H_i$ for $i=1,2,3$ in Figure 5. Therefore, the drawing of the graphs $H_1+D_n$, $H_2+D_n$, and $H_3+D_n$ with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ crossings is obtained. On the other hand, $G+D_n$ is a subgraph of each $H_i+D_n$, and therefore, $\mathrm{cr}(H_i+D_n)\ge \mathrm{cr}(G+D_n)$ for any $i=1,2,3$. Thus, the next results are obvious.

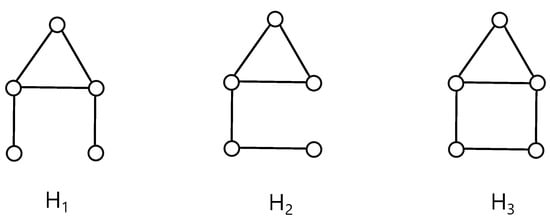
Figure 5. Three graphs $H_1$, $H_2$, and $H_3$ by adding new edges to the graph G.

Corollary 1.

$\mathrm{cr}(H_i+D_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ for $n\ge 1$, where $i=1,2,3$.

We remark that the crossing numbers of the graphs $H_1+D_n$ and $H_3+D_n$ were already obtained by Berežný and Staš [4], and Klešč and Schrötter [7], respectively. Moreover, into the drawing in Figure 4b, it is possible to add n edges, which form the path $P_n$, $n\ge 2$ on the vertices of $D_n$ without another crossing. Thus, the next results are also obvious.

Theorem 2.

$\mathrm{cr}(G+P_n)=\mathrm{cr}(H_2+P_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ for $n\ge 2$.

The crossing number of the graph $H_1+P_n$ has been investigated in [12].