4D,
N
=
1
Matter Gravitino Genomics
Abstract
:1. Introduction
- This paper presents the Majorana representation of the transformation laws of the multiplet described in [28,29,30]. The existence of these transformation laws is discussed in [28,29] as a submultiplet of the overarching transformation laws. In [30], the submultiplet’s tranformation laws are presented in a Weyl representation. It is important to have a Majorana representation of component transformation laws for a multiplet to be decomposed as adinkras as in the previous genomics works [1,2,3].
- The transformation laws for the two matter-gravitino multiplets and are expressed in terms of a field redefinition parameter that preserves the diagonal character of the Lagrangian. The existence of this parameter is pointed out in [30]. As we plan to further SUSY genomics and holography research to higher spin multiplets, where this diagonal parameter continues to be present, it is important to understand this parameter’s significance at the adinkra level.
- This paper demonstrates the utility of the new Mathematica package Adinkra.m (https://hepthools.github.io/Adinkra/). This package is available open-source and will be indispensable in future adinkra research.
- The main purpose of the paper is the adinkranization of the two matter-gravitino multiplets, the calculation of their fermionic holoraumy matrices along with that of , and the comparisons between these three multiplets via the gadget. In calculations of holoraumy and the gadget of these three multiplets, we see the presence of the diagonal Lagrangian parameter. The gadget results presented in this paper will provide a template for researching the significance of this parameter in future, higher spin investigations as pertaining to SUSY genomics and holography. The multiplets investigated in this paper are the base of a tower of higher spin multiplets [36,37,38,39], thus they lay the foundation for future investigations of these higher spin multiplets.
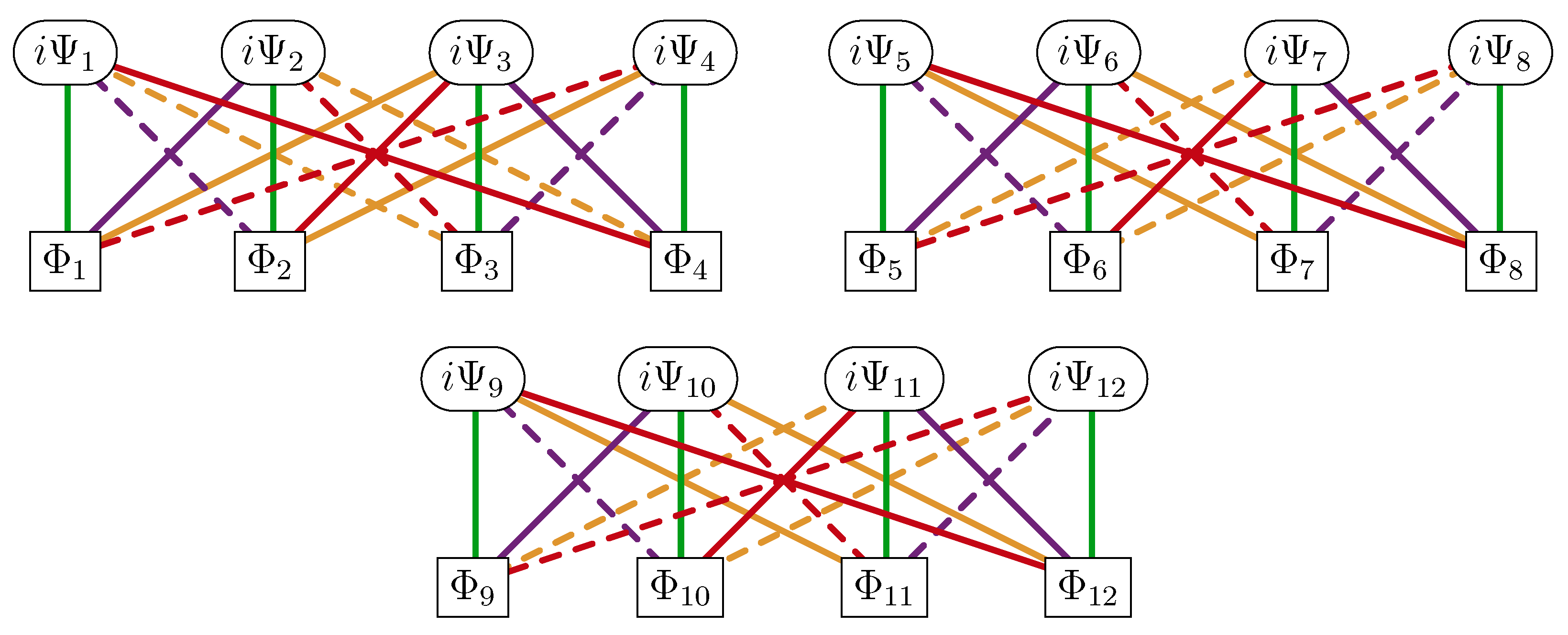
2. Adinkra Review
- The white nodes encode the bosons and the black nodes encode the fermions multiplied by the imaginary number .
- A line connecting two nodes indicates a SUSY transformation law between the corresponding fields.
- Each of the colors encodes a different SUSY transformation as color coded in Equations (3) and (4).
- A solid (dashed) line indicates a plus (minus) sign in SUSY transformations.
- In transforming from a higher node to a lower node (higher mass dimension field to one-half lower mass dimension field), a time derivative appears on the field of the lower node.
3. Supersymmetry Genomics Review
3.1. The 4D, Off-Shell Chiral Multiplet (CM)
- Calculating the trace in Equation (11), which produces the result .
3.2. The 4D, Off-Shell Tensor Multiplet (TM)
3.3. The 4D, Off-Shell Vector Multiplet (VM)
3.4. The 4D, Off-Shell Complex Linear Superfield Multiplet (CLS)
3.5. The 4D, Off-Shell Old-Minimal Supergravity Multiplet (mSG)
3.6. Gadgets
4. The de Wit–van Holten Formulation
4.1. Transformation Laws
4.2. Anti-Commutators
4.3. Lagrangian
5. The Ogievetsky–Sokatchev (OS) Formulation
5.1. Transformation Laws
5.2. Anti-Commutators
5.3. Lagrangian
6. The Non-Minimal Supergravity Formulation
6.1. Transformation Laws
6.2. Anti-Commutators
6.3. Lagrangian
7. Adinkranization of the Multiplets
7.1. Holoraumy and
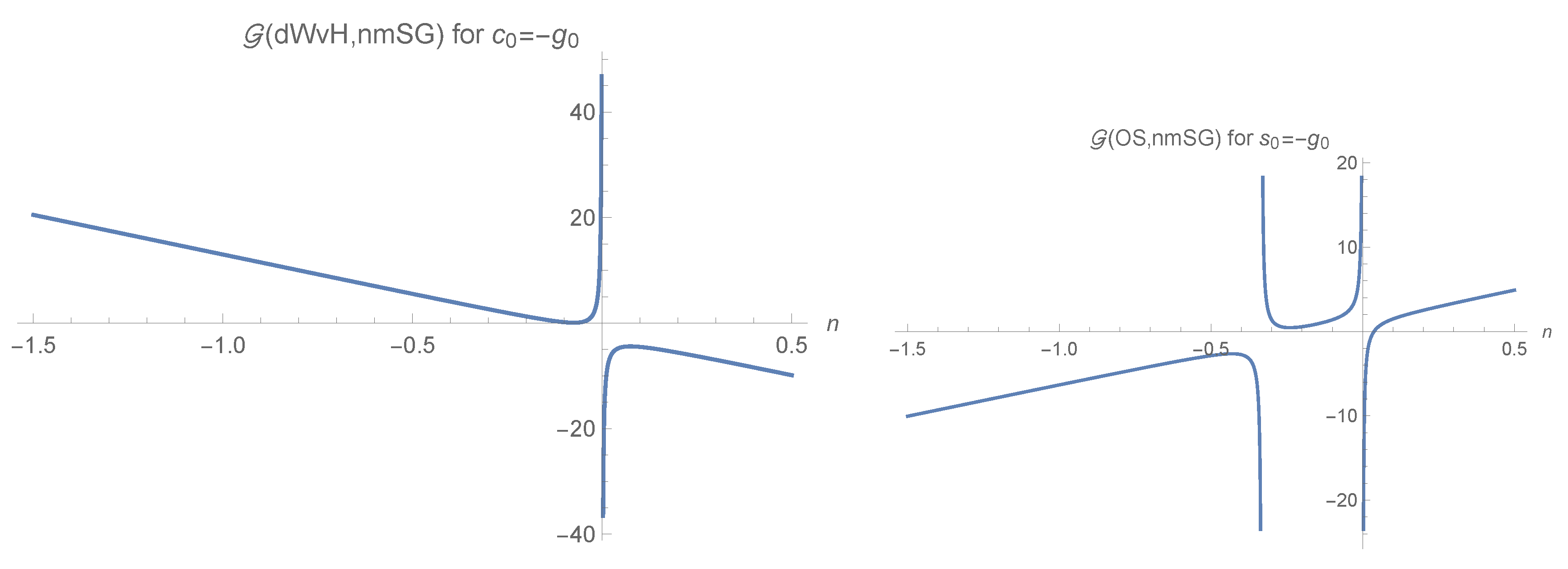
7.2. , Eigenvalues, and Gadgets for the dWvH, OS, and Multiplets
8. Conclusions
“The most effective way to do it, is to do it.”- Amelia Earhart
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof That tIJ =1/2VIJ Satisfies the so(N) Algebra
Appendix B. Explicit LI and RI Matrices
Appendix C. Explicit Form for the Matrices for the dWVH Multiplet in a 20 × 20 Tensor Product Basis
References
- Gates, S.J., Jr.; Gonzales, J.; MacGregor, B.; Parker, J.; Polo-Sherk, R.; Rodgers, V.G.J.; Wassink, L. 4D, N = 1 Supersymmetry Genomics (I). J. High Energy Phys. 2009, 0912, 008. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Hallett, J.; Parker, J.; Rodgers, V.G.J.; Stiffler, K. 4D, N = 1 Supersymmetry Genomics (II). J. High Energy Phys. 2012, 1206, 071. [Google Scholar] [CrossRef]
- Chappell, I.; Gates, S.J., Jr.; Linch, W.D.; Parker, J.; Randall, S.; Ridgway, A.; Stiffler, K. 4D, N = 1 Supergravity Genomics. J. High Energy Phys. 2013, 1310, 004. [Google Scholar] [CrossRef]
- Faux, M.; Gates, S.J., Jr. Adinkras: A Graphical technology for supersymmetric representation theory. Phys. Rev. D 2005, 71, 065002. [Google Scholar] [CrossRef]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. On graph-theoretic identifications of Adinkras, supersymmetry representations and superfields. Int. J. Mod. Phys. A 2007, 22, 869–930. [Google Scholar] [CrossRef]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. Adinkras and the Dynamics of Superspace Prepotentials. High Energy Phys. 2006, arXiv:hep-th/0605269. [Google Scholar]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D.; Miller, R.L. Topology Types of Adinkras and the Corresponding Representations of N-Extended Supersymmetry. arXiv, 2008; arXiv:0806.0050. [Google Scholar]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D.; Miller, R.L. Adinkras for Clifford Algebras, and Worldline Supermultiplets. arXiv, 2008; arXiv:0811.3410. [Google Scholar]
- Douglas, B.L.; Gates, S.J., Jr.; Wang, J.B. Automorphism Properties of Adinkras. arXiv, 2010; arXiv:1009.1449. [Google Scholar]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D.; Miller, R.L. Codes and Supersymmetry in One Dimension. Adv. Theor. Math. Phys. 2011, 15, 1909–1970. [Google Scholar] [CrossRef]
- Zhang, Y.X. Adinkras for Mathematicians. Trans. Am. Math. Soc. 2014, 366, 3325–3355. [Google Scholar] [CrossRef]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. On the matter of N = 2 matter. Phys. Lett. B 2008, 659, 441–446. [Google Scholar] [CrossRef]
- Faux, M. The Conformal Hyperplet. Int. J. Mod. Phys. A 2017, 32, 1750079. [Google Scholar] [CrossRef]
- Faux, M.G.; Landweber, G.D. Spin Holography via Dimensional Enhancement. Phys. Lett. 2009, B681, 161–165. [Google Scholar] [CrossRef]
- Faux, M.G.; Iga, K.M.; Landweber, G.D. Dimensional Enhancement via Supersymmetry. Adv. Math. Phys. 2011, 2011, 259089. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Hübsch, T. On Dimensional Extension of Supersymmetry: From Worldlines to Worldsheets. Adv. Theor. Math. Phys. 2012, 16, 1619–1667. [Google Scholar] [CrossRef]
- Gates, S.J., Jr. The Search for Elementarity Among Off-Shell SUSY Representations. Korea Inst. Adv. Study Newsl. 2012, 5, 19. [Google Scholar]
- Gates, S.J., Jr.; Hübsch, T.; Stiffler, K. Adinkras and SUSY Holography: Some Explicit Examples. Int. J. Mod. Phys. 2014, A29, 1450041. [Google Scholar] [CrossRef]
- Calkins, M.; Gates, D.E.A.; Gates, S.J.; McPeak, B. Is it possible to embed a 4D, supersymmetric vector multiplet within a completely off-shell adinkra hologram? J. High Energy Phys. 2014, 1405, 057. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Hübsch, T.; Stiffler, K. On Clifford-algebraic dimensional extension and SUSY holography. Int. J. Mod. Phys. 2015, A30, 1550042. [Google Scholar] [CrossRef]
- Calkins, M.; Gates, D.E.A.; Gates, S.J., Jr.; Stiffler, K. Adinkras, 0-branes, Holoraumy and the SUSY QFT/QM Correspondence. Int. J. Mod. Phys. 2015, A30, 1550050. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Grover, T.; Miller-Dickson, M.D.; Mondal, B.A.; Oskoui, A.; Regmi, S.; Ross, E.; Shetty, R. A Lorentz covariant holoraumy-induced ’gadget’ from minimal off-shell 4D, N = 1 supermultiplets. J. High Energy Phys. 2015, 1511, 113. [Google Scholar] [CrossRef]
- Gates, D.E.A.; Gates, S.J., Jr. A Proposal on Culling & Filtering a Coxeter Group for 4D, N = 1 Spacetime SUSY Representations. Unpublished work. 2016. [Google Scholar]
- Gates, D.E.A.; Gates, S.J., Jr.; Stiffler, K. A Proposal on Culling & Filtering a Coxeter Group for 4D, N = 1 Spacetime SUSY Representations: Revised. J. High Energy Phys. 2016, 1608, 076. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Guyton, F.; Harmalkar, S.; Kessler, D.S.; Korotkikh, V.; Meszaros, V.A. Adinkras from ordered quartets of BC4 Coxeter group elements and regarding 1,358,954,496 matrix elements of the Gadget. J. High Energy Phys. 2017, 1706, 006. [Google Scholar] [CrossRef]
- Gates, S.J.; Iga, K.; Kang, L.; Korotkikh, V.; Stiffler, K. Generating all 36,864 Four-Color Adinkras via Signed Permutations and Organizing into ℓ- and -Equivalence Classes. Symmetry 2019, 11, 120. [Google Scholar] [CrossRef]
- Gates, S.J.; Kang, L.; Kessler, D.S.; Korotkikh, V. Adinkras from ordered quartets of BC4 Coxeter group elements and regarding another Gadget’s 1,358,954,496 matrix elements. Int. J. Mod. Phys. A 2018, 33, 1850066. [Google Scholar] [CrossRef]
- De Wit, B.; van Holten, J.W. Multiplets of Linearized SO(2) Supergravity. Nucl. Phys. 1979, B155, 530–542. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Vasiliev, M.A. Minimal Set of Auxiliary Fields and S Matrix for Extended Supergravity. Lett. Nuovo Cim. 1979, 25, 79–90. [Google Scholar] [CrossRef]
- Siegel, W.; Gates, S.J., Jr. (3/2, 1) Superfield of O(2) Supergravity. Nucl. Phys. 1980, B164, 484–494. [Google Scholar] [CrossRef]
- Ogievetsky, V.I.; Sokatchev, E. On Gauge Spinor Superfield. JETP Lett. 1976, 23, 58–59. [Google Scholar]
- Ogievetsky, V.I.; Sokatchev, E. Superfield Equations of Motion. J. Phys. 1977, A10, 2021–2030. [Google Scholar] [CrossRef]
- Siegel, W.; Gates, S.J., Jr. Superfield Supergravity. Nucl. Phys. 1979, B147, 77–104. [Google Scholar] [CrossRef]
- Zhang, Y.X. A Unified Enumeration of 1-dimension Garden Algebras and Valise Adinkras. arXiv, 2018; arXiv:1801.02678. [Google Scholar]
- Friend, I.; Kostiuk, J.; Zhang, Y.X. Enumerative Gadget Phenomena for (4,1)-Adinkras. arXiv, 2018; arXiv:1810.05545. [Google Scholar]
- Gates, S.J., Jr.; Kuzenko, S.M.; Sibiryakov, A.G. Towards a unified theory of massless superfields of all superspins. Phys. Lett. B 1997, 394, 343–353. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Koutrolikos, K. On 4D, massless gauge superfields of arbitrary superhelicity. J. High Energy Phys. 2014, 1406, 098. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Koutrolikos, K. On 4D, N = 1 Massless Gauge Superfields of Higher Superspin: Half-Odd-Integer Case. arXiv, 2013; arXiv:1310.7386. [Google Scholar]
- Gates, S.J., Jr.; Koutrolikos, K. On 4D, N = 1 Massless Gauge Superfields of Higher Superspin: Integer Case. arXiv, 2013; arXiv:1310.7385. [Google Scholar]
- Gates, S.J., Jr.; Hallett, J.; Hübsch, T.; Stiffler, K. The Real Anatomy of Complex Linear Superfields. Int. J. Mod. Phys. A 2012, 27, 1250143. [Google Scholar] [CrossRef]
- Doran, C.F.; Hübsch, T.; Iga, K.M.; Landweber, G.D. On General Off-Shell Representations of World Line (1D) Supersymmetry. Symmetry 2014, 6, 67–88. [Google Scholar] [CrossRef]
- Gates, S.J.; Rana, L. A Theory of spinning particles for large N extended supersymmetry. Phys. Lett. B 1995, 352, 50–58. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Rana, L. A Theory of spinning particles for large N extended supersymmetry(II). Phys. Lett. B 1996, 369, 262–268. [Google Scholar] [CrossRef]
- Georgi, H. Lie algebras in particle physics. Front. Phys. 1999, 54, 1–320. [Google Scholar]
- Gates, S.J.; Grisaru, M.T.; Rocek, M.; Siegel, W. Superspace or One Thousand and One Lessons in Supersymmetry. Front. Phys. 1983, 58, 1–548. [Google Scholar]
- Buchbinder, I.L.; Gates, S.J., Jr.; Linch, W.D., III; Phillips, J. New 4-D, N = 1 superfield theory: Model of free massive superspin 3/2 multiplet. Phys. Lett. B 2002, 535, 280–288. [Google Scholar] [CrossRef]
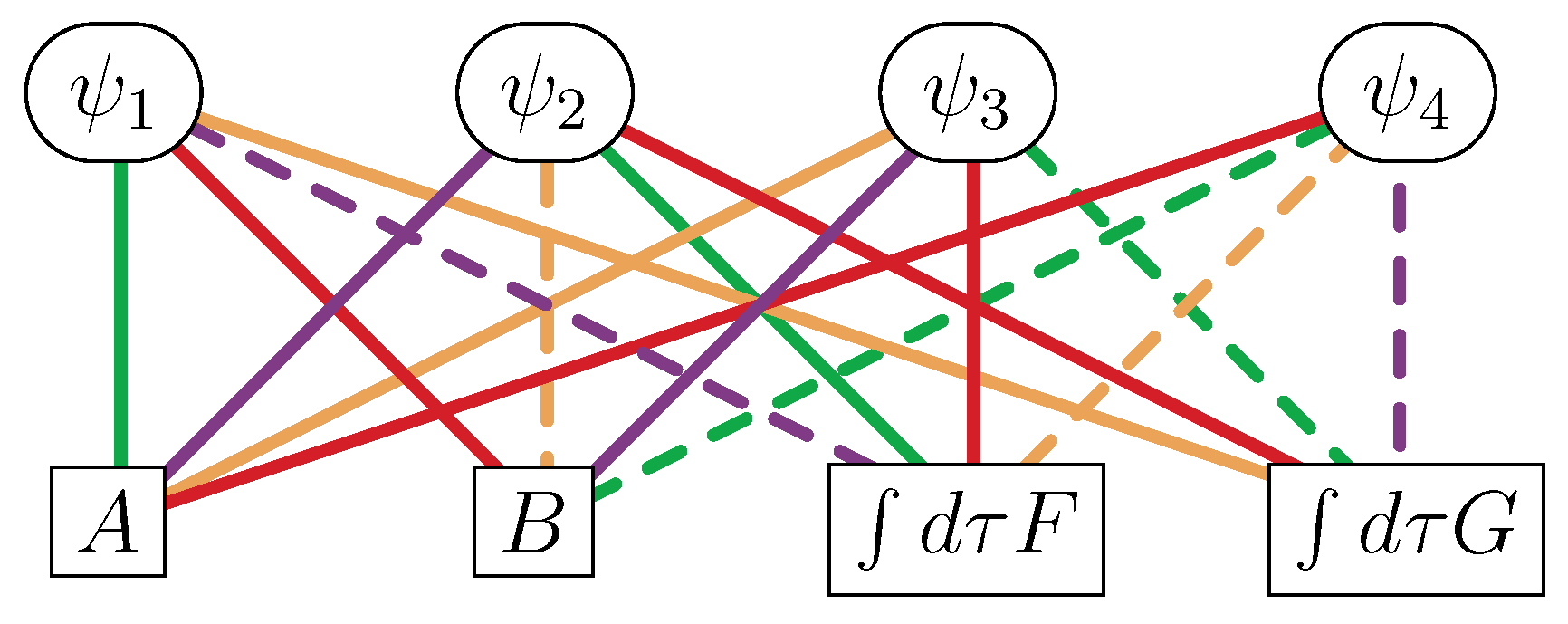

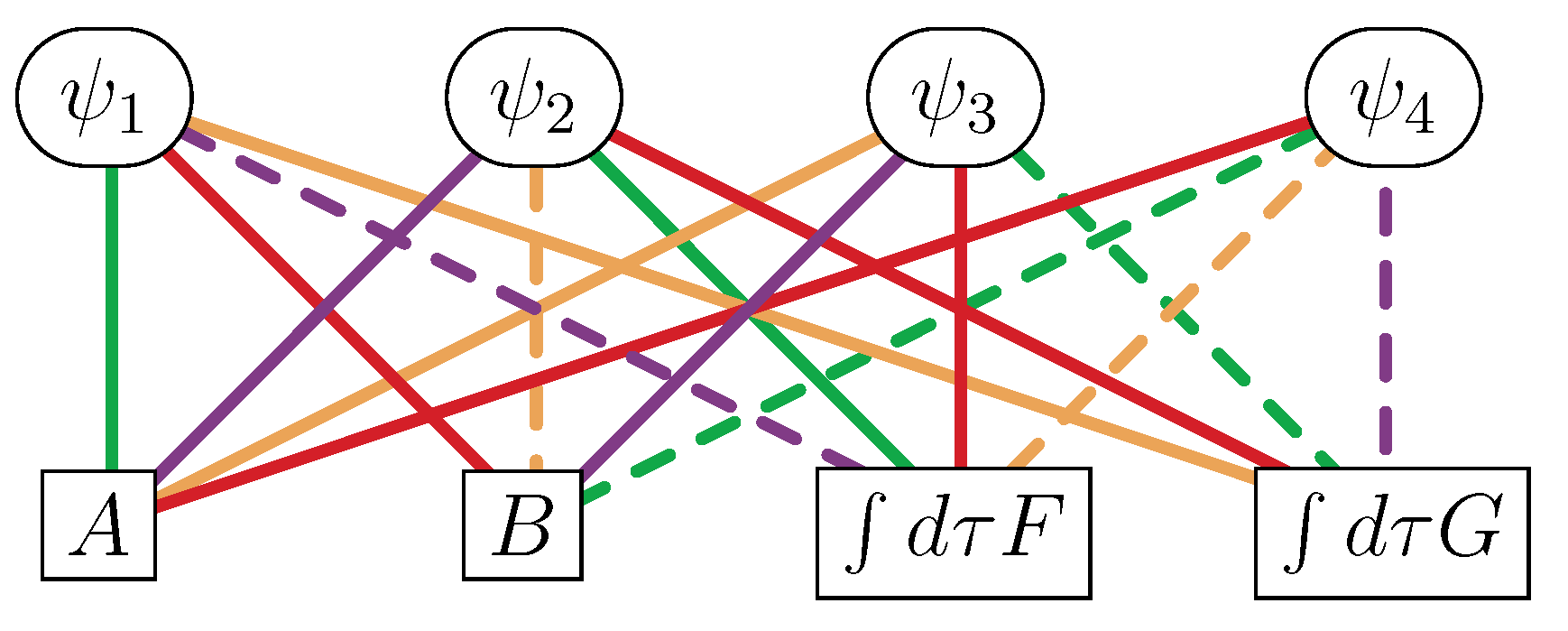
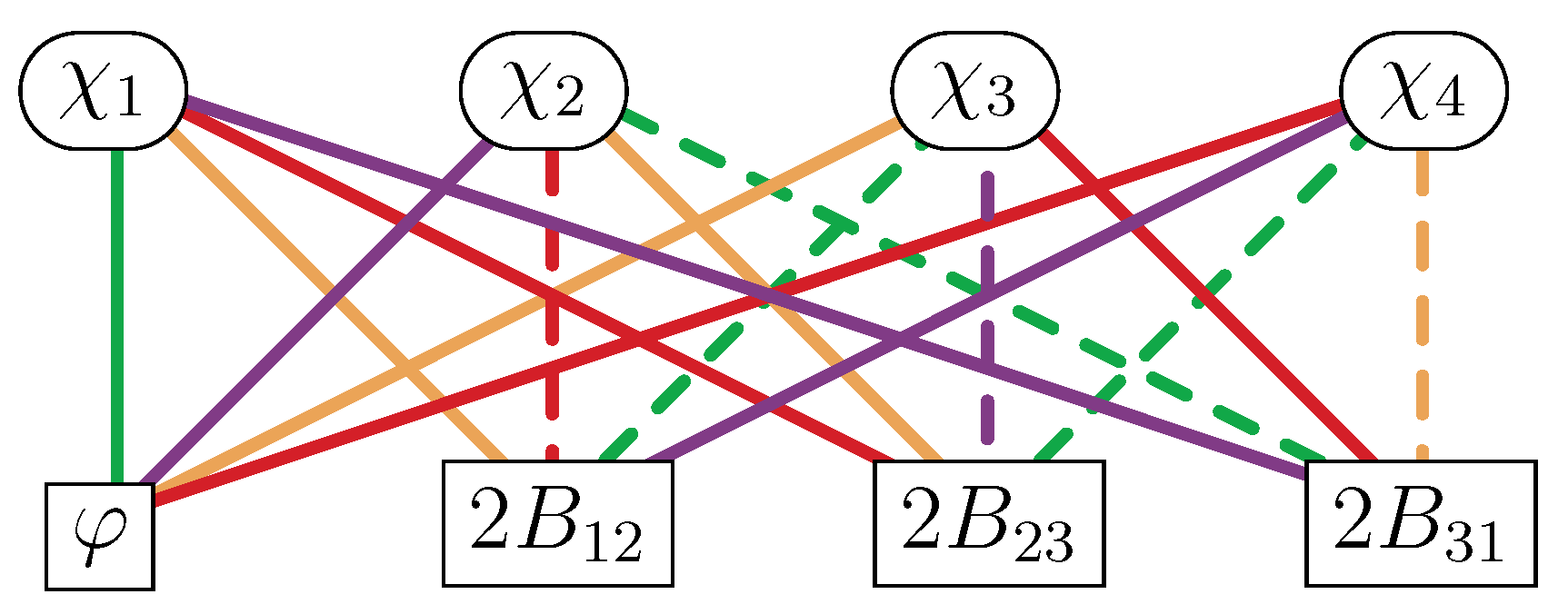
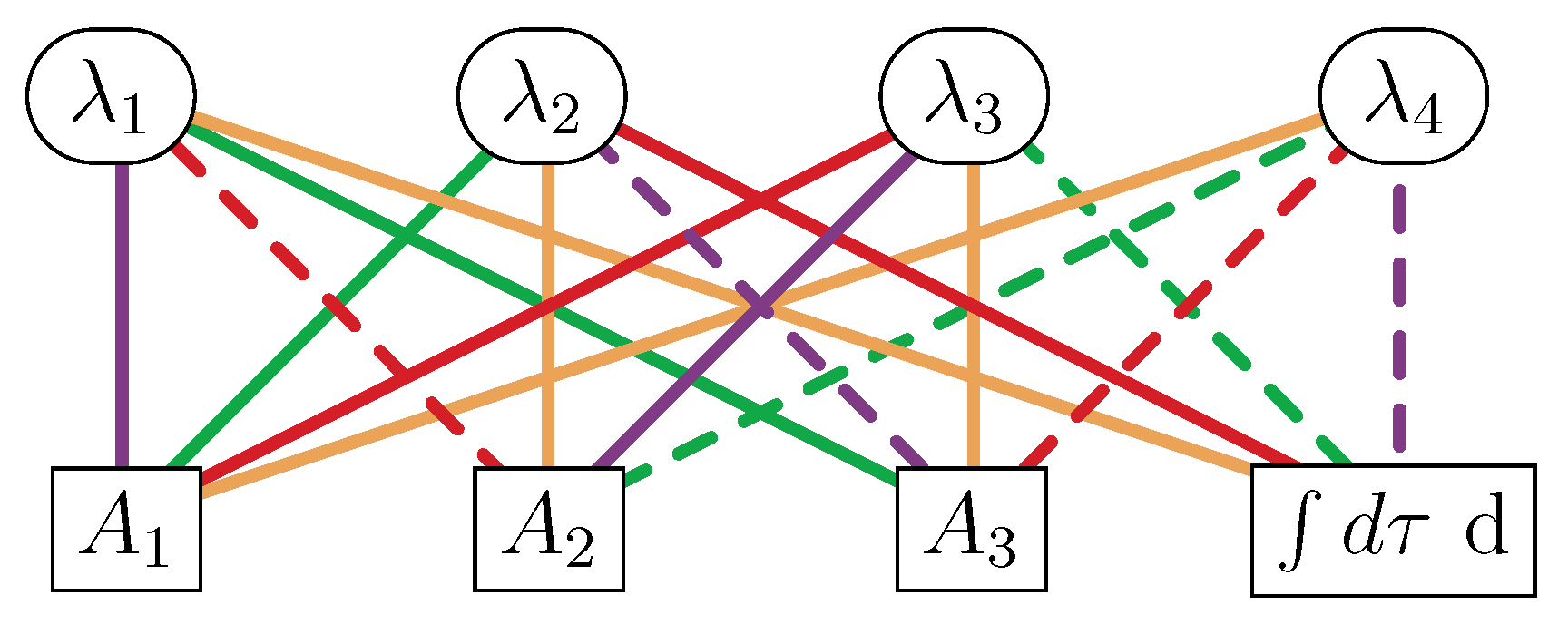
| Multiplet | CM | VM | TM | CLS | mSG | cSG | |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 2 | 2 | 4 | 2 | |
| Multiplet | Minimum | When Minimum | When Equals Five |
|---|---|---|---|
| dWvH | 5 | ||
| OS | 29/7 | ||
| 14/3 | or |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mak, S.-N.H.; Stiffler, K.
4D,
Mak S-NH, Stiffler K.
4D,
Mak, S.-N. Hazel, and Kory Stiffler.
2019. "4D,
Mak, S.-N. H., & Stiffler, K.
(2019). 4D,





