Abstract
In a real-life scenario, it is undoable and unmanageable to solve a decision-making problem with the single stand-alone decision-aid method, expert assessment methodology or deterministic approaches. Such problems are often based on the suggestions or feedback of several experts. Usually, the feedback of these experts are heterogeneous imperfect information collected from various more or less reliable sources. In this paper, we introduce the concept of multi-sets over type-2 fuzzy sets. We have tried to propose an extension of type-1 multi-fuzzy sets into a type-2 multi-fuzzy set (T2MFS). After defining T2MFS, we discuss the algebraic properties of these sets including set-theoretic operations such as complement, union, intersection, and others with examples. Subsequently, we define two distance measures over these sets and illustrate a decision-making problem which uses the idea of type-2 multi-fuzzy sets. Furthermore, an application of a medical diagnosis system based on multi-criteria decision making of T2MFS is illustrated with a real-life case study.
1. Introduction
According to Cantor, a set is a well-defined collection of distinct objects, but let us see what happens if we consider a collection of objects where one or some or all objects occur more than once. The answer to this question is a different type of set known as multi-set or -set which was first studied by Bruijn [1]. Afterwards, Yager [2] proposed a new and more generalized concept of multi-sets named as multi-fuzzy sets (MFS) which can deal with many real life problems with some degree of ease. Sebastian and Ramakrishnan [3] also studied multi-fuzzy sets and concluded that multi-fuzzy set theory is an extension of Zadeh’s fuzzy set theory, Atanassov’s intuitionistic fuzzy set theory and L-fuzzy set theory. Yang et al. [4] discussed applications of multi-fuzzy soft sets in decision making. Furthermore, Das et al. [5] proposed an approach of group multi-criteria decision-making using intuitionistic multi-fuzzy sets.
A type-2 fuzzy set (T2FS) is an extension of ordinary fuzzy sets, i.e., type-1 fuzzy set (T1FS). The membership value of a type-1 fuzzy set is a real number in the closed interval . On the other hand, the membership value of a T2FS is a type-1 fuzzy set. The concept of T2FS was introduced by Zadeh [6,7,8]. Mizumoto and Tanaka [9,10], and Dubois and Prade [11] investigated the logical operations of T2FS. Later, many researchers did a lot of theoretical work on the properties of T2FS [12,13,14] and figured out many applications [15,16,17,18,19,20,21].
Although there are various mathematical tools such as fuzzy sets, rough sets, multi-sets, multi-fuzzy sets, intuitionistic fuzzy sets, and type-2 fuzzy sets to deal with uncertainties [22,23,24], there might be some physical problems where the primary membership function may have more than one secondary membership grade with the same or different values. In those particular cases, the existing mathematical tools might not be adequate. That is why we introduce a new concept of type-2 multi-fuzzy sets. Type-2 multi-fuzzy sets are supposedly a new approach which will be an extension of the existing concepts and shall be helpful to deal with problems related to uncertainties. T2MFS is a type-2 fuzzy set whose primary membership function has a sequence of secondary membership values lying in the closed interval . In this paper, we first give definitions of classical multi-sets, multi-fuzzy sets and type-2 fuzzy sets and also provide examples of each.
The main contributions of this article are highlighted as follows:
- (i)
- A type-2 multi-fuzzy set is proposed in this article.
- (ii)
- Some set-theoretic operations of T2MFS, e.g., complement, inclusion, union, and intersection of T2MFS are presented in this article.
- (iii)
- Two distance measure: (a) Hamming distance and (b) Euclidian distance are proposed in this study.
- (iv)
- A suitable application based on a medical diagnosis system is presented by using the distance measure of T2MFS.
The rest of the paper is organized as follows. Some relevant studies of the literature are surveyed in Section 2. The preliminary concepts of our study are discussed in Section 3. In Section 4, we define type-2 multi-fuzzy set (T2MFS) and give examples. Subsequently, in Section 5, the algebraic operations on T2MFS like complement, inclusion, union, and intersection are discussed. Consequently, in Section 6, set-theoretic properties like idempotency, commutativity, associativity, and distributivity are verified for T2MFSs. In Section 7, we define the two distance measures of T2MFS. We provide a real-life application based on a medical diagnosis system, which applies the concept of type-2 multi-fuzzy sets in Section 8. In Section 9, we conduct a case study based on the application presented in Section 8. Finally, the study is concluded in Section 10.
2. Literature Review
In this section, we present a brief overview of different variants of the multi-fuzzy set (MFS) which have been proposed in previous studies. The survey, by no means, encompasses all the related researches in the literature. However, some related studies having significant contributions are reviewed.
The concept of MFS has originated as an extension of the fuzzy set [25], L-fuzzy set [26] and intuitionistic fuzzy set [27]. In a MFS, the membership function is an ordered sequence of ordinary fuzzy membership functions. Here, an element of the universe can repeat itself with possibly the same or different membership values. Motivated by the study of Yager [2] on MFS, several contributions can be observed in the field of multi-fuzzy sets and its variants. Muthuraj and Balamurugan [28] proposed some algebraic structures of multi-fuzzy subgroup and investigated their properties. Sebastian and Ramakrishnan [29] proposed the multi-fuzzy subgroup and normal multi-fuzzy subgroups. Furthermore, various bridge function like lattice homomorphisms, order homomorphisms, -fuzzy lattices, and strong -fuzzy lattices have been developed by Sebastian and Ramakrishnan [30]. Subsequently, multi-fuzzy topology was proposed by Sebastian and Ramakrishnan [31]. In addition, a progressive development of MFS can be observed from the contributions of several researchers [32,33,34].
Enlightened by the development of MFS, Dey and Pal [35] proposed multi-fuzzy complex numbers and multi-fuzzy complex sets. Using the concepts of their studies, the authors introduced multi-fuzzy complex nilpotent matrices over a distributive lattice [36]. The authors also developed multi-fuzzy vector space and multi-fuzzy linear transformation over a finite-dimensional multi-fuzzy set [37].
Shinoj and John [38] introduced the intuitionistic fuzzy multi-sets (IFMS). After that, several investigations were conducted to develop various features of IFMS. Ejegwa and Awolola [39] determined the binomial probability of IFMS, where for each trial, it was assumed that the probability of the membership degree was constant and the intuitionistic fuzzy multi-set index was negligible. Rajarajeswari and Uma [40] proposed three distance measures and their corresponding similarity measures of IFMS. These measures are based on the Hausdorff distance measure, the geometric distance measure and the normalized distance measure. Subsequently, different studies of IFMS [41,42,43,44] can be observed in the literature. Besides, Das et al. [5] proposed an efficient approach for group multi-criteria decision-making (MCDM) based on IMFS.
3. Preliminaries
Before introducing the concept of type-2 multi-fuzzy sets, we first present some essential concepts of a crisp multi-set or -set, multi-fuzzy sets, type-2 fuzzy sets with examples, and set theoretical operations of multi-fuzzy sets.
3.1. Classical Multi-Sets
A classical multi-set or -set (in short) is a set, where any element of the set may occur more than once. The definition can be found in the work of (Girish and John [45]). An -set drawn from set X is represented by a function Count- or defined as where represents the set of non-negative integers.
Here, is the number of occurrences of the element in the -set . We present the -set drawn from the set as , where is the number of occurrences of the element , in the -set . However, those elements which are not included in the -set have zero count.
Example 1:
Let us consider the universal set of some object asand let objectappear three times,appear five times,appear one time andappear two times in set. Then, this appearance of the objects can be represented in set form. It can also be represented in the form as
which is a-set.
3.2. Multi-Fuzzy Set
A multi-fuzzy set (Yager [2]) is a fuzzy set, where for each element of the universal set there may be more than one membership value. It can be defined mathematically as follows. Let be a nonempty set. A multi-fuzzy set (MFS) on is characterized by a function, count membership of denoted by such that , where is the set of all crisp multi-sets drawn from the unit interval . Then, for any , the value is a crisp multi-set drawn from . For each , the membership sequence is defined as the decreasingly ordered sequence of elements in . It is denoted by , where .
Example 2:
Let us consider fuzzy setas follows
of the universal set. From this fuzzy set, we see that the elementoccurs three times with membership valuesrespectively; the elementoccurs four times with membership valuesrespectively and the elementoccurs once with a membership value. Thus, the set can be rewritten in the form as
which essentially is a multi-fuzzy set.
The graphical representation of the multi-fuzzy set is shown in Figure 1, where we consider , and .
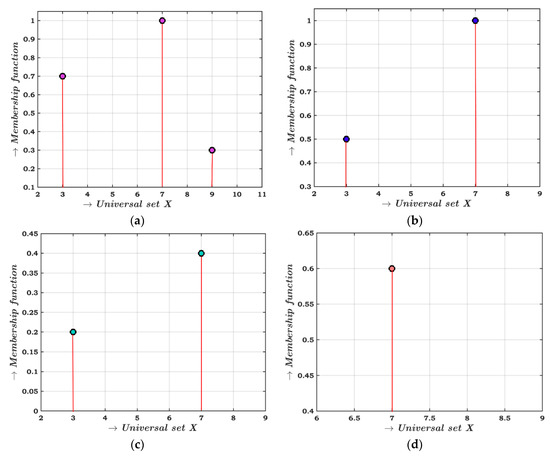
Figure 1.
The membership function of the multi-fuzzy set is represented by four different combinations of membership functions of 3, 7 and 9, where (a) the graphical representation of , (b) the graphical representation of , (c) the graphical representation of and (d) the graphical representation of are presented respectively.
We now discuss some basic operations such as inclusion, equality, union, and intersection of MFSs. Let and be two MFSs defined on .
3.2.1. Inclusion
Example 3:
Let us consider two multi-fuzzy setsandover a nonempty universeas
Then, from the definition it is clear that .
3.2.2. Equality
3.2.3. Union
3.2.4. Intersection
Example 4:
Let us consider two multi-fuzzy sets over a nonempty universe as
and
Then
and
Here,Correspondingly,
3.3. Type-2 Fuzzy Set (T2FS)
A type-2 fuzzy set is a fuzzy set whose membership degree includes uncertainty i.e., membership degree is a type-1 fuzzy set. A T2FS introduces a third dimension to the membership function via the second membership grades. A T2FS is mathematically expressed as follows according to (Mendel and John [46])
where is the secondary membership function and is the primary membership of , which is the domain of . can be expressed as
where denotes union over all admissible and . For a discrete universe of discourse, is replaced by .
For each value of , the secondary membership function is defined as
such that for a particular , the secondary membership grade of is called
Example 5:
Let the set of infant age be represented by a type-2 fuzzy set. Let youthness be the primary membership function ofand the degree of youthness be the secondary membership function. Letbe an age set with the primary membership of the members ofrespectively being,,=. The secondary membership function ofis, i.e.,is the secondary membership grade ofwith primary membership .
In the same way, = and = .
So the discrete type-2 fuzzy set can be represented by
4. Type-2 Multi-Fuzzy Sets (T2MFS)
Let be the universe of discourse. Let be a type-2 fuzzy set defined on and be a primary membership value of an element . Then, is said to be a type-2 multi-fuzzy set if it is characterised by a count function denoted by and is defined as , where is the set of all crisp multi-sets taken from the unit interval which are the secondary membership values of . For each , the secondary membership sequence is defined in decreasing order as and is denoted by . Then, set can be represented as
if the universe is discrete, whereas if is a continuous universe, then can be written as
Let us illustrate this idea with an example.
Example 6:
Let us consider a type-2 fuzzy set T defined in the universal set
From the structure ofwe see that three’s with primary membership values ofhave secondary membership valuesandrespectively; two’s with primary membership values ofhave the corresponding secondary membership values ofand; two’s with a primary membership value ofhave secondary membership values ofrespectively; one y with a primary membership value ofhas a secondary membership value of; and three’s with primary membership values ofwith secondary membership valuesandrespectively. Therefore, can be represented as
Thus, is a type-2 multi-fuzzy set. The graphical representation of T2MFS is shown in Figure 2, where we consider and .
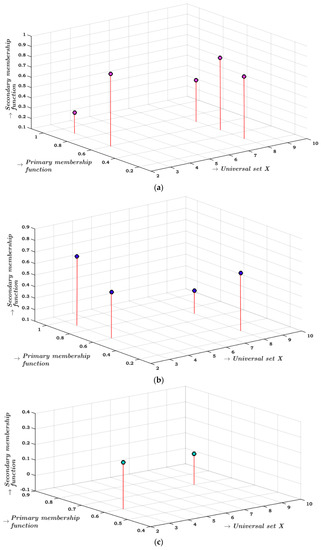
Figure 2.
The membership function of T2MFS is represented by three different combinations of primary membership and secondary membership functions of 3 and 8, where (a) the graphical representation of , (b) the graphical representation of and (c) the graphical representation of are presented respectively.
Again, let us denote the collection of all T2MFSs over the universe by T2MF(). When we define operations between two T2MFSs, say and , the lengths of their secondary membership sequences and for a particular primary membership value of (say ) and for a particular primary membership value of (say ) should be set to be equal. We hence define the length as
and
For the sake of simplicity, we write as . Let us describe this idea by an example.
Example 7:
Let us consider two T2MFSs, sayand as
and
Then
Moreover,
5. Some Operations on T2MFS
In this section, we discuss four fundamental arithmetical operations: (i) complement, (ii) inclusion, (iii) union, and (iv) intersection of T2MFS.
5.1. Complement
Let be a T2MFS over some universe . Then, the complement of denoted by is defined as
where = and is the primary membership function of . Let us give an example to illustrate this idea.
Example 8:
Let us consider the T2MFS used in Example 6.
5.2. Inclusion
Let and be two T2MFSs over some universe . Then we say that if and only if
where and are primary membership functions of and respectively, and and are the secondary membership functions of and respectively. These two sets and are said to be equal if and only if
Let us illustrate this idea by an example.
Example 9:
Let us consider two T2MFSs, sayand , where
and
Then applying the above-mentioned definition, we can see that .
5.3. Union
Let and be two T2MFSs over the universe . Then the set is defined as
where and , , such that , where and are the primary membership functions of and respectively. and are the secondary membership functions of and respectively. Let us illustrate this idea by an example.
Example 10:
Let us consider two T2MFSs, sayand , which are considered in Example 5. Then
and
Then
5.4. Intersection
Let and be two T2MFSs over the universe . Then set is the intersection of and where it is denoted as and is defined as
Here, , , where , and and are the primary membership functions of and respectively. and are the secondary membership functions of and respectively. Subsequently, we illustrate this idea by an example as shown below.
Example 11:
Let us consider two T2MFSs, sayand , where
Then
6. Properties of T2MFS
In this section, we discuss four fundamental properties of T2MFS.
Let , and be three T2MFSs over a universe . Then the following relations hold:
- (i)
- ,
- (ii)
- (iii)
- ,
- (iv)
- ,
- (v)
- ,
The proofs of (i) to (iii) are obvious. We illustrate these results later by example. We now prove the results (iv) and (v).
Proof of (iv).
Similarly, we can prove that . □
Proof of (v).
Similarly, we can prove that . □
Let us illustrate these results by an example.
Example 12:
Let us consider three T2MFSs over a non-empty universe .
For simplicity, we have takenas a singleton set for each .
Then
Therefore, the idempotent property holds.
and
Hence, De Morgan’s laws hold.
and
Consequently, the commutative property holds.
and
Hence, the associative property holds.
and
As a result, the distributive property holds.
7. Distance Measures of T2MFS
Let and be two T2MFSs. Then we can define the following distances as follows:
- (1)
- Hamming Distance
- (2)
- Euclidean Distancewhere and are the primary membership functions of and respectively, and and are the corresponding secondary membership functions of and .Let us now explain this idea with an example.
Example 13:
Letbe a non-empty universe. Letandbe two T2MFSs over which are given as
and
8. Numerical Illustration
Although fuzzy logic is relatively a newer subject than classical mathematical logic, we use the former extensively in our everyday life. We primarily use fuzzy logic in decision-making problems. However, there may be some cases in decision-making where the primary membership function occurs with a sequence of same or different degrees. In that case, we need to use T2MFS to solve the problem. Let us present an example of medical diagnosis after acquiring the necessary information from Reference [38]. Let be a set of patients, be a set of diseases and be a set of symptoms. Let us consider the intensity of the disease symptoms to be the secondary membership functions.
Now, if we look at one set of data, there is a chance that some errors may occur since we know that at different times during a day the disease symptoms have different intensities. To minimize these errors, we study three different samples at three different times of the day. The details of one such example are provided below.
In Table 1, each symptom is described by their primary and secondary membership function.

Table 1.
Symptoms vs. Diseases.
For proper diagnosis of each patient, we take samples at three different times in a day say at AM, PM and PM. We use the Euclidean distance measure (cf. Section 6) to calculate the distance between the patients and the diseases. Here, the Euclidean distance is determined between each patient from every symptoms for each diagnosis .
The data reported in Table 2 is of a T2MFS, where the intensity of the symptoms form a secondary membership sequence. Moreover, in Table 3 and Table 4 the Hamming distance and the Euclidean distance are determined respectively for each patient from the set of diseases.

Table 2.
Patients vs. Symptoms.

Table 3.
Hamming distance between Patients and Diseases.

Table 4.
Euclidean distance between Patients and Diseases.
According to the principle of minimum distance point, a lower distance point indicates a proper diagnosis of a particular disease. While comparing the data reported in Table 3 and Table 4, a similar interpretation is observed. Here, considering both these Table 3 and Table 4, the lowest distance point gives the proper diagnosis, and therefore it can be inferred that patient suffers from and patients and suffer from , whereas, patient suffers from . Hence, out of four patients, we observe that two patients are affected with In addition, one patient is affected with each of the two diseases, and , whereas, none of the patients are diagnosed with .
9. Case Study
For the purpose of simulation, we consider a real case study for 500 patients of the Healthcare Hospital situated in Kolkata, India. Subsequently, we consulted with the specialist doctors of the Healthcare Hospital and received their feedback on the 500 patients at three different times in a day.
A patient suffering from a disease, when visiting a hospital, expresses his/her symptoms, e.g., , , , and to a doctor. Based on these feedbacks, the doctor analyzes the disease (e.g., , , and ) the patient is suffering from. These symptoms and the disease of the patients are represented in linguistic terms which involves uncertainty. As an example, in a day, the of a patient can vary in the morning, afternoon and night. Based on these recorded values of the , the evaluation of different doctors might change as well. For example, if the of a patient is recorded Fahrenheit (), and respectively in the morning, afternoon and night, then one doctor might analyze that the patient is having , while the other doctor might not agree that the patient is suffering from and often agree to observe the for some subsequent days. It can be noted here, that a particular symptom of a patient can fluctuate in a day, and based on these fluctuations, the opinion (analysis) of the experts (doctors) also varies for a particular patient. Therefore, in order to incorporate the uncertainties of the symptoms and the diseases rationally, the parameters of the symptom and the disease of a patient are represented as T2MFS. In our study, the necessary information are received from the doctors of the Healthcare Hospital. It should be mentioned here that while receiving specialist doctors feedback, we consider the set of five symptoms and the four diseases as the same, compared to the one considered in the application mentioned in the numerical illustration section. These data are presented in the tables of the supplementary file. Here, Table 5 and Table 6 report the data of the Healthcare Hospital which are similar to the corresponding data presented in Table 1 and Table 2. Similar to Table 4, in this case study, we determine the Euclidean distances between patients and diseases. However, instead of the corresponding data of four patients as shown in Table 2 and Table 4, Table 6 and Table S1 represent the data of 500 patients. From Table 7, it is observed that 66 patients are affected with Viral Fever. Two-hundred-and-forty-two patients are suspected to have Tuberculosis; 62 patients are suffering from Typhoid and 130 patients are diagnosed with Throat Disease.

Table 5.
Symptoms vs. Diseases in Healthcare Hospital.

Table 6.
Patients vs. Symptoms in Healthcare Hospital.

Table 7.
Patients diagnosed with a particular disease in Healthcare Hospital.
10. Conclusions
In this paper, we have tried to extend the concept of multi-fuzzy set theory to type-2 multi-fuzzy sets. The T2MFS may be applied to various applications in daily life. The algebraic properties of these sets have been verified and two types of distance metrics including Hamming distance and Euclidean distance have been discussed. Moreover, a few illustrative examples and a real-life case study of the medical diagnosis system are presented in this article. In the numerical illustration, we measure the Hamming distance and Euclidean distance of each patient for the set of diseases by considering the symptoms of the disease where both types of distance measurements yield a similar diagnostic result. The lowest distance shows proper diagnosis for both the distance measurements. In addition, as an application of T2MFS, the case-study is also conducted on 500 patients undergoing treatment in a hospital.
As far as the limitation of T2MFS is concerned, it is conceptually difficult to define the T2MFS and its necessary algebraic operations in the continuous domain, since the membership functions of such continuous T2MFS will be difficult to represent.
In the future, researchers may attempt to generalize this concept further by studying higher order multi-fuzzy sets in an abstract setting. Also, this research work might be enhancing the study of T2MFS for uncertain group decision-making (GDM) problems by introducing some aggregated operators where GDM is vital due to the lack of information, the expertise of the experts, risk amendment, etc. Besides, the possible extension of T2MFS in various other domains of research including image processing and data mining can be considered as the possible future area of research.
Supplementary Materials
The following are available online at http://www.mdpi.com/2073-8994/11/2/170/s1, Table S1: Euclidean distance between Patients and Diseases in Healthcare Hospital.
Author Contributions
The individual contribution and responsibilities of the authors were as follows: M.B.K., B.R. and S.M. performed the research study, collected, pre-processed, and analyzed the data and the obtained results, and worked on the development of the paper. S.K. and D.P. provided good advice throughout the research by giving suggestions on, methodology, modelling uncertainty of the patient data, and refinement of the manuscript. All the authors have read and approved the final manuscript.
Funding
This research was funded by Department of Science & Technology (DST), Government of India (No. DST/INSPIRE Fellowship/2015/IF150410).
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Bruijn, N.G. Denumerations of Rooted trees and Multi-sets. Discret. Appl. Math. 1983, 6, 25–33. [Google Scholar] [CrossRef]
- Yager, R.R. On the theory of bags. Int. J. Gen. Syst. 1986, 13, 23–37. [Google Scholar] [CrossRef]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy sets: An extension of fuzzy sets. Fuzzy Inf. Eng. 2011, 3, 35–43. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, X.; Meng, C. The multi-fuzzy soft set and its application in decision making. Appl. Math. Model. 2013, 37, 4915–4923. [Google Scholar] [CrossRef]
- Das, S.; Kar, M.B.; Kar, S. Group multi-criteria decision making using intuitionistic multi-fuzzy sets. J. Uncertain. Anal. Appl. 2013, 10, 1–16. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Mizumoto, M.; Tanaka, K. Some properties of fuzzy sets of type-2. Inf. Control 1976, 31, 312–340. [Google Scholar] [CrossRef]
- Mizumoto, M.; Tanaka, K. Fuzzy sets of type-2 under algebraic product and algebraic sum. Fuzzy Sets Syst. 1981, 5, 277–280. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Application; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Coupland, S.; John, R. A fast geometric method for defuzzification of type-2 fuzzy sets. IEEE Trans. Fuzzy Syst. 2008, 16, 929–941. [Google Scholar] [CrossRef]
- Greenfield, S.; John, R.I.; Coupland, S. A novel sampling method for type-2 defuzzification. In Proceedings of the UKCI, London, UK, 5–7 September 2005; pp. 120–127. [Google Scholar]
- Karnik, N.N.; Mendel, J.M. Centroid of a type-2 fuzzy set. Inf. Sci. 2001, 132, 195–220. [Google Scholar] [CrossRef]
- Garcia, J.C.F. Solving fuzzy linear programming problems with interval type-2 RHS. In Proceedings of the 2009 IEEE International Conference on System, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 262–267. [Google Scholar]
- Stanujkic, D.; Karabasevic, D. An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: a case of website evaluation. Oper. Res. Eng. Sci. Theor. Appl. 2018, 1, 29–39. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Badi, I. Prediction and control of surface roughness for end milling process using ANFIS. Oper. Res. Eng. Sci. Theor. Appl. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Kundu, P.; Kar, S.; Maiti, M. Fixed charge transportation problem with type-2 fuzzy variable. Inf. Sci. 2014, 255, 170–180. [Google Scholar] [CrossRef]
- Kundu, P.; Kar, S.; Maiti, M. Multi-item solid transportation problem with type-2 fuzzy parameters. Appl. Soft Comput. 2015, 31, 61–80. [Google Scholar] [CrossRef]
- Kundu, P.; Majumder, S.; Kar, S.; Maiti, M. A method to solve linear programming problem with interval type-2 fuzzy parameters. Fuzzy Optim. Decis. Mak. 2018. [Google Scholar] [CrossRef]
- Pal, S.S.; Kar, S. A Hybridized Forecasting Method Based on Weight Adjustment of Neural Network Using Generalized Type-2 Fuzzy Set. Int. J. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Vasiljevic, M.; Fazlollahtabar, H.; Stevic, Z.; Veskovic, S. A rough multicriteria approach for evaluation of the supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar] [CrossRef]
- Lukovac, V.; Popovic, M. Fuzzy Delphi approach to defining a cycle for assessing the performance of military drivers. Decis. Mak. Appl. Manag. Eng. 2018, 1, 67–81. [Google Scholar] [CrossRef]
- Pamucar, D.; Cirovic, G. Vehicle route selection with an adaptive neuro fuzzy inference system in uncertainty conditions. Decis. Mak. Appl. Manag. Eng. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Goguen, J.A. L-fuzzy sets. J. Math. Anal. Appl. 1967, 18, 145–174. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Muthuraj, R.; Balamurugan, S. Multi-fuzzy group and its level subgroups. Gen. Math. Notes 2013, 17, 74–81. [Google Scholar]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy Subgroups. Int. J. Contemp. Math. Sci. 2011, 6, 365–372. [Google Scholar]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy extension of crisp functions using bridge functions. Ann. Fuzzy Math. Inform. 2011, 2, 1–8. [Google Scholar]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy topology. Int. J. Appl. Math. 2011, 24, 117–129. [Google Scholar]
- Sebastian, S.; John, R. Multi-fuzzy sets and their correspondence to other sets. Ann. Fuzzy Math. Inform. 2016, 11, 341–348. [Google Scholar]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy sets. Int. Math. Forum 2010, 5, 2471–2476. [Google Scholar]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy extensions of functions. Adv. Adapt. Data Anal. 2011, 3, 339–350. [Google Scholar] [CrossRef]
- Dey, A.; Pal, M. Multi-fuzzy complex numbers and multi-fuzzy complex sets. Int. J. Fuzzy Syst. Appl. 2014, 4, 15–27. [Google Scholar] [CrossRef]
- Dey, A.; Pal, M. Multi-fuzzy complex nilpotent matrices. Int. J. Fuzzy Syst. Appl. 2016, 5, 52–76. [Google Scholar] [CrossRef]
- Dey, A.; Pal, M. Multi-fuzzy vector space and multi-fuzzy linear transformation over a finite dimensional multi-fuzzy set. J. Fuzzy Math. 2016, 24, 103–116. [Google Scholar]
- Shinoj, T.K.; John, S.J. Intuitionistic fuzzy multi-sets and its application in medical diagnosis. Int. J. Math. Comput. Sci. 2012, 6, 121–124. [Google Scholar]
- Ejegwa, P.A.; Awolola, J.A. Intuitionistic fuzzy multiset (IFMS) in binomial distributions. Int. J. Sci. Technol. Res. 2014, 3, 335–337. [Google Scholar]
- Rajarajeswari, P.; Uma, N. On distance and similarity measures of intuitionistic fuzzy multi-set. IOSR J. Math. 2013, 5, 19–23. [Google Scholar] [CrossRef]
- Rajarajeswari, P.; Uma, N. Intuitionistic fuzzy multi relations. Int. J. Math. Arch. 2013, 4, 244–249. [Google Scholar]
- Rajarajeswari, P.; Uma, N. A study of normalized geometric and normalized hamming distance measures in intuitionistic fuzzy multi sets. Int. J. Sci. Res. Eng. Technol. 2013, 2, 76–80. [Google Scholar]
- Rajarajeswari, P.; Uma, N. Zhang and Fu’s similarity measure on intuitionistic fuzzy multi sets. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 12309–12317. [Google Scholar]
- Rajarajeswari, P.; Uma, N. Correlation measure for intuitionistic fuzzy multi sets. Int. J. Res. Eng. Technol. 2014, 3, 611–617. [Google Scholar]
- Girish, K.P.; John, S.J. Multi-set topologies induced by multi-set relations. Inf. Sci. 2012, 188, 298–313. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 307–315. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).