1. Introduction
The investigation of the crossing number of graphs is a classical and very difficult problem provided that computing of the crossing number of a given graph in general is an NP-complete problem. It is well known that the problem of reducing the number of crossings in the graph has been studied in many areas, and the most prominent area is very large-scale integration technology.
In the paper, we will use notations and definitions of the crossing numbers of graphs like in [
1]. We will often use Kleitman’s result [
2] on crossing numbers of the complete bipartite graphs. More precisely, he proved that:
Using Kleitman’s result [
2], the crossing numbers for join of two paths, join of two cycles, and for join of path and cycle were studied in [
1]. Moreover, the exact values for crossing numbers of
and
for all graphs
G of order at most four are given in [
3]. Furthermore, the crossing numbers of the graphs
are known for a few graphs
G of order five and six in [
4,
5,
6,
7,
8,
9,
10]. In all of these cases, the graph
G is connected and contains at least one cycle. Further, the exact values for the crossing numbers
and
have been also investigated for some graphs
G of order five and six in [
5,
7,
11,
12].
The methods presented in the paper are new, and they are based on multiple combinatorial properties of the cyclic permutations. It turns out that if the graph of configurations is used like a graphical representation of the minimum numbers of crossings between two different subgraphs, then the proof of the main theorem will be simpler to understand. Similar methods were partially used for the first time in the papers [
8,
13]. In [
4,
9,
10,
14], the properties of cyclic permutations were also verified with the help of software in [
15]. In our opinion, the methods used in [
3,
5,
7] do not allow establishing the crossing number of the join product
.
2. Cyclic Permutations and Configurations
Let
G be the disconnected graph of order five consisting of one isolated vertex and of one vertex incident with some vertex of the three-cycle. We will consider the join product of the graph
G with the discrete graph on
n vertices denoted by
. The graph
consists of one copy of the graph
G and of
n vertices
, where any vertex
,
, is adjacent to every vertex of
G. Let
,
, denote the subgraph induced by the five edges incident with the vertex
. Thus, the graph
is isomorphic with the complete bipartite graph
and:
In the paper, we will use the same notation and definitions for cyclic permutations and the corresponding configurations for a good drawing
D of the graph
like in [
9,
14]. Let
D be a drawing of the graph
. The rotation
of a vertex
in the drawing
D like the cyclic permutation that records the (cyclic) counter-clockwise order in which the edges leave
has been defined by Hernández-Vélez, Medina, and Salazar [
13]. We use the notation
if the counter-clockwise order the edges incident with the vertex
is
,
,
,
, and
. We have to emphasize that a rotation is a cyclic permutation. In the paper, each cyclic permutation will be represented by the permutation with one in the first position. Let
denote the inverse permutation of
. We will deal with the minimal necessary number of crossings between the edges of
and the edges of
in a subgraph
depending on the rotations
and
.
We will separate all subgraphs , , of the graph into three mutually-disjoint subsets depending on how many of the considered cross the edges of G in D. For , let and . Every other subgraph crosses the edges of G at least twice in D. Moreover, let denote the subgraph for , where . Thus, for a given subdrawing of G, any subgraph is exactly represented by .
Let us suppose first a good drawing
D of the graph
in which the edges of
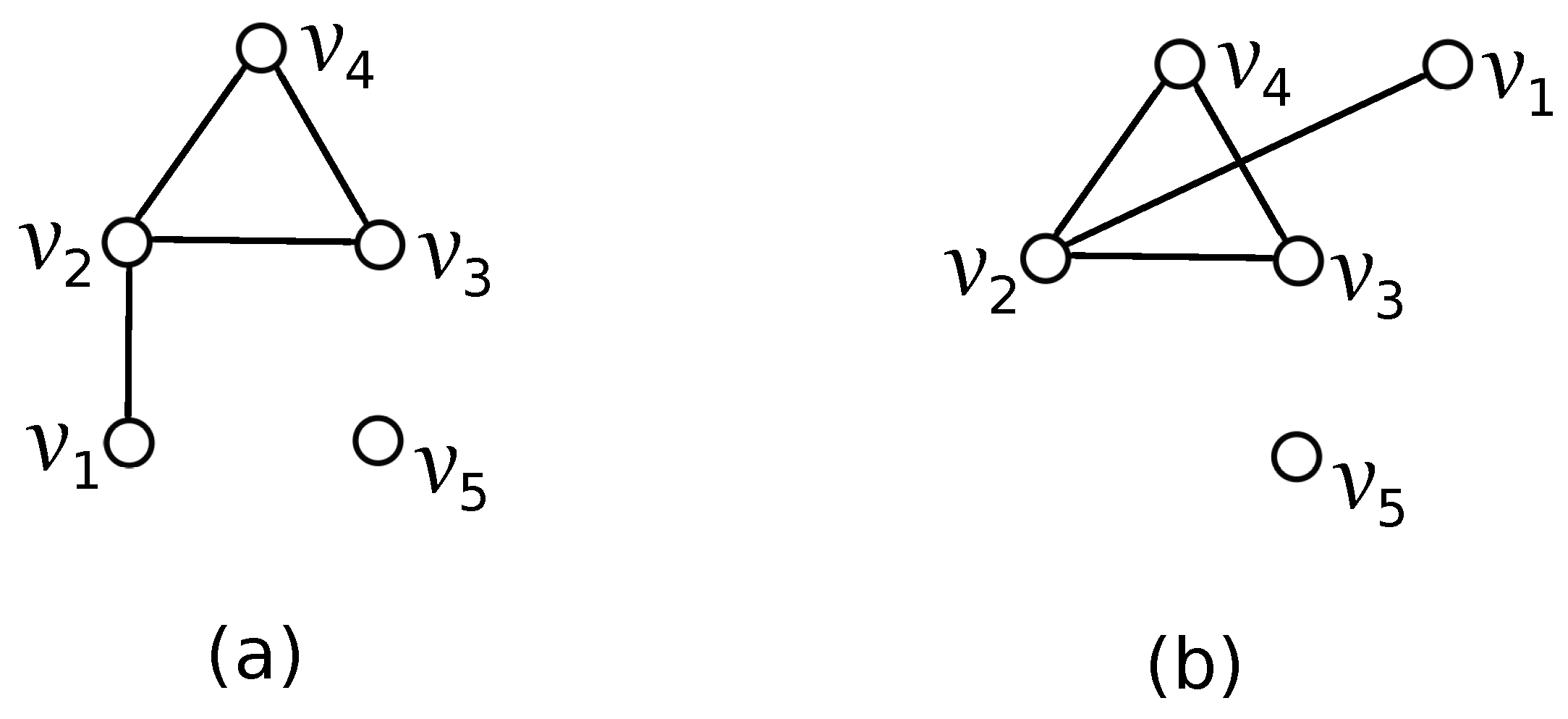
G do not cross each other. In this case, without loss of generality, we can choose the vertex notation of the graph in such a way as shown in
Figure 1a. Our aim is to list all possible rotations
that can appear in
D if the edges of
do not cross the edges of
G. Since there is only one subdrawing of
represented by the rotation
, there are two possibilities for how to obtain the subdrawing of
depending on in which region the edge
is placed. Of course, the vertex
can be placed in one of four regions of the subdrawing
with the vertex
on their boundaries. These
possibilities under our consideration will be denoted by
and
, for
and
. The configuration is of type
A or
B in the considered drawing
D, if the vertex
is placed in the quadrangular or in the triangular region in the subdrawing
, respectively. As for our considerations, it does not play a role in which of the regions is unbounded; assume the drawings shown in
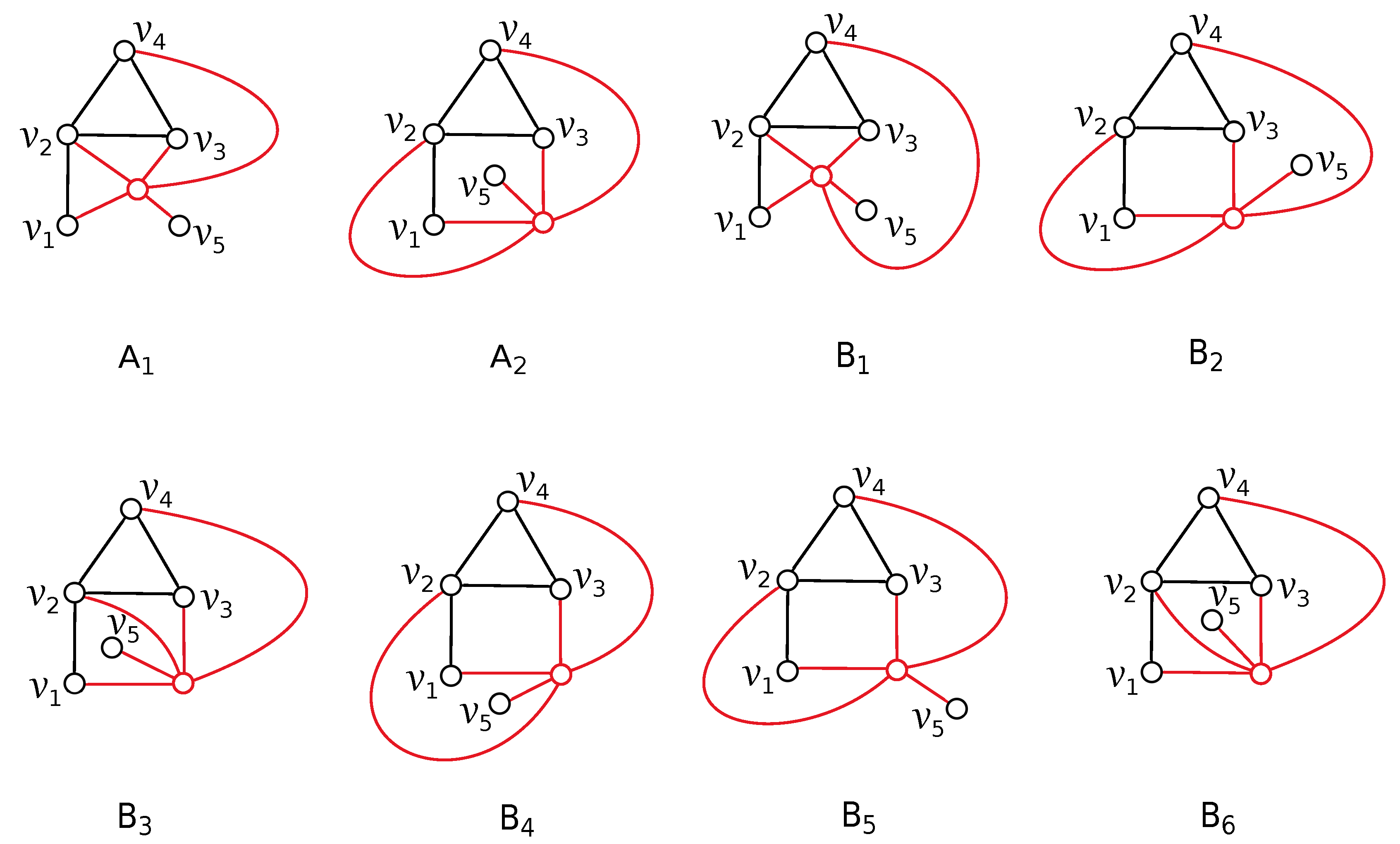
Figure 2. Thus, the configurations
,
,
,
,
,
,
, and
are represented by the cyclic permutations
,
,
,
,
,
,
, and
, respectively. In a fixed drawing of the graph
, some configurations from
need not appear. We denote by
the subset of
consisting of all configurations that exist in the drawing
D.
We remark that if two different subgraphs and with their configurations from cross in a considered drawing D of the graph , then the edges of are crossed only by the edges of . Let X, Y be the configurations from . We briefly denote by the number of crossings in D between and for two different such that , have configurations X, Y, respectively. Finally, let over all good drawings of the graph with . Our aim shall be to establish for all pairs .
The configurations
and
are represented by the cyclic permutations
and
, respectively. Since the minimum number of interchanges of adjacent elements of
required to produce cyclic permutation
is one, any subgraph
with the configuration
of
crosses the edges of
at least once, i.e.,
. Details have been worked out by Woodall [
16]. The same reason gives
,
,
,
,
,
,
, and
for
. Moreover, by a discussion of possible subdrawings, we can verify that
,
,
, and
. Let
be the subgraph having the configuration
, and let
be a subgraph from
with
. Using Woodall’s result
for some nonnegative integer
k, let us also suppose that
. Of course, any subgraph
having the configuration
or
satisfies the mentioned condition. One can easily see that if
, then
. If
and
, then the subdrawing
induced by the edges incident with the vertices
and
crosses the edges of
exactly once, and once, respectively. Thus,
, i.e., the subgraph
has the configuration
. This forces
and
. Similar arguments are applied for
and
. Clearly, also
and
for any
and
. Thus, all lower bounds of the number of crossing of configurations from
are summarized in the symmetric
Table 1 (here,
and
are configurations of the subgraphs
and
, where
are integers from
or
, and
).
Assume a good drawing
D of the graph
with one crossing among edges of the graph
G (in which there is a subgraph
). In this case, without loss of generality, we can choose also the vertex notations of the graph in such a way as shown in
Figure 1b. Since there is only one subdrawing of
represented by the rotation
, we have four possibilities for how to obtain the subdrawing of
depending on in which region the vertex
is placed. Thus, there are four different possible configurations of the subgraph
denoted as
,
,
, and
, with the corresponding rotations
,
,
, and
, respectively. We denote by
the subset of
consisting of all configurations that exist in the drawing
D. The same way as above can be applied for the verification of the lower bounds of the number of crossings of two different configurations from
. Thus, all lower bounds of the numbers of crossings of two configurations from
are summarized in the symmetric
Table 2 (here,
and
are configurations of the subgraphs
and
, where
).
3. The Graph of Configurations
In general, the low possible number of crossings between two different subgraphs in a good subdrawing of
is one of the main problems in the proofs on the crossing number of the join of the graph
G with the discrete graphs
. The lower bounds of the numbers of crossings between two subgraphs, which do not cross the edges of
G, were summarized in the symmetric
Table 1. Since some configurations from the set
need not appear in the fixed drawing of
, we will first deal with the smallest possible values in
Table 1 as with the worst possible case in the mentioned proofs. Thus, a new graphical representation of
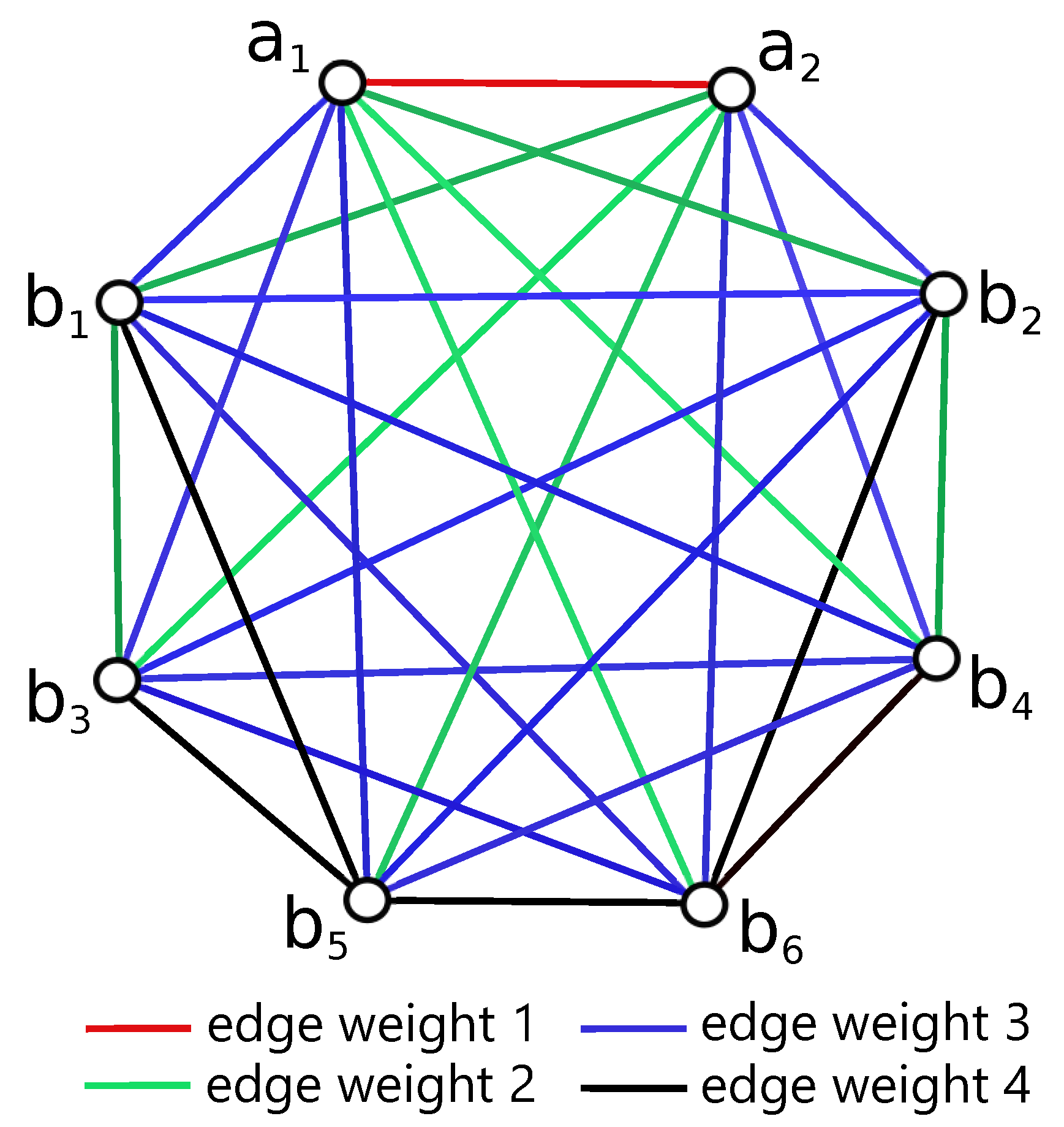
Table 1 by the graph of configurations will be useful.
Let us suppose that
D is a good drawing of the graph
with
, and let
be the nonempty set of all configurations that exist in the drawing
D belonging to the set
. A graph of configurations
is an ordered triple
, where
is the set of vertices,
is the set of edges, which is formed by all unordered pairs of distinct vertices, and a weight function
that associates with each edge of
an unordered pair of two vertices of
. The vertex
for some
if the corresponding configuration
for some
, where
or
. The edge
if
and
are two different vertices of the graph
. Finally,
for the edge
, if
m is the associated lower bound between two different configurations
, and
in
Table 1. Of course,
is the simple undirected edge-weighted graph uniquely determined by the drawing
D. Moreover, if we define the graph
in the same way over the set
, then
is the subgraph of
induced by
for the considered drawing
D. Since the graph
can be represented like the edge-weighted complete graph
, it will be more transparent to follow the subcases in the proof of the main theorem; see
Figure 3.
4. The Crossing Number of
Two vertices and of are antipodal in a drawing of if the subgraphs and do not cross. A drawing is antipodal-free if it has no antipodal vertices. In the rest of the paper, each considered drawing of the graph will be assumed antipodal-free. In the proof of the main theorem, the following lemma related to some restricted subdrawings of the graph is helpful.
Lemma 1. Let D be a good and antipodal-free drawing of , . If are different subgraphs such that , have different configurations from any of the sets , , , and , then: Proof of Lemma 1. Let us suppose the configuration
of the subgraph
, and note that it is exactly represented by
. The unique drawing of the subgraph
contains four regions with the vertex
on their boundaries (
Figure 2). If there is a
with
, then one can easily see that
. Of course, the edge
must cross one edge of the graph
G. If
crosses the edge
, then the subgraph
is represented by
. If the edge
crosses the edge
, then there are only three possibilities for the considered subdrawing of
, i.e., the subgraph
can be represented by three possible cyclic permutations
,
, or
.
For the remaining configurations , , , , and of , using the same arguments, one can easily verify that the rotations of the vertex are from the sets , , , , and , respectively. This forces that there is no subgraph with , where the subgraph has the configuration or . The same reason is given for the case of with the configurations and . Finally, for any . This completes the proof. □
We have to emphasize that we cannot generalize Lemma 1 for all pairs of different configurations from . Let us assume the configurations of and of . For , the reader can easily find a subdrawing of in which . The same remark holds for pairs with , with , and with .
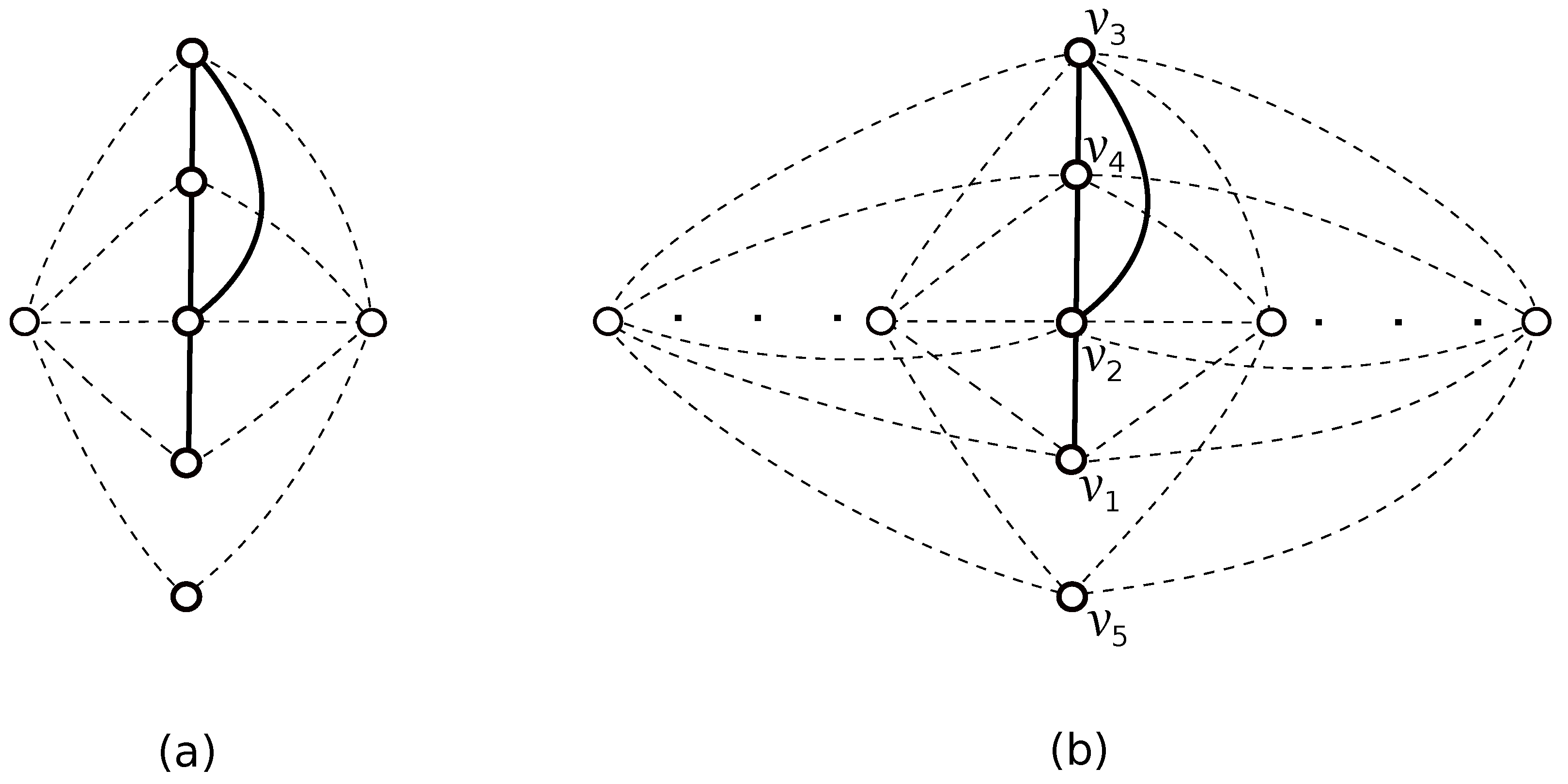
Theorem 1. for .
Proof of Theorem 1. The drawing in
Figure 4b shows that
. We prove the reverse inequality by contradiction. The graph
is planar; hence,
. Since the graph
contains a subdivision of the complete bipartite graph
, we have
. Thus,
by the good drawing of
in
Figure 4a. Suppose now that for
, there is a drawing
D with:
and let
Let us first show that the considered drawing
D must be antipodal-free. As a contradiction, suppose that, without loss of generality,
. Using positive values in
Table 1 and
Table 2, one can easily verify that both subgraphs
and
are not from the set
, i.e.,
. The known fact that
implies that any
,
, crosses the edges of the subgraph
at least four times. Therefore, for the number of crossings in the considered drawing
D, we have:
This contradiction with the assumption (
2) confirms that
D must be an antipodal-free drawing. Moreover, if
and
, the assumption (
3) together with the well-known fact
imply that in
D, there are at least
subgraphs
, which do not cross the edges of
G. More precisely:
i.e.,
This forces that , and . Now, for , we will discuss the existence of possible configurations of subgraphs in the drawing D.
Case 1.
. Without loss of generality, we can choose the vertex notation of the graph
G in such a way as shown in
Figure 1a. Thus, we will deal with the configurations belonging to the nonempty set
. According to the minimum value of the weights of edges in the graph
, we will fix one, or two, or three subgraphs with a contradiction with the condition (
2) in the following subcases:
- i.
, i.e.,
. Without loss of generality, let us consider two different subgraphs
such that
and
have configurations
and
, respectively. Then,
for any
with
by summing the values in all columns in the considered two rows of
Table 1. Moreover,
for any subgraph
with
due to the properties of the cyclic permutations. Hence, by fixing the graph
,
- ii.
, i.e., for any .
Let us assume that
or
, i.e., there is a three-cycle in the graph
with weights of two of all its edges. Without loss of generality, let us consider three different subgraphs
such that
,
m and
have different configurations from
. Then,
for any
with
by
Table 1, and
for any subgraph
by Lemma 1. Thus, by fixing the graph
,
In the next part, let us suppose that and ,
- (1)
for some
or
, where
. Without loss of generality, let us consider two different subgraphs
such that
and
have configurations
and
, respectively. Then,
for any
with
by
Table 1. Moreover,
for any subgraph
with
due to properties of the cyclic permutations. Hence, if we fix the graph
,
- (2)
for any
and
, where
, i.e.,
for any
. Without loss of generality, we can assume that
. Then,
for any
with
. Thus, by fixing the graph
,
Case 2.
. Without loss of generality, we can choose the vertex notation of the graph
G in such a way as shown in
Figure 1b. Thus, we will deal with the configurations belonging to the nonempty set
in the following two cases:
- i.
for some
. Without loss of generality, let us consider two different subgraphs
such that
and
have different configurations from the set
. Then,
for any
with
by
Table 2. Moreover,
for any subgraph
with
due to the properties of the cyclic permutations. Hence, by fixing the graph
,
If and have different configurations from the set , then the same argument can be applied.
- ii.
for any
. Without loss of generality, we can assume that
. Then,
for any
with
. Thus, by fixing the graph
,
Thus, it was shown that there is no good drawing D of the graph with less than crossings. This completes the proof of Theorem 1. □