Edge Even Graceful Labeling of Polar Grid Graphs

Abstract

Edge Even Graceful Labelingwas first defined byElsonbaty and Daoud in 2017. An edge even graceful labeling of a simple graph $G$ with $p$ vertices and $q$ edges is a bijection $f$ from the edges of the graph to the set $\{2,4,\dots ,2q\}$ such that, when each vertex is assigned the sum of all edges incident to it $\mathrm{mod}2r$ where $r=\max \{p,q\}$, the resulting vertex labels are distinct. In this paper we proved necessary and sufficient conditions for the polar grid graph to be edge even graceful graph.

1. Introduction

The field of Graph Theory plays an important role in various areas of pure and applied sciences. One of the important areas in graph theory is Graph Labeling of a graph $G$ which is an assignment of integers either to the vertices or edges or both subject to certain conditions. Graph labeling is a very powerful tool that eventually makes things in different fields very ease to be handled in mathematical way. Nowadays graph labeling has much attention from different brilliant researches ingraph theory which has rigorous applications in many disciplines, e.g., communication networks, coding theory, x-raycrystallography, radar, astronomy, circuit design, communication network addressing, data base management and graph decomposition problems. More interesting applications of graph labeling can be found in [1,2,3,4,5,6,7,8,9,10].

Let $G=(V(G),E(G))$ with $p=\left|V(G)\right|$ and $q=\left|E(G)\right|$ be a simple, connected, finite, undirected graph.

A function $f$ is called a graceful labeling of a graph G if $f:V(G)\to \{0,1,2,\dots ,q\}$ is injective and the induced function $f^{\ast }:E(G)\to \{1,2,\dots ,q\}$ defined as $f^{\ast }(e=uv)=\left|f(u)-f(v)\right|$ is bijective. This type of graph labeling first introducedby Rosa in 1967 [11] as a $\beta -$ valuation, later on Solomon W. Golomb [12] called as graceful labeling.

A function $f$ is called an odd graceful labeling of a graph G if $f:V(G)\to \{0,1,2,\dots ,2q-1\}$ is injective and the induced function $f^{\ast }:E(G)\to \{1,3,\dots ,2q-1\}$ defined as $f^{\ast }(e=uv)=\left|f(u)-f(v)\right|$ is bijective. This type of graph labeling first introducedby Gnanajothi in 1991 [13]. For more results on this type of labeling see [14,15].

A function $f$ is called an edge graceful labeling of a graph G if $f:E(G)\to \{1,2,\dots ,q\}$ is bijective and the induced function $f^{\ast }:V(G)\to \{0,1,2,\dots ,p-1\}$ defined as $f^{\ast }(u)={\displaystyle \sum _{e=uv\in E(G)}f(e)}\mathrm{mod}\hspace{0.17em}p$ is bijective. This type of graph labeling first introducedby Lo in 1985 [16]. For more results on this labeling see [17,18].

A function $f$ is called an edge odd graceful labeling of a graph G if $f:E(G)\to \{1,3,\dots ,2q-1\}$ is bijective and the induced function $f^{\ast }:V(G)\to \{0,1,2,\dots ,2q-1\}$ defined as $f^{\ast }(u)={\displaystyle \sum _{e=uv\in E(G)}f(e)}\mathrm{mod}2q$ is injective. This type of graph labeling first introducedby Solairaju and Chithra in 2009 [19]. See also Daoud [20].

A function $f$ is called an edge even graceful labeling of a graph $G$ if $f:E(G)\to \{2,4,\dots ,2q\}$ is bijective and the induced function $f^{\ast }:V(G)\to \{0,2,4,\dots ,2q-2\}$ defined as $f^{\ast }(u)={\displaystyle \sum _{e=uv\in E(G)}f(e)}\mathrm{mod}2r,$ where $r=\max \{p,q\}$ is injective. This type of graph labeling first introduced by Elsonbaty and Daoud in 2017 [21].

For a summary of the results on these five types of graceful labels as well as all known labels so far, see [22].

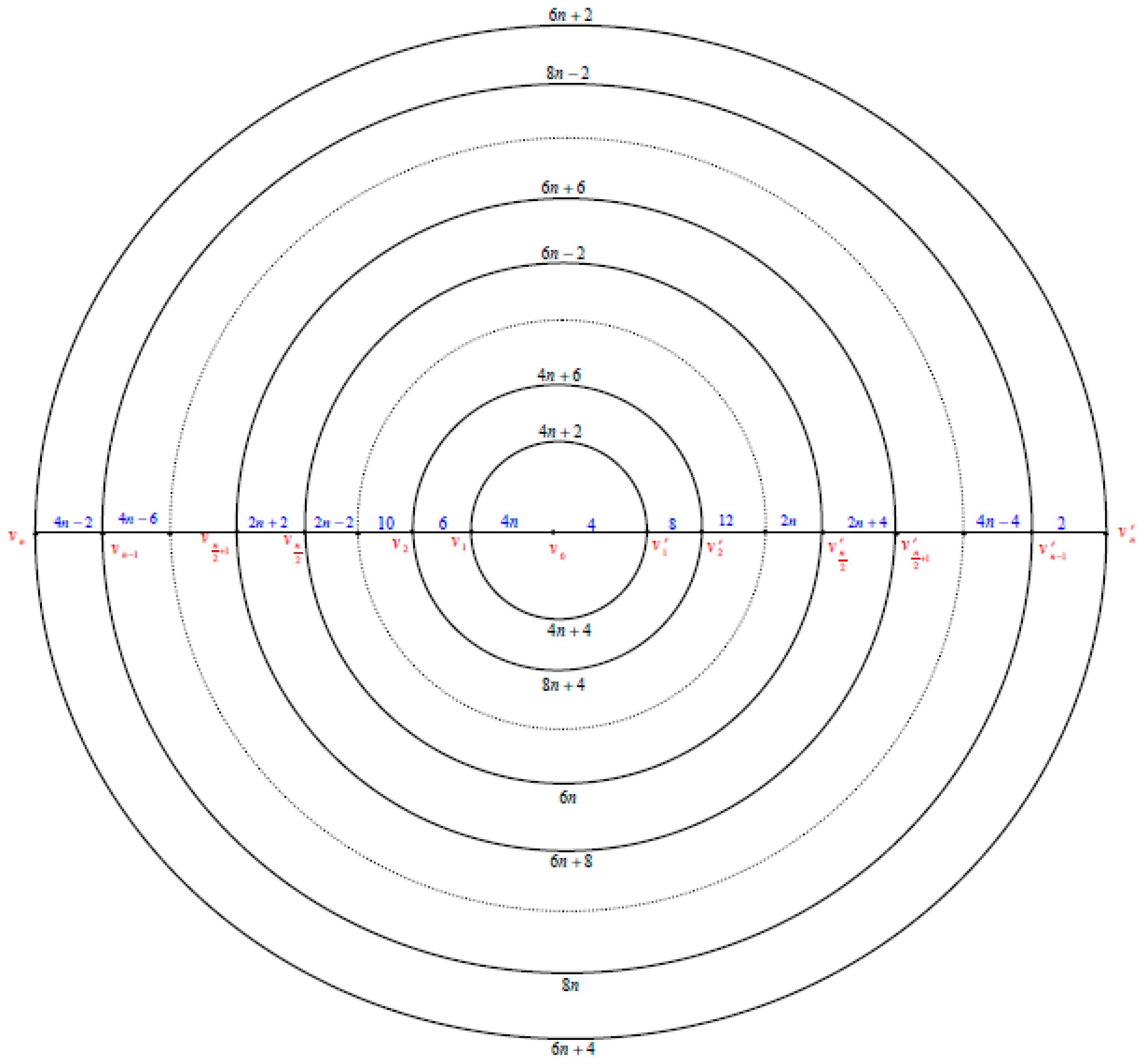
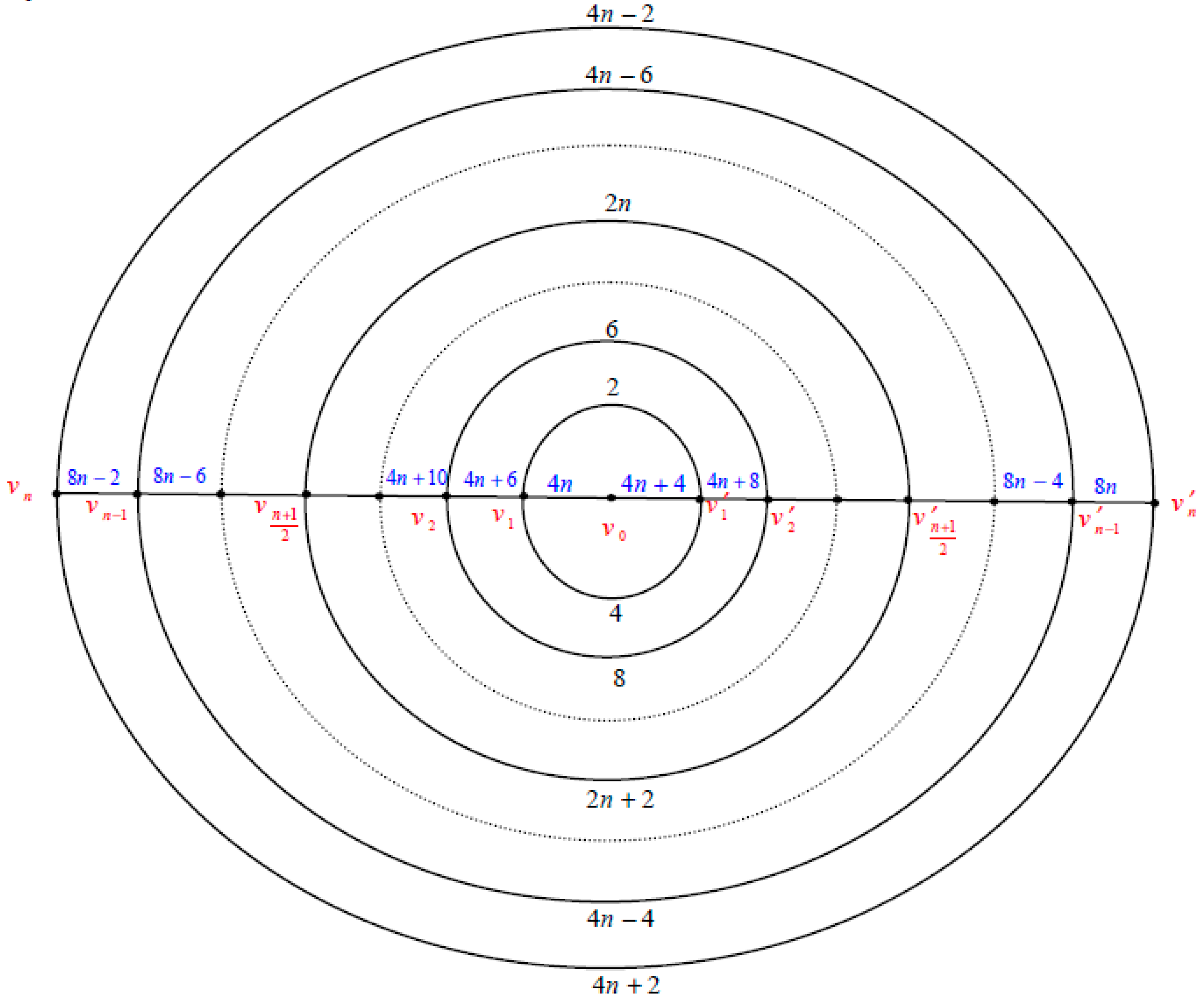
2. Polar Grid Graph $P_{m,n}$

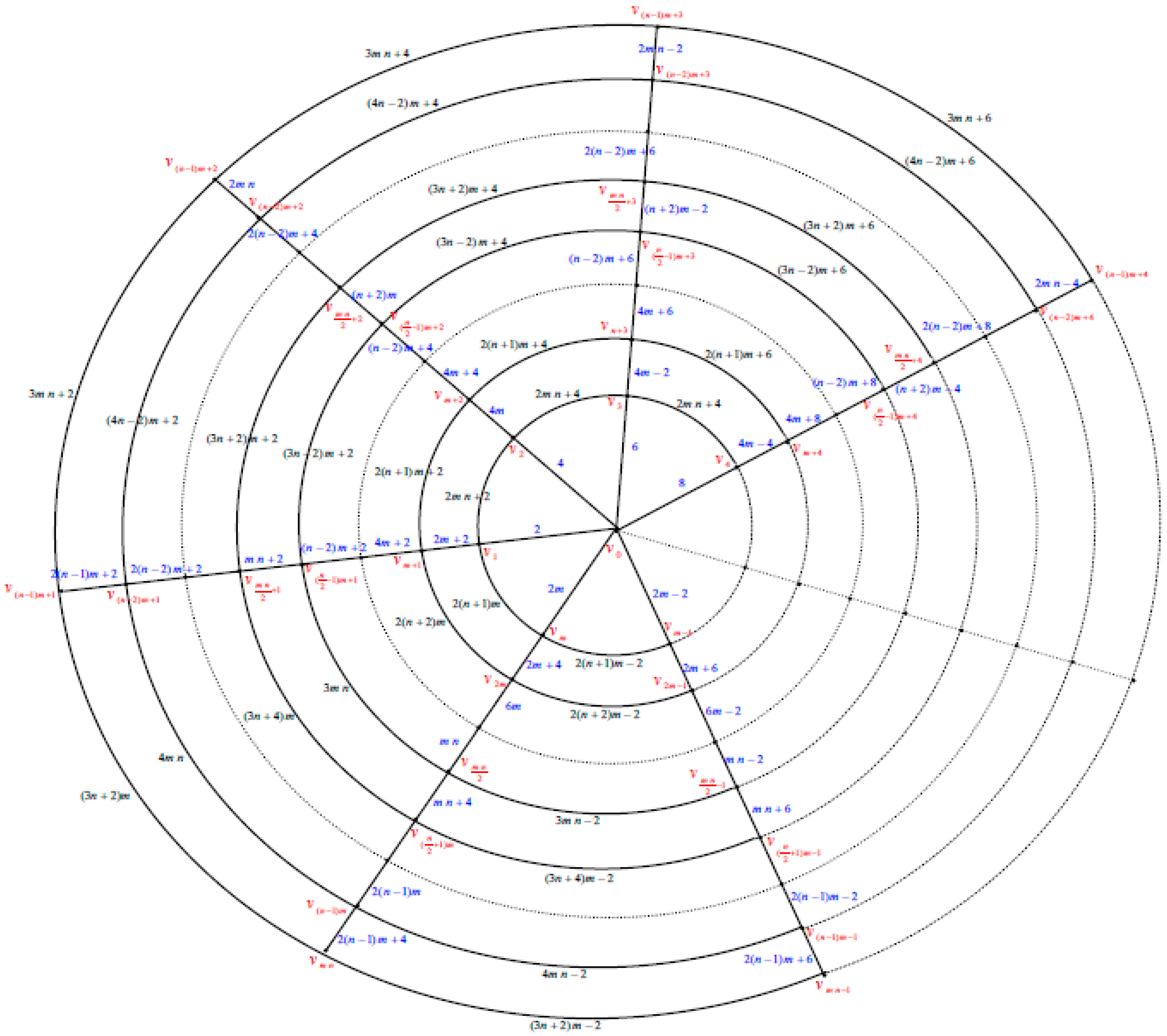
The polargrid graph $P_{m,n}$ is the graph consists of $n$ copies of circles $C_m$ which will be numbered from the inner most circle to the outer circle as $C_m^{(1)},\hspace{0.17em}{C}_m^{(2)},\dots ,\hspace{0.17em}{C}_m^{(n-1)},\hspace{0.17em}{C}_m^{(n)}$ and $m$ copies of paths $P_{n+1}$ intersected at the center vertex $v_0$ which will be numbered as $P_{n+1}^{(1)},\hspace{0.17em}{P}_{n+1}^{(2)},\dots ,\hspace{0.17em}{P}_{n+1}^{(m-1)},\hspace{0.17em}{P}_{n+1}^{(m)}$. See Figure 1.

Figure 1. Polar grid graph $P_{m,n}$.

Theorem 1.

If m and n are even positive integes such that $m\ge 4$ and $n\ge 2$, then the polar grid graph $P_{m,n}$ is an edge even graceful graph.

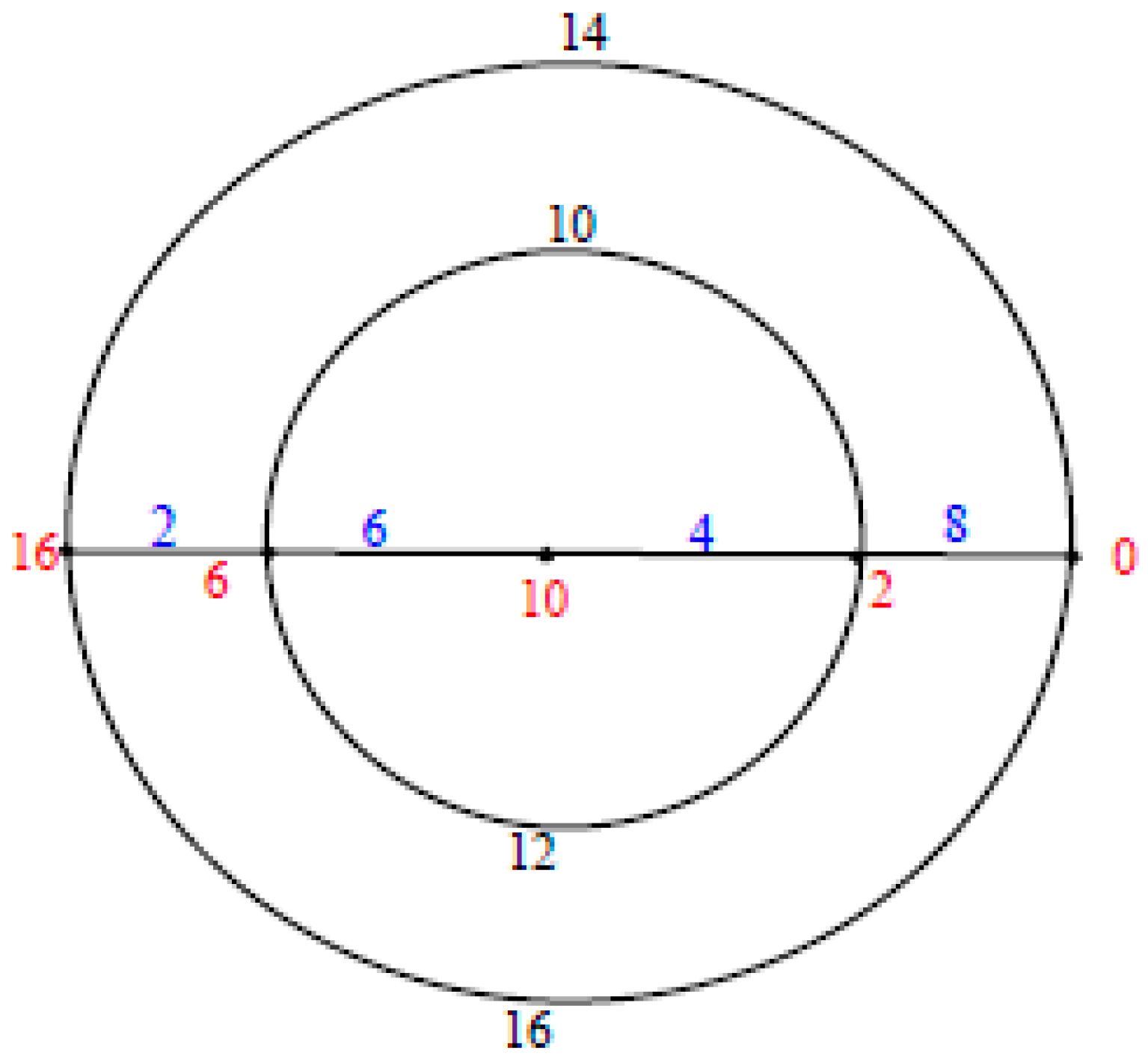
Proof. 

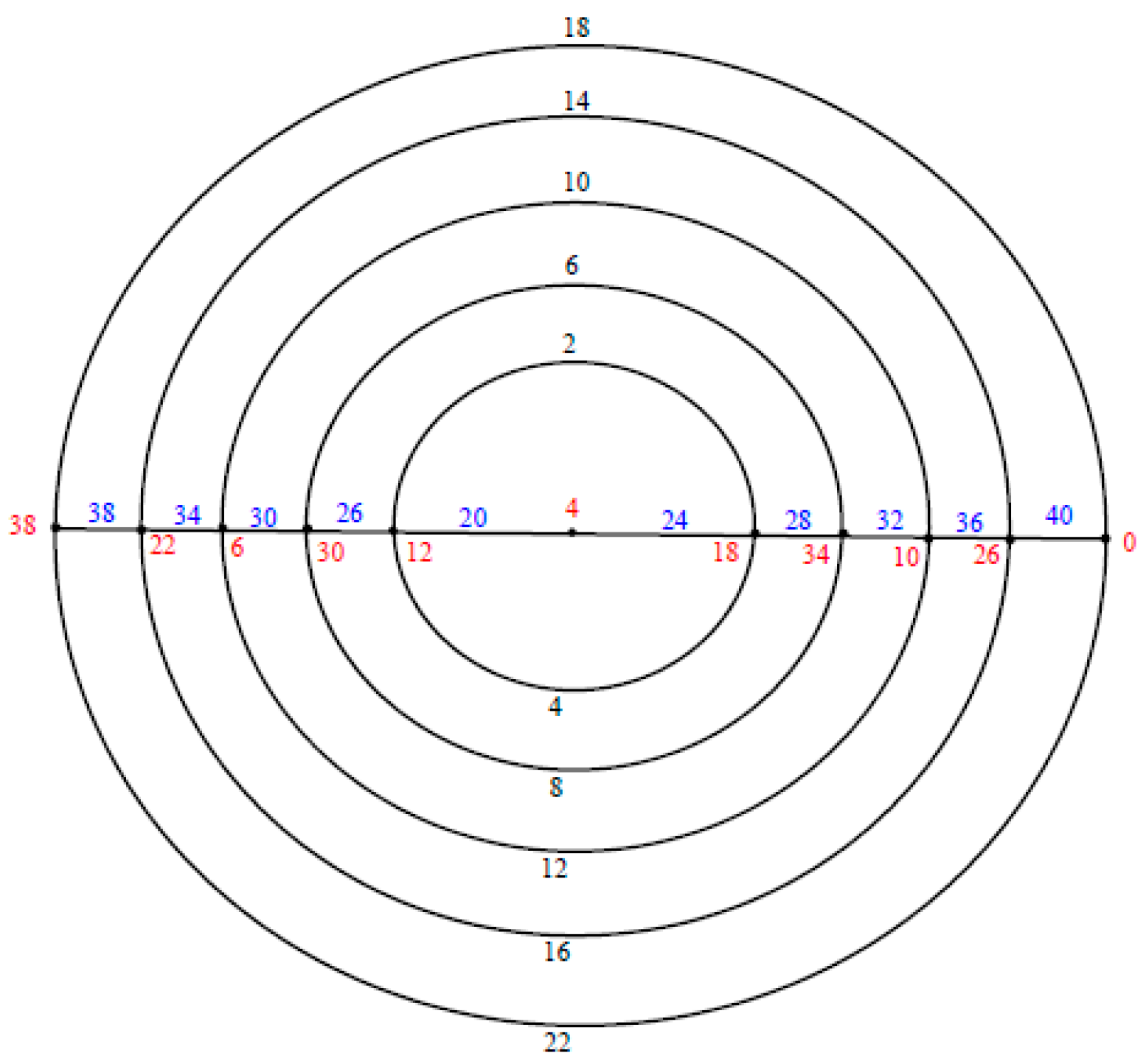
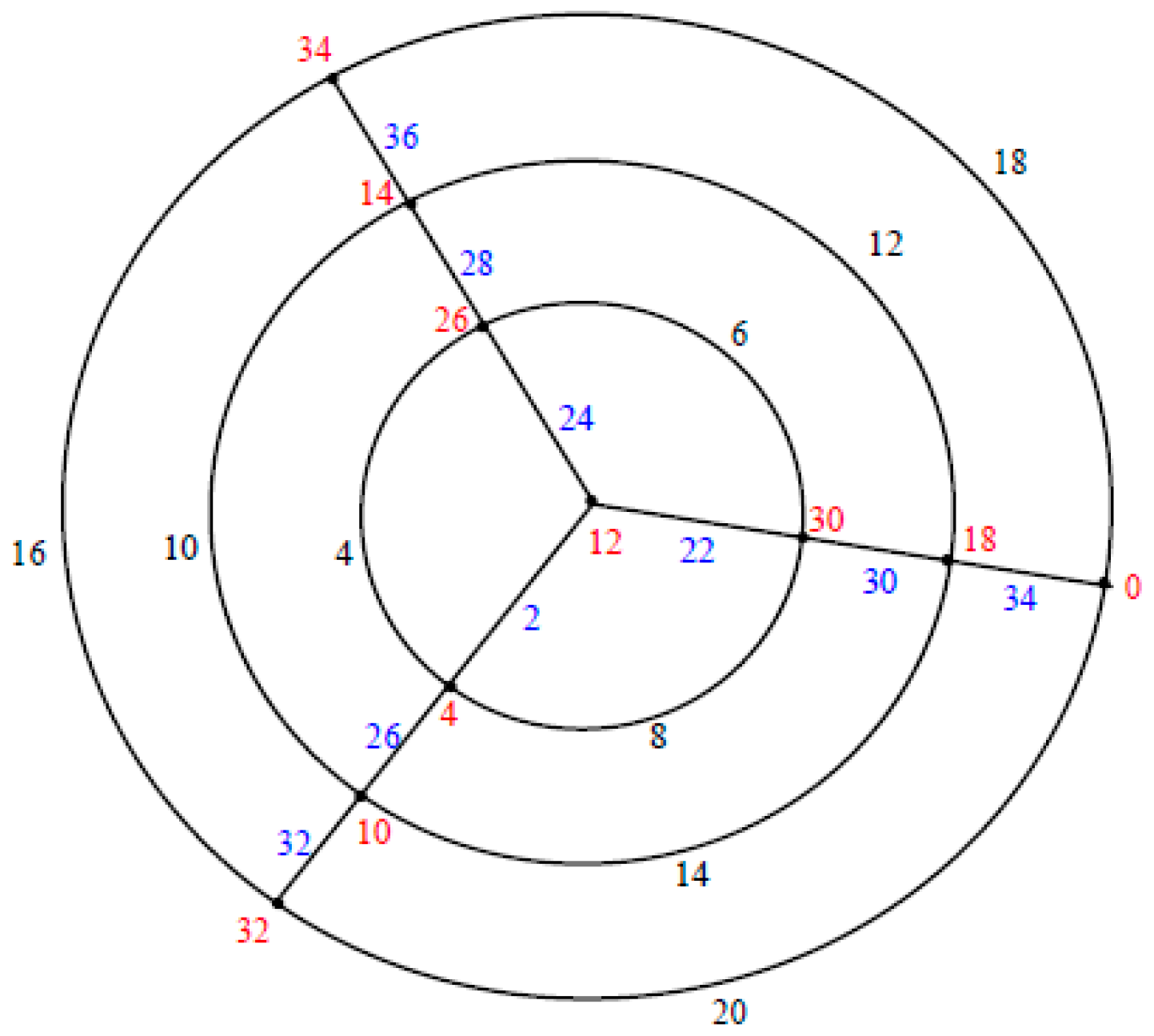
Using standard notation $p=\left|V(P_{m,n})\right|\hspace{0.17em}=mn+1,\hspace{0.17em}q=\left|E(P_{m,n})\right|=2mn$ and $r=\max \{p,q\}=2mn$ Let the polar grid graph $P_{m,n}$ be labeled as in Figure 2. Let $f:E(G)\to \{2,4,\dots ,2q\}.$ □

Figure 2. Labeling ofthe polar grid graph $P_{m,n}$ when n is even, $n\ge 2$.

First we label the edges of paths $P_{n+1}^{(k)},\hspace{0.17em}\le k\le m$ begin with the edges of the path $P_{n+1}^{(1)}$ to the edges of the path $P_{n+1}^{(m)}$ as follows: Move clockwise to label the edges $v_0{v}_1,\hspace{0.17em}{v}_0{v}_2,\hspace{0.17em}\dots ,\hspace{0.17em}{v}_0{v}_{m-1},v_0{v}_m$ by $2,\hspace{0.17em}4,\hspace{0.17em}\dots ,\hspace{0.17em}2m-2,\hspace{0.17em}2m,$ then move anticlockwise to label the edges $v_1{v}_{m+1},v_m{v}_{2m},v_{m-1}{v}_{2m-1},\hspace{0.17em}\dots ,\hspace{0.17em}{v}_3{v}_{m+3},v_2{v}_{m+2}$ by $2m+2,\hspace{0.17em}2m+4,\hspace{0.17em}2m+6,\hspace{0.17em}\dots ,\hspace{0.17em}4m-2,\hspace{0.17em}4m,$ then move clockwise to label the edges $v_{m+1}{v}_{2m+1},v_{m+2}{v}_{2m+2},v_{m+3}{v}_{2m+3},\hspace{0.17em}\dots ,\hspace{0.17em}{v}_{2m-1}{v}_{3m-1},v_m{v}_{3m}$ by $4m+2,\hspace{0.17em}4m+4,\hspace{0.17em}4m+6,\hspace{0.17em}\dots ,\hspace{0.17em}6m-2,\hspace{0.17em}6m$ and so on. Finally move anticlockwise to label the edges $v_{m(n-2)+1}{v}_{m(n-1)+1},\hspace{0.17em}{v}_{m(n-1)-1}{v}_{mn},v_{m(n-1)-1}{v}_{mn-1},\hspace{0.17em}\dots ,\hspace{0.17em}{v}_{m(n-2)+2}{v}_{m(n-1)+2}$ by $2m(n-1)+2,\hspace{0.17em}2m(n-1)+4,$ $2m(n-1)+6,\hspace{0.17em}\dots ,\hspace{0.17em}2mn-2,\hspace{0.17em}2mn$. Second we label the edges of the circles $C_m^{(k)},1\le k\le n$ begin with the edges of the inner most circle $C_m^{(1)}$ to the edges of the circle $C_m^{(\frac{n}{2})}$, then the edges of the outer circle $C_m^{(n)}.$ Finally the edges of circles $C_m^{(\frac{n}{2}+1)},\hspace{0.17em}{C}_m^{(\frac{n}{2}+2)},\hspace{0.17em}\dots ,\hspace{0.17em}{C}_m^{(n-1)}$ respectively as follows: $f(v_{m(k-1)+i}{v}_{m(k-1)+i+1})=2mn+2m(k-1)+2i,\hspace{0.17em}f(v_{km}{v}_{m(k-1)+1})=2mn+2mk,\hspace{0.17em}1\hspace{0.17em}\le i\le m-1,1\le k\le \frac{n}{2};$ $f(v_{m(n-1)+i}{v}_{m(n-1)+i+1})=3mn+2i,\hspace{0.17em}1\hspace{0.17em}\le i\le m-1;\hspace{0.17em}f(v_{km}{v}_{m(k-1)+1})=2mn+(2k+1)m,\hspace{0.17em}\frac{n}{2}+1\le k\le n-1$.

Now the corresponding labels of vertices $\mathrm{mod}4mn$ are assigned as follows:

Case (1) $m\equiv 4k\mathrm{mod}4n,\hspace{0.17em}1\le k\le n-1$ and $m=2\mathrm{mod}4n.$

The labels of the vertices of the inner most circle $C_m^{(1)}$ to the circle $C_m^{(\frac{n}{2})}$ are given by $f^{\ast }(v_{(k-1)m+i})\equiv 4m(2k-1)+4i,\hspace{0.17em}1\le k\le \frac{n}{2},1\le \hspace{0.17em}i\le m$, the labels of the vertices of the outre circle $C_m^{(n)}$ are given by $f^{\ast }(v_{(n-1)m+i})\equiv 2i\hspace{0.17em}+2,\hspace{0.17em}1\le \hspace{0.17em}i\le m$ and the labels of the vertices of the circles $C_m^{(\frac{n}{2}+1)},\hspace{0.17em}\dots ,\hspace{0.17em}{C}_m^{(n-1)}$ are given by $f^{\ast }(v_{(k-1)m+i})\equiv 8m(k-\frac{n}{2})+4i\hspace{0.17em}+2,\hspace{0.17em}1\le \hspace{0.17em}i\le m\hspace{0.17em},\frac{n}{2}+1\hspace{0.17em}\le k\le n-1$.

The label of the center vertex $v_0$ is assigned as follows: when $m=4k\mathrm{mod}4n,\hspace{0.17em}1\le k\le n-1$, $f^{\ast }(v_0)\equiv \frac{m}{2}(2m+2)=m^2+m$, since $m=4k\mathrm{mod}4n$ then $m=4nh+4k$, thus $f^{\ast }(v_0)=m(4k+1)$ and when $m=2\mathrm{mod}4n$, we have $f^{\ast }(v_0)=3m$.

Case (2) $m\equiv (8k-2)\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n}{2}$. In this case the vertex $v_{km-(\frac{m+2}{4})}$ in the circle $C_m^{(k)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{km-(\frac{m+2}{4})}{v}_{km-(\frac{m-2}{4})}$ and $v_{km-(\frac{m-2}{4})}{v}_{km-(\frac{m-6}{4})}$. That is $f(v_{km-(\frac{m+2}{4})}{v}_{km-(\frac{m-2}{4})})=2mn+m(2k-1)+\frac{m+2}{2}$ and $f(v_{km-(\frac{m-2}{4})}{v}_{km-(\frac{m-6}{4})})=2mn+m(2k-1)+\frac{m-2}{2}$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{km-(\frac{m+2}{4})})\equiv m(8k-1)+2,\hspace{0.17em}{f}^{\ast }(v_{km-(\frac{m-2}{4})})\equiv m(8k-1)+4,\hspace{0.17em}{f}^{\ast }(v_{km-(\frac{m-6}{4})})\equiv m(8k-1)+6$ and the label of the center vertex $v_0$ is assigened as $f^{\ast }(v_0)\equiv m(8k-1)$.The rest vertices are labeled as in case(1).

Case (3) $m\equiv (8k+2)\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n}{2}-1$. In this case the vertex $v_{km-(\frac{m+2}{2})}$ in the circle $C_m^{(\frac{n}{2}+k)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{km-(\frac{m+2}{2})}{v}_{km-(\frac{m}{2})}$ and $v_{km-(\frac{m}{2})}{v}_{km-(\frac{m-2}{2})}$. That is $f(v_{km-(\frac{m+2}{2})}{v}_{km-(\frac{m}{2})})=2mn+m(2k+1)+\frac{m+2}{2}$ and $f(v_{km-(\frac{m}{2})}{v}_{km-(\frac{m-2}{2})})=2mn+m(2k+1)+\frac{m-2}{2}$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{km-(\frac{m+2}{2})})\equiv m(8k+3)+2,\hspace{0.17em}{f}^{\ast }(v_{km-(\frac{m}{2})})\equiv m(8k+3)+4,\hspace{0.17em}{f}^{\ast }(v_{km-(\frac{m-2}{2})})\equiv m(8k+3)+6$ and the label of the center vertex $v_0$ is assigened $f^{\ast }(v_0)\equiv m(8k-29)$ as. The rest vertices are labeled as in case(1).

Case (4) $m\equiv 0\mathrm{mod}4n$. In this case the vertex $v_{mn-(\frac{m+2}{2})}$ in the outer circle will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{mn-(\frac{m+4}{2})}{v}_{mn-(\frac{m+2}{2})}$ and $v_{mn}{v}_{m(n-1)+1}$. That is $f(v_{mn-(\frac{m+4}{2})}{v}_{mn-(\frac{m+2}{2})})=m(3n+2)$ and $f(v_{mn}{v}_{m(n-1)+1})=3mn+m-4$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{mn-(\frac{m+4}{2})})\equiv 2m\hspace{0.17em}+2,\hspace{0.17em}{f}^{\ast }(v_{mn-(\frac{m+2}{2})})\equiv 2m\hspace{0.17em}+4,\hspace{0.17em}{f}^{\ast }(v_{mn})\equiv m\hspace{0.17em}-2$ and $f^{\ast }(v_{m(n-1)+1})\equiv 4mn-m$ and the label of the center vertex $v_0$ is assigened as $f^{\ast }(v_0)\equiv m$. The rest vertices are labeled as in case (1).

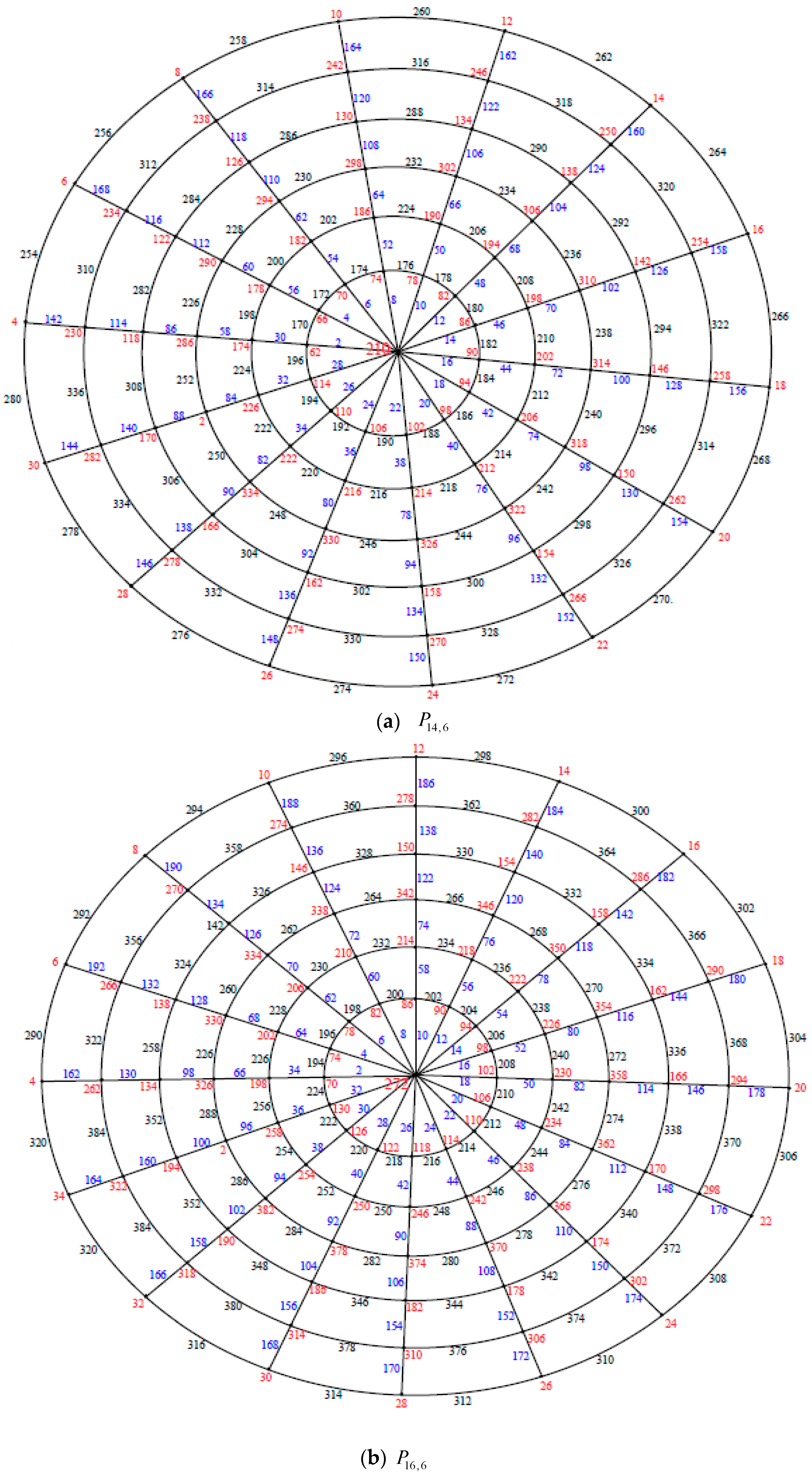
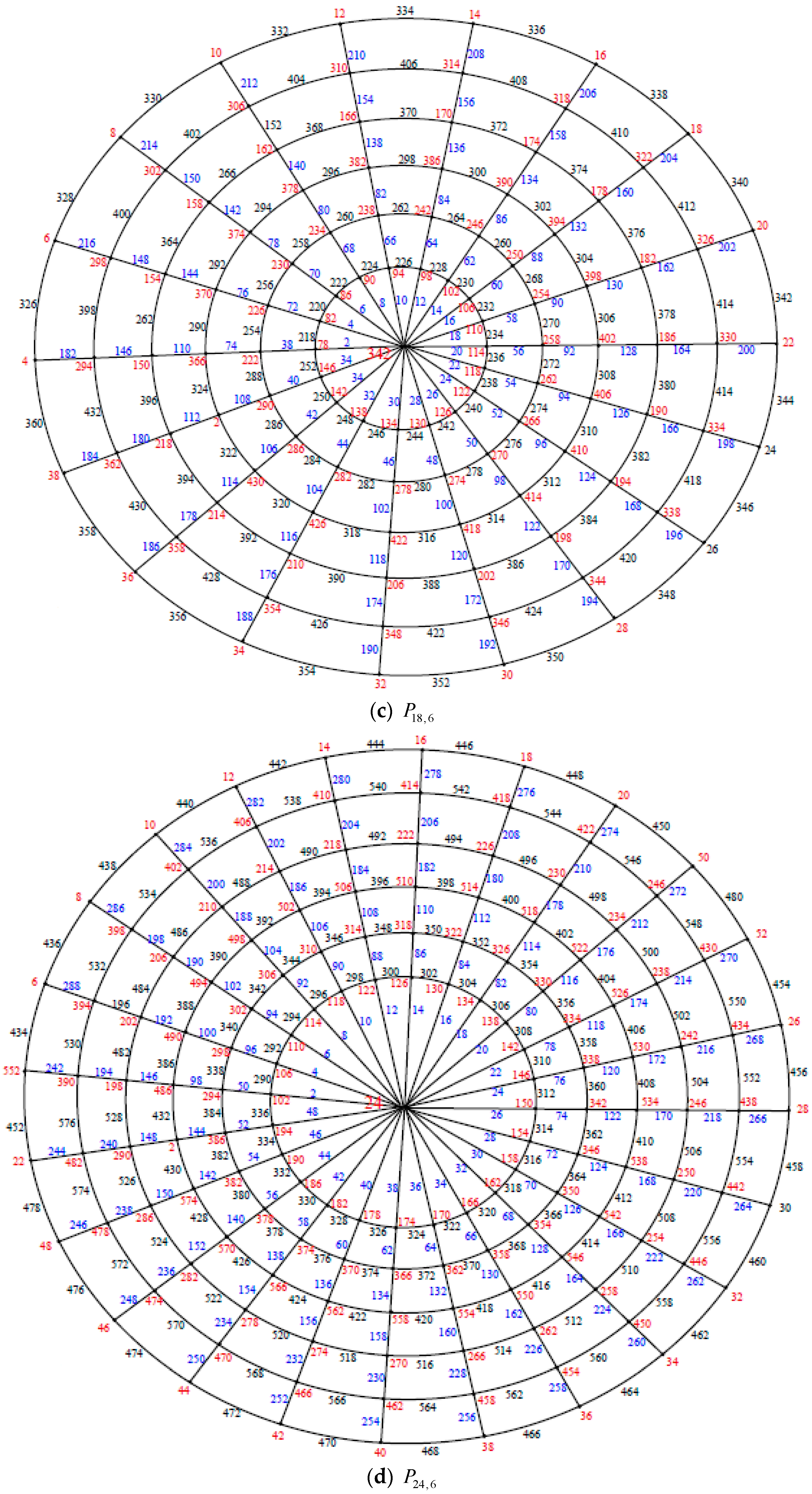
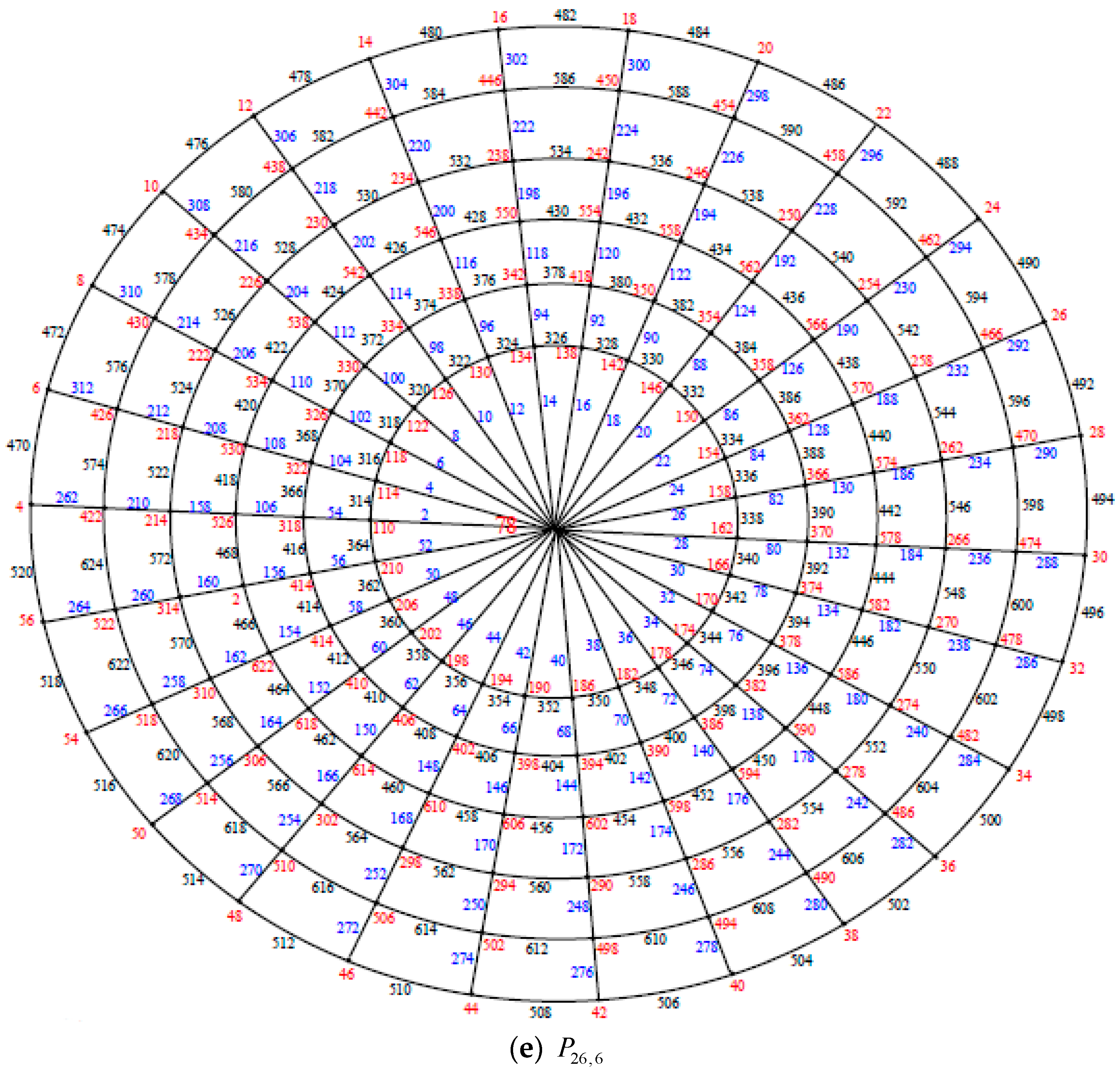
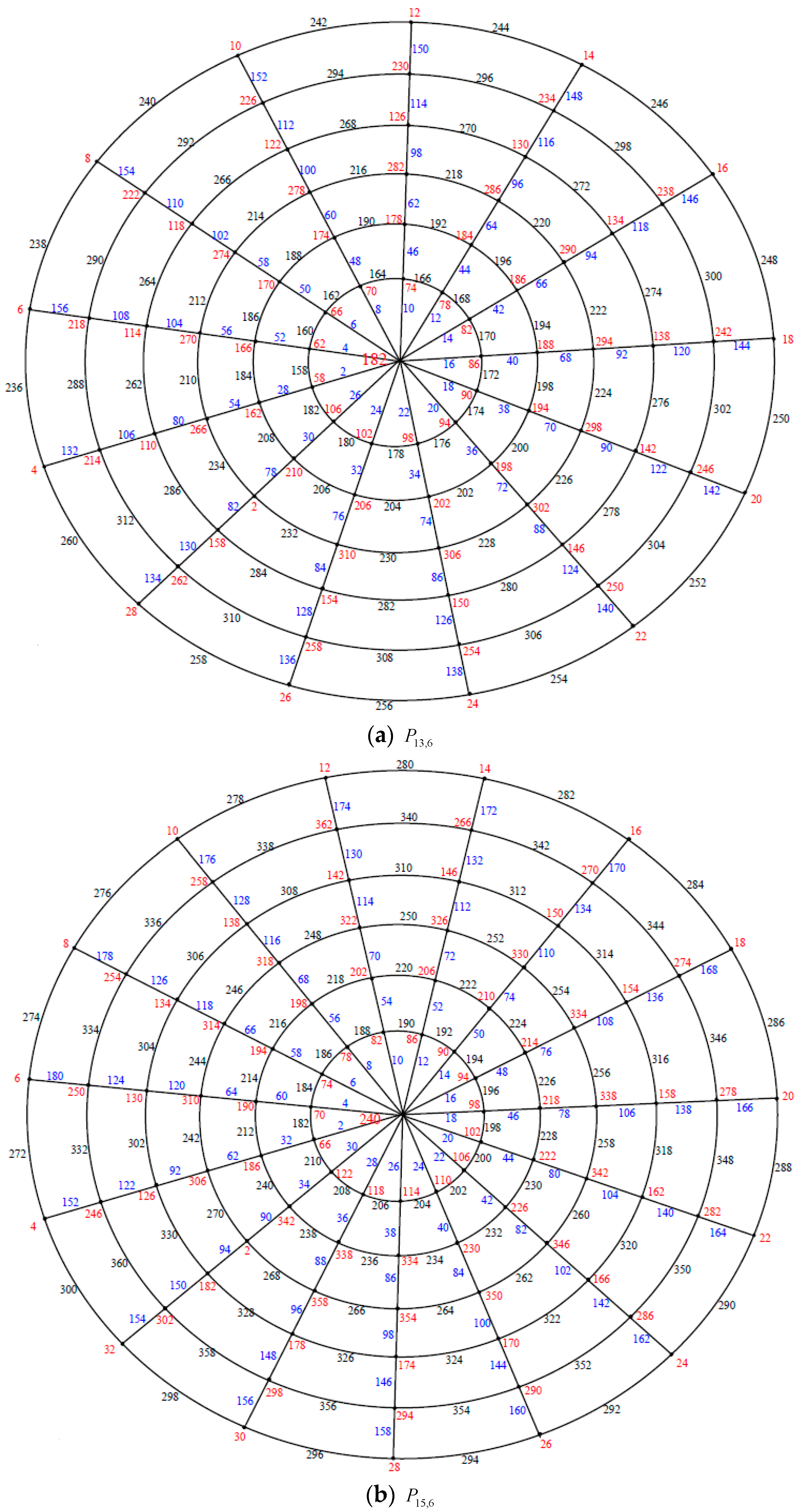
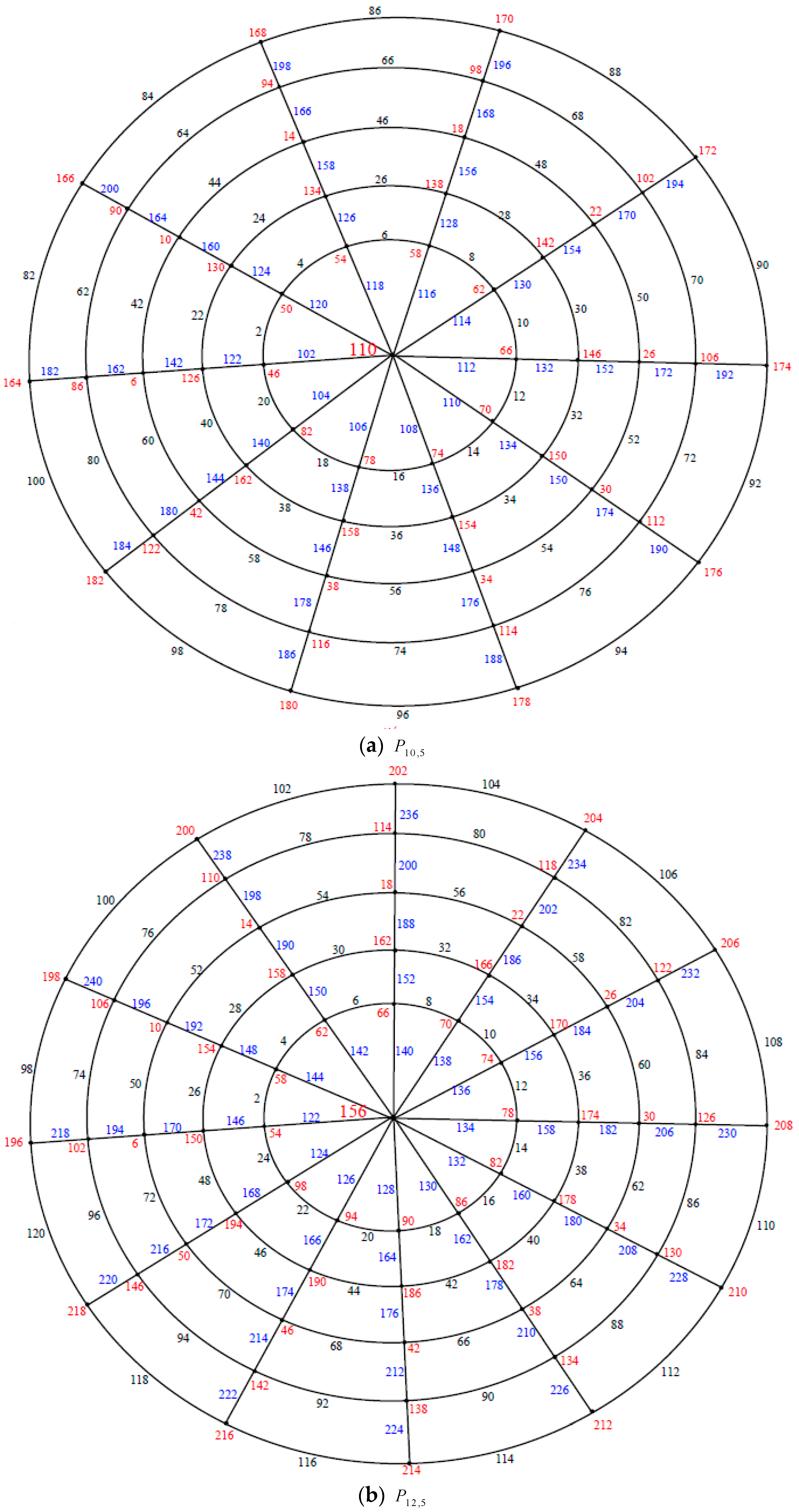
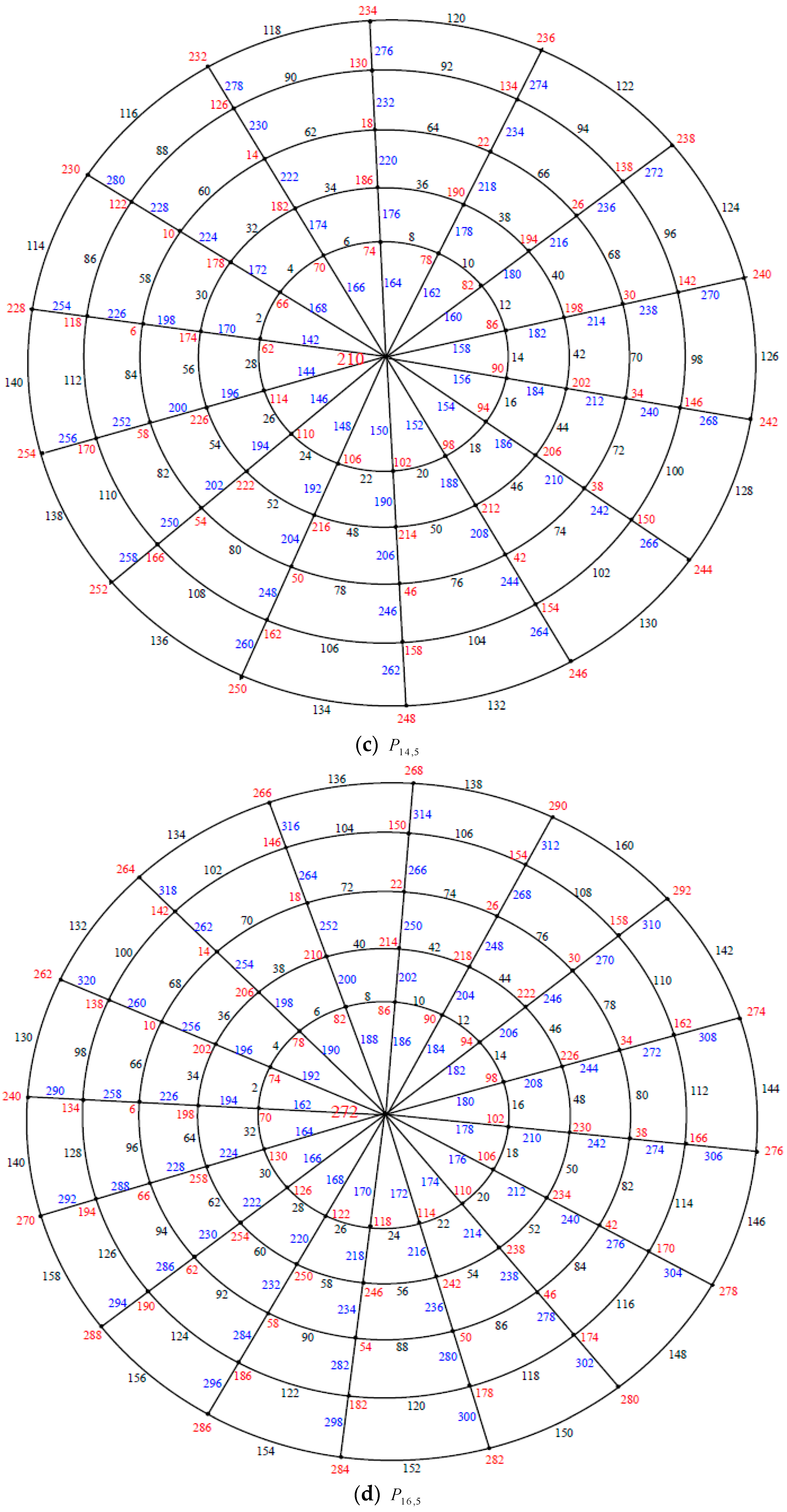
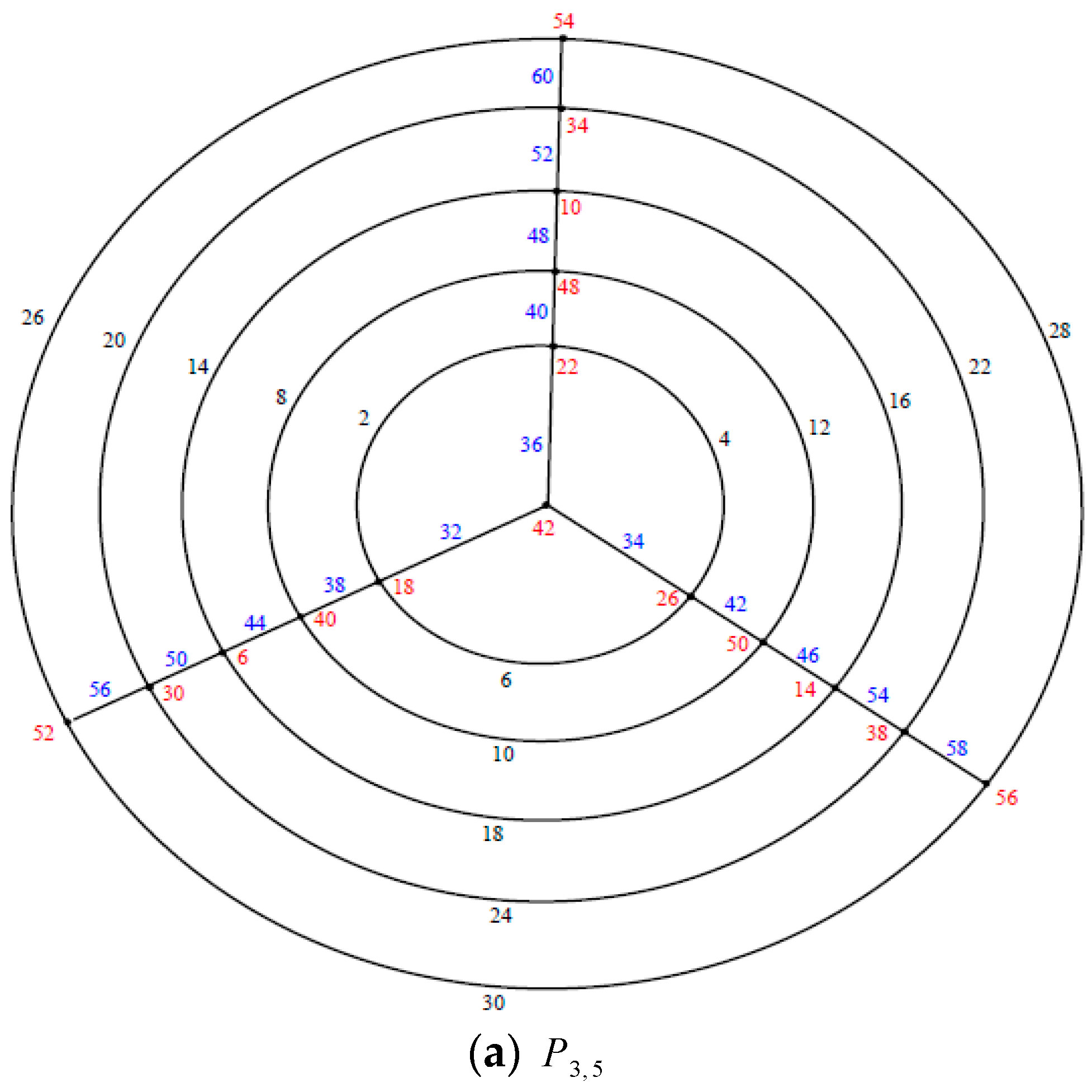
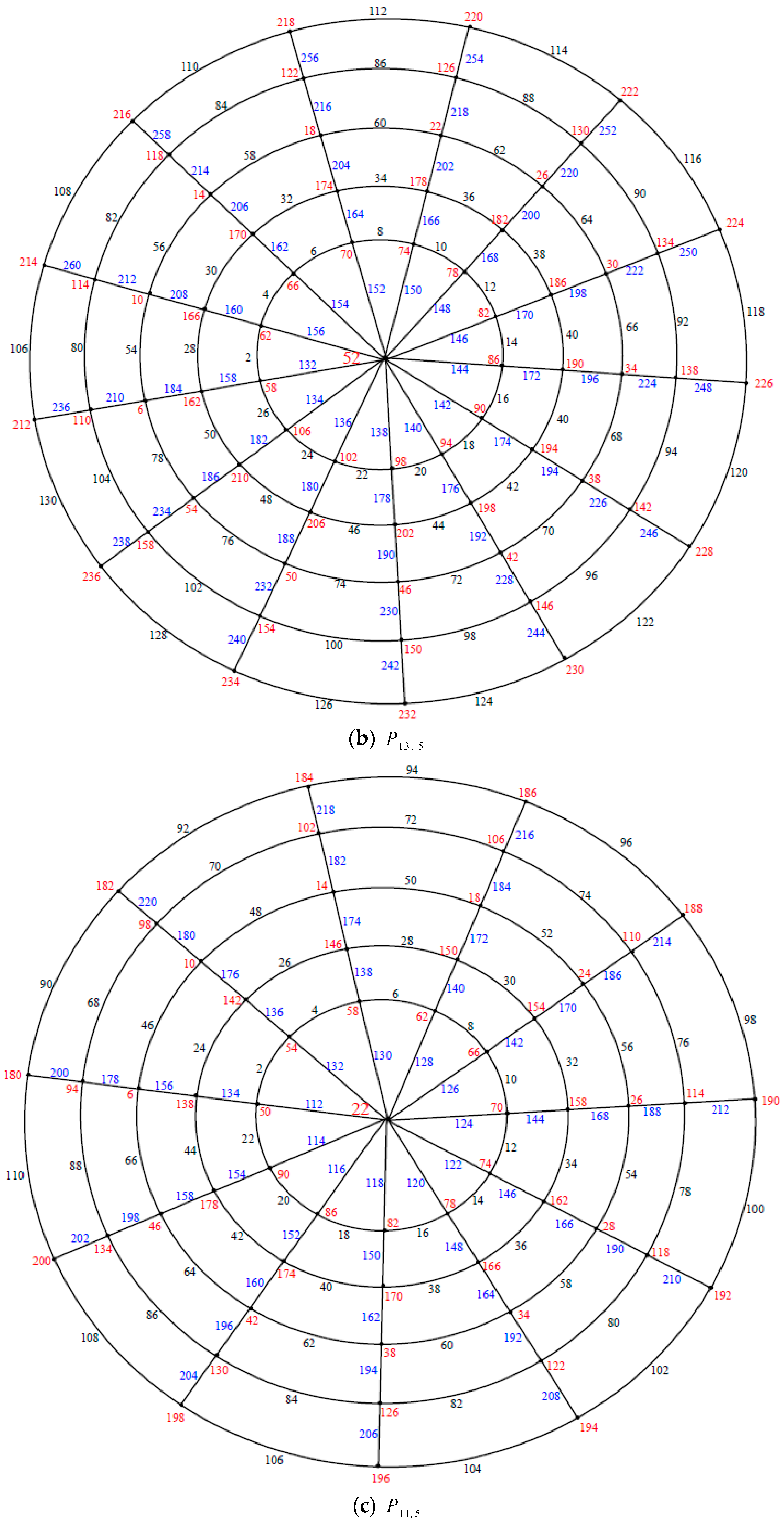
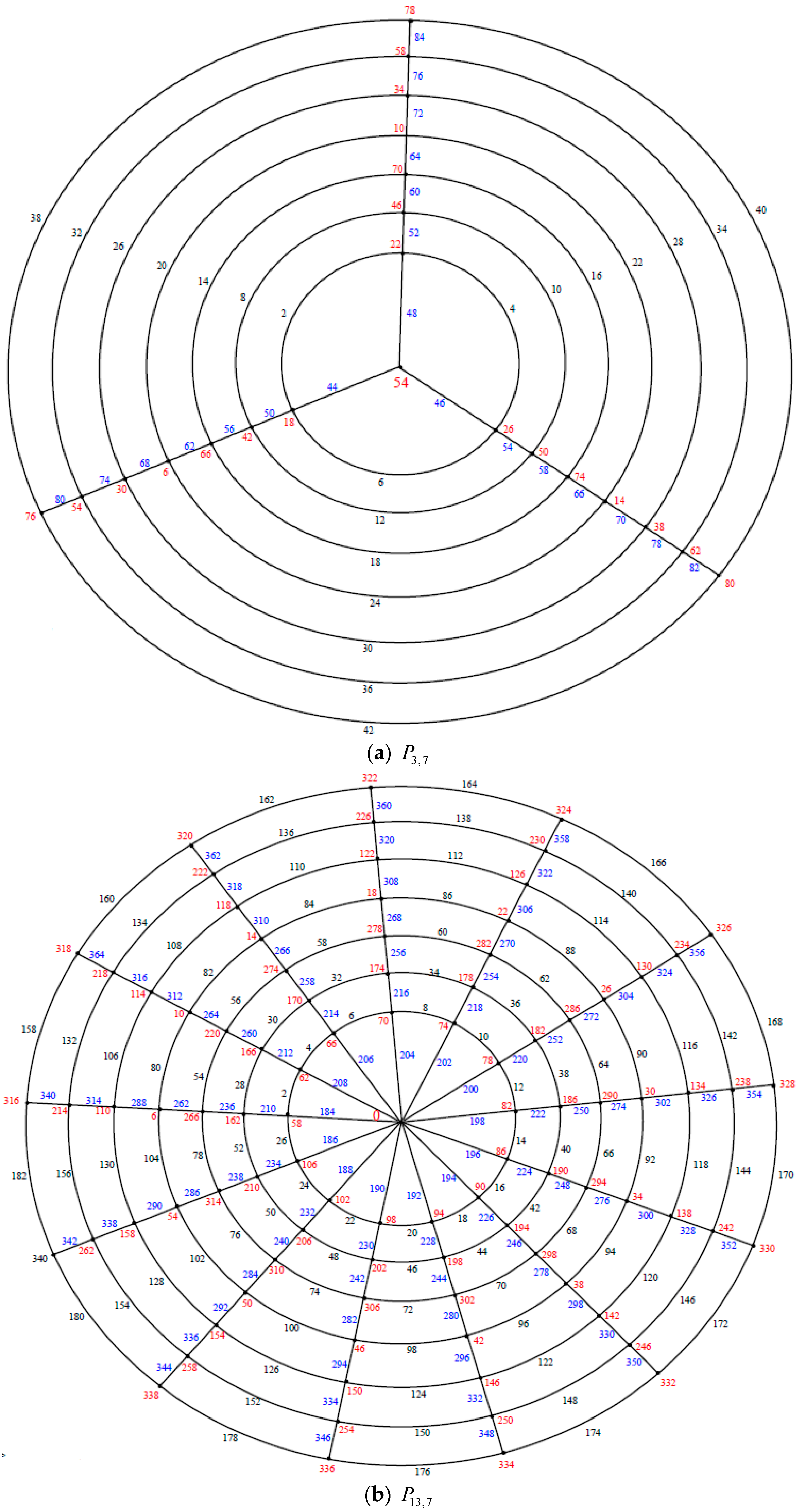
Illustration. 

The edge even graceful labeling of the polar grid graphs $P_{14,6},\hspace{0.17em}{P}_{16,6},\hspace{0.17em}{P}_{18,6},\hspace{0.17em}{P}_{24,6}$ and $P_{26,6}$ respectively are shown in Figure 3.

Figure 3. The edge even graceful labeling of the polar grid graphs $P_{14,6},\hspace{0.17em}{P}_{16,6},\hspace{0.17em}{P}_{18,6},\hspace{0.17em}{P}_{24,6}$ and $P_{26\hspace{0.17em},\hspace{0.17em}6}$.

Remark 1.

In case $m=2$ and n is even, $n>2$.

Let the label of edges of the polar grid graph be as in Figure 4. Thus we have the label of the corresponding vertices are as follows:

Figure 4. Labeling of the polar grid graph $P_{2,n}$, $n$ is even integer greater than $2$.

• $f^{\ast }(v_1)\equiv 4n+12;\hspace{0.17em}{f}^{\ast }(v_i)\equiv 16i-2,\hspace{0.17em}2\le i\le \frac{n}{2};\hspace{0.17em}{f}^{\ast }(v_{\frac{n}{2}+i})\equiv 16i+6,\hspace{0.17em}1\le i\le \frac{n}{2}-1;$
• $f^{\ast }(v_n)\equiv 4;\hspace{0.17em}{f}^{\ast }(v_i^{\prime })\equiv 16i+2,\hspace{0.17em}1\le i\le \frac{n}{2}-1;\hspace{0.17em}{f}^{\ast }({v^{\prime }}_{\frac{n}{2}+i})\equiv 2;\hspace{0.17em}{f}^{\ast }({v^{\prime }}_{\frac{n}{2}+i})\equiv 16i+10,\hspace{0.17em}1\le i\le \frac{n}{2}-2;$
• $f^{\ast }({v^{\prime }}_{n-1})\equiv 4n-4;f^{\ast }({v^{\prime }}_n)\equiv 4n+8\hspace{0.17em}\mathrm{and}\hspace{0.17em}{f}^{\ast }(v_0)\equiv 4n+4$.

Note that $P_{2,2}$ is an edge even graceful graph but not follow this rule. See Figure 5.

Figure 5. The polar grid graph $P_{2,2}$.

Theorem 2.

If $m$ is an odd positive integer greater than $1$ and $n$ an is even positive integer greater than or equal $2$, then the polar grid graph $P_{m,n}$ is an edge even graceful graph.

Proof. 

Let the edges of the polar grid graph $P_{m,n}$ be labeled as in Figure 2. □

Now the corresponding labels of vertices $\mathrm{mod}4mn$ are assigned as follows: There are four cases

Case (1): $m\equiv (4k-1)\mathrm{mod}4n,\hspace{0.17em}1\hspace{0.17em}\le k\le n$

The labels of the vertices of the inner most circle $C_m^{(1)}$ to the circle $C_m^{(\frac{n}{2})}$ are given by $f^{\ast }(v_{(k-1)m+i})\equiv 4m(2k-1)+4i+2,\hspace{0.17em}1\le k\le \frac{n}{2},\hspace{0.17em}1\le i\le m$, the labels of the vertices of the outer circle $C_m^{(n)}$ are given by $f^{\ast }(v_{(n-1)m+i})\equiv 2i+2,\hspace{0.17em}1\le i\le m$ and the labels of the vertices of the circles $C_m^{(\frac{n}{2}+1)},\dots ,\hspace{0.17em}{C}_m^{(n-1)}$ are given by $f^{\ast }(v_{(k-1)m+i})\equiv 8m(k-\frac{n}{2})+4i+2,\hspace{0.17em}1\le i\le m,\hspace{0.17em}\frac{n}{2}+1\le k\le n-1$.

The center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 4mk$, and if $k=n$, we have $f^{\ast }(v_0)\equiv 0$.

Case (2): $m\equiv (8k-3)\mathrm{mod}4n,\hspace{0.17em}1\hspace{0.17em}\le k\le \frac{n}{2}$.

In this case the vertex $v_{km(\frac{m+1}{2})}$ in the circle $C_m^{(k)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{km-(\frac{m+1}{2})}{v}_{km-(\frac{m-1}{2})}$ and $v_{km-(\frac{m-1}{2})}{v}_{km-(\frac{m-3}{2})}.$ That is $f(v_{km-(\frac{m+1}{2})}{v}_{km-(\frac{m-1}{2})})=2mn+m(2k-1)+1$ and $f(v_{km-(\frac{m-1}{2})}{v}_{km-(\frac{m-3}{2})})=2mn+m(2k-1)-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{km-(\frac{m+1}{2})})\equiv 2m(4k-1)+2,\hspace{0.17em}{f}^{\ast }(v_{km-(\frac{m-1}{2})})\equiv 2m(4k-1)+4$ and $f^{\ast }(v_{km-(\frac{m-3}{2})})\equiv 2m(4k-1)+6$. The center vertex $v_0$ is labeled as $f^{\ast }(v_0)=2m(4k-1)$. The rest vertices are labeled as in case (1).

Case (3): $m\equiv (8k+1)\mathrm{mod}4n,\hspace{0.17em}1\hspace{0.17em}\le k\le \frac{n}{2}-1$.

In this case the vertex $v_{m(\frac{n}{2}+k)\hspace{0.17em}(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{n}{2}+k)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{m(\frac{n}{2}+k)-(\frac{m+1}{2})}{v}_{m(\frac{n}{2}+k)\hspace{0.17em}(\frac{m-1}{2})}$ and $v_{m(\frac{n}{2}+k)-(\frac{m-1}{2})}{v}_{m(\frac{n}{2}+k)-(\frac{m-3}{2})}.$ That is $f(v_{m(\frac{n}{2}+k)-(\frac{m+1}{2})}{v}_{m(\frac{n}{2}+k)-(\frac{m-1}{2})}\hspace{0.17em})=3mn+m(2k-1)+1$ and $f(v_{m(\frac{n}{2}+k)-(\frac{m-1}{2})}{v}_{m(\frac{n}{2}+k)-(\frac{m-3}{2})}\hspace{0.17em})=3mn+m(2k+1)-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{n}{2}+k)-(\frac{m+1}{2})})\equiv 2m(4k+1)+2,$ $f^{\ast }(v_{m(\frac{n}{2}+k)-(\frac{m-1}{2})})\equiv 2m(4k+1)+4,$ and $f^{\ast }(v_{m(\frac{n}{2}+k)-(\frac{m-3}{2})})\equiv 2m(4k+1)+6$ and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)=2m(4k+1).$ The rest vertices are labeled as in case (1).

Case (4): $m\equiv 1\mathrm{mod}4n$

In this case the vertex $v_{mn-1}$ in the outer circle $C_m^{(n)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{mn-2}{v}_{mn-1}$ and $v_{mn}{v}_{m(n-1)+1}.$ That is $f(v_{mn-2}{v}_{mn-1})=m(3n+2)$ and $f(v_{mn}{v}_{m(n-1)+1})=m(3n+2)-4$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{mn-2})\equiv 2m+2,\hspace{0.17em}{f}^{\ast }(v_{mn-1})\equiv 2m+4,\hspace{0.17em}{f}^{\ast }(v_{mn})\equiv 2m-2$ and $f^{\ast }(v_{m(n-1)+1})\equiv 0,$ the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 2m.$ The rest vertices are labeled as in case (1).

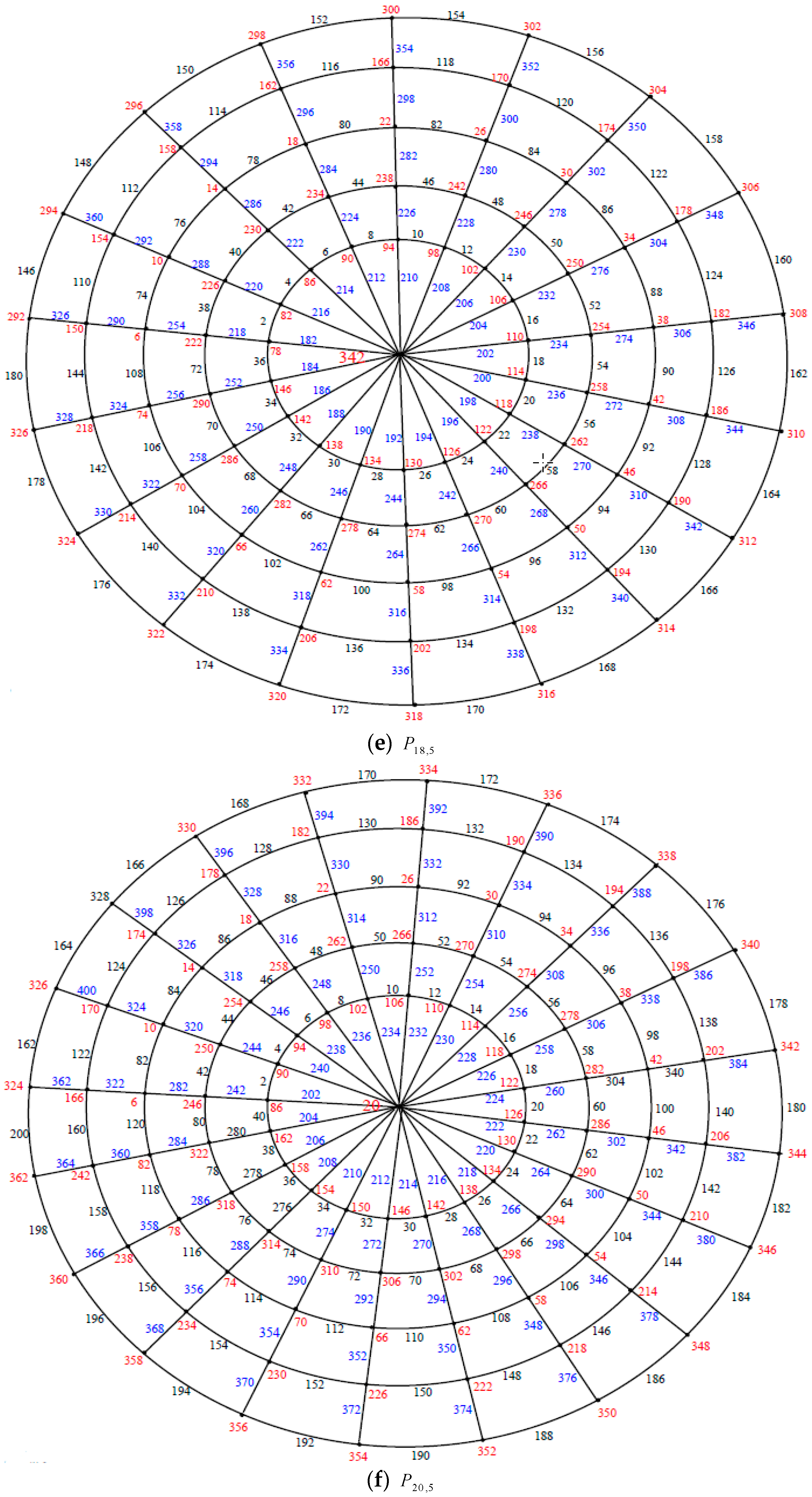
Illustration. 

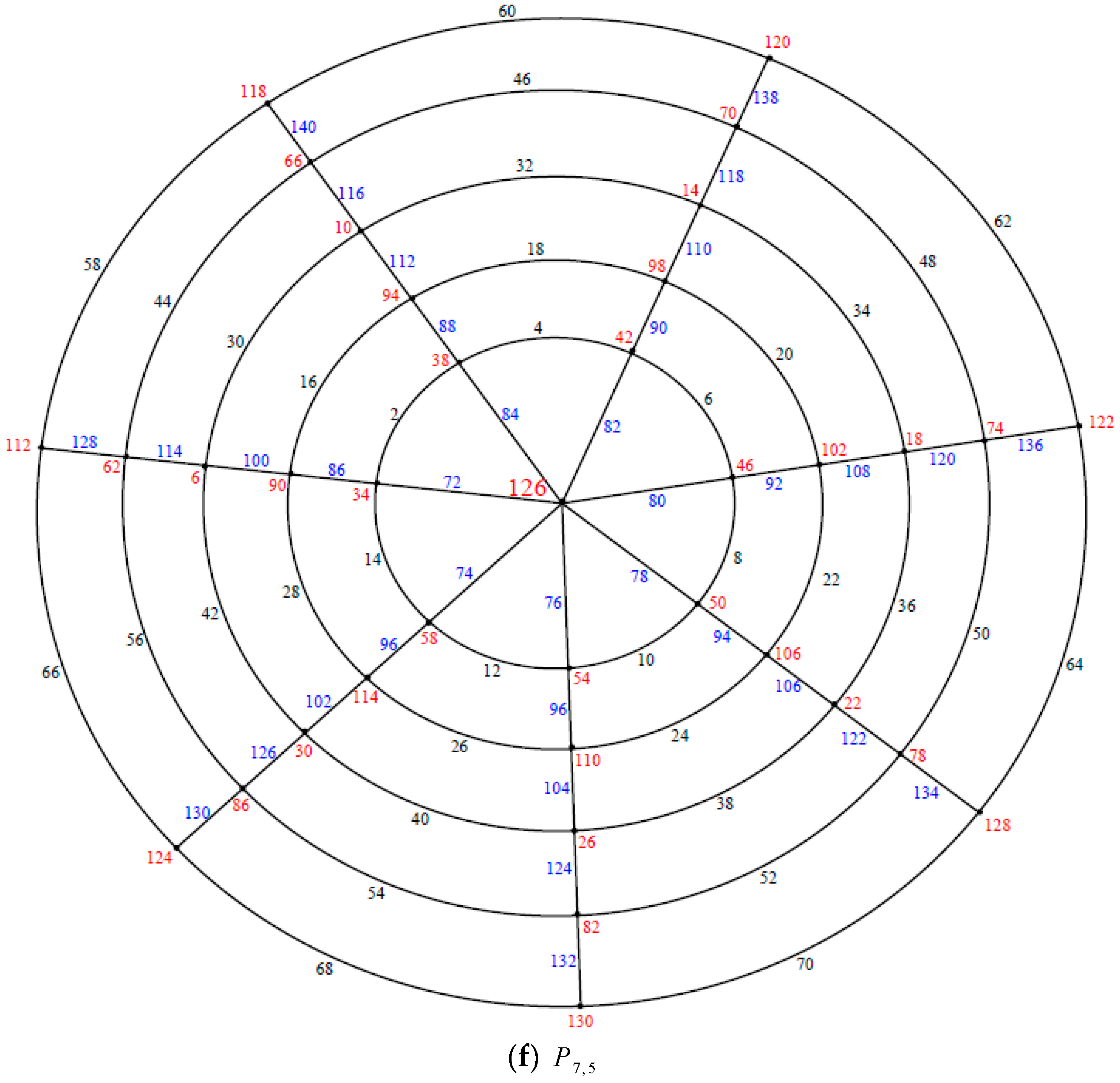
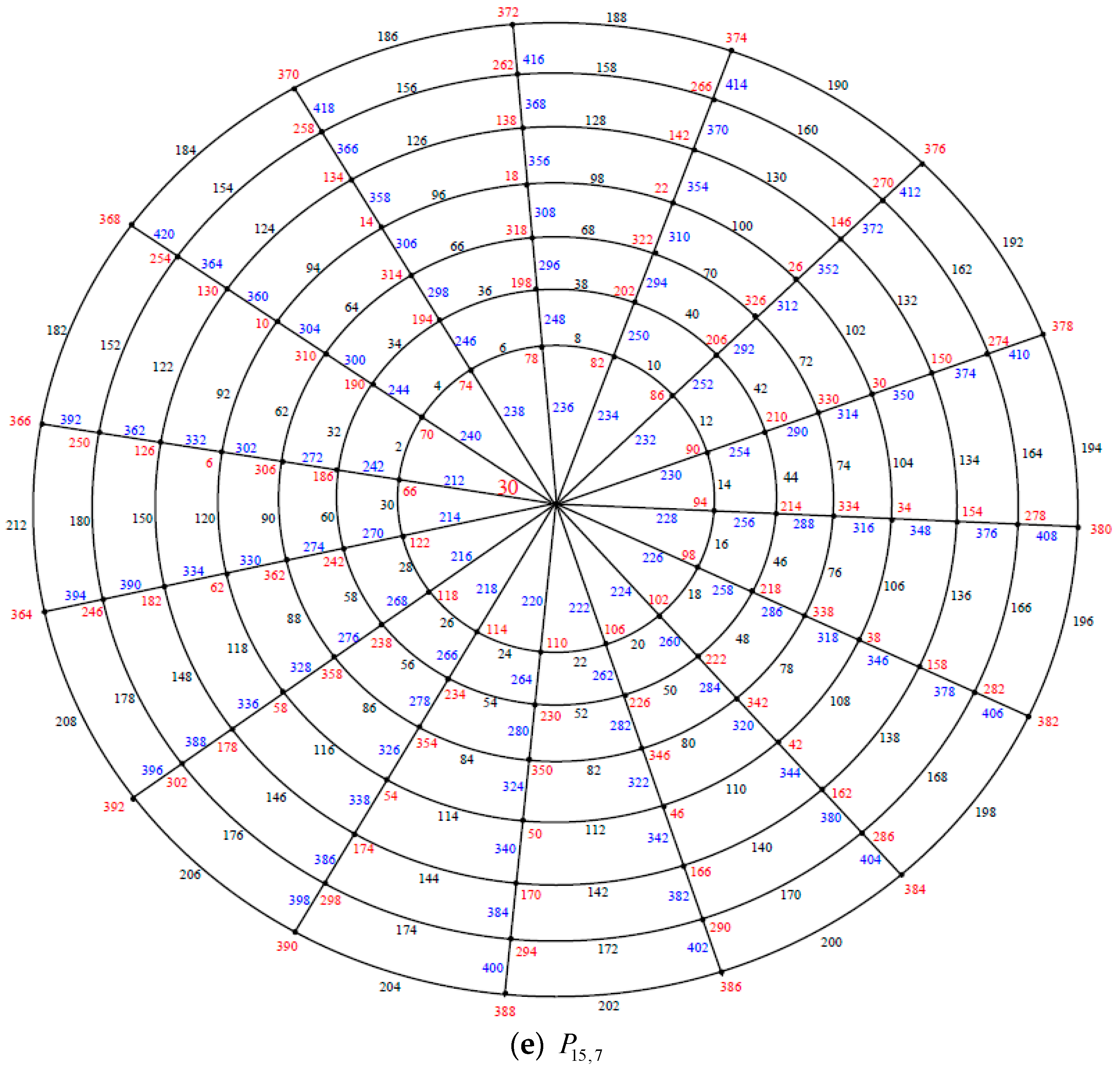
The edge even graceful labeling of the polar grid graphs $P_{13,6},\hspace{0.17em}{P}_{15,6},\hspace{0.17em}{P}_{17,6}$ and $P_{25,6}$ respectively are shown in Figure 6.

Figure 6. The edge even graceful labeling of the polar grid graphs $P_{13,6},\hspace{0.17em}{P}_{15,6},\hspace{0.17em}{P}_{17,6}$ and $P_{25,6}$.

Theorem 3.

If $m$ is an even positive integer greater than or equal $4$ and $n$ is an odd positive integer greater than or equal $3$. Then the polar grid graph $P_{m,n}$ is an edge even graceful graph.

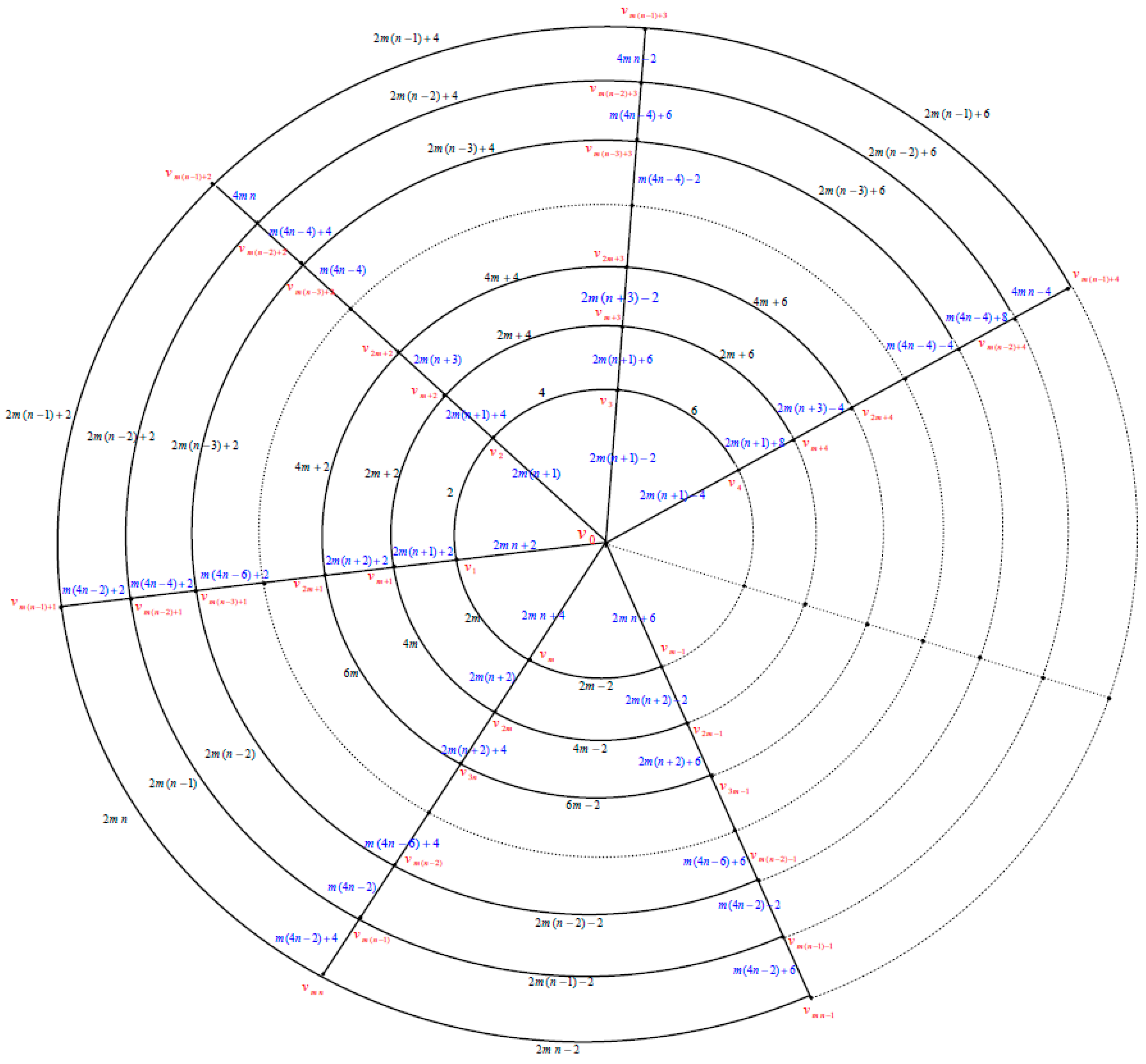
Proof. 

Let the polar grid graph $P_{m,n}$ be labeled as in Figure 7. Let $f:E(G)\to \{2,4,\dots ,2q\}.$ □

Figure 7. Labeling of the polar grid graph $P_{m,n}$ when $n$ is odd and $n\ge 3$.

First we label the edges of the circles $C_m^{(k)},\hspace{0.17em}1\le k\le n$ begin with the edges of the inner most circle $C_m^{(1)}$ to edges of the outer circle $C_m^{(n)}$ as follows:

$$f(v_{m(k-1)+i}{v}_{m(k-1)+i+1})=2m(k-1)+2i,\hspace{0.17em}f(v_{km}{v}_{(k-1)m+1})=2km,\hspace{0.17em}1\le i\le m-1,\hspace{0.17em}1\le k\le n.$$

Second we label the edges of paths $P_{n+1}^{(k)},\hspace{0.17em}1\le k\le m$ begin with the edges of the path $P_{n+1}^{(1)}$ as follows: Move anticlockwise to label the edges $v_0{v}_1,\hspace{0.17em}{v}_0{v}_m,\hspace{0.17em}{v}_0{v}_{m-1},\hspace{0.17em}\dots ,\hspace{0.17em}{v}_0{v}_3,\hspace{0.17em}{v}_0{v}_2$ by $2mn+2,\hspace{0.17em}2mn+4,2mn+6,\hspace{0.17em}\dots ,\hspace{0.17em}2m(n+1)-2,\hspace{0.17em}2m(n+1)$, then move clockwise to label the edges $v_1{v}_{m+1},\hspace{0.17em}{v}_2{v}_{m+2},\hspace{0.17em}{v}_3{v}_{m+3},\dots ,\hspace{0.17em}{v}_{m-1}{v}_{2m-1},\hspace{0.17em}{v}_m{v}_{2m}$ by $2m(n+1)+2,2m(n+1)+4,2m(n+1)+6,\dots ,$ $2m(n+2)-2,2m(n+2),\hspace{0.17em}$ then move anticlockwise to label the edges $v_{m+1}{v}_{2m+1},\hspace{0.17em}{v}_{2m}{v}_{3m},$ $v_{2m-1}{v}_{3m-1},\hspace{0.17em}\dots ,\hspace{0.17em}{v}_{m+3}{v}_{2m+3},\hspace{0.17em}{v}_{m+2}{v}_{2m+2}$ by $2m(n+2)+2,\hspace{0.17em}2m(n+2)+4,2m(n+2)+6,\dots ,$ $2m(n+3)-2,\hspace{0.17em}2m(n+3)$ and so on. Finally move anticlockwise to label the edges $v_{m(n-2)+1}{v}_{m(n-1)+1},\hspace{0.17em}{v}_{m(n-1)+1}{v}_{mn},\hspace{0.17em}{v}_{m(n-1)-1}{v}_{mn-1},\dots ,\hspace{0.17em}{v}_{m(n-2)+3}{v}_{m(m-1)+3},\hspace{0.17em}{v}_{m(n-2)+2}{v}_{m(m-1)+2}$ by $2m(2n-1)+2,2m(2n-1)+4,2m(2n-1)+6,\dots ,4mn-2,4mn$.

The corresponding labels of vertices $\mathrm{mod}4mn$ are assigned as follows: There are four cases

Case (1) $m\equiv 4k\mathrm{mod}4n,\hspace{0.17em}1\le k\le n-2;\hspace{0.17em}m\equiv (4n-2)\mathrm{mod}4n$ and $m\equiv 0\mathrm{mod}4n$

$f^{\ast }(v_{(k-1)m+i})\equiv 4m(2k-1)+4i+2,\hspace{0.17em}1\le i\le m,\hspace{0.17em}1\le k\le n-1.$ That is the labels of the vertices in the most inner circle $C_m^{(1)}$ are assigned by $f^{\ast }(v_i)\equiv 4m+4i+2,\hspace{0.17em}1\le i\le m,$ the labels of the vertices in the circle $C_m^{(2)}$ are assigned by $f^{\ast }(v_{m+i})\equiv 12m+4i+2$, the labels of vertices of the circle $C_m^{(\frac{n-1}{2})}$ are assigned by $f^{\ast }(\frac{v_{m(n-3)}}{2}+i)\equiv 4mn-8m+4i+2$, the labels of vertices of the circle $C_m^{(\frac{n+1}{2})}$ are assigned by $f^{\ast }(\frac{v_{m(n-1)}}{2}+i)\equiv 4i+2$, the labels of vertices of the circle $C_m^{(\frac{n+3}{2})}$ are assigned by $f^{\ast }(\frac{v_{m(n+1)}}{2}+i)\equiv 8m+4i+2,\hspace{0.17em}\dots ,$ the labels of the vertices in the circle $C_m^{(n-1)}$ are assigned by $f^{\ast }(v_{m(n-2)+i})\equiv 4mn-12m+4i+2,\hspace{0.17em}1\le i\le m$ and the labels of the vertices of the outer circle $C_m^{(n)}$ are assigned by $f^{\ast }(v_{m(n-1)+i})\equiv 4mn-4m+2i+2,$ $1\le i\le m.$ The labels of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv m^2(2n+1)$ when $m\equiv 4k\mathrm{mod}4n,$ we have $f^{\ast }(v_0)\equiv m(4k+1)$, when $m\equiv (4n-2)\hspace{0.17em}\mathrm{mod}\hspace{0.17em}4n,$ $f^{\ast }(v_0)\equiv 4mn-m$ and when $m\equiv 0\hspace{0.17em}\mathrm{mod}4n$, $f^{\ast }(v_0)\equiv m.$

Case (2) $m\equiv (8k-2)\mathrm{mod}\hspace{0.17em}4n,\hspace{0.17em}1\le k\le \frac{n-1}{2}.$

In this case the vertex $v_{km-(\frac{m+2}{4})}$ in the circle $C_m^{(k)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the label of two edges $v_{km-(\frac{m+2}{4})}{v}_{km-(\frac{m-2}{4})}$ and $v_{km-(\frac{m-2}{4})}{v}_{km-(\frac{m-6}{4})}$. That is $f(v_{km-(\frac{m+2}{4})}{v}_{km-(\frac{m-2}{4})})=m(2k-1)+\frac{m+2}{2}$ and $f(v_{km-(\frac{m-2}{4})}{v}_{km-(\frac{m-6}{2})})=m(2k-1)+\frac{m-2}{2}$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{km-(\frac{m+2}{4})})\equiv m(8k-1)+2,$ $f^{\ast }(v_{km-(\frac{m-2}{4})})\equiv m(8k-1)+4$ and $f^{\ast }(v_{km-(\frac{m-6}{2})})\equiv m(8k-1)+6$. In this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv m(2mn+m+1)\equiv m(8k-1).$ The rest vertices are labeled as in case (1).

Case (3) $m\equiv (8k-6)\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n-1}{2}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\mathrm{m}\ne 2$. In this case the vertex $v_{m(\frac{n+2k-1}{2})-(\frac{m+2}{4})}$ in the circle $C_m^{(\frac{n+2k-1}{2})}$ will repeat with the center vertex $v_0.$ To avoid this problem we replace the labels of the two edges $v_{m(\frac{n+2k-1}{2})-(\frac{m+2}{4})}{v}_{m(\frac{n+2k-1}{2})-(\frac{m-2}{4})}$ and $v_{m(\frac{n+2k-1}{2})-(\frac{m-2}{4})}{v}_{m(\frac{n+2k-1}{2})-(\frac{m-6}{4})}$. That is $f(v_{m(\frac{n+2k-1}{2})-(\frac{m+2}{4})}{v}_{m(\frac{n+2k-1}{2})-(\frac{m-2}{4})})=mn+2m(k-1)+\frac{m+2}{2}$ and $f(v_{m(\frac{n+2k-1}{2})-(\frac{m-2}{4})}{v}_{m(\frac{n+2k-1}{2})-(\frac{m-6}{4})})=$ $mn+2m(k-1)+\frac{m-2}{2}$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{n+2k-1}{2})-(\frac{m+2}{4})})\equiv m(8k-5)+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{n+2k-1}{2})-(\frac{m-2}{4})})\equiv m(8k-5)+4$ and $f^{\ast }(v_{m(\frac{n+2k-1}{2})-(\frac{m-6}{4})})\equiv$ $m(8k-5)+6$ and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv m(8k-5).$ The rest vertices are labeled as in case (1).

Case (4) $m\equiv (4n-4)\mathrm{mod}4n.$ In this case the vertex $v_{mn-(\frac{m+2}{2})}$ in the outer circle $C_m^{(n)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{mn-(\frac{m+6}{4})}{v}_{mn-(\frac{m+2}{4})}$ and $v_{mn}{v}_{m(n-1)+1}$. That is $f(v_{mn-(\frac{m+6}{4})}{v}_{mn-(\frac{m+2}{4})})=2mn$ and $f(v_{mn}{v}_{m(n-1)+1}\hspace{0.17em})=m(2n-1)-4$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{mn-(\frac{m+6}{4})})\equiv 4mn-2m+2,\hspace{0.17em}{f}^{\ast }(v_{mn-(\frac{m+2}{4})})\equiv 4mn-2m+8,$ $f^{\ast }(v_{mn})\equiv 4mn-3m-2$ and $f^{\ast }(v_{m(n-1)+1})\equiv 4mn-5m$ and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv m(4n-3).$ The rest vertices are labeled as in case (1).

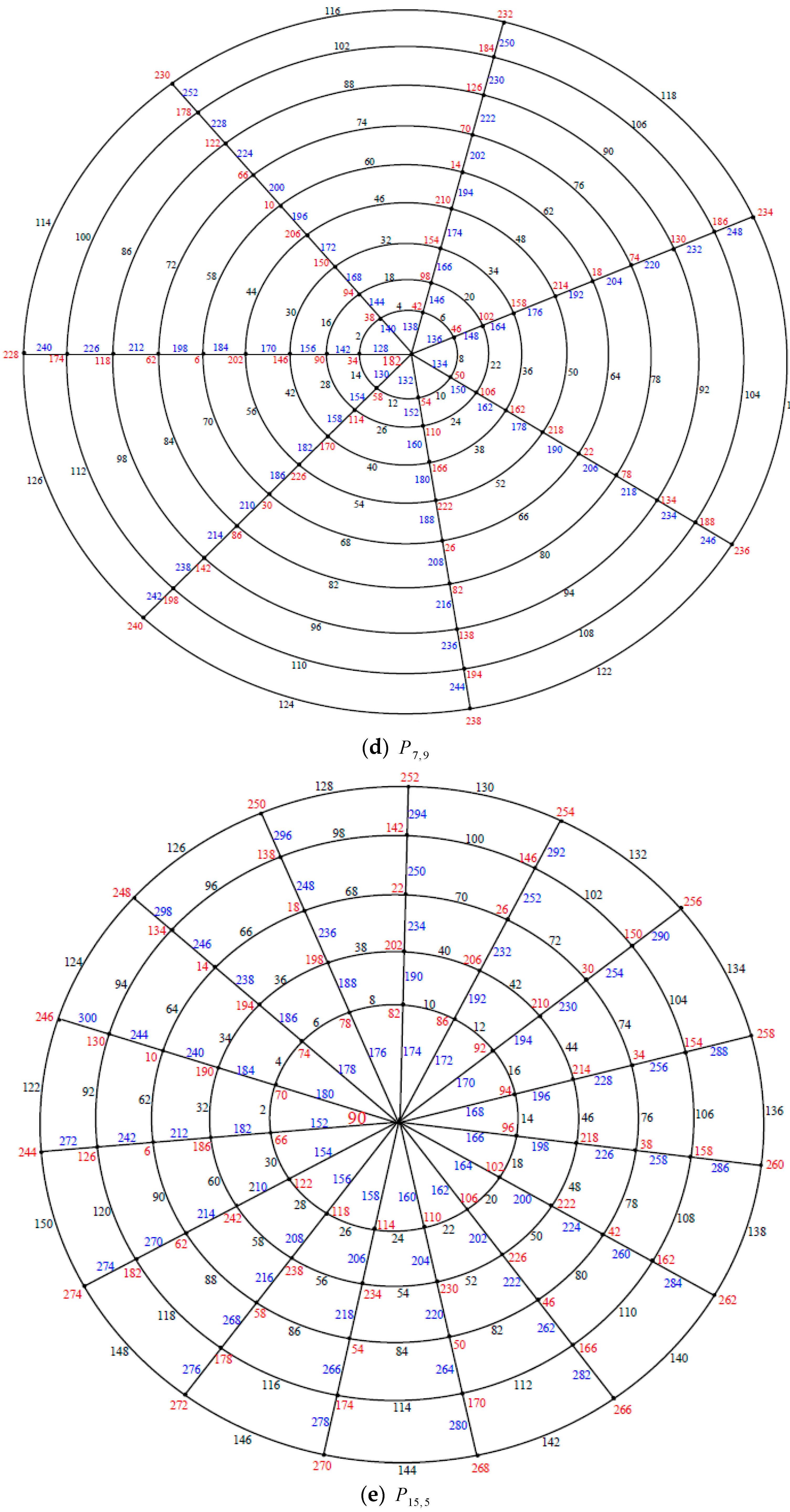
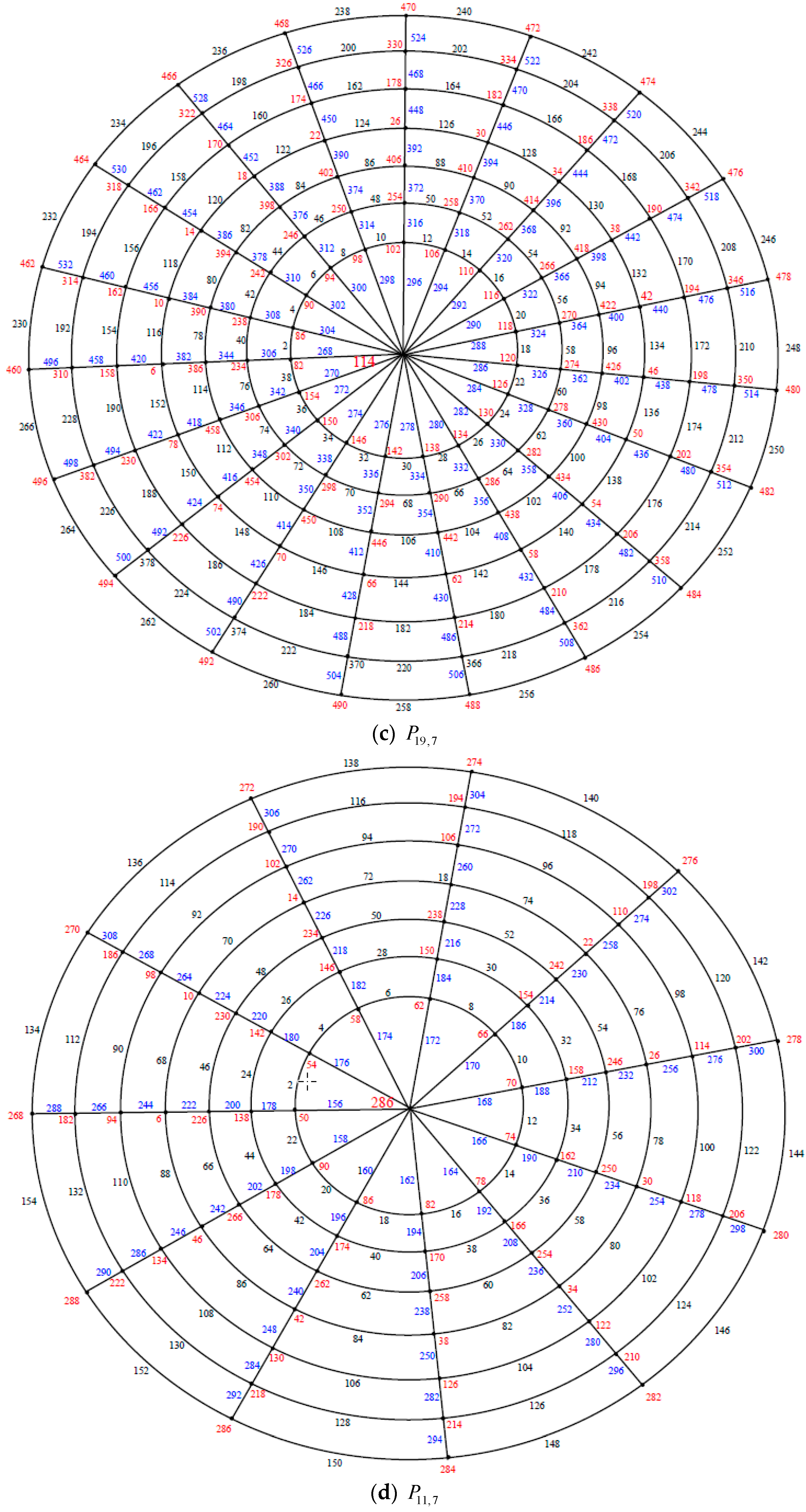
Illustration. 

The edge even graceful labeling of the polar grid graphs $P_{10,5},\hspace{0.17em}{P}_{12,5},\hspace{0.17em}{P}_{14,5},\hspace{0.17em}{P}_{16,5},\hspace{0.17em}{P}_{18,5}$ and $P_{20,5}$ respectively are shown in Figure 8.

Figure 8. The edge even graceful labeling of the polar grid graphs $P_{10,5},\hspace{0.17em}{P}_{12,5},\hspace{0.17em}{P}_{14,5},\hspace{0.17em}{P}_{16,5},\hspace{0.17em}{P}_{18,5}$ and $P_{20,5}$.

Remark 2.

In case $m=2$, $n$ is odd, $n\ge 3$.

Let the label of edges of the polar grid graph $P_{2,n}$ be as in Figure 9. Thus we have the labels of the corresponding vertices as follows: $f^{\ast }(v_1)\equiv 12;\hspace{0.17em}{f}^{\ast }(v_i)\equiv 16i-2,\hspace{0.17em}2\le i\le \frac{n-1}{2};\hspace{0.17em}{f}^{\ast }(v_{\frac{n+2i-1}{2}})\equiv 16i-10,1\le i\le \frac{n-1}{2};\hspace{0.17em}{f}^{\ast }(v_n)\equiv 8n-2;$ $f^{\ast }({v^{\prime }}_i)\equiv 16i+2,\hspace{0.17em}1\le i\le \frac{n-1}{2};\hspace{0.17em}{f}^{\ast }({v^{\prime }}_{\frac{n+1}{2}})\equiv 2;\hspace{0.17em}{f}^{\ast }({v^{\prime }}_{\frac{n+2i-1}{2}})\equiv 16i-6,\hspace{0.17em}2\le i\le \frac{n-1}{2};\hspace{0.17em}{f}^{\ast }({v^{\prime }}_n)\equiv 0$ and $f^{\ast }(v_0)\equiv 4$.

Figure 9. The labeling of the polar grid graph $P_{2,n},\hspace{0.17em}n\ge 3$.

Illustration. 

The edge even graceful labeling of the polar grid graphs $P_{2,5}$ is shown in Figure 10.

Figure 10. The labeling of the polar grid graph $P_{2,5}$.

Theorem 4.

If $m$ and $n$ are odd positive integers greater than $1$. Then the polar grid graph $P_{m,n}$ is an edge even graceful graph.

Proof. 

Let the polar grid graph $P_{m,n}$ be labeled as in Figure 7. Let $f:E(G)\to \{2,4,\dots ,2q\}.$ □

The corresponding labels of vertices $\mathrm{mod}4mn$ are assigned as follows: There are two cases:

Case (1) $n\equiv 1\hspace{0.17em}\mathrm{mod}4$, this case contains five subcases as follows:

SubCase (i) $m\equiv (4k-3)\mathrm{mod}\hspace{0.17em}4n,\hspace{0.17em}2\le k\le n$

$f^{\ast }(v_{(k-1)m+i})\equiv 4m(2k-1)+4i+2,1\le k\le n-1\hspace{0.17em},1\le i\le m.$ That is the labels of vertices of the most inner circle $C_m^{(1)}$ are assigned by $f^{\ast }(v_i)=4m+4i+2$, the labels of vertices of the circle $C_m^{(2)}$ are assigned by $f^{\ast }(v_{m+i})\equiv 12m+4i+2$, the labels of the vertices of the circle $C_m^{(\frac{n-1}{2})}$ are assigned by $f^{\ast }(v_{\frac{m(n-3)}{2}+i})\equiv 4mn-8m+4i+2$, the labels of the vertices of the circle $C_m^{(\frac{n+1}{2})}$ are assigned by $f^{\ast }(v_{\frac{m(n-1)}{2}+i})\equiv 4i+2$, the labels of the vertices of the circle $C_m^{(\frac{n+3}{2})}$ are assigned by $f^{\ast }(v_{\frac{m(n+1)}{2}+i})\equiv 8m+4i+2,\dots ,$ the labels of the vertices of the circle $C_m^{(n-1)}$ are assigned by $f^{\ast }(v_{m(n-2)+i})\equiv 4mn-12m+4i+2,\hspace{0.17em}1\le i\le m$ and the labels of the vertices of the outer circle $C_m^{(n)}$ are assigned by $f^{\ast }(v_{m(n-1)+i})\equiv 4mn-12m+2i+2,\hspace{0.17em}1\le i\le m$. The label of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv 2mn+2m(2k-1)$, when $k=\frac{n+1}{2}$, we have $f^{\ast }(v_0)\equiv 0$.

SubCase (ii) $m\equiv (8k-5)\hspace{0.17em}\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n+1}{2}$, $m\ne 3$. In this subcase the vertex $v_{m(\frac{n+4k-1}{4})-(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{n+4k-1}{4})}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{m(\frac{n+4k-1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{n+4k-1}{4})-(\frac{m-1}{2})}$ and $v_{m(\frac{n+4k-1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{n+4k-1}{4})-(\frac{m-3}{2})}$. That is $f(v_{m(\frac{n+4k-1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{n+4k-1}{4})-(\frac{m-1}{2})})=m[2k+\frac{n-3}{2}]+1$ and $f(v_{m(\frac{n+4k-1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{n+4k-1}{4})-(\frac{m-3}{2})})=m[2k+\frac{n-3}{2}]-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{n+4k-1}{4})-(\frac{m+1}{2})})\equiv 2mn+4m(2k-1)+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{n+4k-1}{4})-(\frac{m-1}{2})})\equiv 2mn+4m(2k-1)+4,$ $f^{\ast }(v_{m(\frac{n+4k-1}{4})-(\frac{m-3}{2})})\equiv 2mn+4m(2k-1)+6,$ and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 2mn+4m(2k-1).$ The rest vertices will be labeled as in subCase (i).

Remark 3.

When $n\equiv 1\hspace{0.17em}\mathrm{mod}4$ and $m=3$, in this case the vertex $v_{3(\frac{n-1}{4})+1}$ in the circle $C_3^{(\frac{n-1}{4}+1)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{3(\frac{n-1}{4})+2}{v}_{3(\frac{n-1}{4})+3}$ and $v_{3(\frac{n-1}{4})+1}{v}_{3(\frac{n-1}{4})+3}$. That is $f(v_{3(\frac{n-1}{4})+2}{v}_{3(\frac{n-1}{4})+3})=3(\frac{n-1}{2})+6$ and $f(v_{3(\frac{n-1}{4})+1}{v}_{3(\frac{n-1}{4})+3})=3(\frac{n-1}{2})+4$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{3(\frac{n-1}{4})+1})\equiv 6n+10,$ $f^{\ast }(v_{3(\frac{n-1}{4})+2})\equiv 6n+18,\hspace{0.17em}{f}^{\ast }(v_{3(\frac{n-1}{4})+3})\equiv 6n+16$ and the center vertex $v_0$ is labeld as $f^{\ast }(v_0)\equiv 6n+12$.

SubCase (iii) $m\equiv (8k-1)\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n-5}{4}.$ In this subcase the vertex $v_{m(\frac{3n+4k+1}{4})-(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{3n+4k-1}{4})}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{m(\frac{3n+4k+1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{3n+4k+1}{4})-(\frac{m-1}{2})}$ and $v_{m(\frac{3n+4k+1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{3n+4k+1}{4})-(\frac{m-3}{2})}$. That is $f(v_{m(\frac{3n+4k+1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{3n+4k+1}{4})-(\frac{m-1}{2})})=\hspace{0.17em}2mn+m[2k-\frac{n+1}{2}]+1$ and $f(v_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})}$ $v_{m(\frac{3n+4k-1}{4})-(\frac{m-3}{2})})=2mn+m[2k-\frac{n+1}{2}]-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{3n+4k+1}{4})-(\frac{m+1}{2})})\equiv 2mn+8km+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})})\equiv \hspace{0.17em}2mn+8km+4,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{3n+4k+1}{4})-(\frac{m-3}{2})})\equiv$ $2mn+8km+6,$ and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 2mn+8km.$ The rest vertices will be labeled as in subCase (i).

SubCase (iv) $m\equiv (8k-1)\mathrm{mod}\hspace{0.17em}4n,\hspace{0.17em}\frac{n+3}{4}\le k\le \frac{n-1}{2}$. In this case the vertex $v_{m(\frac{4k-n+1}{4})-(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{4n-k+1}{4})}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{m(\frac{4k-n+1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{4k-n+1}{4})-(\frac{m-1}{2})}$ and $v_{m(\frac{4k-n+1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{4k-n+1}{4})-(\frac{m-3}{2})}$. That is $f(v_{m(\frac{4k-n+1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{4k-n+1}{4})-(\frac{m-1}{2})})=\hspace{0.17em}m[2k-\frac{n+1}{2}]+1$ and $f(v_{m(\frac{4k-n+1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{4k-n+1}{4})-(\frac{m-3}{2})})=m[2k-\frac{n+1}{2}]-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{4k-n+1}{4})-(\frac{m+1}{2})})\equiv 2mn+8km+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{4k-n+1}{4})-(\hspace{0.17em}\frac{m-1}{2})})\equiv 8km-\hspace{0.17em}2mn+4,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{4k-n+1}{4})-(\frac{m-3}{2})})\equiv$ $8km-2mn+6,$ and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 8km-2mn.$ The rest vertices will be labeled as in subCase (i).

SubCase (v) $m\equiv (2n-3)\hspace{0.17em}\mathrm{mod}4n$. In this case the vertex $v_{mn-1}$ in the outer circle $C_m^{(n)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{mn-2}{v}_{mn-1}$ and $v_{mn}{v}_{m(n-1)+1}$. That is $f(v_{mn-2}\hspace{0.17em}{v}_{mn-1})=2mn-4,\hspace{0.17em}f(v_{mn}{v}_{m(n-1)+1})=2mn$ and we obtain the labels of the corresponding vertices are as follows $f^{\ast }(v_{mn-2})\equiv 4mn-2m+2,\hspace{0.17em}{f}^{\ast }(v_{mn-1})\equiv 4mn-2m+4,$ $f^{\ast }(v_{mn})\equiv 4mn-2m-2$ and $f^{\ast }(v_{m(n-1)+1})\equiv 4mn-4m$, and in this case the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 4mn-2m.$ The rest vertices will be labeled as in subCase (i).

Illustration. 

The edge odd graceful labeling of the polar grid graphs $P_{3,5},P_{13,5},P_{11,5},\hspace{0.17em}{P}_{7,9},\hspace{0.17em}{P}_{15,5}$ and $P_{7,5}$ respectively are shown in Figure 11.

Figure 11. The polar grid graphs $P_{3,5},P_{13,5},\hspace{0.17em}{P}_{11,5},\hspace{0.17em}{P}_{7,9},\hspace{0.17em}{P}_{15,5}$ and $P_{7,5}.$

Case (2) $n\equiv 3\hspace{0.17em}\mathrm{mod}4$. This case contains also five subcases as follows:

SubCase (i) $m\equiv (4k-3)\mathrm{mod}4n,\hspace{0.17em}2\le k\le n$

$f^{\ast }(v_{(k-1)m+i})\equiv 4m(2k-1)+4i+2,1\le k\le n-1,1\le i\le m.$ That is the labels of vertices of the most inner circle $C_m^{(1)}$ are assigned by $f^{\ast }(v_i)\equiv 4m+4i+2$, the label of vertices of the circle $C_m^{(2)}$ are assigned by $f^{\ast }(v_{m+i})\equiv 12m+4i+2$, the labels of vertices of the circle $C_m^{(\frac{n-1}{2})}$ are assigned by $f^{\ast }(v_{\frac{m(n-1)}{2}+i})\equiv 4mn-8m+4i+2$, the labels of vertices of the circle $C_m^{(\frac{n+1}{2})}$ are assigned by $f^{\ast }(v_{\frac{m(n-3)}{2}+i})\equiv 4i+2$, the labels of vertices of the circle $C_m^{(\frac{n+3}{2})}$ are assigned by $f^{\ast }(v_{\frac{m(n+1)}{2}+i})\equiv 8m+4i+2,\dots ,$ the labels of vertices of the circle $C_m^{(n-1)}$ are assigned by $f^{\ast }(v_{m(n-2)+i})\equiv 4mn-12m+4i+2,\hspace{0.17em}1\le i\le m$ and the labels of the vertices of the outer circle $C_m^{(n)}$ are assigned by $f^{\ast }(v_{m(n-1)+i})\equiv 4mn-12m+2i+2,\hspace{0.17em}1\le i\le m$. The label of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv 2mn+2m(2k-1)$, when $k=\frac{n+1}{2}$, we have $f^{\ast }(v_0)\equiv 0$.

SubCase (ii) $m\equiv (8k-5)\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n-3}{4}$, $m\ne 3$

In this subcase the vertex $v_{m(\frac{3n+4k-1}{4})-(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{3n+4k-1}{4})}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{m(\frac{3n+4k-1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})}$ and $v_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{3n+4k-1}{4})-(\frac{m-3}{2})}.$ That is $f(v_{m(\frac{3n+4k-1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})})=2mn+m[2k-\frac{n+3}{2}]+1$ and $f(v_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{3n+4k-1}{4})-(\frac{m-3}{2})})=$ $2mn+m[2k-\frac{n+3}{2}]-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{3n+4k-1}{4})-(\frac{m+1}{2})})\equiv 2mn+4m(2k-1)+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{3n+4k-1}{4})-(\frac{m-1}{2})})\equiv 2mn+4m(2k-1)+4,$ $f^{\ast }(v_{m(\frac{3n+4k-1}{4})-(\frac{m-3}{2})})\equiv 2mn+4m(2k-1)+6,$ and the label of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv 2mn+4m(2k-1).$ That rest vertices will be labeled as in subcase (i).

Remark 4.

When $n\equiv 3\hspace{0.17em}\mathrm{mod}4$ and $m=3$, we have the vertex $v_{3(\frac{3n-1}{4})+1}$ in the circle $C_m^{(\frac{3n-1}{4}+1)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{3(\frac{3n-1}{4})+2}{v}_{3(\frac{3n-1}{4})+3}$ and $v_{3(\frac{3n-1}{4})+1}{v}_{3(\frac{3n-1}{4})+3}.$ That is $f(v_{3(\frac{3n-1}{4})+2}{v}_{3(\frac{3n-1}{4})+3})=3(\frac{3n-1}{2})+6$ and $f(v_{3(\frac{3n-1}{4})+1}{v}_{3(\frac{3n-1}{4})+3})=3(\frac{3n-1}{2})+4$ and we obtain the labes of the corresponding vertices $\mathrm{mod}4mn$ are as follows: $f^{\ast }(v_{3(\frac{3n-1}{4})+1})\equiv 6n+10,$ $f^{\ast }(v_{3(\frac{3n-1}{4})+2})\equiv 6n+18,\hspace{0.17em}{f}^{\ast }(v_{3(\frac{3n-1}{4})+3})\equiv 6n+20$ and the label of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv 6n+12$.

Note that $P_{3,3}$ is an edge even graceful grapg but not follow this rule. See Figure 12.

Figure 12. The polar grid graphs $P_{3,3}$.

SubCase (iii) $m\equiv (8k-1)\mathrm{mod}4n,\hspace{0.17em}\frac{n+5}{4}\le k\le \frac{n+1}{2}$,

In this subcase the vertex $v_{m(\frac{4k-n-1}{4})-(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{4k-n-1}{4})}$ will repeat with the center vertex $v_0.$ To avoid this problem we replace the labels of the two edges $v_{m(\frac{4k-n-1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{4k-n-1}{4})-(\frac{m-1}{2})}$ and $v_{m(\frac{4k-n-1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{4k-n-1}{4})-(\frac{m-3}{2})}$ That is $f(v_{m(\frac{4k-n-1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{4k-n-1}{4})-(\frac{m-1}{2})})=(2k-1)m+1$ and $f(v_{m(\frac{4k-n-1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{4k-n-1}{4})-(\frac{m-3}{2})})=(2k-1)m-1$ and we obtain the labels of the corresponding vertices as follows: $f^{\ast }(v_{m(\frac{4k-n-1}{4})-(\frac{m+1}{2})})\equiv 2m(4k-1)+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{4k-n-1}{4})-(\frac{m-1}{2})})\equiv 2m(4k-1)+4$ and $f^{\ast }(v_{m(\frac{4k-n-1}{4})-(\frac{m-3}{2})})\equiv 2m(4k-1)+6$. The label of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv 2m(4k-1).$ The rest vertices will be labeled as in subCase (i).

SubCase (iv) $m\equiv (8k-1)\mathrm{mod}4n,\hspace{0.17em}1\le k\le \frac{n-1}{2}$

In this subcase the vertex $v_{m(\frac{n+4k+1}{4})-(\frac{m+1}{2})}$ in the circle $C_m^{(\frac{n+4k+1}{4})}$ will repeat with the center vertex $v_0.$ To avoid this problem we replace the labels of the two edges $v_{m(\frac{n+4k+1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{n+4k+1}{4})-(\frac{m-1}{2})}$ and $v_{m(\frac{n+4k+1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{n+4k+1}{4})-(\frac{m-3}{2})}$ That is $f(v_{m(\frac{n+4k+1}{4})-(\frac{m+1}{2})}{v}_{m(\frac{n+4k+1}{4})-(\frac{m-1}{2})})=(2k+\frac{n-1}{2})m+1$ and $f(v_{m(\frac{n+4k+1}{4})-(\frac{m-1}{2})}{v}_{m(\frac{n+4k+1}{4})-(\frac{m-3}{2})})=(2k+\frac{n-1}{2})m-1$ and we obtain the labels of the corresponding vertices as follows $f^{\ast }(v_{m(\frac{n+4k+1}{4})-(\frac{m+1}{2})})=2mn+8km+2,$ $f^{\ast }(v_{m(\frac{n+4k+1}{4})-(\frac{m-1}{2})})=2mn+8km+4,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{n+4k+1}{4})-(\frac{m-3}{2})})=2mn+8km+6$ and the label of the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv 2mn\hspace{0.17em}+8km.$ The rest vertices will be labeled as in subCase (i).

Remark 5.

If $k=\hspace{0.17em}\frac{n+1}{4}$ we have

$$f^{\ast }(v_{m(\frac{n+4k+1}{4})-(\frac{m+1}{2})})=8km-2mn+2,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{n+4k+1}{4})-(\frac{m-1}{2})})=8km-2mn+4,\hspace{0.17em}{f}^{\ast }(v_{m(\frac{n+4k+1}{4})-(\frac{m-3}{2})})=8km-2mn+6$$

and the center vertex $v_0$ is labeled as $f^{\ast }(v_0)\equiv \hspace{0.17em}8km-2mn.$

SubCase (v) $m\equiv (2n-3)\mathrm{mod}4n$

In this subcase the vertex $v_{mn-1}$ in the outer circle $C_m^{(n)}$ will repeat with the center vertex $v_0$. To avoid this problem we replace the labels of the two edges $v_{mn-2}{v}_{mn-1}$ and $v_{mn}{v}_{m(n-1)+1}$. That is $f(v_{mn-2}{v}_{mn-1})=2mn-4,\hspace{0.17em}f(v_{mn}{v}_{m(n-1)+1})=2mn$ and we obtain the labes of the corresponding vertices as follows:

$f^{\ast }(v_{mn-2})=4mn-2m+2,\hspace{0.17em}{f}^{\ast }(v_{mn-1})=4mn-2m+4,\hspace{0.17em}{f}^{\ast }(v_{mn})=4mn-2m-2$ and $f^{\ast }(v_{m(n-1)+1})=4m(n-1)$ and the label of the center vertex $v_0$ is assigned by $f^{\ast }(v_0)\equiv \hspace{0.17em}2m(2n-1).$

The rest vertices will be labeled as in subCase (i).

Illustration. 

The edge odd graceful labeling of the polar grid graphs $P_{3,7},\hspace{0.17em}{P}_{13,7},\hspace{0.17em}{P}_{19,7},\hspace{0.17em}{P}_{11,7}$ and $P_{15,7}$ respectively are shown in Figure 13.

Figure 13. The polar grid graphs $P_{3,7},\hspace{0.17em}{P}_{13,7},\hspace{0.17em}{P}_{19,7},P_{11,7}$ $P_{15,7}$.

3. Conclusions

This paper gives some basic knowledge about the application of Graph labeling and Graph Theory in real life which is the one branch of mathematics. It is designed for the researcher who research in graph labeling and graph Theory. In this paper, we give necessary and sufficient conditions for a polar grid graph to admit edge even labeling. In future work we will study the necessary and sufficient conditions for the cylinder $P_m\times C_n$, torus $C_m\times C_n$ and rectangular $P_m\times P_n$ grid graphs to be edge even graceful.