Parameter Optimization for Computer Numerical Controlled Machining Using Fuzzy and Game Theory
Abstract
:1. Introduction
2. Research Background
2.1. Tool Wear
- T: tool function.
- V: cutting speed.
- f: feed rate.
- D: diameter of milling cutter.
- n, m: constant of tool material properties (acquired by experiment or experience).
- l: cutting length.
- C′: cutting speed of tool life in 1 minute (supplied by tool manufacturer).
- (1)
- According to the formula, a larger depth of cut and higher cutting speed lead to less tool wear.
- (2)
- From expert experience, higher cutting speed and feed rate lead to less tool wear.
- (3)
- According to the formula, lower cutting speed and feed rate lead to less tool wear.
2.2. Cutting Noise
- LPB: the measured value of motor running with no cutting.
- LPA: the measured value of motor running with cutting.
- (1)
- Smaller depth of cut, less noise.
- (2)
- Slower cutting speed, less noise.
- (3)
- Improving the pressure of the tool, less noise.
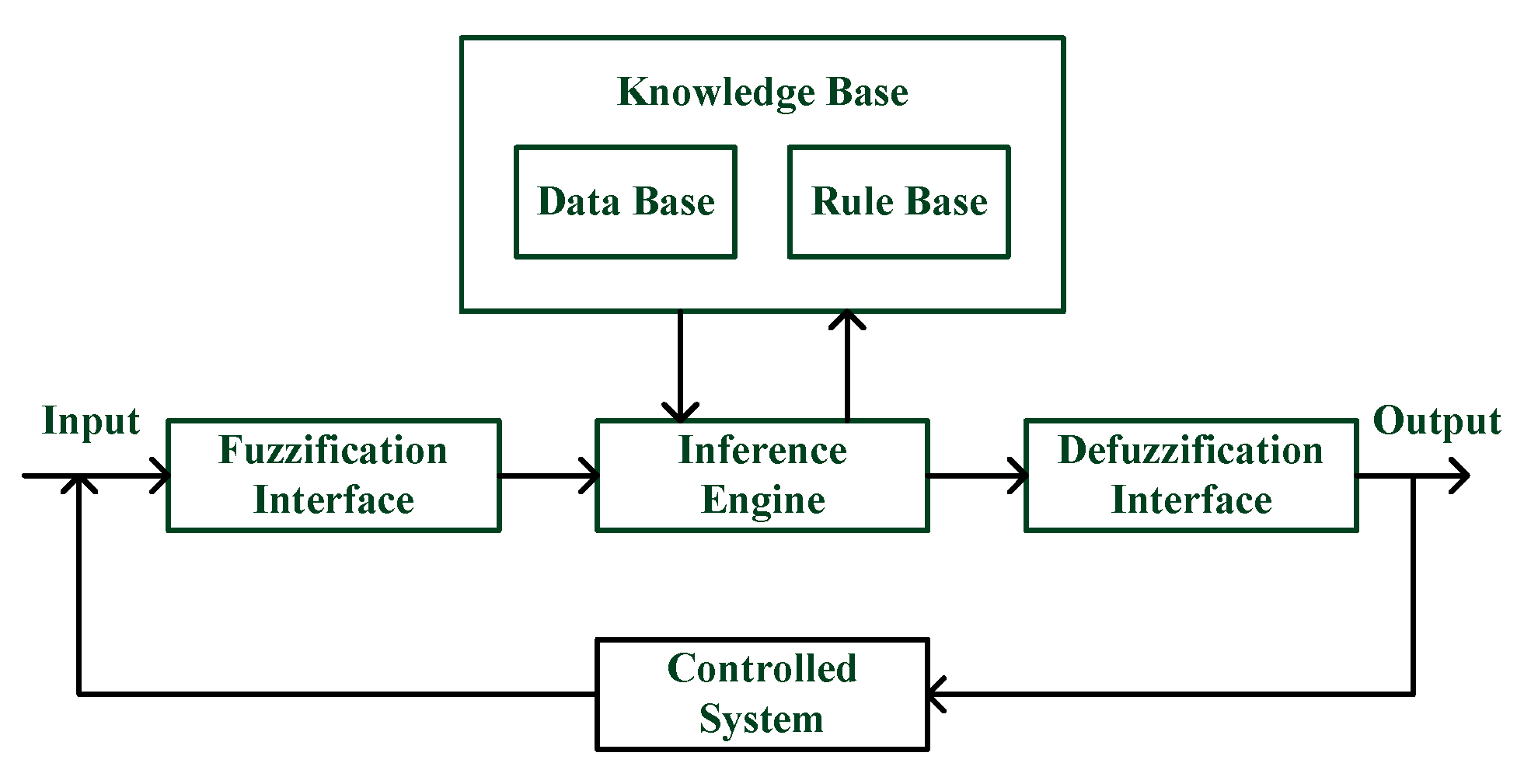
2.3. Fuzzy Theory
2.4. Game Theory
2.4.1. Elements of a Game
- Player: The actor who makes decisions with the greatest goal of pursuing his own interest.
- Nature: If not a contestant, the action taken is determined by a well-known probability.
- Action set: A collection of all possible actions taken by a contestant.
- Payoff Function: The remuneration that a contestant receives when the results of a game are shown, which is generally affected by all participants.
2.4.2. Information Structure
- The identities of the players.
- The moves could be taken by all players.
- The utility function of all players.
2.4.3. Bargaining Games
- : the payoff that both players can get when there is no agreement of the bargain.
- : the payoff that both players can get when there is a agreement of the bargain.
3. Research Design
3.1. Fuzzy Rules Establishment
3.1.1. Tool Wear
3.1.2. Cutting Noise
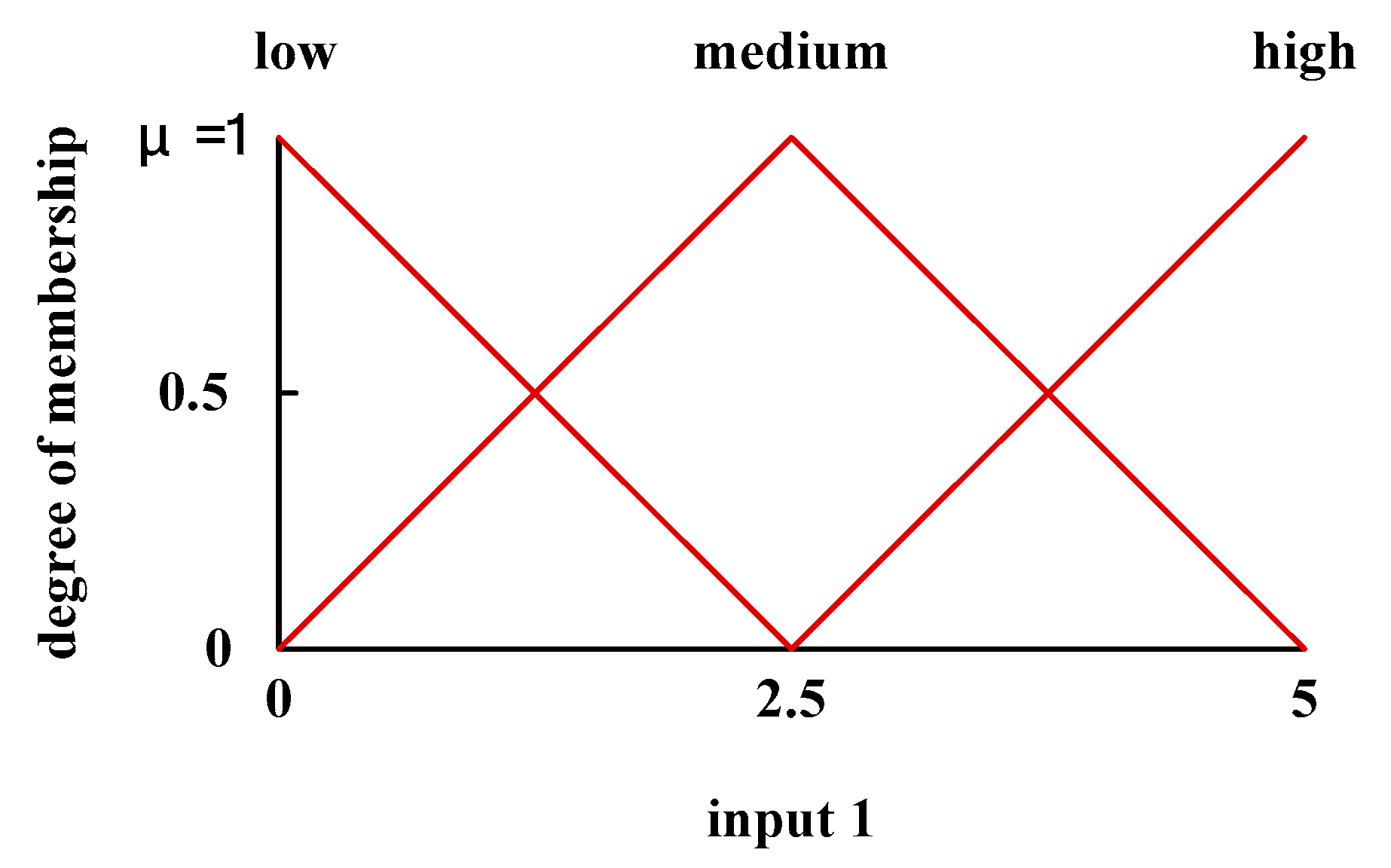
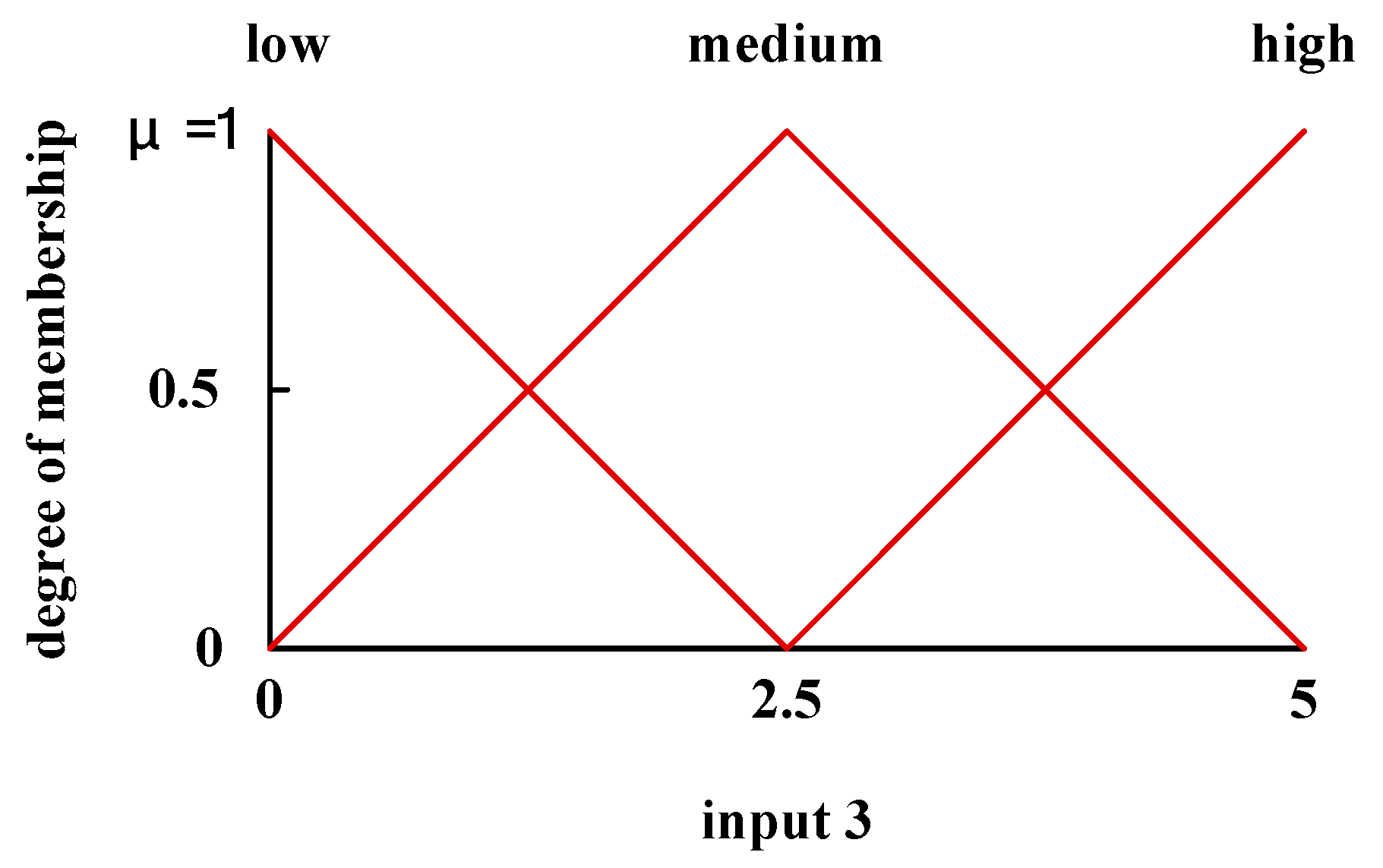
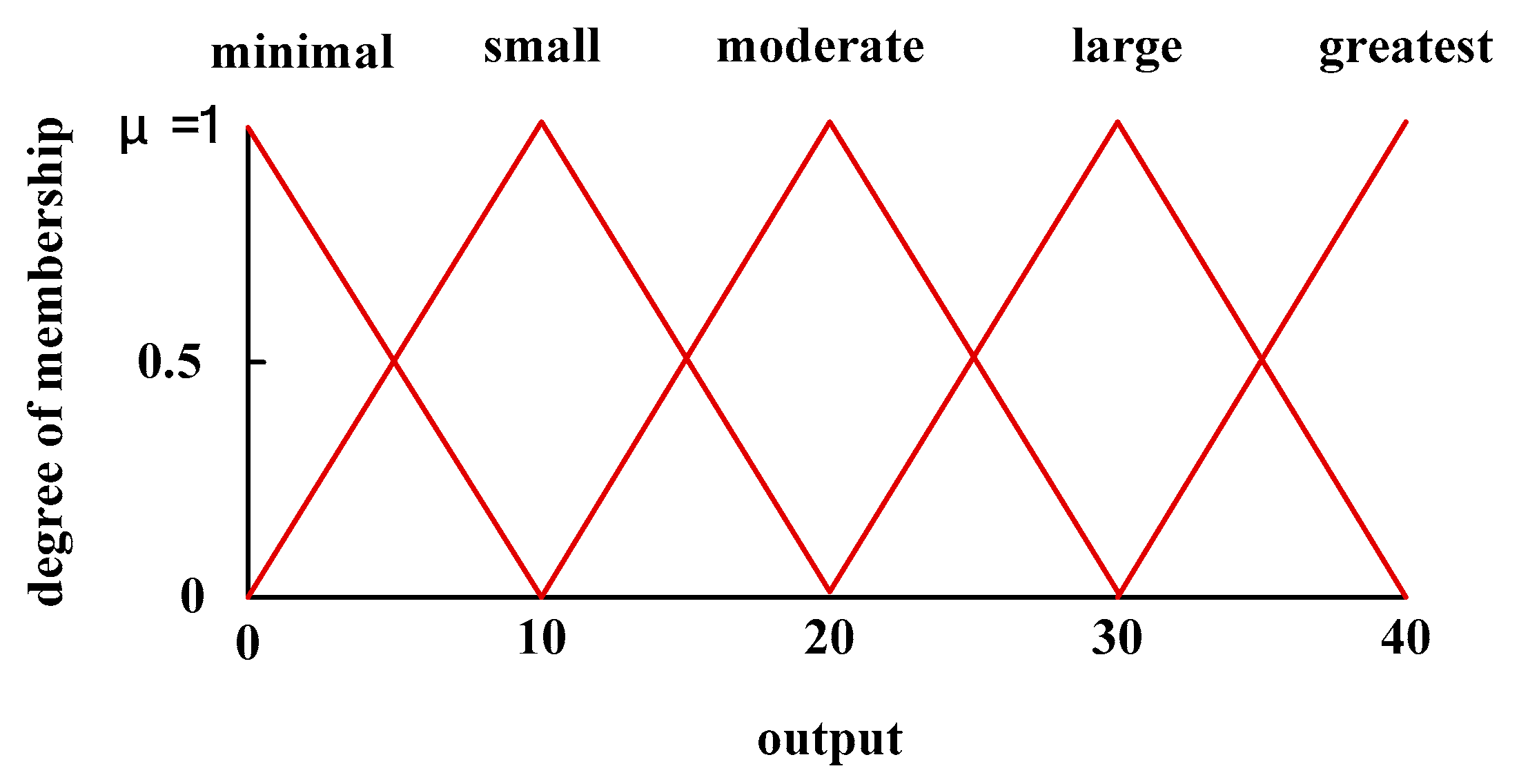
3.2. Variability of the Input and Output Domains
3.3. Combination of Rules and Fuzzy Operation
3.4. Optimal Strategies of Games
3.4.1. Establishment of the Game Model
- (1)
- Cutting speed
- (2)
- Depth of cut
- (3)
- Feed rate
- (4)
- Tool nose runoff
3.4.2. Target of Bargaining Games
3.4.3. Mixed Strategies Game
4. Experimental Verification
4.1. Experimental Condition
- Cutting depth: 0.5 mm, 1 mm, and 1.5 mm.
- Cutting speed: The highest CNC lathe rotational speed of the tool was 3000 rpm, the diameter of the medium-carbon steel S45C used in the turning experiment was ∅45 mm, and its highest cutting speed was 339.292 m per minute. The cutting speed was set as 250 m per minute, 200 m per minute, and 150 m per minute, according to the recommendations given by the disposable blade.
- Feed rate: The feed rate of the precision turning experiment was 0.02 mm per revolution, 0.06 mm per revolution, and 0.1 mm per revolution.
4.2. Result of Single Target Production Quality Verification
4.3. Multi-Quality Optimal Strategy
4.3.1. Establish Initial Payoff Matrix Z2
- A: Tool wear
- B: Cutting noise
- A-1: Cutting speed is “low”, cutting depth is “high”, and feed rate is “high”. (Rule9)
- A-2: Cutting speed is “medium”, cutting depth is “medium”, and feed rate is “low”. (Rule13)
- A-3: Cutting speed is “medium”, cutting depth is “high”, and feed rate is “low”. (Rule16)
- A-4: Cutting speed is “medium”, cutting depth is “high”, and feed rate is “high”. (Rule18)
- B-1: Cutting speed is “low”, cutting depth is “high”, and feed rate is “high”. (Rule9)
- B-2: Cutting speed is “medium”, cutting depth is “medium”, and feed rate is “low”. (Rule13)
- B-3: Cutting speed is “medium”, cutting depth is “high”, and feed rate is “low”. (Rule16)
- B-4: Cutting speed is “medium”, cutting depth is “high”, and feed rate is “high”. (Rule18)
4.3.2. Mixed Strategy as the Problem Solver
4.3.3. Analysis of the Results of Multi-Quality Optimization
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lan, T.S.; Chuang, K.C.; Chen, Y.M. Automated Green Innovation for CNC Machining Design. J. Adv. Mech. Eng. 2018, 10, 1–11. [Google Scholar]
- Lan, T.S.; Chuang, K.C.; Chen, Y.M. Optimization of Machining Parameters Using Fuzzy Taguchi Method for Reducing Tool Wear. J. Appl. Sci. 2018, 8, 1011. [Google Scholar] [CrossRef]
- Lan, T.S.; Chuang, K.C.; Chen, Y.M. Optimal Production Parameters under Considerations of Noise Using Fuzzy Taguchi Method. In Proceedings of the 4th IEEE International Conference on Applied System Innovation, Chiba, Japan, 13–17 April 2018; pp. 354–357. [Google Scholar]
- Zhang, L.; Zhang, B.; Hong, B.; Huang, H.H. Optimization of Cutting Parameters for Minimizing Environmental Impact: Considering Energy Efficiency, Noise Emission and Economic Dimension. J. Precis. Eng. Manuf. 2018, 19, 613–624. [Google Scholar] [CrossRef]
- Hossein, K.A.E.; Kops, N. Investigation on the use of cutting temperature and tool wear in the turning of mild steel bars. J. Mech. Eng. Sci. 2017, 11, 3038–3045. [Google Scholar] [CrossRef]
- Schultheiss, F.; Zhou, J.; Gröntoft, E.; Ståhl, J.E. Sustainable machining through increasing the cutting tool utilization. J. Clean. Prod. 2013, 59, 298–307. [Google Scholar] [CrossRef]
- Weng, Y.Z. Multi-Objective Optimization of CNC Turning Parameters Using Fuzzy Analysis. Master’s Thesis, Tatung University, Taipei City, Taiwan, 2007. [Google Scholar]
- Li, Y.; Wang, H.P.; Wang, F.Y. Multi-objective Design of Process Parameter Based On Game Theory. J. Appl. Mech. Mater. 2011, 121–126, 964–967. [Google Scholar] [CrossRef]
- Zhou, G.; Lu, Q.; Xiao, Z.; Zhou, C.; Tian, C. Cutting parameter optimization for machining operations considering carbon emissions. J. Clean. Prod. 2019, 208, 937–950. [Google Scholar] [CrossRef]
- Tian, C.; Zhou, G.; Zhang, J.; Zhang, C. Optimization of cutting parameters considering tool wear conditions in low-carbon manufacturing environment. J. Clean. Prod. 2019, 226, 706–719. [Google Scholar] [CrossRef]
- Hung, L.T. Cutting Tool Science (Revised Edition); Chuan-Hwa Book Co., Ltd.: Taipei City, Taiwan, 2016. [Google Scholar]
- Chiu, M.C.; Lan, T.S. Noise control Theory and engineering design; Wu-Nan Book Inc.: Taipei City, Taiwan, 2014. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chiu, T.Y. Micro-environment Control by Using Fuzzy Theory. Master’s Thesis, National Chung Hsing University, Taichung City, Taiwan, 2015. [Google Scholar]
- Chen, S.Y. A Comparative Study of Allocation of Projects Benefit with Cooperative Game Theory. Master’s Thesis, National UNITED University, Miaoli County, Taiwan, 2015. [Google Scholar]
- Lan, C.H. Construction of Deduction Fuzzy Optimization System for Multiple-quality Production Using TRIZ and Game Theory. Master’s Thesis, Yu Da University, Miaoli County, Taiwan, 2008. [Google Scholar]
- Shapley, L.S. A Value for n-Person Games. Contributions to the Theory of Games Volume II; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Gao, Y.; Li, Z.; Wang, F.; Wang, F.; Tan, R.R.; Bi, J.; Jia, X. A game theory approach for corporate environmental risk mitigation. J. Resour. Conserv. Recycl. 2018, 130, 240–247. [Google Scholar] [CrossRef]
- Nash, J. The Bargaining Problem. J. Econom. 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Rubinstein, A. Perfect Equilibrium in a Bargaining Model. J. Econom. 1982, 50, 97–109. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Y.; Chan, F. Evidential Supplier Selection Based on DEMATEL and Game Theory. J. Fuzzy Syst. 2018, 20, 1321–1333. [Google Scholar] [CrossRef]
- Marzband, M.; Javadi, M.; Pourmousavi, S.A.; Lightbody, G. An advanced retail electricity market for active distribution systems and home microgrid interoperability based on game theory. J. Electr. Power Syst. Res. 2018, 157, 187–199. [Google Scholar] [CrossRef]
- Rasmusen, E. Games and Information: An Introduction to Game Theory; Blackwell Publishers: Hoboken, NJ, USA, 1989. [Google Scholar]
- Tsiropoulou, E.E.; Kapoukakis, A.; Papavassiliou, S.J. Energy-efficient subcarrier allocation in SC-FDMA wireless networks based on multilateral model of bargaining. In Proceedings of the 2013 IFIP Networking Conference, Brooklyn, NY, USA, 22–24 May 2013. [Google Scholar]

| Perfect Information | Imperfect Information | |
|---|---|---|
| Static | Nash Equilibrium | Bayesian Nash Equilibrium |
| Dynamic | Sub-dame Perfect Nash Equilibrium | Perfect Bayesian Nash Equilibrium |
| Parameter | Cutting Speed | Cutting Depth | Feed Rate | Tool Wear Rate | |
|---|---|---|---|---|---|
| Rule | |||||
| 1 | low | low | low | high | |
| 2 | low | low | moderate | maximum | |
| 3 | low | low | high | high | |
| 4 | low | moderate | low | moderate | |
| 5 | low | moderate | moderate | high | |
| 6 | low | moderate | high | high | |
| 7 | low | high | low | minimum | |
| 8 | low | high | moderate | minimum | |
| 9 | low | high | high | low | |
| 10 | moderate | low | low | maximum | |
| 11 | moderate | low | moderate | maximum | |
| 12 | moderate | low | high | maximum | |
| 13 | moderate | moderate | low | moderate | |
| 14 | moderate | moderate | moderate | moderate | |
| 15 | moderate | moderate | high | high | |
| 16 | moderate | high | low | low | |
| 17 | moderate | high | moderate | minimum | |
| 18 | moderate | high | high | low | |
| 19 | high | low | low | high | |
| 20 | high | low | moderate | maximum | |
| 21 | high | low | high | maximum | |
| 22 | high | moderate | low | moderate | |
| 23 | high | moderate | moderate | low | |
| 24 | high | moderate | high | low | |
| 25 | high | high | low | low | |
| 26 | high | high | moderate | minimum | |
| 27 | high | high | high | low | |
| Parameter | Cutting Speed | Cutting Depth | Feed Rate | Cutting Noise | |
|---|---|---|---|---|---|
| Rule | |||||
| 1 | low | low | low | minimum | |
| 2 | low | low | moderate | minimum | |
| 3 | low | low | high | low | |
| 4 | low | moderate | low | minimum | |
| 5 | low | moderate | moderate | low | |
| 6 | low | moderate | high | moderate | |
| 7 | low | high | low | low | |
| 8 | low | high | moderate | low | |
| 9 | low | high | high | low | |
| 10 | moderate | low | low | moderate | |
| 11 | moderate | low | moderate | moderate | |
| 12 | moderate | low | high | moderate | |
| 13 | moderate | moderate | low | low | |
| 14 | moderate | moderate | moderate | high | |
| 15 | moderate | moderate | high | high | |
| 16 | moderate | high | low | moderate | |
| 17 | moderate | high | moderate | moderate | |
| 18 | moderate | high | high | moderate | |
| 19 | high | low | low | maximum | |
| 20 | high | low | moderate | maximum | |
| 21 | high | low | high | maximum | |
| 22 | high | moderate | low | maximum | |
| 23 | high | moderate | moderate | maximum | |
| 24 | high | moderate | high | maximum | |
| 25 | high | high | low | maximum | |
| 26 | high | high | moderate | maximum | |
| 27 | high | high | high | maximum | |
| Fuzzy Term | 0 | 1.25 | 2.5 | 3.75 | 5 |
| Low | 1 | 0.5 | 0 | 0 | 0 |
| Medium | 0 | 0.5 | 1 | 0.5 | 0 |
| High | 0 | 0 | 0 | 0.5 | 1 |
| Fuzzy Term | 0 | 1.25 | 2.5 | 3.75 | 5 |
| Low | 1 | 0.5 | 0 | 0 | 0 |
| Medium | 0 | 0.5 | 1 | 0.5 | 0 |
| High | 0 | 0 | 0 | 0.5 | 1 |
| Fuzzy Term | 0 | 1.25 | 2.5 | 3.75 | 5 |
| Low | 1 | 0.5 | 0 | 0 | 0 |
| Medium | 0 | 0.5 | 1 | 0.5 | 0 |
| High | 0 | 0 | 0 | 0.5 | 1 |
| No. | Minimal | Small | Moderate | Large | Greatest |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0.84 | 0 | 0 | 0 | 0 |
| 2 | 0.68 | 0 | 0 | 0 | 0 |
| 3 | 0.52 | 0 | 0 | 0 | 0 |
| 4 | 0.36 | 0 | 0 | 0 | 0 |
| 5 | 0.2 | 0.04 | 0 | 0 | 0 |
| 6 | 0.04 | 0.2 | 0 | 0 | 0 |
| 7 | 0 | 0.36 | 0 | 0 | 0 |
| 8 | 0 | 0.52 | 0 | 0 | 0 |
| 9 | 0 | 0.84 | 0 | 0 | 0 |
| 10 | 0 | 1 | 0 | 0 | 0 |
| 11 | 0 | 0.68 | 0 | 0 | 0 |
| 12 | 0 | 0.52 | 0 | 0 | 0 |
| 13 | 0 | 0.36 | 0 | 0 | 0 |
| 14 | 0 | 0.2 | 0.04 | 0 | 0 |
| 15 | 0 | 0.04 | 0.2 | 0 | 0 |
| 16 | 0 | 0 | 0.36 | 0 | 0 |
| 17 | 0 | 0 | 0.52 | 0 | 0 |
| 18 | 0 | 0 | 0.68 | 0 | 0 |
| 19 | 0 | 0 | 0.84 | 0 | 0 |
| 20 | 0 | 0 | 1 | 0 | 0 |
| 21 | 0 | 0 | 0.84 | 0 | 0 |
| 22 | 0 | 0 | 0.68 | 0 | 0 |
| 23 | 0 | 0 | 0.52 | 0 | 0 |
| 24 | 0 | 0 | 0.36 | 0 | 0 |
| 25 | 0 | 0 | 0.2 | 0 | 0 |
| 26 | 0 | 0 | 0.04 | 0.04 | 0 |
| 27 | 0 | 0 | 0 | 0.2 | 0 |
| 28 | 0 | 0 | 0 | 0.36 | 0 |
| 29 | 0 | 0 | 0 | 0.52 | 0 |
| 30 | 0 | 0 | 0 | 0.68 | 0 |
| 31 | 0 | 0 | 0 | 0.84 | 0 |
| 32 | 0 | 0 | 0 | 1 | 0 |
| 33 | 0 | 0 | 0 | 0.84 | 0 |
| 34 | 0 | 0 | 0 | 0.68 | 0.04 |
| 35 | 0 | 0 | 0 | 0.52 | 0.2 |
| 36 | 0 | 0 | 0 | 0.36 | 0.36 |
| 37 | 0 | 0 | 0 | 0.2 | 0.52 |
| 38 | 0 | 0 | 0 | 0.04 | 0.68 |
| 39 | 0 | 0 | 0 | 0 | 0.84 |
| 40 | 0 | 0 | 0 | 0 | 1 |
| Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | Tool Wear (μm−2) |
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 4.38 |
| 3 | 2 | 2 | 1 | 4.13 |
| 3 | 2 | 2 | 2 | 3.87 |
| 1 | 2 | 2 | 1 | 4.21 |
| 2 | 3 | 2 | 2 | 2.97 |
| 1 | 2 | 2 | 3 | 4.13 |
| 2 | 2 | 1 | 1 | 4.38 |
| 2 | 2 | 2 | 1 | 4.04 |
| 2 | 1 | 3 | 3 | 4.13 |
| 1 | 2 | 1 | 3 | 4.55 |
| 1 | 3 | 3 | 2 | 3.38 |
| Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | Cutting Noise (dB) |
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 82.83 |
| 1 | 2 | 2 | 2 | 81.73 |
| 3 | 2 | 2 | 2 | 85.97 |
| 2 | 1 | 2 | 2 | 82.61 |
| 2 | 3 | 2 | 2 | 82.91 |
| 2 | 2 | 1 | 2 | 82.55 |
| 2 | 2 | 3 | 2 | 82.93 |
| 2 | 2 | 2 | 1 | 82.79 |
| 2 | 2 | 2 | 3 | 82.81 |
| 1 | 1 | 1 | 1 | 81.5 |
| 1 | 3 | 3 | 2 | 81.94 |
| B | |||||
|---|---|---|---|---|---|
| B-1 | B-2 | B-3 | B-4 | ||
| A | A-1 | ||||
| A-2 | |||||
| A-3 | |||||
| A-4 | |||||
| B | |||||
|---|---|---|---|---|---|
| B-1 | B-2 | B-3 | B-4 | ||
| A | A-1 | (Pa1,Pb1) | (Pa2,Pb2) | (Pa3,Pb3) | (Pa4,Pb4) |
| A-2 | (Pa5,Pb5) | (Pa6,Pb6) | (Pa7,Pb7) | (Pa8,Pb8) | |
| A-3 | (Pa9,Pb9) | (Pa10,Pb10) | (Pa11,Pb11) | (Pa12,Pb12) | |
| A-4 | (Pa13,Pb13) | (Pa14,Pb14) | (Pa15,Pb15) | (Pa16,Pb16) | |
| B | |||
|---|---|---|---|
| B-1 | B-2 | ||
| A | A-1 | (Pa1,Pb1) | (Pa2,Pb2) |
| A-2 | (Pa3,Pb3) | (Pa4,Pb4) | |
| Player | Optimal Strategy | Adoption Probability (%) |
|---|---|---|
| Tool wear (S) | ||
| Cutting noise (Z) |
| Control Parameter | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| A: Depth of cut (mm) | 0.5 | 1 | 1.5 |
| B: Cutting speed (m/min) | 150 | 200 | 250 |
| C: Feed rate (mm/rev) | 0.02 | 0.06 | 0.1 |
| D: Tool nose runoff (mm) | −0.1 | ±0.03 | 0.1 |
| Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | Tool Wear (μm−2) |
|---|---|---|---|---|
| 200 | 1 | 0.06 | ±0.03 | 4.38 |
| Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | Cutting Noise (dB) |
|---|---|---|---|---|
| 200 | 1 | 0.06 | ±0.03 | 82.83 |
| Tool Wear | Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | (μm−2) |
| Cutting speed | 250 | 1 | 0.06 | ±0.03 | 3.87 |
| Depth of cut | 200 | 1.5 | 0.06 | ±0.03 | 2.97 |
| Feed rate | 200 | 1 | 0.02 | ±0.03 | 4.55 |
| Median | 200 | 1 | 0.06 | ±0.03 | 4.38 |
| Cutting Noise | Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | (dB) |
| Cutting speed | 150 | 1 | 0.06 | ±0.03 | 81.73 |
| Depth of cut | 200 | 0.5 | 0.06 | ±0.03 | 82.61 |
| Feed rate | 200 | 1 | 0.02 | ±0.03 | 82.55 |
| Median | 200 | 1 | 0.06 | ±0.03 | 82.83 |
| B | |||||
|---|---|---|---|---|---|
| B-1 | B-2 | B-3 | B-4 | ||
| A | A-1 | (9.966,9.966) | (9.966,9.966) | (9.966,20) | (9.966,20) |
| A-2 | (20,9.966) | (20,9.966) | (20,20) | (20,20) | |
| A-3 | (9.966,9.966) | (9.966,9.966) | (9.966,20) | (9.966,20) | |
| A-4 | (1.769,9.966) | (1.769,9.966) | (1.769,20) | (1.769,20) | |
| B | |||
|---|---|---|---|
| B-1 | B-2 | ||
| A | A-1 | (9.966,9.966) | (9.966,9.966) |
| A-3 | (9.966,9.966) | (9.966,9.966) | |
| B | |||
|---|---|---|---|
| B-1 | B-2 | ||
| A | A-1 | (3.38,81.94) | (3.38,82.55) |
| A-3 | (4.38,81.94) | (4.38,82.55) | |
| Player | Optimal Strategy | Adoption Probability (%) |
|---|---|---|
| Tool wear (S) | Increasing the cutting depth | 100 |
| Cutting noise (Z) | Reducing the cutting speed | 100 |
| Cutting Speed (m/min) | Depth of Cut (mm) | Feed Rate (mm/rev) | Tool Nose Runoff (mm) | Comparison | ||
|---|---|---|---|---|---|---|
| Multi-Quality Optimization | 150 | 1.5 | 0.1 | ±0.03 | Tool wear | 3.38 (μm−2) |
| Cutting noise | 81.94 (dB) | |||||
| Median | 200 | 1 | 0.06 | ±0.03 | Tool wear | 4.38 (μm−2) |
| Cutting noise | 82.83 (dB) | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuang, K.-C.; Lan, T.-S.; Zhang, L.-P.; Chen, Y.-M.; Dai, X.-J. Parameter Optimization for Computer Numerical Controlled Machining Using Fuzzy and Game Theory. Symmetry 2019, 11, 1450. https://doi.org/10.3390/sym11121450
Chuang K-C, Lan T-S, Zhang L-P, Chen Y-M, Dai X-J. Parameter Optimization for Computer Numerical Controlled Machining Using Fuzzy and Game Theory. Symmetry. 2019; 11(12):1450. https://doi.org/10.3390/sym11121450
Chicago/Turabian StyleChuang, Kai-Chi, Tian-Syung Lan, Lie-Ping Zhang, Yee-Ming Chen, and Xuan-Jun Dai. 2019. "Parameter Optimization for Computer Numerical Controlled Machining Using Fuzzy and Game Theory" Symmetry 11, no. 12: 1450. https://doi.org/10.3390/sym11121450
APA StyleChuang, K.-C., Lan, T.-S., Zhang, L.-P., Chen, Y.-M., & Dai, X.-J. (2019). Parameter Optimization for Computer Numerical Controlled Machining Using Fuzzy and Game Theory. Symmetry, 11(12), 1450. https://doi.org/10.3390/sym11121450





