Optimization of Flocculation Settling Parameters of Whole Tailings Based on Spatial Difference Algorithm
Abstract
:1. Introduction
2. Algorithm Definitions
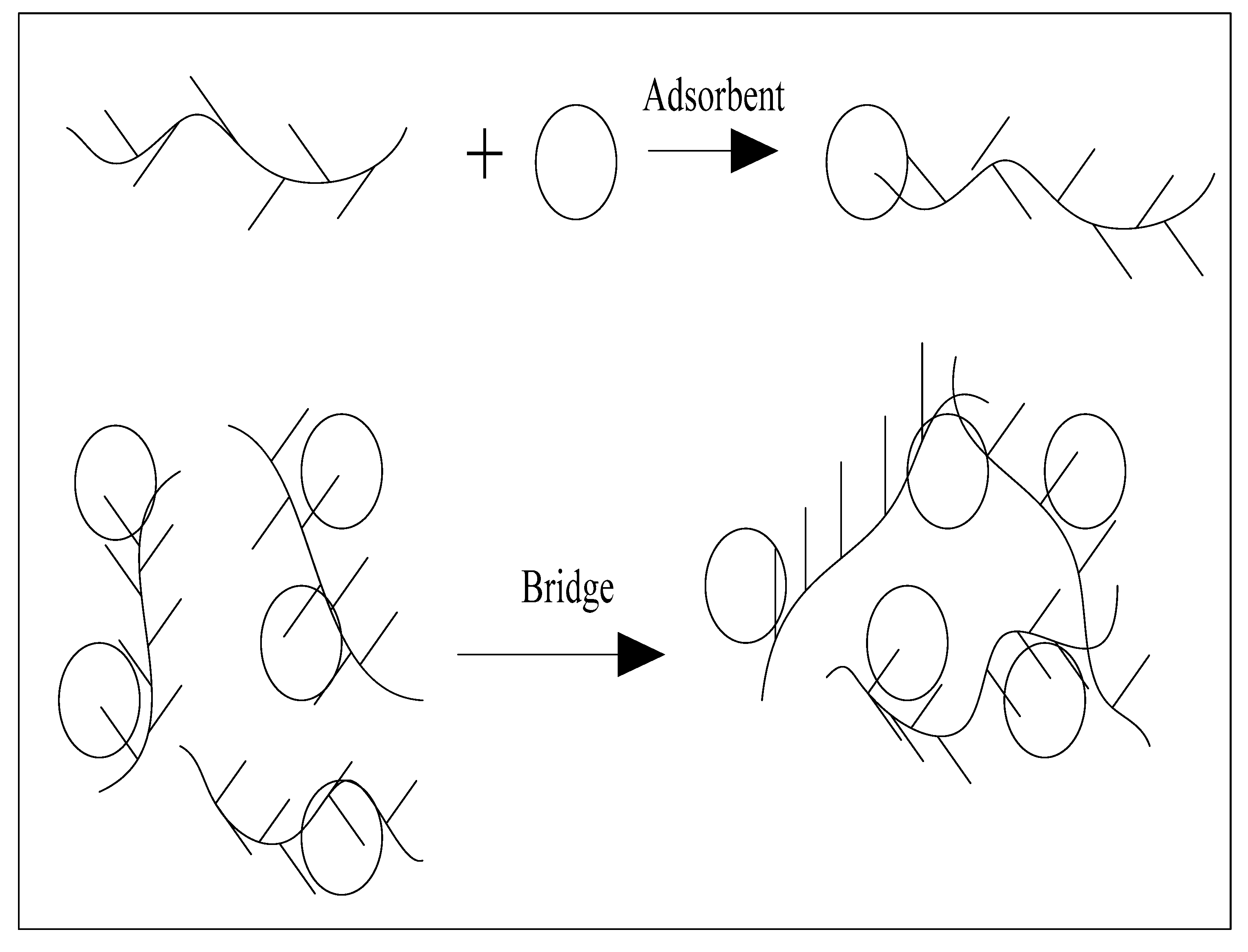
2.1. Mechanism of Flocculation Action
2.2. Input Factor Analysis of Flocculation Settlement Parameters of Whole Tailings
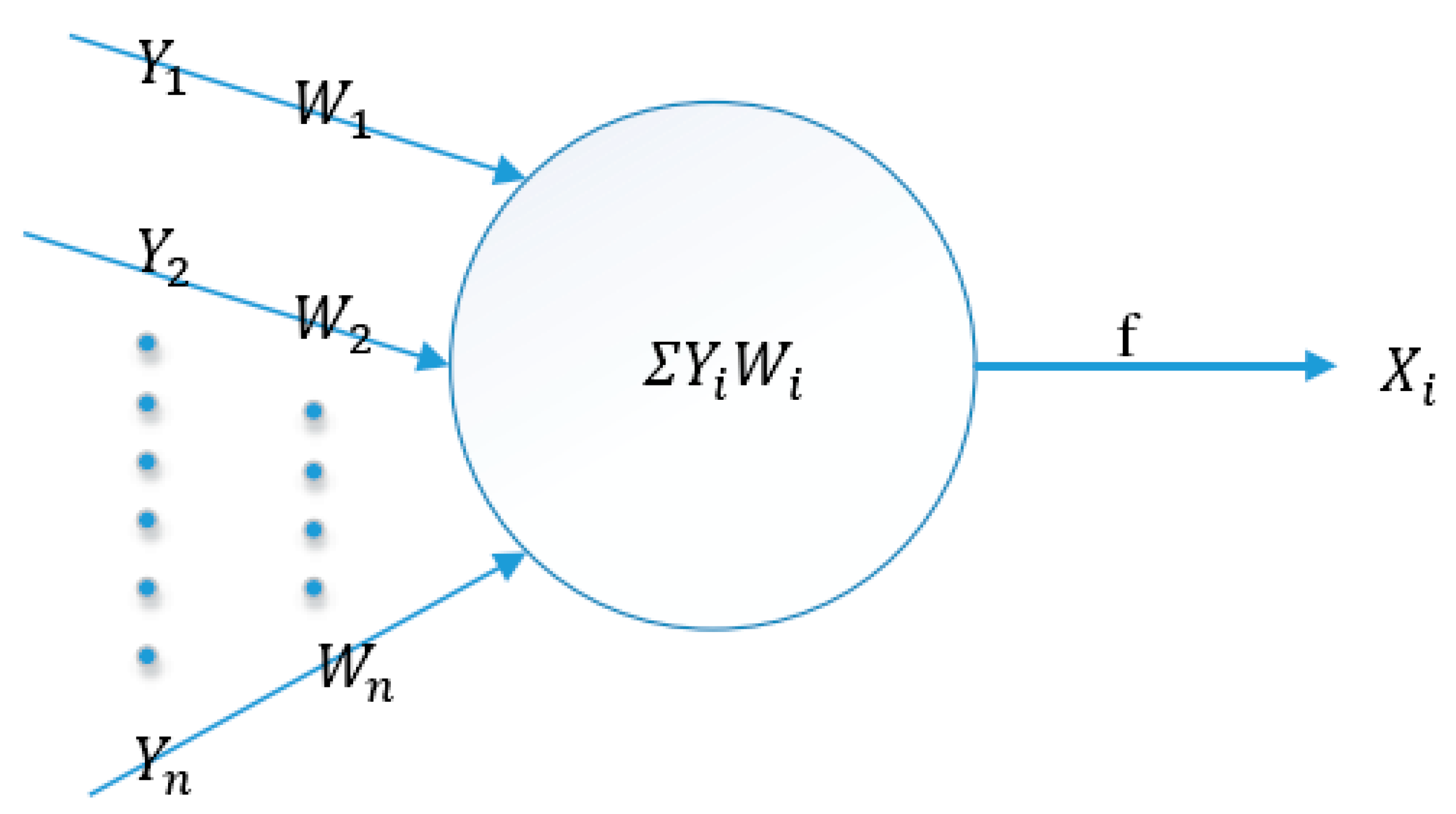
2.3. Analysis of Output Factor of Flocculation Settlement Parameters of Whole Tailings
2.4. Parameter Optimization of Spatial Difference Algorithm
2.4.1. Inverse Distance Weighted (IDW) Difference Method
2.4.2. Spline Method
2.4.3. Kriging Method
2.5. Verification of the Accuracy of the Results of Spatial Difference Optimization Model
3. Results
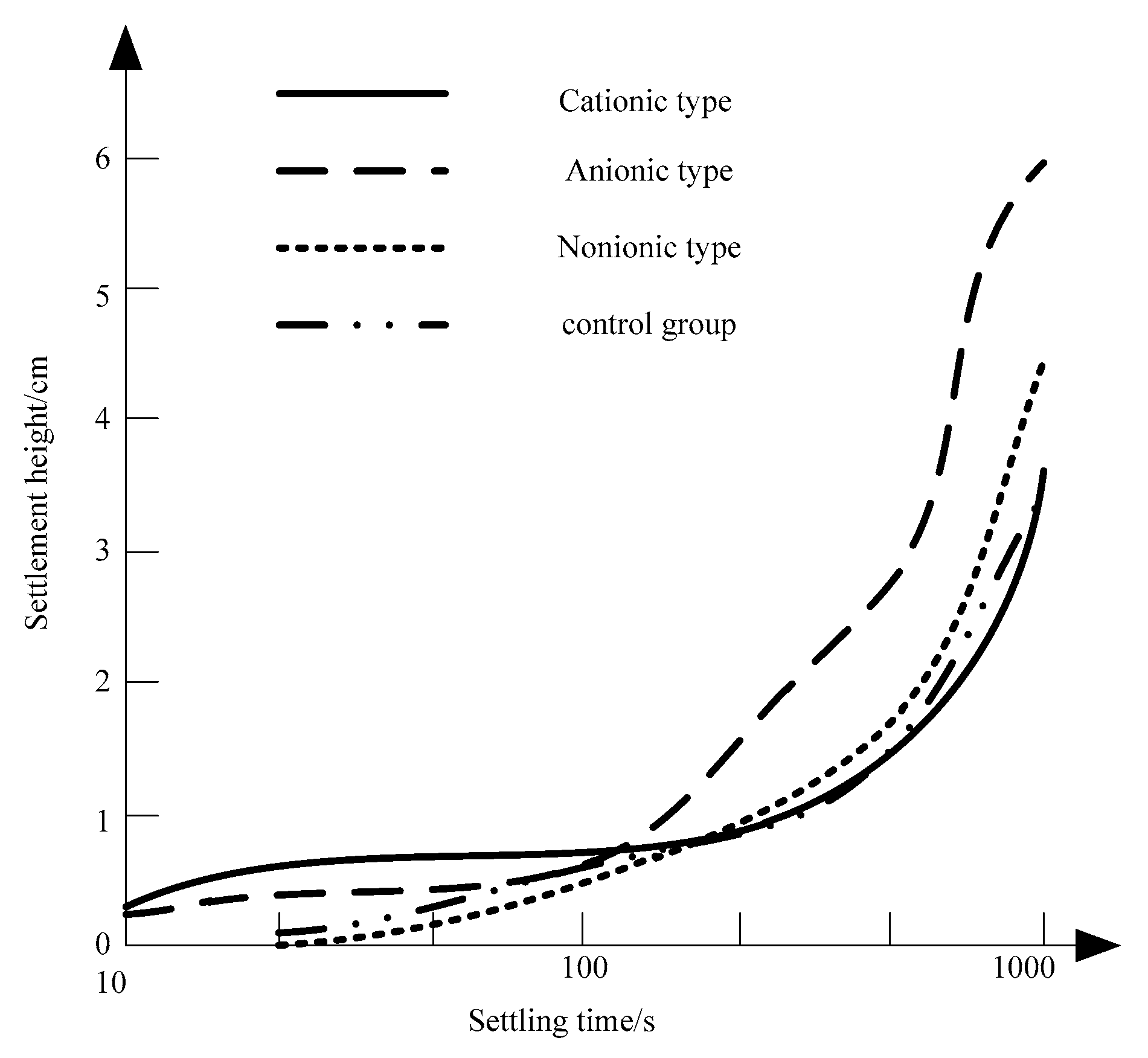
3.1. Physical Properties of Whole Tailings
3.2. Establishment of the Sample Set
3.3. Parameter Optimization Model of Spatial Difference Algorithm
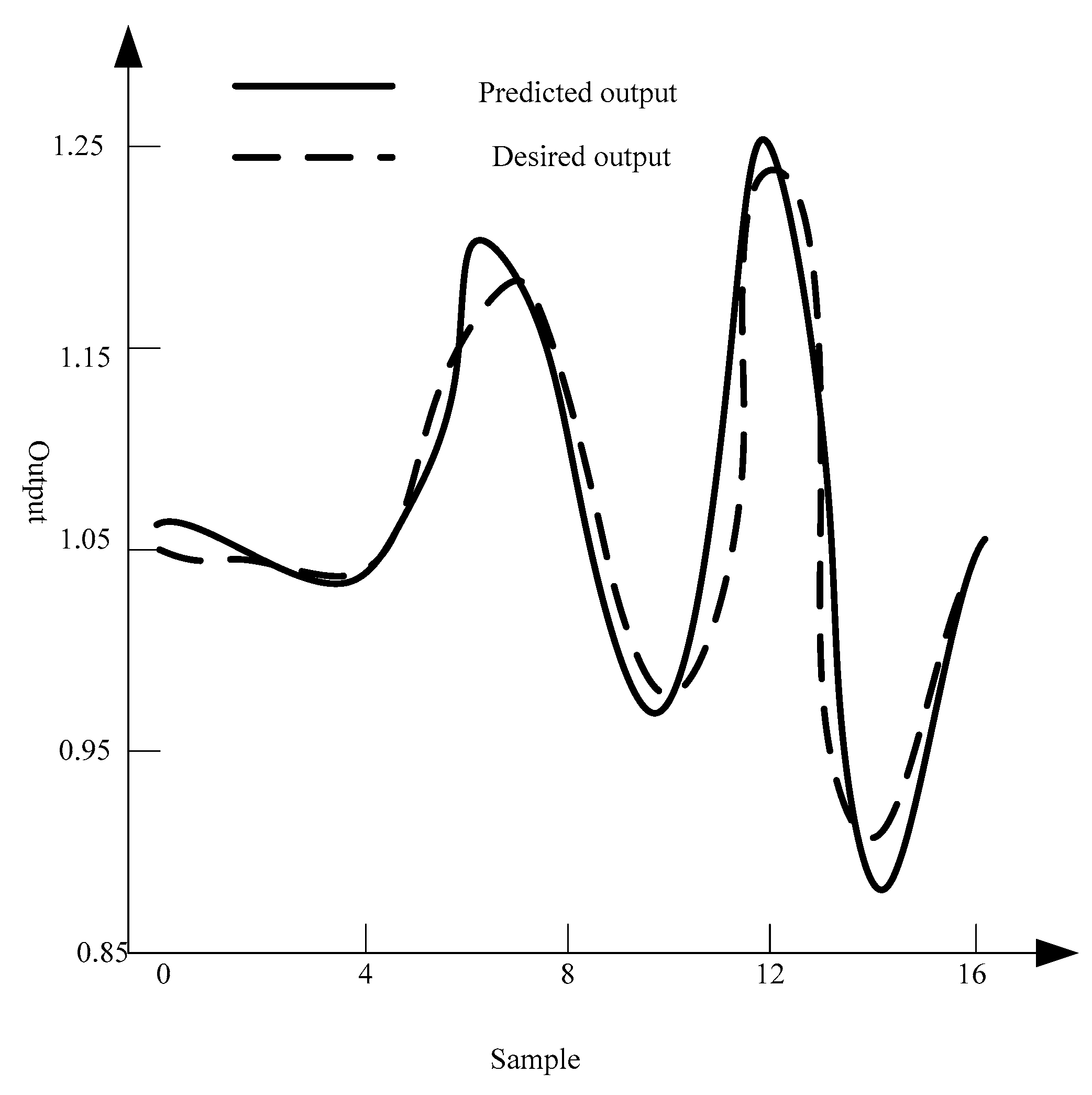
3.4. Error Analysis
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Çırak, M.; Çetin, H. Optimization of Coagulation-Flocculation Process for Treatment of a Colloidal Suspension Containing Dolomite/Clay/Borax. Int. J. Min. Process. 2017, 159, 30–41. [Google Scholar] [CrossRef]
- Lu, Q.; Yan, B.; Xie, L. A Two-Step Flocculation Process on Oil Sands Tailings Treatment Using Oppositely Charged Polymer Flocculation. Sci. Total. Environ. 2016, 565, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Angle, W.; Gharib, S. Effects of Sand and Flocculation on Dewaterability of Kaolin Slurries Aimed at Treating Mature Oil Sands Tailings. Chem. Eng. Res. Des. 2017, 125, 306–318. [Google Scholar] [CrossRef]
- Botha, L.; Soares, P. The Influence of Tailings Composition on Flocculation. Can. J. Chem. Eng. 2015, 93, 1514–1523. [Google Scholar] [CrossRef]
- Demoz, A. Scaling Inline Static Mixers for Flocculation of Oil Sand Mature Fine Tailings. AIChE J. 2015, 61, 1747–1757. [Google Scholar] [CrossRef]
- Mandik, I.; Cheirsilp, B.; Boonsawang, P.; Prasertsan, P. Optimization of Flocculation Efficiency of Lipid-Rich Marine Chlorella sp. Biomass and Evaluation of Its Composition in Different Cultivation Modes. Bioresource Technol. 2015, 182, 89–97. [Google Scholar] [CrossRef]
- Agbovi, K.; Wilson, D. Flocculation Optimization of Orthophosphate with FeCl3 and Alginate Using the Box–Behnken Response Surface Methodology. Ind. Eng. Chem. Res. 2017, 56, 3145–3155. [Google Scholar] [CrossRef]
- Quinlan, J.; Tam, C. Water Treatment Technologies for the Remediation of Naphthenic Acids in Oil Sands Process-Affected Water. Chem. Eng. J. 2015, 279, 696–714. [Google Scholar] [CrossRef]
- Wang, L.; Wan, L.; Zhang, Y.; Lee, D.; Liu, X.; Chen, X.; Tay, J. Mechanism of Enhanced Sb(V) Removal from Aqueous Solution Using Chemically Modified Aerobic Granules. J. Hazard Mater. 2015, 284, 43–49. [Google Scholar] [CrossRef]
- Bayabil, K.; Stoof, R.; Lehmann, C.; Yitaferu, B.; Steenhuis, T. Assessing the Potential of Biochar and Charcoal to Improve Soil Hydraulic Properties in the Humid Ethiopian Highlands: The Anjeni Watershed. Geoderma 2015, 243–244, 115–123. [Google Scholar] [CrossRef]
- Hashemzadeh, F.; Gaffarinejad, A.; Rahimi, R. Porous p-NiO/n-Nb2O5 Nanocomposites Prepared by an EISA Route with Enhanced Photocatalytic Activity in Simultaneous Cr(VI) Reduction and Methyl Orange Decolorization under Visible Light Irradiation. J. Hazard Mater. 2015, 286, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Oladipo, A.; Gazi, M.; Yilmaz, E. Single and Binary Adsorption of Azo and Anthraquinone Dyes by Chitosan-Based Hydrogel: Selectivity Factor and Box-Behnken Process Design. Chem. Eng. Res. Des. 2015, 104, 264–279. [Google Scholar] [CrossRef]
- Motta, L.; Gaikwad, R.; Botha, L.; Soares, J. Quantifying the Effect of Polyacrylamide Dosage, Na+ and Ca2+ Concentrations, and Clay Particle Size on the Flocculation of Mature Fine Tailings with Robust Statistical Methods. Chemosphere 2018, 208, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Botha, L.; Davey, S.; Nguyen, B.; Swarnakar, A.; Rivard, E.; Soares, J. Flocculation of Oil Sands Tailings by Hyperbranched Functionalized Polyethylenes (HBfPE). Miner. Eng. 2017, 108, 71–82. [Google Scholar] [CrossRef]
- Reis, G.; Oliveira, S.; Palhares, N.; Spinelli, L.; Lucas, E.; Vedoy, D.; Asare, E.; Soares, J. Using Acrylamide/Propylene Oxide Copolymers to Dewater and Densify Mature Fine Tailings. Miner. Eng. 2016, 95, 29–39. [Google Scholar] [CrossRef]
- Nassar, N.; Betancur, S.; Acevedo, S.; Franco, C.; Cortés, F. Development of a Population Balance Model to Describe the Influence of Shear and Nanoparticles on the Aggregation and Fragmentation of Asphaltene Aggregates. Ind. Eng. Chem. Res. 2015, 55, 146–148. [Google Scholar] [CrossRef]
- Ochando-Pulido, M.; Stoller, M.; Palma, D.; Martínez-Ferez, A. On the Optimization of a Flocculation Process as Fouling Inhibiting Pretreatment on an Ultrafiltration Membrane during Olive Mill Effluents Treatment. Desalination 2016, 393, 151–158. [Google Scholar] [CrossRef]
- Xiao, S.; Song, Y.; Tian, Z.; Tu, X.; Hu, X.; Liu, R. Enhanced Mineralization of Antibiotic Berberine by the Photoelectrochemical Process in Presence of Chlorides and Its Optimization by Response Surface Methodology. Environ. Earth Sci. 2015, 73, 4947–4955. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Liu, L.; Jiang, X.; Zhang, K.; Zheng, T.; Wang, H. First Evidence of Bioflocculation from ShinellaAlbus with Flocculation Activity on Harvesting of Chlorella Vulgaris Biomass. Bioresource Technol. 2016, 218, 807–815. [Google Scholar] [CrossRef]
- Buyel, F.; Fischer, R. A Juice Extractor Can Simplify the Downstream Processing of Plant-Derived Biopharmaceutical Proteins Compared to Blade-Based Homogenizers. Process.Biochem. 2015, 50, 859–866. [Google Scholar] [CrossRef]
- Mnak, G.; Altun, I.; Olgun, M. Fixed Points of f-contractive Type Fuzzy Mappings. J. Intell. Fuzzy Syst. 2017, 33, 1435–1439. [Google Scholar] [CrossRef]
- Li, P. Content Aware Scheduling Algorithm for SVC Streaming over OFDM. J. ChinaAcad. Electron. Inf. Technol. 2015, 10, 169–174. [Google Scholar]
- Wang, T.; Cai, T.; Duan, X. Digital Realization of Simplified Three-Level SVM for Vienna Rectifier. J. Power Supply 2017, 15, 72–79. [Google Scholar]
- Dewasurendra, M.; Vajravelu, K. On the Method of Inverse Mapping for Solutions of Coupled Systems of Nonlinear Differential Equations Arising in Nanofluid Flow, Heat and Mass Transfer. Appl. Math. Nonlinear Sci. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Delgado, J.; Peña, J.M. Monotonicity Preserving Representations of Curves and Surfaces. Appl. Math. Nonlinear Sci. 2016, 1, 517–528. [Google Scholar] [CrossRef]
- Tan, S.; Wang, H.; Huang, Q. Implement of Five-Level Inverter SVPWM Algorithm Based on FPGA. Chin. J. Power Sources 2015, 39, 2240–2243. [Google Scholar]
- Yao, T.; Zheng, S. FPGA Design Space Circular Interpolation Controller and Implementation. Autom.Instrum. 2015, 1, 161–163. [Google Scholar]
- Wu, F.; Lv, L.; Chen, R. Based on Analysis of Time Scale Cloud Space Grid Resource Scheduling Algorithm. Compu. Simul. 2015, 32, 131–135. [Google Scholar]
- Gao, W.; Wang, W. New Isolated Toughness Condition for Fractional (g, f, n)—Critical Graph. Colloq. Math. 2017, 147, 55–65. [Google Scholar] [CrossRef]
| Particle Size/mm | The Mass Fraction/% |
|---|---|
| > 5.000 | - |
| 2.000 < size ≤ 5.000 | 1.5 |
| 0.500 < size ≤ 2.000 | 10.7 |
| 0.075 < size ≤ 0.250 | 10.9 |
| 0.050 < size ≤ 0.075 | 15.3 |
| 0.005 < size ≤ 0.050 | 54.8 |
| ≤ 0.005 | 5.2 |
| Parameter | The Numerical |
|---|---|
| The proportion of | 2.79 |
| The median grain d50/mm | 0.034 |
| Particle size < 74 μm Particle mass fraction | 75.20 |
| Effective particle size d10 | 0.08 |
| Coefficient of unevenness Cu | 4.7 |
| The permeability coefficient | 2.8 |
| Level | Influencing Factor | |
|---|---|---|
| Flocculation Consumption/(g·t−1) | ||
| T1 | 10 | 15 |
| T2 | 15 | 20 |
| T3 | 20 | 25 |
| T4 | 25 | 30 |
| Experiment No. | Flocculent Unit Consumption q/(g·t−1) | Sedimentation Velocity v/(m·h−1) | |
|---|---|---|---|
| 1 | 10 | 15 | 1.06 |
| 2 | 15 | 15 | 1.09 |
| 3 | 20 | 15 | 1.07 |
| 4 | 25 | 15 | 1.04 |
| 5 | 10 | 20 | 1.14 |
| 6 | 15 | 20 | 1.22 |
| 7 | 20 | 20 | 1.17 |
| 8 | 25 | 20 | 1.10 |
| 9 | 10 | 25 | 1.00 |
| 10 | 15 | 25 | 1.30 |
| 11 | 20 | 25 | 1.27 |
| 12 | 25 | 25 | 1.14 |
| 13 | 10 | 30 | 0.90 |
| 14 | 15 | 30 | 1.12 |
| 15 | 20 | 30 | 1.02 |
| 16 | 25 | 30 | 0.99 |
| Experiment No. | Flocculent Unit Consumption q/(g·t−1) | Sedimentation Velocity v/(m·h−1) | |
|---|---|---|---|
| 1 | 0.171 | 0.379 | 0.008 |
| 2 | 0.389 | 0.379 | 0.009 |
| 3 | 0.586 | 0.379 | 0.008 |
| 4 | 0.794 | 0.379 | 0.007 |
| 5 | 0.171 | 0.586 | 0.011 |
| 6 | 0.389 | 0.586 | 0.014 |
| 7 | 0.586 | 0.586 | 0.012 |
| 8 | 0.794 | 0.586 | 0.009 |
| 9 | 0.171 | 0.794 | 0.005 |
| 10 | 0.379 | 0.794 | 0.018 |
| 11 | 0.586 | 0.794 | 0.016 |
| 12 | 0.794 | 0.794 | 0.011 |
| 13 | 0.171 | 1.000 | 0.000 |
| 14 | 0.379 | 1.000 | 0.010 |
| 15 | 0.586 | 1.000 | 0.060 |
| 16 | 0.794 | 1.000 | 0.005 |
| Serial Number | Actual Value of Settlement Velocity/(cm·h−1) | Optimum Settlement Velocity Value/(cm·h−1) | Relative Error/% |
|---|---|---|---|
| 1 | 302.65 | 313.23 | 3.5 |
| 2 | 167.87 | 172.45 | 2.7 |
| 3 | 112.56 | 111.32 | 1.1 |
| 4 | 156.76 | 155.43 | 0.8 |
| 5 | 213.45 | 215.65 | 1.0 |
| 6 | 222.45 | 219.89 | 1.5 |
| 7 | 324.56 | 325.76 | 0.3 |
| 8 | 325.67 | 332.54 | 2.1 |
| 9 | 312.35 | 315.26 | 0.9 |
| 11 | 265.45 | 270.21 | 1.7 |
| 12 | 225.65 | 228.65 | 1.3 |
| 13 | 314.32 | 318.21 | 1.2 |
| 14 | 253.76 | 256.34 | 1.0 |
| 15 | 235.65 | 237.65 | 0.8 |
| 16 | 218.76 | 220.12 | 0.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Chen, J.; Wang, C. Optimization of Flocculation Settling Parameters of Whole Tailings Based on Spatial Difference Algorithm. Symmetry 2019, 11, 1371. https://doi.org/10.3390/sym11111371
Huang Y, Chen J, Wang C. Optimization of Flocculation Settling Parameters of Whole Tailings Based on Spatial Difference Algorithm. Symmetry. 2019; 11(11):1371. https://doi.org/10.3390/sym11111371
Chicago/Turabian StyleHuang, Yanlong, Jianzhong Chen, and Chuanzhen Wang. 2019. "Optimization of Flocculation Settling Parameters of Whole Tailings Based on Spatial Difference Algorithm" Symmetry 11, no. 11: 1371. https://doi.org/10.3390/sym11111371
APA StyleHuang, Y., Chen, J., & Wang, C. (2019). Optimization of Flocculation Settling Parameters of Whole Tailings Based on Spatial Difference Algorithm. Symmetry, 11(11), 1371. https://doi.org/10.3390/sym11111371





