Dynamic Soft Sensor Development for Time-Varying and Multirate Data Processes Based on Discount and Weighted ARMA Models
Abstract
:1. Introduction
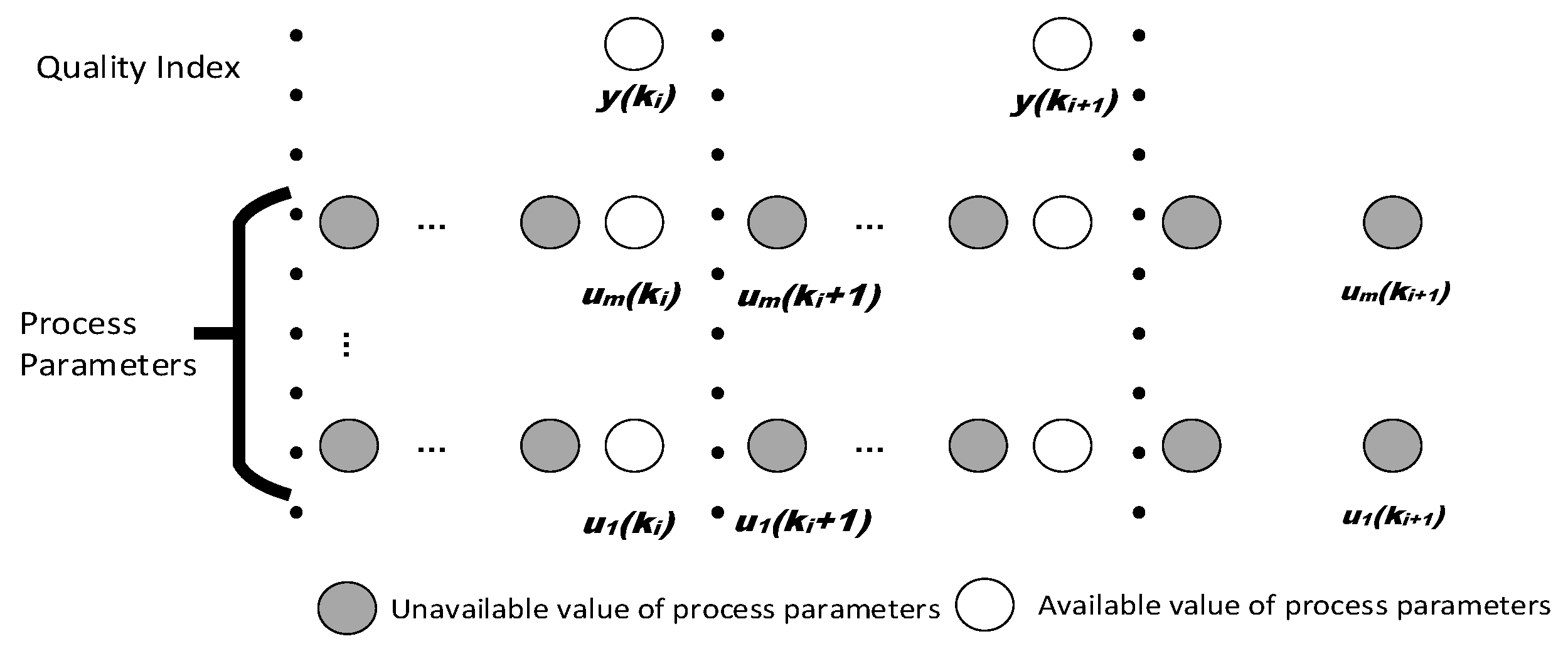
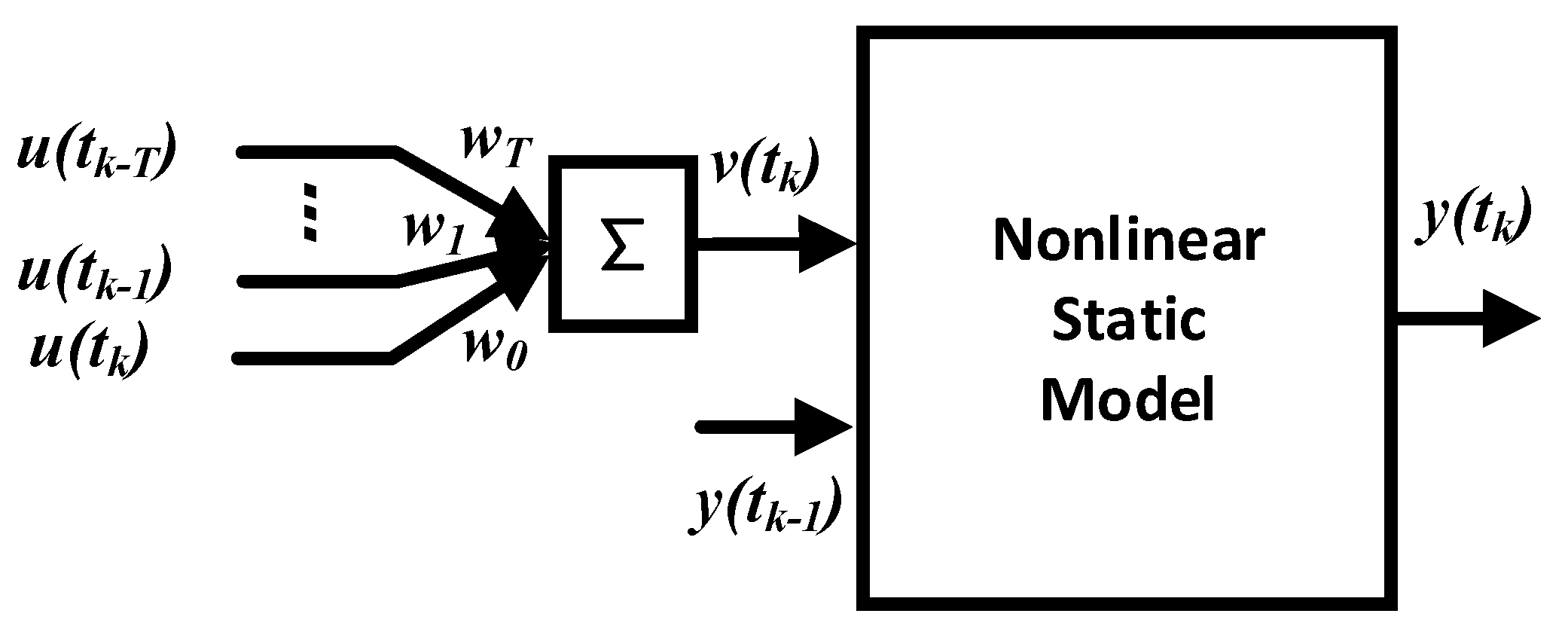
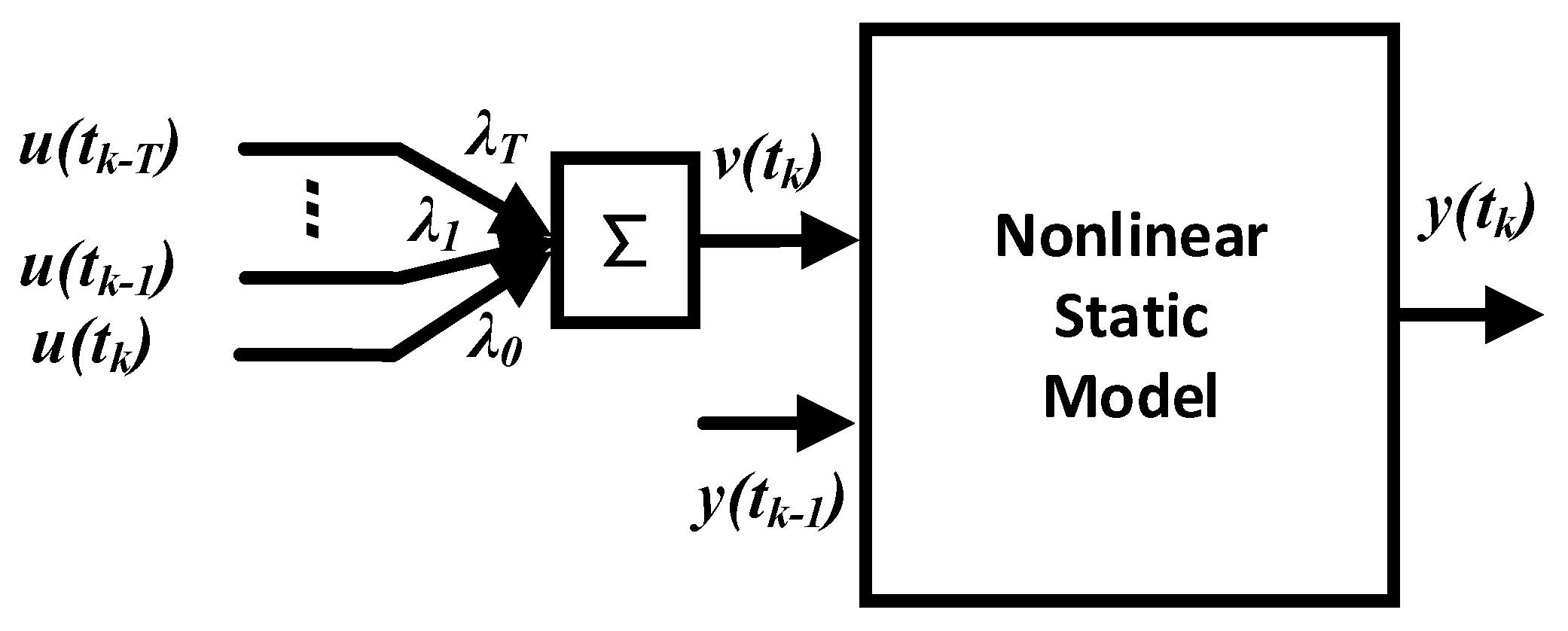
2. Problem Statement
3. DSSMI-AMWPDD
3.1. AMWPDD Sample Data Processing
- (1)
- λ1 + λ2 + …… + λT = 1;
- (2)
- λ1 > λ2 > …… > λT;
3.2. LSSVM-Based SSMI
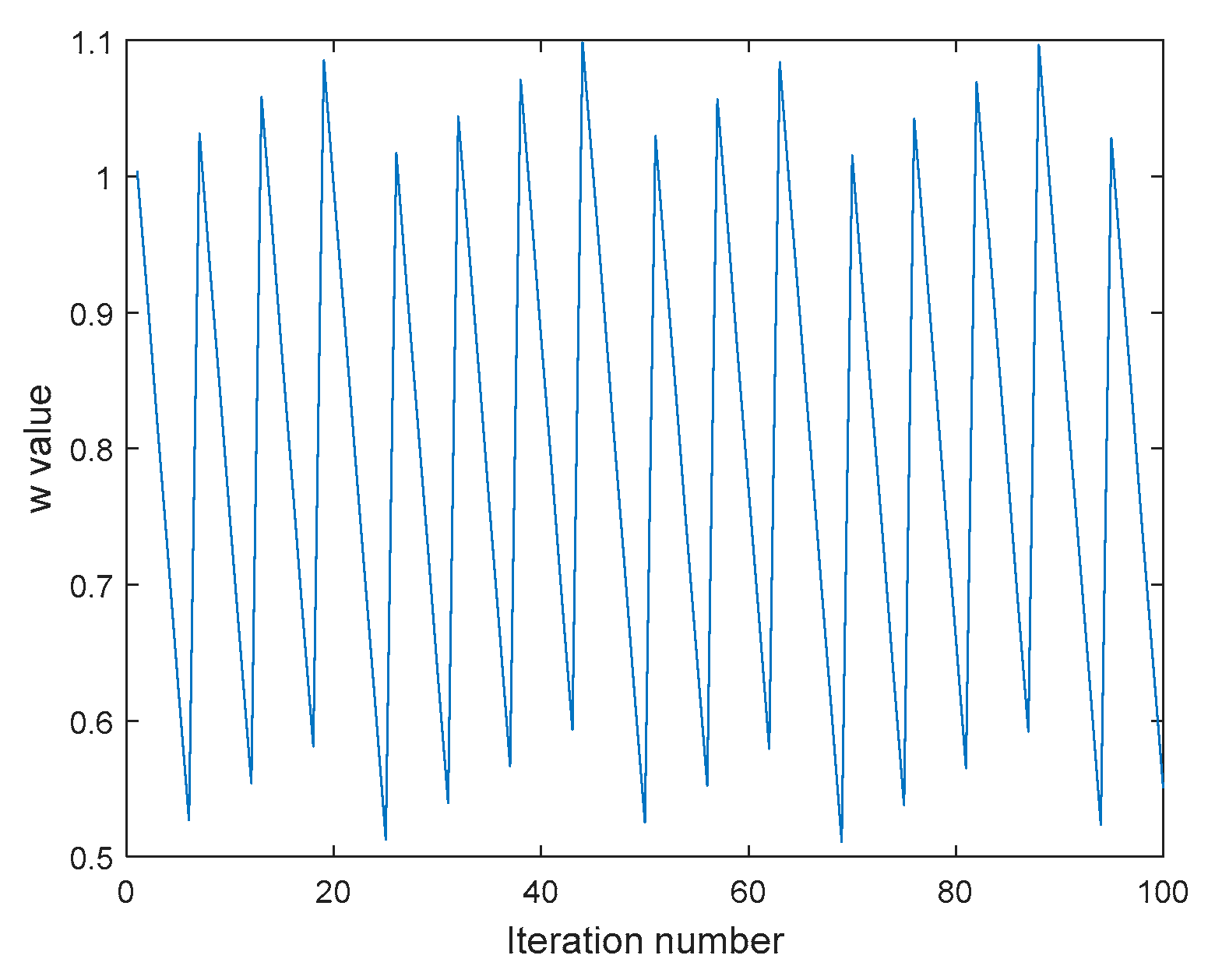
4. Model Parameter Optimization Based on ωDPSO
5. Simulation and Analysis
5.1. CSTR Simulation Experiment and Result Analysis
5.1.1. SSMI Based on Static Data
5.1.2. SSMI Based on Dynamic Fusion Data
5.1.3. Comparison and Analysis
5.2. Simulation Experiment and Result Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Y.; Luo, X. A novel calibration approach of soft sensor based on multirate data fusion technology. J. Process Control 2010, 20, 1252–1260. [Google Scholar] [CrossRef]
- Gopakumar, V.; Tiwari, S.; Rahman, I. A deep learning based data driven soft sensor for bioprocesses. Biol. Eng. J. 2018, 136, 28–39. [Google Scholar] [CrossRef]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Yan, W.; Guo, P.; Tian, Y.; Gao, J. A framework and modeling method of data-driven soft sensors based on semi-supervised gaussian regression. Ind. Eng. Chem. Res. 2016, 55, 7394–7401. [Google Scholar] [CrossRef]
- Zhao, Y.; Fatehi, A.; Huang, B. A data-driven hybrid arx and markov-chain modeling approach to process identification with time varying time delays. IEEE Trans. Ind. Electr. 2017, 64, 4226–4236. [Google Scholar] [CrossRef]
- Wang, X.; Huang, L.; Yang, C. Prediction model of slurry ph based on mechanism and error compensation for mineral flotation process. Chin. J. Chem. Eng. 2018, 26, 174–180. [Google Scholar] [CrossRef]
- Liu, S.M.; Wu, Y.P.; Che, H.; Yipeng, W.; Han, C. Monitoring data quality control for a water distribution system using data self-recognition. J. Tsinghua Univ. (Sci. Technol.) 2017, 57, 999–1003. [Google Scholar] [CrossRef]
- Di, K.S.; Wang, Y.H.; Shang, C.; Huang, D.X. Dynamic soft sensor modeling based on nonlinear slow feature analysis. Comput. Appl. Chem. 2016, 33, 1160–1164. [Google Scholar] [CrossRef]
- Liu, J.; Vitelli, V.; Zio, E.; Seraoui, R. A novel dynamic-weighted probabilistic support vector regression-based ensemble for prognostics of time series data. IEEE Trans. Reliab. 2015, 64, 1203–1213. [Google Scholar] [CrossRef]
- Osorio, D.; Ricardo Pérez-Correa, J.; Agosin, E.; Cabrera, M. Soft-sensor for on-line estimation of ethanol concentrations in wine stills. J. Food Eng. 2008, 87, 571–577. [Google Scholar] [CrossRef]
- Shang, C.; Gao, X.; Yang, F.; Huang, D.X. Novel bayesian framework for dynamic soft sensor based on support vector machine with finite impulse response. IEEE Trans. Control Syst. Technol. 2014, 22, 1550–1557. [Google Scholar] [CrossRef]
- Gao, X.; Yang, F.; Huang, D.; Ding, Y. An iterative two-level optimization method for the modeling of wiener structure nonlinear dynamic soft sensors. Ind. Eng. Chem. Res. 2014, 53, 1172–1178. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, X. Modeling study of nonlinear dynamic soft sensors and robust parameter identification using swarm intelligent optimization CS-NLJ. J. Process Control 2017, 58, 33–45. [Google Scholar] [CrossRef]
- Yuan, P.; Zhang, B.; Mao, Z. A self-tuning control method for wiener nonlinear systems and its application to process control problems. Chin. J. Chem. Eng. 2017, 25, 193–201. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, X. Time series estimation of gas sensor baseline drift using arma and kalman based models. Sens. Rev. 2016, 36, 34–39. [Google Scholar] [CrossRef]
- Sun, W.; He, Y.J.; Chang, H. Forecasting Fossil Fuel Energy Consumption for Power Generation Using QHSA-Based LSSVM Model. Energies 2015, 8, 939–959. [Google Scholar] [CrossRef]
- Hong, X.; Chen, S. The system identification and control of hammerstein system using non-uniform rational b-spline neural network and particle swarm optimization. Neurocomputing 2012, 82, 216–223. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Aburomman, A.A.; Reaz, M.B.I. A novel svm-knn-pso ensemble method for intrusion detection system. Appl. Soft Comput. 2015, 38, 360–372. [Google Scholar] [CrossRef]
- Hu, W.; Yan, L.; Liu, K.; Wang, H. A short-term traffic flow forecasting method based on the hybrid PSO-SVR. Neur. Prof. Lett. 2016, 43, 155–172. [Google Scholar] [CrossRef]
- Ma, D.; Tan, W.; Zhang, Z.; Hu, J. Gas emission source term estimation with 1-step nonlinear partial swarm optimization–Tikhonov regularization hybrid method. Chin. J. Chem. Eng. 2018, 26, 356–363. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, B.; Yang, X.; Wang, X.; Wang, J.; Huang, H. Prediction of flood season precipitation in southwest china based on improved pso-pls. J. Trop. Meteorol. 2018, 2, 163–175. [Google Scholar] [CrossRef]
- Xiao, Y.; Kang, N.; Hong, Y.; Zhang, G. Misalignment Fault Diagnosis of DFWT Based on IEMD Energy Entropy and PSO-SVM. Entropy 2017, 19, 6. [Google Scholar] [CrossRef]
- Guedria, N.B. Improved accelerated PSO algorithm for mechanical engineering optimization problems. Appl. Sofe Comput. 2016, 40, 455–467. [Google Scholar] [CrossRef]
- Cao, P.; Luo, X. Modeling of soft sensor for chemical process. CIESC J. 2013, 64, 788–800. [Google Scholar] [CrossRef]
- Zhang, D.; Cao, J.; Sun, L. Soft sensor modeling of moisture content in drying process based on LSSVM. Int. Conf. Electr. Meas. Instrum. 2009, 2, 989–993. [Google Scholar] [CrossRef]
- Mejri, D.; Limam, M.; Weihs, C. A new dynamic weighted majority control chart for data streams. Soft Comput. 2016, 22, 511–522. [Google Scholar] [CrossRef]
- Brekelmans, R.; Hertog, D.D.; Roos, K.; Eijgenraam, C. Safe dike heights at minimal costs: The nonhomogeneous case. Oper. Res. 2012, 60, 1342–1355. [Google Scholar] [CrossRef]
- Triantafyllopoulos, K. Multivariate discount weighted regression and local level models. Comput. Stat. Data Anal. 2006, 50, 3702–3720. [Google Scholar] [CrossRef]
- Suykens, J.; Johan, A.K. Least squares support vector machines. Int. J. Circ. Theor. Appl. 2002, 27, 605–615. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, Q.; Tang, C.; Liu, X.; Song, J.; Zhou, C. Prediction of reservoir parameters of delta lithologic reservoirs based on support vector regression and well-steering. Oil Geophys. Prospect. 2016, 51. [Google Scholar] [CrossRef]
- Li, C.X.; Ding, X.D.; Zheng, X.F. Predicting non-Gaussian wind velocity using hybridizing intelligent optimization based LSSVM. J. Vib. Shock 2017, 36, 52–58. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Brabanter, J.D.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Roushangar, K.; Saghebian, S.M.; Mouaze, D. Predicting characteristics of dune bedforms using PSO-LSSVM. Int. J. Sediment Res. 2017, 32, 515–526. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, S.; Shen, S.; Guo, L. Particle swarm optimization algorithm with sinusoidal changing inertia weight. Comput. Eng. Appl. 2012, 48, 40–42. [Google Scholar] [CrossRef]
- Zhu, L.X.; Ling, J.; Wang, B.; Hao, J.; Ding, Y. Soft-sensing modeling of marine protease fermentation process based on improved PSO-RBFNN. CIESC J. 2018, 69, 1221–1227. [Google Scholar] [CrossRef]
- Xu, B.; Wang, Y.; Wang, F.; He, M.; Wang, M.; Xie, Y. Prediction of package volume based on improved PSO-BP. Comput. Integr. Manuf. Syst. 2018, 24, 1871–1879. [Google Scholar] [CrossRef]
- Sinha, A.; Mishra, R. Control of a nonlinear continuous stirred tank reactor via event triggered sliding modes. Chem. Eng. Sci. 2018, 187, 52–59. [Google Scholar] [CrossRef] [Green Version]
- Shao, W. Adaptive Soft Sensor Modeling Based on Local Learning; China U Petrol: Qingdao, China, 2016. [Google Scholar]
- Khatibisepehr, S.; Huang, B.; Xu, F.; Espejo, A. A bayesian approach to design of adaptive multi-model inferential sensors with application in oil sand industry. J. Process Control 2012, 22, 1913–1929. [Google Scholar] [CrossRef]

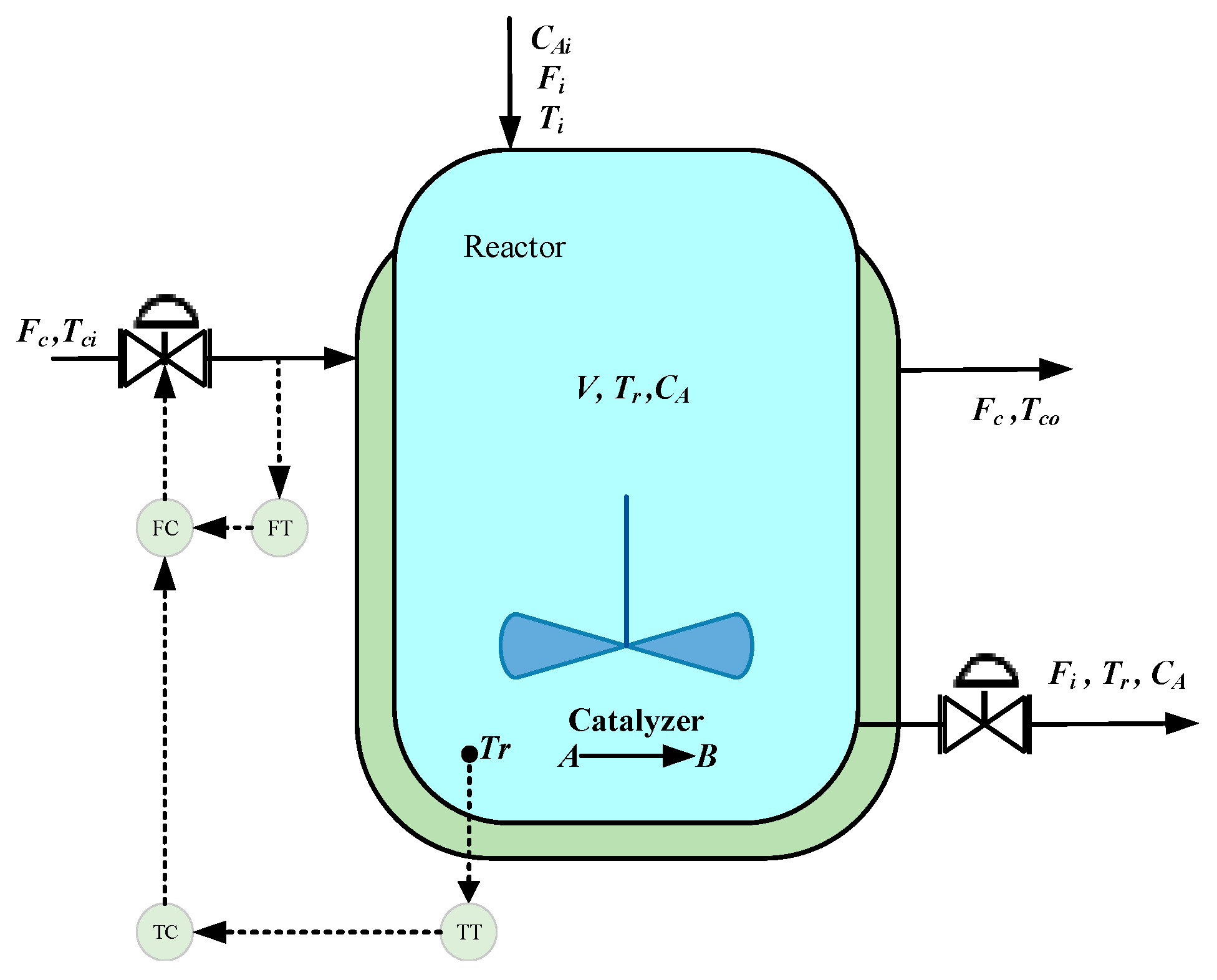
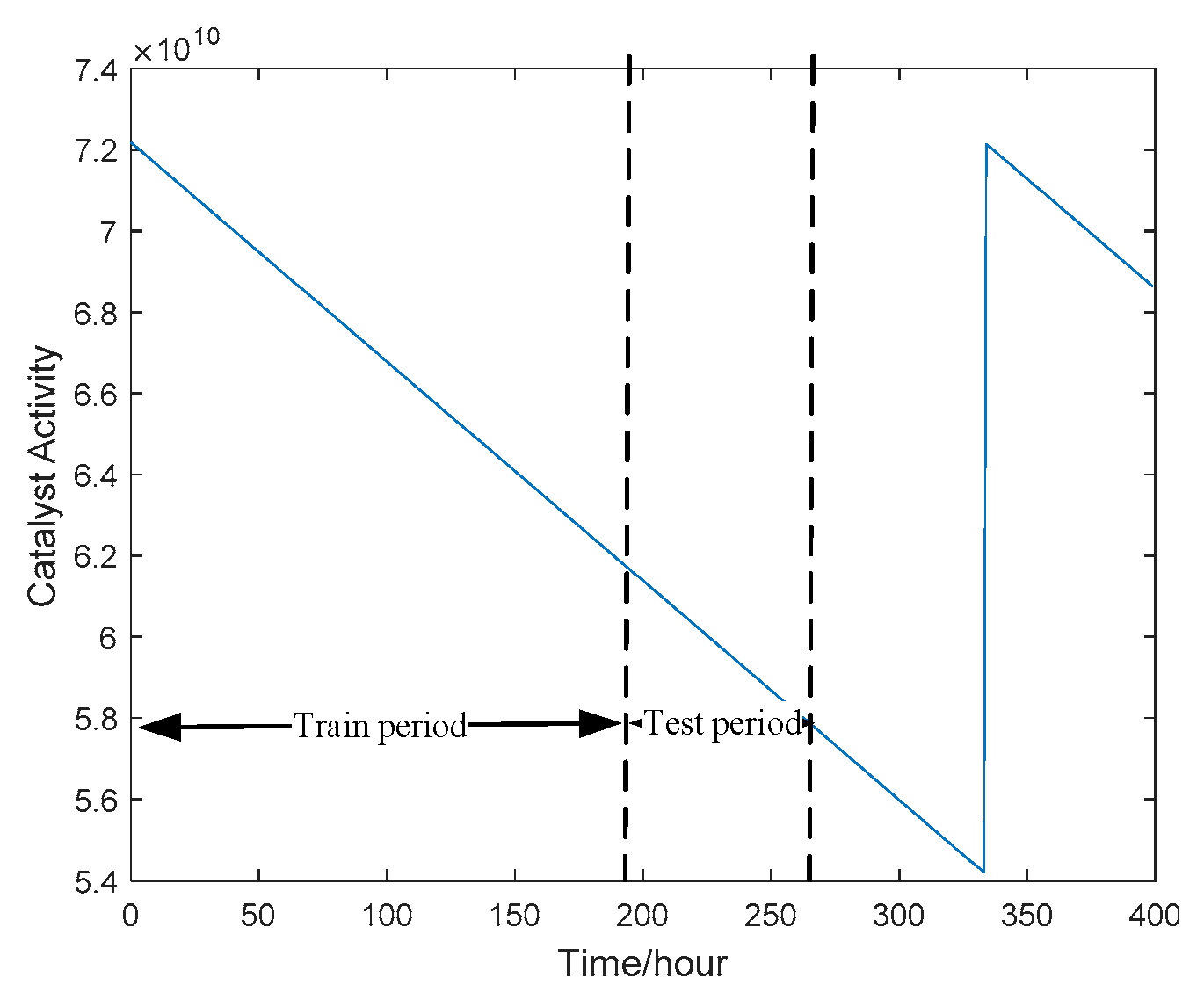
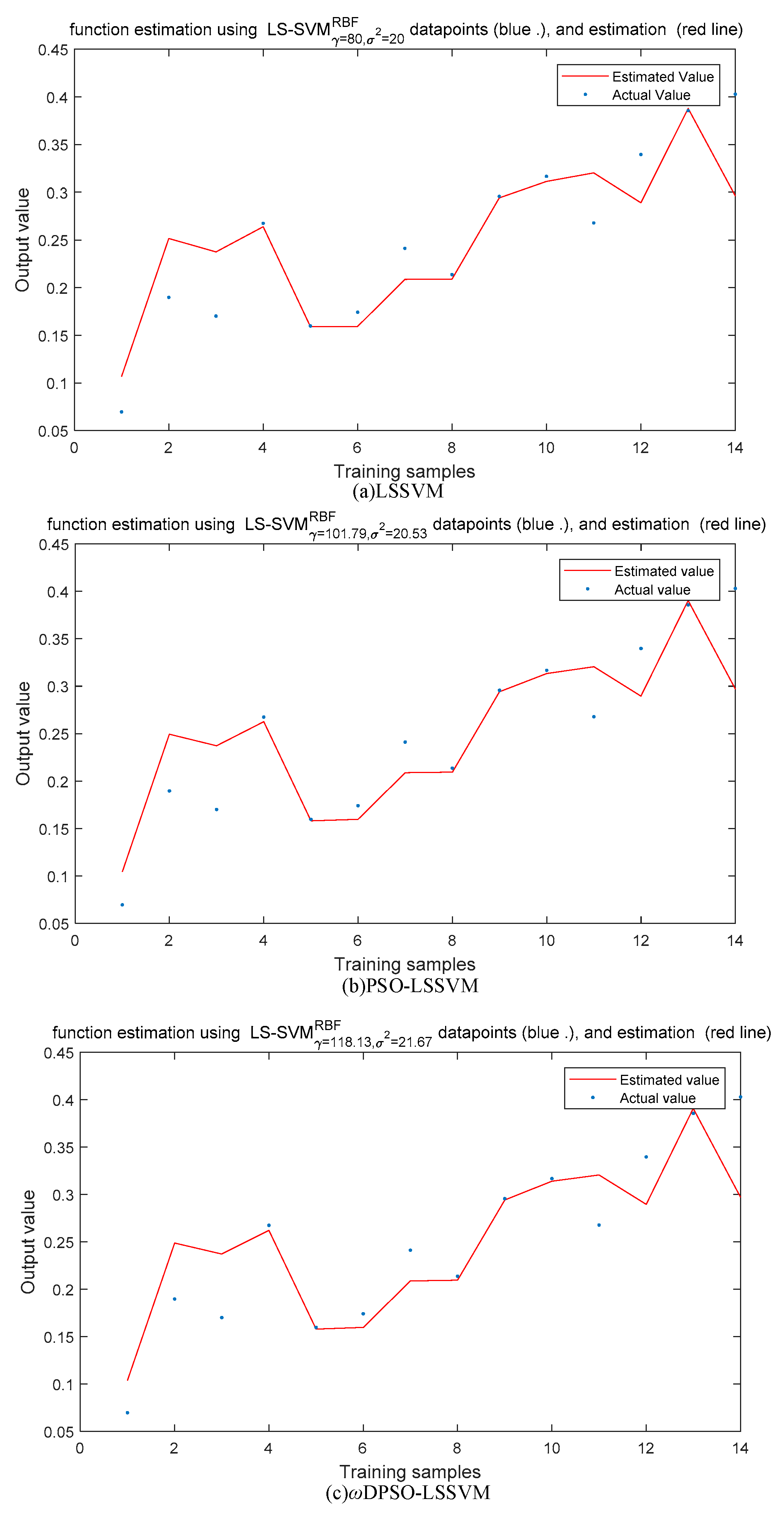
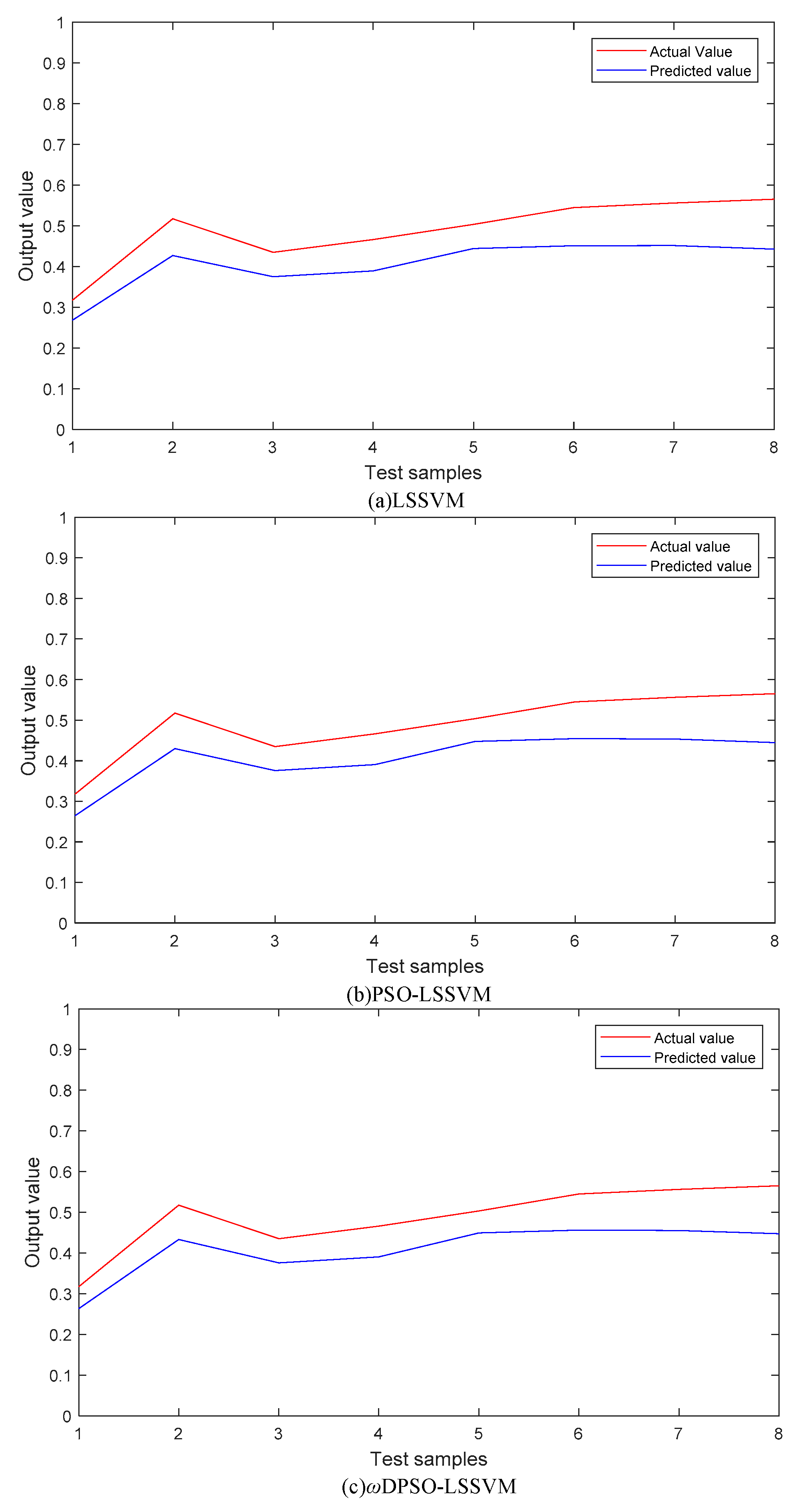


| Parameter | Description | Steady-State Value |
|---|---|---|
| Fi | Feed flow rate | 100 L/min |
| CAi | Reactant concentration in the feed | 1 mol/L |
| Ti | Feed temperature | 350 K |
| V | Reactor volume | 100 L |
| k0 | Reaction speed | 7.2 × 1010 min−1 |
| Cp | Reactant specific heat capacity | 1 cal/g/k |
| hA | Thermal conductivity | 7 × 105 cal/min/K |
| Tci | Cooling water inlet temperature | 350 K |
| Cpc | Cooling water specific heat capacity | 1 cal/g/k |
| Soft Sensor | RMSE | Running Time(s) |
|---|---|---|
| LSSVM | 0.0446 | 0.851 |
| PSO-LSSVM | 0.0440 | 26.520 |
| ωDPSO -LSSVM | 0.0439 | 22.744 |
| Soft Sensor | MAE | RMSE |
|---|---|---|
| LSSVM | 0.0820 | 0.0853 |
| PSO-LSSVM | 0.0807 | 0.0839 |
| ωDPSO -LSSVM | 0.0794 | 0.0823 |
| Soft Sensor | RMSE | Running Time(s) |
|---|---|---|
| LSSVM | 0.0341 | 0.793 |
| PSO-LSSVM | 0.0328 | 28.94 |
| ωDPSO -LSSVM | 0.0327 | 22.143 |
| Soft Sensor | MAE | RMSE |
|---|---|---|
| LSSVM | 0.0529 | 0.0683 |
| PSO-LSSVM | 0.0521 | 0.0650 |
| ωDPSO -LSSVM | 0.0511 | 0.0632 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Dai, Y. Dynamic Soft Sensor Development for Time-Varying and Multirate Data Processes Based on Discount and Weighted ARMA Models. Symmetry 2019, 11, 1414. https://doi.org/10.3390/sym11111414
Li L, Dai Y. Dynamic Soft Sensor Development for Time-Varying and Multirate Data Processes Based on Discount and Weighted ARMA Models. Symmetry. 2019; 11(11):1414. https://doi.org/10.3390/sym11111414
Chicago/Turabian StyleLi, Longhao, and Yongshou Dai. 2019. "Dynamic Soft Sensor Development for Time-Varying and Multirate Data Processes Based on Discount and Weighted ARMA Models" Symmetry 11, no. 11: 1414. https://doi.org/10.3390/sym11111414
APA StyleLi, L., & Dai, Y. (2019). Dynamic Soft Sensor Development for Time-Varying and Multirate Data Processes Based on Discount and Weighted ARMA Models. Symmetry, 11(11), 1414. https://doi.org/10.3390/sym11111414




