Combined Conflict Evidence Based on Two-Tuple IOWA Operators
Abstract
:1. Introduction
2. Preliminaries
2.1. Dempster–Shafer Evidence Theory
2.2. Jousselme Distance
2.3. New Conflict Coefficient
2.4. OWA Operator and IOWA Operator
2.5. Maximum Entropy Method
3. Two-Tuple IOWA Operator and the Determine Weighting Vector of Multi-Source BOEs
3.1. Two-Tuple IOWA Operator
3.2. The Determination of Associated Weight of BOEs
4. New Combination Approach of Conflict Evidence
5. Example and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Li, Y. Improvement of DS evidence theory for multi-sensor conflicting information. Symmetry 2017, 9, 69. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- He, Z.; Jiang, W. A new belief Markov chain model and its application in inventory prediction. Int. J. Prod. Res. 2018, 56, 2800–2817. [Google Scholar] [CrossRef]
- Denoeux, T. 40 years of Dempster-Shafer theory. Int. J. Approx. Reason. 2016, 79, 1–6. [Google Scholar] [CrossRef]
- Chen, J.; Ye, F.; Jiang, T.; Tian, Y. Conflicting information fusion based on an improved ds combination method. Symmetry 2017, 9, 278. [Google Scholar] [CrossRef]
- Jiang, W. A correlation coefficient for belief functions. Int. J. Approx. Reason. 2018, 103, 94–106. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Xu, D.L.; Xue, M. Determining attribute weights for multiple attribute decision analysis with discriminating power in belief distributions. Knowl.-Based Syst. 2018, 143, 127–141. [Google Scholar] [CrossRef] [Green Version]
- Xiao, F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf. Fusion 2019, 46, 23–32. [Google Scholar] [CrossRef]
- Su, X.; Li, L.; Shi, F.; Qian, H. Research on the Fusion of Dependent Evidence Based on Mutual Information. IEEE Access 2018, 6, 71839–71845. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. D number theory based game-theoretic framework in adversarial decision making under a fuzzy environment. Int. J. Approx. Reason. 2019, 106, 194–213. [Google Scholar] [CrossRef]
- Fei, L.; Deng, Y.; Hu, Y. DS-VIKOR: A New Multi-criteria Decision-Making Method for Supplier Selection. Int. J. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- He, Z.; Jiang, W. An evidential dynamical model to predict the interference effect of categorization on decision making. Knowl.-Based Syst. 2018, 150, 139–149. [Google Scholar] [CrossRef]
- Xiao, F. A multiple criteria decision-making method based on D numbers and belief entropy. Int. J. Fuzzy Syst. 2019, 21, 1144–1153. [Google Scholar] [CrossRef]
- Fu, C.; Chang, W.; Xue, M.; Yang, S. Multiple criteria group decision making with belief distributions and distributed preference relations. Eur. J. Oper. Res. 2019, 273, 623–633. [Google Scholar] [CrossRef]
- Han, Y.; Deng, Y. An Evidential Fractal AHP target recognition method. Def. Sci. J. 2018, 68, 367–373. [Google Scholar] [CrossRef]
- Cui, H.; Liu, Q.; Zhang, J.; Kang, B. An improved deng entropy and its application in pattern recognition. IEEE Access 2019, 7, 18284–18292. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S. A game theoretic approach to network reliability assessment. IEEE Trans. Reliab. 2017, 66, 875–892. [Google Scholar] [CrossRef]
- Kang, B.; Zhang, P.; Gao, Z.; Chhipi-Shrestha, G.; Hewage, K.; Sadiq, R. Environmental assessment under uncertainty using Dempster–Shafer theory and Z-numbers. J. Ambient. Intell. Humaniz. Comput. 2019. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Tang, Y. Failure Mode and Effects Analysis based on a novel fuzzy evidential method. Appl. Soft Comput. 2017, 57, 672–683. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y. Engine fault diagnosis based on sensor data fusion considering information quality and evidence theory. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Xiao, F. A Hybrid Fuzzy Soft Sets Decision Making Method in Medical Diagnosis. IEEE Access 2018, 6, 25300–25312. [Google Scholar] [CrossRef]
- Zhang, y.; Jiang, W.; Deng, X. Fault diagnosis method based on time domain weighted data aggregation and information fusion. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X. A new similarity measure between intuitionistic fuzzy sets and the positive definiteness of the similarity matrix. Pattern Anal. Appl. 2017, 20, 215–226. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W.; Wang, Z. Zero-sum polymatrix games with link uncertainty: A Dempster-Shafer theory solution. Appl. Math. Comput. 2019, 340, 101–112. [Google Scholar] [CrossRef]
- Dubois, D.; Liu, W.; Ma, J.; Prade, H. The basic principles of uncertain information fusion. An organised review of merging rules in different representation frameworks. Inf. Fusion 2016, 32, 12–39. [Google Scholar] [CrossRef]
- Han, D.; Yang, Y.; Han, C. Evidence updating based on novel Jeffrey-like conditioning rules. Int. J. Gen. Syst. 2017, 46, 587–615. [Google Scholar] [CrossRef]
- Denœux, T.; Sriboonchitta, S.; Kanjanatarakul, O. Evidential clustering of large dissimilarity data. Knowl.-Based Syst. 2016, 106, 179–195. [Google Scholar] [CrossRef] [Green Version]
- Su, X.; Li, L.; Qian, H.; Mahadevan, S.; Deng, Y. A new rule to combine dependent bodies of evidence. Soft Comput. 2019, 23, 9793–9799. [Google Scholar] [CrossRef]
- Xiao, F. An Improved Method for Combining Conflicting Evidences Based on the Similarity Measure and Belief Function Entropy. Int. J. Fuzzy Syst. 2018, 20, 1256–1266. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, Y. Combining conflicting evidence using the DEMATEL method. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, C.; Deng, X. A new probability transformation method based on a correlation coefficient of belief functions. Int. J. Intell. Syst. 2019, 34, 1337–1347. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. A total uncertainty measure for D numbers based on belief intervals. Int. J. Intell. Syst. 2019. [Google Scholar] [CrossRef]
- Lefevre, E.; Colot, O.; Vannoorenberghe, P. Belief function combination and conflict management. Inf. Fusion 2002, 3, 149–162. [Google Scholar] [CrossRef]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Smets, P. Analyzing the combination of conflicting belief functions. Inf. Fusion 2007, 8, 387–412. [Google Scholar] [CrossRef]
- Deng, X.; Han, D.; Dezert, J.; Deng, Y.; Shyr, Y. Evidence combination from an evolutionary game theory perspective. IEEE Trans. Cybern. 2016, 46, 2070–2082. [Google Scholar] [CrossRef] [PubMed]
- Yager, R.R. On the Dempster-Shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Sun, Q.; Ye, X.q.; Gu, W.k. A new combination rules of evidence theory. Acta Electron. Sin. 2000, 28, 117–119. [Google Scholar]
- Smets, P. Data fusion in the transferable belief model. In Proceedings of the Third International Conference on Information Fusion (FUSIon 2000), Paris, France, 10–13 July 2000; Volume 1, pp. PS21–PS33. [Google Scholar]
- Yong, D.; WenKang, S.; ZhenFu, Z.; Qi, L. Combining belief functions based on distance of evidence. Decis. Support Syst. 2004, 38, 489–493. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Evaluating green supply chain management practices under fuzzy environment: A novel method based on D number theory. Int. J. Fuzzy Syst. 2019, 21, 1389–1402. [Google Scholar] [CrossRef]
- Xiao, F. A novel multi-criteria decision making method for assessing health-care waste treatment technologies based on D numbers. Eng. Appl. Artif. Intell. 2018, 71, 216–225. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, L.; Jiang, W. Uncertainty measurement with belief entropy on the interference effect in the quantum-like Bayesian Networks. Appl. Math. Comput. 2019, 347, 417–428. [Google Scholar] [CrossRef]
- He, Z.; Jiang, W. An evidential Markov decision making model. Inf. Sci. 2018, 467, 357–372. [Google Scholar] [CrossRef] [Green Version]
- Haenni, R. Are alternatives to Dempster’s rule of combination real alternatives?: Comments on “About the belief function combination and the conflict management problem”—-Lefevre et al. Inf. Fusion 2002, 3, 237–239. [Google Scholar] [CrossRef]
- Jousselme, A.L.; Grenier, D.; Bossé, É. A new distance between two bodies of evidence. Inf. Fusion 2001, 2, 91–101. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. In Readings in Fuzzy Sets for Intelligent Systems; Elsevier: Amsterdam, The Netherlands, 1993; pp. 80–87. [Google Scholar]
- Fei, L.; Wang, H.; Chen, L.; Deng, Y. A new vector valued similarity measure for intuitionistic fuzzy sets based on OWA operators. Iran. J. Fuzzy Syst. 2019, 16, 113–126. [Google Scholar]
- Pan, L.; Deng, Y. A New Belief Entropy to Measure Uncertainty of Basic Probability Assignments Based on Belief Function and Plausibility Function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef]
- Yager, R.R.; Kacprzyk, J. The Ordered Weighted Averaging Operators: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- O’Hagan, M. Aggregating template or rule antecedents in real-time expert systems with fuzzy set logic. In Proceedings of the Twenty-Second Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 31 October–2 November 1988; Volume 2, pp. 681–689. [Google Scholar]
- Chiclana, F.; Herrera-Viedma, E.; Herrera, F.; Alonso, S. Some induced ordered weighted averaging operators and their use for solving group decision-making problems based on fuzzy preference relations. Eur. J. Oper. Res. 2007, 182, 383–399. [Google Scholar] [CrossRef]
- Zeng, S.; Merigo, J.M.; Su, W. The uncertain probabilistic OWA distance operator and its application in group decision making. Appl. Math. Model. 2013, 37, 6266–6275. [Google Scholar] [CrossRef]
- Merigo, J.M.; Engemann, K.J.; Palacios-Marques, D. Decision making with Dempster-Shafer belief structure and the OWAWA operator. Technol. Econ. Dev. Econ. 2013, 19, S100–S118. [Google Scholar] [CrossRef]
- Cho, S.B. Fuzzy aggregation of modular neural networks with ordered weighted averaging operators. Int. J. Approx. Reason. 1995, 13, 359–375. [Google Scholar] [Green Version]
- Jiang, W.; Cao, Y.; Deng, X. A Novel Z-network Model Based on Bayesian Network and Z-number. IEEE Trans. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Geng, J.; Ma, X.; Zhou, X.; Wang, H. Saliency-Guided Deep Neural Networks for SAR Image Change Detection. IEEE Trans. Geosci. Remote. Sens. 2019, 1–13. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S.; Sankararaman, S.; Goebel, K. Resilience-based network design under uncertainty. Reliab. Eng. Syst. Saf. 2018, 169, 364–379. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Y.; Tang, Y.; Li, S. An incident information management framework based on data integration, data mining, and multi-criteria decision making. Decis. Support Syst. 2011, 51, 316–327. [Google Scholar] [CrossRef]
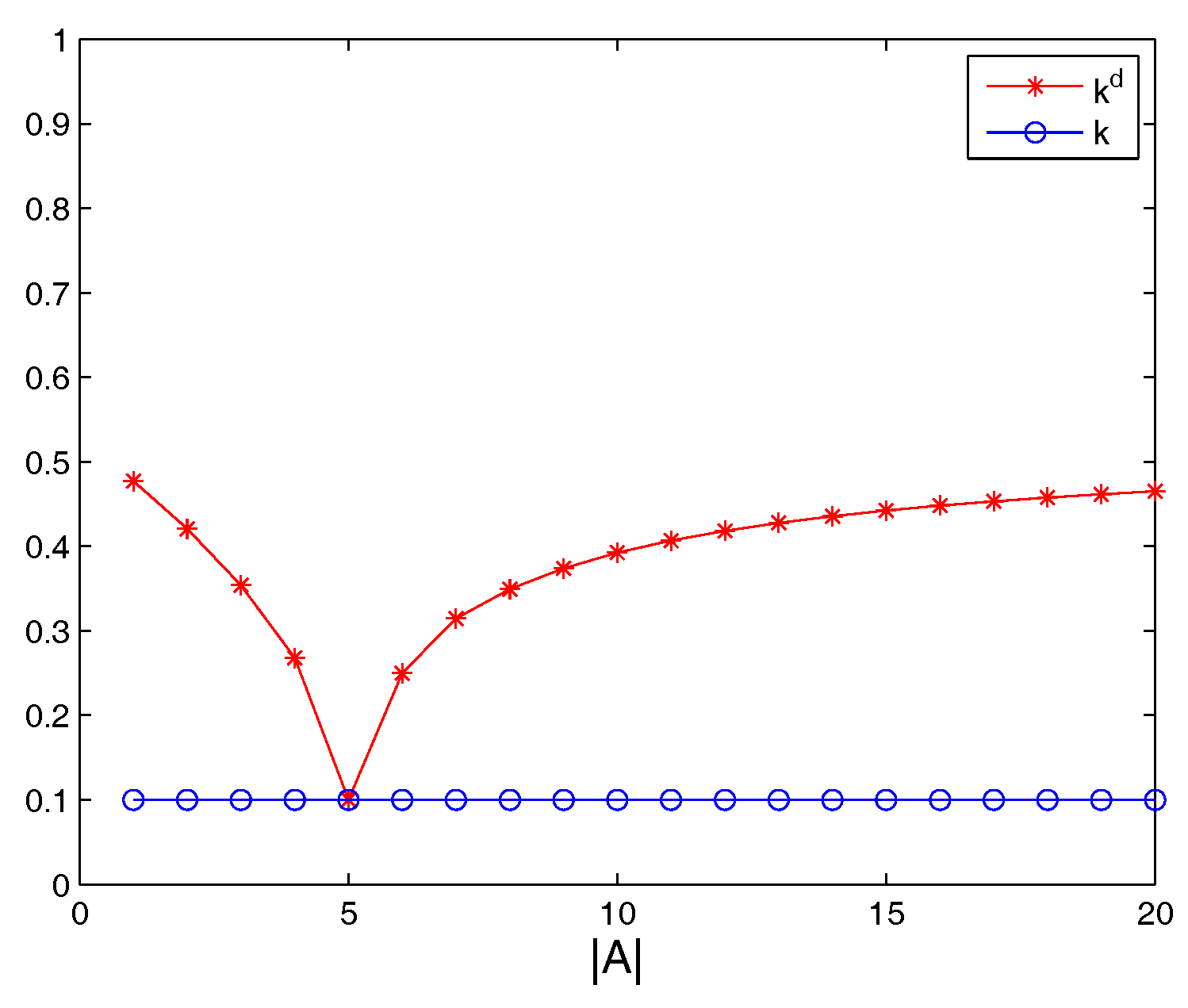
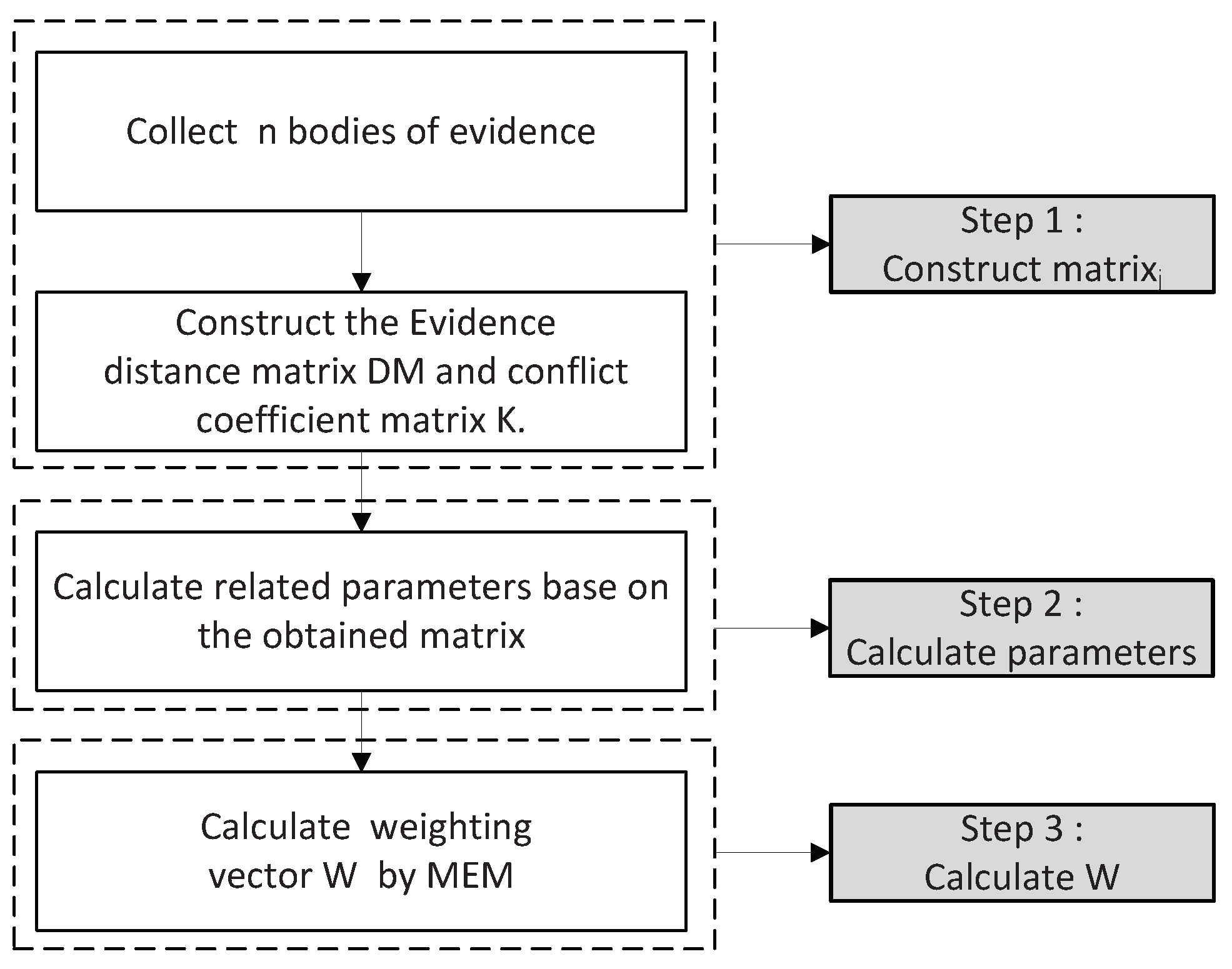
| Case | k | ||
|---|---|---|---|
| 0.8544 | 0.1000 | 0.4772 | |
| 0.7416 | 0.1000 | 0.4208 | |
| 0.6083 | 0.1000 | 0.3541 | |
| 0.4359 | 0.1000 | 0.2680 | |
| 0.1000 | 0.1000 | 0.1000 | |
| 0.4000 | 0.1000 | 0.2500 | |
| 0.5292 | 0.1000 | 0.3146 | |
| 0.5990 | 0.1000 | 0.3495 | |
| 0.6481 | 0.1000 | 0.3740 | |
| 0.6848 | 0.1000 | 0.3924 | |
| 0.7135 | 0.1000 | 0.4068 | |
| 0.7365 | 0.1000 | 0.4183 | |
| 0.7555 | 0.1000 | 0.4277 | |
| 0.7714 | 0.1000 | 0.4357 | |
| 0.7849 | 0.1000 | 0.4425 | |
| 0.7965 | 0.1000 | 0.4482 | |
| 0.8066 | 0.1000 | 0.4533 | |
| 0.8155 | 0.1000 | 0.4577 | |
| 0.8233 | 0.1000 | 0.4617 | |
| 0.8304 | 0.1000 | 0.4652 |
| BOEs | Approach | Target | |||||
|---|---|---|---|---|---|---|---|
| Dempster | 0 | 0.8571 | 0.1429 | 0 | 0 | B | |
| Yager [38] | 0 | 0.1800 | 0.0300 | 0 | 0.7900 | Θ | |
| Murphy [35] | 0.1543 | 0.7469 | 0.0988 | 0 | 0 | B | |
| Deng [41] | 0.1543 | 0.7469 | 0.0988 | 0 | 0 | B | |
| Proposed | 0.1543 | 0.7469 | 0.0988 | 0 | 0 | B | |
| Dempster | 0 | 0.6316 | 0.3684 | 0 | 0 | B | |
| Yager [38] | 0.4345 | 0.097 | 0.0105 | 0.2765 | 0.1815 | A | |
| Murphy [35] | 0.5568 | 0.3562 | 0.0782 | 0.0088 | 0 | A | |
| Deng [41] | 0.6500 | 0.2547 | 0.0858 | 0.0095 | 0 | A | |
| Proposed | 0.7429 | 0.1489 | 0.1019 | 0.0067 | 0 | A | |
| Dempster | 0 | 0.3288 | 0.6712 | 0 | 0 | C | |
| Yager [38] | 0.6430 | 0.0279 | 0.0037 | 0.1603 | 0.1652 | A | |
| Murphy [35] | 0.8653 | 0.0891 | 0.0382 | 0.0074 | 0 | A | |
| Deng [41] | 0.9305 | 0.0274 | 0.0339 | 0.0082 | 0 | A | |
| Proposed | 0.9638 | 0.0049 | 0.0184 | 0.0139 | 0 | A | |
| Dempster | 0 | 0.1404 | 0.8596 | 0 | 0 | C | |
| Yager [38] | 0.7740 | 0.0193 | 0.0011 | 0.0977 | 0.1080 | A | |
| Murphy [35] | 0.9688 | 0.0156 | 0.0127 | 0.0029 | 0 | A | |
| Deng [41] | 0.9846 | 0.0024 | 0.0098 | 0.0032 | 0 | A | |
| Proposed | 0.9897 | 0.0002 | 0.0043 | 0.0058 | 0 | A |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Qin, X.; Zhao, X. Combined Conflict Evidence Based on Two-Tuple IOWA Operators. Symmetry 2019, 11, 1369. https://doi.org/10.3390/sym11111369
Zhou Y, Qin X, Zhao X. Combined Conflict Evidence Based on Two-Tuple IOWA Operators. Symmetry. 2019; 11(11):1369. https://doi.org/10.3390/sym11111369
Chicago/Turabian StyleZhou, Ying, Xiyun Qin, and Xiaozhe Zhao. 2019. "Combined Conflict Evidence Based on Two-Tuple IOWA Operators" Symmetry 11, no. 11: 1369. https://doi.org/10.3390/sym11111369
APA StyleZhou, Y., Qin, X., & Zhao, X. (2019). Combined Conflict Evidence Based on Two-Tuple IOWA Operators. Symmetry, 11(11), 1369. https://doi.org/10.3390/sym11111369




