Exploiting Weak Field Gravity-Maxwell Symmetry in Superconductive Fluctuations Regime
Abstract
:1. Introduction
2. Weak Field Approximation
2.1. Gravito-Maxwell Equations
2.2. Generalized Maxwell Equations
3. The Model
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
 that partially supported this work for dott. A. Gallerati.
that partially supported this work for dott. A. Gallerati.Conflicts of Interest
References
- DeWitt, B.S. Superconductors and gravitational drag. Phys. Rev. Lett. 1966, 16, 1092–1093. [Google Scholar] [CrossRef]
- Kiefer, C.; Weber, C. On the interaction of mesoscopic quantum systems with gravity. Ann. Phys. 2005, 14, 253–278. [Google Scholar] [CrossRef] [Green Version]
- Papini, G. Detection of inertial effects with superconducting interferometers. Phys. Lett. A 1967, 24, 32–33. [Google Scholar] [CrossRef]
- Papini, G. Superconducting and normal metals as detectors of gravitational waves. Lett. Nuovo Cim. 1970, 4S1, 1027–1032. [Google Scholar] [CrossRef]
- Rothen, F. Application de la theorie relativiste des phenomenes irreversible a la phenomenologie de la supraconductivite. Helv. Phys. Acta 1968, 41, 591. [Google Scholar]
- Rystephanick, R. On the london moment in rotating superconducting cylinders. Can. J. Phys. 1973, 51, 789–794. [Google Scholar] [CrossRef]
- Hirakawa, H. Superconductors in gravitational field. Phys. Lett. A 1975, 53, 395–396. [Google Scholar] [CrossRef]
- Minasyan, I. Londons equations in riemannian space. Doklady Akademii Nauk SSSR 1976, 228, 576–578. [Google Scholar]
- Anandan, J. Gravitational and rotational effects in quantum interference. Phys. Rev. D 1977, 15, 1448. [Google Scholar] [CrossRef]
- Anandan, J. Interference, gravity and gauge fields. IL Nuovo Cimento A (1965–1970) 1979, 53, 221–250. [Google Scholar] [CrossRef]
- Anandan, J. Relativistic thermoelectromagnetic gravitational effects in normal conductors and superconductors. Phys. Lett. A 1984, 105, 280–284. [Google Scholar] [CrossRef]
- Anandan, J. Relativistic gravitation and superconductors. Class. Quantum Grav. 1994, 11, A23. [Google Scholar] [CrossRef]
- Ross, D. The london equations for superconductors in a gravitational field. J. Phys. A Math. Gen. 1983, 16, 1331. [Google Scholar] [CrossRef]
- Felch, S.B.; Tate, J.; Cabrera, B.; Anderson, J.T. Precise determination of h/me using a rotating, superconducting ring. Phys. Rev. B 1985, 31, 7006–7011. [Google Scholar] [CrossRef] [PubMed]
- Dinariev, O.Y.; Mosolov, A. A relativistic effect in the theory of superconductivity. Soviet Phys. Doklady 1987, 32, 1987. [Google Scholar]
- Peng, H.; Torr, D.; Hu, E.; Peng, B. Electrodynamics of moving superconductors and superconductors under the influence of external forces. Phys. Rev. B 1991, 43, 2700. [Google Scholar] [CrossRef] [PubMed]
- Peng, H. A new approach to studying local gravitomagnetic effects on a superconductor. Gen. Relat. Grav. 1990, 22, 609–617. [Google Scholar] [CrossRef]
- Peng, H.; Lind, G.; Chin, Y. Interaction between gravity and moving superconductors. Gen. Relat. Grav. 1991, 23, 1231–1250. [Google Scholar] [CrossRef]
- Li, N.; Torr, D. Effects of a gravitomagnetic field on pure superconductors. Phys. Rev. D 1991, 43, 457. [Google Scholar] [CrossRef]
- Li, N.; Torr, D.G. Gravitational effects on the magnetic attenuation of superconductors. Phys. Rev. B 1992, 46, 5489. [Google Scholar] [CrossRef]
- Torr, D.G.; Li, N. Gravitoelectric-electric coupling via superconductivity. Found. Phys. Lett. 1993, 6, 371–383. [Google Scholar] [CrossRef]
- de Andrade, L.G. Torsion, superconductivity, and massive electrodynamics. Int. J. Theor. Phys. 1992, 31, 1221–1227. [Google Scholar] [CrossRef]
- Podkletnov, E.; Nieminen, R. A possibility of gravitational force shielding by bulk YBa2Cu3O7-X superconductor. Phys. C Supercond. 1992, 203, 441–444. [Google Scholar] [CrossRef]
- Li, N.; Noever, D.; Robertson, T.; Koczor, R.; Brantley, W. Static test for a gravitational force coupled to type II YBCO superconductors. Phys. C Supercond. 1997, 281, 260–267. [Google Scholar] [CrossRef]
- de Podesta, M.; Bull, M. Alternative explanation of “gravitational screening” experiments. Phys. C Supercond. 1995, 253, 199–200. [Google Scholar] [CrossRef]
- Unnikrishnan, C. Does a superconductor shield gravity? Phys. C Supercond. 1996, 266, 133–137. [Google Scholar] [CrossRef]
- Tajmar, M.; Plesescu, F.; Seifert, B. Measuring the dependence of weight on temperature in the low-temperature regime using a magnetic suspension balance. Meas. Sci. Technol. 2009, 21, 015111. [Google Scholar] [CrossRef]
- Tajmar, M. Evaluation of enhanced frame-dragging in the vicinity of a rotating niobium superconductor, liquid helium and a helium superfluid. Phys. C Supercond. 2011, 24, 125011. [Google Scholar] [CrossRef]
- Podkletnov, E.; Modanese, G. Investigation of high voltage discharges in low pressure gases through large ceramic superconducting electrodes. J. Low Temp. Phys. 2003, 132, 239–259. [Google Scholar] [CrossRef]
- Poher, C.; Modanese, G. Enhanced induction into distant coils by ybco and silicon-graphite electrodes under large current pulses. Phys. Essays 2017, 30, 435–441. [Google Scholar] [CrossRef]
- Ciubotariu, C.; Agop, M. Absence of a gravitational analog to the meissner effect. Gene. Relat. Grav. 1996, 28, 405–412. [Google Scholar] [CrossRef]
- Agop, M.; Buzea, C.G.; Griga, V.; Ciubotariu, C.; Buzea, C.; Stan, C.; Jatomir, D. Gravitational paramagnetism, diamagnetism and gravitational superconductivity. Aust. J. Phys. 1996, 49, 1063–1074. [Google Scholar] [CrossRef]
- Agop, M.; Ioannou, P.; Diaconu, F. Some implications of gravitational superconductivity. Prog. Theor. Phys. 2000, 104, 733–742. [Google Scholar] [CrossRef]
- Agop, M.; Buzea, C.G.; Nica, P. Local gravitoelectromagnetic effects on a superconductor. Phys. C Supercond. 2000, 339, 120–128. [Google Scholar] [CrossRef]
- Ivanov, B. Gravitational effects in a spherical solenoid. Mod. Phys. Lett. A 1997, 12, 285–294. [Google Scholar] [CrossRef]
- Ahmedov, B. General relativistic thermoelectric effects in superconductors. Gen. Relat. Grav. 1999, 31, 357–369. [Google Scholar] [CrossRef]
- Ahmedov, B.; Kagramanova, V. Electromagnetic effects in superconductors in stationary gravitational field. Int. J. Mod. Phys. D 2005, 14, 837–847. [Google Scholar] [CrossRef]
- Tajmar, M.; de Matos, C.J. Gravitomagnetic field of a rotating superconductor and of a rotating superfluid. Physica 2003, C385, 551–554. [Google Scholar] [CrossRef]
- de Matos, C.J.; Tajmar, M. Gravitomagnetic London moment and the graviton mass inside a superconductor. Physica 2003, C432, 167. [Google Scholar] [CrossRef]
- Tajmar, M.; de Matos, C.J. Extended analysis of gravitomagnetic fields in rotating superconductors and superfluids. Physica 2005, C420, 56. [Google Scholar] [CrossRef]
- Tajmar, M. Electrodynamics in superconductors explained by proca equations. Phys. Lett. A 2008, 372, 3289–3291. [Google Scholar] [CrossRef]
- Ning, W. Gravitational shielding effect in gauge theory of gravity. Commun. Theor. Phys. 2004, 41, 567. [Google Scholar] [CrossRef]
- Chiao, R.Y. The interface between quantum mechanics and general relativity. J. Mod. Opt. 2006, 53, 16–17. [Google Scholar] [CrossRef]
- de Matos, C.J. Gravitoelectromagnetism and dark energy in superconductors. Int. J. Mod. Phys. D 2007, 16, 2599–2606. [Google Scholar] [CrossRef]
- de Matos, C.J. Electromagnetic dark energy and gravitoelectrodynamics of superconductors. Phys. C Supercond. 2008, 468, 210–213. [Google Scholar] [CrossRef] [Green Version]
- de Matos, C.J. Gravitational force between two electrons in superconductors. Phys. C Supercond. 2008, 468, 229–232. [Google Scholar] [CrossRef] [Green Version]
- de Matos, C.J. Physical vacuum in superconductors. J. Supercond. Novel Magn. 2010, 23, 1443–1453. [Google Scholar] [CrossRef]
- de Matos, C.J. Modified entropic gravitation in superconductors. Phys. C Supercond. 2012, 472, 5–9. [Google Scholar] [CrossRef] [Green Version]
- Inan, N.; Thompson, J.; Chiao, R. Interaction of gravitational waves with superconductors. Fortschritte der Physik 2017, 65, 1600066. [Google Scholar] [CrossRef]
- Inan, N. A new approach to detecting gravitational waves via the coupling of gravity to the zero-point energy of the phonon modes of a superconductor. Int. J. Mod. Phys. D 2017, 26, 1743031. [Google Scholar] [CrossRef]
- Atanasov, V. The geometric field (gravity) as an electro-chemical potential in a ginzburg-landau theory of superconductivity. Phys. B Cond. Matter 2017, 517, 53–58. [Google Scholar] [CrossRef]
- Sbitnev, V.I. Quaternion algebra on 4d superfluid quantum space-time: Gravitomagnetism. Found. Phys. 2019, 49, 107–143. [Google Scholar] [CrossRef]
- Modanese, G. Theoretical analysis of a reported weak-gravitational-shielding effect. EPL (Europhys. Lett.) 1996, 35, 413. [Google Scholar] [CrossRef]
- Modanese, G. Role of a “local” cosmological constant in euclidean quantum gravity. Phys. Rev. D 1996, 54, 5002. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Gallerati, A. Superconductor in a weak static gravitational field. Eur. Phys. J. 2017, C77, 549. [Google Scholar] [CrossRef]
- Cyrot, M. Ginzburg-landau theory for superconductors. Rep. Prog. Phys. 1973, 36, 103–158. [Google Scholar] [CrossRef]
- Zagrodziński, J.; Nikiciuk, T.; Abal’osheva, I.; Lewandowski, S. Time-dependent ginzburg–landau approach and its application to superconductivity. Supercond. Sci. Technol. 2003, 16, 936. [Google Scholar] [CrossRef]
- Alstrøm, T.S.; Sørensen, M.P.; Pedersen, N.F.; Madsen, S. Magnetic flux lines in complex geometry type-ii superconductors studied by the time dependent ginzburg-landau equation. Acta Appl. Math. 2011, 115, 63–74. [Google Scholar] [CrossRef]
- Mashhoon, B.; Paik, H.J.; Will, C.M. Detection of the gravitomagnetic field using an orbiting superconducting gravity gradiometer. theoretical principles. Phys. Rev. D 1989, 39, 2825–2838. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Gravitomagnetic effects. IL Nuovo Cimento B 2002, 117, 743–768. [Google Scholar]
- Larkin, A.; Varlamov, A. Fluctuation Phenomena in Superconductors. In Handbook on Superconductivity: Conventional and Unconventional Superconductors; Springer: Berlin, Germany, 2002; p. 1. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984; p. 491. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Macmillan: London, UK, 1973. [Google Scholar]
- Braginsky, V.B.; Caves, C.M.; Thorne, K.S. Laboratory experiments to test relativistic gravity. Phys. Rev. D 1977, 15, 2047. [Google Scholar] [CrossRef]
- Huei, P. On calculation of magnetic-type gravitation and experiments. Gen. Relat. Grav. 1983, 15, 725–735. [Google Scholar] [CrossRef]
- Behera, H. Comments on gravitoelectromagnetism of Ummarino and Gallerati in “Superconductor in a weak static gravitational field” vs. other versions. Eur. Phys. J. 2017, C77. [Google Scholar] [CrossRef]
- Hurault, J. Nonlinear effects on the conductivity of a superconductor above its transition temperature. Phys. Rev. 1969, 179, 494. [Google Scholar] [CrossRef]
- Schmid, A. Diamagnetic susceptibility at the transition to the superconducting state. Phys. Rev. 1969, 180, 527. [Google Scholar] [CrossRef]
- de Gennes, P.-G. Superconductivity of Metals and Alloys; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
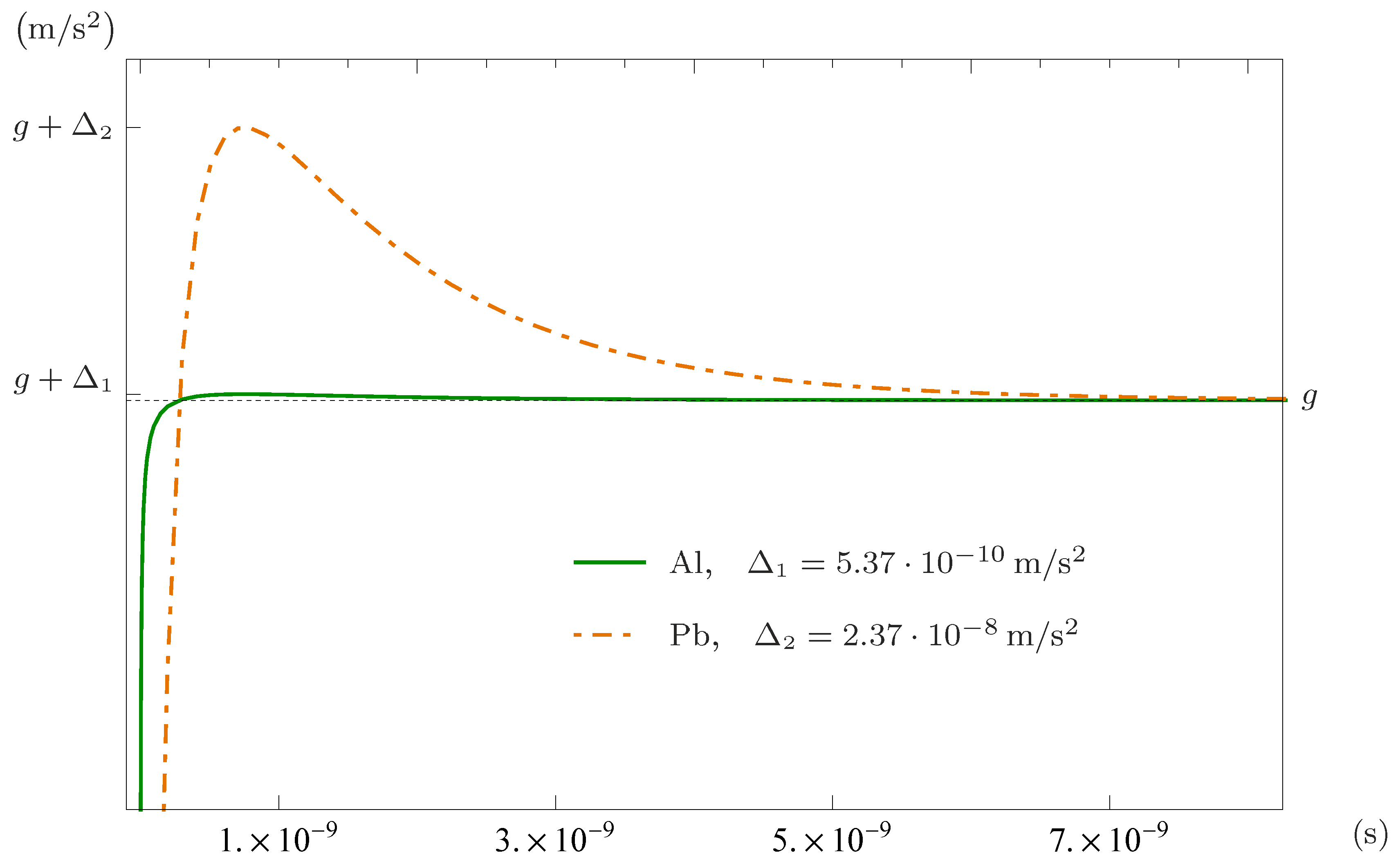
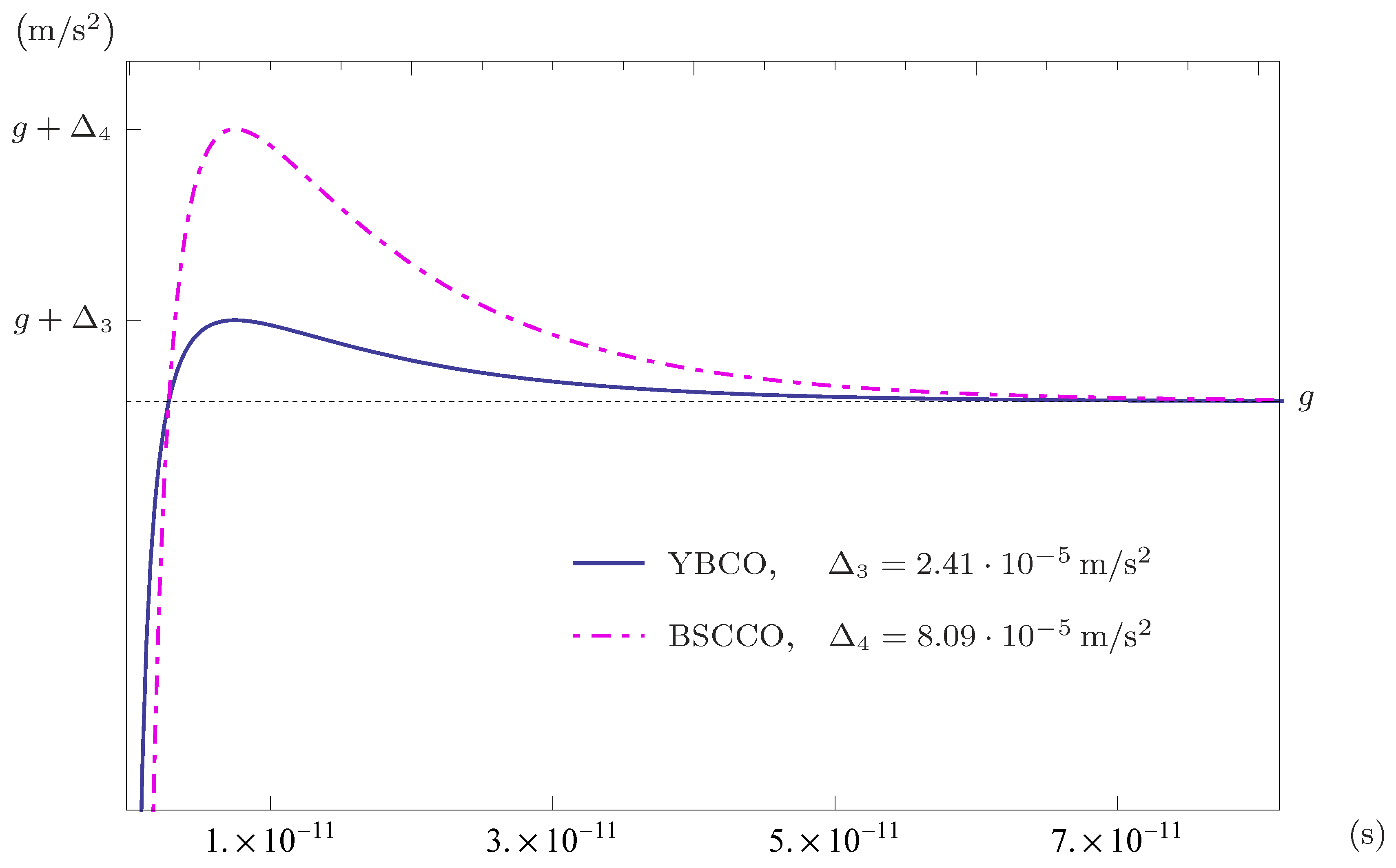
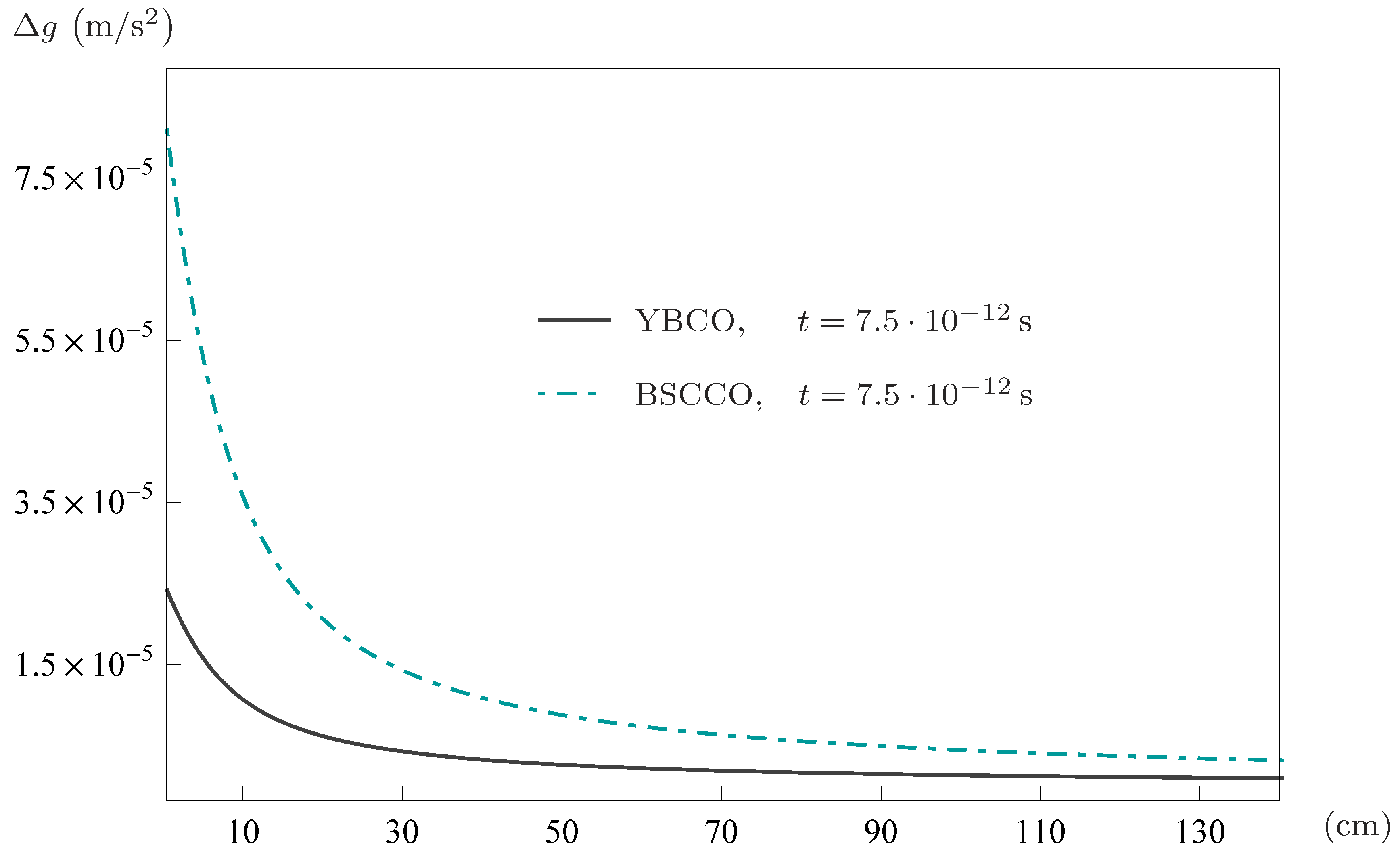
| Al | 15500 | 531313 | ||||
| Pb | 870 | 73924 | ||||
| YBCO | 30 | 895 | ||||
| BSCCO | 10 | 333 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ummarino, G.A.; Gallerati, A. Exploiting Weak Field Gravity-Maxwell Symmetry in Superconductive Fluctuations Regime. Symmetry 2019, 11, 1341. https://doi.org/10.3390/sym11111341
Ummarino GA, Gallerati A. Exploiting Weak Field Gravity-Maxwell Symmetry in Superconductive Fluctuations Regime. Symmetry. 2019; 11(11):1341. https://doi.org/10.3390/sym11111341
Chicago/Turabian StyleUmmarino, Giovanni Alberto, and Antonio Gallerati. 2019. "Exploiting Weak Field Gravity-Maxwell Symmetry in Superconductive Fluctuations Regime" Symmetry 11, no. 11: 1341. https://doi.org/10.3390/sym11111341
APA StyleUmmarino, G. A., & Gallerati, A. (2019). Exploiting Weak Field Gravity-Maxwell Symmetry in Superconductive Fluctuations Regime. Symmetry, 11(11), 1341. https://doi.org/10.3390/sym11111341






