Flexible Birnbaum–Saunders Distribution
Abstract
:1. Introduction
1.1. Asymmetry
1.2. Bimodality
1.3. BS Model
2. Results in Flexible Birnbaum-Saunders
2.1. Interpretation of Parameters.
2.2. Properties
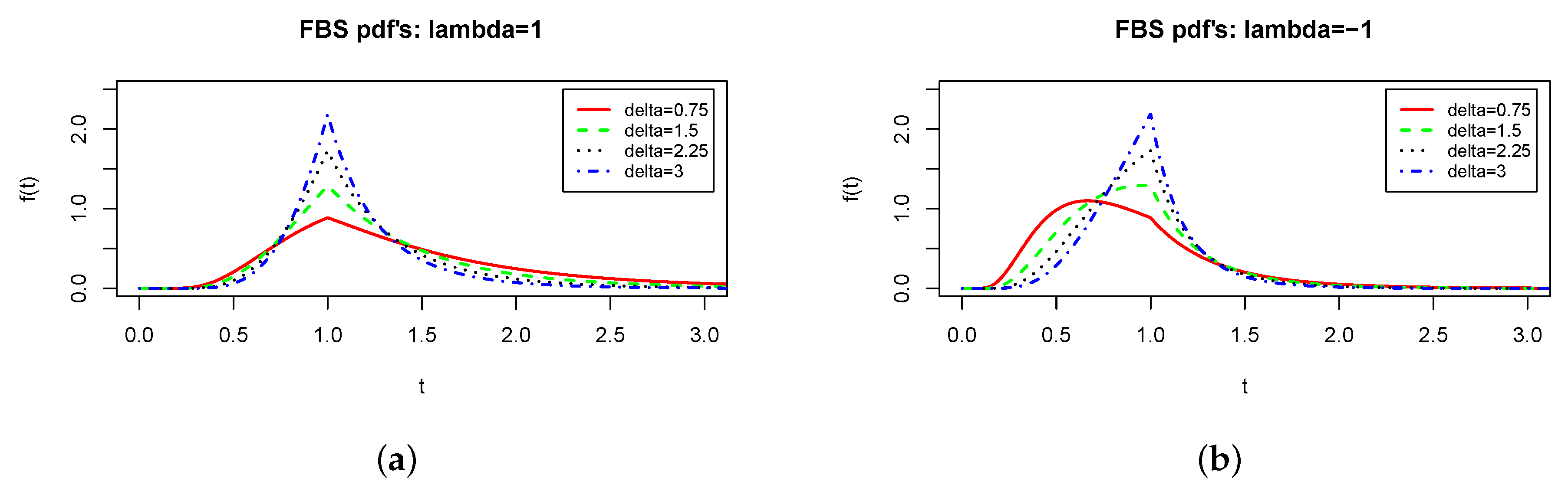
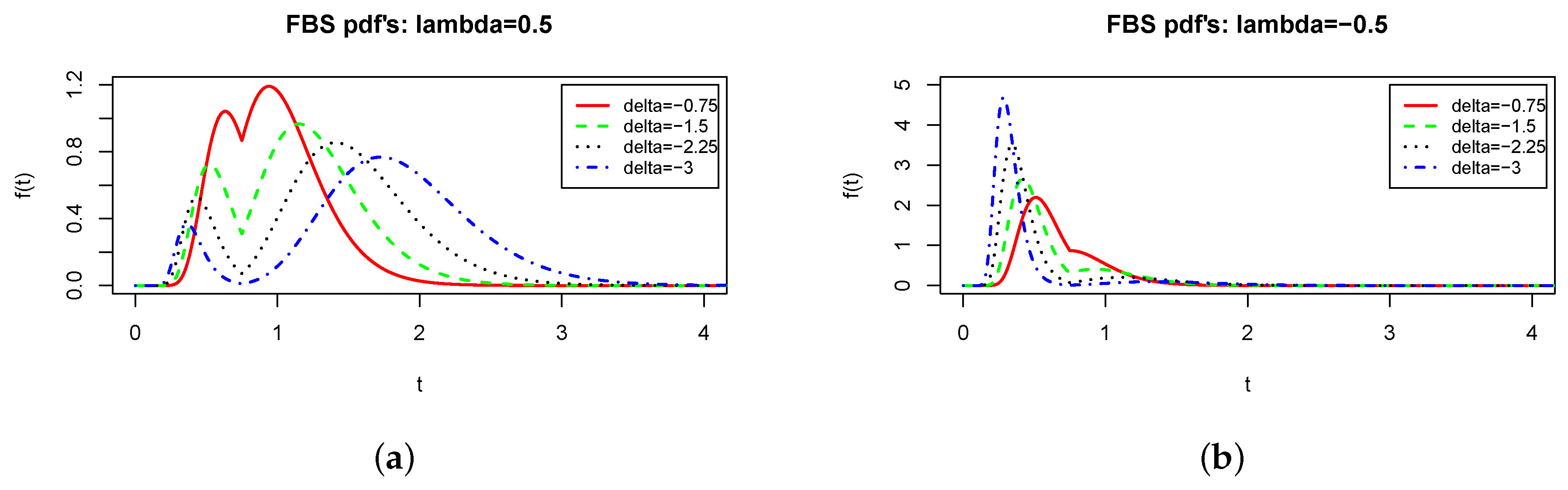
2.2.1. Effect of .
2.2.2. Effect of .
2.2.3. Shape of .
- 1.
- solution of
- 2.
- solution of
- 1.
- Let , . Then Z is unimodal and the mode, , is given by the solution of the non-linear equation
- 2.
- Let , Then T is unimodal and the mode, , is given by the solution of the non-linear equation
- (i)
- Let be the pth quantile of T, .where denotes the pth quantile of
- (ii)
- for .
- (iii)
- .
2.2.4. Lifetime Analysis
- (i)
- The survival function is with given in (9).
- (ii)
- The hazard function, , iswith the cdf of the bivariate normal given in Proposition 1.
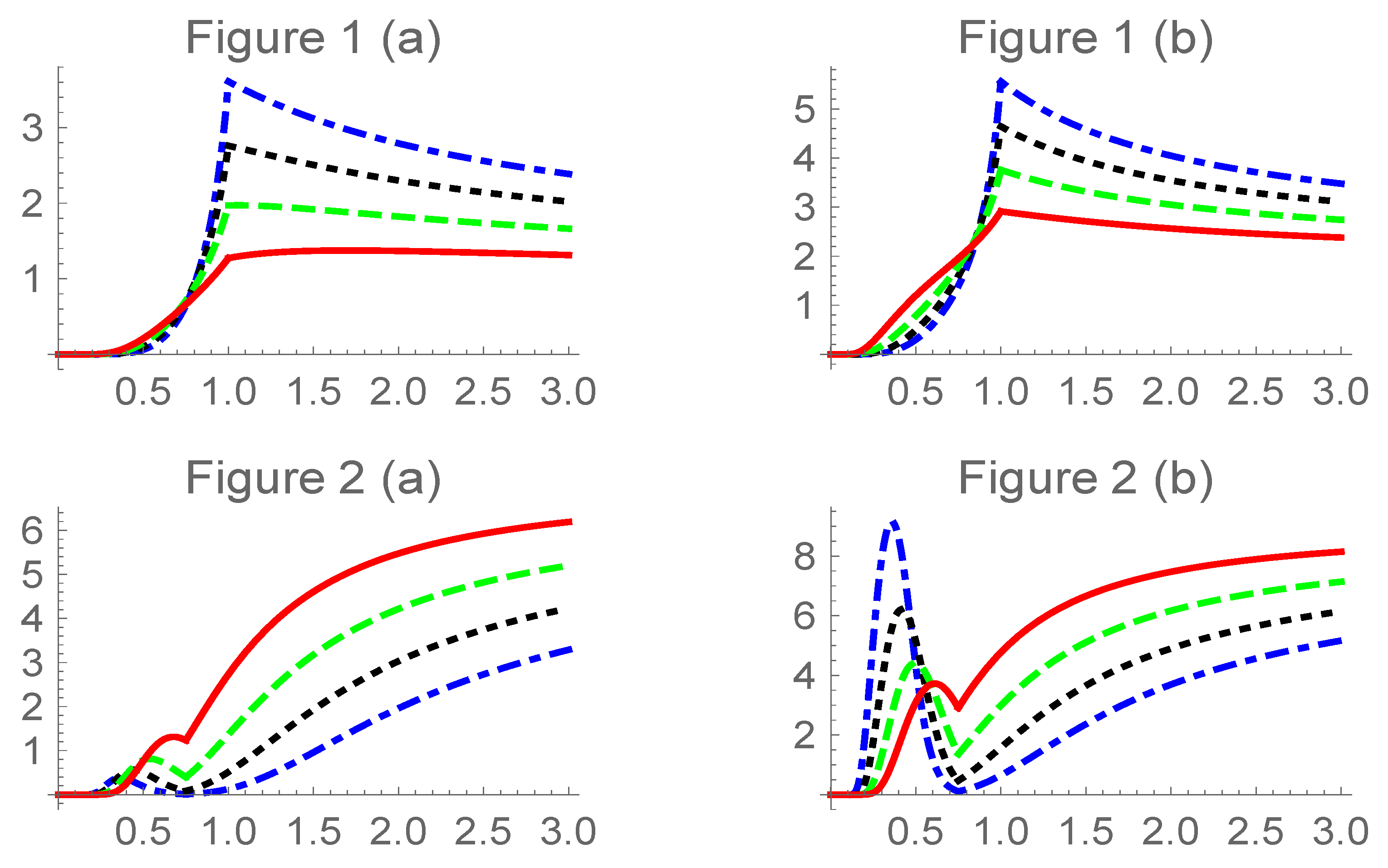
- 1.
- corresponding to Figure 1a,b. These are, first, quickly increasing, later decreasing more slowly or even in a flat way. It can be applied in practical situations in which the risk of failure increases quickly until certain point in which its behaviour becomes flatter. As [23] points out, the flat area is very interesting in survival analysis and reliability contexts.
- 2.
- corresponding to Figure 2a,b are increasing-decreasing-increasing. This kind of hazard functions has been recently introduced and discussed in literature, due to its interest in reliability of systems, see for instance [23] or [24] (and references therein). In plot for Figure 2b, is (quickly) increasing—or (quickly) decreasing. On the other hand, for Figure 2a the initial effect increasing—decreasing is less accentuated.
3. Moments and Maximum Likelihood Estimation
3.1. Maximum Likelihood Estimators
3.2. Expected and Observed Information Matrices
4. Numerical Illustrations
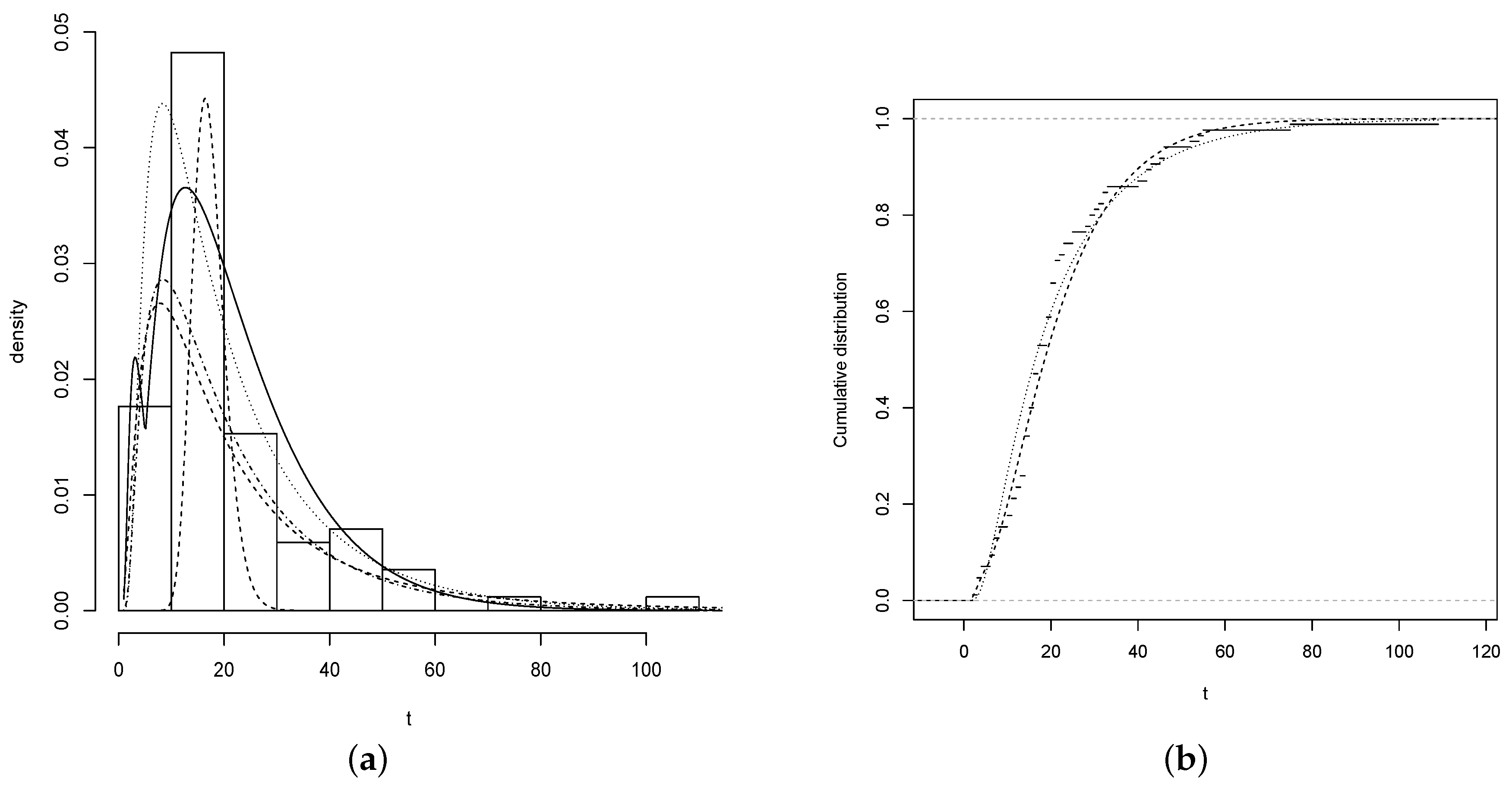
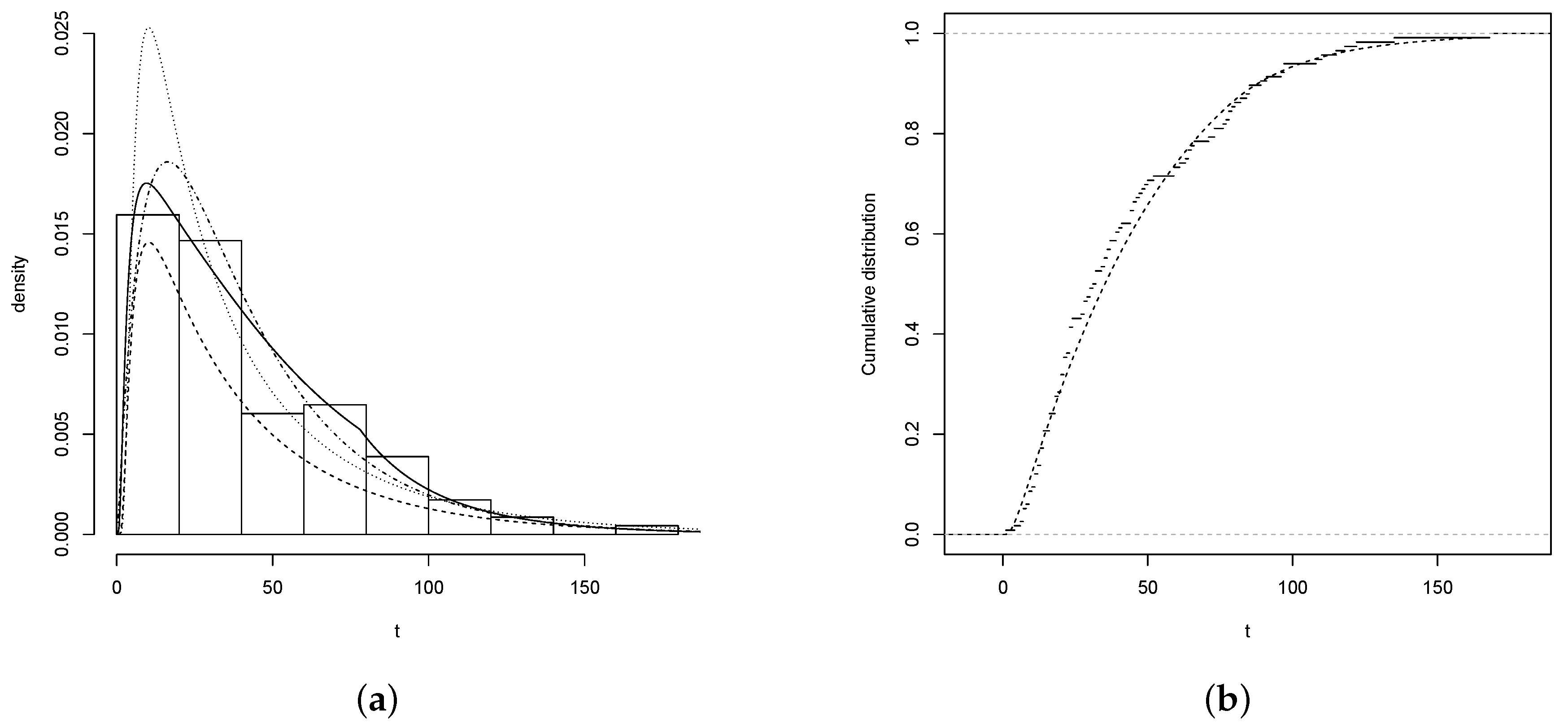
4.1. Nickel Concentration
4.1.1. FBS versus the BS and SBS distributions
4.1.2. FBS versus a Mixture of Normal Distributions
4.1.3. FBS versus a Mixture of Log-Normal Distributions
4.2. Air Pollution
4.2.1. FBS versus the BS and SBS Distributions
4.2.2. FBS versus the Extended BS (EBS) Model
5. Conclusions
- (i)
- the FBS model provides consistently better fits than the BS and SBS models (they can be considered relevant precedents of our proposal)
- (ii)
- the FBS distribution can improve the fit provided by other competing models designed to deal with bimodality (such as a mixture of normal distributions). It can also perform better for unimodal situations in which a generalized BS model with skewness parameters must be applied, such as the EBS model proposed in [16]. We highlight that in both situations FBS provides a better fit with a more parsimonious model (less number of parameters), and the problem of identifiability of mixtures can be circumvented.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- 1.
- 2.
- 3.
- (i)
- (ii)
- Thereforei.e.,
- (iii)
- Let be . In this case , , and . Thereforei.e.,
References
- Birnbaum, Z.W. Effect of linear truncation on a multinormal population. Ann. Math. Statist. 1950, 21, 272–279. [Google Scholar] [CrossRef]
- Gómez, H.W.; Elal-Olivero, D.; Salinas, H.S.; Bolfarine, H. Bimodal Extension Based on the Skew-normal Distribution with Application to Pollen Data. Environmetrics 2009, 22, 50–62. [Google Scholar] [CrossRef]
- Lehmann, E.L. The power of rank tests. Ann. Mathematical Stat. 1953, 24, 23–43. [Google Scholar] [CrossRef]
- Roberts, C. A Correlation Model Useful in the Study of Twins. J. Am. Stat. Assoc. 1966, 61, 1184–1190. [Google Scholar] [CrossRef]
- O’Hagan, A.; Leonard, T. Bayes estimation subject to uncertainty about parameter constraints. Biometrika 1976, 63, 201–203. [Google Scholar] [CrossRef]
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Arnold, B.C.; Gómez, H.W.; Salinas, H.S. On multiple contraint skewed models’. Statistics 2009, 43, 279–293. [Google Scholar] [CrossRef]
- Bolfarine, H.; Martínez–Flórez, G.; Salinas, H.S. Bimodal symmetric-asymmetric families. Commun. Stat. Theory Methods 2018, 47(2), 259–276. [Google Scholar] [CrossRef]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Pewsey, A.; Gómez, H.W.; Bolfarine, H. Likelihood-based inference for power distributions. Test 2012, 21, 775–789. [Google Scholar] [CrossRef]
- Chan, J.; Choy, S.; Makov, U.; Landsman, Z. Modelling insurance losses using contaminated generalised beta type-II distribution. ASTIN Bull. 2018, 48, 871–904. [Google Scholar] [CrossRef]
- Birnbaum, Z.W.; Saunders, S.C. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]
- Birnbaum, Z.W.; Saunders, S.C. A New Family of Life Distributions. J. Appl. Probab. 1969, 6, 319–327. [Google Scholar] [CrossRef]
- Díaz-García, J.A.; Leiva-Sánchez, V. A new family of life distributions based on the elliptically contoured distributions. J. Statist. Plann. Inference 2005, 128, 445–457. [Google Scholar] [CrossRef]
- Vilca-Labra, F.; Leiva-Sanchez, V. A new fatigue life model based on the family of skew-elliptical distributions. Commun. Stat. Theory Methods 2006, 35, 229–244. [Google Scholar] [CrossRef]
- Leiva, V.; Vilca-Labra, F.; Balakrishnan, N.; Sanhueza, A. A skewed sinh-normal distribution and its properties and application to air pollution. Commun. Stat. Theory Methods 2010, 39, 426–443. [Google Scholar] [CrossRef]
- Castillo, N.O.; Gómez, H.W.; Bolfarine, H. Epsilon Birnbaum-Saunders distribution family: Properties and inference. Stat. Pap. 2011, 52, 871–883. [Google Scholar] [CrossRef]
- Gómez, H.W.; Olivares, J.; Bolfarine, H. An extension of the generalized Birnbaum- Saunders distribution. Stat. Probab. Lett. 2009, 79, 331–338. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Generalized Modified Slash Birnbaum-Saunders Distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gómez, H.W. Generalized modified slash distribution with applications. Commun. Stat. Theory Methods 2019. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. An alpha-power extension for the Birnbaum-Saunders distribution. Statistics 2014, 48, 896–912. [Google Scholar] [CrossRef]
- Olmos, N.M.; Martínez-Flórez, G.; Bolfarine, H. Bimodal Birnbaum-Saunders Distribution with Application to Corrosion Data. Commun. Stat. Theory Methods 2017, 46, 6240–6257. [Google Scholar] [CrossRef]
- Shakhatreh, M.; Lemonte, A.; Moreno-Arenas, G. The log-normal modified Weibull distribution and its reliability implications. Reliab. Eng. Syst. Saf. 2019, 188, 6–22. [Google Scholar] [CrossRef]
- Prataviera, F.; Ortega, E.M.M.; Cordeiro, G.M.; Pescim, R.R. A new generalized odd log-logistic flexible Weibull regression model with applications in repairable systems. Reliab. Eng. Syst. Saf. 2018, 176, 13–26. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Kundu, D.; Balakrishnan, N. Modified moment estimation for the two-parameter Birnbaum-Saunders distribution. Comput. Statist. Data Anal. 2003, 43, 283–298. [Google Scholar] [CrossRef]
- Barros, M.; Paula, G.A.; Leiva, V. A new class of survival regression models with heavy-tailed errors: Robustness and diagnostics. Lifetime Data Anal. 2008, 14, 316–332. [Google Scholar] [CrossRef]
- Lemonte, A.; Cribari-Neto, F.; Vasconcellos, K. Improved statistical inference for the two-parameter Birnbaum-saunders distribution. Comput. Stat. Data Anal. 2007, 51, 4656–4681. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Nadarajah, S. A truncated inverted beta distribution with application to air pollution data. Stoch. Environ. Res. Risk Assess. 2008, 22, 285–289. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Gokhale, S.; Khare, M. Statistical behavior of carbon monoxide from vehicular exhausts in urban environments. Environ. Model. Softw. 2007, 22, 526–535. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Flórez, G.; Barranco-Chamorro, I.; Bolfarine, H.; Gómez, H.W. Flexible Birnbaum–Saunders Distribution. Symmetry 2019, 11, 1305. https://doi.org/10.3390/sym11101305
Martínez-Flórez G, Barranco-Chamorro I, Bolfarine H, Gómez HW. Flexible Birnbaum–Saunders Distribution. Symmetry. 2019; 11(10):1305. https://doi.org/10.3390/sym11101305
Chicago/Turabian StyleMartínez-Flórez, Guillermo, Inmaculada Barranco-Chamorro, Heleno Bolfarine, and Héctor W. Gómez. 2019. "Flexible Birnbaum–Saunders Distribution" Symmetry 11, no. 10: 1305. https://doi.org/10.3390/sym11101305
APA StyleMartínez-Flórez, G., Barranco-Chamorro, I., Bolfarine, H., & Gómez, H. W. (2019). Flexible Birnbaum–Saunders Distribution. Symmetry, 11(10), 1305. https://doi.org/10.3390/sym11101305





