Skewness of Maximum Likelihood Estimators in the Weibull Censored Data
Abstract
:1. Introduction
2. The Weibull Censored Data
3. Skewness Coefficient
4. Simulation Study
- The terms and are closer in all the considered combinations, suggesting that approaches in a reasonable way, even when the sample size is small.
- In general terms, approaches well for and . However, for the terms seem discrepant even for .
- Considering the 90 cases for , ranges from , and for C 10%, 25% and 50%, respectively. For , ranges from , and for C 10%, 25% and 50%, respectively. This suggest that a higher percentage of censorship produce a higher skewness in the MLE estimators for the components of .
- Considering the 90 cases for , ranges from , , , and , for and 100, respectively. For , ranges from , , , and for and 100, respectively. This suggest that, as expected, when n increases the skewness coefficient of the MLE estimators for the components of will be more symmetric.
5. Applications
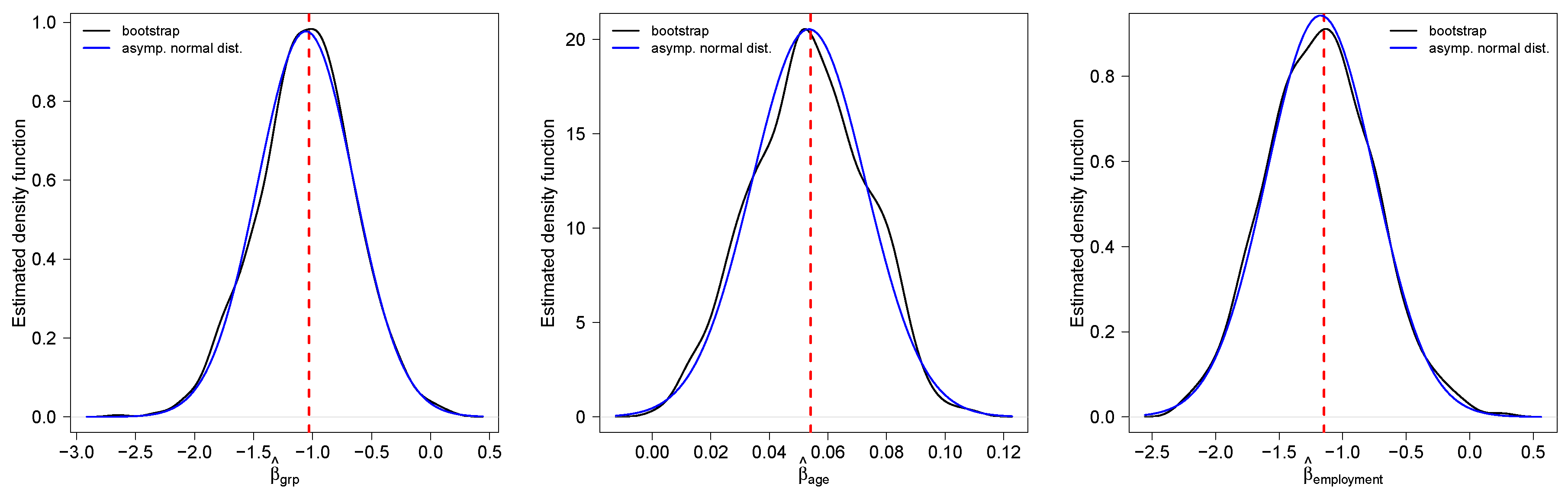
5.1. Smokers Dataset
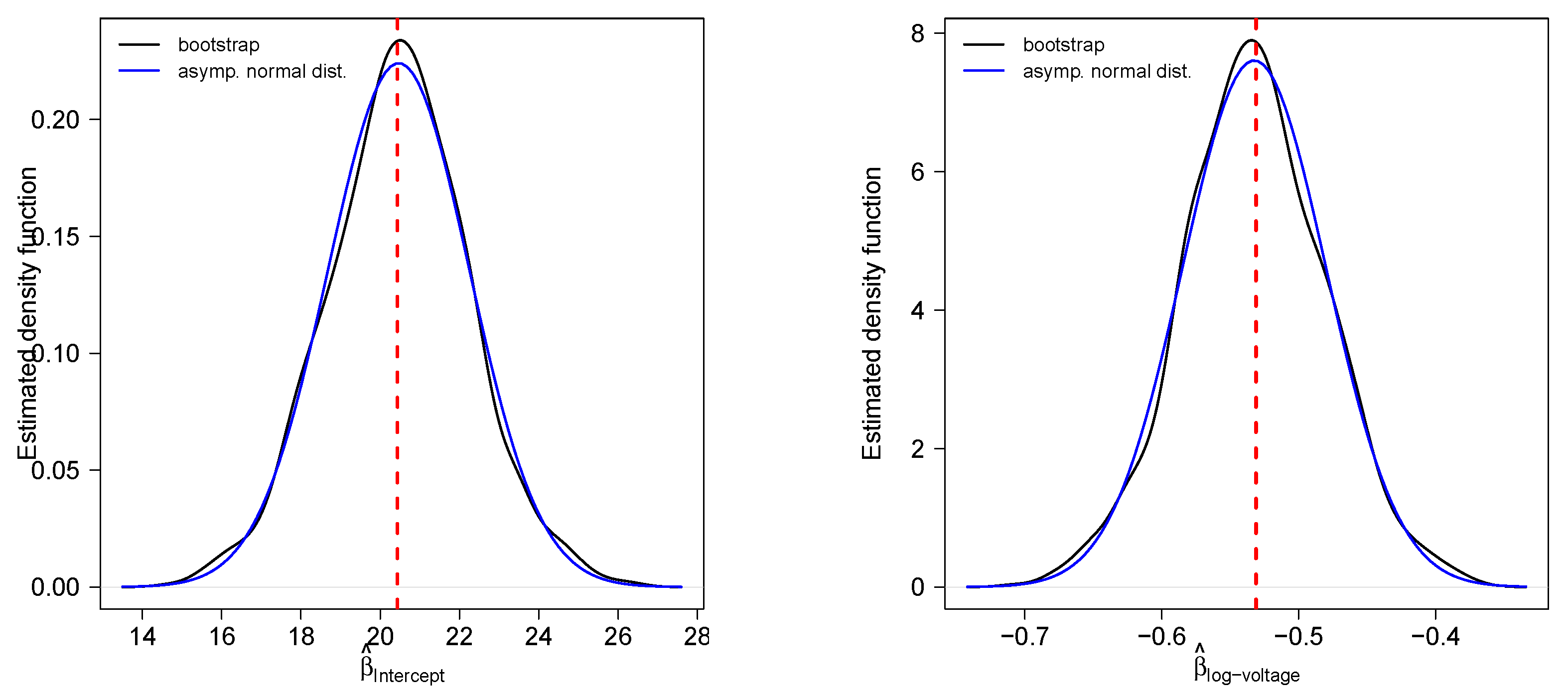
5.2. Insulating Fluids Dataset
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. W’s Quantities
Appendix A.2. Derivatives and Cumulants
References
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistic, 4th ed.; Griffin: London, UK, 1977. [Google Scholar]
- Bowman, K.O.; Shenton, L.R. Asymptotic skewness and the distribution of maximum likelihood estimators. Commun. Stat. Theory Methods 1998, 27, 2743–2760. [Google Scholar] [CrossRef]
- Cordeiro, H.H.; Cordeiro, G.M. Skewness for parameters in generalized linear models. Commun. Stat. Theory Methods 2001, 30, 1317–1334. [Google Scholar] [CrossRef]
- Magalhães, T.M.; Botter, D.A.; Sandoval, M.C.; Pereira, G.H.A.; Cordeiro, G.M. Skewness of maximum likelihood estimators in the varying dispersion beta regression model. Commun. Stat. Theory Methods 2019, 48, 4250–4260. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Colosimo, E.A. Improved likelihood ratio tests for exponential censored data. J. Stat. Comput. Sim. 1997, 56, 303–315. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Colosimo, E.A. Corrected score tests for exponential censored data. Stat. Probab. Lett. 1999, 44, 365–373. [Google Scholar] [CrossRef]
- Magalhães, T.M.; Gallardo, D.I. Bartlett and Bartlett-type corrections for Weibull censored data. Stat. Oper. Res. Trans. 2019. Submitted. [Google Scholar]
- Lemonte, A.J. Non null asymptotic distribution of some criteria in censored exponential regression. Commun. Stat. Theory Methods 2014, 43, 3314–3328. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Nelson, W.; Meeker, W.Q. Theory for optimum accelerated censored life tests for Weibull and extreme value distributions. Technometrics 1978, 20, 171–177. [Google Scholar] [CrossRef]
- Renyi, A. On the theory of order statistics. Acta Math. Hung. 1953, 4, 191–231. [Google Scholar] [CrossRef]
- Devianto, D.; Oktasari, L.; Maiyastri. Some properties of hypoexponential distribution with stabilizer constant. Appl. Math. Sci. 2015, 142, 7063–7070. [Google Scholar] [CrossRef]
| C | |||||||||||
| 20 | −0.235 | −0.080 | −0.095 | 0.052 | 0.207 | 0.197 | 0.071 | 0.245 | 0.234 | ||
| 30 | −0.169 | 0.009 | 0.001 | 0.037 | 0.040 | 0.041 | 0.097 | 0.212 | 0.204 | ||
| 0.5 | 40 | −0.114 | −0.013 | −0.019 | 0.038 | 0.107 | 0.104 | 0.075 | 0.196 | 0.193 | |
| 60 | −0.139 | −0.082 | −0.083 | 0.011 | 0.061 | 0.061 | 0.033 | 0.171 | 0.170 | ||
| 100 | −0.059 | −0.055 | −0.055 | 0.054 | 0.074 | 0.073 | −0.005 | 0.087 | 0.087 | ||
| 20 | −0.198 | 0.017 | 0.004 | −0.008 | 0.225 | 0.197 | 0.068 | 0.298 | 0.284 | ||
| 30 | −0.219 | −0.101 | −0.107 | 0.110 | 0.200 | 0.192 | 0.216 | 0.304 | 0.299 | ||
| 10% | 1.0 | 40 | −0.210 | 0.004 | −0.002 | 0.083 | 0.140 | 0.137 | 0.109 | 0.185 | 0.182 |
| 60 | −0.147 | −0.005 | −0.010 | 0.085 | 0.143 | 0.137 | 0.057 | 0.173 | 0.171 | ||
| 100 | −0.092 | −0.013 | −0.015 | 0.019 | 0.048 | 0.047 | 0.116 | 0.132 | 0.131 | ||
| 20 | −0.232 | 0.006 | 0.005 | 0.094 | 0.143 | 0.131 | 0.022 | 0.093 | 0.087 | ||
| 30 | −0.178 | −0.041 | −0.040 | 0.004 | 0.054 | 0.048 | −0.007 | 0.147 | 0.136 | ||
| 3.0 | 40 | −0.185 | 0.005 | 0.003 | 0.002 | 0.024 | 0.023 | 0.064 | 0.156 | 0.151 | |
| 60 | −0.128 | −0.020 | −0.020 | 0.044 | 0.049 | 0.047 | 0.073 | 0.124 | 0.120 | ||
| 100 | −0.117 | −0.028 | −0.028 | 0.084 | 0.100 | 0.095 | 0.039 | 0.077 | 0.075 | ||
| Parameter | Estimate | s.e. | |
|---|---|---|---|
| 3.1690 | 0.8136 | −0.0478 | |
| −1.0303 | 0.3694 | −0.0529 | |
| 0.0541 | 0.0167 | 0.1251 | |
| −1.1460 | 0.3935 | −0.0753 |
| Parameter | Estimate | s.e. | |
|---|---|---|---|
| 20.4342 | 1.8772 | 0.1451 | |
| −0.5311 | 0.0557 | −0.1517 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magalhães, T.M.; Gallardo, D.I.; Gómez, H.W. Skewness of Maximum Likelihood Estimators in the Weibull Censored Data. Symmetry 2019, 11, 1351. https://doi.org/10.3390/sym11111351
Magalhães TM, Gallardo DI, Gómez HW. Skewness of Maximum Likelihood Estimators in the Weibull Censored Data. Symmetry. 2019; 11(11):1351. https://doi.org/10.3390/sym11111351
Chicago/Turabian StyleMagalhães, Tiago M., Diego I. Gallardo, and Héctor W. Gómez. 2019. "Skewness of Maximum Likelihood Estimators in the Weibull Censored Data" Symmetry 11, no. 11: 1351. https://doi.org/10.3390/sym11111351
APA StyleMagalhães, T. M., Gallardo, D. I., & Gómez, H. W. (2019). Skewness of Maximum Likelihood Estimators in the Weibull Censored Data. Symmetry, 11(11), 1351. https://doi.org/10.3390/sym11111351







