Abstract
In this paper we introduce a new distribution constructed on the basis of the quotient of two independent random variables whose distributions are the half-normal distribution and a power of the exponential distribution with parameter 2 respectively. The result is a distribution with greater kurtosis than the well known half-normal and slashed half-normal distributions. We studied the general density function of this distribution, with some of its properties, moments, and its coefficients of asymmetry and kurtosis. We developed the expectation–maximization algorithm and present a simulation study. We calculated the moment and maximum likelihood estimators and present three illustrations in real data sets to show the flexibility of the new model.
1. Introduction
In recent years, for data with positive support, specifically, lifetime, or reliability, the half-normal (HN) model has been widely used. The probability density function (pdf) is given by
where is the scale parameter and represents the standard normal pdf. We denote this by writing .
Some generalizations for this model are proposed by Cooray and Ananda [1], Cordeiro et al. [2], Bolfarine and Gómez [3] and Gómez and Vidal [4].
Olmos et al. [5] extended the HN distribution by incorporating a kurtosis parameter q, with the purpose of obtaining heavier tails, i.e., it has greater kurtosis than the base model. They called this model the slashed half-normal (SHN) distribution. Its construction is based on considering the quotient of two independent random variables, with random variable in the numerator and the in the denominator (See Rogers and Tukey [6] and Mosteller and Tukey [7] for more details). Thus a model is obtained that has more flexible coefficients of asymmetry and kurtosis than the HN model. We say that a random variable T follows a SHN if its pdf is given by
where is a scale parameter, is a kurtosis parameter, is the cumulative distribution function (cdf) of the gamma distribution and is the pdf of the gamma model with shape and rate parameters a and b, respectively.
Reyes et al. [8] introduced the modified slash (MS) distribution. We say that M has a MS distribution if
the construction of which is based on considering an exponential (Exp) distribution with parameter 2 in the denominator, i.e., they consider that . The motivation of the selection of the distribution is given in Reyes et al. [8]. The result of this work shows that the MS model has a greater coefficient of kurtosis and this characteristic is very important for modeling data sets when they contain atypical observations.
The principal goal of this article is to use the idea published by Reyes et al. [8] to construct an extension of the half-normal model with a greater range in the coefficient of kurtosis than the SHN model, in order to use it to model atypical data. This will allow us obtain a new model generated on the basis of a scale mixture between an HN and a Weibull (Wei) distribution.
The rest of the paper is organized as follows: Section 2 contains the representation of this model and we generate the density of the new family, its basic properties and moments, and its coefficients of asymmetry and kurtosis. In Section 3 we make inferences using the moments and maximum likelihood (ML) methods. In Section 4 we implement the expectation–maximization (EM) algorithm. In Section 5 we carry out a simulation study for parameter recovery. We show three illustrations in real datasets in Section 6 and finally in Section 7 we present our conclusions.
2. An Asymmetric Distribution
In this section we introduce the representation, its pdf, and some important properties and graphs to show the flexibility of the new model.
2.1. New Distribution
The representation of this new distribution is
where and are independent, , . We call the distribution of T the modified slashed half-normal (MSHN) distribution. This is denoted by .
2.2. Density Function
The following Proposition shows the pdf of the MSHN distribution with scale parameter and kurtosis parameter q, generated using the representation given in (3).
Proposition 1.
Proof.
Using the stochastic representation given in (3) and the Jacobian method, we obtain that the density function associated with T is given by
Making the change of variable we have,
Hence, applying the Lemma 1 as set forth in the Appendix A, we obtain the result. □
Figure 1 depicts plots of the density of the MSHN distribution for different values of parameter q.
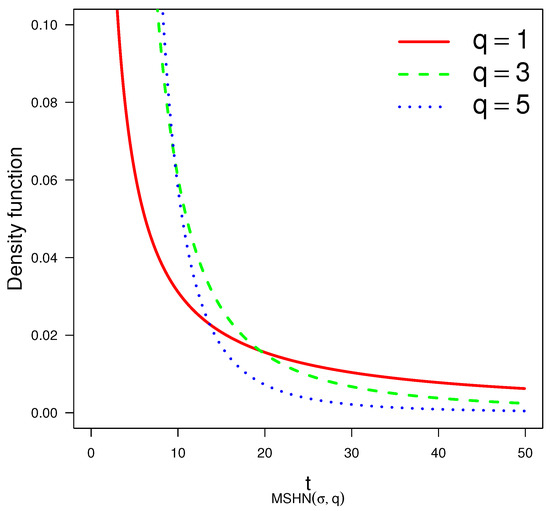
Figure 1.
The density function for different values of parameter q and in the MSHN distribution.
We perform a brief comparison illustrating that the tails of the MSHN distribution are heavier than those of the SHN distribution.
Table 1 shows the tail probability for different values in the SHN and MSHN models. It is immediately apparent that the MSHN tails are heavier than those of the SHN distribution.

Table 1.
Tails comparison for different slashed half-normal (SHN) and modified slashed half-normal (MSHN) distributions.
2.3. Properties
In this sub-section we study some properties of the MSHN distribution.
Proposition 2.
Let , then when the density is
where is the cdf of the standard normal.
Proof.
Using Proposition 1 for , we have,
Changing the variable we obtain the result. □
Proposition 3.
If and then .
Proof.
Since the marginal pdf of T is given by
and using the Lemma 1 in the Appendix A, the result is obtained. □
Proposition 4.
Let . If then T converges in law to a random variable .
Proof.
Let and , where and .
We study the convergence in law of T, since then , we have that . If then , i.e., we have 1 (see Lehmann [9]).
Since , by applying Slutsky’s Lemma (see Lehmann [9]) to , we have
that is, for increasing values of q, T converges in law to a distribution. □
Remark 1.
Proposition 2 shows us that the distribution has a closed-form expression. Proposition 3 shows that an distribution can also be obtained as a scale mixture of an HN and a Wei distribution. This property is very important since it makes it possible to generate random numbers and implement the EM algorithm. Proposition 4 implies that, if then the cdf of an model approaches to the cdf of a distribution.
2.4. Moments
In this sub-section, the following proposition shows the computation of the moments of a random variable . Hence, it also displays the coefficients of asymmetry and kurtosis.
Proposition 5.
Let . Then the r-th moment of T is given by
where denotes the gamma function.
Proof.
Let and using Proposition 3, we have
where , is the r-th moment of the inverse Weibull distribution. □
Corollary 1.
Let . Then the expectation and variance of T are given respectively by
Corollary 2.
Let . Then the coefficients of asymmetry () and kurtosis () are given by
Remark 2.
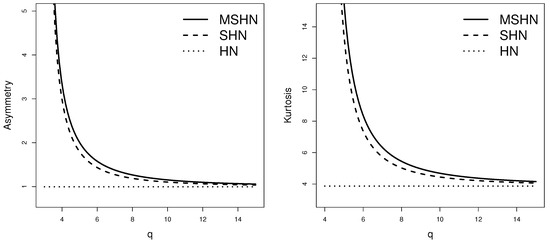
Figure 2 shows graphs of the coefficients of the MSHN distribution compared with those of the SHN distribution. Note that the MSHN distribution presents higher asymmetry and kurtosis values than the SHN distribution. Furthermore, in both distributions when the coefficients of asymmetry and kurtosis converge to and , respectively; they coincide with the coefficients of the HN distribution.

Figure 2.
Graph of the coefficients of asymmetry and kurtosis for the MSHN and SHN distributions.
3. Inference
Proposition 6.
Let be a random sample of size n of the distribution. Then for , the moment estimators of σ and q are given by
where is the mean of the sample and is the mean of the sample for the square of the observations.
Proof.
From Proposition 5, and considering the first two equations in the moments method, we have
Solving the first equation above for we obtain given in (9). Substituting in the second equation above, we obtain the result given in (10). □
4. Em Algorithm
The EM algorithm (Dempster et al. [10]) is a useful method for ML estimation in the presence of latent variables.
To facilitate the estimation process, we introduce latent variables through the following hierarchical representation of the MSHN model:
In this setting, we have that
Therefore, the complete log-likelihood function can be expressed as
where .
Letting , it follows that the conditional expectation of the complete log-likelihood function has the form
where , with and .
As both quantities and have no explicit forms in the context of the MSHN model, they have to be computed numerically. Thus to compute we use an approach similar to that of Lee and Xu ([11], Section 3.1), i.e., considering to be a random sample from the conditional distribution , then can be approximated as
Therefore, the EM algorithm for the MSHN model is given by
- E-step: Given , calculate , for
- CM-step I: Update
- CM-step II: Fix , update by optimizing , where
The E, CM-I and CM-II steps are repeated until a convergence rule is satisfied, say is sufficiently small. Finally, standard errors (SE) can be estimated using the inverse of the observed information matrix.
Remark 3.
- i.
- For , in M-step reduces to those obtained when the HN distribution is used;
- ii.
- An alternative to the CM-Steps II is obtained considering the idea in Lin et al. ([12], Section 3), by using the following estimation:CML-step: Update by maximizing the constrained actual log-likelihood function, i.e.,
5. Simulation
We present a simulation study to assess the performance of the EM algorithm for the parameters and q in the MSHN model. We consider 1000 samples of three sample sizes generated from the MSHN model: , 50 and 100. To generate the following algorithm was used:
- Simulate and .
- Compute .
For each sample generated, the ML estimates were computed using the EM algorithm. Table 2 shows the mean of the bias estimated for each parameter (bias), its SE and the estimated root of the mean squared error (RMSE). From Table 2, we conclude that the ML estimates are quite stable. The bias is reasonable and diminishes as the sample size is increased. As expected, the terms SE and RMSE are closer when the sample size is increased, suggesting that the SE of the estimators is well estimated.

Table 2.
Maximum likelihood (ML) estimations for parameters and q of the MSHN distribution. Standard error (SE), root of the mean squared error (RMSE).
6. Aplications
In this section we provide three applications to real datasets that illustrate the flexibility of the proposed model.
6.1. Application 1
Lyu [13] presents a data set related 104 times with programming in the Centre for Software Reliability (CSR). Some descriptive statistics are: mean = 147.8, variance = 60,071.7, skewness = 3, and kurtosis = 14.6. The moment estimators for the MSHN model were and , which were used as initial values to compute the estimator in Table 3.

Table 3.
ML estimations with the corresponding SE for the models fitted. Half-normal (HN).
For each distribution we report the estimated log-likelihood. To compare the competing models, we consider the Akaike information criterion (AIC) (Akaike [14]) and the Bayesian information criterion (BIC) (Schwarz [15]), which are defined as and , respectively, where k is the number of parameters in the model, n is the sample size and is the maximum value for the log-likelihood function. Table 4 displays the AIC and BIC for each model fitted. Figure 3 presents the histogram of the data fitted with the HN, SHN and MSHN distributions, provided with the ML estimations. The QQ-plot for the MSHN and SHN distributions are presented in Figure 4.

Table 4.
The Akaike information criterion (AIC) and the Bayesian information criterion (BIC) for each model fitted.
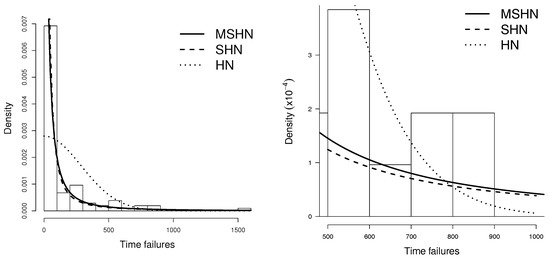
Figure 3.
Histogram fitted with the HN, SHN and MSHN distributions provided with the ML estimations.
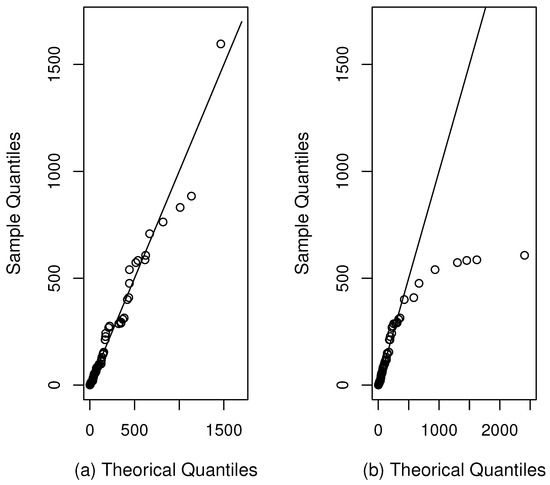
Figure 4.
QQ plots: (a) MSHN distribution and (b) SHN distribution.
6.2. Application 2
The second dataset is taken from Von Alven [16], and represents 46 instances of active repairs (in hours) for an airborne communication transceiver. Some descriptive statistics are: mean = 3.607, variance = 24.445, skewness = 2.888, and kurtosis = 11.802.
Initially we computed the moment estimators for the MSHN distribution, obtaining the following estimations: and . We used these estimations as initial values in computing the ML estimators presented in Table 5. For each distribution we report the estimated log-likelihood.

Table 5.
ML estimations with the corresponding SE for the models fitted.
Table 6 displays the AIC and BIC for each model fitted. Figure 5 presents the histogram of the data fitted with the HN, SHN and MSHN distributions, provided with the ML estimations.

Table 6.
AIC and BIC for each model fitted.
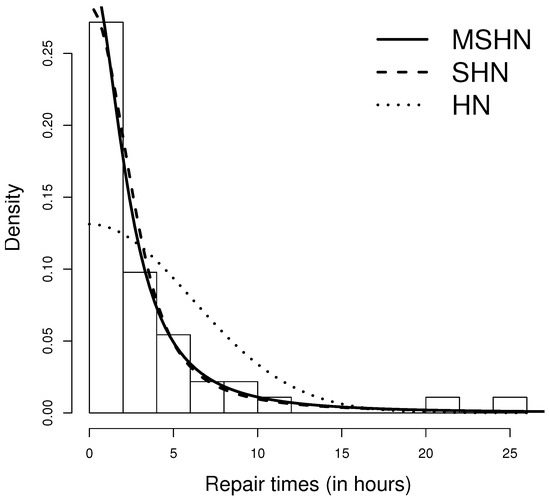
Figure 5.
Histogram fitted with the HN, SHN and MSHN distributions provided with the ML estimations.
6.3. Application 3
The third data set (Linhart and Zucchini [17]) represents 31 times of air conditioning system failure of an aeroplane. Some descriptive statistics are: mean = 55.35, variance = 5132.503, skewness = 1.805, and kurtosis = 5.293.
Initially we computed the moment estimators for the MSHN distribution, and obtained the following estimations: and . We used these estimations as initial values in computing the ML estimators presented in Table 7. For each distribution we report the estimated log-likelihood.

Table 7.
ML estimations with the corresponding SE for the models fitted.
Table 8 displays the AIC and BIC for each model fitted. Figure 6 presents the histogram of the data fitted with the HN, SHN and MSHN distributions, provided with the ML estimations.

Table 8.
AIC and BIC for each model fitted.
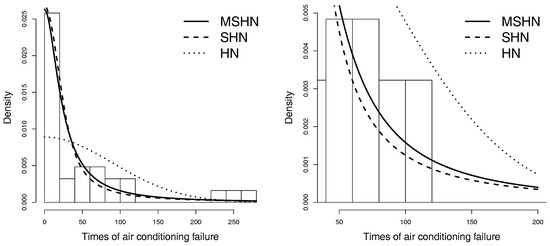
Figure 6.
Histogram fitted with the HN, SHN and MSHN distributions provided with the ML estimations.
7. Conclusions
In this paper, we have introduced a new and more flexible model, as it increases kurtosis and contains, as a particular case, the HN distribution. The EM algorithm is implemented, obtaining acceptable results for the maximum likelihood estimators. In applications using real data it performs very well, better than competing models. Some further characteristics of the MSHN distribution are:
- The MSHN distribution has a greater kurtosis than the SHN distribution, as is clearly reflected in Table 1.
- The proposed model has a closed-form expression and presents more flexible asymmetry and kurtosis coefficients than that of the HN model.
- Two stochastic representations for the MSHN model are presented. One is defined as the quotient between two independent random variables: An HN in the numerator and Exp(2) in the denominator. The other shows that the MSHN distribution is a scale mixture of an HN and a Wei distribution.
- Using the mixed scale representation, the EM algorithm was implemented to calculate the ML estimators.
- Results from a simulation study indicate that with a reasonable sample size, an acceptable bias is obtained.
- Three illustrations using real data show that the MSHN model achieves a better fit in terms of the AIC and BIC criteria.
Author Contributions
N.M.O., O.V., Y.M.G. and Y.A.I. contributed significantly to this research article.
Funding
The research of Neveka M. Olmos and Yuri A. Iriarte was supported by SEMILLERO UA-2019. The research of Yolanda M. Gómez was supported by proyecto DIUDA programa de inserción No. 22367 of the Universidad de Atacama.
Acknowledgments
The authors would like to thank the editor and the anonymous referees for their comments and suggestions, which significantly improved our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Density function of the gamma, exponential and Weibull distributions, respectively, are given by
- Gamma distribution:with, , and .
- Exponential distribution:with, and .
- Weibull distribution:with, , and .
In the following, Lemma presents an important result used in the derivation of the pdf for the MSHN distribution.
Lemma A1.
Prudnikov et al. [18], Equation (2.3.1.13) For , , and . Then
where
Considering , and are coprime integers, where , and is the generalized hypergeometric function defined by
where .
References
- Cooray, K.; Ananda, M.M.A. A Generalization of the Half-Normal Distribution with Applications to Lifetime Data. Commun. Stat. Theory Methods 2008, 37, 1323–1337. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Pescim, R.R.; Ortega, E.M.M. The Kumaraswamy Generalized Half-Normal Distribution for Skewed Positive Data. J. Data Sci. 2012, 10, 195–224. [Google Scholar]
- Gómez, Y.M.; Bolfarine, H. Likelihood-based inference for power half-normal distribution. J. Stat. Theory Appl. 2015, 14, 383–398. [Google Scholar] [CrossRef]
- Gómez, Y.M.; Vidal, I. A generalization of the half-normal distribution. Appl. Math. J. Chin. Univ. 2016, 31, 409–424. [Google Scholar] [CrossRef]
- Olmos, N.M.; Varela, H.; Gómez, H.W.; Bolfarine, H. An extension of the half-normal distribution. Stat. Pap. 2012, 53, 875–886. [Google Scholar] [CrossRef]
- Rogers, W.H.; Tukey, J.W. Understanding some long-tailed symmetrical distributions. Stat. Neerl. 1972, 26, 211–226. [Google Scholar] [CrossRef]
- Mosteller, F.; Tukey, J.W. Data Analysis And Regression; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Reyes, J.; Gómez, H.W.; Bolfarine, H. Modified slash distribution. Statistics 2013, 47, 929–941. [Google Scholar] [CrossRef]
- Lehmann, E.L. Elements of Large-Sample Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Statist. Soc. Ser. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Lee, S.Y.; Xu, L. Influence analyses of nonlinear mixed-effects models. Comput. Stat. Data Anal. 2004, 45, 321–341. [Google Scholar] [CrossRef]
- Lin, T.I.; Lee, J.C.; Yen, S.Y. Finite mixture modeling using the skew-normal distribution. Stat. Sin. 2007, 17, 909–927. [Google Scholar]
- Lyu, M. Handbook of Software Reliability Engineering; IEEE Computer Society Press: Washington, DC, USA, 1996. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Auto. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Von Alven, W.H. Reliability Engineering by ARINC; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1964. [Google Scholar]
- Linhart, H.; Zucchini, W. Model Selection; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 1986. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon & Breach Science Publishers: Amsterdam, The Netherlands, 1986. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).