A General Principle of Isomorphism: Determining Inverses
Abstract
1. Introduction
2. Application of the Realization Theorem in Finding the Inverses
- 1)
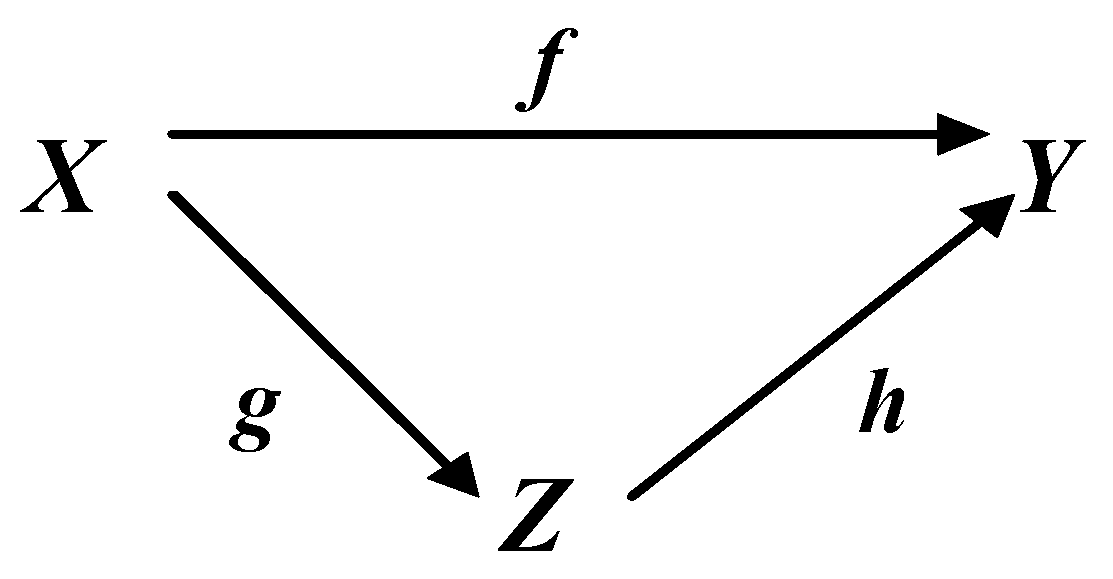
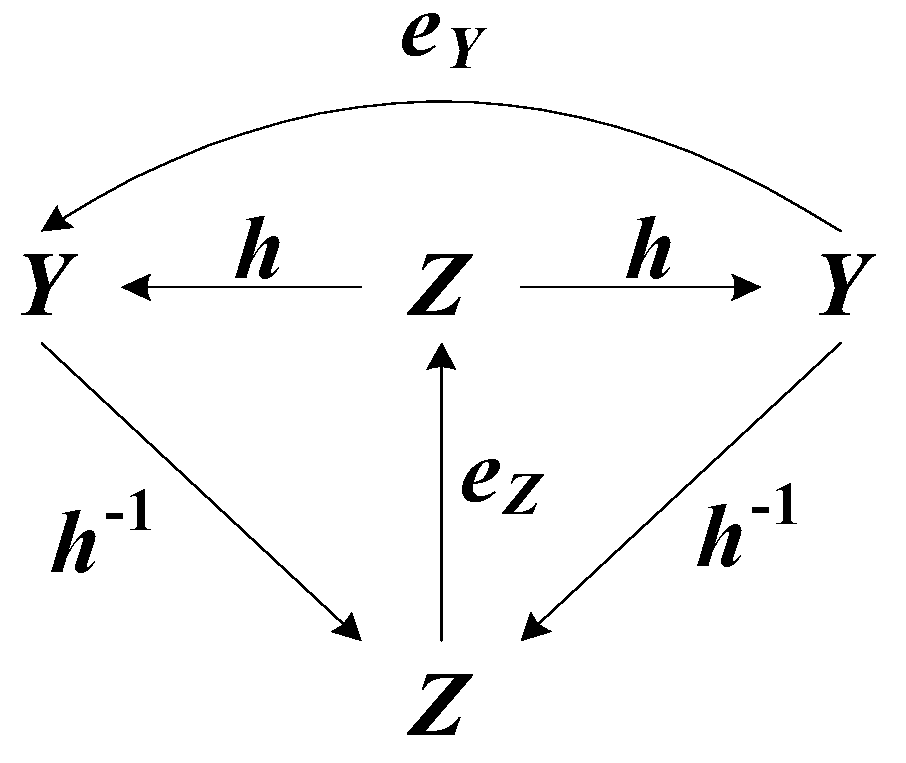
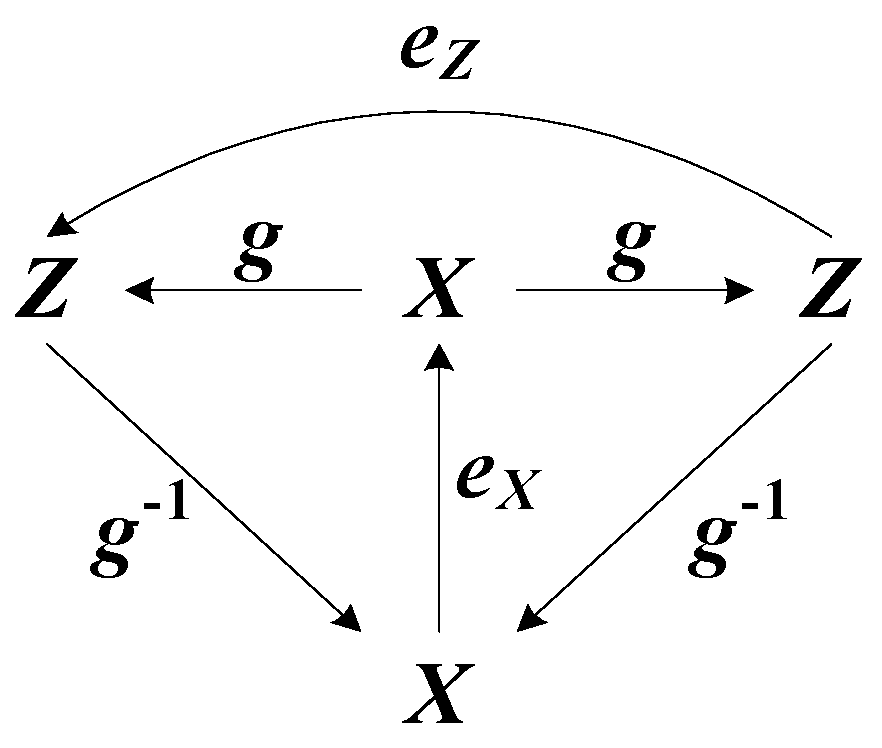
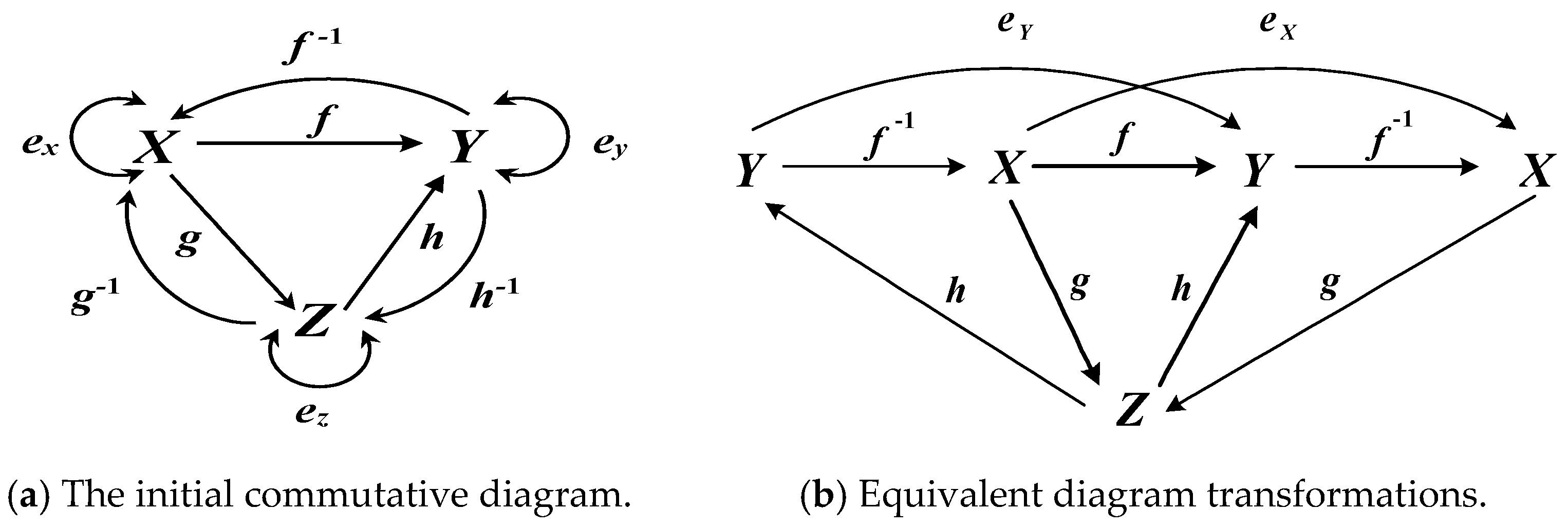
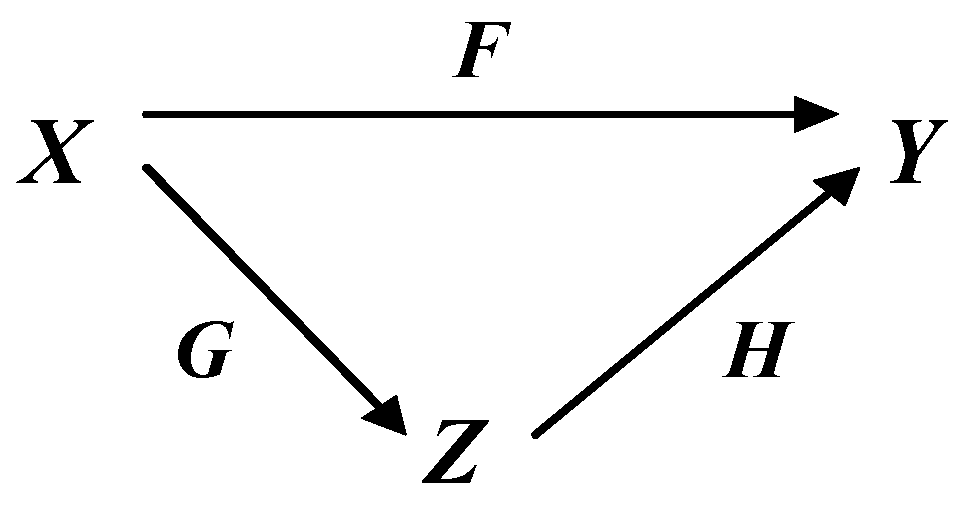
- In the first case, all maps f, g, and h and the composition f = hg in the commutative diagram in Figure 1 are defined initially. In many problems of system theory there is a need to determine the inverses of g−1 and h−1 explicitly;
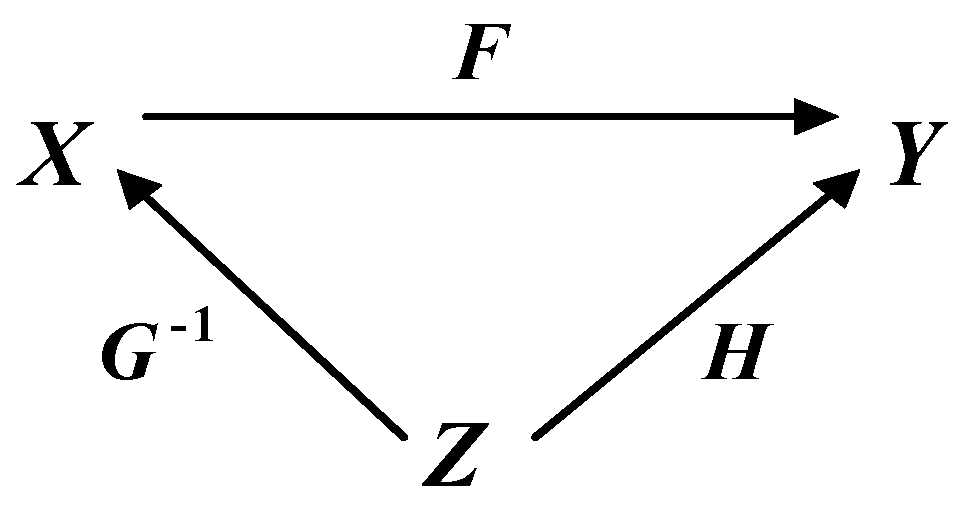
- 2)
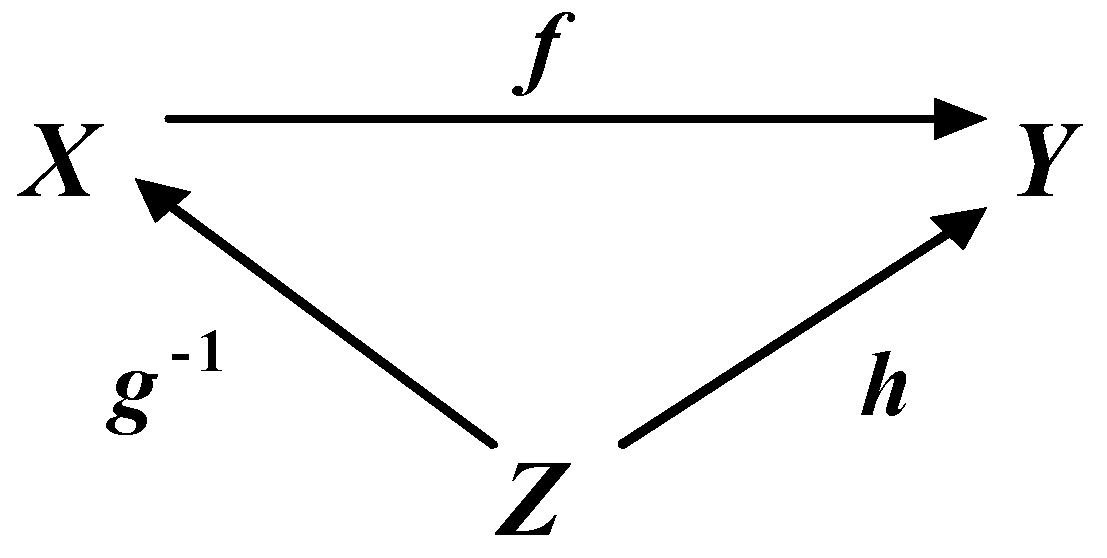
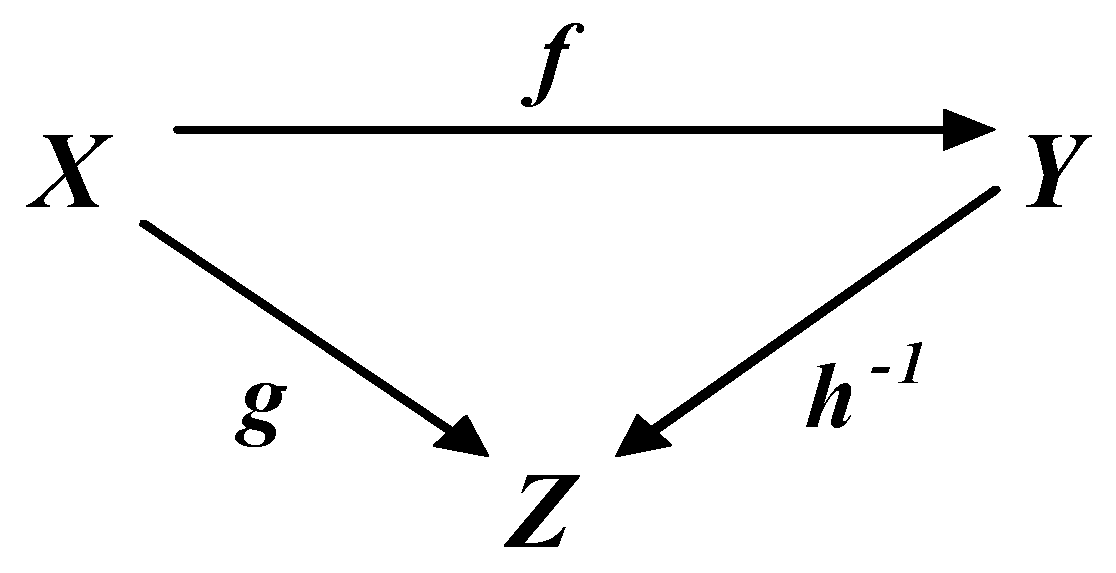
- In the second case, the commutative diagram is converted to the form shown in Figure 2. Here, only the isomorphic map f, some map designated as g−1, and their composition fg−1 are initially known. It is clear that under these conditions the map h commuting the specified composition exists, is uniquely and immediately determined by the formula fg−1 = h. In this case, the mapping of h−1 is unknown and needs to be determined. The inverse of g−1, which also needs to be determined, is also unknown. However, maps g and h−1, inverses to g−1 and h, respectively, can be defined only up to class, that is, they are not unique. This is because, based on the requirements of the realization theorem [3], in this case a pair of mappings (h, g) and their composition hg = f, which implement the isomorphism of f, or a pair of mappings (g−1, h−1) and their composition g−1h−1 = f−1, which implement the isomorphism f−1, are not determined initially and at the same time. Thus, in this second case it is required to find classes of admissible maps h−1 and g that satisfy the condition fg−1 = h and other conditions of the realization theorem, which will be given below. It is obvious that the required classes of maps h−1 and g will be strictly interconnected taking into account these conditions. Once you have defined the classes of valid mappings, you can select one related mappings instance from the corresponding classes, if necessary, and commit those instances to the commutative diagram. Only in this case the only inverses to these instances of mappings will be fixed and can be calculated. Clearly, after fixing specific instances of mappings from valid classes, this case is no different from the first case where all mappings in a commutative diagram are known.
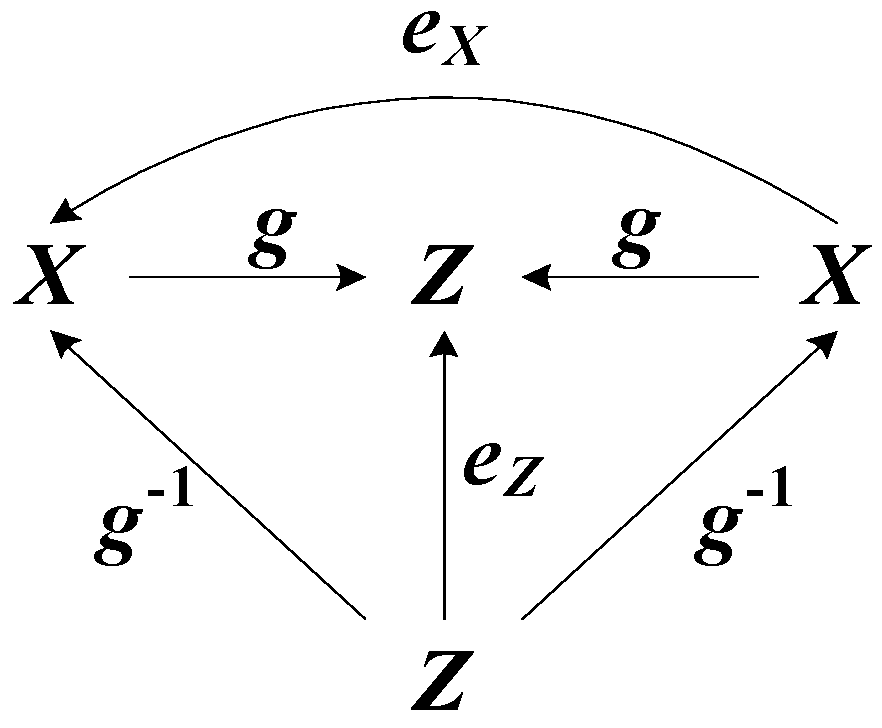
ex = exright = exleft = eyright = eyleft = ey = e.
ezleftezright = gf−1hgf−1h = 〈hg = f〉 = gf−1f f−1h = 〈f−1f = exright, ff−1 = eyleft〉 = gf−1eylefth =
= g exright f−1h = 〈f−1eyleft = f−1, exright f−1 = f−1〉 = g f−1h = ez.
3. Discussion
4. Summary
Funding
Conflicts of Interest
References
- Kulabukhov, V.S. Printsip izomorfnosti v teorii sistem. In Proceedings of the Mezhdunarodnaya Konferentsiya po Problemam Upravleniya, IPU RAN, Moscow, Russia, 29 June–2 July 1999; Volume 1. [Google Scholar]
- Kulabukhov, V.S. Printsip izomorfnosti v zadache realizatsii i yego prilozheniya k analizu svoystv sistem upravleniya. In Proceedings of the XII Vserossiysk, Soveshch, po Problemam Upravleniya VSPU-2014, IPU RAN, Moscow, Russia, 16–19 June 2014; pp. 438–448. [Google Scholar]
- Kulabukhov, V.S. The General Principle of Isomorphism in Systems Theory. Available online: https://cloudofscience.ru/sites/default/files/pdf/CoS_5_400.pdf (accessed on 7 May 2019).
- Kalman, R.E. On the General Theory of Control System. IFAC Proc. Vol. 1960, 1, 18–22. [Google Scholar] [CrossRef]
- Wang, P. Invariance, uncontrollability, and unobservaility in dynamical systems. IEEE Trans. Autom. Control 1965, 10, 366–367. [Google Scholar] [CrossRef]
- Luenberger, D. Observers for multivariable systems. IEEE Trans. Autom. Control 1966, 11, 190–197. [Google Scholar] [CrossRef]
- Zade, L.; Desoer, C.A.; Zadeh, L.A. Teoriia Lineinykh System; Nauka: Moscow, Russia, 1970. [Google Scholar]
- Kalman, R.E.; Arbib, M.A.; Falb, P.L. Ocherki po Matematicheskoi Teorii Sistem; Mir: Moscow, Russia, 1971. [Google Scholar]
- Mesarovic, M.D. Conceptual basis for a mathematical theory of general systems. Kybernetes 1972, 1, 35–40. [Google Scholar] [CrossRef]
- Takahara, Y. Realization Theory for General Stationary Linear Systems and General System Theoretical Characterization of Linear Differential Equation Systems. Trans. Soc. Instrum. Control Eng. 1973, 9, 408–414. [Google Scholar] [CrossRef][Green Version]
- Mesarovic, M.; Takahara, Y. General Systems Theory: Mathematical Foundations (Mathematics in Science and Engineering); Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Sain, M.K. The growing algebraic presence in systems engineering: An introduction. Proc. IEEE 1976, 64, 96–111. [Google Scholar] [CrossRef]
- Agazzi, E. Systems theory and the problem of reductionism. Erkenntnis 1978, 12, 339–358. [Google Scholar] [CrossRef]
- Willems, J.C. In Dynamical Systems and Microphysics. In System Theoretic Foundations for Modelling Physical Systems; Springer: Vienna, Austria, 1980; pp. 279–289. [Google Scholar]
- Li, T. On the realization theory of impulse response sequences. Acta Math. Sci. 1984, 4, 365–376. [Google Scholar] [CrossRef]
- Kalman, P.E. Identifikatsiya sistem s shumami. Uspekhi Mat. Nauk Russ. 1985, 40, 27–41. [Google Scholar]
- Krasovskii, A.A. Handbook on the Theory of Automatic Control; Nauka: Moscow, Russia, 1987. [Google Scholar]
- Proychev, T.P.; Mishkov, R.L. Transformation of nonlinear systems in observer canonical form with reduced dependency on derivatives of the input. Automatica 1993, 29, 495–498. [Google Scholar] [CrossRef]
- Ciccarella, G.; Dalla Mora, M.; Germani, A. A Luenberger-like observer for nonlinear systems. Int. J. Control 1993, 57, 537–556. [Google Scholar] [CrossRef]
- Bukov, V.N.; Kulabukhov, V.S.; Maksimenko, I.M.; Ryabchenko, V.N. Uniqueness of solutions of problems of the theory of systems. Autom. Remote Control 1997, 58, 1875–1885. [Google Scholar]
- Bukov, V.; Kulabuhov, V.; Maximenko, I.; Ryabchenko, V. Uniqueness of a solution of the systems theory problems and functional integration. In Proceedings of the IFAC Conference on Informatics and Control, St. Petersburg, Russia, 9–13 June 1997; Volume 2. [Google Scholar]
- Bukov, V.N. Vlozheniye Sistem. Analiticheskiy Podkhod k Analizu i Sintezu Matrichnykh System; Izd-vo nauchn. Literatury N.F. Bochkarevoy: Kaluga, Russia, 2006. [Google Scholar]
- Bhattacharyya, S.P.; Datta, A.; Keel, L.H. Linear Control Theory: Structure, Robustness and Optimization; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Isidori, A. Nonlinear Control Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Kulabukhov, V. Linear Isomorphic Regulators. In MATEC Web of Conferences, Proceedings of the CMTAI2016, Moscow, Russsia, 15–16 December 2016; MATEC Web of Conferences: Paris, France, 2017; Volume 9, p. 03008. [Google Scholar] [CrossRef]
- Kulabukhov, V.S. Isomorphic observers of the linear systems state. In IOP Conference Seriesm, Proceedings of the Materials Science and Engineering in Aeronautics (MEA2017), Moscow, Russian Federation, 15–16 November 2017; IOP Publishing: Bristol, UK, 2017; Volume 312, p. 012016. [Google Scholar] [CrossRef]
- Kulabukhov, V. Algebraic Formalization of System Design Based on a Purposeful Approach. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 476, p. 012017. [Google Scholar] [CrossRef]
- Kostrikin, A.I. Vvedenie v Algebru: Osnovy Algebry; Fiziko-Matematicheskaia Literatura: Moscow, Russia, 1994. [Google Scholar]
- Homyakov, D.M.; Homyakov, P.M. Fundamentals of System Analysis; Lomonosov Moscow State University: Moscow, Russia, 1996. [Google Scholar]
- Zhilin, D.M. Teoriya Sistem: Opyt Postroyeniya Kursa; KomKniga: Moscow, Russia, 2006. [Google Scholar]
- Volkova, V.N.; Denisov, A.A. Osnovy Teorii Sistem i Sistemnogo Analiza; Izdatel’stvo SPbGTU: Saint-Petesburg, Russia, 1999. [Google Scholar]
- Artyukhov, V.V. Obshchaya Teoriya Sistem: Samoorganizatsiya, Ustoychivost’, Raznoobraziye, Krizisy; Knizhnyy dom LIBROKOM: Moscow, Russia, 2010. [Google Scholar]
- Urmantsev, Y.A. Obshchaya teoriya sistem: Sostoyaniye, prilozheniya i perespektivy razvitiya. In Sistema, Simmetriya, Garmoniya; Mysl’: Moscow, Russia, 1988. [Google Scholar]
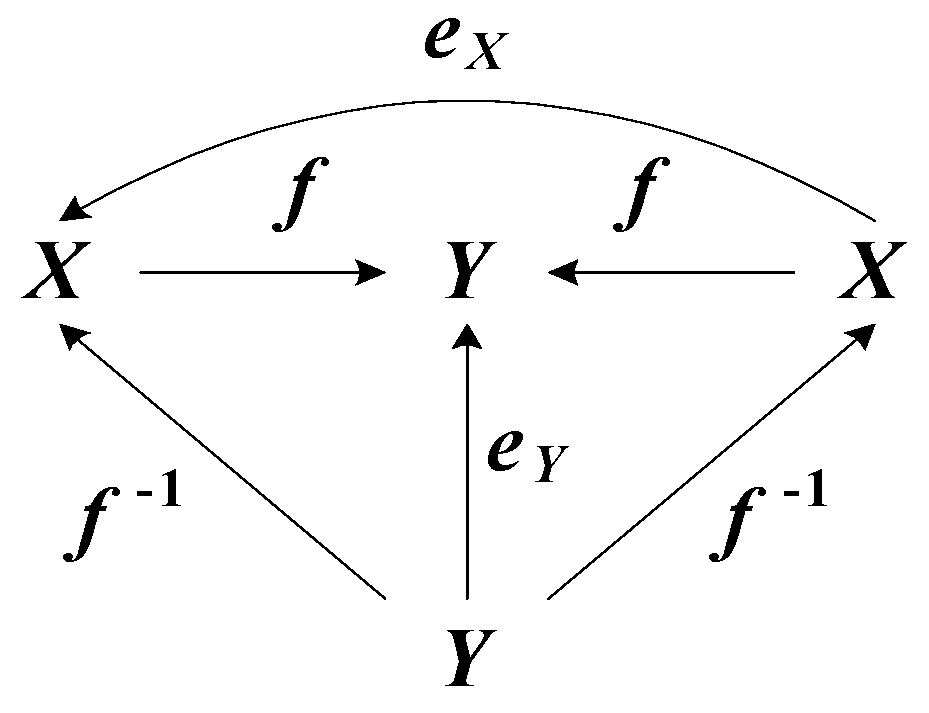
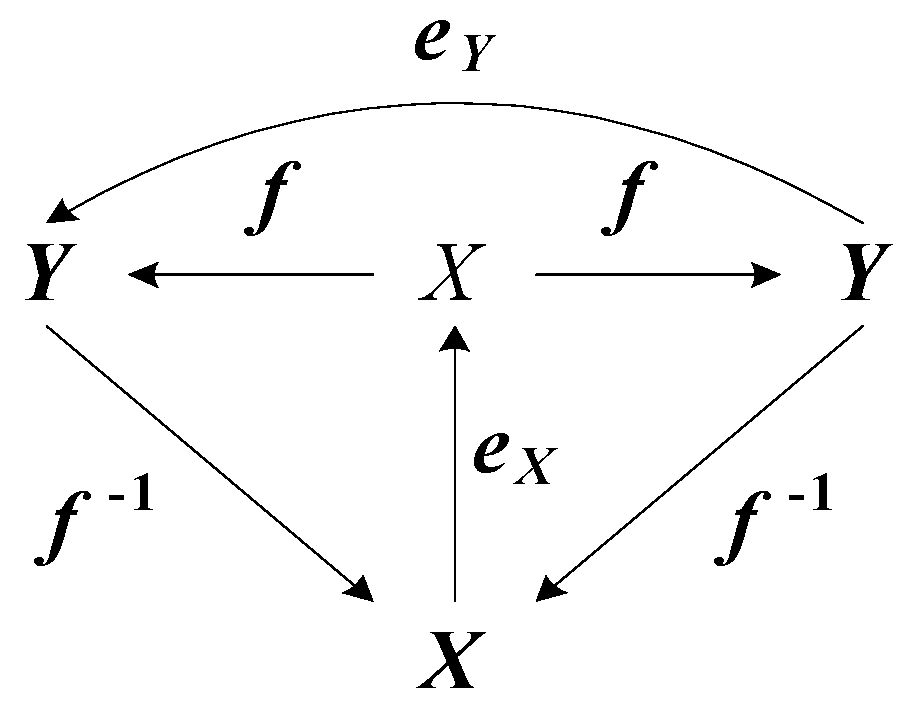
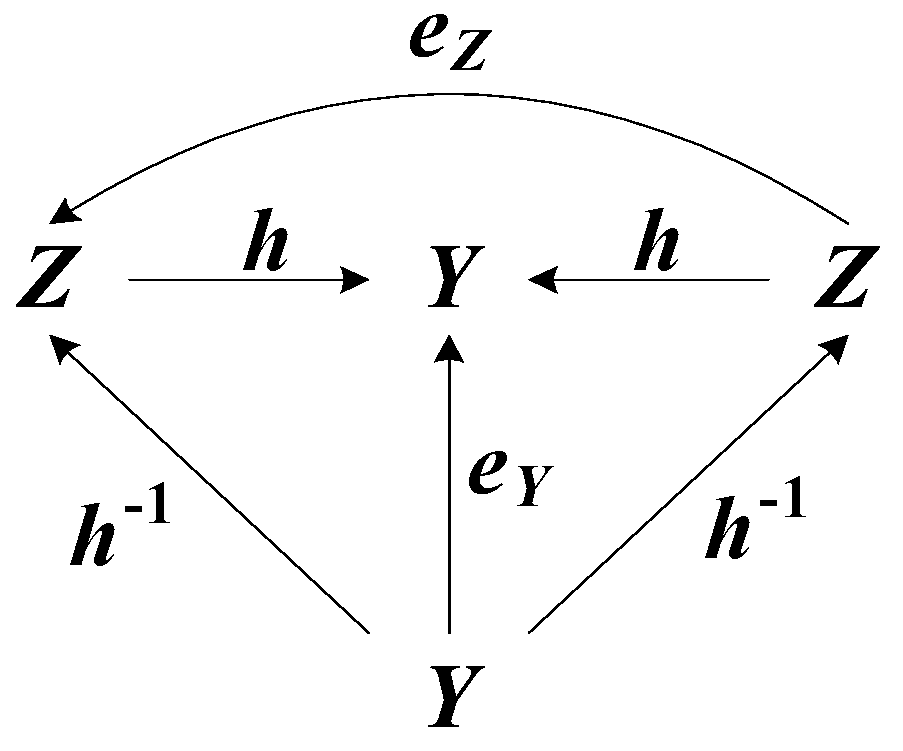
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulabukhov, V.S. A General Principle of Isomorphism: Determining Inverses. Symmetry 2019, 11, 1301. https://doi.org/10.3390/sym11101301
Kulabukhov VS. A General Principle of Isomorphism: Determining Inverses. Symmetry. 2019; 11(10):1301. https://doi.org/10.3390/sym11101301
Chicago/Turabian StyleKulabukhov, Vladimir S. 2019. "A General Principle of Isomorphism: Determining Inverses" Symmetry 11, no. 10: 1301. https://doi.org/10.3390/sym11101301
APA StyleKulabukhov, V. S. (2019). A General Principle of Isomorphism: Determining Inverses. Symmetry, 11(10), 1301. https://doi.org/10.3390/sym11101301



