A Breakdown-Free Block COCG Method for Complex Symmetric Linear Systems with Multiple Right-Hand Sides

Abstract

The block conjugate orthogonal conjugate gradient method (BCOCG) is recognized as a common method to solve complex symmetric linear systems with multiple right-hand sides. However, breakdown always occurs if the right-hand sides are rank deficient. In this paper, based on the orthogonality conditions, we present a breakdown-free BCOCG algorithm with new parameter matrices to handle rank deficiency. To improve the spectral properties of coefficient matrix A, a precondition version of the breakdown-free BCOCG is proposed in detail. We also give the relative algorithms for the block conjugate A-orthogonal conjugate residual method. Numerical results illustrate that when breakdown occurs, the breakdown-free algorithms yield faster convergence than the non-breakdown-free algorithms.

1. Introduction

Consider the following complex symmetric linear system with multiple right-hand sides:

$$AX=B,$$

(1)

with $A\in {\mathbb{C}}^{n\times n}$ non-Hermitian but symmetric (i.e., $A\ne A^H,A=A^T$), $X,B\in {\mathbb{C}}^{n\times p}$, and $1\le p\ll n$. Such systems arise from many practical and important applications, for example, electromagnetic scattering, quantum chemistry, the complex Helmholtz equation, and so on [1,2].

Due to simple calculations and less information required, block Krylov subspace methods are always designed to solve system (1) efficiently [3,4]. Recently, Tadano et al. presented the block conjugate orthogonal conjugate gradient (BCOCG) method [5], which can exploit the symmetry of A naturally. The BCOCG is also deemed a natural generalization of the conjugate orthogonal conjugate gradient (COCG) method [6,7,8] for solving systems (1). Besides COCG-type methods, the COCR method described in [2,7,8] can also exploit the symmetry of A when $p=1$ in (1). In [1], Gu et al. introduced a block version of the COCR method (BCOCR) by employing the residual orthonormalization technique.

However, rank deficiency is a common problem that can lead block Krylov subspace methods to breakdown. The main reason is that the block search direction vectors may be linearly dependent on the existing basis by the increasing of the iteration number [9,10]. Consequently, some useless information will affect the accuracy of the solution and the numerical stability. BCOCG and BCOCR may also encounter such a problem, especially when p of (1) is larger, and we will show this phenomenon in the example section. Hence, it is valuable to solve the rank deficiency problem, and finally to enhance the numerical stability of BCOCG and BCOCR. Motivated by [10], in this paper, we propose a breakdown-free block COCG algorithm (BFBCOCG) and a breakdown-free block COCR algorithm (BFBCOCR) that can efficiently solve the rank deficiency problem of BCOCG and BCOCR, respectively.

The convergence rate of the Krylov subspace method depends on the spectral properties of the coefficient matrix, for example, the eigenvalue or singular value distribution, field of values, condition of the eigensystem, and so on. Fortunately, preconditioning can improve the spectral properties [11]. In this paper, we present the preconditioned version of BFBCOCG and BFBCOCR in detail.

The rest of this paper is organized as follows. In Section 2, based on the orthogonality conditions, we propose the BFBCOCG and BFBCOCR algorithms and their preconditioned variants with their new parameter matrices. Some numerical examples are listed in Section 3 to show the efficiency of our new algorithms. Finally, some conclusions are given in Section 4.

In this paper, ${\mathcal{K}}_{k+1}(A,R_0)$ denotes the $(k+1)$-dimension Krylov subspace $\mathrm{span}\{R_0,A{R}_0,\cdots ,A^k{R}_0\}$, $\overline{A}$ denotes the conjugate of A.

2. The Breakdown-Free Variants of BCOCG and BCOCR

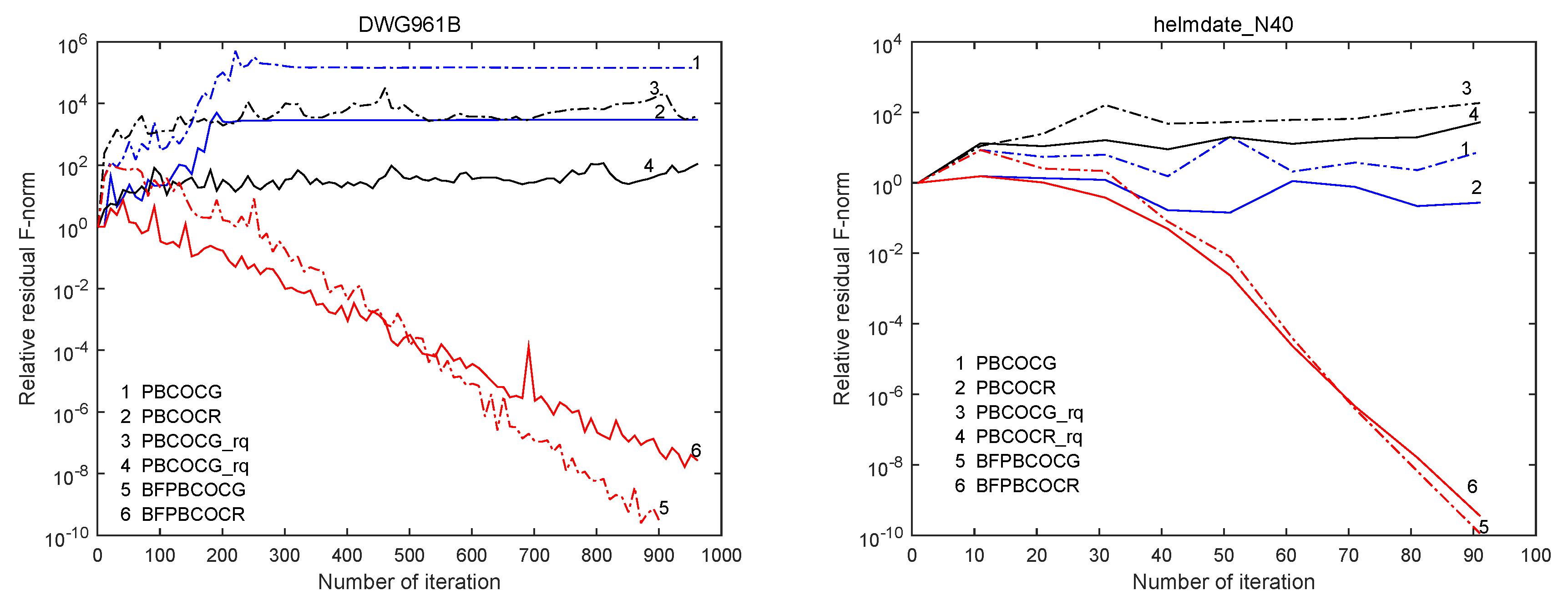
In this section, we present our main algorithms, i.e., the breakdown-free block COCG algorithm (BFBCOCG) and the breakdown-free block COCR algorithm (BFBCOCR) in detail. We first introduce the block COCG (BCOCG) and block COCR (BCOCR) methods briefly and then give the derivation of BFBCOCG and BFBCOCR with their orthogonality properties, respectively. In the end, the preconditioned variants of BFBCOCG and BFBCOCR are also proposed, denoted by BFPBCOCG and BFPBCOCR, respectively. We use an underscore “_” to distinguish the breakdown-free and the non-breakdown-free algorithms.

2.1. BCOCG and BCOCR

Let $X_0$ be an initial approximation, and let $X_{k+1}\in X_0+{\mathcal{K}}_{k+1}(A,R_0)$ be the $k+1$th approximate solution of system (1). Hence, the recurrence relation of BCOCG and BCOCR is as follows: [1]

$$\begin{array}{cc}\hfill & R_0=P_0=B-A{X}_0\in {\mathcal{K}}_1(A,R_0),\hfill \\ \hfill & X_{k+1}=X_k+P_k{\alpha }_k\in X_0+{\mathcal{K}}_{k+1}(A,R_0),\hfill \\ \hfill & R_{k+1}=R_k-A{P}_k{\alpha }_k\in {\mathcal{K}}_{k+2}(A,R_0),\hfill \\ \hfill & P_{k+1}=R_{k+1}+P_k{\beta }_k\in {\mathcal{K}}_{k+2}(A,R_0),\mathrm{for}k=0,1,2\cdots .\hfill \end{array}$$

(2)

The difference between BCOCG and BCOCR is the different calculation formulas of matrices ${\alpha }_k$ and ${\beta }_k$ in (2), which are derived by applying the following orthogonality conditions:

$$R_{k+1}\perp \mathcal{L}\mathrm{and}A{P}_{k+1}\perp \mathcal{L}.$$

(3)

Different choices of $\mathcal{L}$ lead to different algorithms:

• $\mathcal{L}={\mathcal{K}}_{k+1}(\overline{A},{\overline{R}}_0)$ results in BCOCG.
• $\mathcal{L}=\overline{A}{\mathcal{K}}_{k+1}(\overline{A},{\overline{R}}_0)$ results in BCOCR.

2.2. BFBCOCG and BFBCOCR

If the block size p is large, then the vectors of the block search direction will inevitably be linearly dependent on the increasing of the iteration number for BCOCG, hence rank deficiency occurs. In the following, in order to overcome this problem, we consider applying the breakdown-free strategy to BCOCG and propose the breakdown-free block COCG algorithm (BFBCOCG). The rationale of BFBCOCG is extracting an orthogonal basis ${\underline{P}}_{k+1}$ from the current searching space by using the operation $orth(·)$. Thus, compared with (2), the new recurrence relation becomes

$$\begin{array}{cc}\hfill & P_0=R_0=B-A{X}_0,{\underline{P}}_0=orth(P_0)\in {\mathcal{K}}_1(A,R_0),\hfill \\ \hfill & X_{k+1}=X_k+{\underline{P}}_k{\underline{\alpha }}_k\in X_0+{\mathcal{K}}_{k+1}(A,R_0),\hfill \\ \hfill & R_{k+1}=R_k-A{\underline{P}}_k{\underline{\alpha }}_k\in {\mathcal{K}}_{k+2}(A,R_0),\hfill \\ \hfill & {\underline{P}}_{k+1}=orth(P_{k+1})=orth(R_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)\in {\mathcal{K}}_{k+2}(A,R_0),\mathrm{for}k=0,1,2\cdots .\hfill \end{array}$$

(4)

Therefore, again using the orthogonality condition (3), we can get the Lemma 1. Here, we denote ${\underline{U}}_k=A{\underline{P}}_k$.

Lemma 1.

For all $0\le j<k$, $R_j^T{R}_k=0$, ${\underline{P}}_j^T{R}_k=0$, and ${\underline{P}}_j^{T}A{P}_k=0$.

Proof. 

Because $R_j,{\underline{P}}_j\in {\mathcal{K}}_k(A,R_0)$ for all $0\le j<k$, and $R_k\perp {\mathcal{K}}_k(\overline{A},{\overline{R}}_0)$ by (3), thus $R_j^T{R}_k=0$ and ${\underline{P}}_j^T{R}_k=0$. Then ${\underline{P}}_j^{T}A{P}_k=0$ can be obtained by the second orthogonality condition in (3). □

Similarly, the following Theorem 1 is obtained to update the parameters ${\underline{\alpha }}_k$ and ${\underline{\beta }}_k$.

Theorem 1.

Under the orthogonality condition (3), the value of parameters ${\underline{\alpha }}_k$ and ${\underline{\beta }}_k$ in the recurrence relation (4) can be obtained by solving the following equations:

$$\begin{array}{cc}\hfill ({\underline{P}}_k^T{\underline{U}}_k){\underline{\alpha }}_k& ={\underline{P}}_k^T{R}_k,\hfill \\ \hfill (R_k^T{\underline{P}}_k){\underline{\beta }}_k& =R_{k+1}^T{R}_{k+1},\mathit{for}k=0,1,2,\cdots .\hfill \end{array}$$

(5)

Proof. 

From Lemma 1 and (4), we have the following two equations:

$$0={\underline{P}}_k^T{R}_{k+1}={\underline{P}}_k^T(R_k-A{\underline{P}}_k{\underline{\alpha }}_k)={\underline{P}}_k^T{R}_k-{\underline{P}}_k^T{\underline{U}}_k{\underline{\alpha }}_k$$

(6)

and

$$0={\underline{P}}_k^{T}A{P}_{k+1}={\underline{P}}_k^{T}A(R_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)={\underline{U}}_k^T{R}_{k+1}+{\underline{P}}_k^T{\underline{U}}_k{\underline{\beta }}_k.$$

(7)

So, solving (6), we can easily get the ${\underline{\alpha }}_k$.

Pre-multiplying ${\underline{\alpha }}_k^T$ to (7), then from the third equation of (4), we have

$$-{\underline{\alpha }}_k^T{\underline{P}}_k^T{\underline{U}}_k{\underline{\beta }}_k={\underline{\alpha }}_k^T{\underline{U}}_k^T{R}_{k+1}={(R_k-R_{k+1})}^T{R}_{k+1}.$$

From Lemma 1, we have $R_k^T{R}_{k+1}=0$, and by the first equation of (5), one has ${\underline{\alpha }}_k^T{\underline{P}}_k^T{\underline{U}}_k=R_k^T{\underline{P}}_k$. Thus the above equation can be rewritten as

$$R_k^T{\underline{P}}_k{\underline{\beta }}_k=R_{k+1}^T{R}_{k+1},$$

(8)

which can be used to update matrix ${\underline{\beta }}_k$. □

The following Algorithm 1 is the breakdown-free block COCG.

Algorithm 1 Breakdown-free block COCG (BFBCOCG)

1.  Given the initial guess $X_0\in {\mathbb{C}}^{n\times p}$ and a tolerance $tol$; Compute: $R_0=B-A{X}_0$, ${\underline{P}}_0=orth(R_0)$, ${\underline{U}}_0=A{\underline{P}}_0$; 2.  For $k=0,1,2,\cdots$ until $\parallel R_k{\parallel }_F/{\parallel R_0\parallel }_F\le tol$, do Solve: $({\underline{P}}_k^T{\underline{U}}_k){\underline{\alpha }}_k={\underline{P}}_k^T{R}_k$; Update: $X_{k+1}=X_k+{\underline{P}}_k{\underline{\alpha }}_k$, $R_{k+1}=R_k-{\underline{U}}_k{\underline{\alpha }}_k$, Solve: ($R_k^T{\underline{P}}_k){\underline{\beta }}_k=R_{k+1}^T{R}_{k+1}$; Update: ${\underline{P}}_{k+1}=orth(R_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)$, ${\underline{U}}_{k+1}=A{\underline{P}}_{k+1}$; End For

Similar to BFBCOCG, we can also easily get BFBCOCR by using $\mathcal{L}=\overline{A}{\mathcal{K}}_{k+1}(\overline{A},{\overline{R}}_0)$ in the orthogonality condition (3). The following Algorithm 2 is the breakdown-free block COCR.

Algorithm 2 Breakdown-free block COCR (BFBCOCR)

1.  Given the initial guess $X_0\in {\mathbb{C}}^{n\times p}$ and a tolerance $tol$; Compute: $R_0=B-A{X}_0$, ${\underline{P}}_0=orth(R_0)$, ${\underline{U}}_0=A{\underline{P}}_0$; 2.  For $k=0,1,2,\cdots$ until $\parallel R_k{\parallel }_F/{\parallel R_0\parallel }_F\le tol$, do Solve: $({\underline{U}}_k^T{\underline{U}}_k){\underline{\alpha }}_k={\underline{U}}_k^T{R}_k$; Update: $X_{k+1}=X_k+{\underline{P}}_k{\underline{\alpha }}_k$, $R_{k+1}=R_k-{\underline{U}}_k{\underline{\alpha }}_k$, Solve: $(R_k^T{\underline{U}}_k){\underline{\beta }}_k=R_{k+1}^{T}A{R}_{k+1}$; Update: ${\underline{P}}_{k+1}=orth(R_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)$, ${\underline{U}}_{k+1}=A{\underline{P}}_{k+1}$; End For

2.3. BFPBCOCG and BFPBCOCR

As we all know, if the coefficient matrix has poor spectral properties, then the Krylov subspace methods may not robust, while a preconditioning strategy can make it better [11]. The trick is preconditioning (1) with a symmetric positive matrix M, which approximates to the inverse of matrix A; we get the following equivalent system:

$$MAX=MB.$$

(9)

Let $M=L{L}^T$ be the Cholesky decomposition of M. Then system (9) is equivalent to

$$\tilde{A}\tilde{X}=\tilde{B},\mathrm{with}\tilde{A}=L^{T}AL,\tilde{X}=L^{-1}X,\tilde{B}=L^{T}B.$$

(10)

We add a tilde “˜” on the variables derived from the new system. Then applying the BFBCOCG method and its recurrence relations (4) to (10), we have the orthogonality conditions

$${\tilde{R}}_k\perp {\mathcal{K}}_k(\overline{\tilde{A}},{\overline{\tilde{R}}}_0)\mathrm{and}\tilde{A}{\tilde{P}}_k\perp {\mathcal{K}}_k(\overline{\tilde{A}},{\overline{\tilde{R}}}_0).$$

(11)

It is easy to see ${\tilde{R}}_k=L^T{R}_k$, ${\tilde{\underline{P}}}_k=orth({\tilde{R}}_k+{\tilde{\underline{P}}}_{k-1}{\underline{\beta }}_{k-1})\in {\mathcal{K}}_{k+1}(\tilde{A},{\tilde{R}}_0)$. The approximate solution $X_k=L{\tilde{X}}_k$ is from $L{\tilde{X}}_0+L{\mathcal{K}}_k(\tilde{A},{\tilde{R}}_0)=X_0+{\mathcal{K}}_k(MA,M{R}_0)$. Set ${\underline{P}}_k=L{\tilde{\underline{P}}}_k$, then ${\underline{P}}_k\in {\mathcal{K}}_{k+1}(MA,M{R}_0)$. The new recurrence relation becomes

$$\begin{array}{cc}\hfill & R_0=B-A{X}_0,{\underline{P}}_0=orth(P_0)=orth(M{R}_0)\in {\mathcal{K}}_1(MA,M{R}_0),\hfill \\ \hfill & X_{k+1}=X_k+{\underline{P}}_k{\underline{\alpha }}_k\in X_0+{\mathcal{K}}_{k+1}(MA,M{R}_0),\hfill \\ \hfill & R_{k+1}=R_k-A{\underline{P}}_k{\underline{\alpha }}_k\in L^{-T}{\mathcal{K}}_{k+2}(\tilde{A},{\tilde{R}}_0),\hfill \\ \hfill & {\underline{P}}_{k+1}=orth(P_{k+1})=orth(M{R}_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)\in {\mathcal{K}}_{k+2}(MA,M{R}_0),\mathrm{for}k=0,1,2\cdots .\hfill \end{array}$$

(12)

The orthogonality condition (11) become

$$R_k\perp {\mathcal{K}}_k(\overline{MA},\overline{M}{\overline{R}}_0)\mathrm{and}A{P}_k\perp {\mathcal{K}}_k(\overline{MA},{\overline{MR}}_0).$$

(13)

Under the recurrence relation (12) and the orthogonality condition (13), we can get the following Lemma 2 and Theorem 2 to update the matrices ${\underline{\alpha }}_k$ and ${\underline{\beta }}_k$. Here, we omit the proof because it is like the proof of Lemma 1 and Theorem 1. We denote $Z_k=M{R}_k,{\underline{U}}_k=A{\underline{P}}_k$.

Lemma 2.

For all $0\le j<k$, $R_j^T{Z}_k=0$, ${\underline{P}}_j^T{R}_k=0$, and ${\underline{P}}_j^{T}A{P}_k=0$.

Remark 1.

Under the preconditioned strategy, the relations of the block residuals are changed from orthogonal for BFBCOCG to M-orthogonal for BFPBCOCG. Here, two vectors x and y are M-orthogonal, meaning $x{\perp }_{M}y$, i.e., $y^{H}Mx=0$.

Theorem 2.

Under the orthogonality condition (13), the value of parameters ${\underline{\alpha }}_k$ and ${\underline{\beta }}_k$ in the recurrence relations (12) can be obtained by solving the following equations:

$$\begin{array}{cc}\hfill {\underline{P}}_k^T{\underline{U}}_k{\underline{\alpha }}_k& ={\underline{P}}_k^T{R}_k,\hfill \\ \hfill (R_k^T{\underline{P}}_k){\underline{\beta }}_k& =R_{k+1}^T{Z}_{k+1},\mathrm{for}k=0,1,2,\cdots .\hfill \end{array}$$

The following Algorithm 3 is the breakdown-free preconditioned block COCG algorithm.

Algorithm 3 Breakdown-free preconditioned block COCG (BFPBCOCG)

1.  Given the initial guess $X_0\in {\mathbb{C}}^{n\times p}$ and a tolerance $tol$; Compute: $R_0=B-A{X}_0$, $Z_0=M{R}_0$, ${\underline{P}}_0=orth(Z_0)$, ${\underline{U}}_0=A{\underline{P}}_0$; 2.  For $k=0,1,2,\cdots$ until $\parallel R_k{\parallel }_F/{\parallel R_0\parallel }_F\le tol$, do Solve: $({\underline{P}}_k^T{\underline{U}}_k){\underline{\alpha }}_k={\underline{P}}_k^T{R}_k$; Update: $X_{k+1}=X_k+{\underline{P}}_k{\underline{\alpha }}_k$, $R_{k+1}=R_k-{\underline{U}}_k{\underline{\alpha }}_k$, $Z_{k+1}=M{R}_{k+1}$; Solve: $(R_k^T{\underline{P}}_k){\underline{\beta }}_k=R_{k+1}^T{Z}_{k+1}$; Update: ${\underline{P}}_{k+1}=orth(Z_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)$, ${\underline{U}}_{k+1}=A{\underline{P}}_{k+1}$; End For

Change the orthogonality conditions (11) to the following conditions:

$${\tilde{R}}_k\perp \overline{\tilde{A}}{\mathcal{K}}_k(\overline{\tilde{A}},{\overline{\tilde{R}}}_0)\mathrm{and}\tilde{A}{\tilde{P}}_k\perp \overline{\tilde{A}}{\mathcal{K}}_k(\overline{\tilde{A}},{\overline{\tilde{R}}}_0).$$

(14)

The breakdown-free preconditioned block COCR (BFPBCOCR) can be deduced with the similar derivation of BFPBCOCG. Algorithm 4 shows the code of BFPBCOCR.

Algorithm 4 Breakdown-free preconditioned block COCR (BFPBCOCR)

1.  Given the initial guess $X_0\in {\mathbb{C}}^{n\times p}$ and a tolerance $tol$; Compute: $R_0=B-A{X}_0$, $Z_0=M{R}_0$, ${\underline{P}}_0=orth(Z_0)$, ${\underline{U}}_0=A{\underline{P}}_0$; 2.  For $k=0,1,2,\cdots$ until $\parallel R_k{\parallel }_F/{\parallel R_0\parallel }_F\le tol$, do Solve: $({\underline{U}}_k^{T}M{\underline{U}}_k){\underline{\alpha }}_k={\underline{U}}_k^T{Z}_k$; Update: $X_{k+1}=X_k+{\underline{P}}_k{\underline{\alpha }}_k$, $R_{k+1}=R_k-{\underline{U}}_k{\underline{\alpha }}_k$, $Z_{k+1}=M{R}_{k+1}$; Solve: $(Z_k^T{\underline{U}}_k){\underline{\beta }}_k=Z_{k+1}^{T}A{Z}_{k+1}$; Update: ${\underline{P}}_{k+1}=orth(Z_{k+1}+{\underline{P}}_k{\underline{\beta }}_k)$, ${\underline{U}}_{k+1}=A{\underline{P}}_{k+1}$; End For

At the end of this section, we will give the complexity for six algorithms. They are the block COCG algorithm, block COCR algorithm, breakdown-free block COCG algorithm, breakdown-free block COCR algorithm, breakdown-free preconditioned block COCG algorithm, and breakdown-free preconditioned block COCR algorithm, which are denoted by BCOCG, BCOCR, BFBCOCG, BFBCOCR, BFPBCOCG, BFPBCOCR, respectively. The pseudocodes of BCOCG and BCOCR are from [1]. Table 1 shows the main costs per cycle of the six algorithms. Here, we denote as “block vector” the matrix with size $n\times \times p$, “bdp” the dot product number of two block vectors, “bmv” the product number of a matrix with $n\times p$ and a block vector, “bsaxpy” the number of two block vectors summed with one of the block vectors being from multiplying a block vector to a $p\times p$ matrix, “LE” the number of solving linear equations with a $p\times p$ coefficient matrix, and “bSC” the storage capacity of block vectors.

Table 1. Main costs per cycle for six algorithms.

	BCOCG	BCOCR	BFBCOCG	BFBCOCR	BFPBCOCG	BFPBCOCR
bdp	2	2	3	3	3	3
bmv	1	1	1	2	2	4
LE	2	2	2	2	2	2
bsaxpy	3	4	3	3	3	3
bSC	4	5	4	4	5	5

From Table 1, we can see the last four algorithms need one more dot product of two block vectors than the original two algorithms, i.e., BCOCG and BCOCR. For the product number of a matrix with a block vector, BFBCOCR and BFPBCOCR are both twice BFBCOCG and BFPBCOCG, respectively. This may result in more time to spend in BFBCOCR and BFPBCOCR, especially for a problem with a dense matrix. We reflect on the phenomenon in Example 1.

3. Numerical Examples

In this section, examples are given to demonstrate the effectiveness of our new algorithms. All examples are operated through MATLAB 8.4 (R2014b) on a laptop with an Intel Core i5-6200U CPU 2.3 GHz memory 8GB under the Win10 operating system.

We evaluate the algorithms according to the iteration number ($Iter$), CPU time ($CPU$), and ${log}_{10}$ of the Frobenius norm for the true relative residual ${log}_{10}\frac{\parallel B-A{X}_k{\parallel }_F}{{\parallel B\parallel }_F}$ ($TRR$). All algorithms are started with $X_0=zeros(n,p)$ and stopped with $\frac{\parallel B-A{X}_k{\parallel }_F}{{\parallel B\parallel }_F}\le {10}^{-10}$. Symbol † means no convergence within 1000 iterations. The bold values in the following tables represent the shortest CPU time.

Example 1.

In this example, six algorithms without preconditioning are compared. They are BCOCG, BCOCR, BFBCOCG, BFBCOCR, the block COCG method with residual orthonormalization (BCOCG_rq) [1], and the block COCR method with residual orthonormalization (BCOCR_rq) [1]. Two types of matrices are tested. The first type contains three matrices, $cube1800$, $parallelepipede$, and $sphere2430$, which are all dense and from monostatic radar cross-section calculations, and obtained from the GitHub repository (https://github.com/Hsien-Ming-Ku/Test_matrices/tree/master/Example2). The dimensions n of these matrices are 1800, 2016, 2430, respectively. The second type contains $helmdate\text{\_}N40$, $helmdate\text{\_}N80$, and $helmdate\text{\_}N160$, which are all from the discretization of the Helmholtz equation [12]. Their dimensions n are 1681, 6561, 25921, respectively. The right-hand sides are chosen as $B=(1+i)[rand(n,6),ones(n,2)]$, so that the block size $p=8$, and B is rank deficiency. Here, $i=\sqrt{-1}$. Table 2 and Table 3 give the results.

Table 2. The numerical results for the first type from Example 1.

Algorithm	cube1800			parallelepipede			sphere2430
	CPU	Iter	TRR	CPU	Iter	TRR	CPU	Iter	TRR
BCOCG	†	†	†	†	†	†	†	†	†
BCOCR	†	†	†	†	†	†	4.4542	190	−10.2579
BCOCG_rq	†	†	†	†	†	†	†	†	†
BCOCR_rq	†	†	†	†	†	†	†	†	†
BFBCOCG	2.5071	161	−10.1050	3.5124	179	−10.2753	4.3642	172	−10.0783
BFBCOCR	4.4694	162	−10.3856	5.8695	164	−10.2095	8.8278	171	−10.1099

Table 3. The numerical results for the second type from Example 1.

Algorithm	helmdate_N40			helmdate_N80			helmdate_N160
	CPU	Iter	TRR	CPU	Iter	TRR	CPU	Iter	TRR
BCOCG	†	†	†	†	†	†	†	†	†
BCOCR	†	†	†	†	†	†	†	†	†
BCOCG_rq	†	†	†	†	†	†	†	†	†
BCOCR_rq	†	†	†	†	†	†	†	†	†
BFBCOCG	0.2599	155	−10.3166	2.0171	364	−10.0025	†	†	†
BFBCOCR	0.3132	173	−10.1085	1.9872	332	−10.3876	38.2284	876	−10.0528

From Table 2 and Table 3, we can see that for these rank-deficiency problems, the breakdown-free algorithms perform better than the non-breakdown-free algorithms in CPU time and iteration number. For the first type of problem, although the iterations of BFBCOCR are fewer than BFBCOCG, the CPU time is nearly double because the matrices are all dense and the product number of matrix and block vectors for BFBCOCR is one more than BFBCOCG per iteration. For the first two matrices of the second type of problem, the difference between BFBCOCG and BFBCOCR is not obvious, the main reason being that the matrices are sparse. However, for the third matrix $helmdate\text{\_}N160$, only BFBCOCR can solve the problem. This indicates that for the matrices from the discretization of the Helmholtz equation, BFBCOCR performs the most robust compared to the other five algorithms.

Example 2.

To make it fair, all algorithms compared in this example are preconditioned; they are the preconditioned version sof the same six algorithms as in Example 1 and are denoted by PBCOCG, PBCOCR, BFPBCOCG, BFPBCOCR, PBCOCG_rq, and PBCOCR_rq, respectively. The preconditioning strategy we used is IC(3) in [13]. IC(3) produces $L{L}^T$ for a complex symmetric A, and if L is nonsingular, then we can use $L{L}^T$ as a preconditioner. We test three matrices. The first matrix is $bwg961b$, which is from the NEP collection [14] for electrical engineering and has dimension $n=961$. The second and third matrices are $helmdate\text{\_}N40$ and $helmdate\text{\_}N80$, respectively. The right-hand sides are chosen as $B=(1+i)[rand(n,8),ones(n,2)]$ so that the block size $p=10$, and B is rank deficiency. Numerical results are shown in Table 4 and Figure 1.

Table 4. The numerical results for Example 2.

Algorithm	dwg961b			helmdate_N40			helmdate_N80
	CPU	Iter	TRR	CPU	Iter	TRR	CPU	Iter	TRR
PBCOCG	†	†	†	†	†	†	†	†	†
PBCOCR	†	†	†	†	†	†	†	†	†
PBCOCG_rq	†	†	†	†	†	†	†	†	†
PBCOCR_rq	†	†	†	†	†	†	†	†	†
BFPBCOCG	1.7563	904	−10.0333	0.3238	91	−10.2684	†	†	†
BFPBCOCR	†	†	†	0.4824	91	−10.0138	3.5199	197	−10.1141

Figure 1. Relative residual F-norm for matrices $dwg961b$ and $helmdate\text{\_}40N$ in Example 2.

From the results, we can see that the breakdown-free algorithms perform better than the non-breakdown-free algorithms. Especially in Figure 1, the convergence curve of the four non-breakdown-free algorithms has not dropped, while the breakdown-free ones quickly drop to the accuracy. For matrix $bwg961b$, from Table 4 and Figure 1 we can see that the convergence curves of BFPBCOCG and BFPBCOCR are both downward-trending, while BFPBCOCG performs smoother. For matrix $helmdate\text{\_}N40$, the difference between BFPBCOCG and BFPBCOCR is not big. For matrix $helmdate\text{\_}N80$, BFPBCOCG does not converge, but BFPBCOCR converges quickly. This illustrates that for the matrices from the discretization of the Helmholtz equation, BFPBCOCR has an advantage over the other five preconditioned algorithms in terms of robustness.

4. Conclusions

In this paper, we presented a breakdown-free block conjugate orthogonal conjugate gradient algorithm for complex symmetric linear systems with multiple right-hand sides. Based on the orthogonality conditions, we gave its two new parameter matrices. The preconditioned version is also proposed in detail. At the same time, we also present the breakdown-free version for the block conjugate A-orthogonal conjugate residual method with its preconditioned version. From the numerical examples, we realized that when the right-hand sides are rank deficiency, our four new algorithms perform better than other algorithms. Moreover, for Helmholtz equation problems, BFBCOCR and BFPBCOCR show more stable behavior than BFBCOCG and BFPCOCG; while for dense matrices problems, BFBCOCG and BFPBCOCG converge faster than BFBCOCR and BFPBCOCR. However, there is still a lack of theoretical analysis for the advantages of BFBCOCG and BFBCOCR, and even of BFPBCOCG and BFPBCOCR. All of these require further investigations.