1. Introduction
Video frame interpolation is one of the computer vision techniques that synthesizes single or multiple intermediate frames between two temporally adjacent frames. It is also known as high frame rate conversion, and aims to make videos to be more seamless and visually appealing. Conventional video frame interpolation methods [
1,
2,
3] are typically pixel blending fashion, and use motion estimation mainly based on optical flow estimation. As reported in these researches, obtaining high quality optical flow is crucial in generating good interpolation results.
Recently, applying a deep convolutional neural network to video frame interpolation has been multifariously examined in many researches [
4,
5,
6], since it has shown considerable performance over various computer vision problems. Liu et al. [
4] proposed a network to generate intermediate frames by warping the input frames using estimated optical flow. To train the network, they introduced self-supervised learning, which implicitly affects the network to produce better optical flow. Their method shows better results compared to those models trained in a supervised fashion. However, their method often yields critical artifacts, such as halo and ghost, for occlusion or large motion, which makes optical flow estimation frequently fail. Liu et al. [
7] proposed cycle consistency loss which affects the trained model to produce better optical flow by enforcing the similarity between the input frames and the mapped-back frames. They also introduced the motion linearity and edge-guided training to handle the large motion and rich texture problem. Nevertheless, the method yet shows poor results for complex motion and occlusion.
There have been various approaches to handle such occlusion problems. Tianfan et al. [
8] designed a network composed of three sub-networks whose objective is different. The first and second network both estimate optical flow and occlusion mask from input frames. The last network synthesizes intermediate frame with estimated optical flow and occlusion mask. Jiang et al. [
5] proposed a visibility map for occlusion reasoning. The visibility map allows the blending process to exclude the contribution of occluded pixels to the interpolated frame. For the same reasoning, Bao et al. [
9] proposed a network exploiting depth information. The network predicts not only optical flow, but also depth map, which explicitly detects the occlusion. They also proposed depth-aware flow projection layers that generate intermediate optical flow, which preferably samples closer objects than farther ones. For occlusion, these methods show overwhelmingly better results compared to the state-of-the-art methods. However, these methods yield poor interpolation results for high resolution video frames such as 4K images, which contains wider and larger motion.
Niklaus et al. [
10] proposed a context-aware network that utilizes both optical flow and contextual information. Unlike most video interpolation methods, the network architecture is based upon GridNet [
11], which combines warping and pixel blending into a single step. Their work achieved state-of-the-art performance. However, this method is still unable to perform on high resolution video frames, due to its complex network structure, which requires a huge amount of memory. Meyer et al. [
12] exploited a convolutional neural network to directly estimate the phase decomposition of the intermediate frame. Their method seems to work better for large motion, but it is inferior to the existing methods for rich texture. Niklaus et al. [
6] proposed a pixel-wise frame interpolation network that predicts N × N spatially adaptive kernels. The kernels contain the combination of optical flow and pixel warping information between input frames. Their method obtains high quality interpolation results. However, this method demands higher computational power and more memory in order to perform on high resolution video frames. Niklaus et al. [
13], for memory efficiency, proposed a method that approximates a 2D interpolation kernel with two separable 1D kernels. Yet their method suffers from high computation cost, and is unable to perform on 4K video frames.
In recent researches, some approaches have been proposed to process high resolution video interpolation. Amersfoort et al. [
14] proposed a residual learning method with a multi-scale generative adversarial network. The network reconstructs the high resolution intermediate frame in a coarse-to-fine fashion. Their method runs 47× faster than the existing methods on 360 × 640 image resolution, while producing comparable visual quality. Peleg et al. [
15] proposed an interpolated motion based the high resolution video frame interpolation method. Similar to the work of Amersfoort, they first predict each vertical and horizontal motion in low resolution, as well as an occlusion map. Then, a high resolution intermediate frame is constructed in a block-wise manner. Their method, on the Caffe [
16] platform, runs significantly faster than the existing methods on high resolution videos, while maintaining quantitative quality. Ahn et al. [
17] proposed a hybrid task-based network composed of two sub-networks which each have different objectives. Each first and second network conducts temporal and spatial interpolation, respectively. They achieved the state-of-the-art performance in both quantitative evaluation and running time on 4K videos.
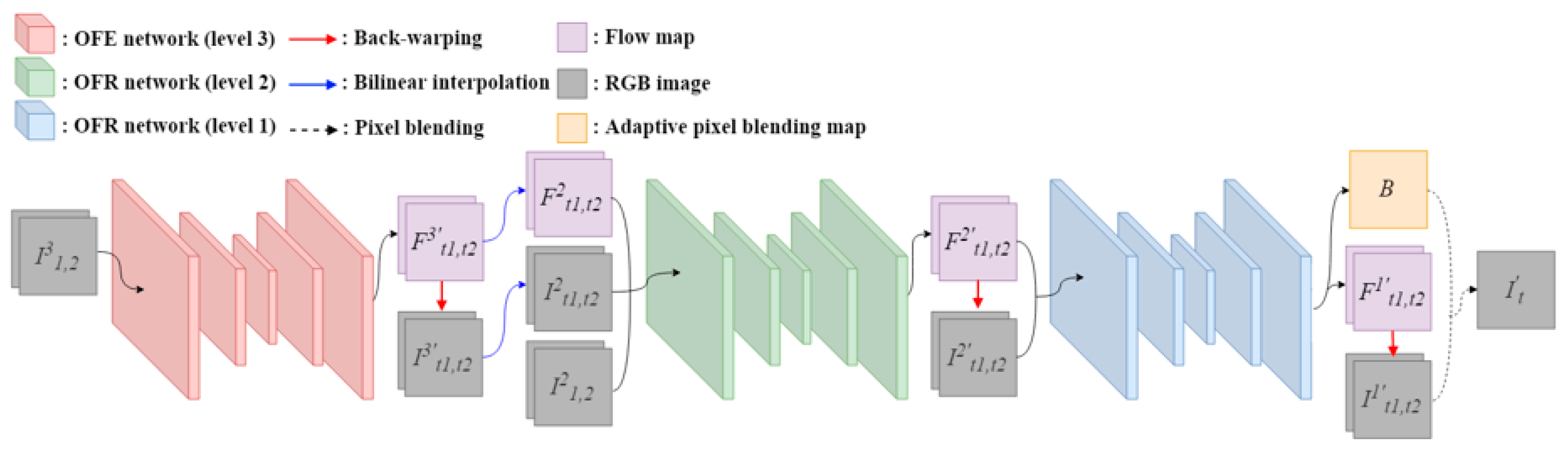
In this paper, we propose a novel fast 4K video frame interpolation method using a multi-scale motion reconstruction network. The proposed network is composed of three sub-networks: An optical flow estimation (OFE) network and two multi-scale optical flow reconstruction (OFR) networks. The OFE network predicts bi-directional optical flow in quarter resolution of input frames. The OFR networks reconstruct the intermediate optical flow into half and original resolution, respectively. This structure allows the network to stably reconstruct high resolution optical flow by applying multi-scale losses. Furthermore, we propose consistency and adversarial loss terms. The consistency loss explicitly enforces the trained network to avoid blur artifact and produce better results. The adversarial loss intuitively helps the model to generate seamless and natural results.
Figure 1 shows the interpolation examples for the existing state-of-the-art methods for 4K frames. Compared to these methods, the proposed method is able to handle large motion and complex structural changes.
2. Proposed Method
Figure 2 shows the architecture of the proposed video frame interpolation network. Our method produces the interpolated frame in a pixel blending manner with warped frames using an optical flow map. The entire network is composed of an optical flow estimation (OFE) network and two multi-scale optical flow reconstruction (OFR) networks. We use three-level pyramidal image representation for multi-scale inputs, which means each network takes different levels of input. Given two input frames
and
, we make three-level pyramidal images
and
,
k {1,2,3}. The first level of pyramidal frames
and
are identical to
and
. The second level frames
and
are obtained by downscaling the
and
, respectively. The same process is conducted to generate the third level frames,
and
The OFE network predicts the optical flow map in low resolution, and OFR networks reconstruct the map in a higher resolution which is the original size of the input frames.
2.1. Optical Flow Estimation
The proposed OFE network aims to predict high quality optical flow in a computationally efficient way. To obtain high quality optical flow, as studied in Jiang’s work [
5], it is necessary that the receptive field of the convolutional filter is large enough to capture large motions. However, one can argue about the optimal size of the receptive field due to the trade-off between the slowness of convolutional operation and the quality of the produced optical flow. Thus, instead of increasing the size of the receptive field, we use downscaled input frames to predict the optical flow. We found this approach allows the network to handle large motions well, without having the heavy computational cost associated with increasing the size of the receptive field.
The OFE network takes the third level of pyramidal input frames
and
, and predicts the bi-directional optical flow maps
and
in a quarter of the resolution of the original input frames. That is,
and
,
k , where
H and
W are the height and width of the original input frames. The intermediate frames
and
are obtained as below.
where,
denotes a back-warp warping function. The intermediate frames
,
and the predicted optical flow maps
and
are upscaled into
,
and
,
, and then they are fed into the first OFR network with the second level of pyramidal input frames
and
. That is, the input of the first OFR network
satisfies as follows:
,
. In this paper, we used bilinear interpolation for the upscaling operation. The optical flow reconstruction process is described in
Section 2.2.
The proposed OFE network is built based upon U-Net [
18]. It is composed of an encoder, a decoder and two additional convolutional layers, followed by a leaky rectified linear unit (Leaky ReLU) [
19] at the front of the network. We set the receptive field filter size to 7 for the first two convolutional layers and to 3 for the rest of the convolutional layers. The encoder has five hierarchical layers, and each hierarchical layer is composed of one average pooling layer and two convolutional layers, followed by a Leaky ReLU. The decoder also has five hierarchical layers with the same structure as the hierarchical layers of encoder, except the decoder has an upscaling layer instead of an average pooling layer before the convolutional layers. There are five skip connections from the encoder to the decoder. The last convolutional layer of each hierarchical layer in the decoder concatenates the last layer of each hierarchical layer in the encoder with its previous layer.
2.2. Optical Flow Reconstruction
The proposed OFR networks aim to reconstruct the optical flow in the original resolution from the predicted low resolution optical flow. This coarse-to-fine approach is often used in previous studies [
14,
17] in order for computational efficiency. However, this approach tends to yield blurry results because it directly reconstructs pixel information. In order to avoid this problem, the proposed approach reconstructs optical flow information instead of pixel information. We also developed the OFR networks with a multi-scale reconstruction scheme. This affects the networks to stably reconstruct a high resolution optical flow. The first OFR network takes
as its input, and then produces the optical flow maps
and
in half of the resolution of the original input frames, which means
, where
k . Similar to the process of the OFE network, the intermediate frames
and
are obtained as follows.
The intermediate frames , and the predicted optical flow maps , are used for the second OFR network. The input of the second OFR network satisfies: , . Note that still has half the resolution of the original input frames. Finally, the second OFR network produces the original resolution optical flow maps and as well as the parameters for the adaptive pixel blending map B. The final intermediate frame is obtained as below.
Here,
denotes element-wise multiplication. The adaptive pixel blending map
B controls the contribution of the input frames. For example, when the pixel p exists in both frame
and
,
B is set to 0.5, and when the p exists in frame
only, then
B is set to 1. We implemented this by using a sigmoid activation function which maps the resulting values in between 0 to 1. This approach is often studied to handle the occlusion problem in the previous researches [
5,
15]. However, for some challenging cases such as complex structural changes or large motion, their method often fails to determine the contribution of the input frames. In this case, they tend to sample pixels equally from both frames, and this yields a ghost artifact. To handle this problem, the proposed method predicts the adaptive pixel blending map by adjusting the slope of our sigmoid function with a learnable parameter. The adaptive pixel blending map
B is obtained as below.
where,
and
are the output of the second OFR network. First parameter
determines the slope of this sigmoid activation function, and the second parameter
acts as input for the activation function. This approach enforces the pixel blending map to sample pixels from the preferable frame and thus to avoid that ghost artifact. The benefits of using the adaptive pixel blending map are studied in
Section 3.3.
The OFR networks have the similar architecture as the OFE network, but they differ in the number of channels for input and output. The first and second OFR networks take 16-channel and 10-channel inputs, respectively, while the OFE network has a 6-channel input. For output, the second OFR network produces a 6-channel, while the OFE and the first OFR networks have a 4-channel output. The decoder of the second OFR network has an additional hierarchical layer.
2.3. Loss Function
We use various loss terms to train the proposed network. Our loss l is defined as below.
We first consider pixel-wise color loss , which measures the difference between the interpolated frame and its ground-truth . The color loss is calculated as by Equation (6).
To preserve details of the interpolated frame, we use feature-based perceptual loss [
20]
which is frequently used for generating visually seamless results in many video frame interpolation methods [
5,
10,
13,
17]. The perceptual loss
is defined as below.
where
denotes the output of conv4_3 layer in the VGG16 [
21] network, trained using ImageNet [
22].
We also use warping loss
to measure the accuracy of the predicted optical flow in each level of pyramidal image representation. Similar to Jiang et al. [
5], the warping loss
is defined as below.
Besides, we use consistency loss
to prevent the trained network from producing overly smoothed results. Similar to Liu et al. [
7], the consistency loss measures the difference between the input frames and mapped-back frames from the interpolated frame. The consistency loss
is defined as below.
Even though we use the consistency loss to handle the over-smoothed problem, the interpolated frame still tends to be smoothed due to the OFR networks which often make drastic optical flow changes. In order to suppress these drastic optical flow changes, we introduce a multi-scale smoothness loss which measures the difference between the reconstructed optical flow map and its reference optical flow map. We experimentally found that this affects the network to stably reconstruct our high resolution optical flow map. The smoothness loss
is defined as below.
where,
and
denote a bilinear upsampling operation and element-wise multiplication. The advantage of the proposed smoothness loss is studied in
Section 3.2.
Finally, we propose the adversarial loss with the discriminator network in order to produce more visually pleasing results. The adversarial loss
is defined as below.
where,
D and
G denote the discriminator network and the proposed frame interpolation network, respectively. The discriminator network takes either the interpolated frame or its ground truth. While the proposed interpolation network attempts at fooling the discriminator network, the discriminator network predicts whether the input is interpolated, or whether they are original ones. The adversarial network has the similar architecture with the OFE network. It has a 3-channel for the input and a 1-channel for the output. The weights of each loss terms are as follows:
= 1.0,
= 0.01,
= 0.5,
= 0.25,
= 0.8, and
= 0.001. We empirically determined these weights through extensive experiments.
2.4. Training
We collected high-resolution videos with various frame rates from YouTube. Following Ahn et al. [
17], we downscaled the collected videos in order to reduce the degradation problem due to video compression. To make triplet input samples, we crop 512 × 512 patches from temporally adjacent frames. Since the proposed network is self-supervised, an additional label for the triplet dataset is unnecessary. The total number of datasets is about 230,000 triplet samples. To train the proposed interpolation network, we use Adam optimizer [
23] with 800 epochs, an initial learning rate of 0.0001, and a batch size of 12. The learning rate is decreased by a factor of 10 for every 300 epochs. We applied various kinds of data augmentation, including random horizontal and vertical flips, frame order swap and temporal gap adjustment. The temporal gap adjustment especially provides the network with rich motion information.
3. Experimental Results
The public datasets often used for evaluation in many video-frame interpolation researches [
4,
5,
7,
13,
24] are the Middleburry optical flow benchmark [
25] and UCF101 [
26]. Since these datasets have very limited low image resolution, they are not suitable for the proposed method which handles high resolution video frames. There are some studies that provide the evaluation results produced from high resolution video datasets. Niklaus et al. [
13] and Bao et al. [
9] conducted evaluation on HD video, and Peleg et al. [
15] upscaled the Vimeo dataset [
27] into higher resolution (1344 × 768) for performance comparison. Ahn et al. [
17] compare and report the performance of their method on Ultra Video [
28] and SJTU Media [
29] datasets whose image resolutions are 4K.
To evaluate and compare the performance of the proposed method, we choose Ultra Video and SJTU Media datasets, because they have 4K image resolution and are suitable for our target. In addition, for various dataset comparisons to the state-of-art methods, we also consider the Vimeo dataset with the same experimental condition introduced in [
15].
For the algorithm, we choose SepConv-
[
13], SuperSloMo [
5], and Ahn et al. [
17], which are available for evaluation and can interpolate a high-resolution video frame such as a 4K image. We also consider IM-Net [
15] for Vimeo dataset evaluation since they provide the evaluation results in their research.
We report PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity) [
30], which are often used to evaluate the performance of video frame interpolation algorithms. We also compare the inference time to show the effectiveness of the proposed method.
3.1. Quantitative Evaluation
Since the Ultra Video and SJTU Media datasets have the YCbCr color format, we converted them into the red-green-blue (RGB) color format for evaluation. However, as Ahn et al. uses the YCbCr color format, we converted their results to the RGB color format to compare the performance in the same domain. The rest of the methods are conducted in the RGB color format.
Table 1 shows the comparison results to state-of-the-art methods that are operable for 4K videos. For the SJTU Media dataset, the proposed method obtained the best results in PSNR of 31.84 dB. The performance gap to the second best method was 0.09 dB. For the Ultra Video, the proposed method outperformed the state-of-the-art methods in both the PSNR and SSIM evaluations. The proposed method achieved PSNR of 28.71 dB, which is 0.23 dB greater than the result of SuperSloMo that showed the second best performance. The proposed method showed a relatively wide performance gap compared to the performance gap for SJTU Meida dataset, because the Ultra Video dataset tends to have more large motions and complex structural changes.
Although the proposed method aims to interpolate 4K video frames, for the more reliable experiments, we considered the Vimeo dataset which contains real-life videos. The Vimeo dataset has 3782 triplet samples extracted from publicly available videos. The dataset has a relatively smaller image size, which is 448 × 256. Thus, for consistency, we followed Peleg et al. and upscaled the dataset into 1344 × 768, using Lastname et al. [
31]. Although IM-Net is publicly unavailable, they provide the quantitative evaluation results for the Vimeo dataset.
Table 2 summarizes the PSNR and SSM evaluation results for the Vimeo dataset. The proposed method achieved PSNR of 33.76 dB and outperformed the state-of-the-art methods. The performance gap between the proposed method and the second best method was 0.27 dB.
Finally, as shown in the
Table 3, we demonstrated that the proposed method performs faster than the existing methods that are operable for 4K videos, while maintaining comparable interpolation quality. To evaluate run time comparison, we calculated the average inference time for interpolating 1000 video frames. Disk read time is excluded in inference time, which means we measure the elapsed time between two points: The first point, which is right after the video frame, is obtained in the input buffer, the second point is when the output buffer received the result from the network. We applied this protocol both for the proposed method and the reference methods.
The proposed method produced a 4K frame in 380 ms using a Titan Xp on a PyTorch [
32] platform. Under the same condition, SepConv, SuperSloMo and Ahn et el. took 1670, 1080 and 620 ms, respectively. We also implemented the proposed method based on CUDA and cuDNN [
33] to improve the run time speed. With CUDA and cuDNN, the proposed method can interpolate a 4K frame in 210 ms. For FHD videos, on the PyTorch platform, the proposed method took 115 ms and 48 ms using CUDA and cuDNN while IM-Net, which is implemented based on Caffe [
16], took 4855 ms. In conclusion, the proposed method runs up to 4.39× faster than the existing methods for 4K videos on the same platform.
3.2. Visual Comparison
In this section, we investigate how the proposed method handles challenging cases for 4K frames.
Figure 3 demonstrates the visual comparison for each state-of-the-art method. The first and second samples are examples of large motion. SepConv and Ahn et al., which are kernel-based approaches, cannot handle large motion, because the motion is beyond their kernel size. SuperSloMo also yields poor results in this case. As shown in
Figure 3, the proposed method handles large motion better than the existing methods and produces a more visually appealing result. We attribute this to the proposed smoothness loss and OFR networks which utilize multi-scale coarse-to-fine fashion. As the proposed network takes downscaled frames as input, the motion is also reduced, and the network can avoid such challenging cases. Furthermore, the smoothness loss allows the OFR networks to stably reconstruct a high resolution optical flow map, which directly affects the results. The third sample is the doors of a racetrack. As the doors are opening, they make complex structural changes and occlusion. The proposed method handles this problem better than the existing methods. Ahn et al. shows comparable results because their method works well with samples which have strong edges, since they use edge loss for training.
3.3. Ablation Study
We report on the ablation study to examine how the different parts of the proposed method effect the results.
Table 4 summarizes the ablation study results for the proposed loss functions and the architecture.
We perform frame interpolation without the high resolution optical flow map produced by the proposed optical flow reconstruction network. Instead of using the predicted high resolution optical flow map, we simply upscaled the
and
which are outputs of the OFE network, using a bilinear interpolation operation. Then the interpolated optical flow map is used for interpolation. That is, we used the bilinear interpolated optical map instead of
and
in Equation (3).
Table 4 shows that the proposed OFR networks are the most significant and increase the quantitative accuracy with a large gap compared to the ablation network. To examine the effectiveness of the adaptive pixel blending map, we trained the proposed network without the first parameter in Equation (4). That is, we used the sigmoid function with a fixed slope. As shown in
Table 4, the network trained with the adaptive pixel blending map is superior to its ablation network.
For the rest of the ablation study, we trained the proposed network with different loss terms and examined the effectiveness of each proposed loss. Firstly, we trained the network without our multi-scale smoothness loss. The network trained with the multi-scale smoothness loss was superior to the ablation model. We found that multi-scale smoothness loss encourages the reconstructed flow map to be more seamless and to suppress drastic flow changes. The consistency loss is the second most significant of the proposed loss terms, and it increases the quantitative accuracy. Especially, for the Vimeo dataset, the consistency loss achieved higher improvement compared to the OFR networks. We also studied the proposed adversarial loss. Intuitively, using the adversarial loss enforces the network to produce a more visually seamless result.
Table 4 proves that the trained network benefits from the adversarial loss in terms of PSNR and SSIM.