Abstract
Spatially uniform optical excitations can induce Floquet topological band structures within insulators which can develop similar or equal characteristics as are known from three-dimensional topological insulators. We derive in this article theoretically the development of Floquet topological quantum states for electromagnetically driven semiconductor bulk matter and we present results for the lifetime of these states and their occupation in the non-equilibrium. The direct physical impact of the mathematical precision of the Floquet-Keldysh theory is evident when we solve the driven system of a generalized Hubbard model with our framework of dynamical mean field theory (DMFT) in the non-equilibrium for a case of ZnO. The physical consequences of the topological non-equilibrium effects in our results for correlated systems are explained with their impact on optoelectronic applications.
Keywords:
topological excitations; Floquet; dynamical mean field theory; non-equilibrium; stark-effect; semiconductors PACS:
71.10.-w theories and models of many-electron systems; 42.50.Hz strong-field excitation of optical transitions in quantum systems; multi-photon processes; dynamic Stark shift; 74.40+ Fluctuations; 03.75.Lm Tunneling, Josephson effect, Bose-Einstein condensates in periodic potentials, solitons, vortices, and topological excitations; 72.20.Ht high-field and nonlinear effects; 89.75.-k complex systems
1. Introduction
Topological phases of matter [1,2,3] have captured our fascination over the past decades, revealing properties in the sense of robust edge modes and exotic non-Abelian excitations [4,5]. Potential applications of periodically driven quantum systems [6] are conceivable in the subjects of semiconductor spintronics [7] up to topological quantum computation [8] as well as topological lasers [9,10] in optics and random lasers [11]. Already topological insulators in solid-state devices such as HgTe/CdTe quantum wells [12,13], as well as topological Dirac insulators such as BiTe and BiSn [14,15,16] were groundbreaking discoveries in the search for the unique properties of topological phases and their technological applications.
In non-equilibrium systems, it has been shown that time-periodic perturbations can induce topological properties in conventional insulators [17,18,19,20] which are trivial in equilibrium otherwise. Floquet topological insulators include a very broad range of physical solid state and atomic realizations, driven at resonance or off-resonance. These systems can display metallic conduction, which is enabled by quasi-stationary states at the edges [17,21,22]. Their band structure may have the form of a Dirac cone in three-dimensional systems [23,24], and Floquet Majorana fermions [25] have been conceptionally developed. Graphene and Floquet fractional Chern insulators have been recently investigated [26,27,28].
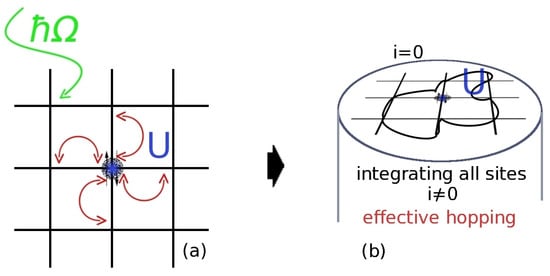
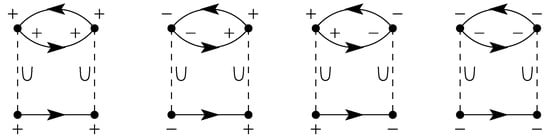
In this article, we show that Floquet topological quantum states can evolve in correlated electronic systems of driven semi-conductors in the non-equilibrium. We investigate bulk matter in the centrosymmetric, cubic rocksalt configuration, see Figure 1. The non-equilibrium is in this sense defined by the intense external electromagnetic driving field, which induces topologically dressed electronic states and the evolution of dynamical gaps, see Figure 2. These procedures are expected to be observable in pump-probe experiments on time scales below the thermalization time. We show that the expansion into Floquet modes [29], see Figure 3, is leading to results of direct physical impact in the sense of modeling the coupling of a classical electromagnetic external driving field to the correlated quantum many body system. Our results derived by Dynamical Mean Field Theory (DMFT) in the non-equilibrium provide novel insights in topologically induced phase transitions of driven otherwise conventional three-dimensional semiconductor bulk matter and insulators.
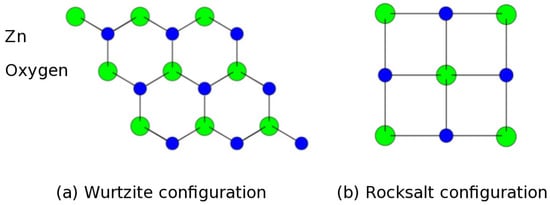
Figure 1.
ZnO structure (ab-plane). (a) non-centrosymmetric, hexagonal, wurtzite configuration; (b) centrosymmetric, cubic, rocksalt configuration (Rochelle salt) [30,31,32]. The rocksalt configuration is distinguished by a tunable gap from 1.8 eV up to 6.1 eV, a gap value of 2.45 eV is typical for the monocrystal rocksalt configuration without oxygen vacancies [33,34]. As such, the rocksalt configuration could be suited for higher harmonics generation under non-equilibrium topological excitation [35,36].
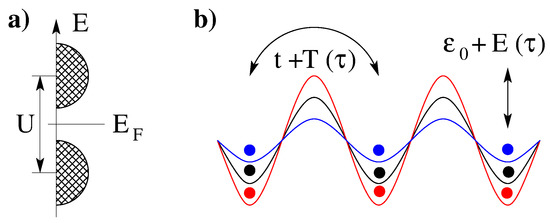
Figure 2.
Insulator to metal transition caused by photo-excitation. (a) schematic split of energy bands due to the local Coulomb interaction U. The gap is determined symmetrically to the Fermi edge ; (b) the periodic in time driving yields an additional hopping contribution of electrons on the lattice (black) and the renormalization of the local potential, , as a quasi-energy. Colors of the lattice potential represent the external driving in time.
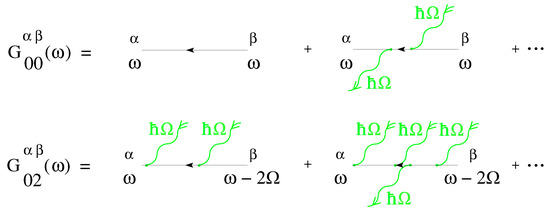
Figure 3.
Schematic representation of the Floquet Green’s function and the Floquet matrix in terms of absorption and emission of external energy quanta . represents the sum of all balanced contributions; describes the net absorption of two photons. are the Keldysh indices.
3. Floquet Spectra of Driven Semiconductors
From the numerically computed components of the Green’s function, we define [37] the local density of states (LDOS), , where momentum is integrated out and Floquet indices are summed
In combination with the lifetime as the inverse of the imaginary part of the self-energy, , and the non-equilibrium distribution function
the local density of states can be experimentally determined as the compelling band structure of the non-equilibrium system.
We show results for optically excited semiconductor bulk, with a band gap in the equilibrium of 2.45 eV and typical parameters for ZnO. ZnO in either configuration [33,34,64,65,66] is a very promising material for the construction of micro-lasers, quantum wells and optical components. In certain geometries and in connection to other topological insulators, it is already used for the engineering of ultrafast switches. ZnO, see Figure 1, is broadly investigated in the non-centro-symmetric wurtzite configuration and very recently in the centro-symmetric rocksalt configuration [31,32]. Its bandgap is estimated to be of 1.8 eV up to 6.1 eV depending on various factors as the pressure during the fabrication process. In either crystal configuration, the production of second or higher order harmonics under intense external excitations [67] is searched. It is of high interest for novel types of lasers.
3.1. Development and Lifetimes of Floquet Topological Quantum States in the Non-Equilibrium
In Figure 6, we investigate a wide gap semi-conductor band structure, and the band gap in equilibrium is assumed to be eV. The semiconductor bulk shall be exposed to an external periodic-in-time driving field. The system is so far considered as pure bulk, so we are investigating Floquet topological effects in the non-equilibrium without any other geometrical influence. The excitation intensity in the results of Figure 6a is considered to be 5.0 MW/cm and 10.0 MW/cm in Figure 6b. DMFT as a solver for correlated and strongly correlated electronics as such is a spatially independent method. It is designed to derive bulk effects, whereas all k-dependencies have been integrated as the fundamental methodology. Therefore, we are not analyzing the k-resolved information of the Brillouin zone. As long as no artificial coarse graining with a novel length scale in the sense of finite elements or finite volumes is included, DMFT results in one, two and three dimensions are independent of any spatial information. In fact, however, the energy dependent LDOS profoundly changes with a varying excitation frequency and with a varying excitation intensity as well, which gives evidence that also the underlying k-dependent band structure is topologically modulated. A non-trivial topological structure of the Hilbert space is generated by external excitations even though our system in equilibrium is fully periodic in space and time. The time dependent external electrical field generates a temporally modulated magnetic field which results in a dynamical Wannier-Stark effect and the generation of Floquet states. Floquet states are the temporal analogue to Bloch states, and thus the argumentation by Zak [61] in principle applies for the generation of the Berry phase , since the solid is exposed to an externally modulated electromagnetic potential [62,68,69,70]. The Floquet quasi-energies, see Figure 3, are labeled by the Floquet modes in dependency to the external excitation frequency, and to the external excitation amplitude. The topological invariants, the Chern number as a sum over all occupied bands and the invariants include the Berry flux . The winding number is also consistently associated with the argument of collecting a non-zero Berry flux. We consider both regimes, where the driving frequency is smaller than the width of the semiconductor gap in equilibrium and also where it is larger and a very pronounced topology of states is generated. While the system is excited and thus evolving in non-equilibrium, a Berry phase is acquired and a non-zero Berry flux and thus a non-zero Chern number are characterizing the topological band structure as to be non-trivial. For one-dimensional, models [61,71] with the variation of the external excitation frequency replica of Floquet bands with a quantized change of the Berry phase emerge in the spectrum. In three dimensions, the Berry phase is associated with the Wyckoff positions of the crystal and the Brillouin zone [61], and, as such, it cannot be derived by the pure form of the DMFT. -dependent information can be derived by so-called real-space or cluster DMFT solutions (R-DMFT or CDMFT) [72,73,74,75]; however, they have not been generalized to the non-equilibrium for three-dimensional systems. It is important to note that the system out of equilibrium acquires a non-zero Berry phase and Coulomb interactions lead to a Mott-type gap that closes due to the superposition by crossing Floquet bands; however, the opening of non-equilibrium induced Mott-gap replica can also be found for eV. The replica are complete at eV; see Figure 6a. For the increase of , these gap replica are again intersected by the next order of Floquet sidebands. The closing of the Mott-gap and the opening of side Mott-gaps, in the spectrum due to topological excitation, are classified as non-trivial topological effects. In Figure 7a, we present results of the LDOS for the same system of optically excited cubic ZnO rocksalt excited by an external laser energy of eV and an increasing excitation intensity, Figure 7b shows the corresponding inverse lifetime and Figure 7c shows the corresponding non-equilibrium distribution of electrons . In addition, for very small excitation intensities, the result for the non-equilibrium distribution function shows a profound deviation from the Fermi step in equilibrium. These occupied non-equilibrium states have a finite lifetime, especially at the inner band edges, which is a sign of the Franz-Keldysh effect [76,77,78,79], here in the sense of a topological effect, which is accessible in a pump-probe experiment.
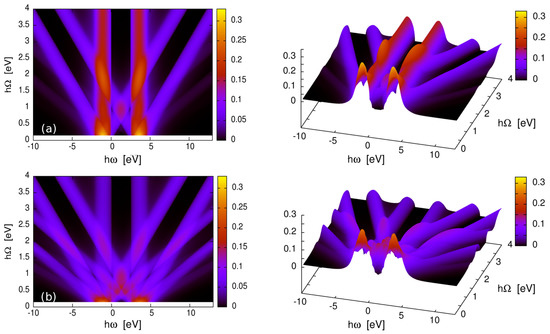
Figure 6.
Floquet topological quantum states of the semiconductor bulk in the non-equilibrium. (a) the evolution of the LDOS in the non-equilibrium for varying excitation laser frequencies up to eV is shown. The excitation intensity 5.0 MW/cm is constant. The bandgap of ZnO rocksalt in equilibrium is 2.45 eV, see Figure 2, the gap is vanishing with the increase of the driving frequency and dressed states emerge as a consequence of the non-equilibrium AC-Stark effect [82,83]. The split bands are superposed by a doublet of Floquet fans which intersect. The formation of topological subgaps, see e.g., at eV occurs; (b) the evolution of the LDOS for the excitation intensity of 10.0 MW/cm is shown. Spectral weight is shifted to a multitude of higher order Floquet-bands, while the original split band characteristics almost vanishes apart from the near-gap band edges. A variety of Floquet gaps is formed. At any crossing point, topologically induced transitions are possible, and the generation of higher harmonics can be enhanced. Panels on the right display the topology of the LDOS. The subgaps are very pronounced and the intersection of bands is visible as an increase of the LDOS which can be measurable in a pump-probe experiment. For a detailed discussion, please see Section 3.
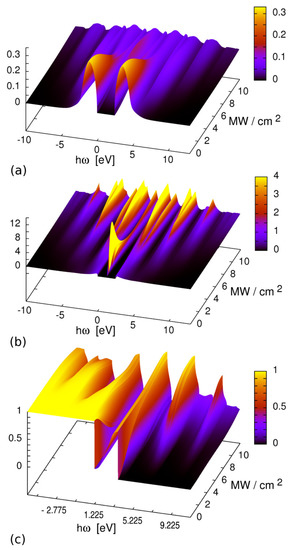
Figure 7.
(a) energy spectra of Floquet topological quantum states of the semiconductor bulk in the non-equilibrium. The evolution of the LDOS is displayed for the single excitation energy of eV, wavelength nm and an increasing external driving intensity up to 10.0 MW/cm. Spectral weight is shifted by excitation to Floquet sidebands and a sophisticated sub gab structure is formed. In the non-equilibrium, such topological effects in correlated systems are non-trivial. The bandgap in equilibrium is 2.45 eV, the Fermi edge is 1.225 eV, and the width of each band is 2.45 eV as well; (b) inverse lifetime of Floquet states of electromagnetically driven ZnO rocksalt bulk in the non-equilibrium; (c) non-equilibrium distribution function of electrons in optically driven bulk ZnO rocksalt. Parameters in (b,c) are identical to (a). For a detailed discussion, please see Section 3.
The change of the polarization of the external excitation modifies the physical situation and the result. In particular, circular and elliptically polarized light can be formally written as a superposition of linear polarized waves. Thus, in the pure uncorrelated case, , one could think that the setup can be formally implemented in the sense of coupled matrices. In the strongly correlated system at hand, the physics is fundamentally different. The solution for the strongly correlated case, , in the non-equilibrium, including DMFT, will become more sophisticated since the coupled matrices will result in the entanglement of processes in some sense. This can be deduced from the result in Figure 7b, which displays the modification of non-equilibrium life-times of electronic states due to the varying excitation amplitudes. Such a modification is also qualitatively found for varying excitation frequencies.
The classification of correlated topological systems is an active research field [26,80,81]. At this point, we refer to Section 3.3 in this article, where we show, in our theoretical results the analysis of the single Floquet modes. For the investigation of the LDOS and the occupation number , as well as for the lifetimes of the non-equilibrium states, an artificial cut-off of the Floquet series, as it is described in the literature, does not make sense from the numerical physics point of view of DMFT in frequency space. This would hurt basically conservation laws and the cut-off would lead to a drift of the overall energy of the system; see Section 3.3. However, according to the bulk-boundary correspondence [2,3], the results of this work for bulk will be observed in a pump-probe experiment at the surface of the semiconductor sample. In the following, we discuss the development of Floquet topological states for an increasing external driving frequency , see Figure 6, and, for an increasing amplitude of the driving, see Figure 7.
3.2. Topological Generation of Higher Harmonics and of Optical Transparency
When we increase the external excitation energy of the system from 0 eV to eV, Floquet topological quantum states as well as the topologically induced Floquet band gaps for bulk matter are developed. Both valence and conduction band split in a multitude of Floquet sub-bands which cross each other. In Figure 6a, the evolution of a very clear Floquet fan for the valence as well as for the conduction band of the correlated matter in the non-equilibrium is found. When the excitation energy is increased up to eV, the original band gap is subsequently closing, and the first crossing point in the semiconductor gap along the Fermi edge is found at eV. With the increase of the excitation intensity, see Figure 6b, higher order Floquet sidebands are gaining spectral weight, and we find the next prominent crossing point at the Fermi edge for eV. Band edges of higher order Floquet bands form crossing points with those of the first order. For an excitation energy of eV, the crossing points of the first side bands (02) with the higher number side bands are found at the atomic energy of eV and eV, so above the valence band edge and deep in the gap of the semiconductor. Semiconductors are well known for fundamental absorption at the band edge of the valence band. We find here that the absorption coefficient of the semiconductor is topologically modulated. Non-trivial transitions at the crossing points of Floquet-valence subbands and Floquet-conduction subbands become significant. A higher order Floquet subband is usually physically reached by absorption or generation of higher harmonic procedures and we find a high probability for a topologically induced direct transitions from the fundamental to higher order bands for those points in the spectrum where a Floquet band edge intersects with the inner band edge of the equilibrium valence band. At any band edge directional scattering can be expected if the lifetimes of states are of a value that is applicable to the expected scattering processes. In general, the optical refractive index is topologically modulated, and electromagnetically induced transparency will become observable for intense excitations. The topologically induced Floquet bands overlap and cross each other. Consequentially, very pronounced features and narrow subgaps are formed in the LDOS, which correspond with sharp spikes in the expected life-times in the non-equilibrium. Floquet replica of valence and conduction bands are formed and the dispersion is renormalized. We also find regions for excitation energies from eV up to eV and from eV up to eV, which can be interpreted as a topologically induced metallic phase. These states are the result of the Franz-Keldysh effect [76,77,78,79] or AC-Stark effect, which is well known for high intensity excitation of semiconductor bulk and quantum wells [82,83].
From the viewpoint of correlated electronics in the non-equilibrium, we interpret our results as follows. For finite excitation frequencies, an instantaneous transition to the topologically induced Floquet band structure and a renormalized dispersion is derived. In the bulk system clear Floquet bands develop, if the sample is excited by an intense electrical field. This is observable in Figure 6.
In Figure 7, we display the same system as in Figure 6 for constant driving energy of eV and an increasing driving intensity up to 10.0 MW/cm. We find the development of side bands and an overall vanishing semiconductor gap is found, which marks the transition from the semi-conductor to the topologically highly variable and switchable conductor in the non-equilibrium.
In this article, we do not investigate the coupling to a geometrical edge or a resonator mode. This will lead in the optical case to additional contributions in Equation (1) for the mode itself and the coupling term of the resonator or edge mode to the electron system of the bulk . and a are the creator and the annihilator of the photon, and g is the variable coupling strength of the photonic mode to the electronic system [84]. From our results, here we can conclude already that, for semi-conductor cavities and quantum wells as well as for structures which enhance so called edge states, these geometrical edge or surface resonances will induce an additional topological effect within the full so far excitonic spectrum. It is an additional effect that occurs beyond the bulk boundary correspondence. Dressed states may release energy quanta, e.g., light, or an electronic current into the resonator component [38]. Thus, we expect from our results that such modes may become a sensible switch in non-equilibrium.
It can be expected as well that novel topological effects in the non-equilibrium occur from the geometry. If the energy of the system is conserved, these modes will have always an influence on the full spectrum of the LDOS, when the system is otherwise periodic in space and time. Thus, it is to clarify whether such modes may be of technological use. For the investigation of ZnO as a laser material, the influences of surface resonators will be subject to further investigations. It is on target to find out all the signatures of a topologically protected edge mode in correlated and strongly correlated systems out of equilibrium, and to classify the significance of topological effects for the occurrence of the electro-optical Kerr effect, the magneto-optical Kerr effect (MOKE) or the surface magneto-optical Kerr effect (SMOKE). We believe that in correlated many-body systems out of equilibrium a bulk boundary correspondence is given and will be experimentally found. Those results become modified or enhanced by a coupling of bulk states with the geometry of a micro- or a nanostructure and their geometrical resonances.
3.3. Consistency of the Numerical Framework
The consistency of the numerical formalism is generally checked by the sum over all Floquet indices with the physical meaning that energy conservation must be guaranteed in the non-equilibrium. Consequentially, we do not take into account thermalization procedures and the system’s temperature remains constant. The analysis of the numerical validity as the normalized and frequency integrated density of states
is confirmed in this work for summing over Floquet indices up to the order of 10. We discuss in Figure 8 on the l.h.s. the Floquet contributions with increasing number in steps of . With an increasing order of the Floquet index, the amplitude of the Floquet contribution decreases towards the level of numerical precision of the DMFT self-consistency. This is definitely reached for and thus it is the physical argument to cut the Floquet expansion off for . As a systems requirement, the Floquet contributions are perfectly mirror symmetric with respect to the Fermi edge, whereas the sum of both contributions is directly symmetric with respect to the Fermi edge. These symmetries are generally a proof of the validity of the numerical Fourier transformation and the numerical scheme. The order of magnitude of each Floquet contribution with a higher order than is almost falling consistently with the rising Floquet index. We display results for the external laser wavelength of nm and the laser intensity of 3.8 MW/cm; the ZnO gap is assumed to be eV, which is ZnO rocksalt as a laser active material. We include Floquet contributions up to a precision of with regard to their effective difference from the final result on the r.h.s of Figure 8 as the sum to the nth-order. It corresponds to the accuracy of the self-consistent numerics.
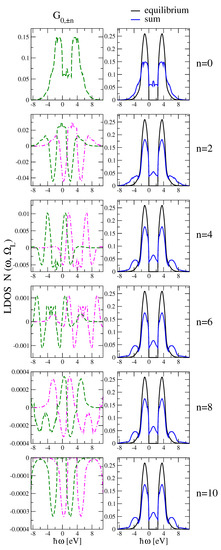
Figure 8.
Floquet contributions and accuracy check of the numerical results for the LDOS of driven semiconductor bulk. The bandgap in equilibrium is eV, the Fermi edge is eV. For discussion, please see Section 3.3.
The Floquet contributions, Figure 8, as such consequentially do not have a direct physical interpretation, however, the sum of all contributions is the local density of states, the LDOS, as a material characteristics. Whereas the lowest order Floquet contribution, compare Equation (2), is symmetric to the Fermi edge but strictly positive, higher order contributions are mirror symmetric to each other and in sum they can have negative contributions to the result of the LDOS. The order of the Floquet contribution n numbers the evolving Floquet side bands which emerge in the LDOS, compare Figure 6a. The increase of mathematical and numerical precision has direct consequences for the finding and the accuracy of physical results, and the investigation of the coupling of the driven electronic system of the bulk with edge and surface modes will therefore profit. Bulk-surface coupling effects in nanostructure and waveguides are of great technological importance and the advantage of this numerical approach in contrast to time dependent DMFT frameworks in this respect is obvious.
4. Conclusions
We investigated in this article the development of Floquet topological quantum states in wide band gap semiconductor bulk as a correlated electronic system with a generalized Hubbard model and with dynamical mean field theory in the non-equilibrium. We found that optical excitations induce a non-trivial band structure and, in several frequency ranges, a topologically induced metal phase is found as a result of the AC-Stark effect. The intersection of Floquet bands and band edges induces novel transitions, which may lead to up- and downconversion effects as well as to higher harmonic generation. The semiconductor absorption coefficient is topologically modulated. Non-trivial transitions at the crossing points of the underlying equilibrium band structure with the intersecting Floquet fans become possible and their efficiency is depending on the excitation power. We also find the development of pronounced novel sub gaps as areas of electromagnetically induced transparency. We also presented a consistency check as a physical consequence of the Floquet sum, which ensures numerically energy conservation. Our results for semiconductor bulk can be tested optoelectronic and magneto-optoelectronic experiments; they may serve as a guide towards innovative laser systems. The bulk semiconductor under topological non-equilibrium excitations as such has to be reclassified. It will be of great interest to investigate the interplay of topological bulk effects with additional surface resonances, a polariton coupling, or a surface magneto-optical modulation.
Author Contributions
Both authors equally contributed to the presented work. Both authors were equally involved in the preparation of the manuscript. Both authors have read and approved the final manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank H. Monien, H. Wittel and F. Hasselbach for highly valuable discussions.
Conflicts of Interest
The authors declare that there are no conflict of interests.
References
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed]
- Moore, G.; Read, N. Nonabelions in the fractional quantum hall effect. Nucl. Phys. B 1991, 360, 362. [Google Scholar] [CrossRef]
- Goldmann, N.; Dalibard, J. Periodically Driven Quantum Systems: Effective Hamiltonians and Engineered Gauge Fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef]
- Zutic, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. A Self-Consistent Quantum Field Theory for Random Lasing. Appl. Sci. 2019, 9, 2477. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef] [PubMed]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin hall insulator state in HgTe quantum wells. Science 2007, 318, 766. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase: Experimental observation of first strong topological insulator. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Discovery (theoretical prediction and experimental observation) of a large-gap topological-insulator class with spin-polarized single-Dirac-cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.-X.; Qi, X.-L.; Dai, X.; Fang, Z.; Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Lindner, N.H.; Refael, G.; Galitski, V. Floquet Topological Insulator in Semiconductor Quantum Wells. Nat. Phys. 2011, 7, 490–495. [Google Scholar] [CrossRef]
- Katan, Y.T.; Podolsky, D. Modulated Floquet Topological Insulators. Phys. Rev. Lett. 2013, 110, 016802. [Google Scholar] [CrossRef]
- Rudner, M.S.; Lindner, N.H.; Berg, E.; Levin, M. Anomalous Edge States and the Bulk-Edge Correspondence for Periodically Driven Two-Dimensional Systems. Phys. Rev. X 2013, 3, 031005. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, B. Effects of light on quantum phases and topological properties of two-dimensional Metal-organic frameworks. Sci. Rep. 2016, 4, 41644. [Google Scholar] [CrossRef]
- Kitagawa, T.; Oka, T.; Brataas, A.; Fu, L.; Demler, E. Transport properties of nonequilibrium systems under the application of light: Photoinduced quantum Hall insulators without Landau levels. Phys. Rev. B 2011, 84, 235108. [Google Scholar] [CrossRef]
- Gu, Z.; Fertig, H.A.; Arovas, D.P.; Auerbach, A. Floquet Spectrum and Transport through an Irradiated Graphene Ribbon. Phys. Rev. Lett. 2011, 107, 216601. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Lindner, N.H.; Bergman, D.L.; Refael, G.; Galitski, V. Topological Floquet spectrum in three dimensions via a two-photon resonance. Phys. Rev. B 2013, 87, 235131. [Google Scholar] [CrossRef]
- Jiang, L.; Kitagawa, T.; Alicea, J.; Akhmerov, A.R.; Pekker, D.; Refael, G.; Cirac, J.I.; Demler, E.; Lukin, M.D.; Zoller, P. Majorana Fermions in Equilibrium and in Driven Cold-Atom Quantum Wires. Phys. Rev. Lett. 2011, 106, 220402. [Google Scholar] [CrossRef] [PubMed]
- D’Alessio, L. Rigol, Dynamical preparation of Floquet Chern insulators. Nat. Commun. 2015, 6, 8336. [Google Scholar] [CrossRef]
- Grushin, A.G.; Gomez-Leon, A.; Neupert, T. Floquet Fractional Chern Insulators. Phys. Rev. Lett. 2014, 112, 156801. [Google Scholar] [CrossRef]
- Bergholtz, E.; Liu, Z. Topological Flat Band Models and Fractional Chern Insulators. Int. J. Mod. Phys. B 2013, 27, 1330017. [Google Scholar] [CrossRef]
- Floquet, G. Sur les équations différentielles linéaires à coefficients périodiques. Ann. l’ Ecole Norm. Sup. 1883, 12, 47–88. [Google Scholar] [CrossRef]
- Razavi-Khosroshahi, H.; Edalati, K.; Wu, J.; Nakashima, Y.; Arita, M.; Ikoma, Y.; Sadakiyo, M.; Inagaki, Y.; Staykov, A.; Yamauchi, M.; et al. High-pressure zinc oxide phase as visible-light-active photocatalyst with narrow band gap. J. Mater. Chem. A 2017, 5, 20298–20303. [Google Scholar] [CrossRef]
- Fritsch, D.; Schmidt, H.; Grundmann, M. Pseudopotential band structures of rocksalt MgO, ZnO, and Mg 1 x Zn x O. Appl. Phys. Lett. 2006, 88, 134104. [Google Scholar] [CrossRef]
- Dixit, H.; Saniz, R.; Lamoen, D.; Partoens, B. The quasiparticle band structure of zincblende and rocksalt ZnO. J. Phys. Condens. Matter 2010, 22, 125505. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Lin, Z.; Lin, W.; Zhang, J.; Ding, K.; Wang, Y.; Zheng, Q.; Zhan, Z.; Yan, F.; Chen, D.; et al. Research progress in ZnO single-crystal: Growth, scientific understanding, and device applications. Chin. Sci. Bull. 2014, 59, 1235–1250. [Google Scholar] [CrossRef]
- Park, W.I.; Jun, Y.H.; Jung, S.W.; Yi, G.-C. Exciton emissions observed in ZnO single crystal nanorods. Appl. Phys. Lett. 2003, 82, 964–966. [Google Scholar] [CrossRef]
- Faisal, F.H.M.; Kaminski, J.Z. Floquet-Bloch theory of high-harmonic generation in periodic structures. Phys. Rev. A 1997, 56, 748. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Evolution of Floquet topological quantum states in driven semiconductors. Eur. Phys. J. B 2019, 92, 215. [Google Scholar] [CrossRef]
- Frank, R. Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations. New J. Phys. 2013, 15, 123030. [Google Scholar] [CrossRef]
- Frank, R. Coherent control of Floquet-mode dressed plasmon polaritons. Phys. Rev. B 2012, 85, 195463. [Google Scholar] [CrossRef]
- Frank, R. Non-equilibrium polaritonics - Nonlinear effects and optical switching. Ann. Phys. 2013, 525, 66–73. [Google Scholar] [CrossRef]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Restrepo, S.; Cerrillo, J.; Bastidas, V.M.; Angelakis, D.G.; Brandes, T. Driven Open Quantum Systems and Floquet Stroboscopic Dynamics. Phys. Rev. Lett. 2016, 117, 250401. [Google Scholar] [CrossRef]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004-1. [Google Scholar] [CrossRef]
- Kalthoff, M.H.; Uhrig, G.S.; Freericks, J.K. Emergence of Floquet behavior for lattice fermions driven by light pulses. Phys. Rev. B 2018, 98, 035138. [Google Scholar] [CrossRef]
- Sentef, M.A.; Claassen, M.; Kemper, A.F.; Moritz, B.; Oka, T.; Freericks, J.K.; Devereaux, T.P. Theory of Floquet band formation and local pseudospin textures in pump-probe photoemission of graphene. Nat. Commun. 2015, 6, 7047. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Fan, S. Topologically non-trivial Floquet band structure in a system undergoing photonic transitions in the ultra-strong coupling regime. Phys. Rev. A 2015, 92, 053822. [Google Scholar] [CrossRef]
- Lubatsch, A.; Kroha, J. Optically driven Mott-Hubbard systems out of thermodynamical equilibrium. Ann. Phys. 2009, 18, 863–867. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Metzner, W.; Vollhardt, D. Correlated Lattice Fermions in d = ∞ Dimensions. Phys. Rev. Lett. 1989, 62, 324. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, P.; Monien, H. Nonequilibrium dynamical mean-field theory of a strongly correlated system. arXiv, 2002; arXiv:0202046. [Google Scholar]
- Maier, T.; Jarrell, M.; Pruschke, T.; Hettler, M.H. Quantum cluster theories. Rev. Mod. Phys. 2005, 77, 1027. [Google Scholar] [CrossRef]
- Freericks, J.K.; Turkowski, V.M.; Zlatic, V. Nonequilibrium Dynamical Mean-Field Theory. Phys. Rev. Lett. 2006, 97, 266408. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, N.; Oka, T.; Aoki, H. Nonequilibrium Steady State of Photoexcited Correlated Electrons in the Presence of Dissipation. Phys. Rev. Lett. 2009, 103, 047403. [Google Scholar] [CrossRef] [PubMed]
- Lin, N.; Marianetti, C.A.; Millis, A.J.; Reichman, D.R. Dynamical Mean-Field Theory for Quantum Chemistry. Phys. Rev. Lett. 2011, 106, 096402. [Google Scholar] [CrossRef] [PubMed]
- Zgid, D.; Chan, G.K.-L. Dynamical mean-field theory from a quantum chemical perspective. J. Chem. Phys. 2011, 134, 094115. [Google Scholar] [CrossRef] [PubMed]
- Aoki, H.; Tsuji, N.; Eckstein, M.; Kollar, M.; Oka, T.; Werner, P. Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 2014, 86, 779. [Google Scholar] [CrossRef]
- Frank, R. Population trapping and inversion in ultracold Fermi gases by excitation of the optical lattice-Non-equilibrium Floquet-Keldysh description. Appl. Phys. B 2013, 113, 41–47. [Google Scholar] [CrossRef][Green Version]
- Sorantin, M.E.; Dorda, A.; Held, K.; Arrigoni, E. Impact ionization processes in the steady state of a driven Mott-insulating layer coupled to metallic leads. Phys. Rev. B 2018, 97, 115113. [Google Scholar] [CrossRef]
- Hofstetter, W.; Qin, T. Topological singularities and the general classification of Floquet-Bloch systems. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 082001. [Google Scholar] [CrossRef]
- Qin, T.; Hofstetter, W. Nonequilibrium steady states and resonant tunneling in time-periodically driven systems with interactions. Phys. Rev. B 2018, 97, 125115. [Google Scholar] [CrossRef]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal High-Frequency Behavior of Periodically Driven Systems: From Dynamical Stabilization to Floquet Engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747–2750. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2009, 82, 1959–2007. [Google Scholar] [CrossRef]
- Gresch, D.; Autes, G.; Yazyev, O.V.; Troyer, M.; Vanderbilt, D.; Bernevig, B.A.; Soluyanov, A.A. Z2Pack: Numerical implementation of hybrid Wannier centers for identifying topological materials. Phys. Rev. B 2017, 95, 075146. [Google Scholar] [CrossRef]
- Chang, P.-C.; Lu, J.G. Temperature dependent conduction and UV induced metal-to-insulator transition in ZnO nanowires. Appl. Phys. Lett. 2008, 92, 212113. [Google Scholar] [CrossRef]
- Chang, P.-C.; Chien, C.-J.; Stichtenoth, D.; Ronning, C.; Lu, J.G. Finite size effect in ZnO nanowires. Appl. Phys. Lett. 2007, 90, 113101. [Google Scholar] [CrossRef]
- Koster, R.S.; Changming, M.F.; Dijkstra, M.; van Blaaderen, A.; van Huis, M.A. Stabilization of Rock Salt ZnO Nanocrystals by Low-Energy Surfaces and Mg Additions: A First-Principles Study. J. Phys. Chem. C 2015, 119, 5648–5656. [Google Scholar] [CrossRef]
- Wegener, M. Extreme Nonliner Optics; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 3-540-22291-X. [Google Scholar]
- King-Smith, R.D.; Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 1993, 47, 1651–1654. [Google Scholar] [CrossRef]
- Vanderbilt, D.; King-Smith, R.D. Electric polarization as a bulk quantity and its relation to surface charge. Phys. Rev. B 1993, 48, 4442. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Dal Lago, V.; Atala, M.; Foa Torres, L.E.F. Floquet topological transitions in a driven one-dimensional topological insulator. Phys. Rev. A 2015, 92, 023624. [Google Scholar] [CrossRef]
- Gull, E.; Millis, A.; Lichtenstein, A.I.; Rubtsov, A.N.; Troyer, M.; Werner, P. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 2011, 83, 349. [Google Scholar] [CrossRef]
- Snoek, M.; Titvinidze, I.; Toke, C.; Byczuk, K.; Hofstetter, W. Antiferromagnetic order of strongly interacting fermions in a trap: Real-space dynamical mean-field analysis. New J. Phys. 2008, 10, 093008. [Google Scholar] [CrossRef]
- Peters, R.; Yoshida, T.; Sakakibara, H.; Kawakami, N. Coexistence of light and heavy surface states in a topological multiband Kondo insulator. Phys. Rev. B 2016, 93, 235159. [Google Scholar] [CrossRef]
- Peters, R.; Yoshida, T.; Kawakami, N. Magnetic states in a three-dimensional topological Kondo insulator. Phys. Rev. B 2018, 98, 075104. [Google Scholar] [CrossRef]
- Franz, W. Einfluß eines elektrischen Feldes auf eine optische Absorptionskante. Z. Naturforschung A 1958, 13, 484–489. [Google Scholar] [CrossRef]
- Keldysh, L.V. The Effect of a Strong Electric Field on the Optical Properties of Insulating Crystals. J. Exptl. Theoret. Phys. 1957, 33, 994–1003, reprinted in Soviet Phys. JETP 1958, 6, 763–770. Available online: jetp.ac.ru/cgi-bin/dn/e_007_05_0788.pdf (accessed on 4 October 2019).
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. J. Exptl. Theoret. Phys. 1964, 47, 1945–1957, reprinted in Soviet Phys. JETP 1964, 20, 1307–1314. Available online: jetp.ac.ru/cgi-bin/dn/e_020_05_1307.pdf (accessed on 4 October 2019).
- Ivanov, A.L.; Keldysh, L.V.; Panashchenko, V.V. Low-threshold exciton-biexciton optical Stark effect in direct-gap semiconductors. Zh. Eksp. Teor. Fiz. 1991, 99, 641–658. [Google Scholar]
- Manmana, S.; Essin, A.M.; Noack, R.M.; Gurarie, V. Topological invariants and interacting one-dimensional fermionic systems. Phys. Rev. B 2012, 86, 205119. [Google Scholar] [CrossRef]
- Rachel, S. Interacting topological insulators: A review. Rep. Prog. Phys. 2018, 81, 116501. [Google Scholar] [CrossRef]
- Miller, D.A.B.; Chemla, D.S.; Damen, T.C.; Gossard, A.C.; Wiegmann, W.; Wood, T.H.; Burrus, C.A. Band-Edge Electroabsorption in Quantum Well Structures: The Quantum-Confined Stark Effect. Phys. Rev. Lett. 1984, 53, 2173–2176. [Google Scholar] [CrossRef]
- Chemla, D.S.; Knox, W.H.; Miller, D.A.B.; Schmitt-Rink, S.; Stark, J.B.; Zimmermann, R. The excitonic optical stark effect in semiconductor quantum wells probed with femtosecond optical pulses. J. Lumin. 1989, 44, 233–246. [Google Scholar] [CrossRef]
- Forn-Diaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005-1. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).