Antimatter Quantum Interferometry

Abstract

The wave–particle duality hypothesis for massive particles has been confirmed by an overwhelming variety of indirect experimental evidence. In addition, direct interferometric tests have been made on particles like electrons, neutrons and even a few molecules, explicitly showing wave-like diffraction and interference phenomena. Of particular interest in this direction, single particle interference has also been demonstrated, but only for the electron case. No such kind of direct information was available for antiparticles or antimatter in general. After briefly discussing the subjects of antimatter research and interferometry, I present here the first evidence of single particle antimatter interference, made with positrons.

1. Introduction

The wave–particle duality hypothesis for massive particles was introduced by de Broglie almost a century ago: The Planck constant h relates the momentum p of a massive particle to its de Broglie wavelength: λ_dB = h/p [1]. This relation, together with the uncertainty principle and the superposition principle, is at the heart of quantum mechanics. These principles have now been tested in an overwhelming variety of experiments over more than 100 years.

Of particular interest is the direct evidence of wave-like behavior of quantum massive particles showing diffraction and interference phenomena, for the first time with electrons [2,3]. Neutrons were shown to display wave behavior in crystals [4], in the gravitational Colella–Overhauser–Werner set of experiments [5,6] and later on using single and double slit diffraction [7]. Wave-like behavior is nowadays established also for molecules like Na₂ [8], and up to the complexity of fullerene [9].

Among the direct tests of wave-like nature of massive particles, a special place is held by experiments where a single particle propagates through an interferometric system. According to Feynman, this ideal experiment constitutes a decisive proof, a test “that has in it the heart of quantum mechanics” [10].

Single-particle experiments were conducted for the first time with electrons in 1976 by G. Merli, G.F. Missiroli and G. Pozzi, in a configuration featuring an electronic biprism, equivalent to the double slit suggested by Feynman [11]. Several decades later, the same experiment was also realized with material slits [12]. At the same time, no direct information on antiparticle wave properties was detected, with the only exception that of an indication of positron diffraction [13].

2. Antimatter

Antimatter, introduced following the Dirac equation in 1928 [14], was observed a few years later in cosmic rays [15]. The general relation between particle and antiparticle properties is the CPT (charge-parity-time reversal) theorem [16], that holds for quantum field theories in a flat spacetime.

While antiparticles are routinely produced by cosmic (and man-made) accelerators, their presence in our environment is negligible and experimentation always requires dedicated sources. CPT symmetry can be studied in principle on any existing antiparticle; however, neutral antimatter (or symmetric matter–antimatter) systems are of particular interest because of the possibility of testing the weak equivalence principle (WEP). The production of cold anti-hydrogen atoms at the CERN Antiproton Decelerator [17,18] has been a milestone in this direction, followed by anti-hydrogen confinement [19] and the development of an antiatom beam [20].

The simplest and most symmetric matter–antimatter system, positronium (Ps, the e⁺ e^- bound system), was discovered by M. Deutsch in 1951 [21]. It is constituted by an electron and a positron and has been the subject of intense investigation in the last decades, holding the promise to allow tests of fundamental laws (see [22] and references therein).

In addition to searching for violations of fundamental laws per se, antimatter studies are relevant to the goal of understanding the fundamental baryonic and leptonic asymmetry in the Universe [23]. The most natural mechanism that could predict the asymmetry relies in fact on the Sakharov conditions [24] being verified at the grand unification scale of energy ($\approx {10}^{16}$ GeV) and their possible interplay with CPT conservation [25]. Antimatter studies (at both low and high energies) might be necessary to solve this fundamental riddle, related to our own very existence.

3. Antimatter Interferometry

In spite of all the progress in studies about antimatter, no experiments featuring antiparticle interference have ever been done. Preliminary ideas about interferometry for antimatter were considered mainly in the frame of inertial sensing and possible measurements of gravitation for antimatter [26].

Generally speaking, antimatter poses a special problem because of its paucity in terrestrial and astronomical environments. For instance, the antiproton-to-proton ratio in cosmic rays is about 10⁻⁵ and virtually no antiparticle can survive in the environment because of immediate annihilation with ordinary matter. For these reasons, controlled sources of antiparticles are restricted to high-energy accelerators or radioactive sources. Interferometry also requires antimatter at relatively low energies, suitable for controlled propagation or even confinement, as is the case for the above-mentioned Antiproton Decelerator or the radioactive ²²Na positron sources.

Considering the case of positrons, for instance, the available radioactive sources and the following treatment necessary to lower the energy (generally in the keV range) results in beam intensities of the order of 10⁴ particles per second. In comparison, electron sources can easily reach the mA range—11 orders of magnitude higher!

The QUPLAS (Quantum interferometry and gravitation with positronium) research group has undertaken a systematic program of study on positrons and positronium, whose first step, called QUPLAS-0 has been interferometry with a keV positron beam. Positronium and antimatter interferometry requires addressing specific problems in addition to the scarcity of antiparticles, including the background produced by annihilations, the finite lifetime of Ps (only 142 ns for the longest-living ortho-Ps state) and the detection of the interferometric pattern [27].

4. Types of Interferometry

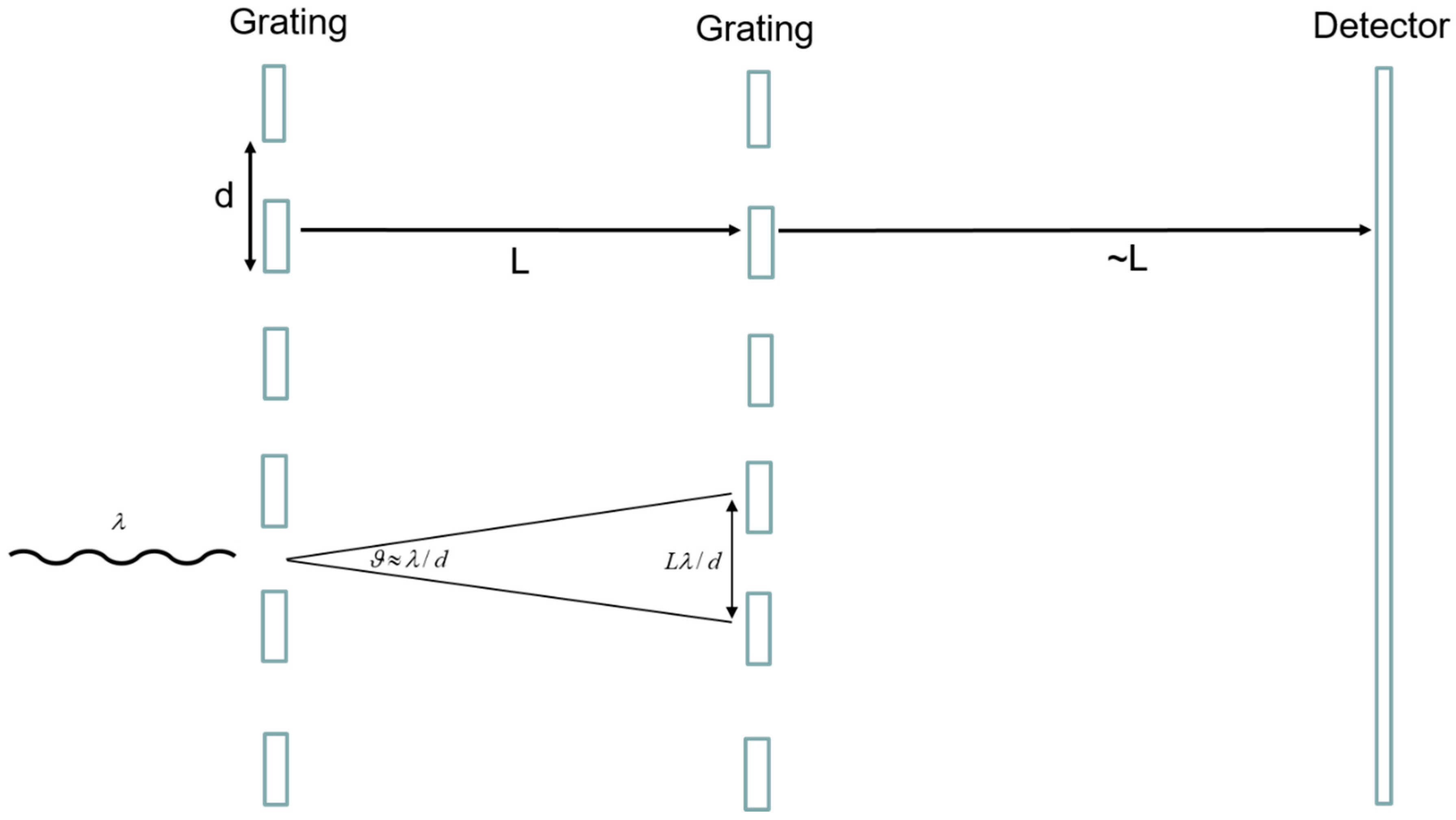
Quantum interferometry can be realized in several different ways. Defining relevant quantities in one of the simplest configurations (two gratings and a detector, Figure 1), one can single out the relevant parameters as:

• The wavelength of the radiation (the de Broglie wavelength of the particle) $\lambda$.
• The periodicity of the grating used to evidence the diffraction/interference effect $d$.
• The longitudinal scale $L$ that is related to the integrating distance or to the observation distance.

The relations which are considered always valid are:

$$\lambda <<d\lambda <L$$

(1)

where the first one is often called the large aperture condition. At this point we can form the quantities:

$$D_T=d/\lambda >>1D_L=L/d$$

(2)

With respect to $\lambda$, D_T is a measure of the dominance of the transverse scale, while D_L indicates the level of longitudinal dominance. If, D_T is big in such a way as to also predominate over D_L then

$$D_T>D_L\to L<d{}^2/\lambda$$

(3a)

If, on the other hand, it is D_L which dominates D_T, then one has

$$D_T<D_L\to L>d{}^2/\lambda$$

(3b)

Condition (3a) indicates the so-called moiré regime, or near field interferometry. Under these conditions, the wave-like nature of the particle is not yet evident and the regime is a corpuscular or ballistic one, which is basically the classical physics case. One can have a better appreciation of this when considering a setup like the one in Figure 1. Because of diffraction, for a single slit on grating A the coherence area on B will be Lλ/d. If (3a) holds, then the moiré condition reads Lλ/d < d and the wave-like nature of the particle will not manifest itself. This regime, more than interferometry, should be more aptly called deflectrometry.

The quantity:

$$L_T=\frac{d^2}{\lambda }$$

(4)

is called the Talbot length and is a characteristic of both the grating period and the wavelength under consideration. Three regimes can then be defined whenever (1) is satisfied:

• $L<<L_T$: moiré regime, where particles behave like classical bullets (deflectometry).
• $L\approx L_T$: Talbot–Lau regime, where particles start to show interference.
• $L>>L_T$: Fraunhofer regime, where the usual far-field approximation holds.

The Talbot (called the Talbot–Lau regime when multi-slit gratings are used) is an “intermediate field” situation, where the second order term of the development in the Kirchoff integral expansion of wave optics is kept; by contrast, only the first order is considered in the Fraunhofer mode.

The moiré and Talbot regimes have in common the repetition of the produced pattern at integer (and, less evidently, fractional) multiples of the Talbot length. In spite of this numerical similarity, a purely projective effect is at work in the moiré case, while Talbot-mode repetitions are due to a quantum mechanical effect. In other words, the periodicity of the repetition patterns has a purely geometrical origin in the moiré case, while also having a dependence on λ for the Talbot; in this latter case, a change in energy of the particles would also change the longitudinal position of the maxima of the interference pattern.

The Talbot and Fraunhofer configurations both feature the wavelength quantum mechanical dependence of the interference pattern. However, the Talbot case strictly requires the monochromaticity of the beam (and the energy will dictate the position of the repetition pattern). The Fraunhofer case has much less sensitivity to energy so that, when the interference pattern is established, it will always be present at any distance, provided the far-field condition L >> L_T is satisfied. However, the Fraunhofer interference will require a good initial collimation of the beam.

In order to tackle the problem of antimatter interferometry, the positron or the antiproton are the simplest particles of choice. Positron sources are available at linear accelerator (LINAC) machines or by exploiting radioactive sources such as the β⁺ emitter ²²Na source. Antiprotons are available at particle accelerators since they will need to be produced at very high energy. The Antiproton Decelerator at CERN is the only machine dedicated to the production of antiprotons at the MeV scales or below that can prove adequate for interferometry.

5. The Experiment

The QUPLAS-0 experiment, which I will discuss here, is the first stage of the QUPLAS (quantum interferometry and gravitation with positronium) program and consisted in producing the first interferometric pattern with an antiparticle: the positron. For this particular task, a ²²Na radioactive source followed by a beam line, an interferometer and a nuclear emulsion detector were used.

For this case, moiré and Talbot configurations are interesting, because of the large momentum acceptance of these configurations. The Fraunhofer requirement of a good beam collimation in fact typically implies a heavy loss of statistics. In addition, the Talbot configuration should be preferred over the moiré in order to put in evidence the quantum mechanical origin of the effect.

After a careful study, the Talbot–Lau setup was considered to be the most promising for the task [28]. One of the main reasons for this is the inevitably poor level of coherence of the beam as well as the need to produce an interference pattern of a minimum periodicity of a few microns to make detection feasible. With reference to Figure 2, the first grating periodicity was $d_1$= 1.2 μm and the second was $d_2$= 1 μm, with 50% open fraction in both cases. The gratings and the detector were positioned such that $L_1$≅ 12 cm and $L_2$≅ 60 cm (or $L_2$= 5$L_1$). This is an example of the so-called Talbot–Lau asymmetric magnifying configuration [25] with a magnification factor of 5, so that the periodicity to be detected at the detector position is of ≅ 5$d_1$= 6 μm. The pattern is therefore detectable by the nuclear emulsion, which has a resolution of about 1 μm [29].

The configuration of the interferometer and detector system was such as to be resonant at the energy of 14 keV according to the equation

$$\frac{L_1}{L_2}=\frac{d_1}{d_2}-1$$

(5)

which implicitly contains the Talbot length and the wavelength of the particle by means of (4).

In the final configuration in Figure 2, the emulsion detector was tilted by 45 degrees; this was due to the uncertainty on the longitudinal location of the Talbot revival which is affected by several uncertainties on grating parameters and misalignments (see discussion in [30]).

The experiment made use of the positron beam of the L-NESS Laboratory of the Politecnico di Milano in Como (Italy). The beam had an intensity of about $8\times {10}^3{e}^{+}/s$ and an angular divergence of a few $mrad$. The positron source is followed by a tungsten (100) moderator and an electrostatic beamline, so that its energy can be tuned between a few keV and 20 keV (with a resolution better than 1%) while maintaining a beam spot of about 2 $\mathrm{mm}$.

6. Results

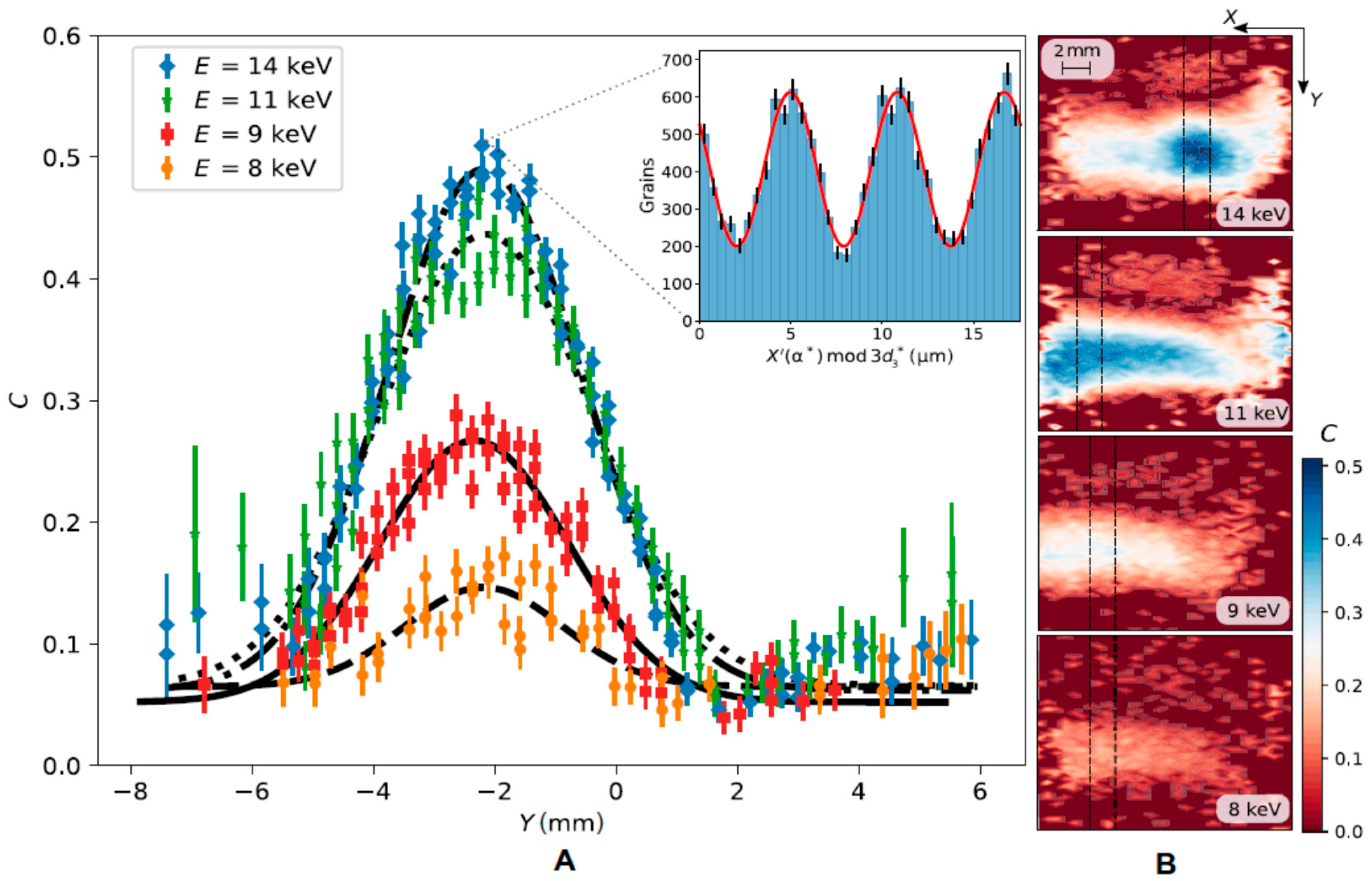
The QUPLAS-0 data taking took place in 2018, and consisted in a series of exposures of emulsions to the L-NESS positron beam at different energies. After the analysis, the resulting patterns on the detector were studied at 8,9,11 and 14 keV (Figure 3).

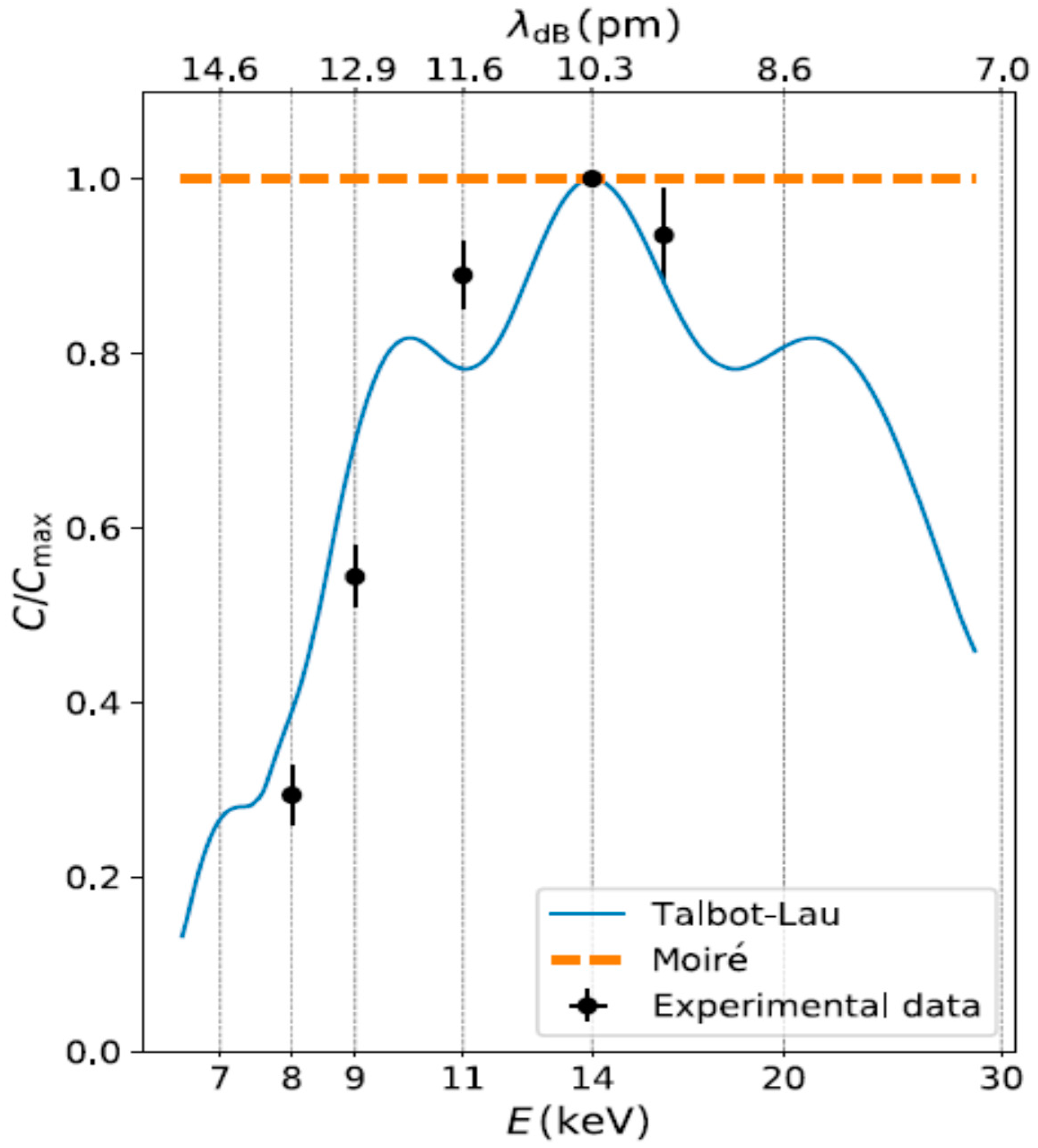
In order to investigate the origin of the signal, one has to study the behavior of the visibility (or contrast C = (I_max − I_min)/(I_max + I_min) as a function of the energy, which corresponds to changing the wavelength of the positrons. The result of such a study for energies 8, 9, 11, 14, 16 keV is shown in Figure 4. It clearly indicates the quantum mechanical origin of the effect which is energy dependent. By contrast, in the moiré regime no such behavior is expected since the particles would behave classically.

The result is the first demonstration of antimatter interferometry. In addition, since the flux of particles is at most ~10⁴ per second, generated by the time-incoherent ²²Na source, and the transit time through the interferometer is 10⁻⁸ s, this turns out to be a single-particle experiment, being therefore the antimatter version of the celebrated Merli–Missiroli–Pozzi single electron result [11].

7. Conclusions

Quantum interferometry of antimatter has been made for the first time by means of Talbot–Lau interferometry on positrons. This is also the second demonstration ever of single-particle interference obtained with an elementary constituent of the standard model.