Cloud-Based Multi-Robot Path Planning in Complex and Crowded Environment with Multi-Criteria Decision Making Using Full Consistency Method
Abstract
1. Introduction
2. Related Work
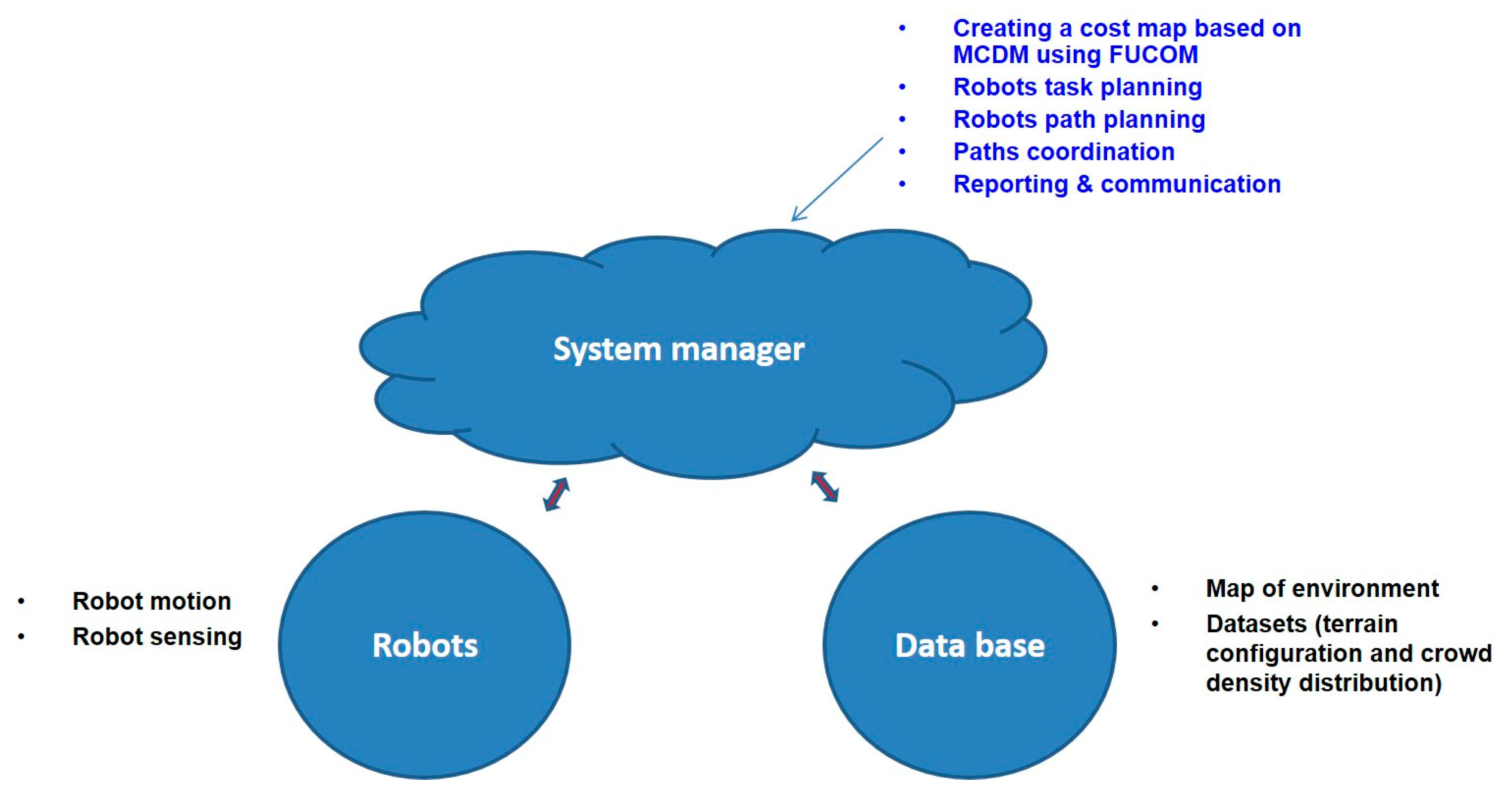
3. System Overview
3.1. D* Lite Algorithm
- g(s)—the minimum cost of moving from sstart to s, i.e., c(sstart, s), found so far;
- h(s) or heuristic value—estimates the minimum cost of moving from s to sgoal. Using heuristic value ensures that the search tree is directed towards the most optimistic cells in terms of belonging to the optimal path from start to goal cell. This speeds up the search.
- f(s) = g(s) + h(s)—estimates the minimum cost of moving from sstart via s to sgoal; and,
- parent(s) or parent pointer—points to the predecessor s’ of s from which is derived g(s), s’ is called the parent of s. The parent pointers are used to extract the path after the search terminates.
3.2. Full Consistency Method (FUCOM)
4. Multi-Criteria Decision Making Model and Procedure
- C1—the convenience of the terrain configuration for robots motion, a 0–10 scaled grading scheme (0 = ‘favorable terrain’ to 10 = ‘extremely unfavorable terrain’),
- C2—the risk related to the loss of communication with the cloud, a 0–10 scaled grading scheme (0 = ‘low risk’ to 10 = ‘high risk’),
- C3—the risk related to the human-robot interactions (slows down the robots motion), a 0–10 scaled grading scheme (0 = ‘low risk’ to 10 = ‘high risk’), and
- C4—the robot safety related to conditions dependent on specific mission (0 = ‘safe conditions’ to 10 = ‘extremely unsafe conditions’).
5. Simulation and Results
- start1 (x, y) = (1, 21), goal1 (x, y) = (73, 100)
- start2 (x, y) = (20, 1), goal2 (x, y) = (100, 91)
- start3 (x, y) = (35, 15), goal3 (x, y) = (100, 100).
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lozano-Perez, T. Spatial planning: A configuration space approach. IEEE Trans. Comput. 1983, 32, 108–120. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Wiktor, A.; Scobee, D.; Messengery, S.; Clark, C. Decentralized and complete multi-robot motion planning in confined spaces. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1168–1175. [Google Scholar]
- Ferguson, D.; Stentz, A. Field D*: An Interpolation-based Path Planner and Replanner. In Robotics Research—Results of the 12th International Symposium of Robotics Research; Springer: Berlin/Heidelberg, Germany, 2005; pp. 239–253. [Google Scholar]
- Aroor, A.; Epstein, S.L. Toward Crowd-Sensitive Path Planning. In Proceedings of the AAAI Fall 2017 Symposium on Human-Agent Groups, Arlington, VA, USA, 9–11 November 2017; pp. 238–245. [Google Scholar]
- Pamučar, D.; Stević, Ž.; Sremac, S. A new model for determining weight coefficients of criteria in MCDM models: Full consistency method (FUCOM). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Durmić, E. The evaluation of the criteria for sustainable supplier selection by using the FUCOM method. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 91–107. [Google Scholar] [CrossRef]
- Badi, I.; Abdulshahed, A. Ranking the Libyan airlines by using Full consistency method (FUCOM) and Analytical hierarchy process (AHP). Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 1–14. [Google Scholar] [CrossRef]
- Nunić, Z. Evaluation and selection of the PVC carpentry manufacturer using the FUCOM-MABAC model. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 13–28. [Google Scholar] [CrossRef]
- Pamučar, D.; Lukovac, V.; Božanić, D.; Komazec, N. Multi-criteria FUCOM-MAIRCA model for the evaluation of level crossings: Case study in the Republic of Serbia. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 108–129. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. D* Lite. In Proceedings of the Eighteenth National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; pp. 476–483. [Google Scholar]
- Wagner, G.; Choset, H. M*: A complete multirobot path planning algorithm with performance bounds. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3260–3267. [Google Scholar]
- Bennewitz, M.; Burgard, W.; Thrun, S. Optimizing schedules for prioritized path planning of multi-robot systems. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Cirillo, M.; Uras, T.; Koenig, S. A lattice-based approach to multi-robot motion planning for non-holonomic vehicles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 232–239. [Google Scholar]
- Apoorva, A.; Gautam, R.; Kala, R. Motion Planning for a Chain of Mobile Robots Using A* and Potential Field. Robotics 2018, 7, 20. [Google Scholar] [CrossRef]
- Biswas, S.; Anavatti, G.S.; Garratt, A.M. A Time-Efficient Co-Operative Path Planning Model Combined with Task Assignment for Multi-Agent Systems. Robotics 2019, 8, 35. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Yun, S.C.; Ganapathy, V.; Chien, T.W. Enhanced D* Lite Algorithm for mobile robot navigation. In Proceedings of the IEEE Symposium on Industrial Electronics and Applications, Penang, Malaysia, 3–5 October 2010. [Google Scholar]
- Singh, S.; Simmons, R.; Smith, T.; Stentz, A.; Verma, V.; Yahja, A.; Schwehr, K. Recent Progress in Local and Global Traversability for Planetary Rovers. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000. [Google Scholar]
- Wettergreen, D.; Dias, B.; Shamah, B.; Teza, J.; Tompkins, P.; Urmson, C.; Wagner, M.; Whittaker, W. First Experiments in Sun-Synchronous Exploration. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002. [Google Scholar]
- Kelly, A.; Amidi, O.; Happold, M.; Herman, H.; Pilarsky, T.; Rander, P.; Stentz, A.; Vallidis, N.; Warner, R. Toward Reliable Autonomous Vehicles Operating in Challenging Environments. In Proceedings of the International Symposium on Experimental Robotics, Singapore, 18–21 June 2004; pp. 599–608. [Google Scholar]
- Goldberg, S.; Maimone, M.; Matthies, L. Stereo Vision and Rover Navigation Software for Planetary Exploration. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002. [Google Scholar]
- Stentz, A. The Focussed D* Algorithm for Real-Time Replanning. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1652–1659. [Google Scholar]
- Stentz, A.; Hebert, M. A Complete Navigation System for Goal Acquisition in Unknown Environments. In Proceedings of the International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August 1995. [Google Scholar]
- Stentz, A. Optimal and Efficient Path Planning for Unknown and Dynamic Environments. Int. J. Robot. Autom. 2003, 10, 58–71. [Google Scholar]
- Brumitt, B.; Stentz, A. GRAMMPS: A generalized mission planner for multiple mobile robots in unstructured environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20 May 1998. [Google Scholar]
- Al-Mutib, K.; AlSulaiman, M.; Emaduddin, M.; Ramdane, H.; Mattar, E. D* Lite Based Real-Time Multi-Agent Path Planning in Dynamic Environments. In Proceedings of the Third International Conference on Computational Intelligence, Modelling & Simulation, Langkawi, Malaysia, 20–22 September 2011. [Google Scholar]
- Peng, J.-H.; Li, I.-H.; Chien, Y.-H.; Hsu, C.-C.; Wang, W.-Y. Multi-Robot Path Planning Based on Improved D* Lite Algorithm. In Proceedings of the IEEE 12th International Conference on Networking, Sensing and Control, Taipei, Taiwan, 9–11 April 2015. [Google Scholar]
- Aroor, A.; Epstein, S.L.; Korpan, R. Online Learning for Crowd-sensitive Path Planning. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1702–1710. [Google Scholar]
- Chan, A.B.; Vasconcelos, N. Bayesian Poisson regression for crowd counting. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 545–551. [Google Scholar]
- Tavana, M.; Bourgeois, B.S. A multiple criteria decision support system for autonomous underwater vehicle mission planning and control. Int. J. Oper. Res. 2010, 7, 216–239. [Google Scholar] [CrossRef]
- Choudhary, S.; Carlone, L.; Nieto, C.; Rogers, J.; Liu, Z.; Christensen, H.I.; Dellaert, F. Multi Robot Object-based SLAM. In Proceedings of the International Symposium on Experimental Robotics, Tokyo, Japan, 3–6 October 2016; pp. 729–741. [Google Scholar]
- Benavidez, P.; Muppidi, M.; Rad, P.; Prevost, J.J.; Jamshidi, M.; Brown, L. Cloud-based realtime robotic Visual SLAM. In Proceedings of the Annual IEEE International Systems Conference, Vancouver, BC, Canada, 13–16 April 2015; pp. 773–777. [Google Scholar]
- He, H.; Kamburugamuve, S.; Fox, G.C.; Zhao, W. Cloud based Real-time Multi-robot Collision Avoidance for Swarm Robotics. Int. J. Grid Distrib. Comput. 2016, 9, 339–358. [Google Scholar] [CrossRef]
- Hunziker, D.; Gajamohan, M.; Waibel, M.; D’Andrea, R. Rapyuta: The RoboEarth Cloud Engine. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 438–444. [Google Scholar]
- Saha, O.; Dasgupta, P. A Comprehensive Survey of Recent Trends in Cloud Robotics Architectures and Applications. Robotics 2018, 7, 47. [Google Scholar] [CrossRef]
- Likhachev, M.; Ferguson, D.; Gordon, G.; Stentz, A.; Thrun, S. Anytime search in dynamic graphs. J. Artif. Intell. 2008, 172, 1613–1643. [Google Scholar] [CrossRef]
- Likhachev, M.; Gordon, G.; Thrun, S. ARA*: Anytime A* with provable bounds on sub-optimality. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–13 December 2003; pp. 767–774. [Google Scholar]
- Likhachev, M.; Ferguson, D.; Gordon, G.; Stentz, A.; Thrun, S. Anytime Dynamic A*: An Anytime, Replanning Algorithm. In Proceedings of the International Conference on Automated Planning and Scheduling, Monterey, CA, USA, 5–10 June 2005; pp. 262–271. [Google Scholar]


| Criteria | C3 | C2 | C1 | C4 |
|---|---|---|---|---|
| 1 | 1 | 1 | 5 |
| Criteria | C3 | C2 | C1 | C4 |
|---|---|---|---|---|
| 1 | 4 | 7 | 7 |
| D* Lite without MCDM | D* Lite with MCDM1 | D* Lite with MCDM2 | |
|---|---|---|---|
| Risky Actions | 887 | 798 (−10.1%) | 719 (−18.9%) |
| Distance | 407.16 | 425.32 (+4.4%) | 435.35 (+6.9%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zagradjanin, N.; Pamucar, D.; Jovanovic, K. Cloud-Based Multi-Robot Path Planning in Complex and Crowded Environment with Multi-Criteria Decision Making Using Full Consistency Method. Symmetry 2019, 11, 1241. https://doi.org/10.3390/sym11101241
Zagradjanin N, Pamucar D, Jovanovic K. Cloud-Based Multi-Robot Path Planning in Complex and Crowded Environment with Multi-Criteria Decision Making Using Full Consistency Method. Symmetry. 2019; 11(10):1241. https://doi.org/10.3390/sym11101241
Chicago/Turabian StyleZagradjanin, Novak, Dragan Pamucar, and Kosta Jovanovic. 2019. "Cloud-Based Multi-Robot Path Planning in Complex and Crowded Environment with Multi-Criteria Decision Making Using Full Consistency Method" Symmetry 11, no. 10: 1241. https://doi.org/10.3390/sym11101241
APA StyleZagradjanin, N., Pamucar, D., & Jovanovic, K. (2019). Cloud-Based Multi-Robot Path Planning in Complex and Crowded Environment with Multi-Criteria Decision Making Using Full Consistency Method. Symmetry, 11(10), 1241. https://doi.org/10.3390/sym11101241






