Approximate Multi-Degree Reduction of SG-Bézier Curves Using the Grey Wolf Optimizer Algorithm
Abstract
1. Introduction
2. The Definition of SG-Bézier Curves
3. Grey Wolf Optimizer (GWO) Algorithm
3.1. The Basic Principles of Grey Wolf Optimizer
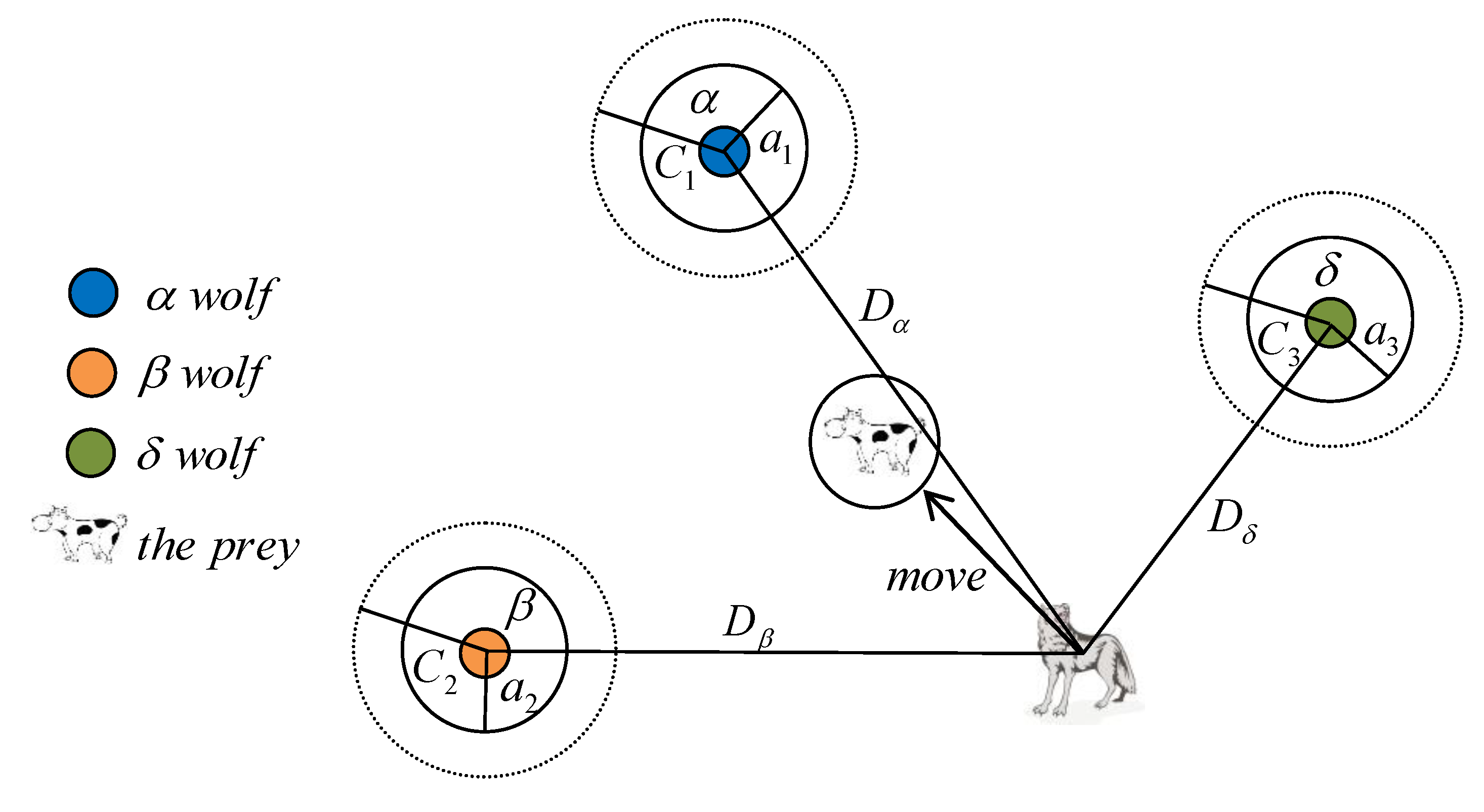
3.1.1. Social Hierarchy
3.1.2. Encircling Prey
3.1.3. Attack Prey
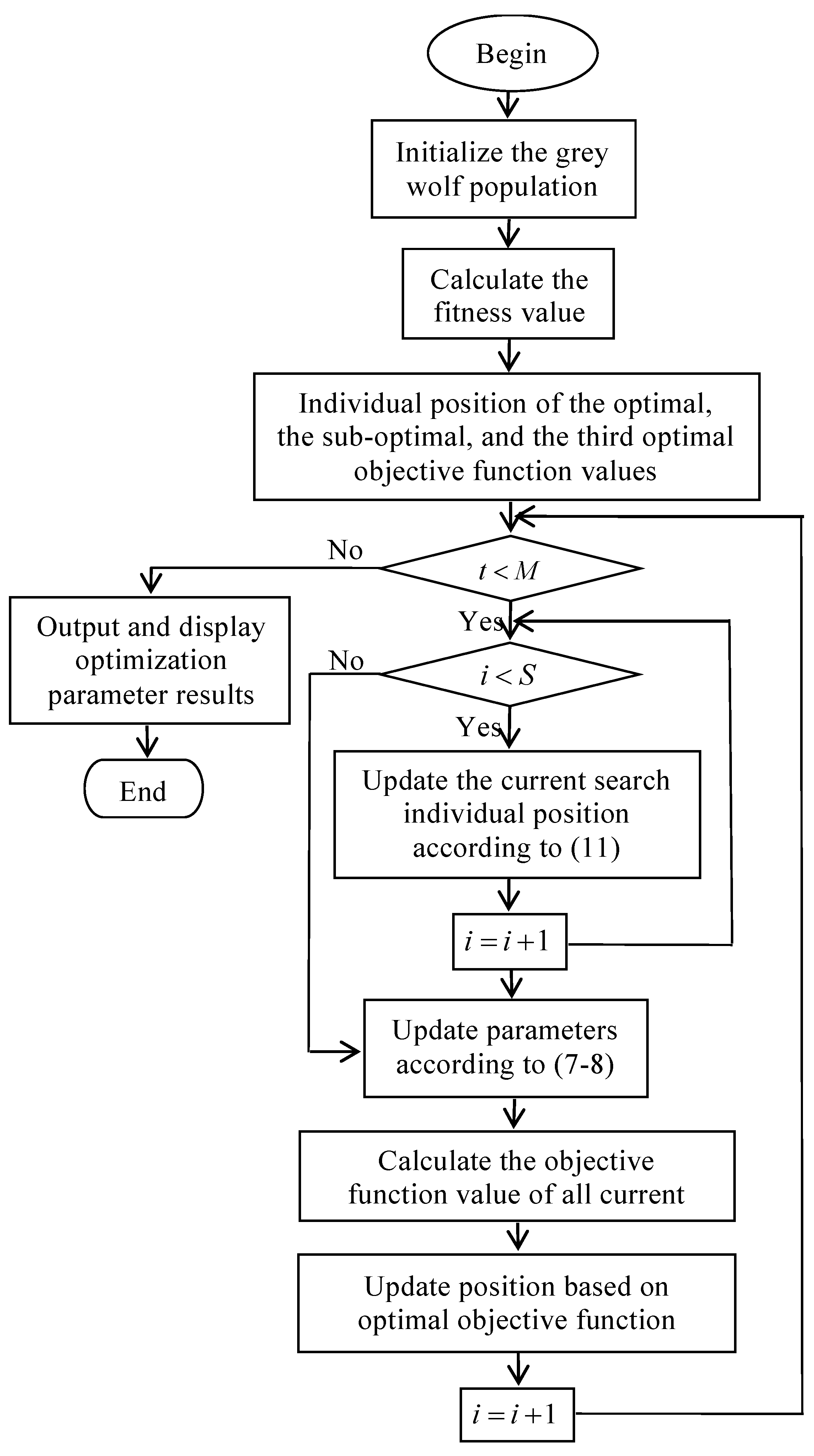
3.2. Algorithmic Flow of Grey Wolf Optimizer
4. Degree Reduction of SG-Bézier Curves with the Grey Wolf Optimizer
4.1. The Basic Idea of SG-Bézier Curve Degree Reduction
4.2. Initialization of the Grey Wolf Population
4.3. Selection of Fitness Function
4.4. The Algorithm Description for Degree Reduction of SG-Bézier Curves
| Algorithm 1 Grey wolf optimizer algorithm: Steps to the degree reduction of SG-Bézier curves. | |
| Step 1 | Input the degree and control points sequence of SG-Bézier curves before degree reduction {P0, P1, …, Pn}. |
| Step 2 | Draw SG-Bézier curve before degree reduction and its control polygon. |
| Step 3 | Initialize the parameters, set the population size and the maximum number of iterations MaxIter, determine the number of points on the curve selected in the error analysis before and after the reduction, and give the upper and lower bounds of the search individual information dimension and the search individual information dimension. |
| Step 4 | According to Equation (17), generate the initial population Qj(j = 0, 1, …, m). |
| Step 5 | According to Equation (19), calculate the fitness value of the grey wolf individual, rank all the fitness values, and record the position Qα, Qβ, Qδof the optimal grey wolf α, the sub-optimal grey wolf β and the third optimal grey wolf ω. |
| Step 6 | According to Equation (12), update the position of the current grey wolf. |
| Step 7 | Update parameters a, A and C by Equations (7)–(9). |
| Step 8 | Calculate the fitness values of all grey wolves after being updated, and determine the new Qα, Qβ and Qδ. |
| Step 9 | To determine whether the maximum number of iterations is reached, yes, execute Step 10; No, repeat Step 5–Step 9. |
| Step 10 | Output optimization parameter result Qα. |
| Step 11 | Draw SG-Bézier curve and its control polygon after degree reduction. |
| Algorithm 2 The pseudo-code of the GWO algorithm: Degree reduction of SG-Bézier curve | |
| Input Parameters: s: Population size; d: Dimensions of searching individuals; lb: The lower bound of searching individual dimension; ub: The upper bound of searching individual dimension; N: The number of points on the curve selected during error analysis before and after the reduction; m: Maximum number of iterations; | |
| 01 | wolf population initialization(wolf_size); |
| 02 | fitness evaluate(wolf population); /*Calculating individual fitness of grey wolf*/ |
| 03 | while (evaluation_number<max_evaluation_number) do/*Termination condition*/ |
| 04 | select the first best three wolves(wolf population); /*Select the optimal, sub-optimal, and second optimal wolf*/ |
| 05 | while (i < m) do |
| 06 | new position of the wolf update(the current wolf); /*Update the location of the current search individuals*/ |
| 07 | evaluation_number + 1; |
| 08 | end |
| 09 | update(a,A,C) |
| 10 | fitness evaluate(new position of the wolf); |
| 11 | evaluation_number + 1; |
| 12 | end |
| 13 | select the best wolf(the entire wolves); |
| 14 | output |
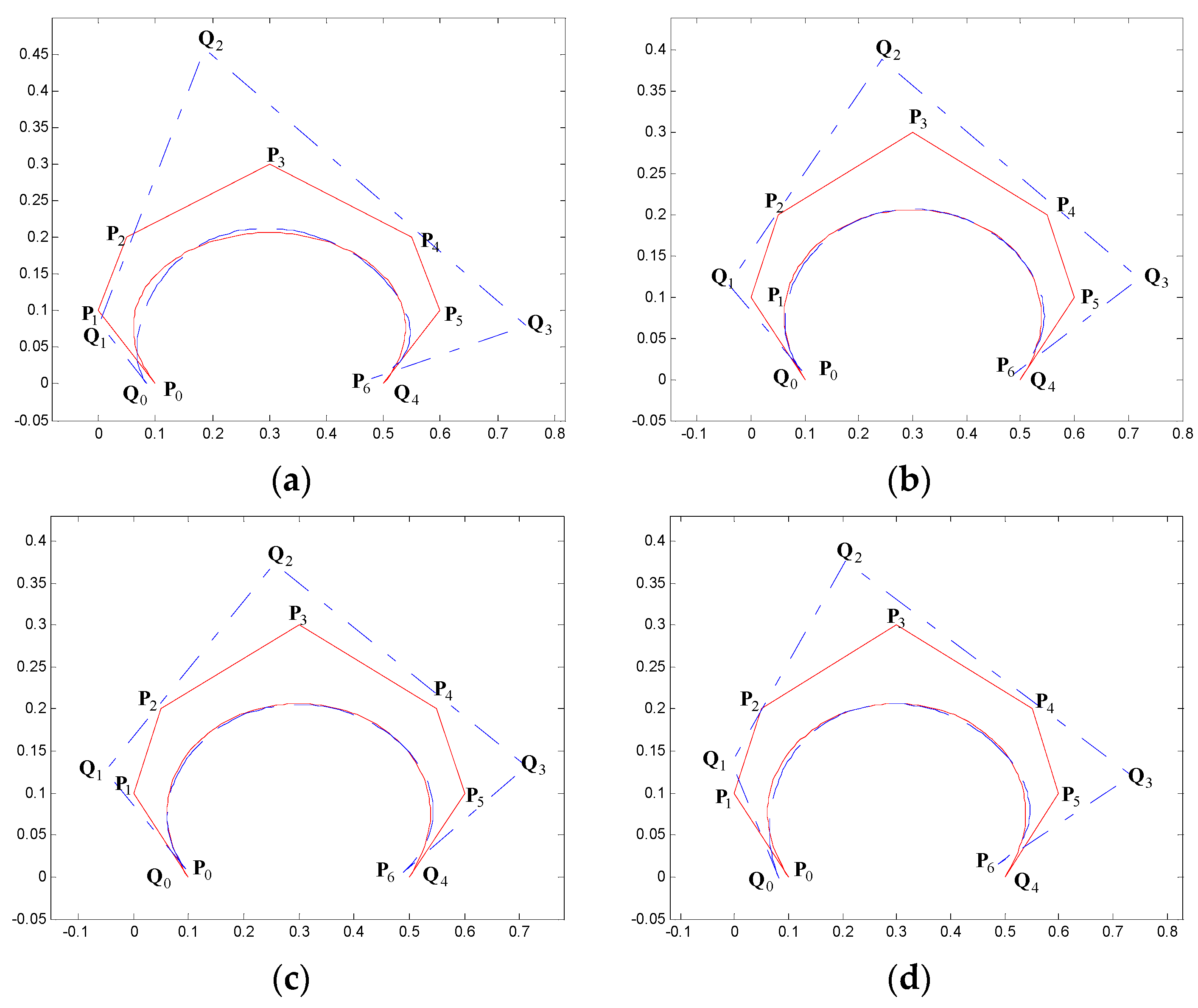
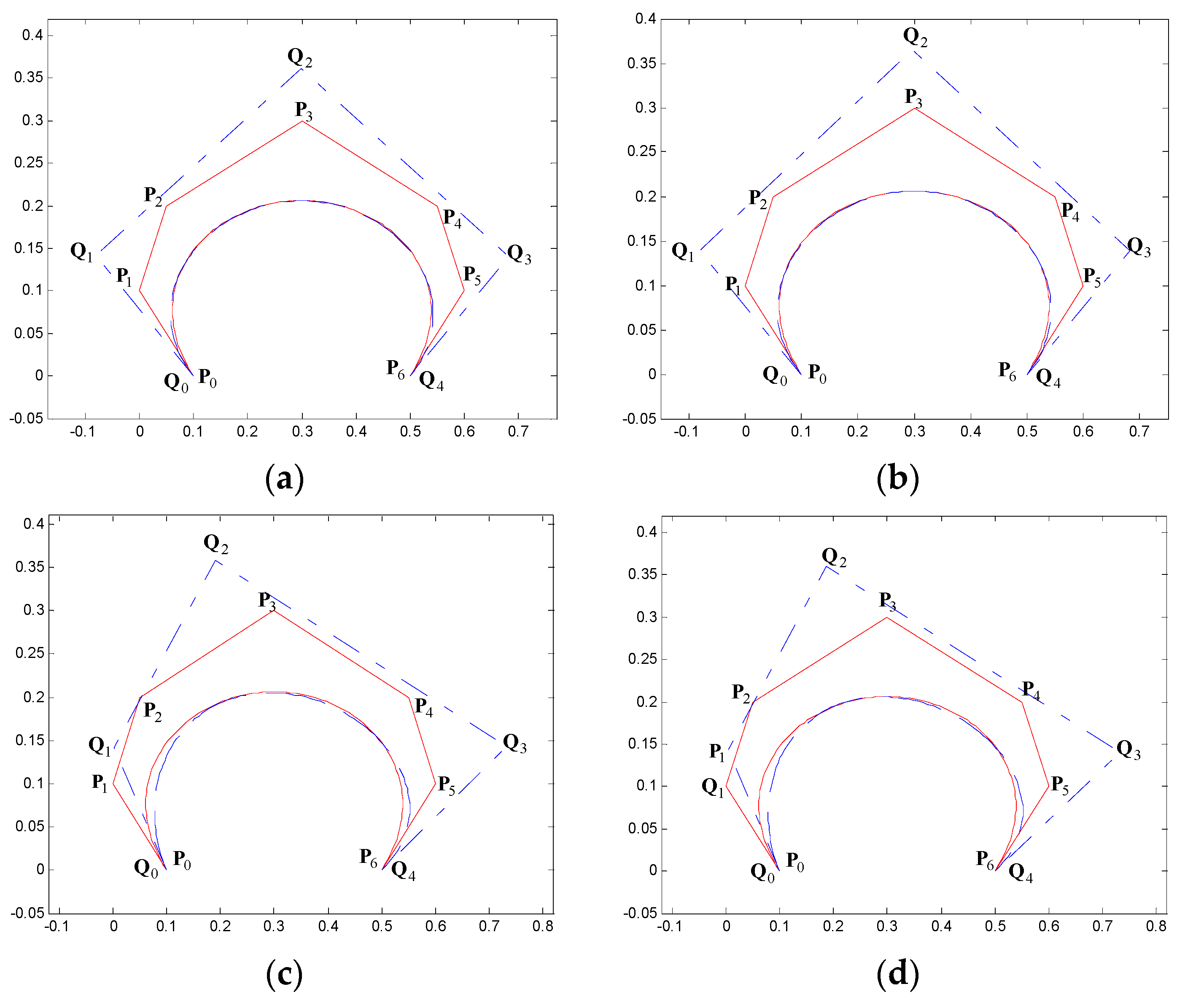
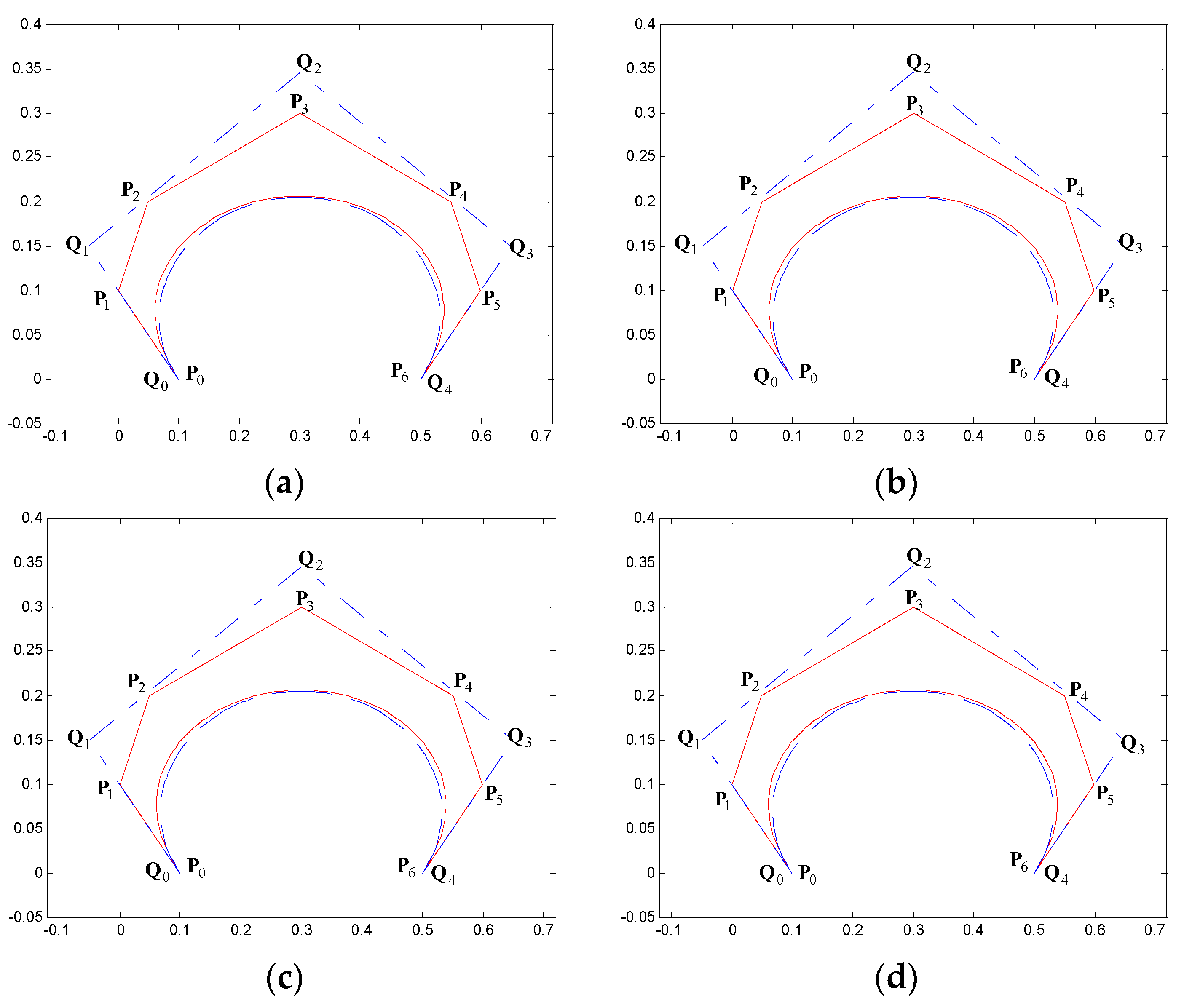
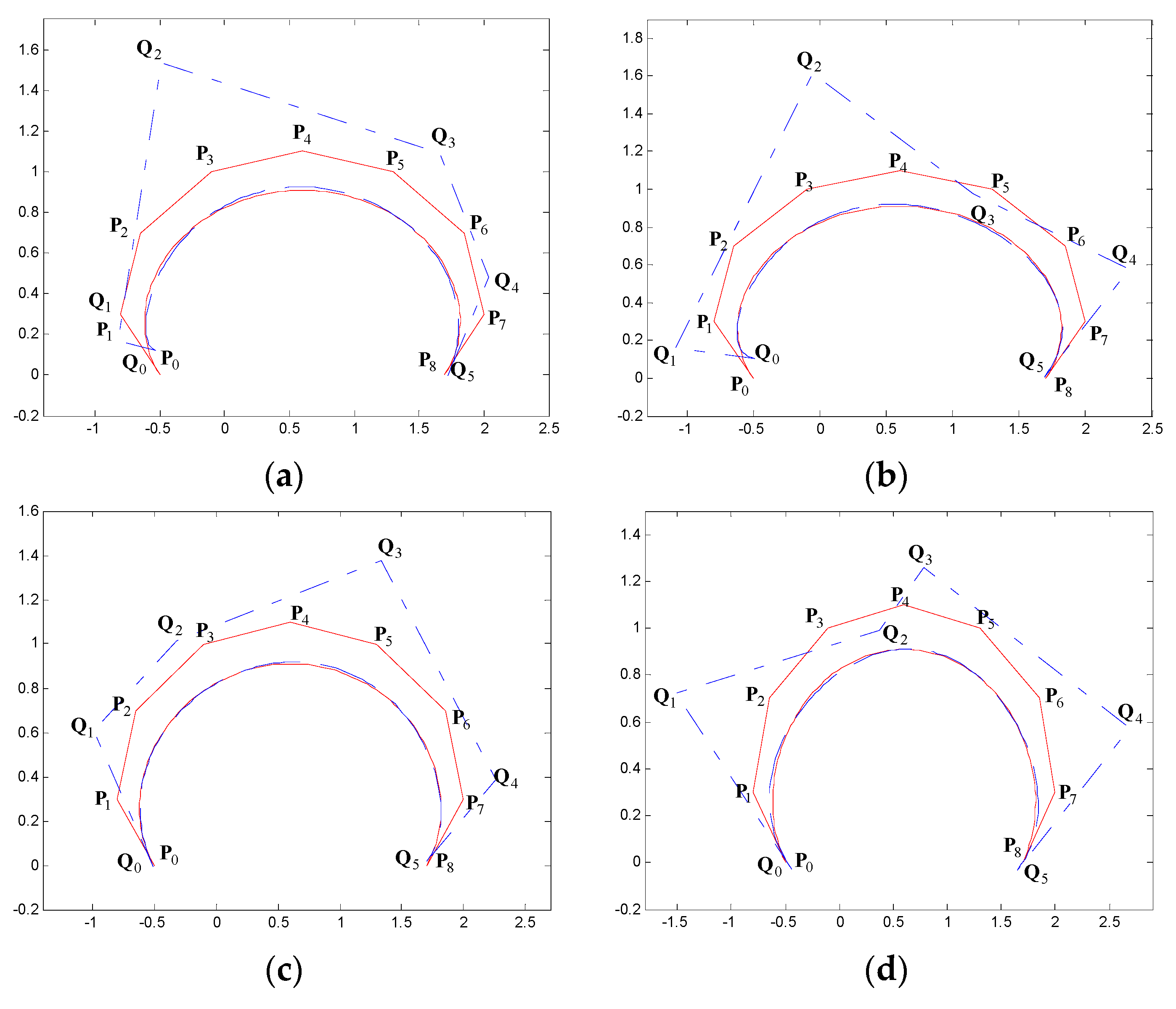
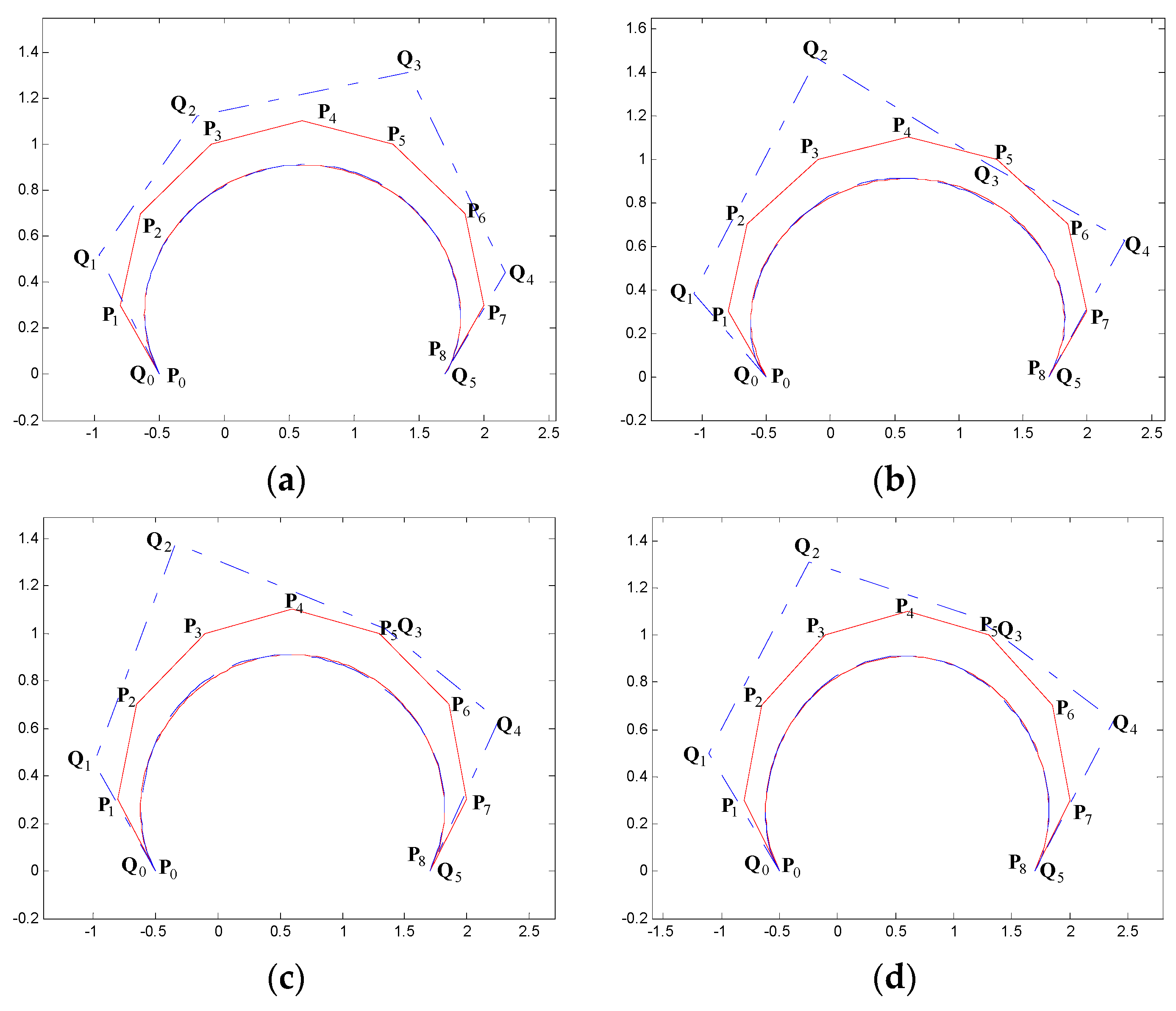
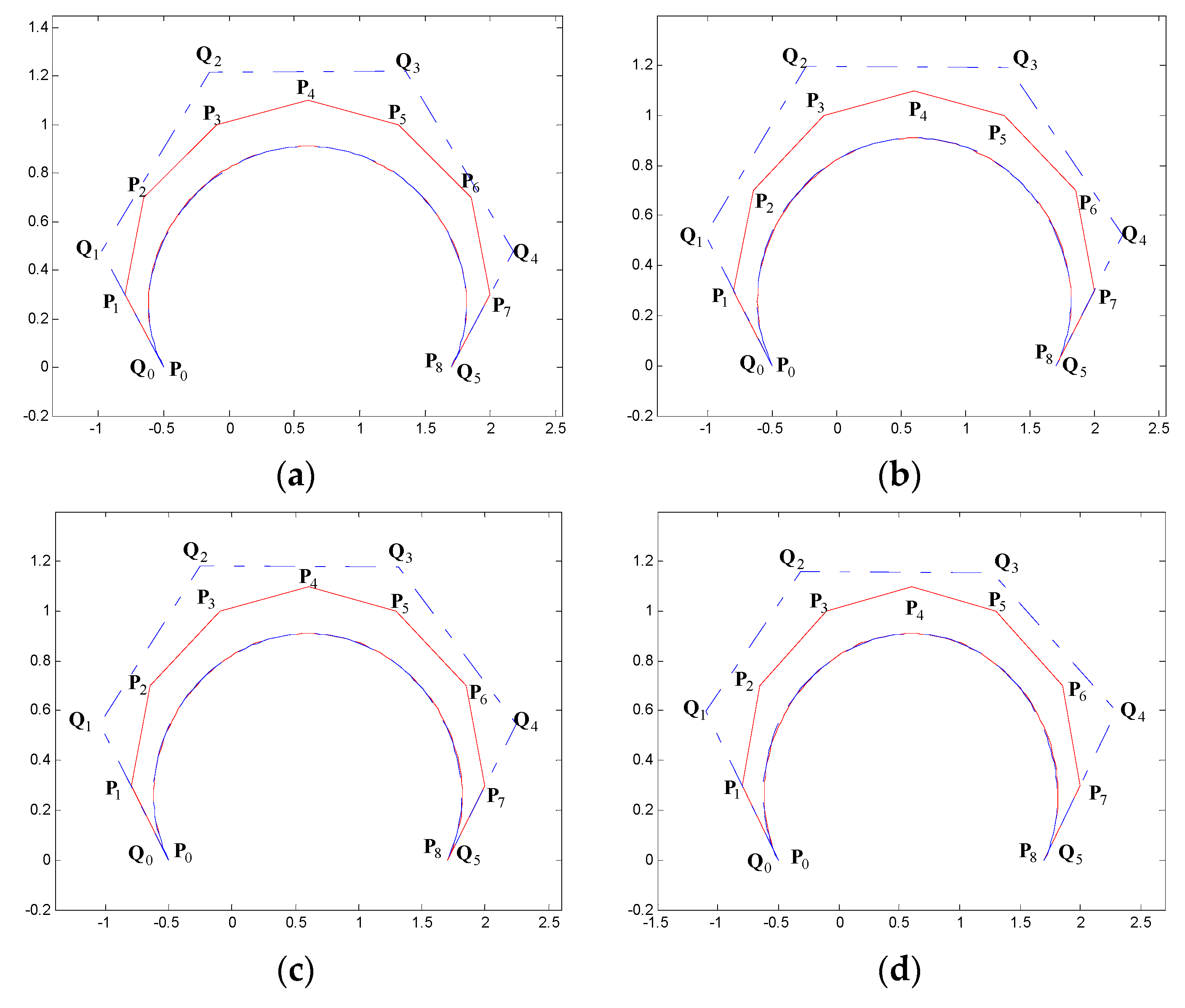
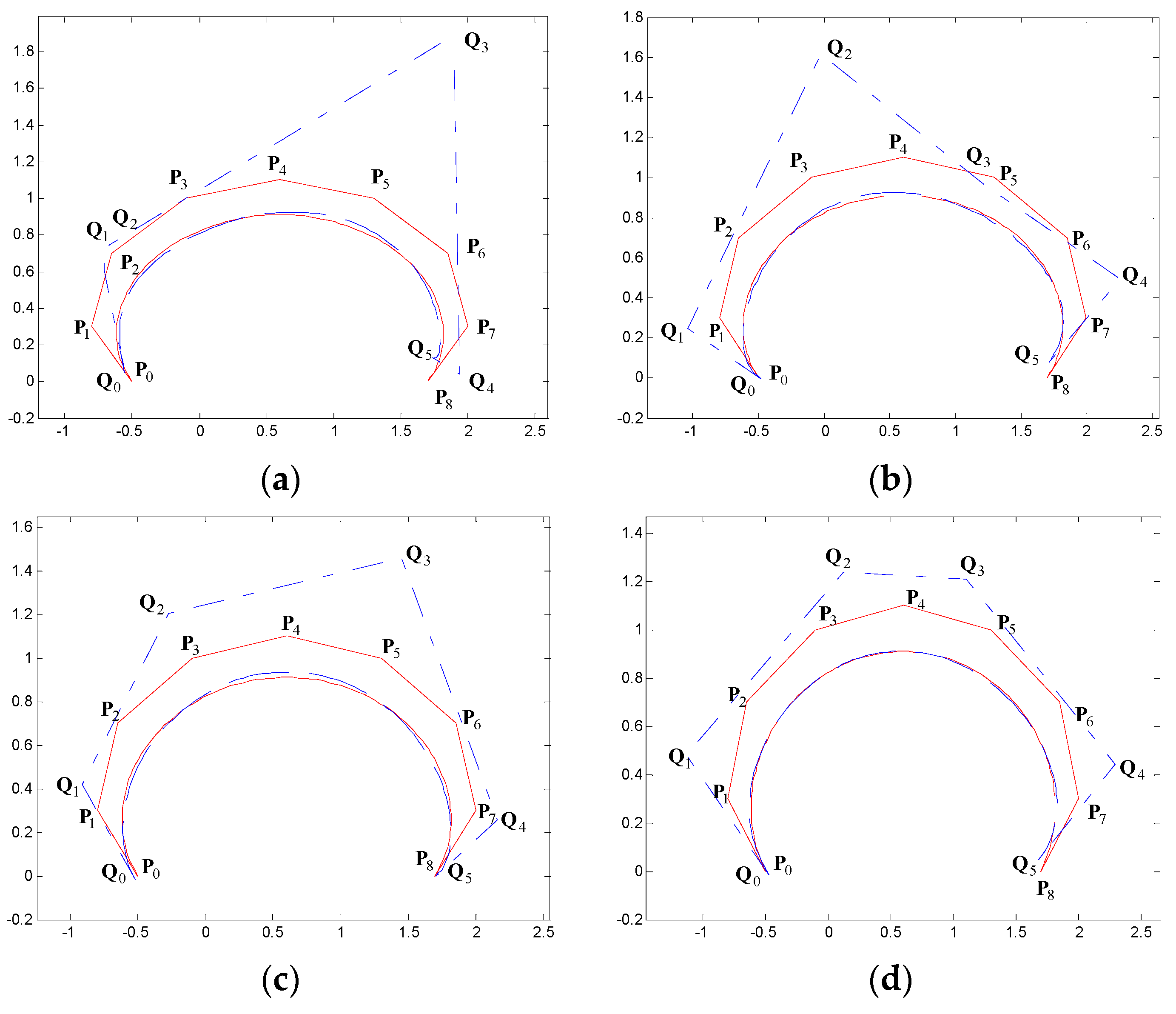
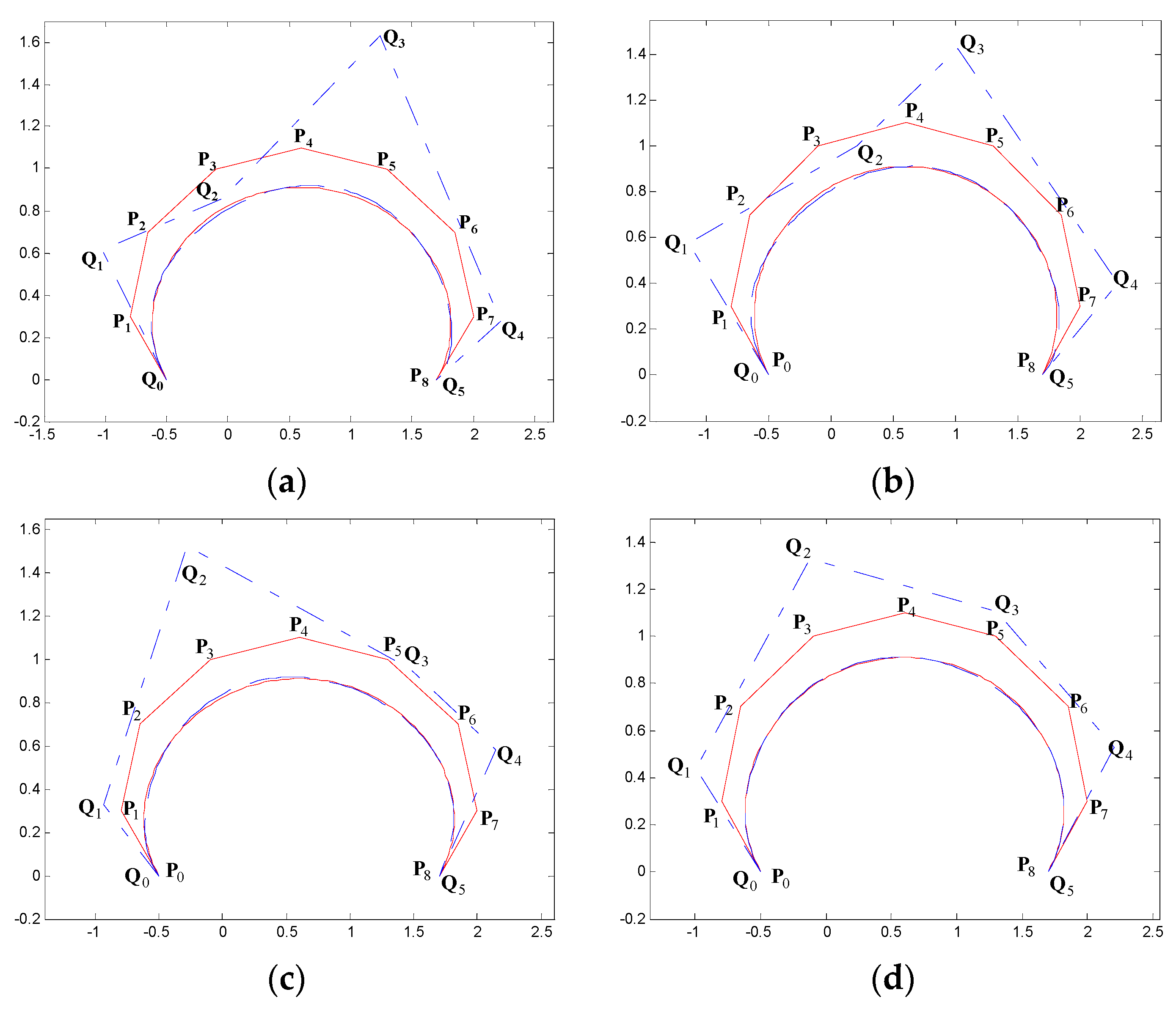
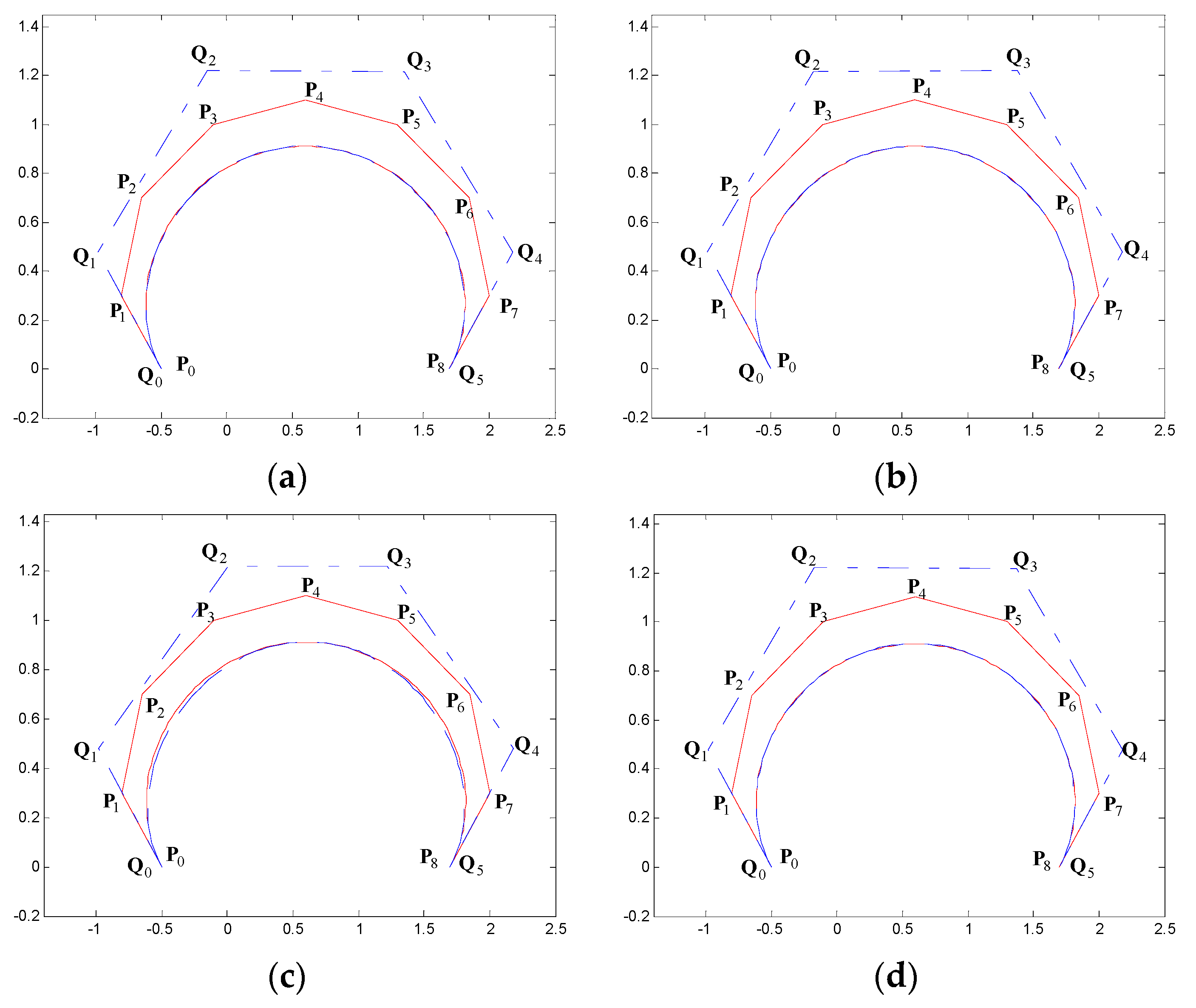
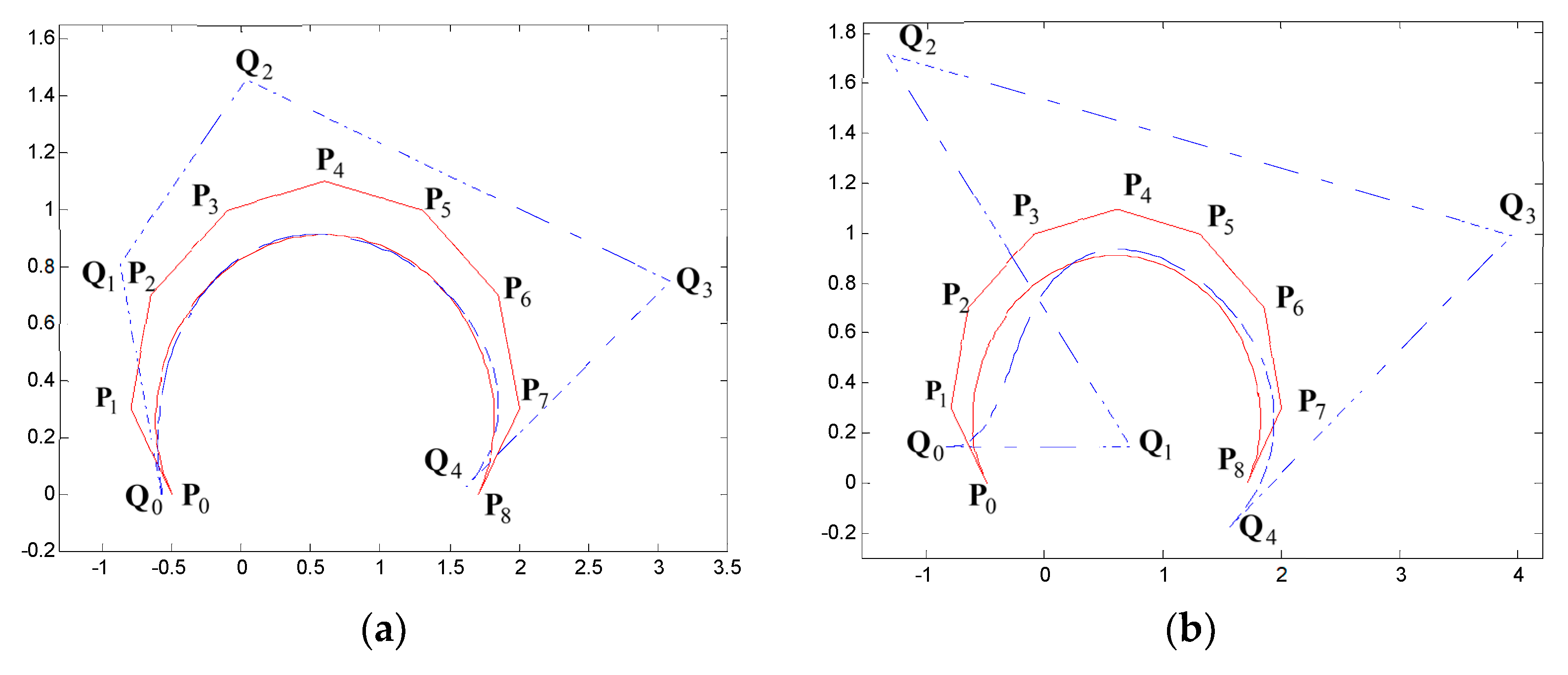
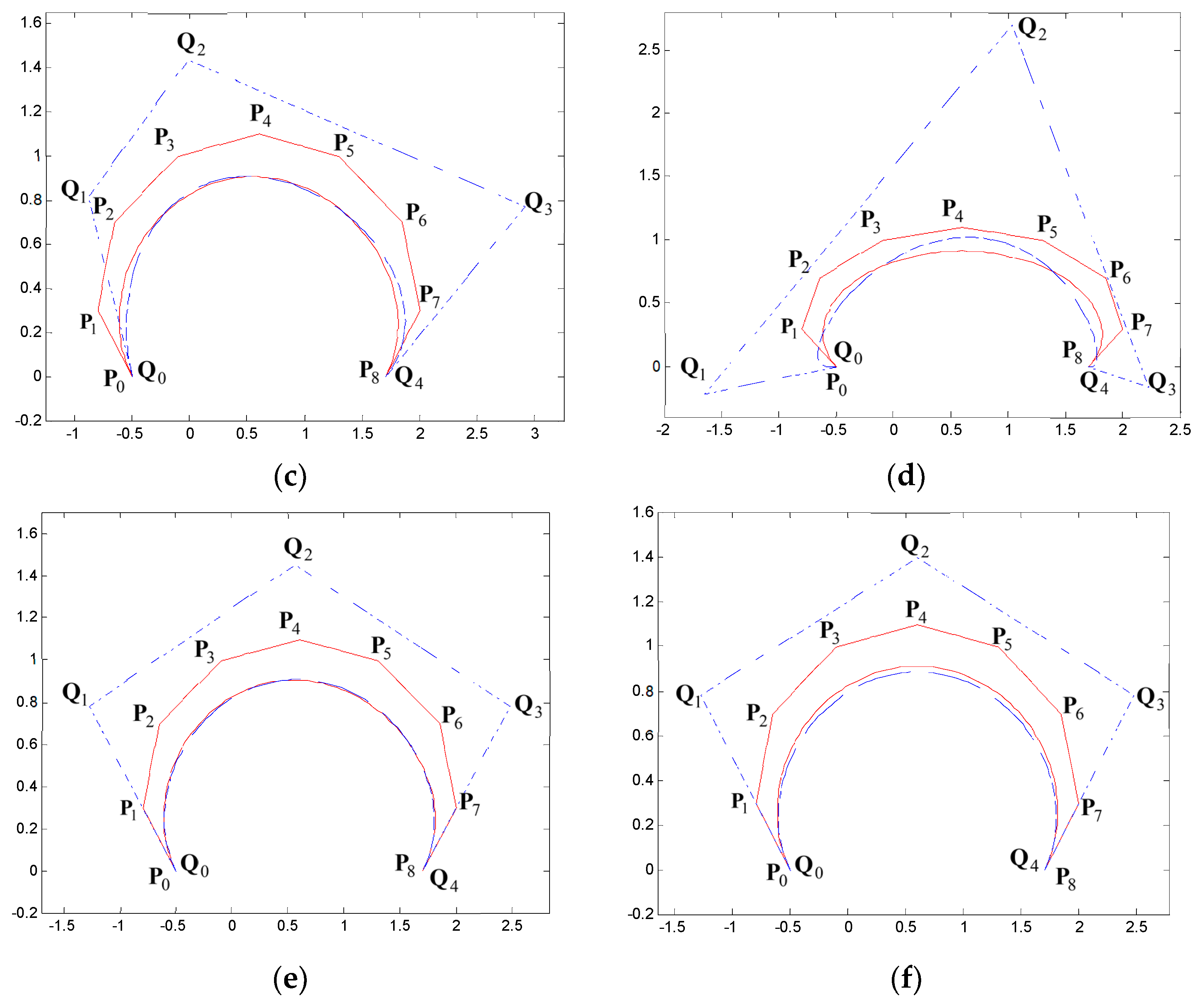
5. Examples of Degree Reduction Approximation Curves
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farin, G. Curves and Surfaces for CAGD: A Practical Guide, 5th ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Mamar, E. Shape preserving alternatives to the rational Bézier model. Comput. Aided Geom. Des. 2001, 18, 37–60. [Google Scholar] [CrossRef]
- Qinyu, C.; Guozhao, W. A class of Bézier-like curves. Comput. Aided Geom. Des. 2003, 20, 29–39. [Google Scholar]
- Oruc, H.; Phillips, G.H. q-Bézier Bernstein polynomials and Bézier curves. J. Comput. Appl. Math. 2003, 151, 1–12. [Google Scholar] [CrossRef]
- Hu, G.; Wu, J.L.; Qin, X.Q. A new approach in designing of local controlled developable H-Bézier surfaces. Adv. Eng. Softw. 2018, 121, 26–38. [Google Scholar] [CrossRef]
- Han, X. Cubic trigonometric polynomial curves with a shape parameter. Comput. Aided Geom. Des. 2004, 21, 535–548. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Q. Planar cubic hybrid hyperbolic polynomial curve and its shape classification. Prog. Nat. Sci. 2004, 14, 41–46. [Google Scholar] [CrossRef]
- Zhang, J.; Krause, F.L.; Zhang, H. Unifying C-curves and H-curves by extending the calculation to complex numbers. Comput. Aided Geom. Des. 2005, 22, 865–883. [Google Scholar] [CrossRef]
- Hu, G.; Bo, C.C.; Qin, X.Q. Continuity conditions for tensor product Q-Bézier surfaces of degree (m, n). Comput. Appl. Math. 2018, 37, 4237–4258. [Google Scholar] [CrossRef]
- Han, X.A.; Ma, Y.C.; Huang, X. The cubic trigonometric Bézier curve with two shape parameters. Appl. Math. Lett. 2009, 22, 226–231. [Google Scholar] [CrossRef]
- Han, X.A.; Huang, X.; Ma, Y.C. Shape analysis of cubic trigonometric Bézier curves with a shape parameter. Appl. Math. Comput. 2010, 217, 2527–2533. [Google Scholar] [CrossRef]
- Rachid, A.; Yusuke, S.; Taishin, N. Gelfond-Bézier curves. Comput. Aided Geom. Des. 2013, 30, 199–225. [Google Scholar]
- Qin, X.Q.; Hu, G.; Yang, Y.; Wei, G. Construction of PH splines based on H-Bézier curves. Appl. Math. Comput. 2014, 238, 460–467. [Google Scholar] [CrossRef]
- Farin, G. Class a Bézier curves. Comput. Aided Geom. Des. 2006, 23, 573–581. [Google Scholar] [CrossRef]
- Han, X.A.; Ma, Y.; Huang, X. A novel generalization of Bézier curve and surface. J. Comput. Appl. Math. 2008, 217, 180–193. [Google Scholar] [CrossRef]
- Yang, L.; Zeng, X.M. Bézier curves and surfaces with shape parameter. Int. J. Comput. Math. 2009, 86, 1253–1263. [Google Scholar] [CrossRef]
- Hu, G.; Cao, H.X.; Zhang, S.X.; Guo, W. Developable Bézier-like surfaces with multiple shape parameters and its continuity conditions. Appl. Math. Model. 2017, 45, 728–747. [Google Scholar] [CrossRef]
- Yan, L.; Liang, J. An extension of the Bézier model. Appl. Math. Comput. 2011, 218, 2863–2879. [Google Scholar] [CrossRef]
- Qin, X.Q.; Hu, G.; Zhang, N.J.; Shen, X.; Yang, Y. A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degree n with multiple shape parameters. Appl. Math. Comput. 2013, 223, 1–16. [Google Scholar] [CrossRef]
- Hu, G.; Wu, J.L.; Qin, X.Q. A novel extension of the Bézier model and its applications to surface modeling. Adv. Eng. Softw. 2018, 125, 27–54. [Google Scholar] [CrossRef]
- Hu, G.; Bo, C.; Wu, J.L.; Wei, G.; Hou, F. Modeling of free-form complex curves using SG-Bézier curves with constraints of geometric continuities. Symmetry 2018, 10, 545. [Google Scholar] [CrossRef]
- Zhao, Y. Research on degree reduction of C-Bézier curves based on generalized inverse matrix. Netw. Secur. Technol. Appl. 2010, 10, 38–40. [Google Scholar]
- Chen, G.; Wang, G.J. Degree reduction approximation of Bézier curves by generalized inverse matrices. J. Comput. Aided Des. Comput. Graph. 2001, 12, 435–439. [Google Scholar]
- Cai, H.J.; Wang, G.J. Constrained approximation of rational Bézier curves based on a matrix expression of its end points continuity condition. Comput. Aided Des. 2010, 42, 495–504. [Google Scholar] [CrossRef]
- Gospodarczyk, P. Degree reduction of Bézier curves with restricted control points area. Comput. Aided Des. 2015, 62, 143–151. [Google Scholar] [CrossRef]
- Ahn, Y.J. Using Jacobi polynomials for degree reduction of Bézier curves with Ck-constraints. Comput. Aided Geom. Des. 2003, 20, 423–434. [Google Scholar] [CrossRef]
- Lee, B.G.; Park, Y.; Yoo, J. Application of Legendre-Bernstein basis transformations to degree elevation and degree reduction. Comput. Aided Geom. Des. 2002, 19, 709–718. [Google Scholar] [CrossRef]
- Rababah, A.; Lee, B.G.; Yoo, J. A simple matrix form for degree reduction of Bézier curves using Chebyshev-Bernstein basis transformations. Appl. Math. Comput. 2006, 181, 310–318. [Google Scholar] [CrossRef]
- Ahn, Y.J.; Lee, B.G.; Park, Y.; Yoo, J. Constrained polynomial degree reduction in the L2-norm equals best weighted Euclidean approximation of Bézier coefficients. Comput. Aided Geom. Des. 2004, 21, 181–191. [Google Scholar] [CrossRef]
- Ait-Haddou, R.; Bartoň, M. Constrained multi-degree reduction with respect to Jacobi norms. Comput. Aided Geom. Des. 2016, 42, 23–30. [Google Scholar] [CrossRef]
- Lu, J.; Qin, X. Degree reduction of S-λ curves using a genetic simulated annealing algorithm. Symmetry 2019, 11, 15. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural Comp. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Mirjalili, S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Tech. J. Eng. Appl. Sci. 2014, 4, 373–379. [Google Scholar] [CrossRef]
- Song, H.; Sulaiman, M.; Mohamed, M. An application of grey wolf optimizer for solving combined economic emission dispatch problems. Int. Rev. Model. Simul. 2014, 7, 838–844. [Google Scholar]
- Caponetto, R.; Fortuna, L.; Graziani, S.; Xibilia, M.G. Genetic algorithms and applications in system engineering: A survey. Trans. Inst. Meas. Control 1993, 15, 143–156. [Google Scholar] [CrossRef]


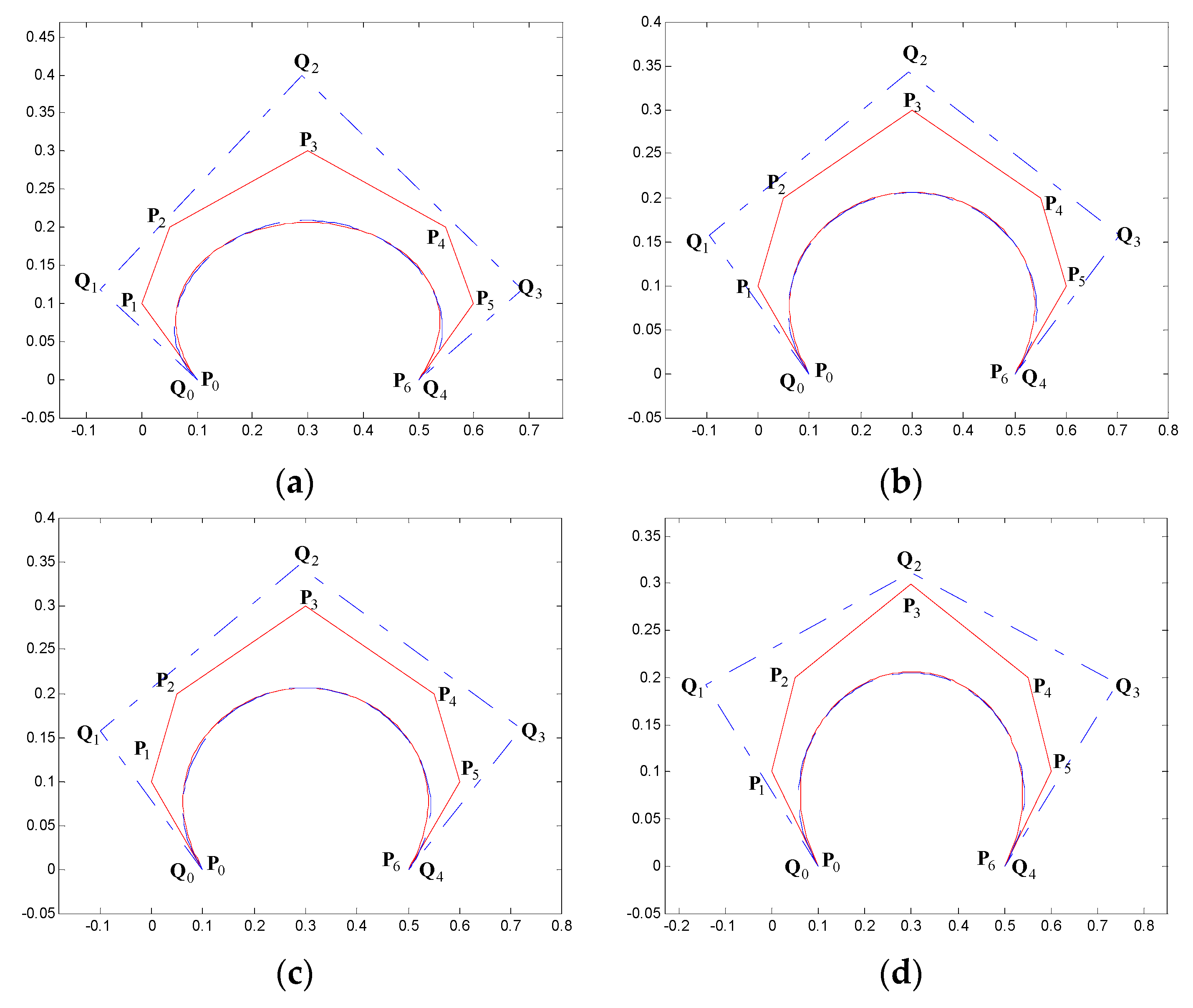
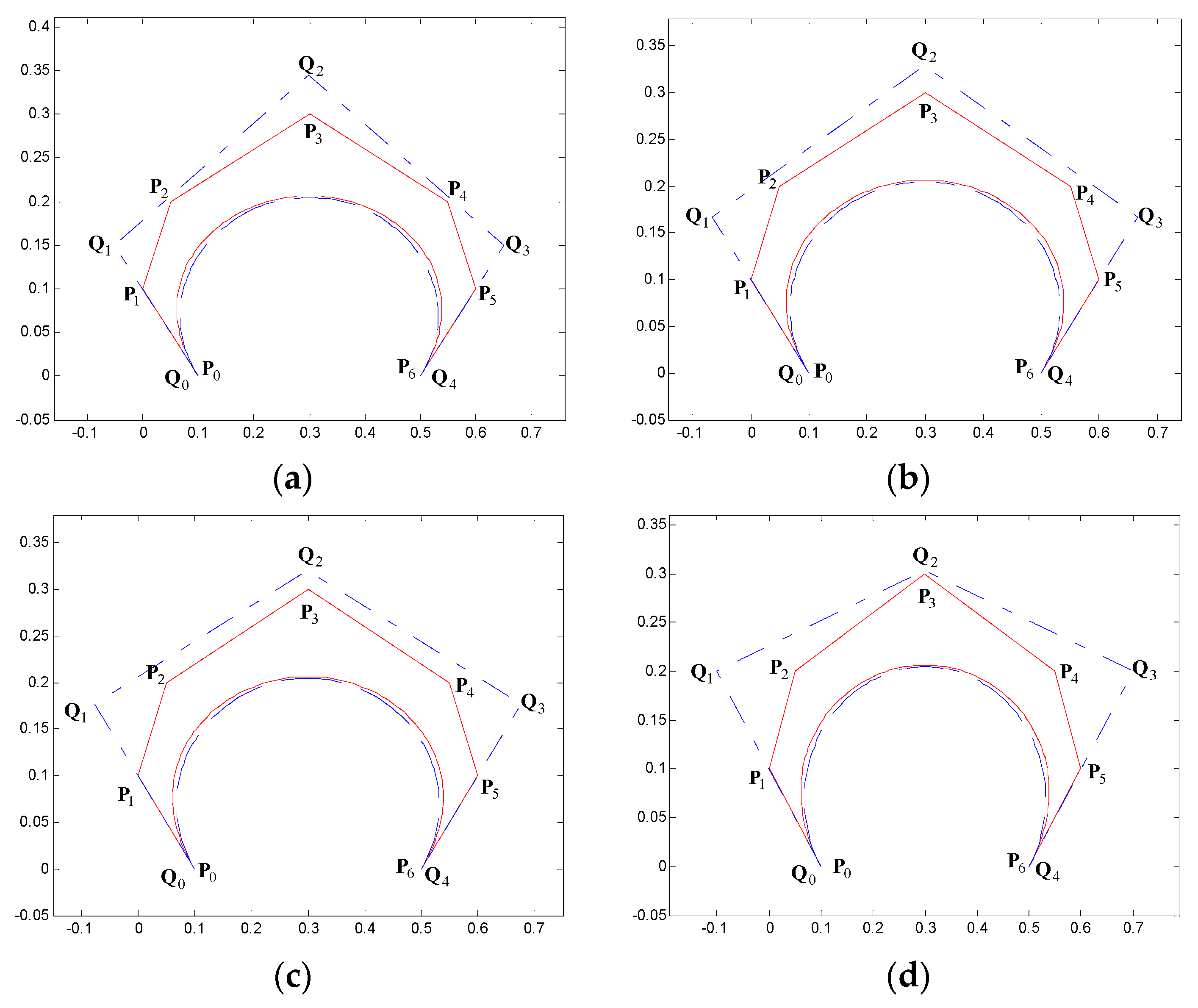
| n | Parameters |
|---|---|
| even | , , |
| odd | , , |
| Constraint Condition | ω = 0 | ω = 0.2 | ω = 0.3 | ω = 0.5 |
|---|---|---|---|---|
| Unrestricted | 4.9914 × 10−3 | 8.6669 × 10−3 | 7.4429 × 10−3 | 9.5617 × 10−3 |
| C0 constraint | 4.1972 × 10−3 | 2.7182 × 10−3 | 3.1251 × 10−3 | 2.6399 × 10−3 |
| C1 constraint | 9.1096 × 10−3 | 9.1890 × 10−3 | 9.1935 × 10−3 | 9.1096 × 10−3 |
| Shape Parameters | Unrestricted | C0 Constraint | C1 Constraint |
|---|---|---|---|
| ω = 0, λ2 = 3, µ1 = 3, µ2 = 3; λ1 = 2 | 1.0108 × 10−2 | 2.6558 × 10−3 | 9.1097 × 10−3 |
| ω = 0, λ1 = 3, µ1 = 3, µ2 = 3; λ2 = 4 | 4.4997 × 10−3 | 2.6803 × 10−3 | 9.1097 × 10−3 |
| ω = 0, λ1 = 3, λ2 = 3, µ2 = 3; µ1 = 2 | 4.0165 × 10−3 | 1.0576 × 10−2 | 9.1097 × 10−3 |
| ω = 0, λ2 = 3, µ1 = 3; λ1 = 2, µ2 = 2 | 7.3299 × 10−3 | 1.0956 × 10−2 | 9.1097 × 10−3 |
| Constraint Condition | ω = 0 | ω = 0.2 | ω = 0.3 | ω = 0.5 |
|---|---|---|---|---|
| Unrestricted | 2.5164 × 10−2 | 1.9874 × 10−2 | 9.4116 × 10−3 | 2.2389 × 10−2 |
| C0 constraint | 4.9315 × 10−3 | 1.2441 × 10−2 | 8.8423 × 10−3 | 7.3303 × 10−3 |
| C1 constraint | 2.9630 × 10−3 | 2.7537 × 10−3 | 3.9361 × 10−3 | 6.7623 × 10−3 |
| Shape Parameters | Unrestricted | C0 Constraint | C1 Constraint |
|---|---|---|---|
| ω = 0, λ2 = 3, λ3 = 3, µ1 = 3, µ2 = 3; λ1 = 2 | 3.3712 × 10−2 | 1.8863 × 10−2 | 2.7072 × 10−3 |
| ω = 0, λ3 = 3, µ1 = 3, µ2 = 3; λ1 = 2, λ2 = 4 | 2.6413 × 10−2 | 1.7231 × 10−2 | 1.6661 × 10−3 |
| ω = 0, λ3 = 3, µ2 = 3; λ1 = 2, λ2 = 4, µ1 = 2 | 3.0435 × 10−2 | 1.4649 × 10−2 | 2.0349 × 10−2 |
| ω = 0, λ1 = 3, λ2 = 3, µ1 = 3; λ3 = 2, µ2 = 2 | 1.3253 × 10−2 | 5.2874 × 10−3 | 1.4618 × 10−3 |
| Method | Unrestricted | C0 Constraint | C1 Constraint |
|---|---|---|---|
| GWO method | 6.1586 × 10−3 | 4.7146 × 10−3 | 7.4163 × 10−3 |
| GA method | 1.3546 × 10−1 | 1.0971 × 10−1 | 2.4860 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Qiao, Y.; Qin, X.; Wei, G. Approximate Multi-Degree Reduction of SG-Bézier Curves Using the Grey Wolf Optimizer Algorithm. Symmetry 2019, 11, 1242. https://doi.org/10.3390/sym11101242
Hu G, Qiao Y, Qin X, Wei G. Approximate Multi-Degree Reduction of SG-Bézier Curves Using the Grey Wolf Optimizer Algorithm. Symmetry. 2019; 11(10):1242. https://doi.org/10.3390/sym11101242
Chicago/Turabian StyleHu, Gang, Yu Qiao, Xinqiang Qin, and Guo Wei. 2019. "Approximate Multi-Degree Reduction of SG-Bézier Curves Using the Grey Wolf Optimizer Algorithm" Symmetry 11, no. 10: 1242. https://doi.org/10.3390/sym11101242
APA StyleHu, G., Qiao, Y., Qin, X., & Wei, G. (2019). Approximate Multi-Degree Reduction of SG-Bézier Curves Using the Grey Wolf Optimizer Algorithm. Symmetry, 11(10), 1242. https://doi.org/10.3390/sym11101242







