Heat Transfer Analysis of a Magneto-Bio-Fluid Transport with Variable Thermal Viscosity Through a Vertical Ciliated Channel
Abstract
1. Introduction
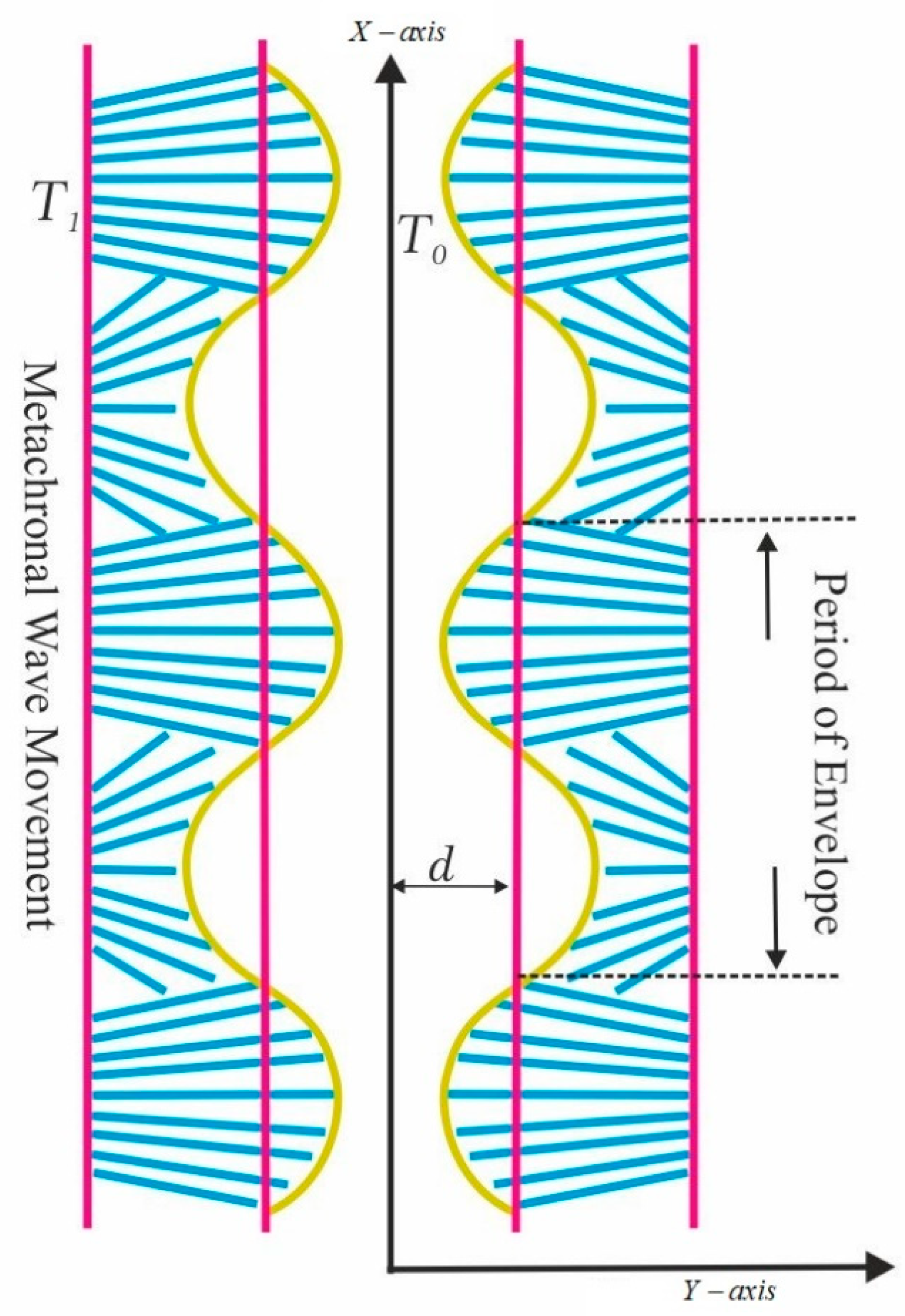
2. Statement of the Problem
3. Solution Methodology
4. Results and Discussions
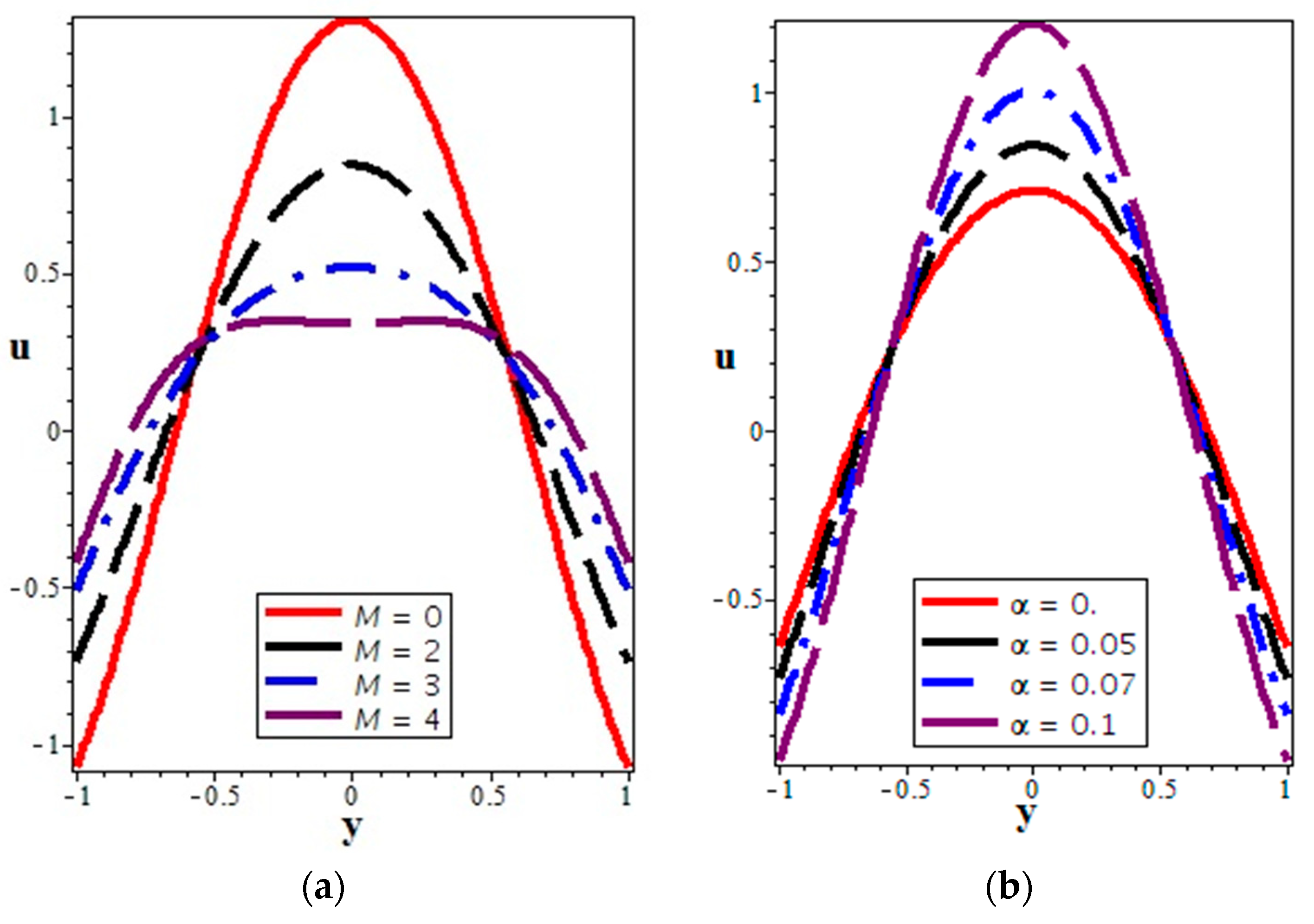
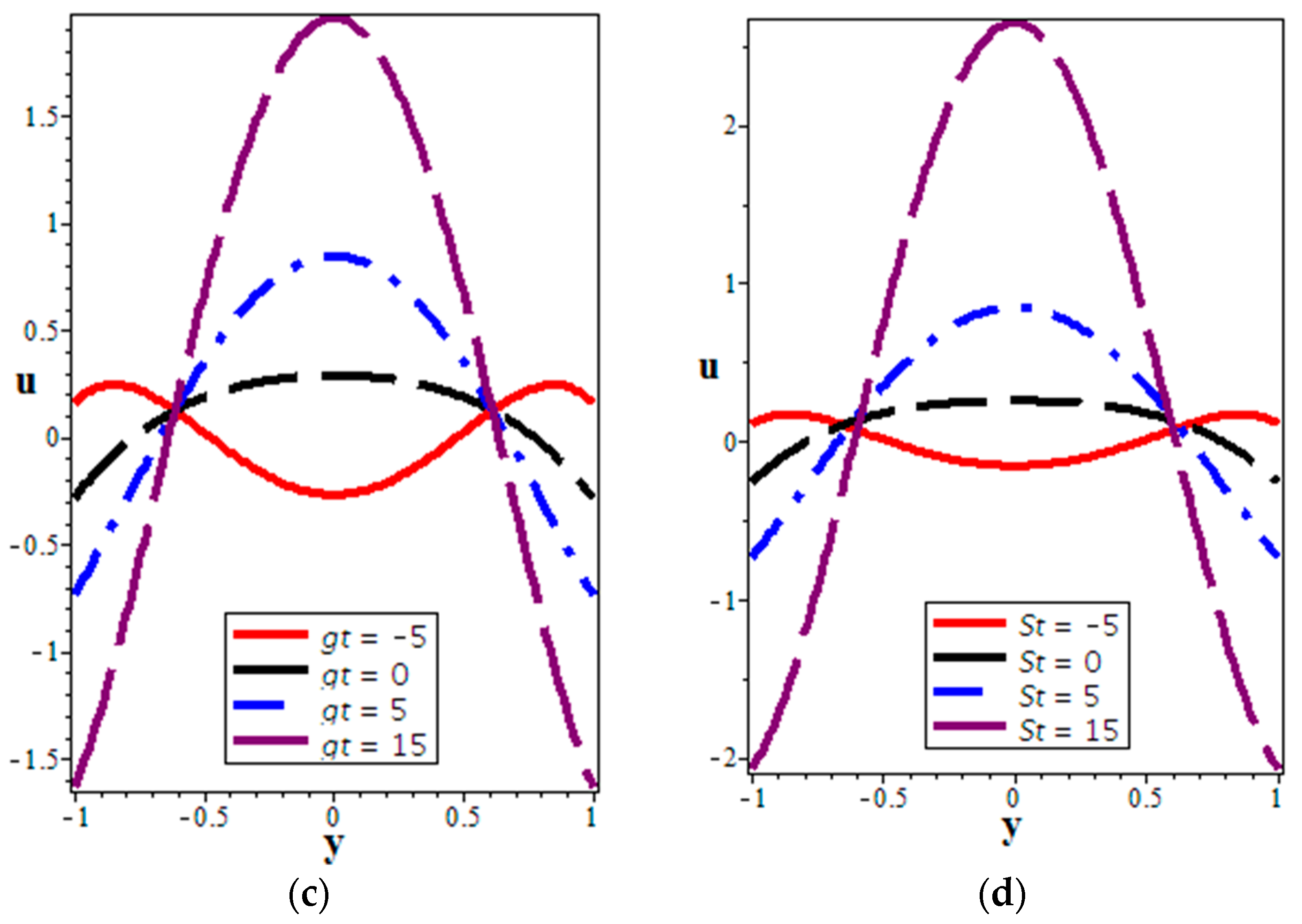
4.1. Velocity Distribution
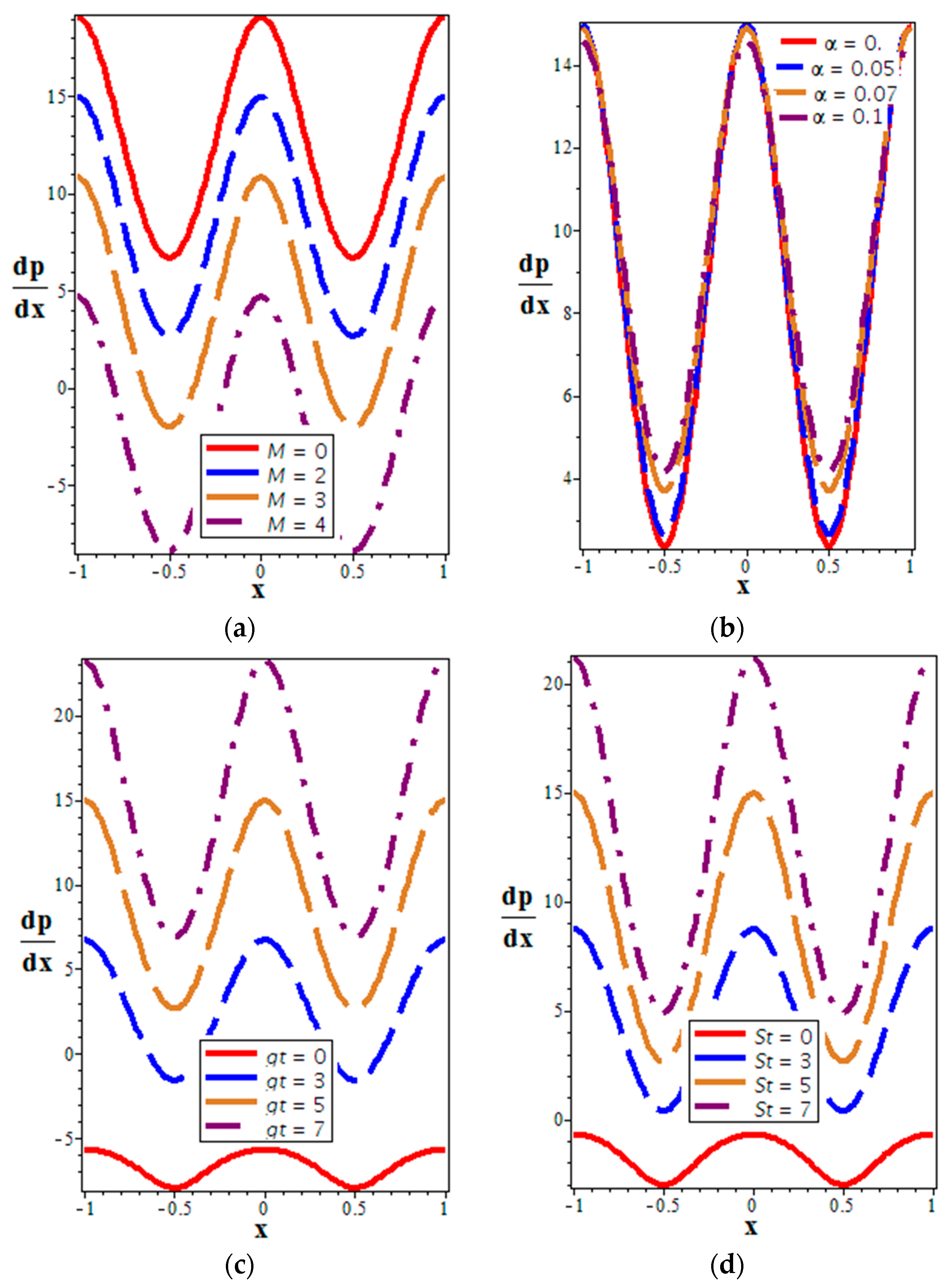
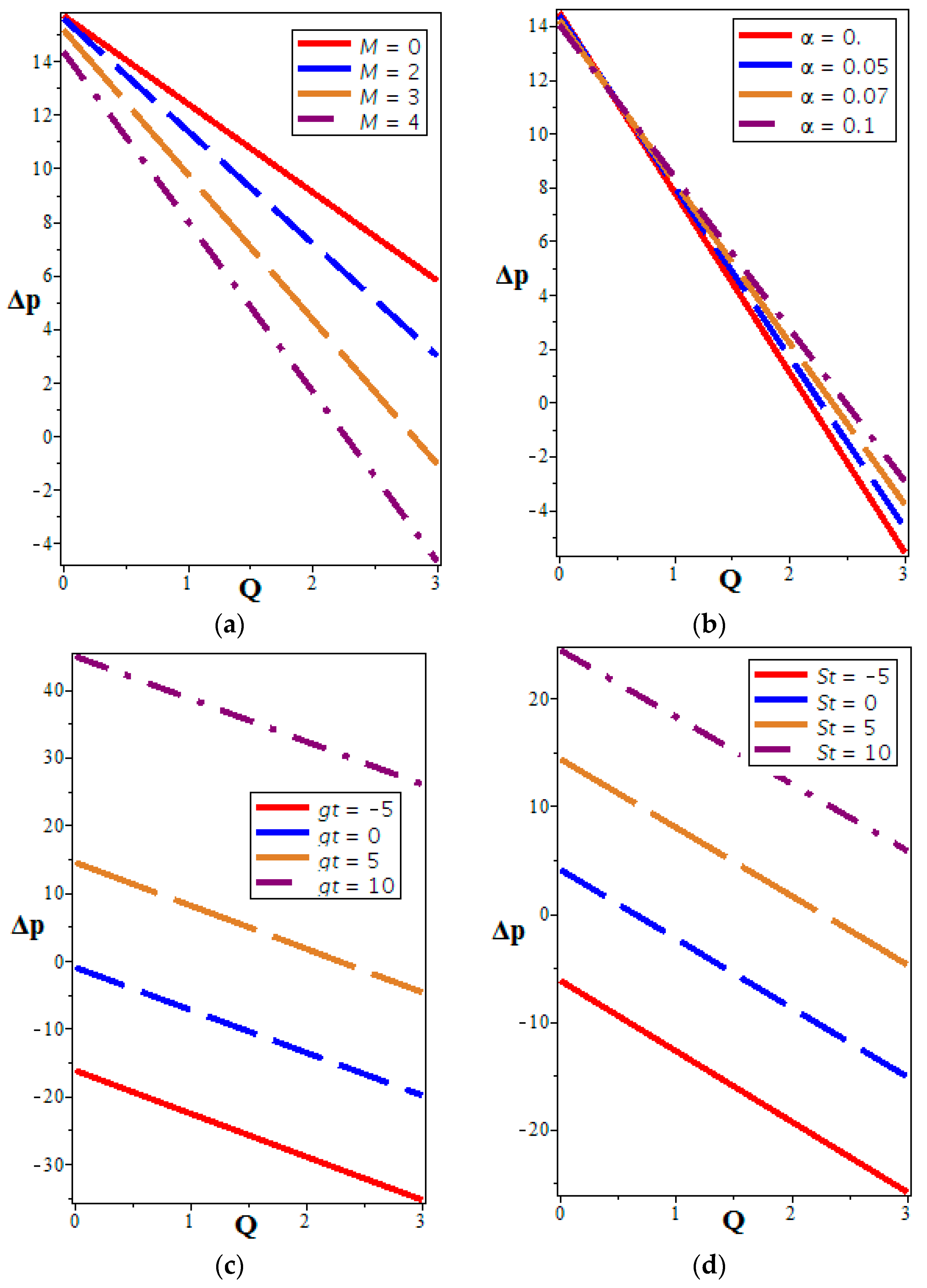
4.2. Pressure Distribution
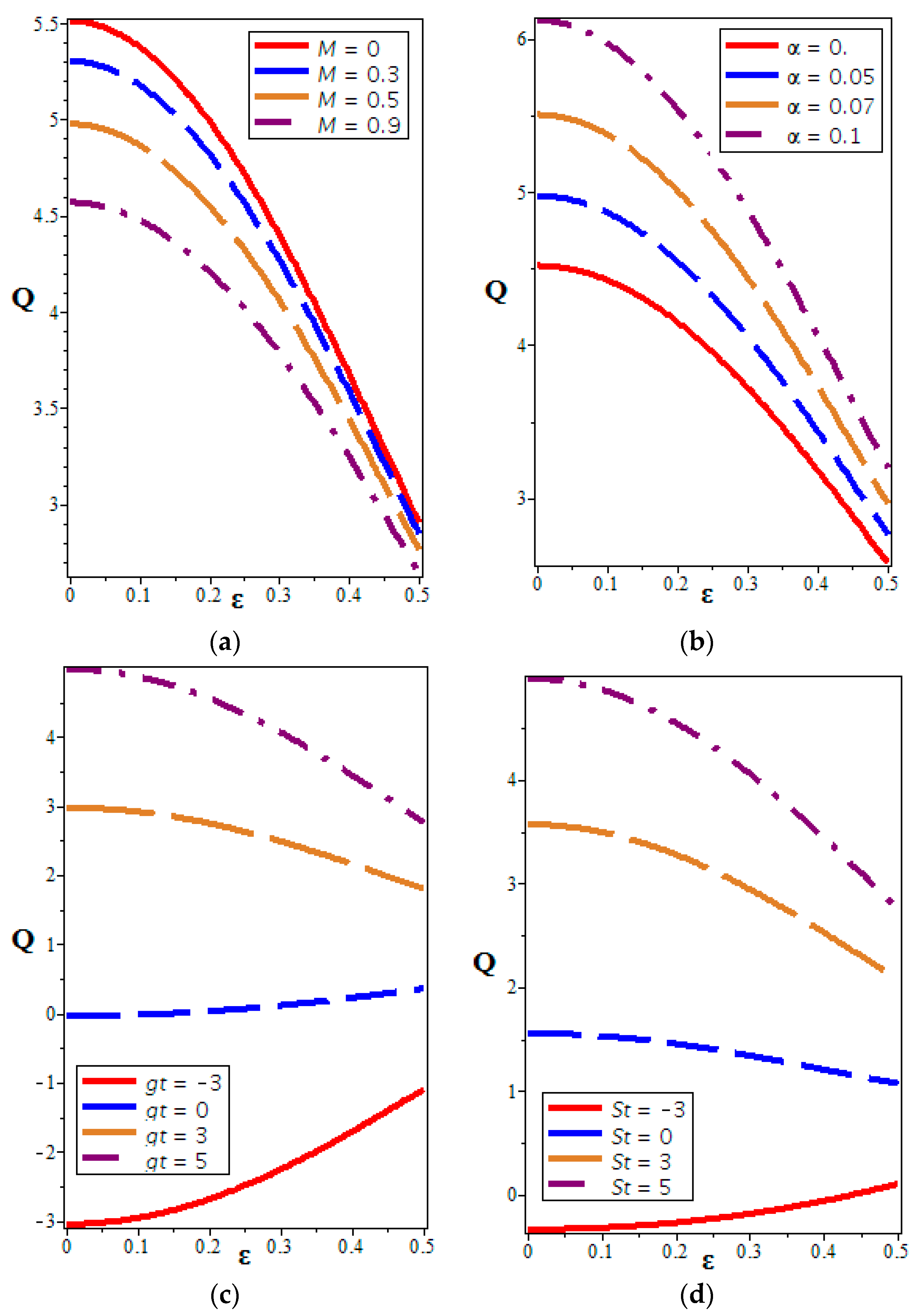
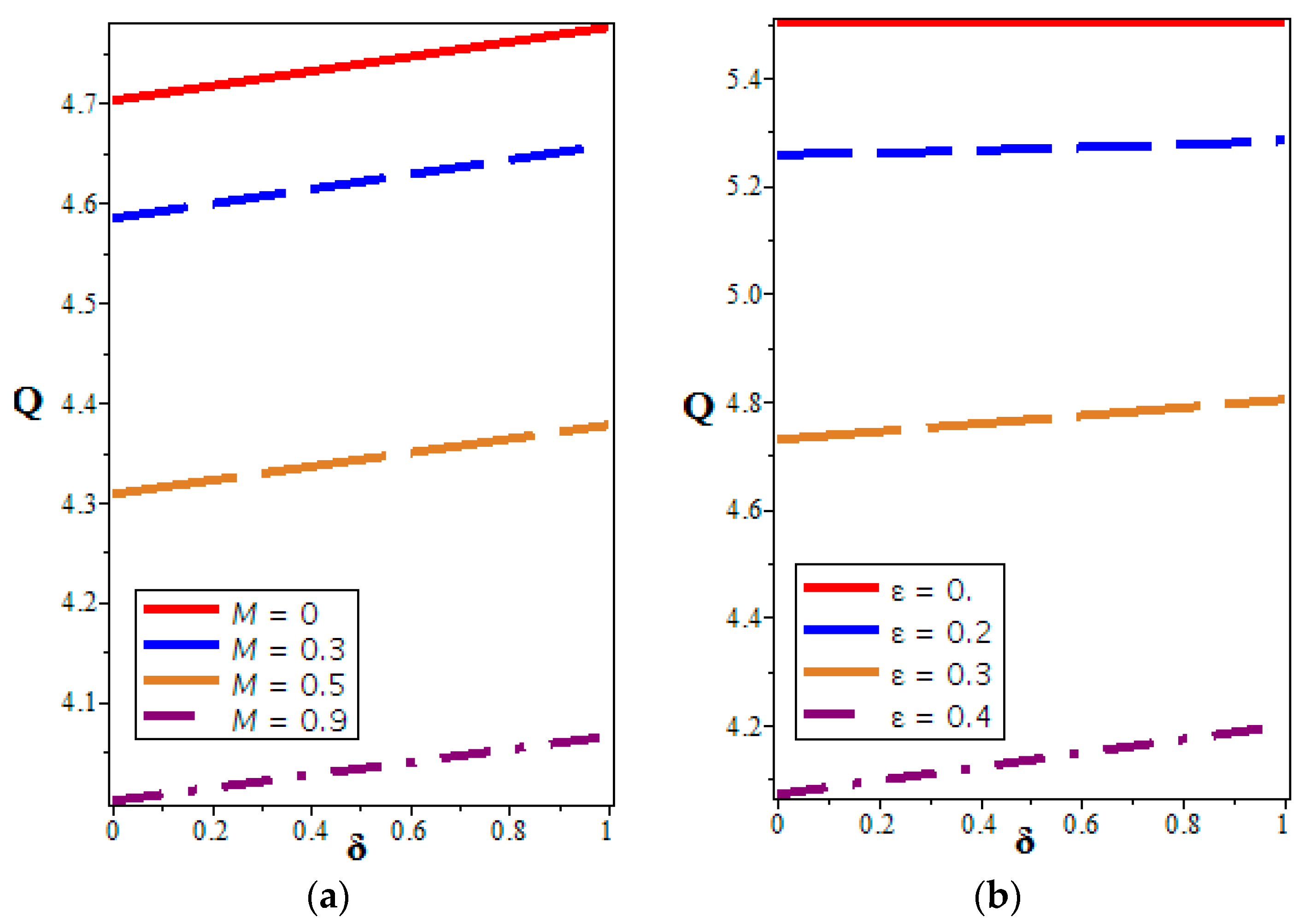
4.3. Volume Flow Rate
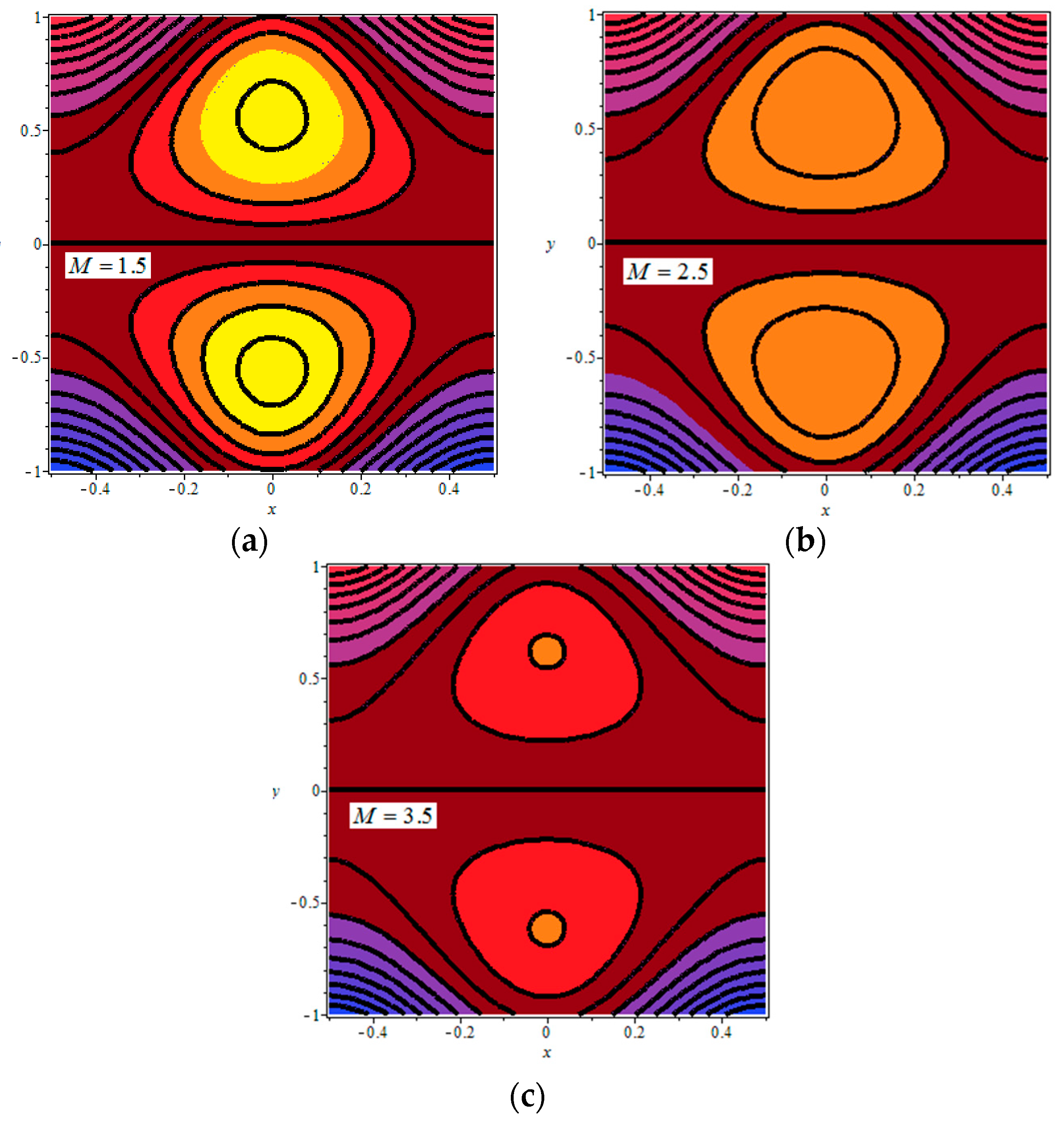
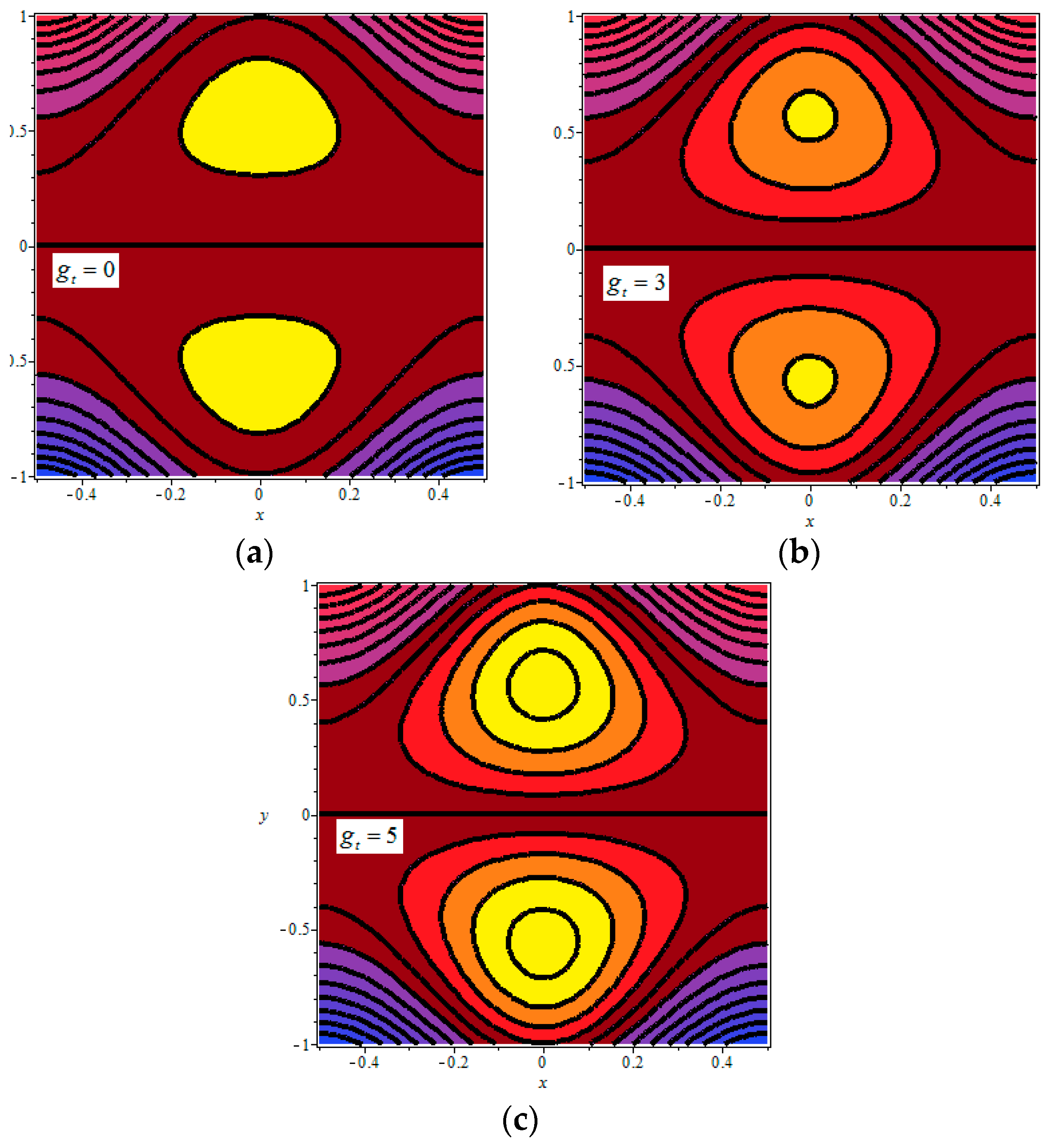
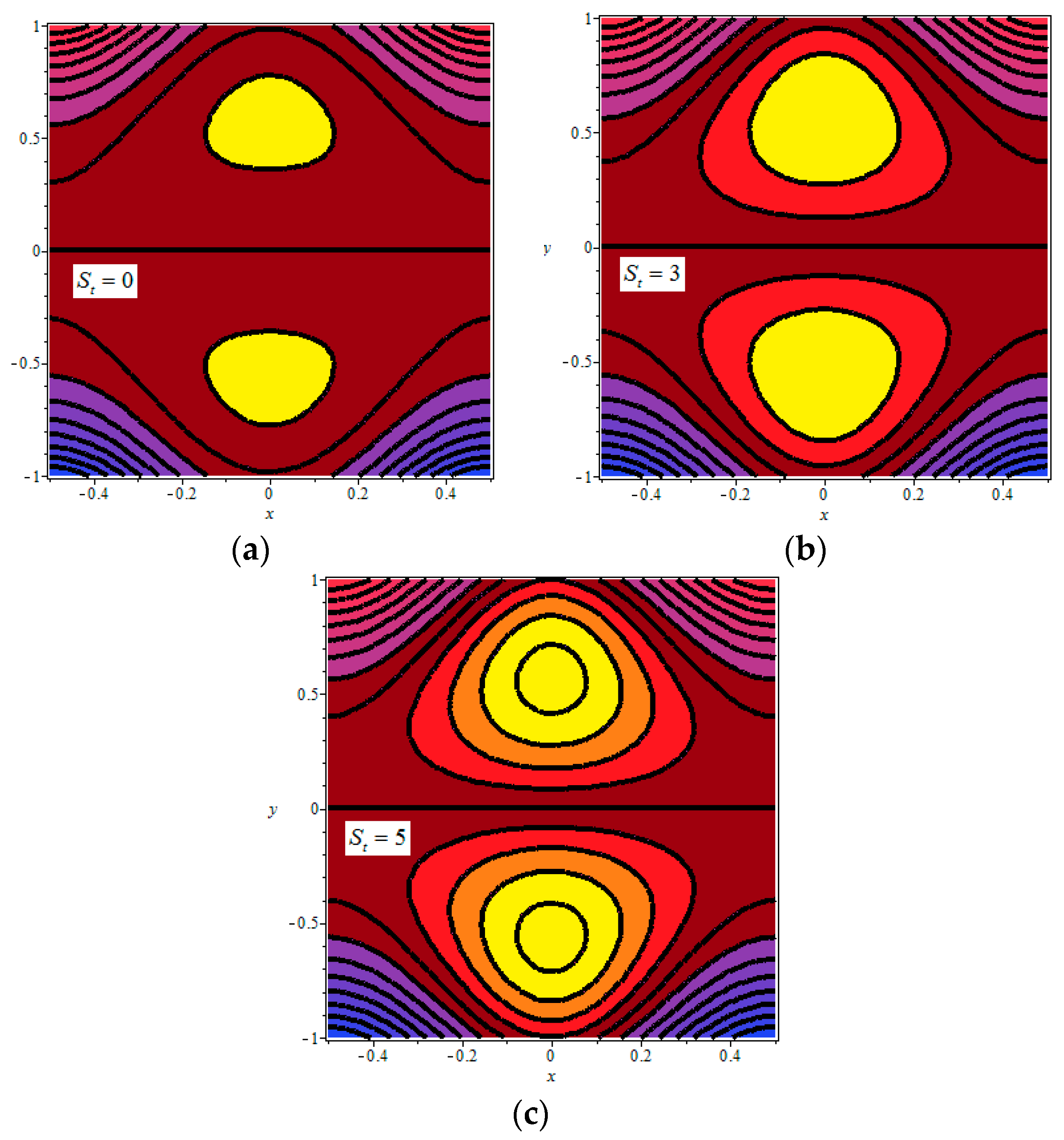
4.4. Trapping Phenomenon
5. Application: Physiological Transport of Semen
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Blake, J.R.; Sleigh, M.A. Mechanics of Ciliary Locomotion. Biol. Rev. 1974, 49, 85–125. [Google Scholar] [CrossRef] [PubMed]
- Liron, N.; Mochon, S. Stokes flow for a stokeslet between two parallel flat plates. J. Eng. Math. 1976, 10, 287. [Google Scholar] [CrossRef]
- Sleigh, M.A. The Biology of Cilia and Flagella; MacMillian: New York, NY, USA, 1962. [Google Scholar]
- Ibanez-Tallon, I.; Heintz, N.; Omran, H. To beat or not to beat: Role of cilia in development and disease. Hum. Mol. Genet. 2003, 12, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Dauptain, A.; Favier, J.; Battaro, A. Hydrodynamics of ciliary propulsion. J. Fluids Struct. 2008, 24, 1156–1165. [Google Scholar] [CrossRef]
- Velez-Cordero, J.R.; Lauga, E. Waving transport and propulsion in a generalized Newtonian fluid. J. Non-Newton. Fluid Mech. 2013, 199, 37–50. [Google Scholar] [CrossRef]
- Brown, J.M.; Witman, G.B. Cilia and Diseases. Biosciences 2014, 64, 1126–1137. [Google Scholar] [CrossRef]
- Hanasoge, S.; Hesketh, P.J.; Alexeev, A. Metachronal motion of artificial cilia. Soft Matter. 2018, 14, 3689–3693. [Google Scholar] [CrossRef]
- Lardner, T.J.; Shack, W.J. Cilia Transport. Bull. Math. Biophys. 1972, 34, 25–35. [Google Scholar] [CrossRef]
- Agrawal, L.; Anawaruddin. Cilia transport of bio-fluid with variable viscosity. Indian J. Pure Appl. Math. 1984, 15, 1128–1139. [Google Scholar]
- Mills, Z.G.; Aziz, A.; Alexeev, A. Beating synthetic cilia enhance heat transport in micro fluidic channels. Soft Matter. 2012, 8, 11508–11513. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Farooq, A.A.; Rana, M.A. Hydromagnetic flow of Newtonian fluid due to ciliary motion in a channel. Magnetohydrodynamics 2014, 50, 109–122. [Google Scholar]
- Nadeem, S.; Sadaf, H. Trapping study of nanofluids in an annulus with cilia. AIP Adv. 2015, 5, 127204. [Google Scholar] [CrossRef]
- Sadaf, H.; Nadeem, S. Influences of slip and Cu-blood nanofluid in a physiological study of cilia. Comput. Methods Programs Biomed. 2016, 131, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Farooq, A.A.; Siddiqui, A.M. Mathematical model for the ciliary induced transport of seminal liquids through the ductuli efferentes. Int. J. Biomath. 2017, 10, 1750031. [Google Scholar] [CrossRef]
- Farooq, A.A. On the transport of epididymal fluid induced by metachronal wave of cilia. J. Eng. Math. 2018, 110, 167–180. [Google Scholar] [CrossRef]
- Ponalagusamy, R. Mathematical analysis of flow of non-Newtonian fluid due to metachronal beating of cilia in a tube and its physiological applications. Appl. Math. Comput. 2018, 337, 545–561. [Google Scholar] [CrossRef]
- Nadeem, S.; Sadaf, S. Metachronal wave of cilia transport in a curved channel. Z. Naturforsch. 2015, 70, 33–38. [Google Scholar] [CrossRef]
- Farooq, A.A.; Tripathi, D.; Elnaqeeb, T. On the propulsion of micropolar fluid inside a channel due to ciliary induced metachronal wave. Appl. Math. Comput. 2019, 347, 225–235. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Beg, O.A.; Khan, Z.H. MHD dissipative flow and heat transfer of Casson fluid due to metachronal wave propulsion of beating cilia with thermal and velocity slip effects under oblique magnetic field. Acta Astronaut. 2016, 128, 1–12. [Google Scholar] [CrossRef]
- Shaheen, A.; Nadeem, S. Metachronal wave analysis for non-Newtonian fluid under Thermophoresis and Brownian motion effects. Results Phys. 2017, 7, 2950–2957. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H. Influence of magnetic field for metachoronical beating of cilia for nanofluid with Newtonian heating. J. Magn. Magn. Mater. 2015, 381, 235–242. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H.; Nadeem, S. Metachronal beating of cilia under influence of Hartmann layer and heat transfer. Eur. Phys. J. Plus 2014, 129, 176. [Google Scholar] [CrossRef]
- Tripathi, D.; Bég, O.A. A study of unsteady physiological magneto-fluid flow and heat transfer through a finite length channel by peristaltic pumping. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2012, 226, 631–644. [Google Scholar] [CrossRef]
- Nadeem, S.; Hayat, T.; Akbar, N.S.; Malik, M.Y. On the influence of heat transfer in peristalsis with variable viscosity. Int. J. Heat Mass Transf. 2009, 52, 4722–4730. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Influence of temperature dependent viscosity on peristaltic transport of a Newtonian fluid: Application of an endoscope. Appl. Math. Comput. 2010, 216, 3606–3619. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Effects of heat transfer on the peristaltic transport of MHD Newtonian fluid with variable viscosity: Application of Adomian decomposition method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3844–3855. [Google Scholar] [CrossRef]
- Shit, G.C.; Ranjit, N.K.; Shina, A. Adomian Decomposition Method for Magnetohydrodynamic flow of blood induced by peristaltic waves. J. Mech. Med. Biol. 2017, 17, 1750007. [Google Scholar] [CrossRef]
- Rathod, V.P.; Laxni, D. Effects of heat transfer on the peristaltic MHD flow of a Binghamfluid through a porous medium in a channel. Int. J. Biomath. 2014, 7, 1450060. [Google Scholar] [CrossRef]
- Manzoor, N.; Maqbool, K.; Beg, O.A.; Shaheen, S. Adomian decomposition solution for propulsion of dissipative magnetic Jeffrey biofluid in a ciliated channel containing a porous medium with forced convection. Heat Transf. Asian Res 2018, 48, 556–581. [Google Scholar] [CrossRef]
- Kefayati, G. Lattice Boltzmann simulation of double-diffusive natural convection of viscoplastic fluids in a porous cavity. Phys. Fluids 2019, 31, 1. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. Three-dimensional Lattice Boltzmann simulation on thermosolutal convection and entropy generation of Carreau-Yasuda fluids. Int. J. Heat Mass Transf. 2019, 131, 346–364. [Google Scholar] [CrossRef]
- Kefayati, G.H.; Hosseinizadeh, S.F.; Gorji, M.; Sajjadi, H. Lattice Boltzmann simulation of natural convection in tall enclosures using water/SiO2 nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 798–805. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical Simulation and Mathematical Modeling of Electro-Osmotic Couette–Poiseuille Flow of MHD Power-Law Nanofluid with Entropy Generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Two-Phase Couette Flow of Couple Stress Fluid with Temperature Dependent Viscosity Thermally Affected by Magnetized Moving Surface. Symmetry 2019, 11, 647. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions. Symmetry 2019, 11, 207. [Google Scholar] [CrossRef]
- Saeed, A.; Islam, S.; Dawar, A.; Shah, Z.; Kumam, P.; Khan, W. Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry 2019, 11, 439. [Google Scholar] [CrossRef]
- Alzahrani, E.; Shah, Z.; Alghamdi, W.; Zaka Ullah, M. Darcy–Forchheimer Radiative Flow of Micropoler CNT Nanofluid in Rotating Frame with Convective Heat Generation/Consumption. Processes 2019, 7, 666. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching sheet. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef]
- Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes 2019, 7, 262. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafee, A.; Khan, I.; Tlili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef]
- Marin, M.; Vlase, S.; Ellahi, R.; Bhatti, M. On the Partition of Energies for the Backward in Time Problem of Thermoelastic Materials with a Dipolar Structure. Symmetry 2019, 11, 863. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids thin film flow of Reiner-Philippoff fluid over an unstable stretching surface with Brownian motion and thermophoresis effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative heat and mass transfer analysis of micropolar nanofluid flow of Casson fluid between two rotating parallel plates with effects of Hall current. J. Heat Transf. 2019, 141, 022401. [Google Scholar] [CrossRef]
- Ameen, I.; Shah, Z.; Islam, S.; Nasir, S.; Khan, W.; Kumam, P.; Thounthong, P. Hall and Ion-Slip Effect on CNTS Nanofluid over a Porous Extending Surface through Heat Generation and Absorption. Entropy 2019, 21, 801. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F. Convective heat transfer of Titania nanofluids of di_erent base fluids in cylindrical annulus with discrete heat source. Heat Tran. Asian Res. 2019, 48, 135–147. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Bessaih, R. Oscillatory Magnetohydrodynamic Natural Convection of Liquid Metal between Vertical Coaxial Cylinders. J. Appl. Fluid Mech. 2016, 9, 1655–1665. [Google Scholar] [CrossRef]
- Saeed, A.; Shah, Z.; Islam, S.; Jawad, M.; Ullah, A.; Gul, T.; Kumam, P. Three-Dimensional Casson Nanofluid Thin Film Flow over an Inclined Rotating Disk with the Impact of Heat Generation/Consumption and Thermal Radiation. Coatings 2019, 9, 248. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Kumam, P.; Shah, Z.; Farooq, A.A.; Nawaz, R.; Dawar, A.; Islam, S.; Thounthong, P. Darcy–Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions. Entropy 2019, 21, 867. [Google Scholar] [CrossRef]
- Shah, Z.; Ullah, A.; Bonyah, E.; Ayaz, M.; Islam, S.; Khan, I. Hall effect on Titania nanofluids thin film flow and radiative thermal behavior with different base fluids on an inclined rotating surface. AIP Adv. 2019, 9, 055113. [Google Scholar] [CrossRef]

| 0 | 0 | 0 | 0 | 0.02204 | 0.00012 |
| 0.01 | 0.1 | 0.1 | 0.05957 | 0.00032 | |
| 0.02 | 0.1 | 0.1 | 0.06443 | 0.00035 | |
| 0.03 | 0.1 | 0.1 | 0.07071 | 0.00038 | |
| 0.1 | 0.01 | 0.1 | 0.1 | 0.05932 | 0.00032 |
| 0.02 | 0.1 | 0.1 | 0.06411 | 0.00034 | |
| 0.03 | 0.1 | 0.1 | 0.07029 | 0.00031 | |
| 0.01 | 0.3 | 0.1 | 0.13398 | 0.00073 | |
| 0.01 | 0.5 | 0.1 | 0.20864 | 0.00113 | |
| 0.01 | 0.1 | 0.3 | 0.06249 | 0.00034 | |
| 0.01 | 0.1 | 0.5 | 0.06569 | 0.00035 | |
| 0.3 | 0.01 | 0.1 | 0.1 | 0.05716 | 0.00031 |
| 0.5 | 0.01 | 0.1 | 0.1 | 0.05208 | 0.00028 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad Farooq, A.; Shah, Z.; Alzahrani, E.O. Heat Transfer Analysis of a Magneto-Bio-Fluid Transport with Variable Thermal Viscosity Through a Vertical Ciliated Channel. Symmetry 2019, 11, 1240. https://doi.org/10.3390/sym11101240
Ahmad Farooq A, Shah Z, Alzahrani EO. Heat Transfer Analysis of a Magneto-Bio-Fluid Transport with Variable Thermal Viscosity Through a Vertical Ciliated Channel. Symmetry. 2019; 11(10):1240. https://doi.org/10.3390/sym11101240
Chicago/Turabian StyleAhmad Farooq, Ali, Zahir Shah, and Ebraheem O. Alzahrani. 2019. "Heat Transfer Analysis of a Magneto-Bio-Fluid Transport with Variable Thermal Viscosity Through a Vertical Ciliated Channel" Symmetry 11, no. 10: 1240. https://doi.org/10.3390/sym11101240
APA StyleAhmad Farooq, A., Shah, Z., & Alzahrani, E. O. (2019). Heat Transfer Analysis of a Magneto-Bio-Fluid Transport with Variable Thermal Viscosity Through a Vertical Ciliated Channel. Symmetry, 11(10), 1240. https://doi.org/10.3390/sym11101240







