Abstract
The progress in the research of various areas of robotics, artificial intelligence, and other similar scientific disciplines enabled the application of multi-robot systems in different complex environments and situations. It is necessary to elaborate the strategies regarding the path planning and paths coordination well in order to efficiently execute a global mission in common environment, prior to everything. This paper considers the multi-robot system based on the cloud technology with a high level of autonomy, which is intended for execution of tasks in a complex and crowded environment. Cloud approach shifts computation load from agents to the cloud and provides powerful processing capabilities to the multi-robot system. The proposed concept uses a multi-robot path planning algorithm that can operate in an environment that is unknown in advance. With the aim of improving the efficiency of path planning, the implementation of Multi-criteria decision making (MCDM) while using Full consistency method (FUCOM) is proposed. FUCOM guarantees the consistent determination of the weights of factors affecting the robots motion to be symmetric or asymmetric, with respect to the mission specificity that requires the management of multiple risks arising from different sources, optimizing the global cost map in that way.
1. Introduction
Path planning is of fundamental importance in mobile robotics. Algorithms for path planning are intendend to generate a collision free path between the start and the goal point within the configuration space of the robot, satisfying, at the same time, a certain optimization criteria. Configuration space implies the concept that completely specifies the robot location in its workspace including specification of all degrees of freedom [1]. Path planning for multi-robot systems is much harder than for a single robot, since the size of the joint configuration space grows exponentially in the number of robots [2]. Consequently, algorithms for single robot path planning cannot be directly applied to the multi-robot systems.
The existing methods for multi-robot path planning, from the aspect of implemented algorithms, can be divided into two general approaches [3]. The coupled approach regards the group of robots as a single entity, such that all paths are planned simultaneously in a joint or composite configuration space and therefore could guarantee completeness, but these solutions do not scale well with large robot teams and they usually cannot be solved in real-time. The decoupled approach first computes separate paths for the individual robots and then employs different strategies to resolve possible conflicts. These solutions are usually fast enough for real-time applications, but they can not guarantee completeness and the robots might easily get stuck in common deadlock situations.
Planning the motion of a team of robots that perform tasks in a real environment involves a large number of challenges. Firstly, the real environment is usually highly dynamic place, so it is difficult to provide a precise planning map (the current map is out of date for a short period of time). Secondly, the time that is available to robots for deliberation is usually very limited—they must quickly make decisions and act according to them.
This paper considers the multi-robot system with a high level of autonomy that is based on the cloud technology and intended for execution of tasks in a complex and crowded environment. A common approach for path planning in robotics is to integrate an approximate, but fast global planner with a precise local planner [4]. This mean that, in a crowded environment, the global planner usually computes paths that ignore the crowds. Subsequently, the local planner takes into account the crowds, as well as kinematic and dynamic constraints of the robot and creates feasible local trajectories. However, if a global planner totaly ignores the costs of navigation through a crowd, such a plan might prove inefficient [5]. Moreover, complex environments may have, besides crowds and static obstacles, other characteristics that influence the motion of robots and that are desirable to consider during the path planning on the global level.
With the aim of taking into consideration the crowds in the initial phase of planning on global level (to form a global cost map), as well as other conditions of the environment, the implementation of multi-criteria decision making (MCDM) is presented in this paper. Particular attention is paid to the problem of determining the criteria weights and, for that purpose, the FUCOM [6] is proposed. The FUCOM belongs to new methods for the determination of the weight coefficients of criteria in MCDM. The application of this method is growing due to its advantages that will be described in detail in this paper. Some implementations of FUCOM can be found in [7,8,9,10]. According to our knowledge, the FUCOM-based approach has not been used so far for path planning in robotics.
The necessary environmental information for MCDM according to this paper is provided from external datasets in combination with data that were collected with robots onboard sensors. Another approach is only based on robots online learning of the environment, but this technique will be the topic of our next research. For global path, a planning graph-based D* Lite algorithm is used [11]. It is adjusted with the aim of application for the multi-robot path planning. Decoupled approach is implemented with a paths coordination strategy.
The goal of proposed approach is to ensure a global cost map for the computing of initial paths, which is similar to the real one as much as possible. In this way, we will try to reduce the total cost of the paths i.e., to manage the risks in path planning in crowded environment, keeping the robots at a certain safe distance from the crowd, but while taking into consideration, at the same time, other conditions of the environment. The application of FUCOM method provides an efficient strategy for solving this problem.
This paper is organized, as follows. Section 2 presents an overview of selected papers that deal with graph-based search in path planning, crowd-sensitive path planning, as well as using MCDM in the forming of cost map. Section 3 describes system architecture and its main “components”—D* Lite algorithm and FUCOM method. Section 4, Section 5 and Section 6 introduce the model and procedure for the forming of cost map based on MCDM while using FUCOM, describing the path planning in simulated environment, and giving discussions of the results. Finally, Section 7 presents conclusions.
2. Related Work
Similar to the path planning problem for single robot, graph search methods that are based on the A* algorithm are frequently used in path planning for multi-robot systems. In [12], the M* algorithm is proposed that employs so-called subdimensional expansion to plan in the joint configuration space, while using A* as the underlying path planning algorithm. It starts by planning in low-dimensional subspace representing configuration spaces of individual robots and increases the dimensionality when the need for coordination is detected. A method for optimizing the priorities for decoupled and prioritized A*-based path planning algorithm for multi-robot system is presented in [13]. This method is a randomized approach that repeatedly reorders the agents to find a sequence for which a solution can be computed and to minimize the overall path lengths. A lattice-based method to multi-robot path planning for non-holonomic vehicles with implemented A* algorithm is presented in [14]. This method generates kinematically feasible motions for multi-robot system. In [15], the A* algorithm in combination with potential field approach is used for path planning of a given set of mobile robots, while moving and avoiding obstacles in a chained fashion. The [16] focuses on consideration of path planning and controlling a group of autonomous agents to accomplish multiple tasks in dynamic environments. It represents the approach in researching that emphasizes the influence of implemented multi-robot task allocation approach on the efficiency of path planning.
The extension of A*, D* algorithm, is a well-known informed incremental graph search algorithm for partially-known environment. D* Lite is an alternative to D* that is at least as efficient as D*, but is algorithmically different and simpler [17]. It is one of most popular path planning algorithms, which is extensively used for mobile robot navigation in a complex environment [18]. The D*-based global path planner has been successfully demonstrated in a lot of practical applications [19,20,21]. Several robots have used the D* algorithm in combination with the Morphin local planner (which version provides local navigational autonomy for the NASA Mars Exploration Rovers [22]) to drive autonomously on rough terrain over long distances [23,24,25]. The D* algorithm is also successfully used as a planner for multi-robot systems [26], as well as D* Lite [27,28].
Crowd-sensitive path planning for single robot or multi-robot systems has been a very popular topic in the robotics community in recent years. In [5] and [29], four A*-based crowd-sensitive path planners (CSA*, Flow-A*, Risk-A*, and CUSUM-A*) are presented. All of them are intended for global navigation in a crowded environment, making the assumption that the robot is only limited to onboard two-dimensional (2D) range sensors. This approach formulates the problem as Bayesian online learning. Each cell in the crowd density map is modeled as a Poisson distribution with rate λ. A Poisson distribution is commonly used to model natural discrete events, including crowd counting [30]. Initially, when the robot has no information regarding the crowd, each of these algorithms generate plans that are identical to those of A*. However, as the robot travels and observes the crowd, it updates its cost map. Once enough information is gathered through map updates, the cost maps force the planner to efficiently avoid crowded areas. CSA* simply avoids crowded areas. On other side, Flow-A* learns and incorporates the direction of crowd flow in the environment to allow for the robot to follow social norms (avoid going against the flow of the crowd). However, people usually change their behavior in the presence of robots. In such scenarios, the learned model should account for such interactions. Risk-A* uses that approach and improves safety. To detect and adjust for temporal changes in crowd patterns, a statistical change detection technique can be used. These methods allow for CUSUM-A* to forget old models and learn new ones that reflect the current state of the environment. CSA*, Flow-A*, Risk-A*, and CUSUM-A* are intended primarily for indoor crowded environments, but a similar approach can be applied in the outdoor crowded environment. However, they only take one factor that influences the motion of robots on the global level into account. In reality, there are usually more such factors.
Dynamic decision support system (DSS) for mission planning and control of autonomous underwater vehicles (AUVs) in complex environments with real-world operational constraints is proposed in [31]. The component of DSS that is intended to reduce the AUV path solution space in complex environments is based on a MCDM while using the analytic network process (ANP) and fuzzy logic. The ANP is used to define the importance weight of the path planning decision factors (ten factors). The ANP is chosen because it is a more general form of the analytic hierarchy process (AHP). ANP does not require independence and it allows for decision factors to ‘influence’ or ‘be influenced’ by other factors in the model. Although this method is applied to planning and control of underwater gliders, it was concluded that the presented approach has much broader applications to unmanned vehicles in general.
3. System Overview
Some of typical forms of the application of multi-robot systems include the following: transport of goods and materials into industrial centers and stores, cleaning of closed and open areas, participation in search and rescue missions, reconnaissance, elimination of the consequences of emergencies, execution of military missions, etc. Prior to everything it is necessary to elaborate well the strategies regarding the allocation of tasks among the robots, path planning, and paths coordination in order to efficiently execute a global mission in any kind of common environment.
With the aim of a wider application of multi-robot systems, agents are supposed to be as simple as possible, energy efficient, low-cost, but still smart enough to reliably perform an assigned task with a high level of autonomy. These two goals are contradictory to each other. Cloud computing is a key enabler for solving these challenges. The idea is to design and create the architecture in which the multi-robot system uses the benefits of converged infrastructure and the resources of the cloud (information, memory, communication, and other) [32,33,34,35,36]. In practice, this usually means that on the cloud level gathering of information and their processing is performed, while the robots, as cloud service users, obtain only data and commands necessary for a direct execution of the allocated tasks. The overview of cloud architecture and whole system considered in this paper is presented in Figure 1.
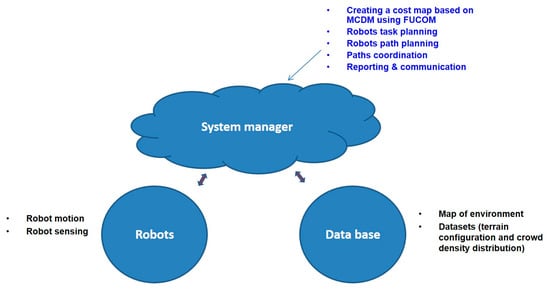
Figure 1.
Block diagram of the system architecture.
The “data base” module provides a map of the environment, as well as information regarding terrain configuration and crowd density distribution.
“Robots” module simulates the motion of robots in accordance to the given commands and data, as well as their sensor activities (environment perception). Robots have a mode for an emergency stop in case of unpredicted situations. The proposed multi-robot system in this project consists of three robots (homogenous system).
The “system manager” module is a cloud level, i.e., it provides the execution of the most demanding tasks necessary for functioning of the multi-robot system, such as: creating a cost map based on MCDM while using FUCOM, robot task planning, path planning/replanning of each robot, paths coordination, solving the conflict situations, and mapping updating based on data collected with robots’ sensors.
Figure 2 provides allocation of the computation time between the modules in one iteration of randomly chosen scenario.
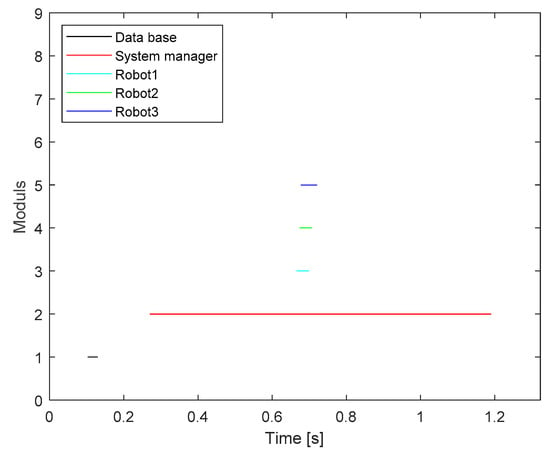
Figure 2.
Gantt chart of computation time allocation between the modules.
Out of the Figure 2, it may be seen that this approach significantly unloads the robots at the expense of using the cloud resources. The “system manager” executes the most demanding operations related to creating a global cost map that is based on MCDM using FUCOM, robots task planning, paths planning and replanning, paths coordination, etc. Only data and commands that are necessary for a direct execution of given tasks are delivered to the robots as the users of the cloud services. As a part of sequences that are related to the robots activity, the cumulative time of their motion and perception with their own sensors is shown.
As the described architecture is of a modular type, it can be expanded in many ways and adjusted for other scenarios. In that sense, the architecture can be, depending on the actual need, simply adjusted for the multi-robot system with a larger number of robots of homogenous or heterogenous structure.
3.1. D* Lite Algorithm
The environment may be represented as a 2D traversability grid with uniform resolution, in which each cell has allocated a real-valued traversal cost larger than zero, reflecting the difficulty of navigation in the appropriate area in order to plan the robot motion. This traversability grid is usually approximated as a discrete graph and after that some graph-based search technique can be applied for path planning. One way to do this is to allocate the node to each cell center, with the edges that connect the node to each adjacent cell center (node). The cost of each edge is a combination of the traversal costs of the two cells that it crosses through and the length of the edge [4].
While keeping this in mind, suppose that S is a set of nodes in one such graph. Each node s, where s ∈ S, represents one cell of the map and it is associated with nodes representing neighboring fields. The set of successors of node s is denoted by Succ(s), while the set of predecessors of node s is denoted by Pred(s). For any pair of nodes s, s’ ∈ S, where s’ ∈ Succ(s), we define cost of transition from s to s’, denoted by c(s, s’), to be positive: 0 < c(s, s’) ≤ ∞. In general case c(s, s’) ≠ c(s’, s). The cost of transition from node s0 to node sк, where s0, sк ∈ S, is defined as the sum of the sequential cost of transitions between neighboring nodes (edge costs) in the set of nodes {s0, s1, …, sк−1, sк}, i.e., as (c(s0, s1) + … + c(si−1, si) + … + c(sk−1, sk)), where c(si−1, si) represents the cost of moving from si−1 to si and si ∈ Succ(si−1), 1 ≤ i ≤ k. The least-cost path from s0 to sк is denoted with c*(s0, sк). For s0 = sк, we define c*(s0, sк) = 0.
The goal of least-cost path search algorithms, such as A*, is to find a path from sstart to sgoal whose cost is minimal, i.e., equal to c*(sstart, sgoal). D* Lite algorithm, as well as A*, during operation forms and maintains (updates) the value of four functions that describe cell s:
- g(s)—the minimum cost of moving from sstart to s, i.e., c(sstart, s), found so far;
- h(s) or heuristic value—estimates the minimum cost of moving from s to sgoal. Using heuristic value ensures that the search tree is directed towards the most optimistic cells in terms of belonging to the optimal path from start to goal cell. This speeds up the search.
- f(s) = g(s) + h(s)—estimates the minimum cost of moving from sstart via s to sgoal; and,
- parent(s) or parent pointer—points to the predecessor s’ of s from which is derived g(s), s’ is called the parent of s. The parent pointers are used to extract the path after the search terminates.
Moreover, in addition to the above functions, D* Lite, as well as A*, forms and maintains (updates) a priority queue or list OPEN. The OPEN list contains all inconsistent cells detected so far during the search, which are candidates for further processing in terms of the propagation of the inconsistency. A cell s becomes inconsistent if, during the search, its g(s) is reduced. At each step, the algorithm adds to the search tree the cell from the OPEN list, which, at that moment, has the smallest key value (for A* algorithm key(s) = f(s)), until it reaches the goal cell. By processing the cells from the OPEN list in the order corresponding to the minimum value of the key, the algorithm extends from the start to the goal cell the path that has the lowest total cost. Therefore, the cells that were taken from the OPEN list and processed in this way are said to be expanded. The process itself is called the expansion of the cell.
A* algorithm, unlike D* Lite, implies that the search for a solution is always done over the same graph and with unchanged transition costs between the cells. In the real world, however, there are usually situations in which at the moment of starting the motion, the environment in which the robot is sent is only partially known. In addition, dynamic changes of the environment might appear or occur during the robot motion. In such situations, the path planning process usually starts with the assumption that all areas that are unknown at the initial moment are free to pass, while the robot during the motion by its sensors explores the terrain and collects information for map updating. The changes in the map involve the changing of the graph that the algorithm uses to generate a path. In such circumstances, it may happen that the solution that is reached by the A* algorithm is not optimal or even valid. Therefore, А* algorithm in this case calculates the path from scratch (in regard to the current position of the robot), without using the results from the previous iterations. In these scenarios, the class of algorithms known as incremental algorithms is efficient, while bearing in mind that, in the situation when new information occurs, they use the search results from the previous iterations to the maximum possible extent, in order to correct the current or find a new valid solution. D* Lite belongs to this class of algorithms. It can be said that D* Lite is extension of A*, which is able to cope much more efficiently with changes to the graph used for planning.
To be able to do this, in addition to the g value D* Lite forms and maintains (updates) for each cell one-step lookahead cost rhs, that represents the path cost estimate that is derived from looking at the g values of its neighbors: rhs(s) = mins’∈Succ(s)(c(s, s’) + g(s’)) or zero if s is the goal cell. In implementation, each cell maintains a pointer to the cell from which it derives its rhs value, so the robot should follow the pointers from its current cell to pursue an optimal path to the goal.
A cell is consistent if its g and rhs values are equal, otherwise it is inconsistent (it is called overconsistent if g > rhs and underconsistent if g < rhs). Overconsistent cells propagate path cost reductions, while underconsistent cells propagate path cost enlargements through the environment.
Like A*, D* Lite algorithm also uses a heuristic to focus and to speed up the search. D* Lite also maintains a priority queue or list of inconsistent cells (OPEN) to be expanded in the current search iteration. The prioritization of cells in the OPEN list during the expansion is also done based on the assigned key value. However, unlike the A* algorithm, in D* Lite the key value has the form of a row vector 1 × 2: key(s) = [k1(s), k2(s)] = [min(g(s), rhs(s)) + h(sstart, s); min(g(s), rhs(s))]. The key value of the cell s is less than the key value of the cell s’, denoted key(s) ≤ key(s’), which means that s is a cell with a higher priority, if k1(s) < k1(s’) or both k1(s) = k1(s’) and k2(s) ≤ k2(s’).
The measure of search efficiency for graph-based algorithms is a number of expanded cells [37,38]. A sloution is reached much more quickly by expanding a fewer cells.
D* Lite generates an initial solution in a similar manner as the backward version of A* algorithm (i.e., search is performed from sgoal to sstart). If the robot detects changes in the environment during the motion (i.e., the cost of some edge is altered), D* Lite first updates the rhs values of all of the cells directly affected by the changed edge cost. After that, priority queue OPEN is updated, i.e., the algorithm places new inconsistent cells onto the queue. Subsequently, the cells are expanded from the updated OPEN list according to the prioritization based on the assigned key value. This ensures the propagation of inconsistency. In this way, D* Lite algorithm checks the validity of the current path and corrects it if necessary. D* Lite is efficient because it processes only those cells that are directly affected by the changes. In other words, while using the previously obtained results to calculate the corrected path, D* Lite does not replan from scratch over the entire graph as A*. As a result, it can be up to two orders of magnitude more efficient than A*.
Figure 3 presents the pseudocode of basic version of D* lite [39].

Figure 3.
D* Lite algorithm (basic version).
The principle of D* Lite that is presented in Figure 3 can be summarized as follows:
D* Lite performs searches by assigning the current cells of the robot and target to the start and goal cells of each search, respectively. The initialization process sets both the initial g and rhs values of all cells except the goal cell to infinity (lines 15–16). The goal cell is inserted into the priority queue (OPEN) because it is initially inconsistent (line 17). D* Lite then finds a cost-minimal path from the start cell to the goal cell (line 19). In real implementation line 20 means that the computed path is being traversed by the robot (the robot makes a steps transition cell by cell along the path i.e., sstart is changing). As the robot travels, it, at the same time, observes the environment. If changes in edge costs in some robot step are detected, D* Lite updates the rhs values of each cell immediately affected by the changed edge costs and places those cells that have been made inconsistent onto the OPEN queue (lines 21–23). D* Lite then propagates the effects of these rhs values changes to the rest of the cell space and checks/replans the path through recalling ComputePath() function (line 19) until it terminates again. Line 18 in real implementation means that the whole process ends when it becomes sstart = sgoal.
As we said earlier, in this paper, the D* Lite algorithm is adjusted with the aim of application for the multi-robot path planning. The decoupled approach is implemented with the paths coordination strategy. Robots share the knowledge about the environment through the cloud in order to perform a mission cooperatively.
3.2. Full Consistency Method (FUCOM)
The FUCOM method is used to define the importance weight of the decision factors. FUCOM is one of the newer models that is, like Analytical Hierarchy Process (AHP) and Best Worst Method (BWM), based on the principles of pairwise comparison of criteria and the validation of results through a deviation from maximum consistency [6]. FUCOM is a model that, to some extent, eliminates the drawbacks of the BWM and AHP models. Benefits that are determinative for the application of FUCOM include a small number of pairwise comparison of criteria (only n − 1 comparison, n = number of criteria), the ability to validate the results by defining the deviation from maximum consistency (OMK) of comparison, and taking into consideration the transitivity during pairwise comparison. As well as with other subjective models for determining the weight of the criteria (AHP, BWM, etc), there is a subjective influence of the decision-maker in the FUCOM model on the final values of the weight of the criteria. This particularly refers to the first and second steps of FUCOM, in which decision-makers rank the criteria according to their personal preferences and perform a pairwise comparison of ranked criteria. However, unlike other subjective models, FUCOM showed minor deviations in the obtained values of the weight of the criteria from the optimum values [6]. Additionally, the methodological procedure of FUCOM eliminates the problem of redundancy of pairwise comparison, which is present in some subjective models for determining the weight of the criteria.
Assume that there are n evaluation criteria in a multi-criteria model that are denoted as wj, j = 1, 2, …, n and that their weight coefficients need to be determined. Subjective models for determining weights based on pairwise comparison of criteria require the decision-maker to determine the degree of influence between the criteria. In accordance with the defined settings, the next section presents the FUCOM algorithm, Figure 4 [6].

Figure 4.
FUCOM algorithm.
4. Multi-Criteria Decision Making Model and Procedure
We use a grid-based approach for map representation in order to navigate through the environment. This means that the map of area of interest is converted into 2D uniform grid of squares, referred to as ‘cells’. Each cell is assigned a price that depends on four criteria.
Criteria (factors):
- C1—the convenience of the terrain configuration for robots motion, a 0–10 scaled grading scheme (0 = ‘favorable terrain’ to 10 = ‘extremely unfavorable terrain’),
- C2—the risk related to the loss of communication with the cloud, a 0–10 scaled grading scheme (0 = ‘low risk’ to 10 = ‘high risk’),
- C3—the risk related to the human-robot interactions (slows down the robots motion), a 0–10 scaled grading scheme (0 = ‘low risk’ to 10 = ‘high risk’), and
- C4—the robot safety related to conditions dependent on specific mission (0 = ‘safe conditions’ to 10 = ‘extremely unsafe conditions’).
The team of experts in charge of mission planning is responsible for decision-making. The assumption is that experts have years of experience in the field of robot path planning, as well as that they have access to information regarding conditions of the environment in which the robots move. Defining wij as the weight of factor j defined by expert i (i = 1,2, …, I; j = 1,2, …, J) and Cmij as the score of jth factor for cell m provided by the ith expert (i = 1,2, …, I; j = 1,2, …, J; m = 1,2, …, M), we find Cm, the ‘path planning index’ of the mth cell. Here, equation (1) is used to aggregate the score of jth factor given by I experts for cell m, as well as its total score for all J factors:
The final path planning indices are next converted into a colour-coded system that reflects the risk level in a cell. In this way, the map is composed of green, yellow, orange, and red risk categories. Green is the lowest risk level that represents cells with 0 ≤ Cm ≤ 2.5. Yellow marks a moderate risk level and it represents cells with 2.5 ≤ Cm ≤ 5. Orange indicates a high risk and it represents cells with 5.0 ≤ Cm ≤ 7.5 and red symbolises severe risk and represents cells with 7.5 ≤ Cm ≤ 10. Each risk level implies its unique cost of transition through the cell. This approach provides risk-sensitive planning.
Data processing according to the previously mentioned steps can take considerable amount of computing time. Hence, forming the datasets of traversal costs at the cloud level in the phase of preprocessing using its resources is proposed.
5. Simulation and Results
Crowds may behave differently in the presence of the robots. Some people make way for the robots, others hinder their motion. Areas that are attractive to children can be more risky than other crowded areas. In any case, approaching the robot to a person or vice versa unacceptably close represents a risky action to a greater or lesser extent.
The global cost map here is represented as a discrete grid with 100 × 100 cells. A complex environment was simulated to evaluate the performance of the proposed concept. In addition to static obstacles, the presence of pedestrians in initially free cells in the environment was simulated, with the probability of occurrence in proportion to the scores of appropriate criteria.
In such generated scenarios, we evaluated the path planning performance under D* Lite without MCDM and D* Lite with MCDM by total travel distance and total number of risky actions (those that brought the robot within distance of two cells from a pedestrian). The robot should do so quickly, travel relatively short distances, avoid collisions, and take relatively few risks. One such scenario is presented in Figure 5, with specifications as follows.
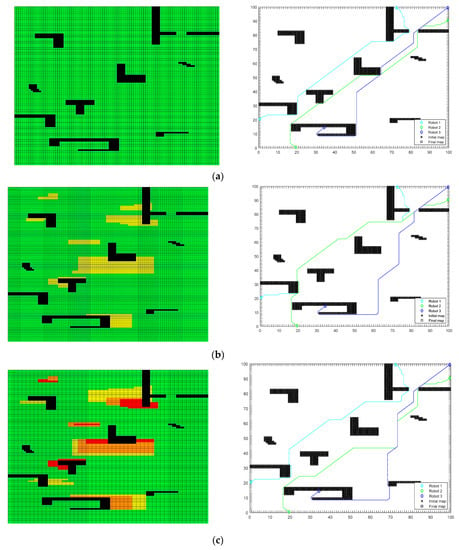
Figure 5.
Scenario cost map (left) and path planning results (right): (a) D* Lite without multi-criteria decision making (MCDM); (b) D* Lite with MCDM1; and, (c) D* Lite with MCDM2.
Start and goal positions of robots:
- start1 (x, y) = (1, 21), goal1 (x, y) = (73, 100)
- start2 (x, y) = (20, 1), goal2 (x, y) = (100, 91)
- start3 (x, y) = (35, 15), goal3 (x, y) = (100, 100).
The first MCDM model—D* Lite with MCDM1
Determining criteria wegihts:
Step 1. The decision-makers performed the ranking of the criteria: C3 ≥ C2 ≥ C1 > C4.
Step 2. The decision-makers performed the pairwise comparison of the ranked criteria from Step 1. The comparison was made with respect to the first-ranked C3 criterion. The comparison was based on the scale . Thus, the priorities of the criteria () for all of the criteria ranked in Step 1 were obtained (Table 1).

Table 1.
Priorities of criteria.
Based on the obtained priorities of the criteria, the comparative priorities of the criteria are calculated: and .
Step 3. The final values of weight coefficients should meet the following two conditions: (1) The first condition: and ; (2) The second condition: The final values of the weight coefficients should meet the condition of mathematical transitivity, i.e., that and . The final model for determining the weight coefficients can be defined as:
By solving the problem with Lingo 17.0 software (Chicago, IL, USA), the final values of the weight coefficients and deviation from full consistency (DFC) of the results are obtained.
The second MCDM model—D* Lite with MCDM2
Determining criteria wegihts:
Step 1. Ranking of the criteria: C3 > C2 > C1 ≥ C4.
Step 2. In the second step, the decision-maker performed the pairwise comparison of the ranked criteria from Step 1. The comparison was made with respect to the first-ranked C3 criterion. The comparison was based on the scale . Thus, the priorities of the criteria () for all of the criteria ranked in Step 1 were obtained (Table 2).

Table 2.
Priorities of criteria.
Based on the obtained priorities of the criteria, the comparative priorities of the criteria are calculated: , , and .
Step 3. Nonlinear model constraints: (1) The first constraint: , , and ; (2) The second constraint: The final values of the weight coefficients should meet the condition of mathematical transitivity, i.e., that and . The final model for determining the weight coefficients can be defined as:
By solving the problem with Lingo 17.0 software, the final values of the weight coefficients and the DFC of the results are obtained.
Table 3 presents the results of the experiment, averaged over 15 trials.

Table 3.
D* Lite with MCDM improves navigation performance.
6. Discussion
Initially, when there is no information about the crowds, plans that are identical to basic version of D* Lite are generated and they can move robots directly through the crowd, as is shown in Figure 5a. Crowds can slow, divert, or halt the robot, and thereby increase its travel time and risky actions. On the other side, forming the global cost maps that were based on the gathered information about the environment, expert knowledge, and MCDM using FUCOM force the planner to tend to avoid crowded areas, but while taking into consideration at the same time other conditions of the environment—Figure 5b,c.
Experts, according to their personal preferences, determine the values of the criteria for cells in grid map (by analyzing available information about the environment), as well as the weights of the criteria (with respect to the particular situation and mission). It is logical that, for maps with a large number of cells, the value of the criteria will be assigned at the level of the regions, where the region includes a group of cells with the same or similar value of the considered criterion by the expert preference.
The application of FUCOM provides an efficient determination the weights of factors that decisively affect the robots motion to be symmetric or asymmetric, with respect to the particular environment and having in mind the mission specificity and objectives, optimizing the global cost map in that way. This refers to the fact that, in most situations, the robots motion in a crowded environment is subordinated to the pedestrians, while certain missions require emergency response of the robots, when they are in some way assigned higher priority in movement. This must be taken into account when defining the global cost map for path planning.
Based on Table 3, it can be concluded that the distance traveled was not statistically significantly different with any of the tested approaches. The most significant differences are in risky actions: D* Lite with MCDM2 took fewer risky actions than D* Lite without MCDM for 18.9%, while D* Lite with MCDM1 took fewer risky actions than D* Lite without MCDM for 10.1%. This is mainly because, in the case of testing D* Lite with MCDM2, the FUCOM model puts greater weight on the criterion related to the crowd than in the case of testing D* Lite with MCDM1. In this way, the possibility of managing the overall risk is provided.
As D* Lite is global planner, the choice of a local collision-avoidance planner directly impacts the number of risky actions and performance of the proposed approach.
7. Conclusions
This paper considers the multi-robot system with a high level of autonomy, based on the cloud technology and intended for the execution of tasks in a complex and crowded environment.
The cloud approach shifts the computation load from agents to the cloud and provides powerful processing capabilities to the multi-robot system. This allows for the onboard systems of the robots to be greatly reduced, keeping only sensors, communication, actuation, and manipulation modules. The implemented multi-robot path planning algorithm uses common data base and it can operate in an environment that is unknown in advance.
Mission control is based on human expert knowledge of robots capabilities, as well as on available information regarding environmental conditions. The application of MCDM using FUCOM provides an adaptive approach to path planning, in terms of optimizing the global cost map while taking into account all of the factors affecting the robots motion in the environment and having in mind a mission specificity that requires the management of risks that arise from different sources.
We tested a presented approach in simulation on complex scenarios and demonstrated an improvement of global path planning through the statistically significant reductions in the number of risky actions. A limitation of this approach is that it needs external information regarding the environment, not only those gathered with robots’ sensors.
Author Contributions
Conceptualization, N.Z., D.P. and K.J.; Methodology, N.Z., D.P. and K.J.; Validation, N.Z., D.P. and K.J.; Investigation, N.Z. and D.P.; Data Curation, N.Z., D.P. and K.J.; Writing—Original Draft Preparation, N.Z., D.P. and K.J.; Writing—Review & Editing, N.Z., D.P. and K.J.; Visualization, N.Z. and D.P.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lozano-Perez, T. Spatial planning: A configuration space approach. IEEE Trans. Comput. 1983, 32, 108–120. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Wiktor, A.; Scobee, D.; Messengery, S.; Clark, C. Decentralized and complete multi-robot motion planning in confined spaces. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1168–1175. [Google Scholar]
- Ferguson, D.; Stentz, A. Field D*: An Interpolation-based Path Planner and Replanner. In Robotics Research—Results of the 12th International Symposium of Robotics Research; Springer: Berlin/Heidelberg, Germany, 2005; pp. 239–253. [Google Scholar]
- Aroor, A.; Epstein, S.L. Toward Crowd-Sensitive Path Planning. In Proceedings of the AAAI Fall 2017 Symposium on Human-Agent Groups, Arlington, VA, USA, 9–11 November 2017; pp. 238–245. [Google Scholar]
- Pamučar, D.; Stević, Ž.; Sremac, S. A new model for determining weight coefficients of criteria in MCDM models: Full consistency method (FUCOM). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Durmić, E. The evaluation of the criteria for sustainable supplier selection by using the FUCOM method. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 91–107. [Google Scholar] [CrossRef]
- Badi, I.; Abdulshahed, A. Ranking the Libyan airlines by using Full consistency method (FUCOM) and Analytical hierarchy process (AHP). Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 1–14. [Google Scholar] [CrossRef]
- Nunić, Z. Evaluation and selection of the PVC carpentry manufacturer using the FUCOM-MABAC model. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 13–28. [Google Scholar] [CrossRef]
- Pamučar, D.; Lukovac, V.; Božanić, D.; Komazec, N. Multi-criteria FUCOM-MAIRCA model for the evaluation of level crossings: Case study in the Republic of Serbia. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 108–129. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. D* Lite. In Proceedings of the Eighteenth National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; pp. 476–483. [Google Scholar]
- Wagner, G.; Choset, H. M*: A complete multirobot path planning algorithm with performance bounds. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3260–3267. [Google Scholar]
- Bennewitz, M.; Burgard, W.; Thrun, S. Optimizing schedules for prioritized path planning of multi-robot systems. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Cirillo, M.; Uras, T.; Koenig, S. A lattice-based approach to multi-robot motion planning for non-holonomic vehicles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 232–239. [Google Scholar]
- Apoorva, A.; Gautam, R.; Kala, R. Motion Planning for a Chain of Mobile Robots Using A* and Potential Field. Robotics 2018, 7, 20. [Google Scholar] [CrossRef]
- Biswas, S.; Anavatti, G.S.; Garratt, A.M. A Time-Efficient Co-Operative Path Planning Model Combined with Task Assignment for Multi-Agent Systems. Robotics 2019, 8, 35. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Yun, S.C.; Ganapathy, V.; Chien, T.W. Enhanced D* Lite Algorithm for mobile robot navigation. In Proceedings of the IEEE Symposium on Industrial Electronics and Applications, Penang, Malaysia, 3–5 October 2010. [Google Scholar]
- Singh, S.; Simmons, R.; Smith, T.; Stentz, A.; Verma, V.; Yahja, A.; Schwehr, K. Recent Progress in Local and Global Traversability for Planetary Rovers. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000. [Google Scholar]
- Wettergreen, D.; Dias, B.; Shamah, B.; Teza, J.; Tompkins, P.; Urmson, C.; Wagner, M.; Whittaker, W. First Experiments in Sun-Synchronous Exploration. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002. [Google Scholar]
- Kelly, A.; Amidi, O.; Happold, M.; Herman, H.; Pilarsky, T.; Rander, P.; Stentz, A.; Vallidis, N.; Warner, R. Toward Reliable Autonomous Vehicles Operating in Challenging Environments. In Proceedings of the International Symposium on Experimental Robotics, Singapore, 18–21 June 2004; pp. 599–608. [Google Scholar]
- Goldberg, S.; Maimone, M.; Matthies, L. Stereo Vision and Rover Navigation Software for Planetary Exploration. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002. [Google Scholar]
- Stentz, A. The Focussed D* Algorithm for Real-Time Replanning. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1652–1659. [Google Scholar]
- Stentz, A.; Hebert, M. A Complete Navigation System for Goal Acquisition in Unknown Environments. In Proceedings of the International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August 1995. [Google Scholar]
- Stentz, A. Optimal and Efficient Path Planning for Unknown and Dynamic Environments. Int. J. Robot. Autom. 2003, 10, 58–71. [Google Scholar]
- Brumitt, B.; Stentz, A. GRAMMPS: A generalized mission planner for multiple mobile robots in unstructured environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20 May 1998. [Google Scholar]
- Al-Mutib, K.; AlSulaiman, M.; Emaduddin, M.; Ramdane, H.; Mattar, E. D* Lite Based Real-Time Multi-Agent Path Planning in Dynamic Environments. In Proceedings of the Third International Conference on Computational Intelligence, Modelling & Simulation, Langkawi, Malaysia, 20–22 September 2011. [Google Scholar]
- Peng, J.-H.; Li, I.-H.; Chien, Y.-H.; Hsu, C.-C.; Wang, W.-Y. Multi-Robot Path Planning Based on Improved D* Lite Algorithm. In Proceedings of the IEEE 12th International Conference on Networking, Sensing and Control, Taipei, Taiwan, 9–11 April 2015. [Google Scholar]
- Aroor, A.; Epstein, S.L.; Korpan, R. Online Learning for Crowd-sensitive Path Planning. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1702–1710. [Google Scholar]
- Chan, A.B.; Vasconcelos, N. Bayesian Poisson regression for crowd counting. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 545–551. [Google Scholar]
- Tavana, M.; Bourgeois, B.S. A multiple criteria decision support system for autonomous underwater vehicle mission planning and control. Int. J. Oper. Res. 2010, 7, 216–239. [Google Scholar] [CrossRef]
- Choudhary, S.; Carlone, L.; Nieto, C.; Rogers, J.; Liu, Z.; Christensen, H.I.; Dellaert, F. Multi Robot Object-based SLAM. In Proceedings of the International Symposium on Experimental Robotics, Tokyo, Japan, 3–6 October 2016; pp. 729–741. [Google Scholar]
- Benavidez, P.; Muppidi, M.; Rad, P.; Prevost, J.J.; Jamshidi, M.; Brown, L. Cloud-based realtime robotic Visual SLAM. In Proceedings of the Annual IEEE International Systems Conference, Vancouver, BC, Canada, 13–16 April 2015; pp. 773–777. [Google Scholar]
- He, H.; Kamburugamuve, S.; Fox, G.C.; Zhao, W. Cloud based Real-time Multi-robot Collision Avoidance for Swarm Robotics. Int. J. Grid Distrib. Comput. 2016, 9, 339–358. [Google Scholar] [CrossRef]
- Hunziker, D.; Gajamohan, M.; Waibel, M.; D’Andrea, R. Rapyuta: The RoboEarth Cloud Engine. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 438–444. [Google Scholar]
- Saha, O.; Dasgupta, P. A Comprehensive Survey of Recent Trends in Cloud Robotics Architectures and Applications. Robotics 2018, 7, 47. [Google Scholar] [CrossRef]
- Likhachev, M.; Ferguson, D.; Gordon, G.; Stentz, A.; Thrun, S. Anytime search in dynamic graphs. J. Artif. Intell. 2008, 172, 1613–1643. [Google Scholar] [CrossRef]
- Likhachev, M.; Gordon, G.; Thrun, S. ARA*: Anytime A* with provable bounds on sub-optimality. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–13 December 2003; pp. 767–774. [Google Scholar]
- Likhachev, M.; Ferguson, D.; Gordon, G.; Stentz, A.; Thrun, S. Anytime Dynamic A*: An Anytime, Replanning Algorithm. In Proceedings of the International Conference on Automated Planning and Scheduling, Monterey, CA, USA, 5–10 June 2005; pp. 262–271. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).