Study of a Null-Flux Coil Electrodynamic Suspension Structure for Evacuated Tube Transportation
Abstract
1. Introduction
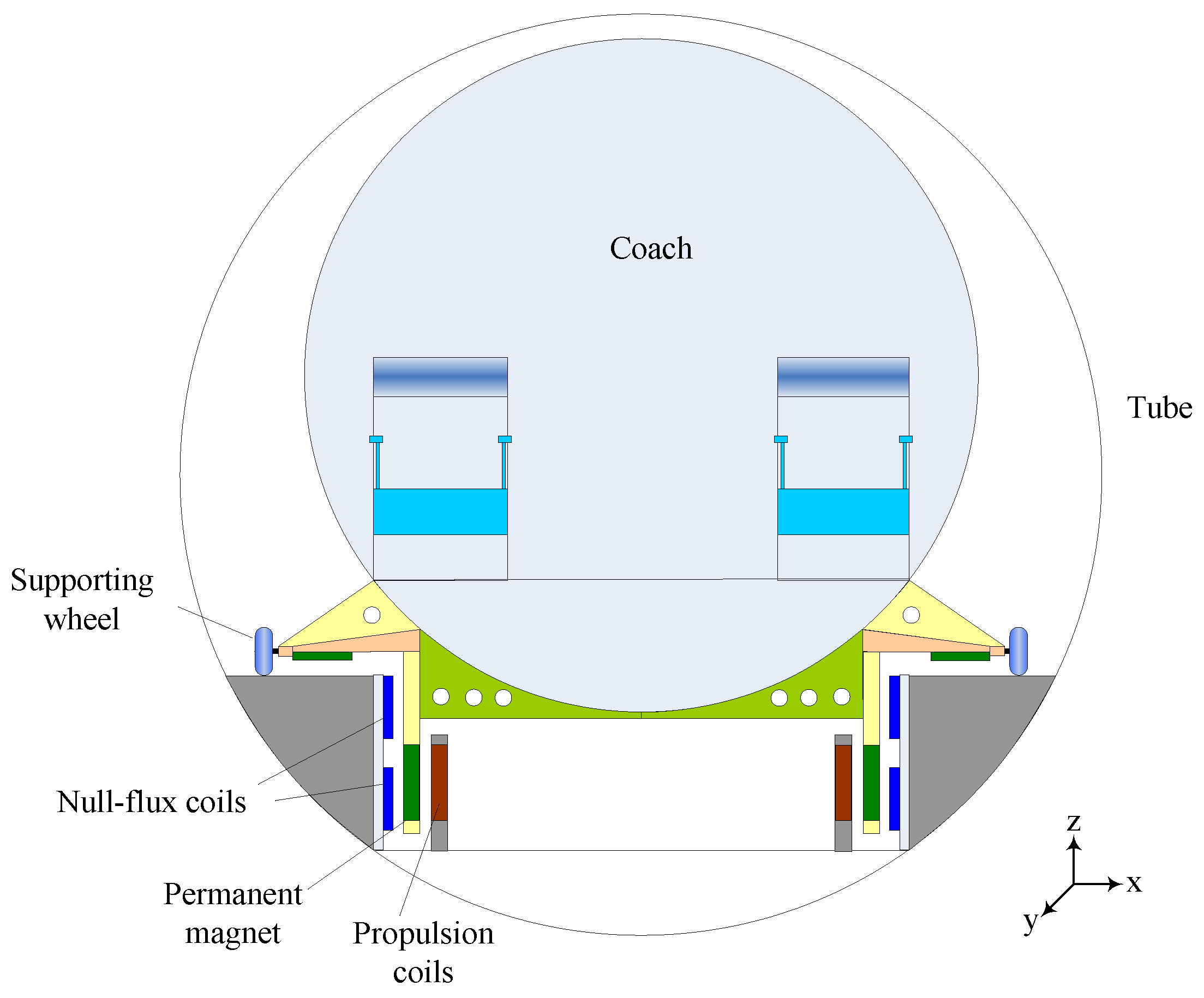
2. Proposed ETT System
3. Analysis of the Null-Flux Coil EDS Structure
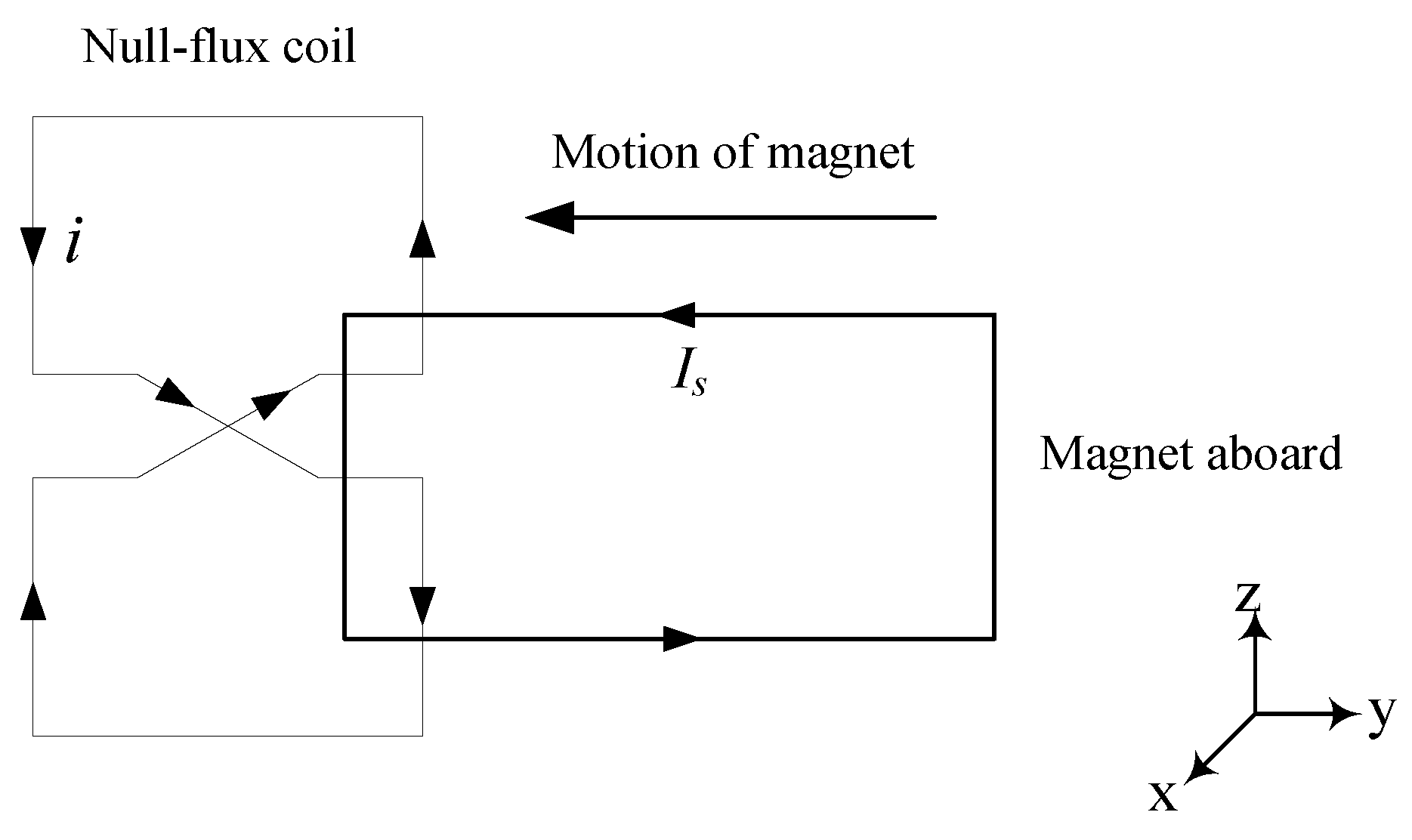
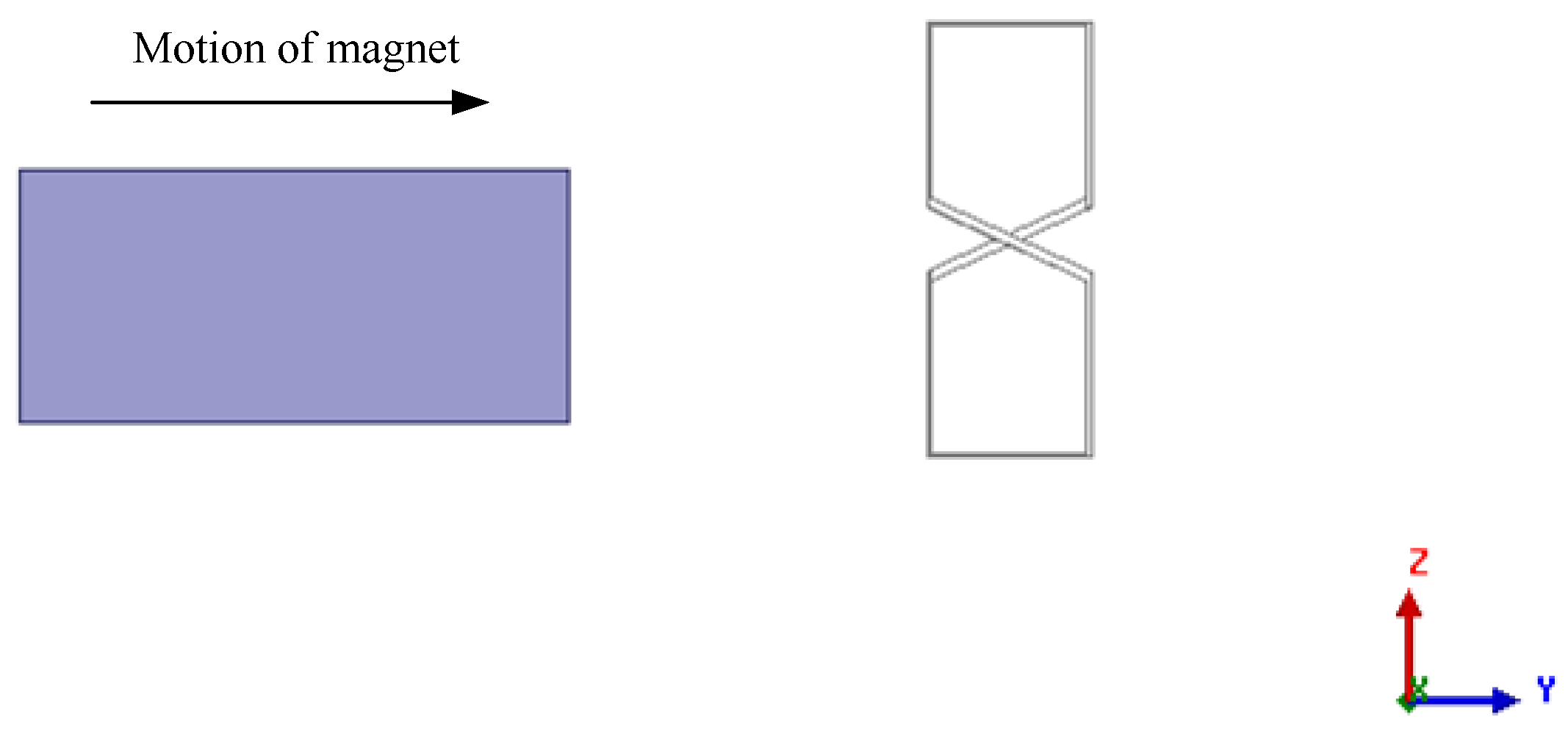
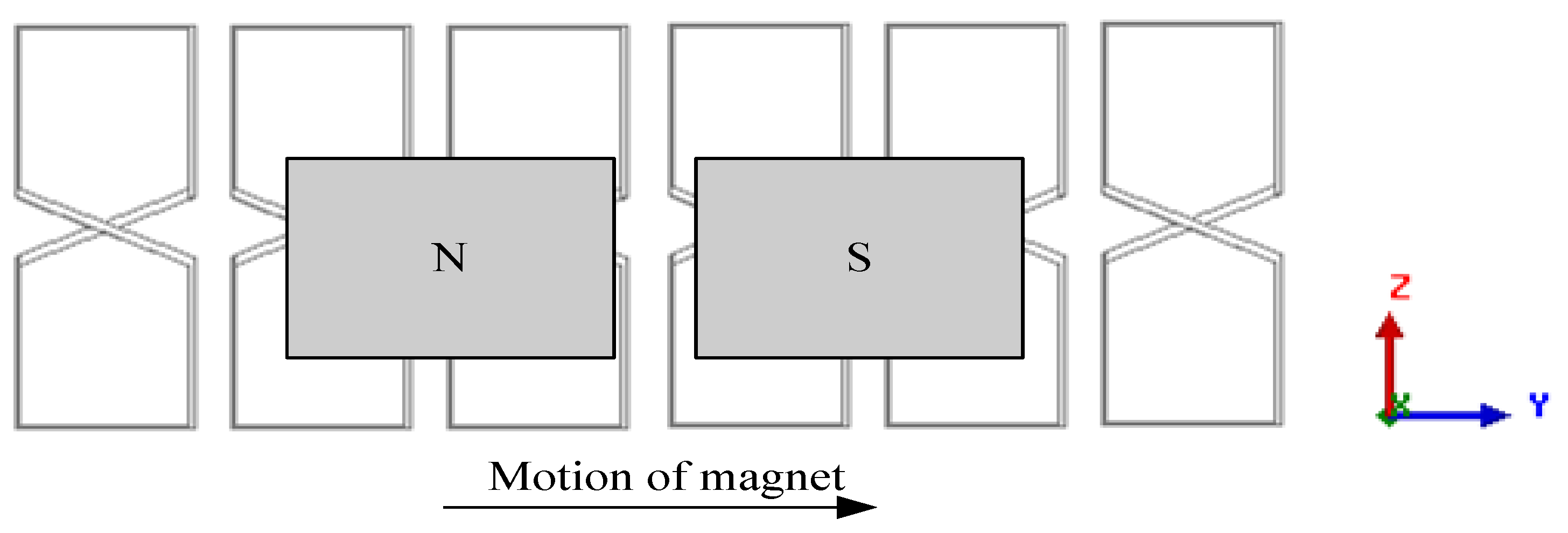
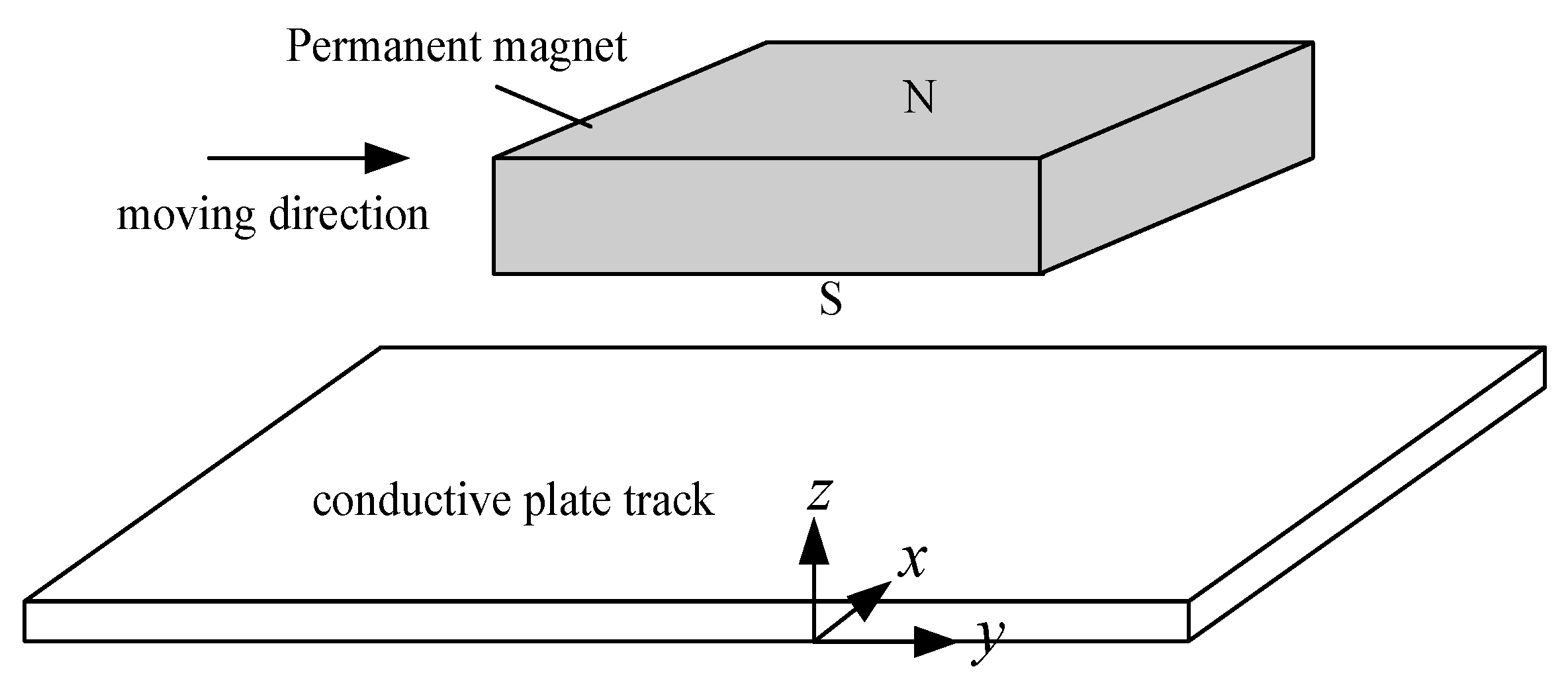
3.1. Working Principles of Null-Flux Coil Structure
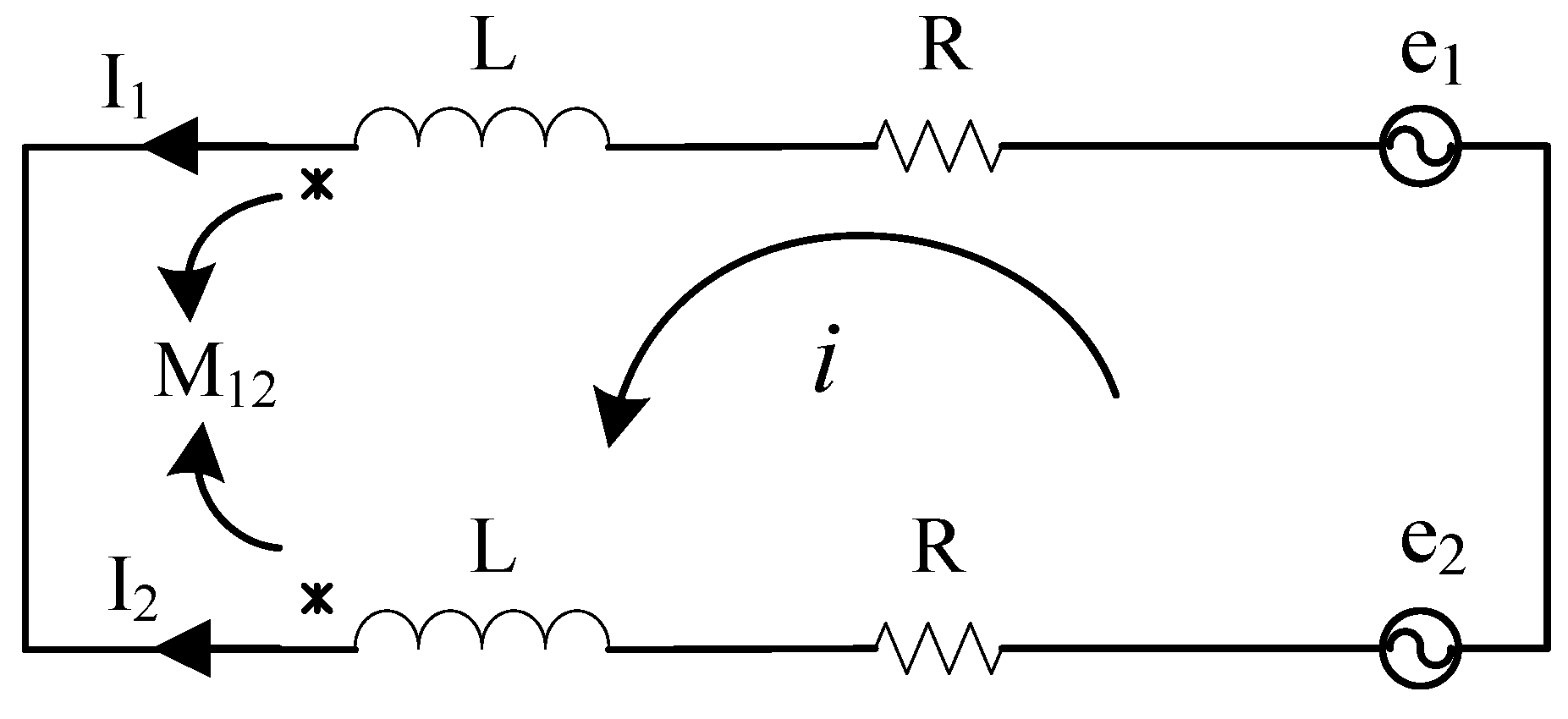
3.2. Equivalent Circuit of Null-Flux Coil Levitation Structure
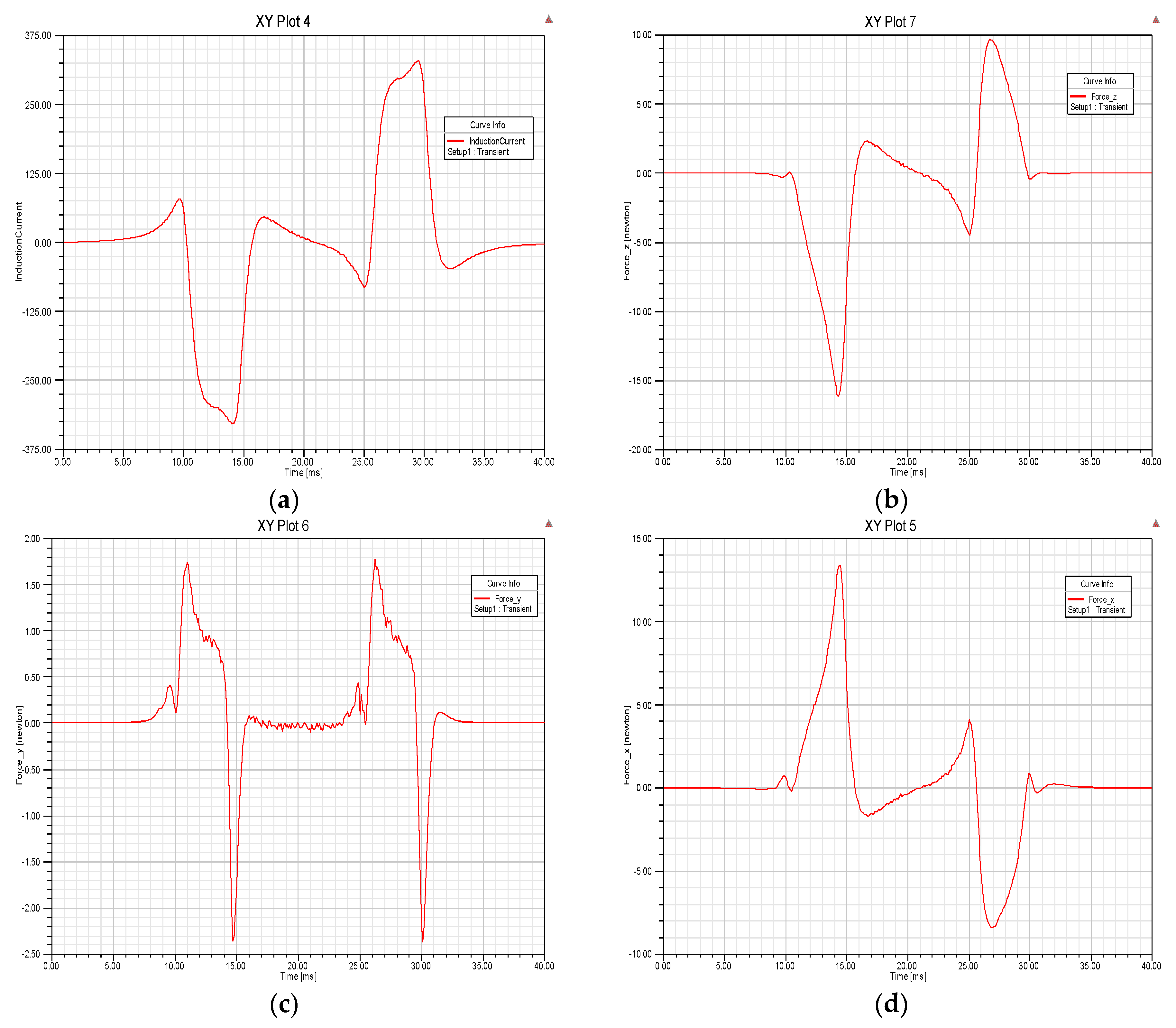
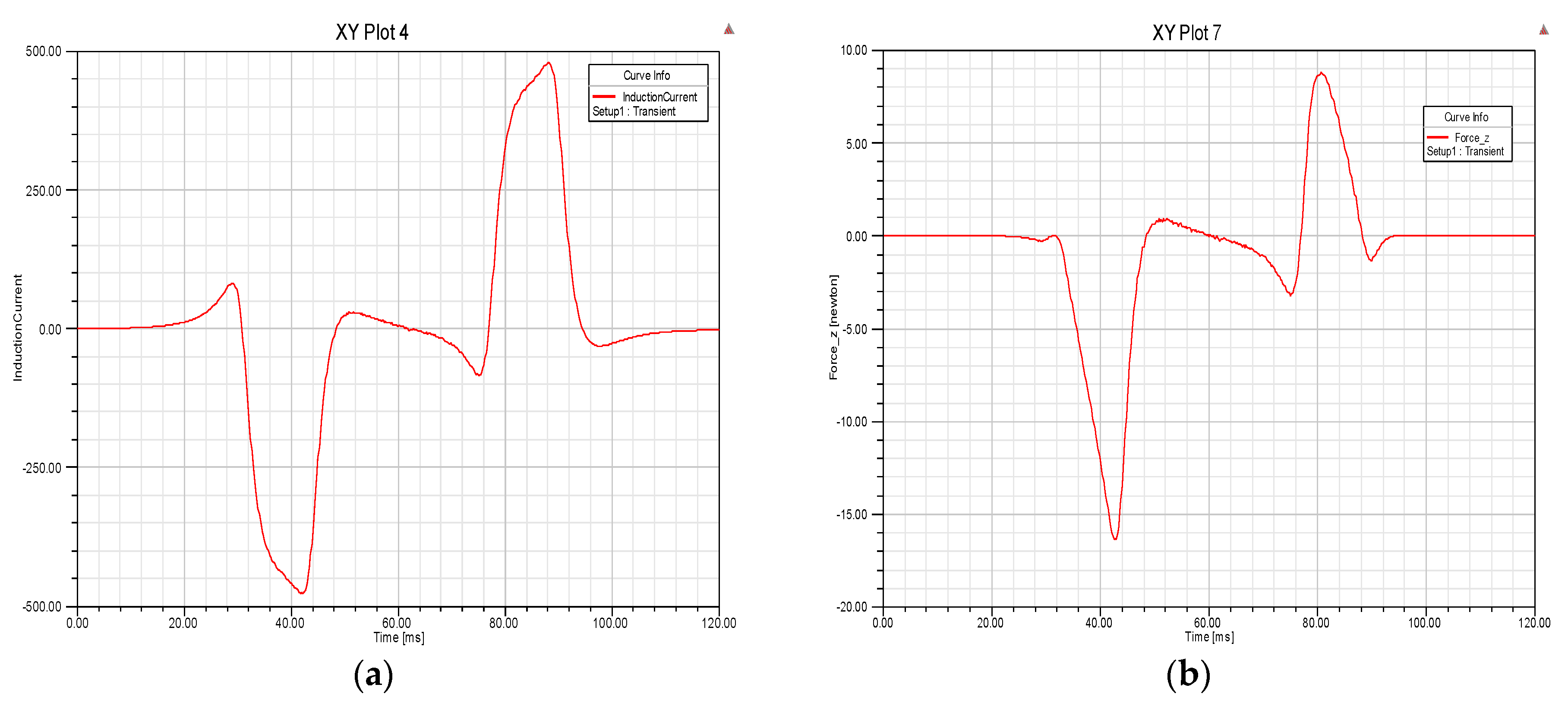
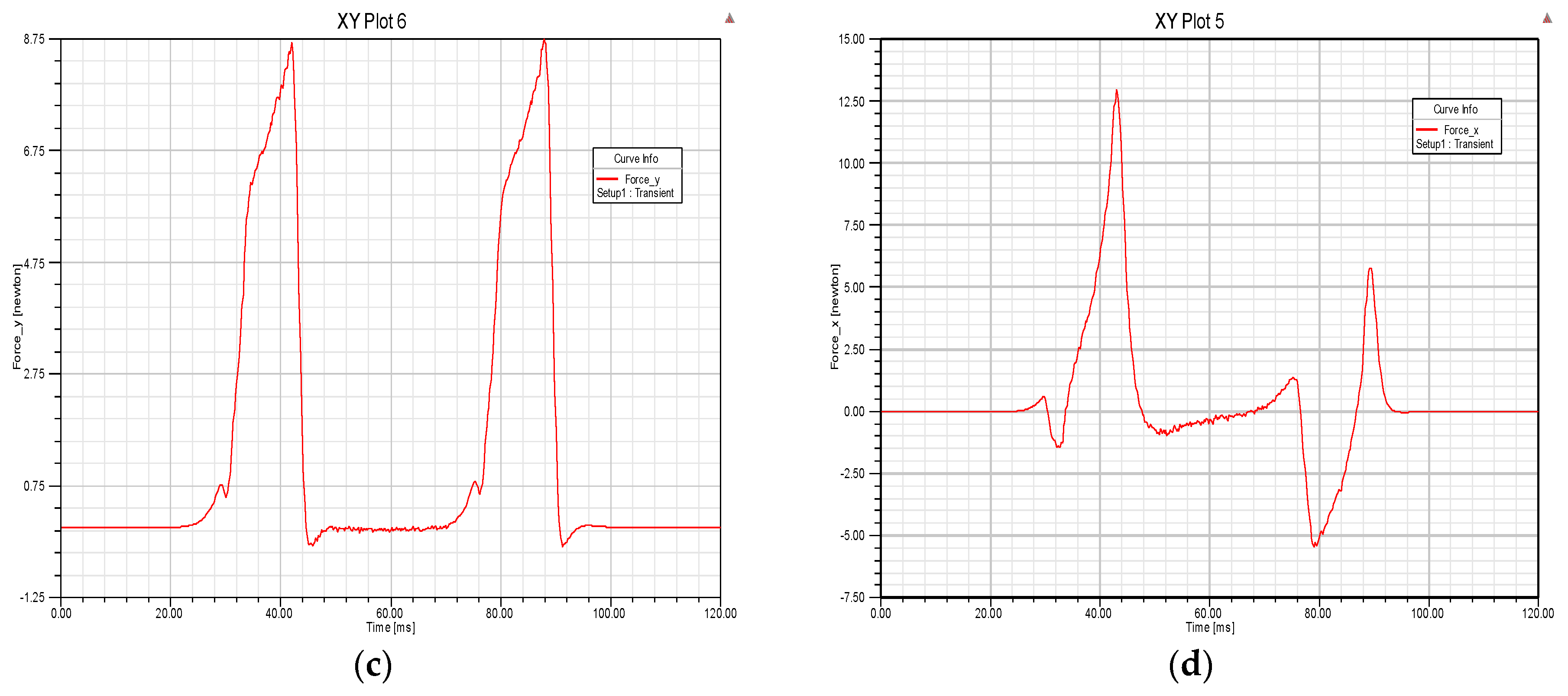
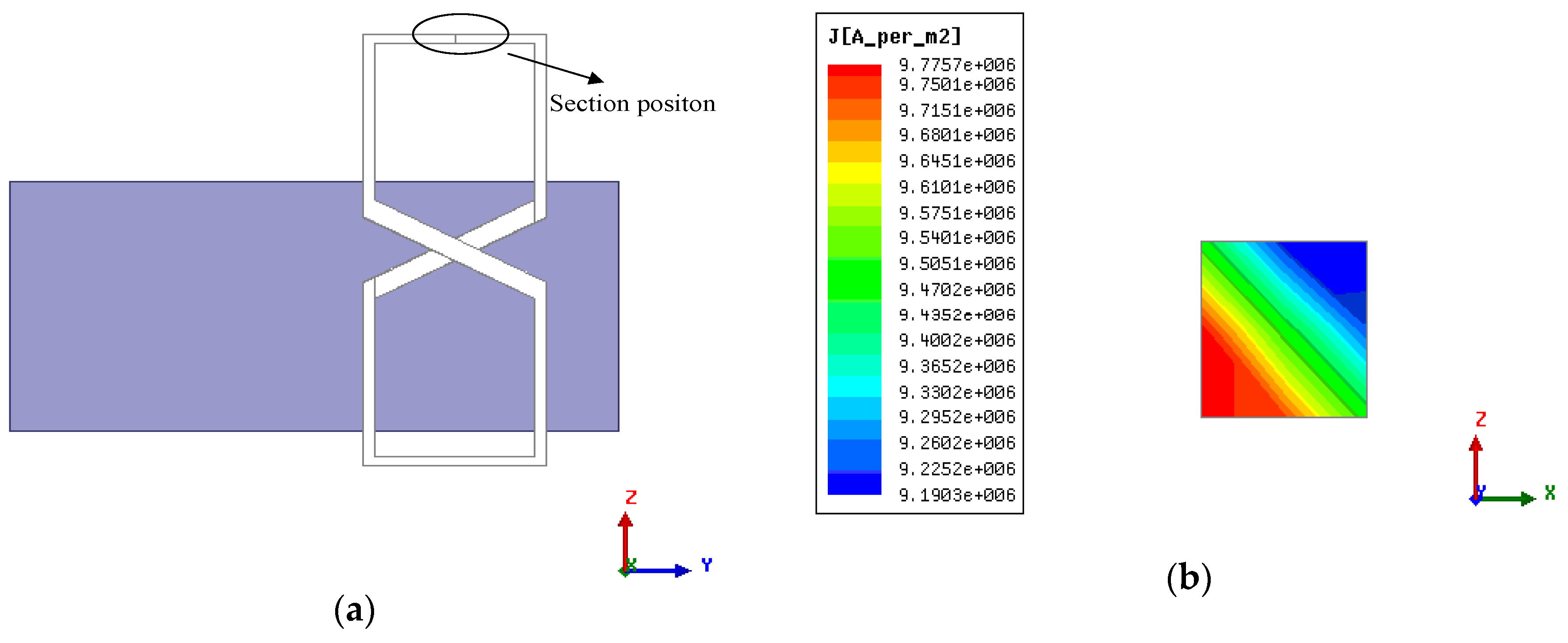
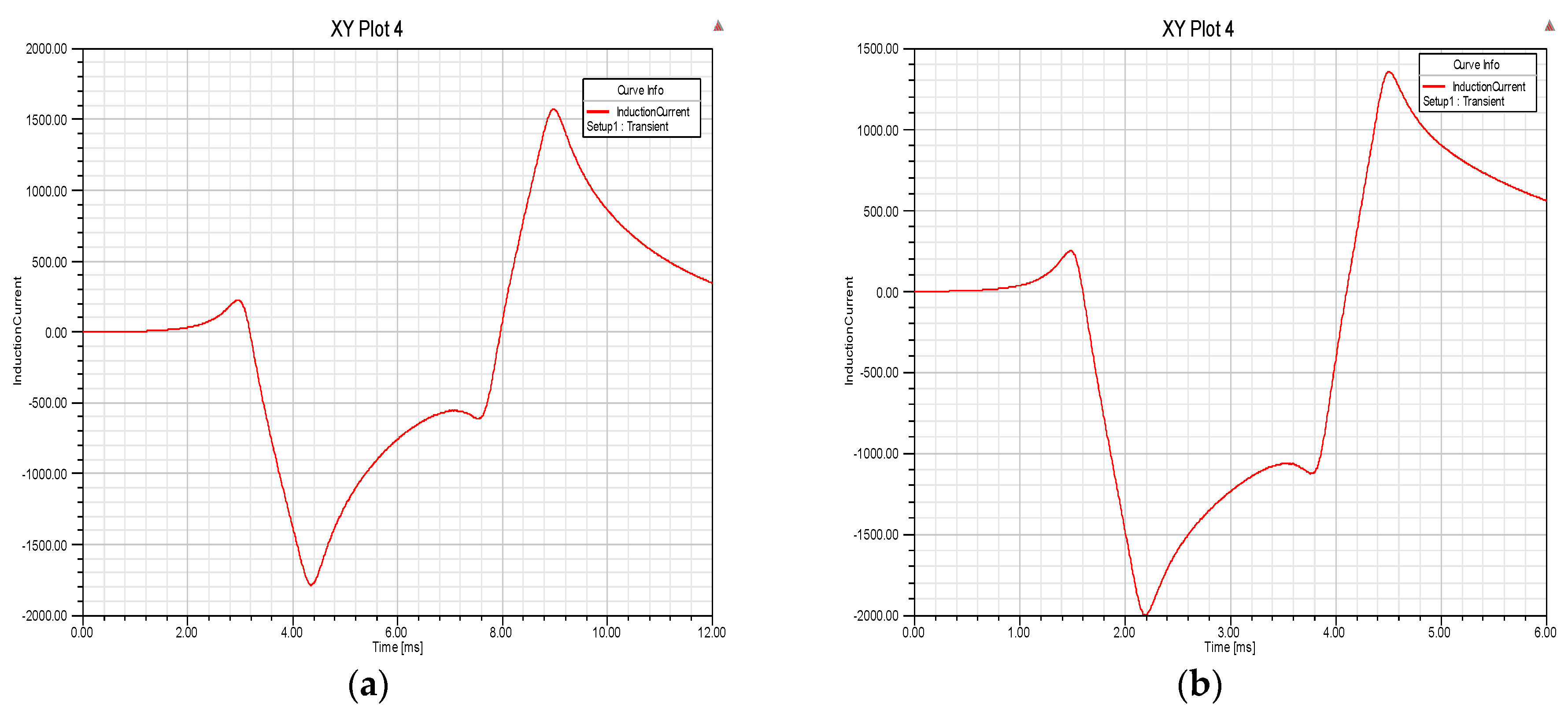
3.3. Verification of Dynamic Circuit Theory
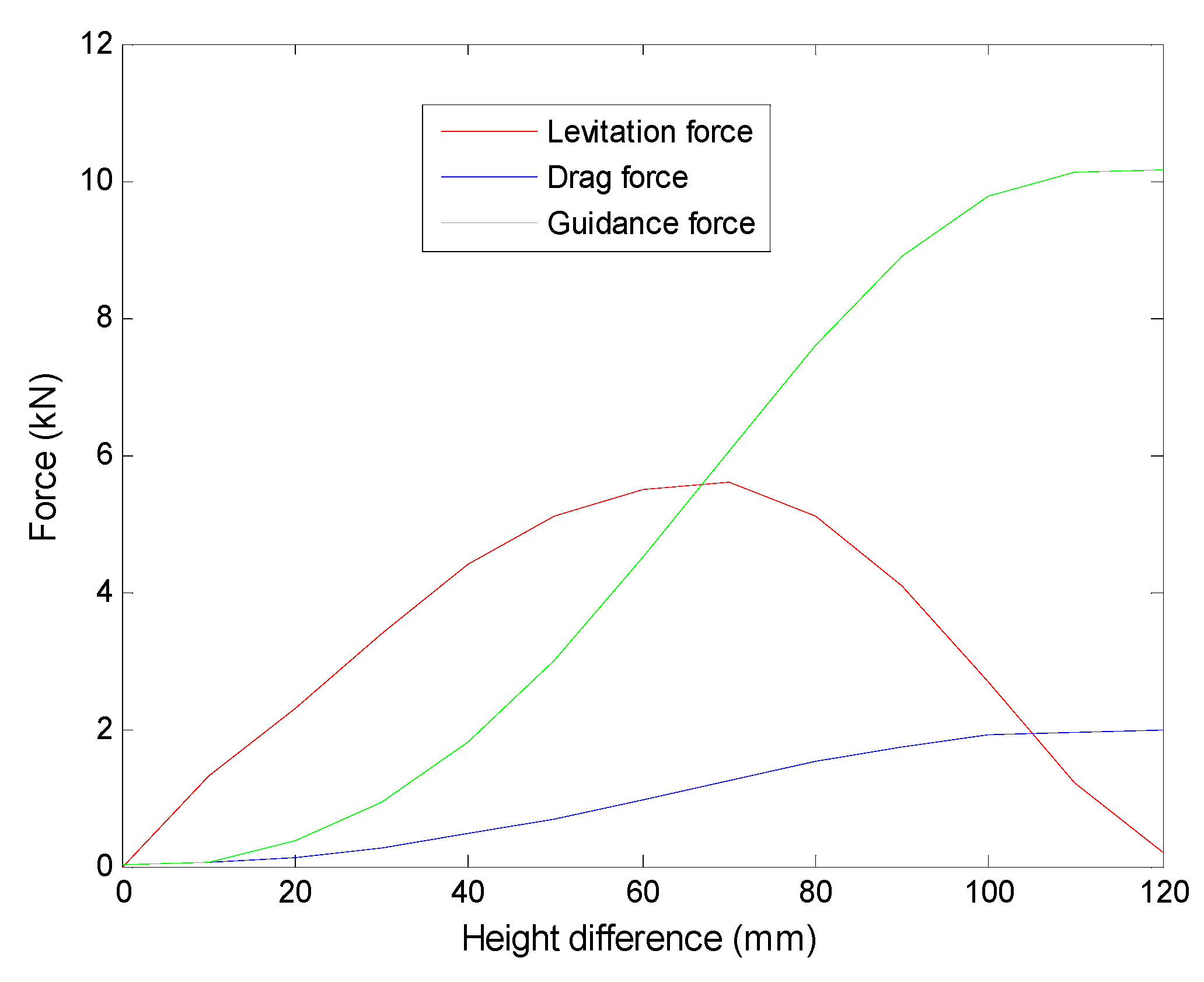
3.4. Characteristics of Magnetic Forces
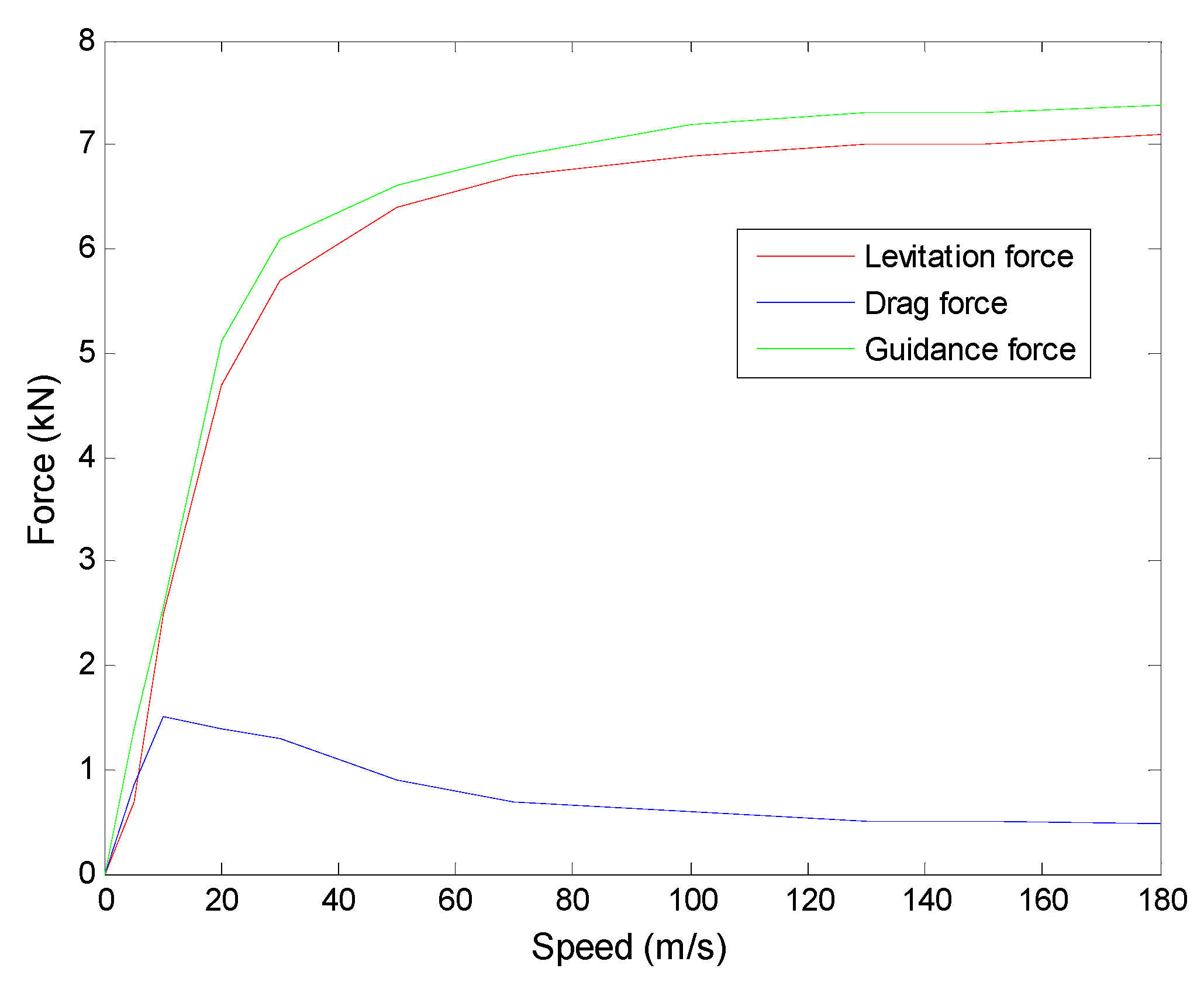
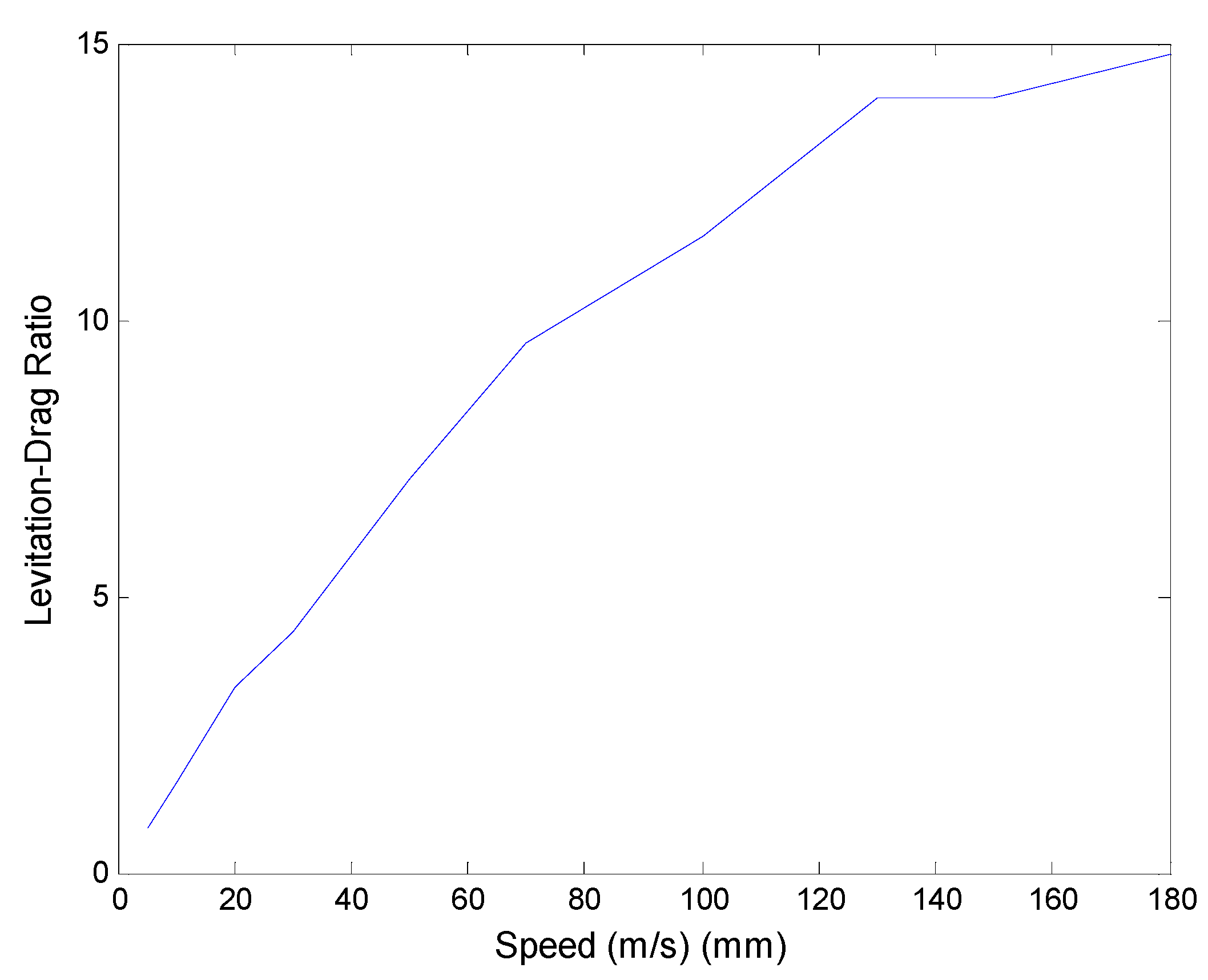
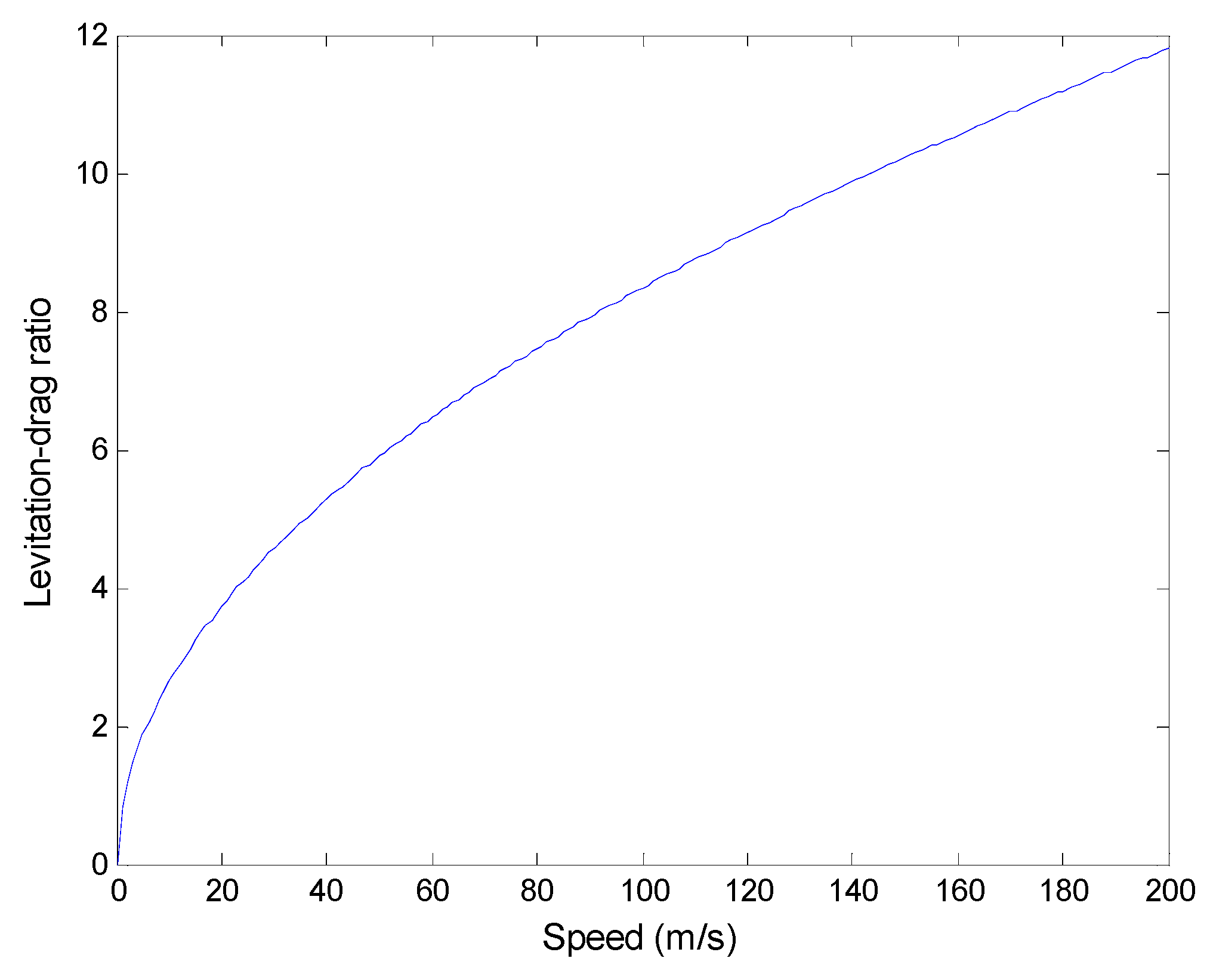
3.4.1. Effects of Speed
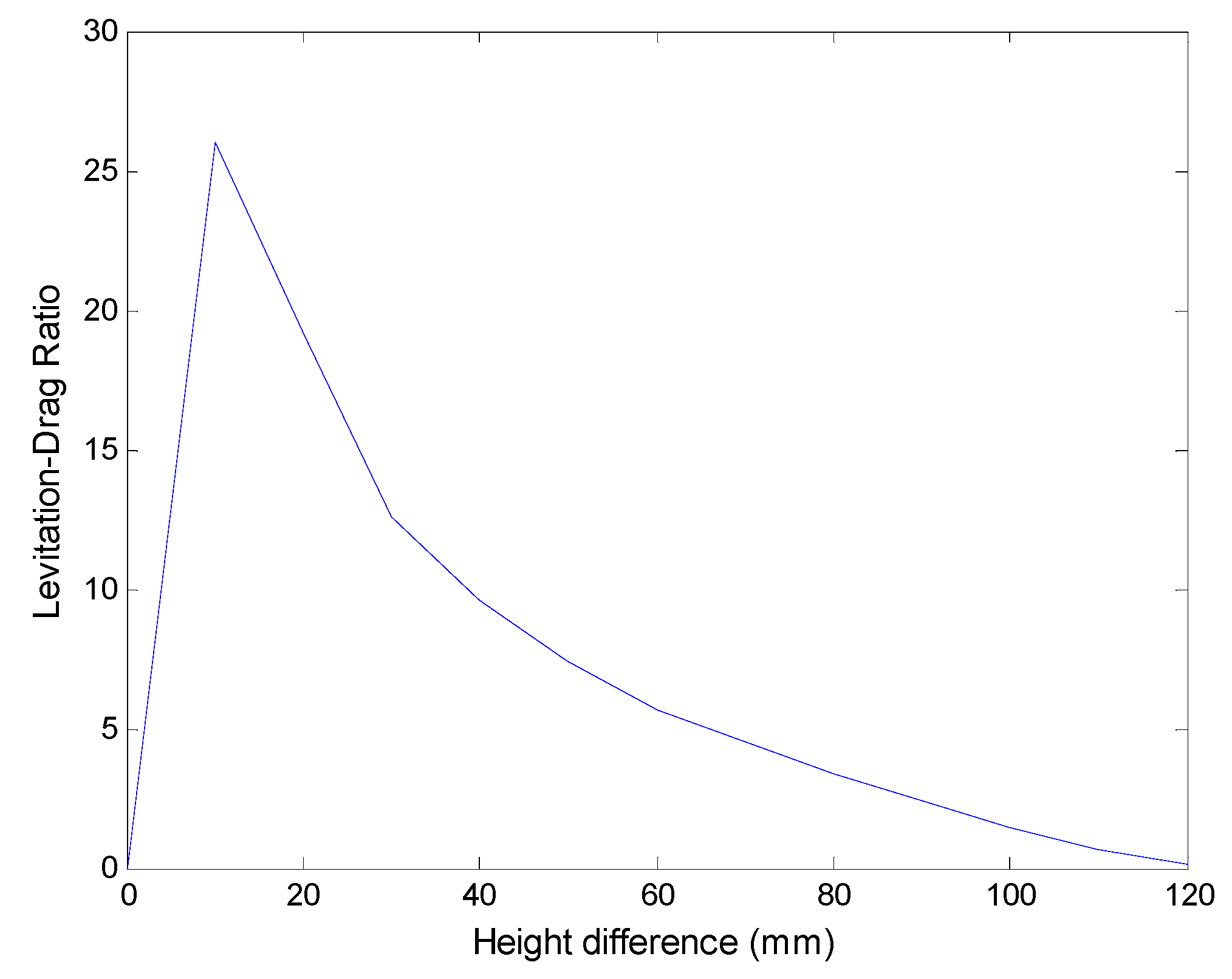
3.4.2. Levitation Working Point
3.4.3. Guidance Stiffness
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhai, M.; Long, Z.; Li, X. A New Strategy for Improving the Tracking Performance of Magnetic Levitation System in Maglev Train. Symmetry 2019, 11, 1053. [Google Scholar] [CrossRef]
- Bonfitto, A.; Tonoli, A.; Silvagni, M. Sensorless active magnetic dampers for the control of rotors. Mechatronics 2016, 47, 195–207. [Google Scholar] [CrossRef]
- Circosta, S.; Bonfitto, A.; Lusty, C.; Keogh, P.; Amati, N.; Tonoli, A. Analysis of a Shaftless Semi-Hard Magnetic Material Flywheel on Radial Hysteresis Self-Bearing Drives. Actuators 2018, 7, 87. [Google Scholar] [CrossRef]
- Galluzzi, R.; Amati, N.; Tonoli, A. Modeling, Design and Validation of Magnetic Hysteresis Motors. IEEE Trans. Ind. Electron. 2019. [Google Scholar] [CrossRef]
- Lee, H.W.; Kim, K.C.; Lee, J. Review of maglev train technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar] [CrossRef]
- Zhou, D.; Hansen, C.H.; Li, J. Suppression of maglev Vehicle-Girder Self-Excited vibration using virtual tuned mass damper. J. Sound Vib. 2011, 330, 883–901. [Google Scholar] [CrossRef]
- Yan, L. Suggestion for selection of Maglev option for Beijing-Shanghai high-speed line. IEEE Trans. Appl. Supercond. 2004, 14, 936–939. [Google Scholar] [CrossRef]
- Goddard, R.H. Vacuum Tube Transportation System. U.S. Patent US2511979A, 20 June 1950. [Google Scholar]
- Hyperloop Alpha. Available online: http://www.spacex.com/hyperloopalpha (accessed on 12 August 2013).
- Xu, J.; Geng, Q.; Li, Y.; Li, J. Design, Fabrication and Test of an HTS Magnetic Suspension Experimental System. IEEE Trans. Appl. Supercond. 2016. [Google Scholar] [CrossRef]
- Lee, C.Y.; Jo, J.M.; Han, Y.J. Design, Fabrication, and Operating Test of the Prototype HTS Electromagnet for EMS-Based Maglev. IEEE Trans. Appl. Supercond. 2012. [Google Scholar] [CrossRef]
- Bonfitto, A.; Castellanos Molina, L.M.; Tonoli, A.; Amati, N. Offset-Free Model Predictive Control for Active Magnetic Bearing Systems. Actuators 2018, 7, 46. [Google Scholar] [CrossRef]
- Davey, K. Analysis of an electrodynamic Maglev system. IEEE Trans. Magn. 1999, 35, 4259–4267. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, D.; Chen, Q.; Yu, P.; Li, J. Design and Analysis of a Plate Type Electrodynamic Suspension Structure for Ground High Speed Systems. Symmetry 2019, 11, 1117. [Google Scholar] [CrossRef]
- Long, Z.; He, G.; Xue, S. Study of EDS & EMS Hybrid Suspension System with Permanent-Magnet Halbach Array. IEEE Trans. Magn. 2011, 47, 4717–4724. [Google Scholar] [CrossRef]
- Hsu, Y.H.; Langhom, A.; Ketchen, D.; Holland, L.; Minto, D.; Doll, D. Magnetic levitation upgrade to the Holloman High Speed Test Track. IEEE Trans. Appl. Supercond. 2009, 19, 2074–2077. [Google Scholar] [CrossRef]
- Okubo, T.; Ueda, N.; Ohashi, S. Effective Control Method of the Active Damper System against the Multidirectional Vibration in the Superconducting Magnetically Levitated Bogie. IEEE Trans. Appl. Supercond. 2016. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, W.; Zheng, J.; Wang, B.; Ren, Y.; Zheng, X.; Zhang, J. A High Temperature Superconducting Maglev-Evacuated Tube Transport (HTS Maglev-ETT) Test System. IEEE Trans. Appl. Supercond. 2017, 27, 6. [Google Scholar] [CrossRef]
- Ding, J.; Yang, X.; Long, Z.; Dang, N. Three Dimensional Numerical Analysis and Optimization of Electromagnetic Suspension System for 200 km/h Maglev Train Considering Eddy Current Effect. IEEE Access 2018, 6, 1547–1555. [Google Scholar] [CrossRef]
- Du, J.; Ohsaki, H. Numerical analysis of eddy current in the EMS-Maglev system. In Proceedings of the 6th International Conference on Electrical Machines and Systems, 2003. ICEMS 2003, Beijing, China, 9–11 November 2003. [Google Scholar]
- Abdelrahman, A.S.; Sayeed, J.; Youssef, M.Z. Hyperloop transportation system: Analysis, design, control and implementation. IEEE Trans. Ind. Electron. 2018, 65, 7427–7436. [Google Scholar] [CrossRef]
- Ji, W.Y.; Jeong, G.; Park, C.B.; Jo, I.H.; Lee, H.W. A study of Non-Symmetric Double-Sided linear induction motor for Hyperloop all-in-one system (Propulsion, Levitation, and Guidance). IEEE Trans. Magn. 2018. [Google Scholar] [CrossRef]
- Danby, G.T.; Powell, J.R. Design Approaches and Parameters for Magnetically Levitated Transport Systems: Superconductivity and Its Applications; Elsevier Science Publishing Co., Inc.: London, UK, 1988; pp. 318–342. [Google Scholar]
- He, J.; Coffey, H.T. Magnetic damping forces in figure-eight-shaped null-flux coil suspension systems. IEEE Trans. Magn. 1997, 33, 4230–4232. [Google Scholar] [CrossRef]
- He, J.; Rote, D.M.; Coffey, H.T. Electrodynamic Forces of the Cross-Connected Figure-Eight Null-Flux Coil Suspension System. In Proceedings of the International Conference On Magnetically Levitated Systems and Linear Drives, Argonne, IL, USA, 19–21 May 1993. [Google Scholar]
- Post, R.F.; Ryutov, D. The Inductrack concept: A new approach to magnetic levitation. In Office of Scientific & Technical Information Technical Reports; Lawrence Livermore National Lab.: Livermore, CA, USA, 1996. [Google Scholar] [CrossRef]

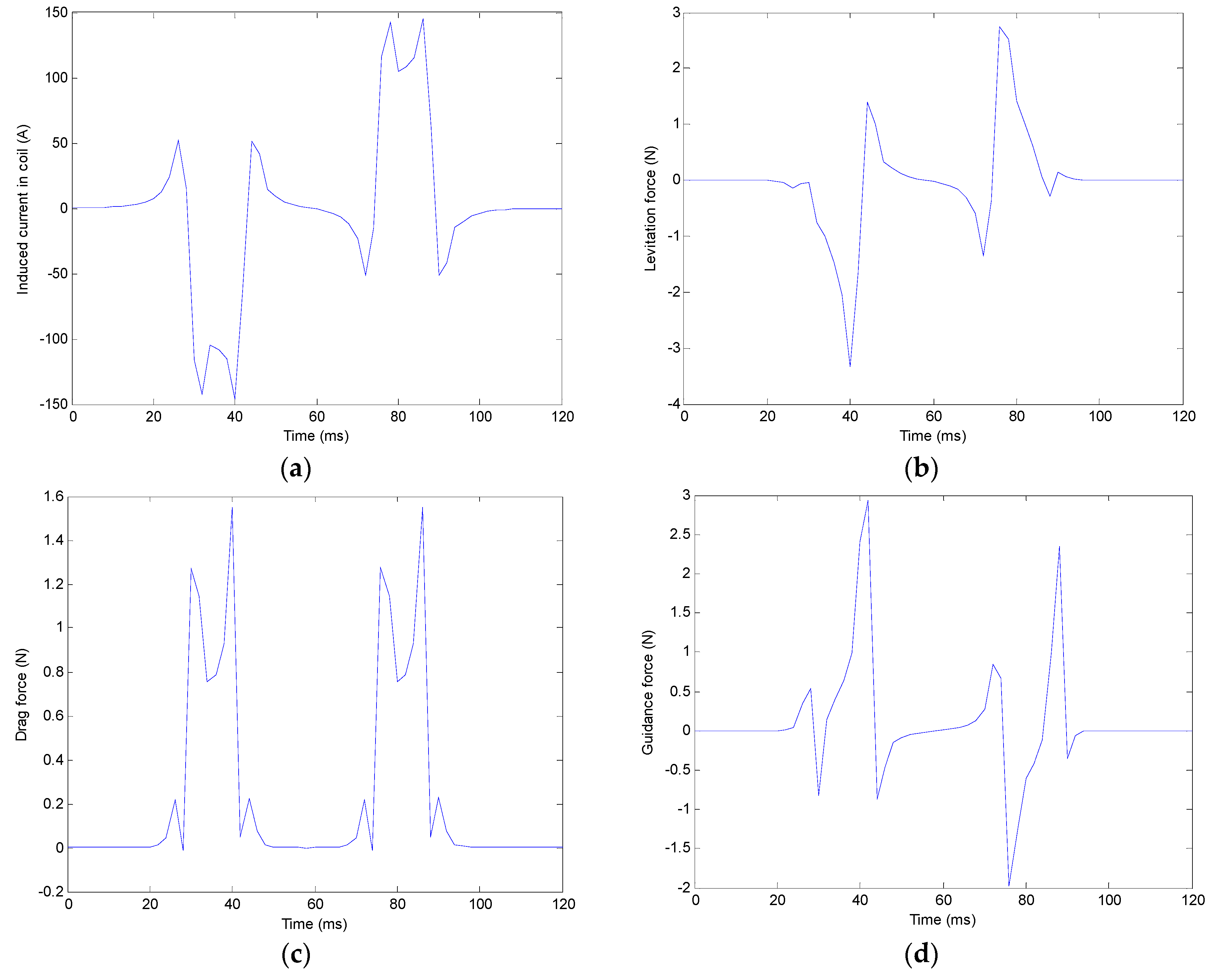
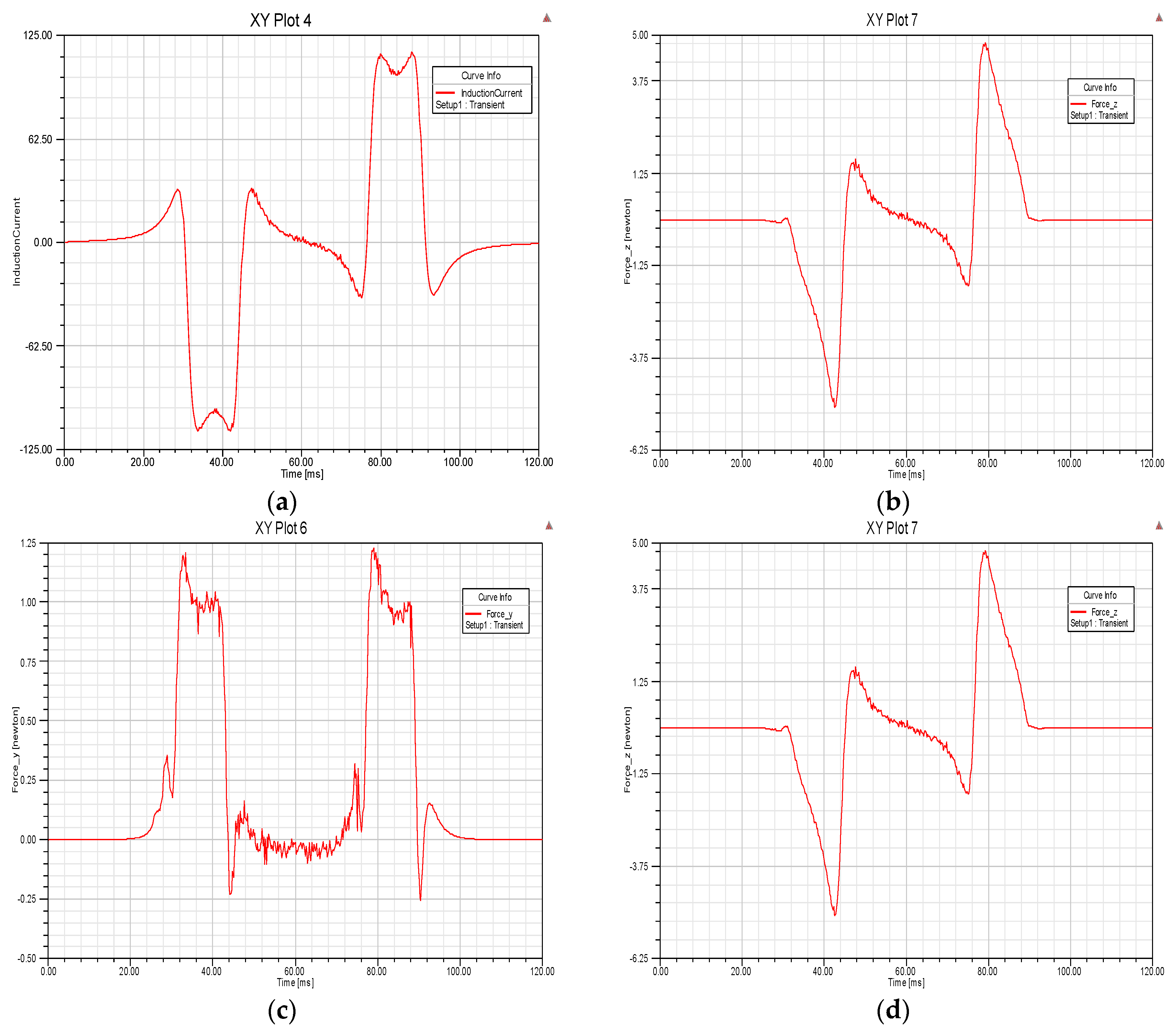
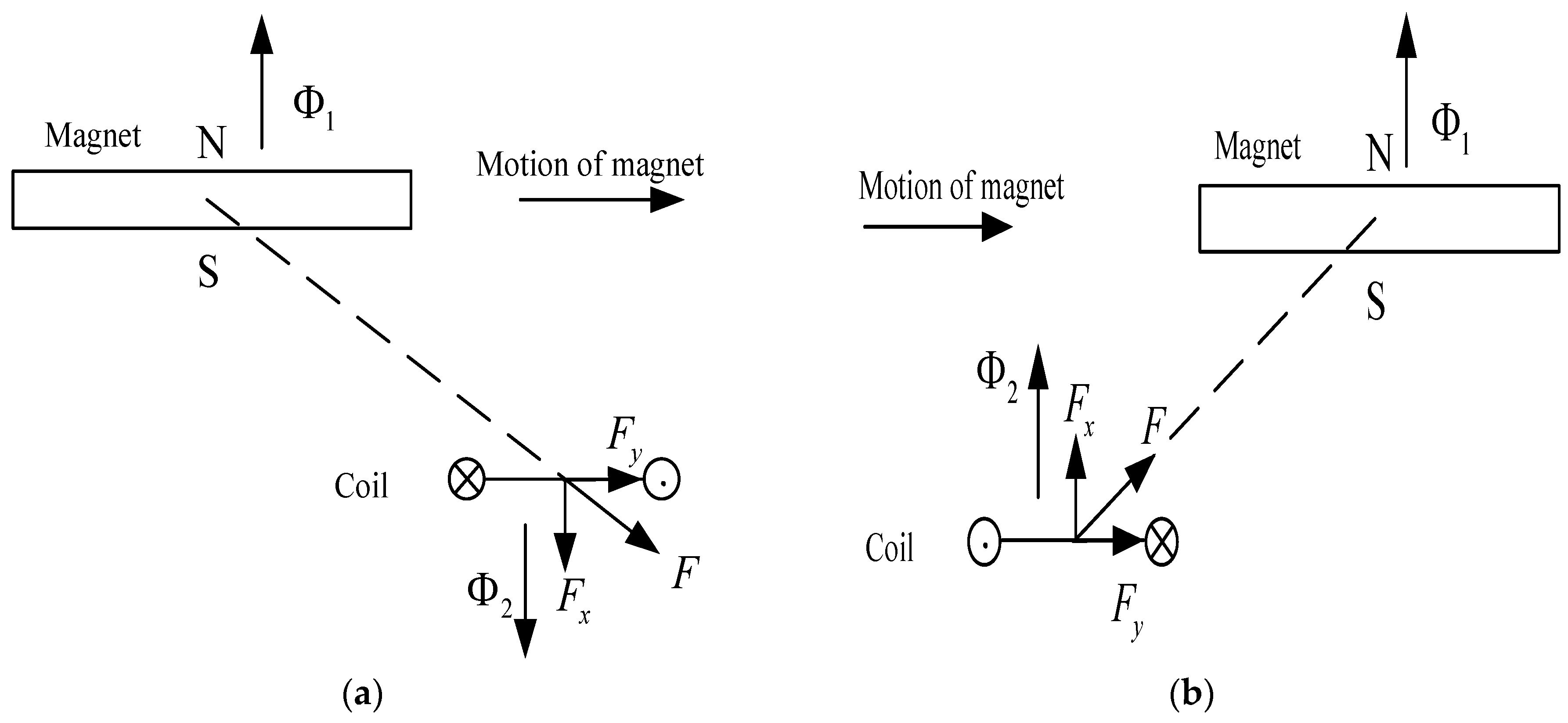
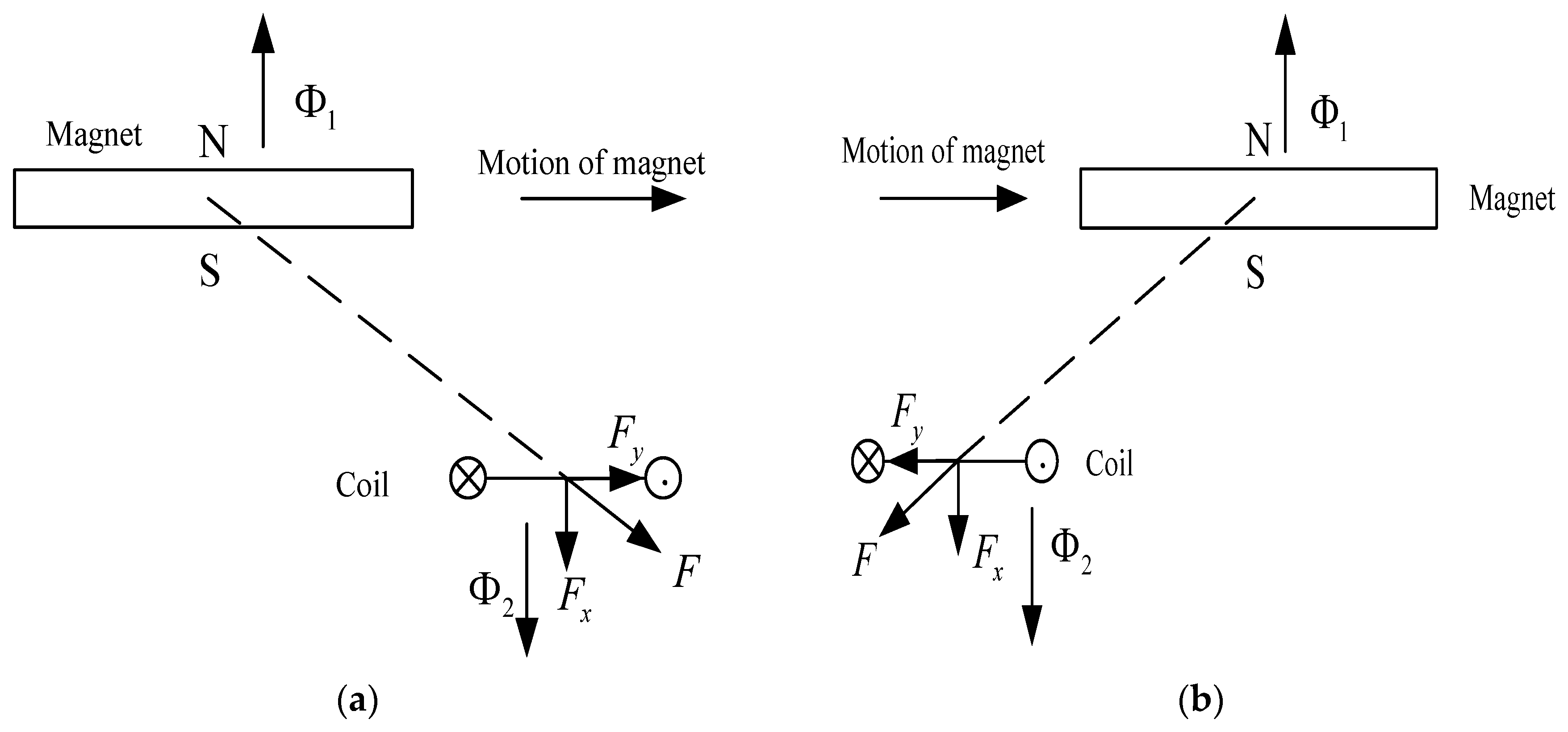

| Variable | Value | Unit |
|---|---|---|
| Length of magnet (axis Y) | 460 | mm |
| Height of magnet (axis Z) | 210 | mm |
| Thickness of magnet (axis X) | 20 | mm |
| Remanence of permanent magnet (PM) | 1.33 | T |
| Coercivity of PM | 962 | kA/m |
| Length of null-flux coil | 137 | mm |
| Height of null-flux coil | 365 | mm |
| Sectional area of null-flux coil | 16 | mm2 |
| Height of gap between the upper and the lower loops | 30 | mm |
| Resistivity of the coil (Cu) | 1.75 × 10−8 | |
| Lateral gap between the coil and the magnet (axis X) | 10 | mm |
| Height difference between the mid-lines of the magnet and the coil (axis Z) | 70 | mm |
| Speed of the magnet (axis Y) | 10 | m/s |
| Variable | Value | Unit |
|---|---|---|
| Length of PM (axis Y) | 550 | mm |
| Height of PM (axis Z) | 220 | mm |
| Thickness of PM (axis X) | 50 | mm |
| Pole pitch of magnets | 600 | mm |
| Remanence of PM | 1.33 | T |
| Coercivity of PM | 962 | kA/m |
| Length of null-flux coil | 340 | mm |
| Height of null-flux coil | 450 | mm |
| Height of gap between the upper and the lower loops | 35 | mm |
| Sectional area | 128 | mm2 |
| Gap between the neighboring coils | 45 | mm |
| Resistivity of the coil (Cu) | 1.75 × 10−8 | |
| Height difference between the mid-lines of the magnet and the coil (axis Z) | 70 | mm |
| Lateral gap between the coil and the magnet (axis X) | 15 | mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Li, J.; Zhou, D. Study of a Null-Flux Coil Electrodynamic Suspension Structure for Evacuated Tube Transportation. Symmetry 2019, 11, 1239. https://doi.org/10.3390/sym11101239
Guo Z, Li J, Zhou D. Study of a Null-Flux Coil Electrodynamic Suspension Structure for Evacuated Tube Transportation. Symmetry. 2019; 11(10):1239. https://doi.org/10.3390/sym11101239
Chicago/Turabian StyleGuo, Zhaoyu, Jie Li, and Danfeng Zhou. 2019. "Study of a Null-Flux Coil Electrodynamic Suspension Structure for Evacuated Tube Transportation" Symmetry 11, no. 10: 1239. https://doi.org/10.3390/sym11101239
APA StyleGuo, Z., Li, J., & Zhou, D. (2019). Study of a Null-Flux Coil Electrodynamic Suspension Structure for Evacuated Tube Transportation. Symmetry, 11(10), 1239. https://doi.org/10.3390/sym11101239





