An Improved Integer Transform Combining with an Irregular Block Partition
Abstract
:1. Introduction
2. Related Works
2.1. Weng et al.’s Method
2.2. Alattar’s Method
3. The Proposed Scheme
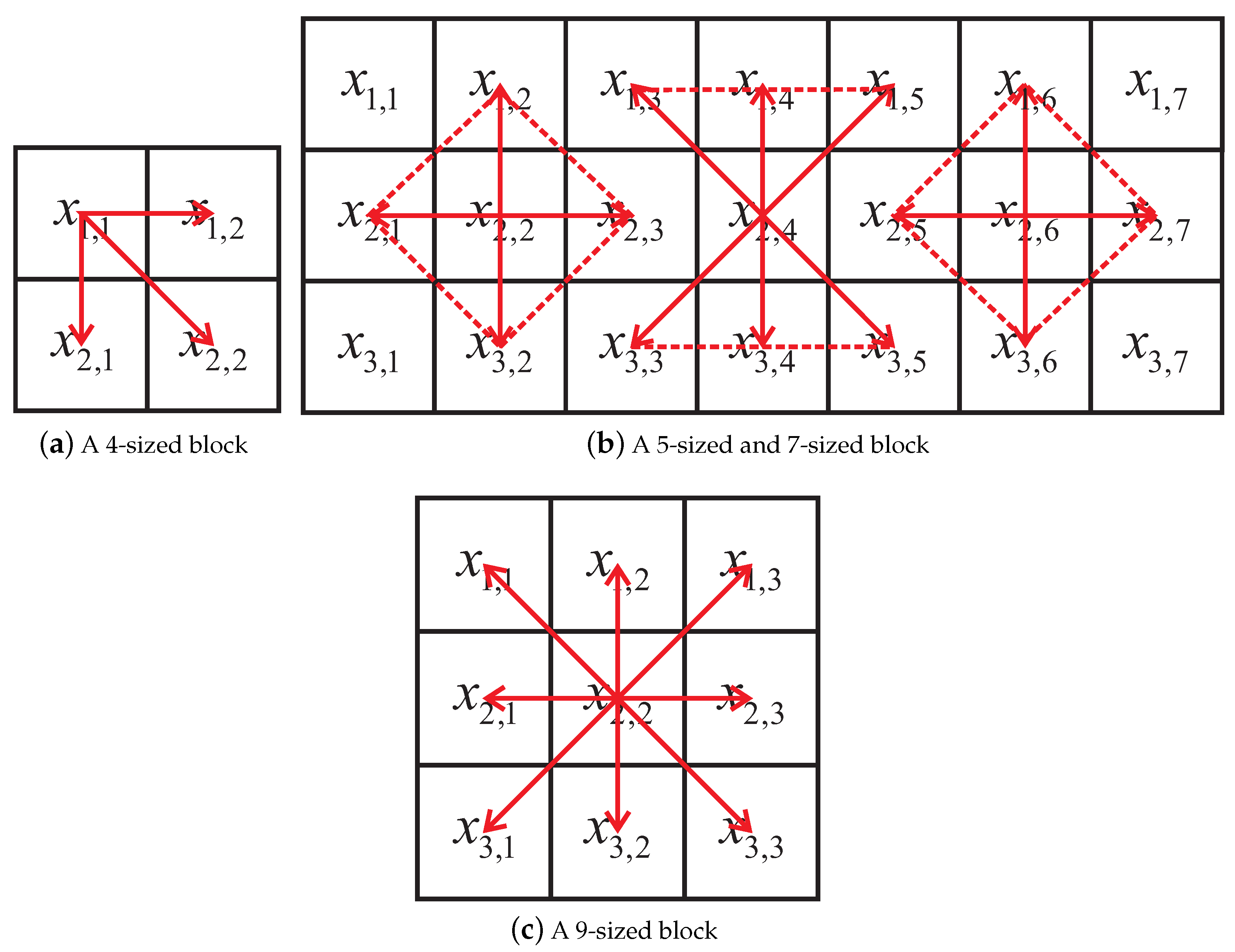
3.1. Irregular Block Partition
3.2. Performance Analysis
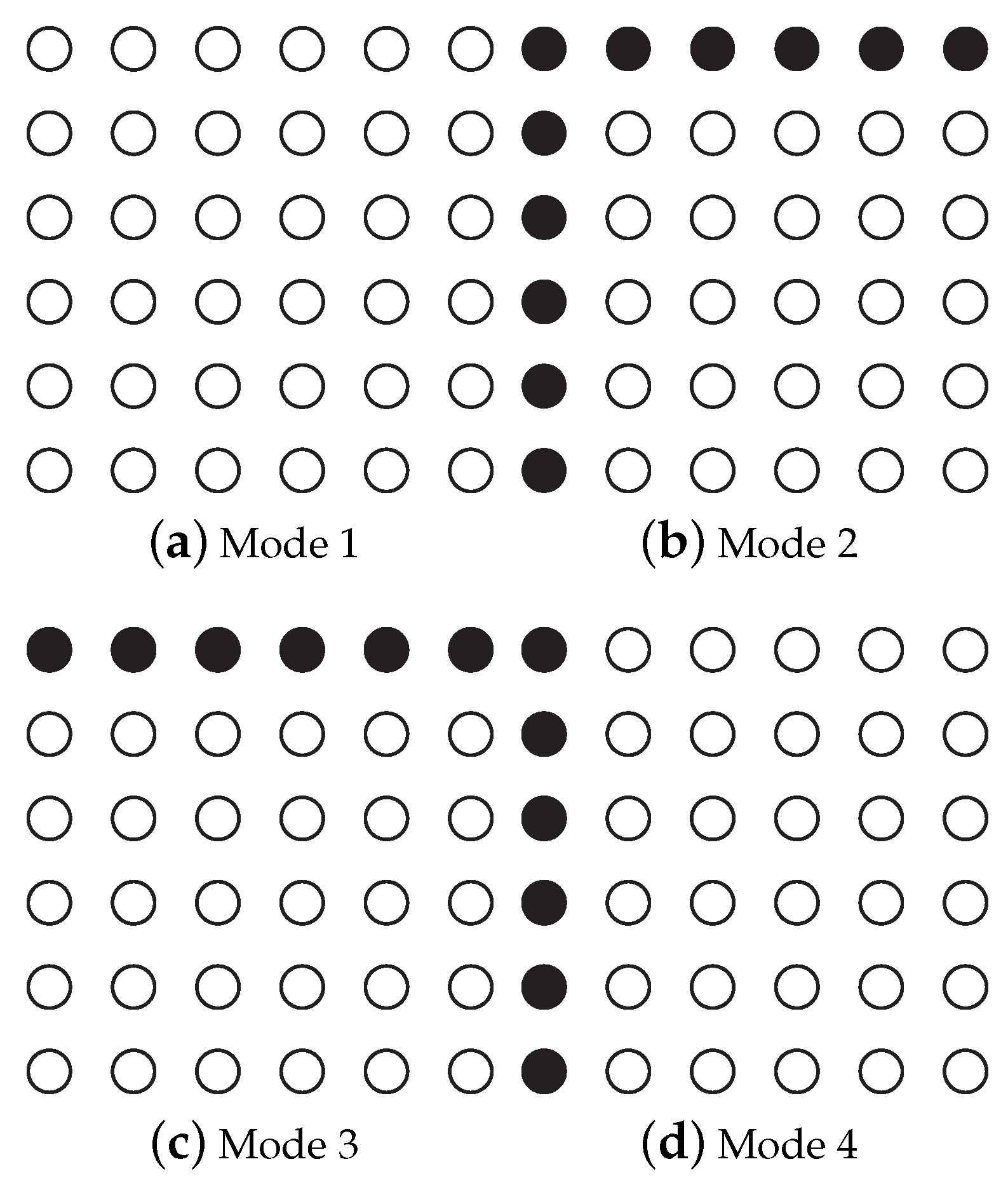
3.3. Block Selection
3.4. Two-Layer Embedding
4. Embedding and Extraction Procedures
4.1. Embedding Procedure
- (1)
- One-layer embedding
- Data bits embeddingif=;elseifendFor the blocks without adjacent pixels, they are ignored in the embedding procedure to ensure reversibility. We employ to describe the number of data bits embedded into the host image, which is equivalent to the number of difference values belonging to .
- Overhead information embeddingThe overhead information is obtained according to the description above. Suppose denotes the required payload, and it is partitioned into two parts which correspond to the first and second embedding layers, respectively. stands for the to-be-embedded payload of the current layer, while represents the maximal embedding capacity. Firstly, is embedded into the blocks in according to the step of data bits embedding. Secondly, for the first modified pixels, we collect their LSBs (least significant binary) and append them to the payload . In this way, the locations of their LSBs are vacant so that they can be occupied by the overhead information. Finally, the rest of the payload along with LSBs are embedded into the remaining blocks in according to the step of data bits embedding.
- (2)
- Watermarked image obtaining
- IfThe payload can be satisfied by one-layer embedding. Therefore, a watermarked image is created after (1) is performed.elseifTwo-layer embedding is adopted to achieve required payload . The remaining payload is defined as . Suppose , then we repeat (1) for the second-layer embedding.end
4.2. Extraction Procedure
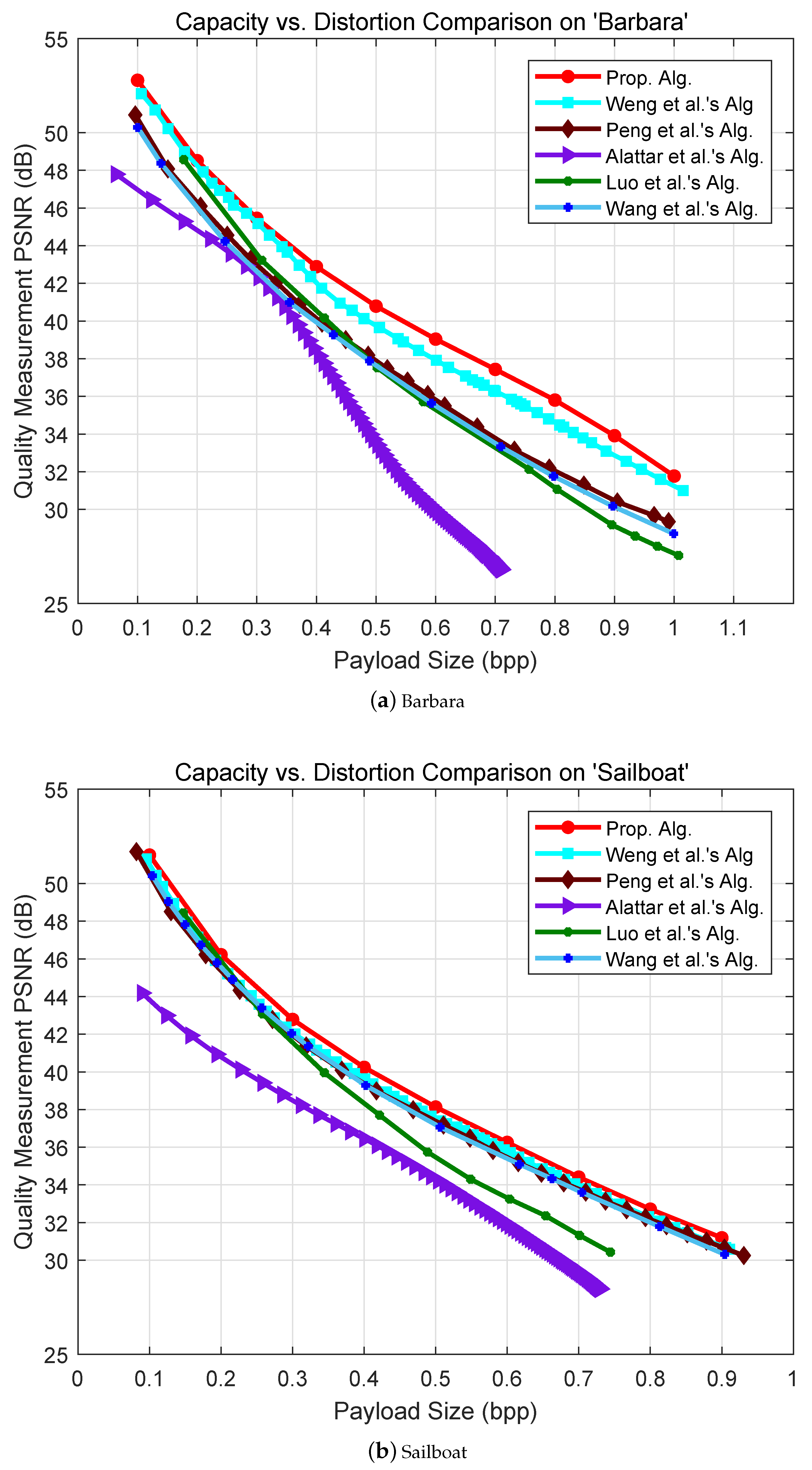
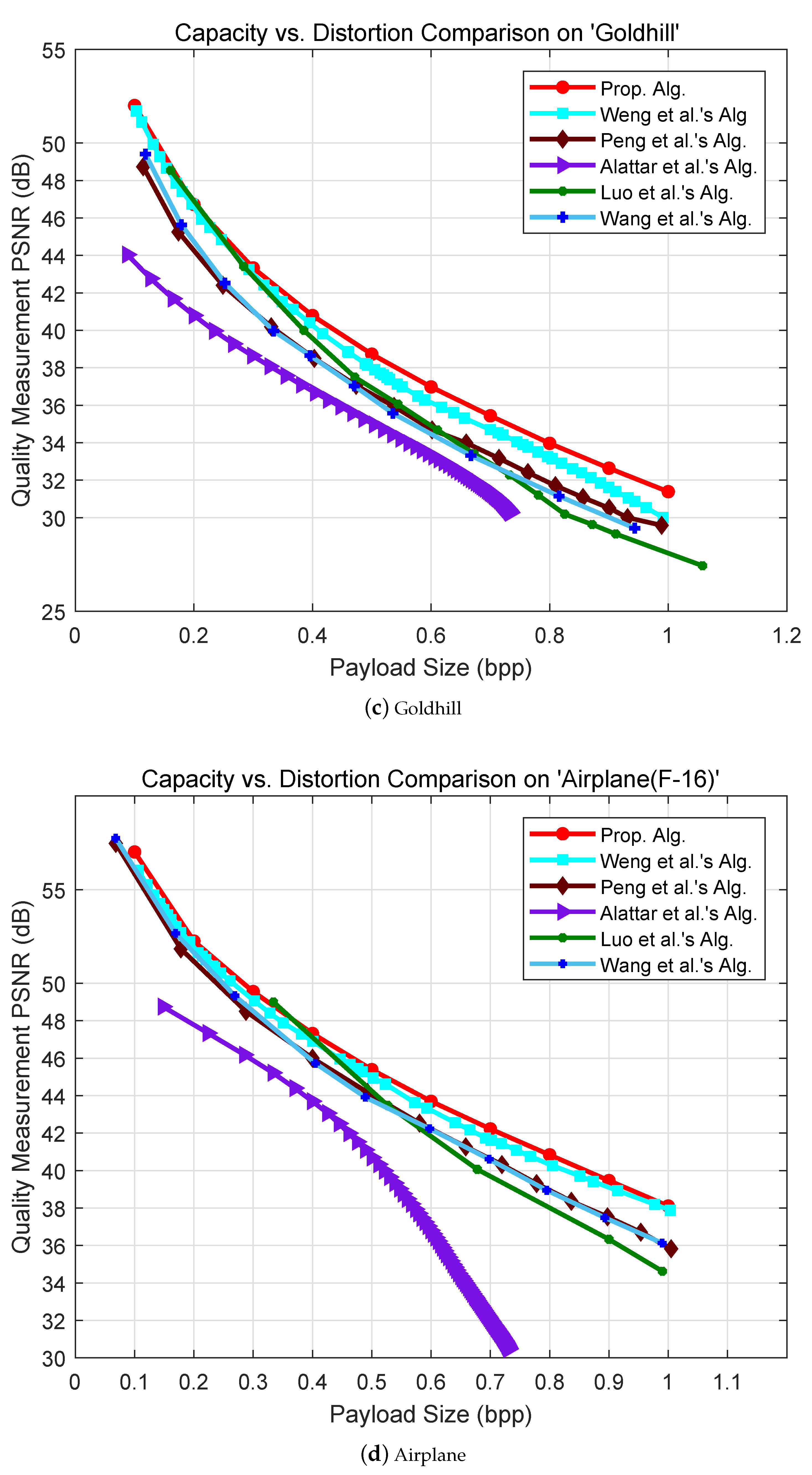
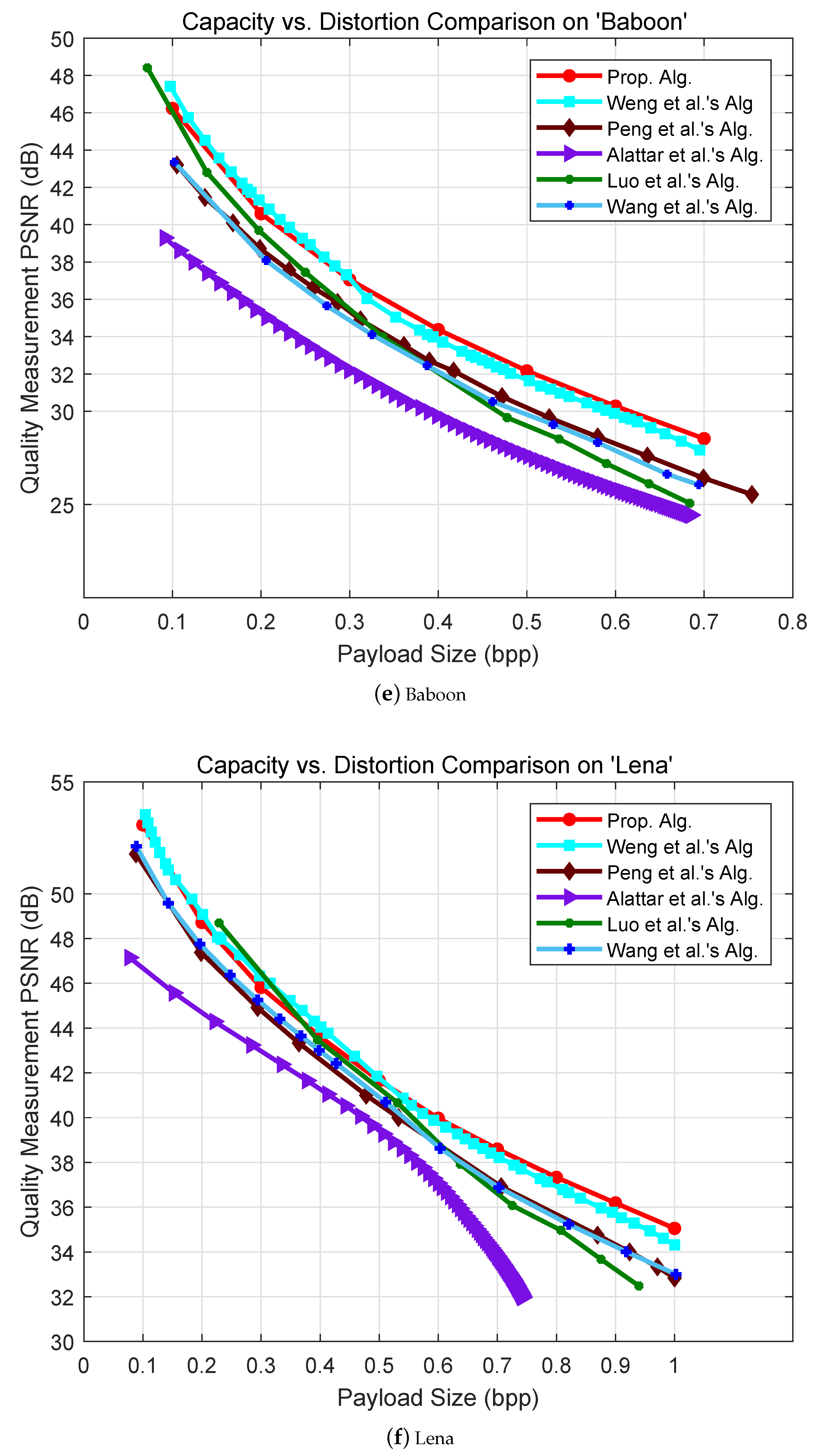
5. Experimental Results
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Celik, M.U.; Sharma, G.; Tekalp, A.M.; Saber, E. Lossless generalized-LSB data embedding. IEEE Trans. Image Process. 2005, 12, 157–160. [Google Scholar] [CrossRef]
- Tian, J. Reversible data embedding using a difference expansion. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 890–896. [Google Scholar] [CrossRef]
- Shi, Y.Q.; Ni, Z.C.; Zou, D.; Liang, C.Y.; Xuan, G.R. Lossless Data Hiding: Fundamentals, Algorithms and Applications. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems, Vancouver, BC, Canada, 23–26 May 2004; Volume 2, pp. 33–36. [Google Scholar]
- Thodi, M.; Rodriguez, J.J. Prediction-error based reversible watermarking. In Proceedings of the 2004 International Conference on Image Processing, Singapore, 24–27 October 2004; Volume 3, pp. 1549–1552. [Google Scholar]
- Alattar, A.M. Reversible watermark using the difference expansion of a generalized integer transform. IEEE Trans. Image Process. 2004, 13, 1147–1156. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, X.L.; Yang, B.; Guo, Z.M. Efficient Generalized Integer Transform for Reversible Watermarking. IEEE Signal Process. Lett. 2010, 17, 567–570. [Google Scholar] [CrossRef]
- Peng, F.; Li, X.; Yang, B. Adaptive reversible data hiding scheme based on integer transform. Signal Process. 2012, 92, 54–62. [Google Scholar] [CrossRef]
- Weng, S.W.; Pan, J.S. Integer transform based reversible watermarking incorporating block selection. J. Vis. Commun. Image Represent. 2016, 35, 25–35. [Google Scholar] [CrossRef]
- Ni, Z.; Shi, Y.Q.; Ansari, N.; Su, W. Reversible data hiding. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 354–362. [Google Scholar]
- Li, X.L.; Li, B.; Yang, B.; Zeng, T.Y. General Framework to Histogram-Shifting-Based Reversible Data Hiding. IEEE Trans. Image Process. 2013, 22, 2181–2191. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Lee, H.K.; Li, J. DE-based reversible data hiding with improved overflow location map. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 250–260. [Google Scholar]
- Sachnev, V.; Kim, H.J.; Nam, J.; Suresh, S.; Shi, Y.Q. Reversible Watermarking Algorithm Using Sorting and Prediction. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 989–999. [Google Scholar] [CrossRef]
- Tsai, P.Y.; Hu, Y.C.; Yeh, H.L. Reversible image hiding scheme using predictive coding and histogram shifting. Signal Process. 2009, 89, 1129–1143. [Google Scholar] [CrossRef]
- Tai, W.L.; Yeh, C.M.; Chang, C.C. Reversible data hiding based on histogram modification of pixel differences. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 906–910. [Google Scholar]
- Hong, W.; Chen, T.S.; Shiu, C.W. Reversible data hiding for high quality images using modification of prediction errors. J. Syst. Softw. 2009, 82, 1833–1842. [Google Scholar] [CrossRef]
- Luo, L.; Chen, Z.; Chen, M.; Zeng, X.; Xiong, Z. Reversible image watermarking using interpolation technique. IEEE Trans. Inf. Forensic Secur. 2010, 5, 187–193. [Google Scholar]
- Hong, W. An efficient prediction-and-shifting embedding technique for high quality reversible data hiding. EURASIP J. Adv. Signal Process. 2010, 2010. [Google Scholar] [CrossRef]
- Coltuc, D. Improved embedding for prediction-based reversible watermarking. IEEE Trans. Inf. Forensic Secur. 2011, 6, 873–882. [Google Scholar] [CrossRef]
- Gao, X.; An, L.; Yuan, Y.; Tao, D.; Li, X. Lossless data embedding using eneralized statistical quantity histogram. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 1061–1070. [Google Scholar]
- Li, X.L.; Yang, B.; Zeng, T.Y. Efficient Reversible Watermarking Based on Adaptive Prediction-ErrorExpansion and Pixel Selection. IEEE Trans. Image Process. 2011, 20, 3524–3533. [Google Scholar]
- Wu, H.T.; Huang, J.W. Reversible image watermarking on prediction errors by efficient histogram modification. Signal Process. 2012, 92, 3000–3009. [Google Scholar] [CrossRef]
- Coatrieux, G.; Pan, W.; Cuppens-Boulahia, N.; Cuppens, F.; Roux, C. Reversible watermarking based on invariant image classification and dynamic histogram shifting. IEEE Trans. Inf. Forensic Secur. 2013, 8, 111–120. [Google Scholar] [CrossRef]
- Jung, S.; Ha, L.; Ko, S. A new histogram modification based reversible data hiding algorithm considering the human visual system. IEEE Signal Process. Lett. 2011, 18, 95–98. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.; Wu, M. An improved human visual system based reversible data hiding method using adaptive histogram modification. Opt. Commun. 2013, 291, 87–97. [Google Scholar] [CrossRef]
- Weng, S.W.; Pan, J.S. Reversible watermarking based on multiple predictionmodes and adaptive watermark embedding. Multimed. Tools Appl. 2013, 72, 3063–3083. [Google Scholar] [CrossRef]


| One-Layer Embedding | Two-Layer Embedding | |||
|---|---|---|---|---|
| Image | Lena | Barbara | Lena | Barbara |
| 8 | 8 | 5 | 5 | |
| 7 | 9 | 6 | 6 | |
| 0 | 0 | 10 | 8 | |
| 0 | 0 | 1 | 2 | |
| Payload (proposed, in bpp) | 0.5 | 0.4 | 0.5 | 0.4 |
| PSNR (proposed, in dB) | 41.20 | 41.89 | 41.65 | 42.88 |
| Lena | Baboon | ||
|---|---|---|---|
| Payload (in bpp) | (in bits) | Payload (in bpp) | (in bits) |
| 0.1 | 40 | 0.1 | 40 |
| 0.2 | 40 | 0.2 | 40 |
| 0.3 | 40 | 0.3 | 40 |
| 0.4 | 40 | 0.4 | 40 |
| 0.5 | 40 | 0.5 | 64 |
| 0.6 | 40 | 0.6 | 80 |
| 0.7 | 40 | 0.7 | 136 |
| 0.8 | 40 | - | - |
| 0.9 | 40 | - | - |
| 1.0 | 40 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, S.; Chen, Y.; Hong, W.; Pan, J.-S.; Chang, C.-C.; Liu, Y. An Improved Integer Transform Combining with an Irregular Block Partition. Symmetry 2019, 11, 49. https://doi.org/10.3390/sym11010049
Weng S, Chen Y, Hong W, Pan J-S, Chang C-C, Liu Y. An Improved Integer Transform Combining with an Irregular Block Partition. Symmetry. 2019; 11(1):49. https://doi.org/10.3390/sym11010049
Chicago/Turabian StyleWeng, Shaowei, Yi Chen, Wien Hong, Jeng-Shyang Pan, Chin-Chen Chang, and Yijun Liu. 2019. "An Improved Integer Transform Combining with an Irregular Block Partition" Symmetry 11, no. 1: 49. https://doi.org/10.3390/sym11010049
APA StyleWeng, S., Chen, Y., Hong, W., Pan, J.-S., Chang, C.-C., & Liu, Y. (2019). An Improved Integer Transform Combining with an Irregular Block Partition. Symmetry, 11(1), 49. https://doi.org/10.3390/sym11010049








