1. Introduction
Digital images are used extensively in various fields, such as the media, publishing, medicine and the military. Therefore, the protection of the copyright and the integrity of digital images is very important and relevant techniques have been developed for this purpose, such as image hashing [
1] and watermarking [
2].
As a branch of watermarking, data hiding is an important technology for providing security for confidential information. Data hiding technology can embed secret data imperceptibly into digital images with various formats [
3]. Depending on whether the cover image can be recovered after embedding the secret data, data hiding methods are classified into two categories, that is, irreversible and reversible data hiding.
Reversible data hiding (RDH) technology embeds the secret data into the cover image in a reversible way [
4]. To date, many RDH methods that work with plaintext images have been proposed. The basic ideas of these methods are different expansion (DE) [
5,
6], histogram shift (HS) [
7,
8], pixel value ordering (PVO) [
9,
10] and the modification of prediction errors [
11,
12]. All of these methods use the spatial correlation and the redundancy of plaintext images to embed additional bits. When a plaintext image is encrypted, these methods cannot work on “noisy” encrypted images, which means that almost all spatial correlation and redundancy are lost.
Recently, RDH in encrypted images (RDHEI) get the attention of researchers. The problem of RDHEI is how to embed secret data into encrypted images reversibly without decryption. RDHEI technology is useful for application in the cloud. To protect privacy, images always are encrypted before they are transmitted to the cloud. Therefore, in the cloud, data must be embedded directly into encrypted images for data management, authentication or other purposes.
To date, several RDHEI methods have been designed, several of which use pixel-bit modification to embed secret bits into encrypted images and recover the images by using the spatial correlation after image decryption. In Reference [
13], encrypted image was divided into non-overlapping blocks and a secret bit was embedded in a block. To embed a secret bit, half of the pixels in a block are selected randomly and the three least significant bits (LSBs) of these pixels are flipped. To recover the image and extract the embedded bits after decryption, the flipped pixels are detected by estimating the smoothness of each block. The method in Reference [
13] was improved in Reference [
14,
15,
16,
17]. In Reference [
14], the side-match strategy was used to improve the precision of the estimation of the smoothness of the blocks. In Reference [
15], more precise functions for estimating the smoothness were used and adjacent pixels in the neighboring blocks were taken into account to estimate the smoothness of the blocks. In Reference [
16], the approach used to select the pixels to be flipped was improved for better quality of the decrypted image and the smoothness of the block was estimated based on the content of the image to reduce errors associated with extracting the bits. In Reference [
17], each block was divided into two or more sub-blocks. By selectively flipping three LSBs of the sub-blocks, two or more bits can be embedded into one block to improve the capacity. In Reference [
18], the secret bits were embedded into randomly-selected pixels in the encrypted image. By using a designed pixel-value predictor after decryption, the modified pixels can be detected to achieve the secret data and the recovered image. A method for improving [
18] was proposed in Reference [
19] and the improved method involved improving the way pixels were selected to be embedded to enlarge the capacity and BCH coding was used to reduce errors in extracting the bits. In Reference [
20], the secret bits were embedded by substituting the most significant bits (MSBs) of the pixels in the encrypted image and recovering the substituted MSBs by MSB prediction after decryption.
Several methods have used compression coding to compress the encrypted image to reserve additional room for embedding data. In Reference [
21], the pixels in the encrypted image are divided randomly into groups. The LSBs of all pixels in each group are compressed by a designed compression matrix to accommodate additional bits. In Reference [
22], the image was divided into non-overlapping
blocks, which were encrypted. Then, the encrypted blocks were classified into a smooth set and a complex set. The LSBs of the blocks in the smooth set were compressed to make room for the embedded bits. In Reference [
23], the image also was divided into
blocks and encrypted at the block level. For the encrypted blocks, run-length coding or matrix compression was chosen to compress the blocks according to the effect of compression. In Reference [
24], the MSBs of 75% of the pixels in the encrypted image were compressed by distributed-source encoding to reserve room. In Reference [
25], the LDPC code was used to compress the fourth LSBs of half of the pixels in the encrypted image to make room.
Several methods used the design of a special encryption scheme to transfer the spatial correlation in the plaintext image into the encrypted image and they used RDH methods, such as histogram shift, different expansion and pixel value ordering to embed secret bits. In Reference [
26], a cross division scheme was used to divide the plaintext image into groups of the same size and the neighboring pixels belonged to the same group. All pixels in the same group were encrypted by using the same key to maintain the spatial correlation between the neighboring pixels. Then, a difference histogram can be generated from the encrypted groups and a histogram shift scheme can be used to embed secret bits based on the histogram. In Reference [
27], the plaintext image was divided into non-overlapping
blocks and the pixels in the same block were encrypted using the same key. Then, a pixel value ordering scheme was used to embed secret bits into the encrypted blocks. In Reference [
28], the plaintext image was divided into non-overlapping
blocks and the image was encrypted by block permutation. An adaptive block-level predictor was designed to generate a set of prediction errors from the encrypted image. Based on the set of prediction errors, a difference expansion scheme was used to embed the secret bits. In Reference [
29], the original image is transformed by integer wavelet transform before image encryption, then a histogram shift scheme can be used on the encrypted coefficients to embed secret bits.
Current studies of RHDEI are focused on improving the embedding rate and the visual quality of the marked decrypted image (i.e., the decrypted image that contains the embedded data). The efficiency of conducting the RDHEI methods should be taken into account considering that the data scales of the images have become very large in many applications in recent years and the cloud would receive a large number of the encrypted images from different data owners. With the aim of supporting the real-time application of RDHEI, we propose a novel, real-time RDHEI method that is based on (7, 4) Hamming coding and MSB prediction. The proposed method considers the capacity and visual quality as well as the execution time. The contributions in this paper are listed as follows:
We proposed a (7, 4) Hamming code-based encoding scheme to embed secret bits into the LSBs of the encrypted image. The scheme can modify only 0–2 LSBs to embed 3 secret bits. Therefore, after data embedding, the visual quality of the marked decrypted image is high.
We introduced an MSB prediction scheme with an error prediction map to implement error-free recovery of a portion of the MSBs. Therefore, these MSBs become reversible and modifiable. The information for recovering the modified LSBs can be embedded into the modifiable MSBs.
We proposed a novel RDHEI method by using the (7, 4) Hamming coding-based encoding scheme and the MSB prediction scheme.
- (a)
The method is a separable method. The receiver can obtain the secret data from the encrypted image without decryption and image recovery.
- (b)
The method is free of errors. The extracted secret data have no incorrect bits. The recovered image is totally the same as the original image.
- (c)
The method has high fidelity of the marked decrypted image.
- (d)
The method is efficient from the standpoint of computation. It can use less execution time for embedding secret data than the existing RDHEI methods. Therefore, it is suitable for real-time applications of RDHEI in the cloud.
The rest of the paper is organized as follows. In
Section 2, the (7, 4) Hamming code encoding and the MSB prediction are introduced. In
Section 3, we propose the novel real-time RDHEI method using the (7, 4) Hamming code and the MSB prediction. In
Section 4, the experimental results of the proposed method are provided and compared with the results of existing RDHEI methods. In
Section 5, we present our conclusions concerning the methods we have developed and proposed.
2. (7, 4) Hamming Code-Based Encoding and MSB Prediction
2.1. The Hamming Code
The Hamming code is one of the most extensively used error correcting codes and it can locate and correct an error in a single bit. The codeword of the (n, k) Hamming code consists of n bits that consist of two parts, that is, the first k bits of the codeword are message bits and the remaining bits, that is, n − k bits, are additional bits that are called parity check bits, which are used to detect and correct the single bit error. One of the most common Hamming code schemes is the (7, 4) Hamming code, which uses a 7-bit codeword that consists of four message bits and three parity-check bits. Below, we show an example of how the (7, 4) Hamming code encodes four message bits into one 7-bit codeword and corrects the single bit error in the codeword.
To do its work, the (7, 4) Hamming code must generate a pair of matrices in advance, that is, the code generator matrix,
G and the parity check matrix,
H. An example of the two matrices is shown as:
Any four message bits can be encoded into a 7-bit Hamming codeword by modulo-2 matrix multiplication. First, the four message bits are regarded as a
vector; then, the vector is multiplied by the
generator matrix,
G, to generate the
vector in which the first four elements are the same as the four message bits and the last three elements are the parity check code. For example, from the four message bits
M = (1110)
2, the 7-bit Hamming codeword,
C, is generated:
Therefore, the codeword C of M is (1110000)2.
To check whether the single bit error has occurred at the receiver’s side, the 7-bit codeword
C that is received is transformed into a
vector and the parity check matrix,
H, is multiplied by the vector using modulo-2 matrix multiplication. If the result of the multiplication is an all-zero
vector, the codeword has no single bit error. Otherwise, the result is equal to one of the matrix columns of
H, denoted as the
ith column and the receiver can detect that the
ith bit is incorrect and correct it. For example, if the codeword
C = (1110000)
2 generated by
G is transformed into
Cerr = (1010000)
2 due to the single bit error, the error can be detected by:
Since the result R is equal to the second column of H, the receiver can detect the second bit of the codeword is an incorrect bit and correct the bit, so that Cerr is recovered to C. Notice that the single bit error can be detected in either message bits or parity-check bits.
2.2. Hamming Code-Based Encoding
Based on the (7, 4) Hamming code, we designed an encoding scheme to embed three secret bits into any seven bits that were extracted randomly from the LSBs of the encrypted image. The basic idea of the Hamming code-based encoding scheme is using the single bit error information of the 7-bit Hamming codewords to represent the secret bits. For a given parity check matrix H, any 7-bit Hamming codeword can be classified as a ‘non-bit-error codeword’ or an ‘ith-bit-error codeword’ () according to Equation (2). The ith-bit-error codeword is the codeword of which the ith bit is detected as an incorrect bit by using the parity check matrix H and the non-bit-error codeword is the codeword of which no bit is detected as an incorrect bit by the H. In the Hamming code-based encoding scheme, the non-bit-error codeword is used to represent the three secret bits (000)2 and the 1st-bit-error codeword, 2nd-bit-error codeword, …, 7th-bit-error codeword are used to represent the three secret bits (001)2, (010)2, …, (111)2.
For a given encrypted image, the image can be randomly divided into groups which contains seven pixels respectively. For any 7-pixel group {P1, P2, …, P7}, the LSBs of all the pixels in the group can be extracted as a 7-bit Hamming codeword C = (b1, b2, b3, b4, b5, b6, b7). To embed three secret bits in C, the Hamming code-based encoding scheme can encode C into a non-bit-error codeword or an ith-bit-error codeword () to represent three secret bits by modifying at most 2 bits of C. The detailed procedure of the Hamming code-based encoding is given as follow:
- Step 1
For the 7-bit codeword C = (b1, b2, b3, b4, b5, b6, b7), we calculate according to Equation (2), where H is the parity check matrix. If R is an all-zero vector, C is a non-bit-error codeword. Otherwise, R must be identical to one column of H. Denoting the index of the column as i, C is an ith-bit-error codeword.
- Step 2
If C is the codeword which represents the three secret bits to be embedded, nothing needs to be done. Otherwise, go to Step 3.
- Step 3
If C is a non-bit-error codeword, C can be encoded into any kth-bit-error codeword by flipping its kth bit bk (). If C is an ith-bit-error codeword (), C can be encoded into a non-bit-error codeword by flipping the ith bit bi or a kth-bit-error codeword by flipping the ith and kth bits. Therefore, by flipping at most 2 bits, C can be encoded into the Hamming codeword which represents the three secret bits to be embedded.
Figure 1 shows an examples of the Hamming code-based encoding scheme. For the given parity check matrix
H, to embed the secret bits (010)
2, the codeword
C1 is the 2nd-bit-error codeword which represents (010)
2, so nothing needs to be done. To embed the secret bits (111)
2, the codeword
C2 is the 4th-bit-error codeword, so the 4th bit and the 7th bit of
C2 are flipped to encode
C2 into a 7th-bit-error codeword which represents (111)
2.
By the proposed Hamming code-based encoding scheme, secret bits can be embedded into 7-bit Hamming codewords that consists of the LSBs of the encrypted image. However, after embedding, the original codewords cannot be recovered directly from the encoded codewords. For reversibility, we designed an MSB prediction scheme to make a portion of the MSBs of the encrypted image modifiable. The information for the recovery of the LSBs can be embedded in the modifiable MSBs and the modifiable MSBs can be recovered without any error. Details of the MSB prediction scheme are given in
Section 2.3.
2.3. MSB Prediction
To recover the modified LSBs of the encrypted image, additional information for recovery should be recorded in the encrypted image. To accommodate the additional information, we designed an MSB prediction scheme that can recover a portion of the modified MSBs by the spatial correlation and the neighboring unmodified pixels after decryption. Therefore, these MSBs are reversible and they can be modified to accommodate additional information for the recovery of the modified LSBs.
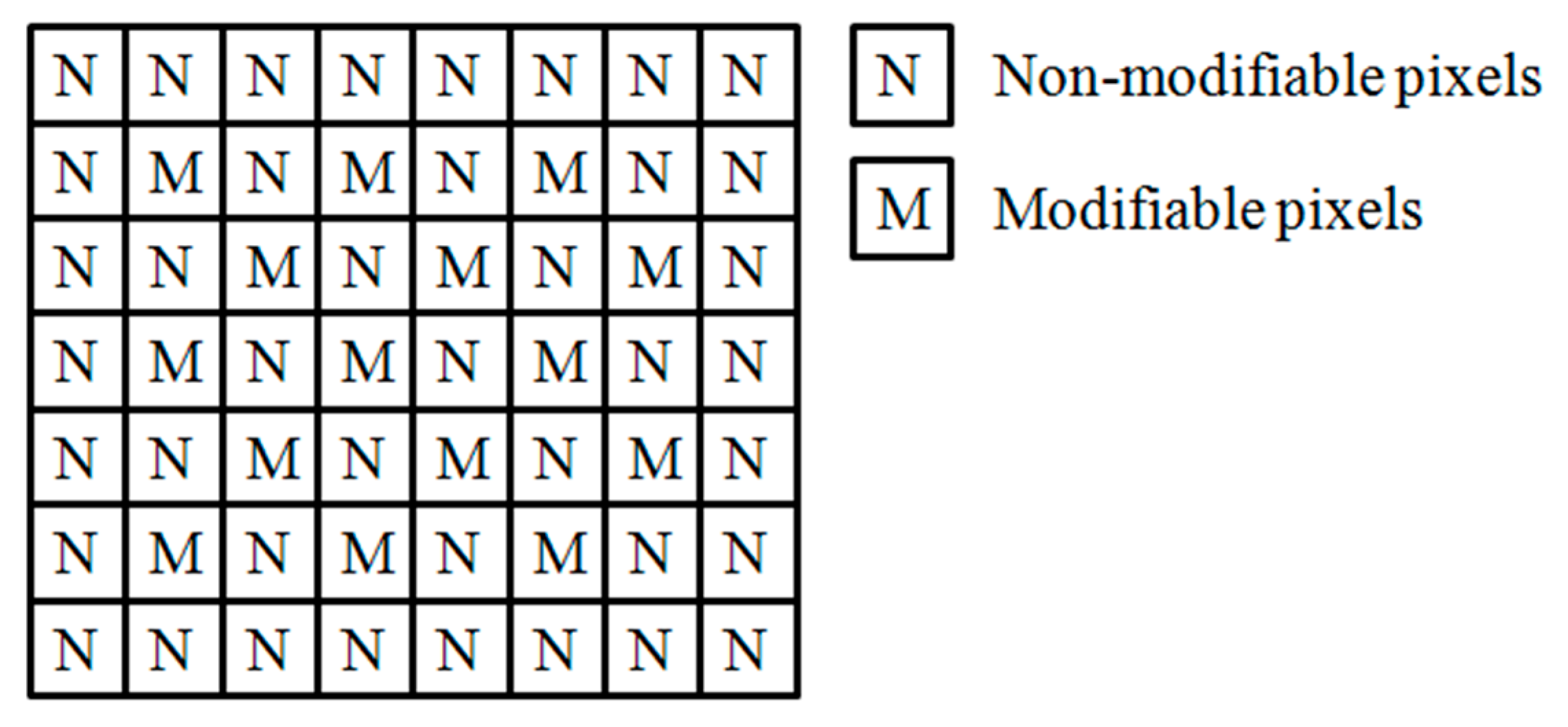
To make a portion of the MSBs reversible, we divided the cover image into two sets, that is, modifiable pixels and non-modifiable pixels.
Figure 2 shows that, for each modifiable pixel
P(
i,
j), its four neighboring pixels
P(
i − 1,
j),
P(
i + 1,
j),
P(
i,
j − 1) and
P(
i,
j + 1) are set to be non-modifiable. The LSBs of the modifiable pixels are used to embed the secret data and the MSBs of the modifiable pixels are used to accommodate additional information for the recovery of the LSBs. The non-modifiable pixels are not modified. After the recovery of the LSBs and decryption, the non-modifiable pixels are used to recover the modified MSBs of the modifiable pixels by MSB prediction.
For a modifiable pixel,
P(
i,
j), of which the MSB potentially has been modified, the MSB prediction scheme recovers the original MSB of the pixel as follows. First, the estimated value of the
P(
i,
j) is calculated by:
Then, the prediction errors of the two candidates, that is,
P(
i,
j) and
Pf(
i,
j), where
Pf(
i,
j) is calculated by flipping the MSB of
P(
i,
j), are calculated by:
According to the prediction errors, the original pixel value of
P(
i,
j) is recovered by:
By using the MSB prediction, the modification of the MSBs of the modifiable pixels can be detected and recovered. Therefore, in the encrypted image, the MSBs of the modifiable pixels can be substituted with the addition information for the recovery of the LSBs.
Since the plaintext image has a spatial correlation and MSB significantly affects the pixel value, the modification of the MSB can be detected correctly by the MSB prediction scheme in most cases. However, if the image has some complex regions in which the spatial correlation between the neighboring pixels is weak, it is possible that the estimated value of the modifiable pixel will be quite different from the original pixel value. In this case, the MSB prediction would choose the wrong candidate as the original pixel value. To recover the modified MSBs with no error, before image encryption, an error prediction map is generated from the original image. The details of the error prediction map are given in
Section 2.4.
2.4. Error Prediction Map
To prevent errors in the recovery of the modifiable MSBs, an error prediction map was designed to help the MSB prediction. The error prediction map was generated from the original image before image encryption. The procedure of generating the error prediction map was:
- Step 1
For the original modifiable pixel, P, use Equation (3) to calculate the estimated value, Pe.
- Step 2
Flip the MSB of P to generate the value of the flipped pixel, Pf.
- Step 3
Calculate the prediction error, PE, of P and the PEf of Pf using Equations (4) and (5), respectively.
- Step 4
If PE > PEf or PE = PEf and the MSB of the estimated value Pe is the same as Pf, the MSB of P cannot be recovered correctly after MSB has been modified. Denote P as the ‘Error prediction pixel’ by recording the coordinate of P.
- Step 5
Repeat Steps 1–4 until all the error prediction pixels in the original image have been recorded.
After image encryption, the generated error prediction map can be encrypted and embedded into the MSBs of the modifiable pixels with its size information by MSB substitution. For an image with the size of
,
bits are required for each error prediction pixel and
bits are required for the size information. In most cases, the error prediction pixels are quite a small portion of all the modifiable pixels in the original image. The detailed discussion on how the size of the error prediction map affect the embedding capacity is given in
Section 3.2.
For a modifiable pixel
P(
i,
j) of which the MSB is potentially modified and its MSB-flipped pixel
Pf(
i,
j) which is generated by flipping the MSB of
P(
i,
j), if the coordinate (
i,
j) is recorded as the error prediction pixel in the error prediction map, the original pixel value of
P(
i,
j) is recovered by:
3. The Proposed Method
Based on the (7, 4) Hamming coding-based encoding and the MSB prediction with the error prediction map, a novel, real-time, error-free RDHEI method is proposed in this section and
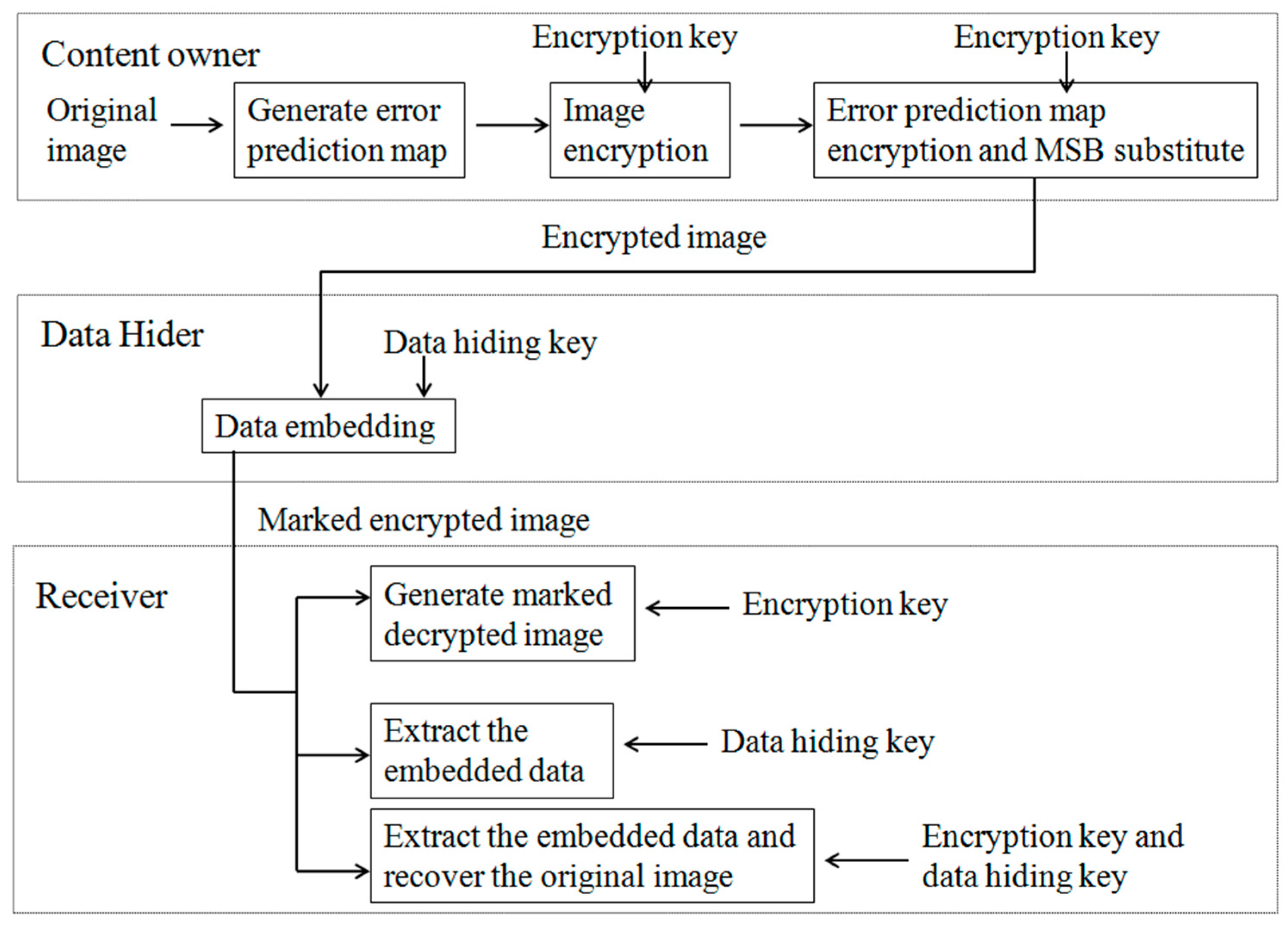
Figure 3 shows an overview of the proposed method. At the content owner’s side, the content owner can generate the error prediction map from the original image. Then, the image and the error prediction map are encrypted and the encrypted error prediction map is accommodated in the MSBs of the encrypted image. At the data hider’s side, the data hider can use the (7, 4) Hamming coding-based encoding to embed secret data. At the receiver’s side, if the receiver only has the encryption key, a marked decrypted image that has high visual quality can be generated. The secret data can be obtained from the encrypted image by using the data hiding key only. The original image can be retrieved when the receiver uses data hiding key and the encryption key together.
3.1. Image Encryption
The stream cipher is used for bit-wise image encryption. Assume that the original image is a standard grayscale image in which the pixels consist of 8 bits. The 8 bits of a pixel,
, are denoted as
–
, where
The steps in the detailed procedure of image encryption are:
- Step 1
Generate the error prediction map from the original image, I.
- Step 2
For each non-modifiable pixel, eight pseudo-random bits, that is,
–
, are generated by using the image encryption key and all of the bits of the pixel are encrypted by:
- Step 3
For each modifiable pixel, six pseudo-random bits, that is,
–
, are generated by using the image encryption key and the six bits,
–
, of the pixel are encrypted by:
Since and are the first and second LSBs, respectively, they are similar to random bits and reflect almost no meaningful content. By using the unencrypted LSBs, the embedded secret data can be obtained from either the encrypted image or the marked decrypted image.
- Step 4
To encrypt the n-bit error prediction map, generate n pseudo-random bits by using the encryption key and do the bit-XOR encryption.
- Step 5
Substitute the MSBs of the first l + n modifiable pixels with the l-bit size information of the error prediction map and the n-bit error prediction map.
After image encryption, the encrypted image, EI, can be sent to the data hider for embedding secret data.
3.2. Data Embedding
At the phase of data embedding, the (7, 4) Hamming code-based encoding is used to embed the secret data into the LSBs of the encrypted modifiable pixels of the encrypted image EI. The steps in the detailed procedure of image encryption are as follows:
- Step 1
According to the size information of the error prediction map, all the modifiable pixels in the encrypted image are divided into two sets: the first set, denoted as FP = {FP1, FP2, …, FPl+n}, contains the first l + n modifiable pixels of which the MSBs indicate the information of the error prediction map. The second set, denoted as RP = {RP1, RP2, …, RPfin}, contains the rest of the modifiable pixels of which the MSBs can be modified to embed the information for image recovery.
- Step 2
To embed secret bits, all the modifiable pixels are divided into 7-pixel groups as follow:
By using the data hiding key, each time the data hider pseudo-randomly selects one pixel from FP and six pixels from RP to form a 7-pixel group, , until or RP does not have enough pixels.
If and RP still has enough pixels, the data hider uses the data hiding key to pseudo-randomly divide RP into 7-pixel groups as .
For each group, the first and second LSBs of all the pixels are used to form Hamming codewords and the six MSBs of the 2nd–7th pixels are used to record the original information of Hamming codes for image recovery. To protect the information of the error prediction map, the MSB of the first pixel cannot be modified.
- Step 3
For each 7-pixel group, the 7-bit Hamming codeword is extracted from the first LSBs of all the pixels in the group to embed three secret bits. By using the parity check matrix
H, the 7-bit Hamming codeword is classified as one of the eight types of 7-bit Hamming codewords (the eight types are the non-bit-error Hamming codeword and the seven
ith-bit-error codewords (
)). For image recovery, the MSBs of the 2nd, 3rd and 4th pixels are modified to record the original type of the codeword (As given in
Section 2.2, the non-bit-error codeword is represented by (000)
2, the 1st-bit-error codeword is represented by (001)
2 and so on). Finally, the 7-bit Hamming codeword is encoded to represent the three secret bits by using the Hamming code-based encoding scheme in
Section 2.2.
- Step 4
After all the groups have been processed in Step 3, the second LSB layer can be used to embed secret bits. For each 7-pixel group, the 7-bit Hamming codeword is extracted from the second LSBs of all the pixels in the group. The procedure of data embedding is the same as the procedure in Step 3, except that the original codeword is recorded by the MSBs of the 5th, 6th and 7th pixels.
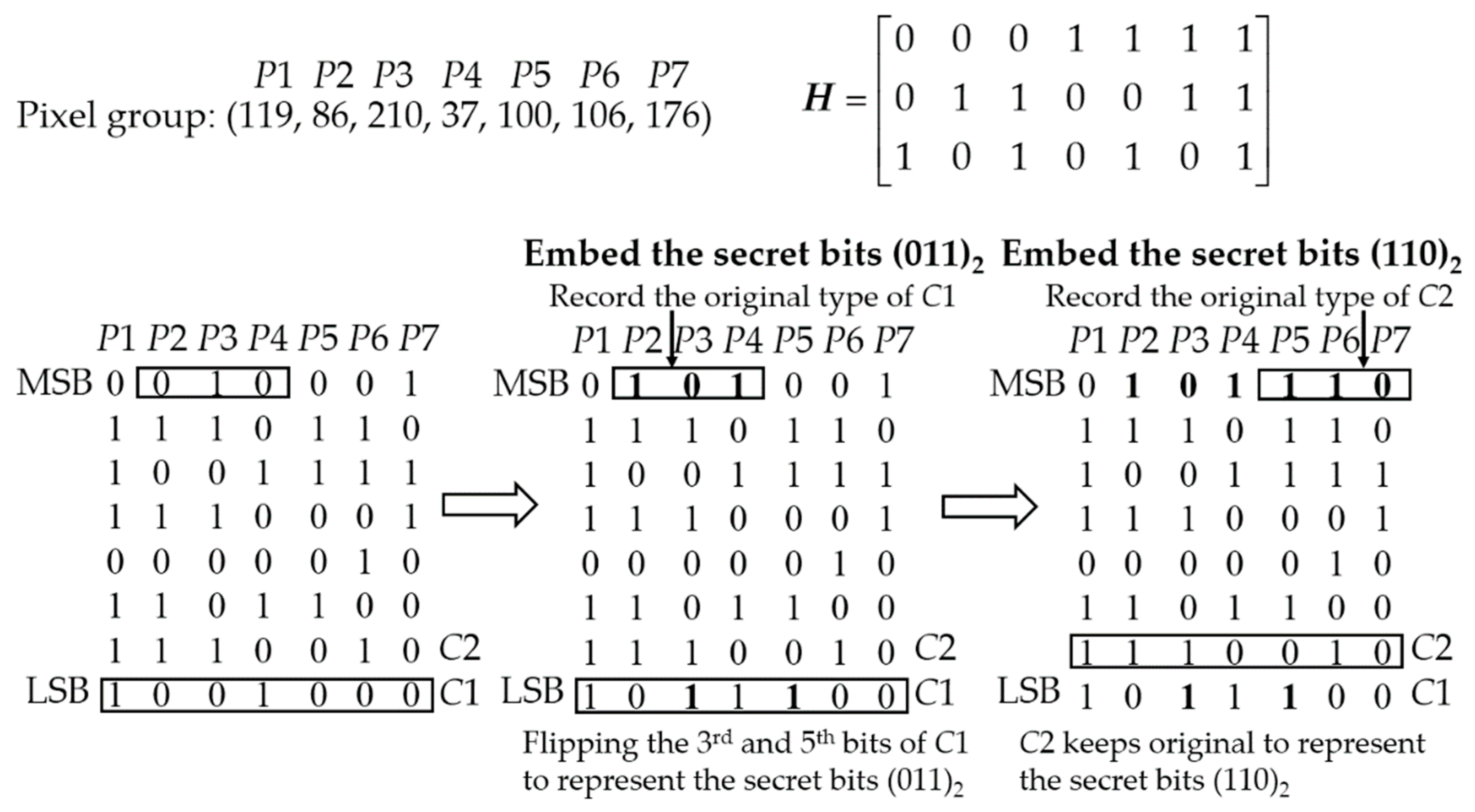
Figure 4 shows an example how the secret bits are embedded to the first LSBs and the second LSBs of all the pixels in the 7-pixel group. To embed the secret bits (011)
2 into the first LSBs of the pixels, the Hamming codeword consisting of the first LSBs
C1 = (1001000)
2 is classified as the 5th-bit-error codeword, then the MSBs of the 2nd, 3rd and 4th pixels are modified to (101)
2 to record the type of the original
C1. Then the 5th bit and the 3rd bit of
C1 are flipped to encode
C1 into a 3rd-bit-error codeword to represent the secret bits (011)
2. To embed the secret bits (110)
2 into the second LSBs of the pixels, the Hamming codeword consisting of the second LSBs
C2 = (1110010)
2 is classified as the 6th-bit-error codeword, then the MSBs of the 5th, 6th and 7th pixels are modified to (110)
2 to record the type of the original
C2. Since
C2 represents the secret bits (110)
2, nothing needs to be done to encode
C2.
According the procedure of data embedding, the embedding capacity is determined by the number of the 7-pixel groups. When the number of the pixels in FP is not larger than one-seven of the number of the modifiable pixels, the number of the 7-pixel groups is at the maximum value , where MPN is the number of the modifiable pixels. Therefore, if the size of all the information of the error prediction map is not larger than , the error prediction map does not affect the embedding capacity. In most cases, the size of the error prediction map are too small to affect the embedding capacity, due to the precise prediction of the MSBs of the modifiable pixels.
For an image with the size of , there are at most modifiable pixels. So the maximum number of the 7-pixel groups is . For each group, the computation complexity of embedding three secret bits is O(1). Therefore, the computation complexity of data embedding in the proposed method is O(MN).
After embedding data, the marked encrypted image is sent to the receiver. To extract the secret data, the data hiding key and the parity check matrix H should be shared with the receiver in advance.
3.3. Image Recovery and Data Extraction
The receiver can obtain different data from the marked encrypted image by using different keys.
3.3.1. Obtain the Marked Decrypted Image
If the receiver only has the encryption key, the receiver can obtain the marked decrypted image, which is very similar to the original image. The secret data still exist in the marked decrypted image and can be obtained by using the data hiding key. The procedure of generating the marked decrypted image is as follows:
- Step 1
Extract the l-bit size information from the first l MSBs of the modifiable pixels of the marked encrypted image and then extract the encrypted error prediction map according to the size information.
- Step 2
Decrypt the marked encrypted image and the error prediction map.
- Step 3
For each modifiable pixel P, calculate the estimated pixel value Pe by the four neighboring non-modifiable pixels of P according to Equation (3).
- Step 4
Calculate the prediction error .
- Step 5
Flip the MSB of P to generate a new pixel value Pf and calculate the prediction error .
- Step 6
According to the error prediction map, if P is not denoted as the error prediction pixel, the MSB of P is recovered by PE and PEf according to Equation (6). Otherwise, the MSB of P is recovered by PE and PEf according to Equation (7).
- Step 7
Repeat Steps 3–6 until all the MSBs of the modifiable pixels have been recovered.
Figure 5 shows an example of MSB recovery of the modifiable pixel
P. By flipping the MSB of
P,
Pf is generated. The four neighboring pixels of
P are non-modifiable pixels which cannot be modified in the procedure of data embedding. By the four neighboring pixels, the estimated value
Pe is calculated. Then the two prediction errors
PE and
PEf are calculated. Since
P is not an error prediction pixel according to the error prediction map and
PE >
PEf,
Pf is the original pixel value according to Equation (6).
To obtain the marked decrypted image, the MSBs of the modifiable pixels are recovered without recovering the modified LSBs of the modifiable pixels. However, compared with the MSB, the LSB have very little impact on the pixel value. In most cases, the modified LSBs cannot affect the results of the MSB recovery. Therefore, without recovering LSBs, the MSBs of the modifiable pixels are still highly likely to be recovered correctly. The generated marked decrypted image is very similar to the original image and it contains the secret data which can be extracted by the data hiding key.
3.3.2. Data Extraction
By using the data hiding key and the parity check matrix H, the receiver can obtain the secret data from the encrypted image or from the marked decrypted image. The procedure for obtaining the secret data is:
- Step 1
Use the data hiding key to divide all the modifiable pixels into the 7-pixel groups.
- Step 2
For each 7-pixel group, extract the 7-bit Hamming codeword from the first LSBs of all the pixels in the group. By using the parity check matrix H, the 7-bit Hamming codeword can be classified as a non-bit-error codeword or an ith-bit-error codeword (). Since the Hamming codeword has been encoded to represent the three secret bits in the procedure of data embedding. Therefore, the three secret bits can be directly obtained according to the Hamming codeword.
As given in
Section 2.2, the non-bit-error codeword represents the three secret bits (000)
2 and the 1st-bit-error codeword, 2nd-bit-error codeword, … and 7th-bit-error codeword represent the three secret bits (001)
2, (010)
2, …, (111)
2.
- Step 3
If all of the groups are processed in Step 2 and not all the embedded bits are extracted, extract the embedded bits from the second LSB layer of each group until all of the embedded bits have been extracted. The process of extraction is the same as Step 2.
Figure 6 shows an example of extracting secret bits from the first and the second LSBs of all the pixels in the 7-pixel group. The Hamming codeword
C1 is extracted from the first LSBs of all the pixels. By using the parity check matrix
H,
C1 is classified as a 3rd-bit-error codeword. So the embedded secret bits are (011)
2. The codeword
C2 is extracted from the second LSBs of all the pixels.
C2 is classified as 6th-bit-error codeword and the embedded secret bits are (110)
2.
3.3.3. Image Recovery
If the receiver has the encryption key, the data hiding key and the parity check matrix, H, the original version of the marked encrypted image can be recovered without any error. The procedure for recovering the image is:
- Step 1
Use the data hiding key to divide all the modifiable pixels into the 7-pixel groups.
- Step 2
For each group, extract the 7-bit Hamming codeword C1 from the first LSBs of all the pixels in the group and use the parity check matrix H to classify C1 into a non-bit-error codeword or an ith-bit-error codeword ().
- Step 3
Extract the MSBs of the 2nd–4th pixels in the group. The three MSBs represent the original type of C1. If C1 matches the original type represented by the three MSBs, C1 is unmodified and does not need to be recovered. Otherwise, C1 is recovered to its original type as follow:
If C1 is a non-bit-error codeword, C1 is recovered to the kth-bit-error codeword by flipping the kth bit of C1 ().
If C1 is an ith-bit-error codeword, C1 is recovered to the non-bit-error codeword by flipping the ith bit of C1 or the kth-bit-error codeword by flipping the ith and kth bits of C1.
- Step 4
Extract the 7-bit Hamming codeword C2 from the second LSBs of all the pixels in the group and the MSBs of the 5th–7th pixels in the group which represent the original type of C2. Then C2 is recovered to its original version the same as Step 3.
- Step 5
Repeat Steps 2–4 until all the first and second LSBs have been recovered.
- Step 6
Recover all of the MSBs of the modifiable pixels of the decrypted image. The recovery of the MSBs is the same as the procedure of obtaining the marked decrypted image in
Section 3.3.1. Since the LSBs are recovered, all of the modified MSBs can be recovered free of errors. Therefore, the original image has been retrieved with no error.
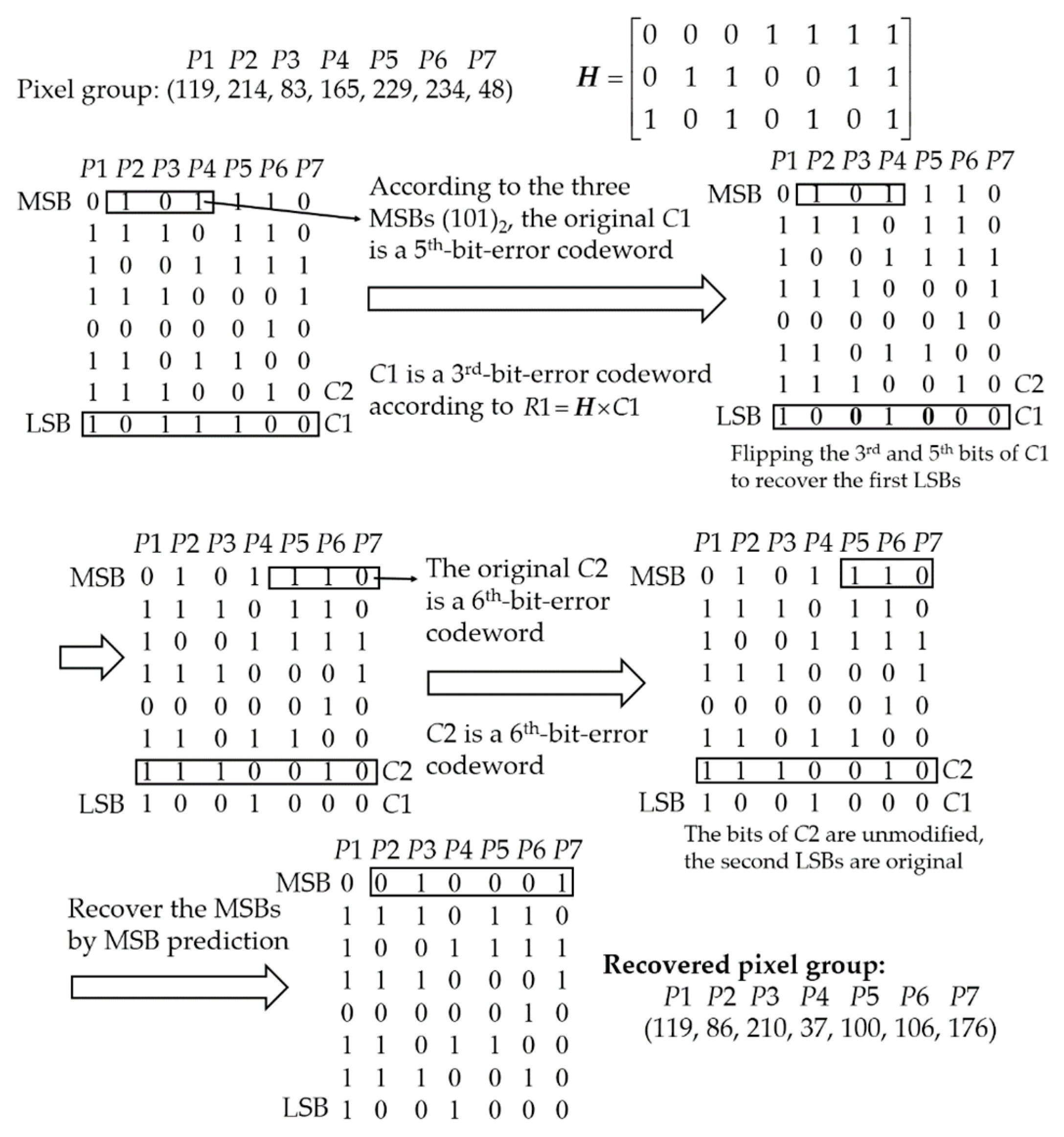
Figure 7 shows an example of recovering the LSBs and MSBs of the modifiable pixels in the group. First, the Hamming code
C1 = (1011100)
2 is extracted from the first LSBs of all the pixels and its original type information (101)
2 is extracted from the MSBs of
P2,
P3 and
P4. By using the parity check matrix
H,
C1 is classified as a 3rd-bit-error codeword. According to the original type information (101)
2,
C1 is a 5th-bit-error codeword, so the 3rd and 5th bits of
C1 are flipped to recover the original LSBs. Then, the Hamming code
C2 = (1110010)
2 is extracted from the second LSBs of all the pixels and its original type information (110)
2 is extracted from the MSBs of
P5,
P6 and
P7. Since
C2 is a 6th-bit-error codeword which matches the original type information (110)
2, the bits of
C2 are unmodified in the procedure of data embedding and do not need to be recovered. After recovering the first and second LSBs, the MSBs of
P2,
P3, …,
P7 are recovered by the neighboring non-modifiable pixels and the error prediction map.
4. Experimental Results
In this section, we evaluate the performance of the proposed method. The evaluations include capacity, visual quality and execution time. The results are compared with the existing RDHEI methods described in References [
15,
18,
27].
Figure 8 shows the six 512 × 512 standard grayscale test images [
30]. The experimental programs were implemented in MATLAB 2012 and run on a computer with 3.6 GHZ Intel i7-4790 CPU and 8 GB memory using the Windows 7 OS.
Figure 9 shows the images of Lena generated by the proposed method.
Figure 9b shows the marked encrypted image with 0.2126 bpp. The image is almost noise-like and the content is secure.
Figure 9c shows the marked decrypted image generated from
Figure 9b with PSNR = 57.73; this image is highly similar to
Figure 9a.
Figure 9d is the recovered image, which is identical to
Figure 9a.
Table 1 shows the embedding rates of the proposed scheme and the three existing methods. Since data extraction errors may occur in Reference [
15,
18], their embedding rates were multiplied with a weighted value, that is,
, where
p is the error rate and
H is the binary entropy function [
31]. Compared with the competitors, the proposed method can achieve a stable and relatively higher capacity. That means that the number of error prediction pixels is small and that there are sufficient modifiable MSBs to support data embedding.
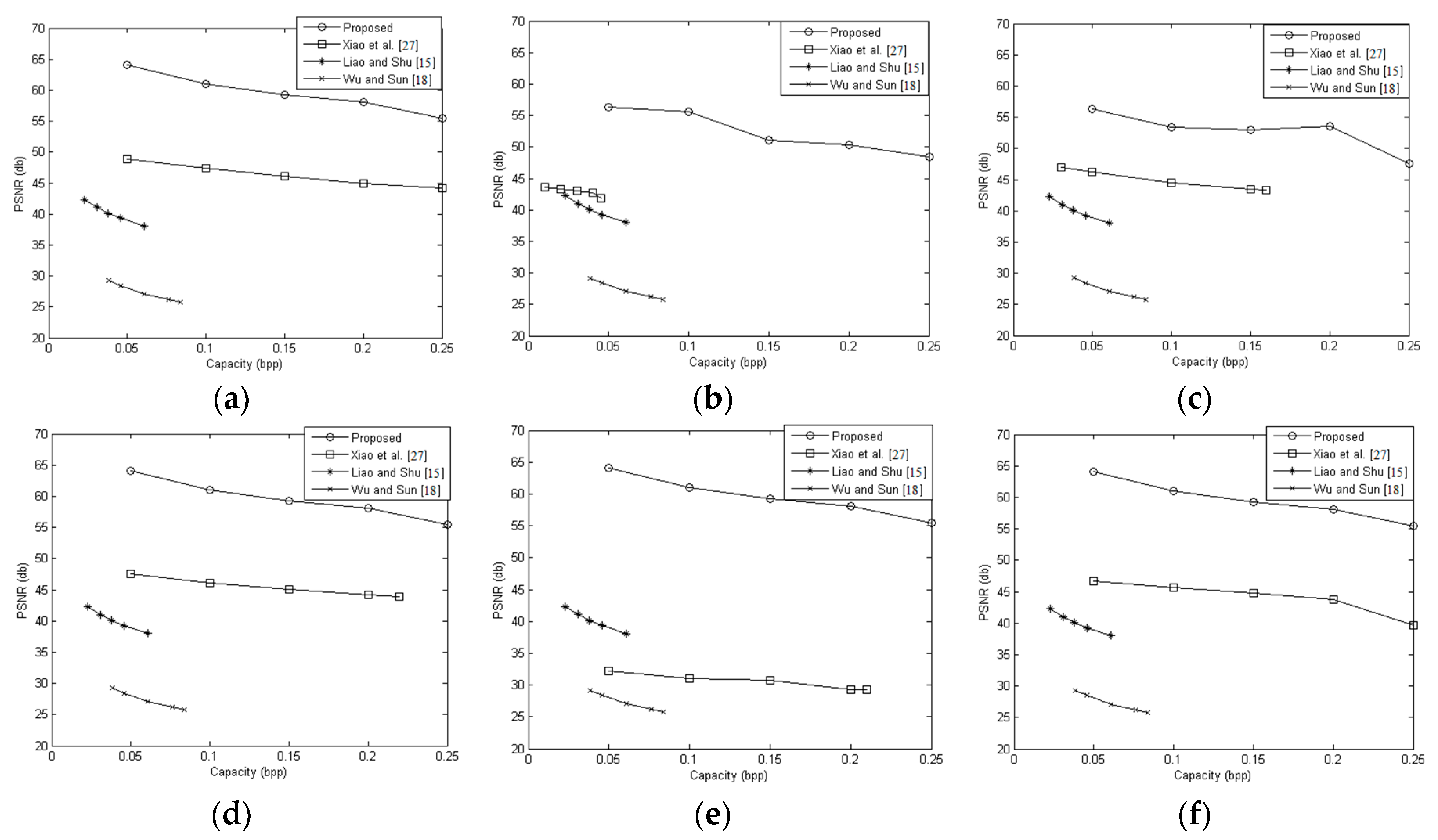
For different embedding rates, the results of the PSNR of the marked decrypted images are shown in
Figure 10. For the smooth images (Airplane, Lena, Peppers and Zelda), the PSNR values of the proposed method were greater than 55 dB at 0.25 bpp. For the complex images (Baboon, Barbara), the PSNR values still were greater than 45 dB at 0.25 bpp. These results showed that the proposed scheme outperformed the other RDHEI methods. This is because, in the proposed method, only a few of the LSBs were modified to embed data and most of the modified MSBs can be recovered correctly. The reason why the PSNR values of the complex images are worse than the PSNR values of the smooth images is that: to obtain the marked decrypted images, for each modifiable pixels, the MSB is recovered without recovering the modified LSBs in advance. In the complex images, more modifiable pixels are estimated inaccurately, so the modified LSBs of these pixels are more likely to affect the results of the comparison between two prediction errors of each estimated pixel. That results in more errors in the MSB recovery of the decrypted marked images.
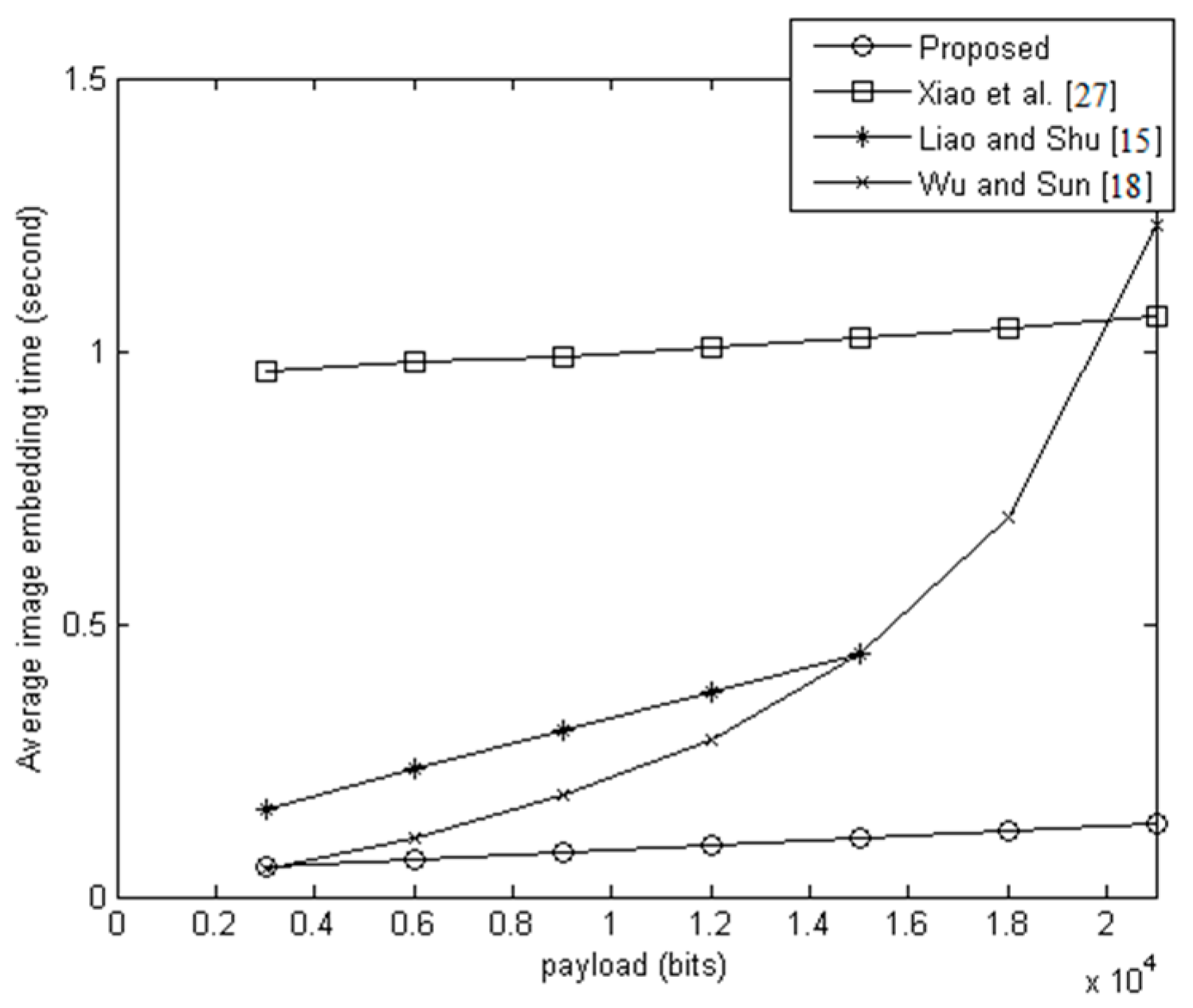
Considering that the cloud must receive and process large numbers of encrypted images from different content owners, the efficiency of data embedding is very important.
Figure 11 shows the average execution time of the four methods for embedding data in 100 images. The images were selected randomly from BossBase-1.01 [
32].
Figure 11 shows that, for the same payloads, the average execution time of the proposed method was less than the average execution times of the other three methods. There are three reasons the proposed method can embed data more efficiently than the other methods. First, in the proposed method, the secret bits can be embedded into any pixel group without addressing any special case, while the other methods need to find the available regions in the image for data embedding ([
18,
27]). Second, the proposed method needs to modify only 5 bits, at most, to embed 3 secret bits, while the other methods must modify more pixels to embed only 1 bit ([
15,
18]). Third, the proposed method embeds secret bits by a simple matrix multiplication, while the other methods need to perform complex operations such as data compression and bit-map embedding ([
27]).