Risk Level Evaluation on Construction Project Lifecycle Using Fuzzy Comprehensive Evaluation and TOPSIS

Abstract

A risk is a predominant problem in the developing countries construction projects. Although numerous studies have been concerned on risk, there is a limited study on a mechanism to identify the typical risks and effects level. This paper presents an approach for evaluating the risks in case of schedule delays at the various lifecycles of construction projects. The methodology applied is an integrated model of the technique for order preference by similarity to ideal solution (TOPSIS) and fuzzy comprehensive evaluation (FCE). In this study, common criteria, sub-criteria, and attributes are constructed to make a decision concerning the influence level of risk of delay at the construction project lifecycle. The results showed that the construction stage (44%) is highly influenced, the second highly influenced stage is post construction (37%), and the least risked stage is pre-construction (35%). The construction projects in Ethiopia have faced an average delay risk of 38% at a high and very high-risk level. This work is expected to serve as a tool to assist managers in the management and control of schedule delays to mitigate their risks.

1. Introduction

Construction projects have a complex nature owing to the site work difficulty, labour change for every site, adverse weather effect, and the higher exposure to error [1]. Consequently, numerous types of risks are occurred in different phases of projects and have an impact on time overrun, cost overrun, quality, and safety [2]. Schedule delay risk has many effects such as increased cost, late completion, disruption, third-party claims, loss of productivity and quality, disputes, and termination of contracts [3]. Therefore, controlling risks in a construction project has been a fundamental part of management in construction projects for decades [4].

A schedule is the main concern for construction projects, because of it influenced by several risks, such as environmental condition, equipment efficiency, productivity, material delivery, and soil types [5]. These factors are caused to delay and cost overruns that often jeopardize safety and quality performance [6]. For example, 13% of the Australian construction projects have faced 40% time overrun [7]. In the United Arab Emirates (UAE), the construction projects encountered 50% schedule delay [8]. In Malaysia, the government projects faced approximately 20% of delay [9]. Construction projects in Saudi Arabia experienced 70% time overrun, among 56% of consultants and 76% of contractors experienced 10–30% of delay, which causes to approximately 50% of cost overruns [10]. In Ethiopia, 40–60% of the construction projects occurred delay [11]. The studies indicate that the risk of schedule delay in developed and developing countries is critical and requires further investigation.

Risk of Schedule delay has a major negative effect on participating parties and projects [12]. Schedule delay often occurs because of many reasons attributable to owners or contractors. The significant contribution of owners often related to issues such as the settlement of claims, slow decision-making, early planning and design, change in the scope, schedule delay in payment, and excessive bureaucracy. Conversely, the contribution of contractors includes cash flow problems, difficulty in obtaining permits, and ineffective planning and scheduling [13]. The main groups of schedule delay factors were classified as owner, contractor, design, consultant, labour, equipment, material, external, and project-related [14]. The other important schedule delay factors mentioned are a slow decision by authorities, lack of funding, errors in work, improper planning, and lack of need identification [15].

Different scholars have conducted different studies on risk. However, the problem of risk is still prevalent. Moreover, the problem requires a pioneering decision-making mechanism to evaluate risk [16]. The evaluation of risk helps to quantify the risks level to mitigate their effects. Therefore, managers need to emphasize on a decision-making mechanism for schedule risk evaluation [6]. The evaluation mechanism should consider the risk throughout the construction lifecycle. Evaluation of risks on construction projects improves quality, safety, reduces cost, and increases the satisfaction of stakeholders.

The objective of this study is to evaluate the delay risk level at the construction lifecycle and comparing the lifecycle to each other. The study evaluates the risk impact level for criteria and sub-criteria based on the different attributes. Finally, the study proposes a method for delay risk evaluation using an integrated decision model of the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) and fuzzy comprehensive evaluation (FCE).

2. Literature Review

Improper risk management is found to be the main cause for the time overrun, cost overrun, and the problem of quality and safety [4]. Risk management is a crucial and important part of the decision-making process for construction projects to reduce risk [17]. Risk management has been investigated from a different viewpoint among certain countries because of the fact that the risk effect varies in different instances [18]. Various researchers have studied the causes and effects of risk for decades to identify the risk factors. Most of the previous studies focused more on the identification of general risk factors and effects than identifying the typical level of impact at the different construction lifecycles.

The studies in different countries identified different risk problems using different methods. However, the method has a certain limitation. One of the most vital methods is the application of the integrated methods of a relative importance index and fuzzy analytical hierarchy process, have been used to reduce risk [19]. This assessment method has limitations in imprecision and involves subjective judgment [14]. The integration of interpretive structural modelling with fuzzy logic has an important role in risk assessment. The model used a computer program to form a relationship between factors in a system [18]. However, this method overlooked the weight of the relationship between factors that makes difficult to use in a complex system [20]. Bayesian belief network developed to quantify the probability of delay risk in construction project considering the cause-effect relations among factors [21,22]. In addition, System Dynamic (SD) plays a respective advantage for schedule delay risk effects investigation based on the causal loop diagrams considering the simulation-based scheduling [23]. Although the System Dynamics and Bayesian Belief Network are important for risk assessment, the methods had restrictions on the structural relationship. Different studies may have different structures of relations and assumptions between factors, this makes confined the models because it may vary from one expert to another [24,22]. The structural equation modelling considers the complex nature of factors and used a causal relationships modelling technique for analyzing the relationship between the factors [25]. However, the method has a certain curb that the risk paths in the design and the dynamic behaviour of the risk factors were not considered [18]. The different methods may have different contribution with certain limitations, especially for risk assessment [26]. In addition, the different studies in the different methods have still lacked a systematic approach to consider the complex and dynamic nature of construction projects risk for better understanding and effective risk management [27]. The aforementioned methods contributed for better assessment of schedule delay risk but the studies still have some confined. First, the evaluation of risk impact level throughout the construction lifecycle has limitations. Second, the assessment methods have been identifying the relations and ranking of factors, but most of the studies were confined to evaluate the level of impact of factors on different construction activities.

To fill this gap, this study aims to propose a hybrid model for delay risk assessment in construction projects with the aid of FCE and TOPSIS. The hybrid model helps managers to have appropriate decision-making mechanism to minimize schedule risk impact. The integrated model of FCE and TOPSIS is an important mechanism to detect typical delay risk impact in construction projects, which is beyond the identification of factors and relationships between factors.

3. Research Methodology

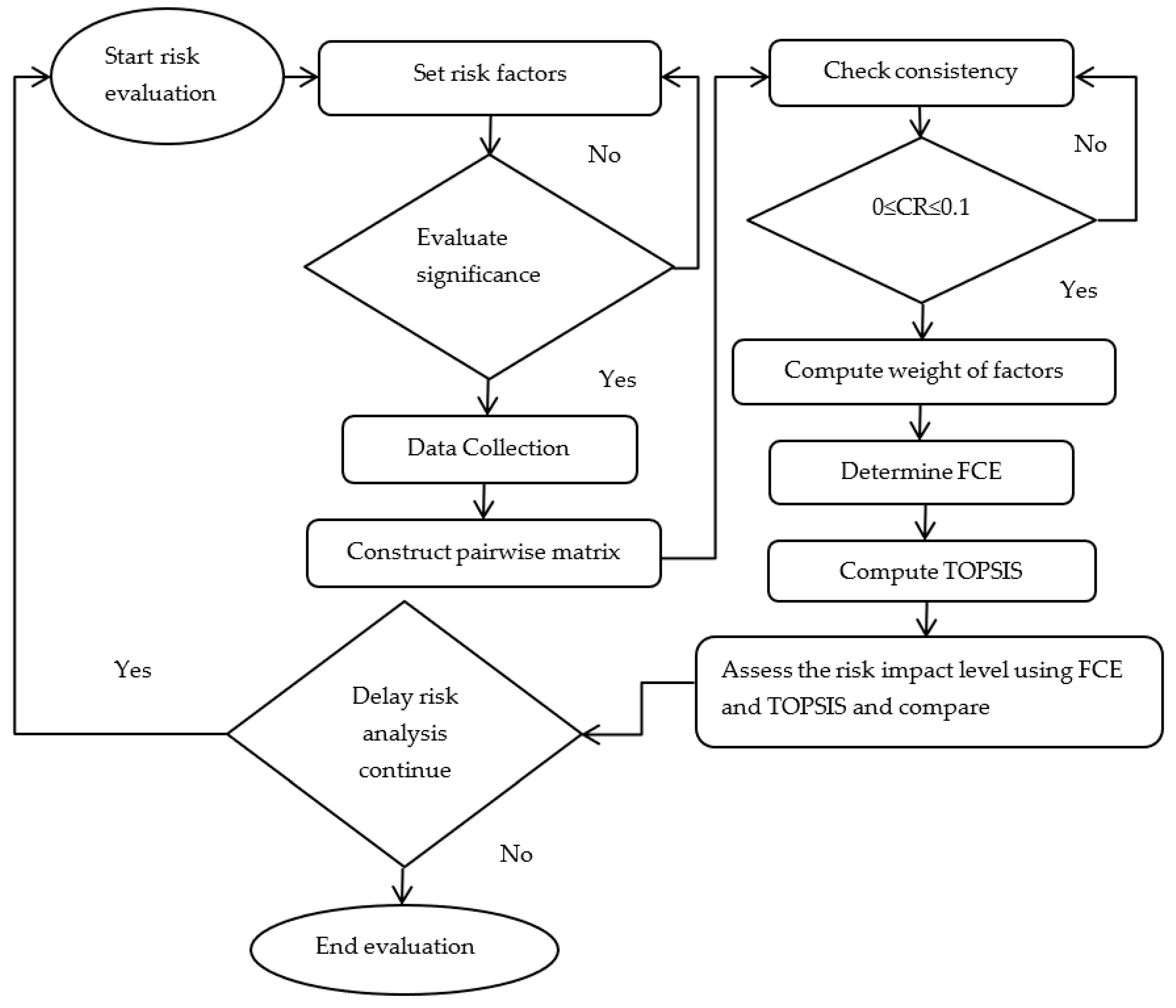
FCE and TOPSIS are essential for selecting and ranking a set of factors with usually incommensurate and independent attributes [28]. FCE and TOPSIS are supporting tools for decision-making in a finite number of alternatives [29]. The integrated model plays the respective advantage of flexibility in order to achieve a better result and make the right decision by identifying the typical level delay risk on construction activities. The layout of the evaluation mechanism of schedule delay risk using integrated models of FCE and TOPSIS is described in Figure 1.

3.1. Set Significant Delay Risk Factors

Set significant delay risk factors: it involves the identification and classification of delay risk factors and their consequences [19]. The procedure of selecting factors expressed as, based on the extensive literature review, a questionnaire for pilot study was developed, then the pilot study was assessed in fifteen different projects and participant were interviewed and responded to the questionnaire. Next based on the literature review and pilot study final questionnaire was developed. Finally, the developed questionnaire was validated to confirm clarity, completeness, and applicability in the case study.

In this study, the construction project lifecycle considers the three basic stages of pre-construction stage, construction stage, and post-construction stage according to the pilot to fit for the empirical assessment. The risk factors listed in

Table 1. Schedule delay risk factors evaluation indexing system and reference.

Criteria Related	Sub-Criteria Related	Attribute Related	Reference
(A) Responsibility	A1 Client	A11 Lack of on-time payments and finance	[4,30,31,19]
		A12 Client interference	[4,31,32]
		A13 Leisureliness in decision-making	[15,19]
		A14 Late at delivery of site for design and construction	[4,30,17]
		A15 Inadequate feasibility study	[4,31,19]
		A16 Poor coordination and communication with other	[4,31,19]
	A2 Contractor	A21 Problems related to subcontractor	[4,31,19]
		A22 Poor site performance and management	[33,15]
		A23 Ineffective scheduling and planning	[30,4,32,19]
		A24 Improper construction methods	[33,19,22]
		A25 Poor coordination and communication with other	[4,30,31]
		A26 Inadequate experience of the contractor	[25,19,22]
		A27 Rework for unsatisfactory work	[19,22,17]
	A3 Consultant	A31 Inadequate consultant experience	[15,19]
		A32 Late in receiving and approving of work	[4,30,19,22]
		A33 Late in performing inspection and testing and poor supervision	[34]
		A34 Poor coordination and communication with other	[19]
	A4 Designer	A41 In adequate details and unclear specification	[25,30,33,19]
		A42 Late design documents and design	[19]
		A43 Design errors and mistakes	[4,30,31,19]
		A44 Misunderstanding requirements of client’s	[15]
(B) Resource	B1 Material	B11 Absence of quality materials	[4,30,31]
		B12 Leisurely delivery of material	[25,30,19,17]
		B13 Changes in specifications and material types	[25,31]
		B14 Damage of materials	[25,32,17]
		B15 Inflation of price for materials	[32,4,33,31]
	B2 Finance	B21 Problem for a financial claim	[25]
		B22 Problem of funding processes from government	[2,15]
		B23 Late release budget	[2,35]
		B24 Global financial crisis	[25,33,19,17]
	B3 Labor	B31 Less productivity	[25,4,17]
		B32 Low morale and motivation	[18]
		B33 Unqualified workers	[30,23,19,17]
		B34 Discipline problem (conflicts)	[15]
		B35 Labour injuries and accidents	[32,17]
	B4 Equipment	B41 Insufficient or equipment shortage	[4,33,22]
		B42 Low efficiency and productivity of equipment	[34]
		B42 Lack of spare parts and failures of equipment	[30,4,31,17]
		B43 Problem of mobilization and allocation	[16]
		B45 Equipment outdated	[16,34]
(C) Contrac condition		C1 Absence of alternative dispute resolution (ADR)	[30,4,33]
		C2 Discrepancies and mistakes in contract	[33]
		C3 Unrealistic cost and duration contract	[4,30,17]
		C4 Poor incentives and inadequate penalties in contract	[4]
		C5 Insufficient details of the contract documents	[25,33]
		C6 Absence of clear understanding for contract	[25,15]
(D) External		D1 Adverse weather condition	[4,30,32,22]
		D2 Force of majeure	[4,30,31,19]
		D3 Corruption	[35]
		D4 Effect of cultural and social factors	[33,19]
		D5 Government commitment and policy	[30,4,31,19]
		D6 Unavailability of utilities in a site	[25,32]

were selected based on the impact that directly or indirectly associated with the three-construction lifecycle. However, the influence level of risk is completely different among the lifecycles, which is essential for decision-making in risk. The final questionnaire was consisted of four criteria, eight sub-criteria, and fifty-two attributes, as summarized in Table 1. Then based on this questionnaire data were collected.

3.2. Fuzzy Comprehensive Evaluation (FCE)

FCE model is used to obtain reliable results in evaluating alternatives widely in an uncertain environment [35]. The FCE approach has strong evaluation abilities that lead to appropriate decision-making. The FCE generates the weight of factors and priorities factors based on expert judgment [36]. FCE determines the risk of criteria and sub-criteria of delay factors on the construction project lifecycle. To get priorities in an organized way, the FCE technique requires to decompose the decision through the following steps, based on the different studies aforementioned.

Firstly, set criteria, sub-criteria, and attributes. This step was segmented the complex problem of delay risk factors into a structured hierarchy of three levels, which are level one (criteria), level two (sub-criteria), and level three (attributes), as shown in Table 1.

Secondly, develop a pairwise comparison matrix. This matrix was constructed using the rate of scale that denotes how much one element dominates over another with respect to a given attribute. The scale value measures the degree of relative importance in a pairwise comparison matrix using linguistic variables for delay risk factors, as described in

Table 2. The Linguistic Variables for Schedule Delay Risk Factor.

Linguistic Terms	Fuzzy Number
Very small risk level	1
Small risk level	3
Medium risk level	5
High risk level	7
Very high risk level	9

.

The matrix for pairwise comparison was developed based on the judgment of respondents, as described in the matrix (1):

$$A=[\begin{array}{cccc}1& \frac{w_1}{w_2}& \dots & \frac{w_1}{w_n}\\ \frac{w_2}{w_1}& 1& \dots & \frac{w_2}{w_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{w_{\mathrm{n}}}{w_1}& \frac{w_{\mathrm{n}}}{w_2}& \dots & 1\end{array}]=[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}].$$

(1)

where $A$ is the matrix with $a_{ij}$ element of the pairwise matrix in $i$ column and $j$ row and the rated weight of factors $W=\left(w_1,w_2,\dots ,w_n\right),\mathrm{where}\left(i,j=1,2,\dots ,n\right)$ and $n$ is the number of factors.

Thirdly, estimate normalized weight. It computed from the pairwise matrix using the arithmetic mean. The normalized weight computed by Equation (2):

$$w_i=\frac{{\overline{w}}_i}{{{\displaystyle \sum }}_{i=1}^n{\overline{w}}_i} \mathrm{but} {\overline{w}}_i={\displaystyle \sum }_{j=1}^n{a}_{ij} \left(i=1, 2,\dots ,n\right) \mathrm{and} \left(j=1,2,3,\dots ,n\right).$$

(2)

where $w_i$ is normalized weight from the cumulative weight $\overline{w}=\left({\overline{w}}_1,{\overline{w}}_2,\dots ,{\overline{w}}_n\right)$.

Determining consistency ratio aids to identify consistency of decision. First, compute random indexing (RI) and consistency index (CI) then determine the consistency ratio (CR). Finally, if CR is greater than or equal to zero and less than or equal to 0.1, the judgment is consistent [37]. The relations for the checking consistency can be expressed as Equations (3):

$$CR=\frac{CI}{RI} \mathrm{but} CI= \frac{{\lambda }_{max}-n }{n-1} \mathrm{Where}; {\lambda }_{max}={\displaystyle \sum }_i^n{a}_{ij}\times w_i .$$

(3)

Finally, compute multi-comprehensive evaluation. In a multi-comprehensive evaluation, the first step is to establish a grade factor and element set. According to the delay risk factors in Table 1, the main element set is $U=\left\{A, B, C, D\right\},$ which represents responsibility, resource, contract condition, and external related factors, respectively. The five grade factors determined by $V=\left\{v_1 v_2 v_{3 }{v}_4 v_5\right\},$ which represents very small risk level (1), small risk level (2), medium risk level (3), high-risk level (4), and very high-risk level (5), respectively. The second step, establish a single fuzzy matrix. The single fuzzy matrix uses the respondent’s rate to evaluate the risk level of attributes. The single fuzzy matrix computed using Equation (4):

$$r_{ik}=\frac{r_i}{N}\mathrm{then} R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& \begin{array}{ccc}{r}_{13}& r_{14}& r_{15}\end{array}\\ r_{21}& r_{22}& \begin{array}{ccc}{r}_{23}& r_{24}& r_{25}\end{array}\\ \begin{array}{c}⋮\\ r_{n1}\end{array}& \begin{array}{c}⋮\\ r_{n2}\end{array}& \begin{array}{ccc}\begin{array}{c}⋮\\ r_{n3}\end{array}& \begin{array}{c}⋮\\ r_{n4}\end{array}& \begin{array}{c}⋮\\ r_{n5}\end{array}\end{array}\end{array}\right].$$

(4)

where $n$ is attributes or element set, grade factor $k$ = $\{1,2,3,4,5$}, the rate of respondents for grade factor $r_i$, the total population of respondents $N$ and single fuzzy matrix $R$.

Lastly, evaluate the comprehensive and multi comprehensive. Comprehensive evaluation compiles a single fuzzy matrix of attributes with a normalized weight of sub-criteria from the pairwise matrix to priorities influence of sub-criteria. This can be expressed using Equation (5):

$$B_i=W_i\times R_i=\left[\begin{array}{c}{W}_1\\ W_2\\ \dots \\ W_n\end{array}\right]\times \left[\begin{array}{ccc}{r}_{11}& r_{12}& \begin{array}{ccc}{r}_{13}& r_{14}& r_{15}\end{array}\\ r_{21}& r_{22}& \begin{array}{ccc}{r}_{23}& r_{24}& r_{25}\end{array}\\ \begin{array}{c}⋮\\ r_{n1}\end{array}& \begin{array}{c}⋮\\ r_{n2}\end{array}& \begin{array}{ccc}\begin{array}{c}⋮\\ r_{n3}\end{array}& \begin{array}{c}⋮\\ r_{n4}\end{array}& \begin{array}{c}⋮\\ r_{n5}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccc}{b}_{i1}& b_{i2}& \begin{array}{ccc}{b}_{i3}& b_{i4}& b_{i5}\end{array}\end{array}\right].$$

(5)

where normalized weight of sub-criteria $W_i$, single fuzzy matrix $R_i$, and $B_i$ is prioritized result of sub-criteria, namely $\left[\begin{array}{ccc}{b}_{i1}& b_{i2}& \begin{array}{ccc}{b}_{i3}& b_{i4}& b_{i5}\end{array}\end{array}\right]$.

The multi-comprehensive evaluation used to priorities the influence of criteria on alternatives. It can be computed based on Equation (6):

$$B_i=W_i\times R_i=\left[\begin{array}{c}{W}_1\\ W_2\\ \dots \\ W_n\end{array}\right]\times \left[\begin{array}{ccc}{b}_{11}& b_{12}& \begin{array}{ccc}{b}_{13}& b_{14}& b_{15}\end{array}\\ b_{21}& b_{22}& \begin{array}{ccc}{b}_{23}& b_{24}& b_{25}\end{array}\\ \begin{array}{c}⋮\\ b_{n1}\end{array}& \begin{array}{c}⋮\\ b_{n2}\end{array}& \begin{array}{ccc}\begin{array}{c}⋮\\ b_{n3}\end{array}& \begin{array}{c}⋮\\ b_{n4}\end{array}& \begin{array}{c}⋮\\ b_{n5}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccc}{b}_{i1}& b_{i2}& \begin{array}{ccc}{b}_{i3}& b_{i4}& b_{i5}\end{array}\end{array}\right].$$

(6)

where $B_i$ is prioritized result of criteria, $R_i$ is a matrix of prioritized result from Equation (5) and $W_i$ is a normalized weight of criteria from the pairwise matrix

3.3. Technique For Order Preference by Similarity to Ideal Solution (TOPSIS)

TOPSIS is important to reasonable and rational decision-making under uncertainty, subjectivity, ambiguity, and biases [29]. TOPSIS suggests both the best and worst alternatives. The best alternative has the short distance from the positive ideal solution and the farthest distance from the negative ideal solution and vice versa [28].

In this study, precise scores of alternatives were determined by formulating a decision matrix from the linguistic variables and then forming a normalized decision matrix. Multiplying the normalized decision matrix with the normalized weight of fuzzy comprehensive evaluation has a result of weighted normalized decision matrix of attributes. Based on the weighted normalized decision matrix, the negative and positive ideal solutions, Euclidean distance, and closeness coefficient were computed. Comparing the closeness coefficient, the typical delay risk on construction project lifecycle was detected. The procedure for implementing TOPSIS presented as:

Firstly, compute normalized decision matrix. This matrix is important because each factor has a different rated value and this rate values should convert into a single unit to enable direct comparison. The normalized decision matrix computed using Equation (7):

$$r_{ij}=\frac{a_{ij}}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{a}_{ij}^2}},j=1,2,3,\dots ,nJ,i=1,2,3,\dots ,n$$

(7)

where $r_{ij}$ is normalized decision matrix, $a_{ij}$ is rated value of $i{}^{th}$ factor and $j{}^{th}$ alternative and $n$ is the total number of alternatives in the construction lifecycle.

Secondly, estimate the weighted normalized decision matrix. In this phase, the normalized weight from the pairwise matrix of fuzzy comprehensive evaluation multiplied with the normalized decision matrix. The weighted normalized decision matrix $v_{ij}$ calculated based on expression as (8):

$$v_{ij}=w_i\times r_{ij},j=1,2,3,\dots ,nJ,i=1,2,3,\dots ,n.$$

(8)

where $w_i$ is the normalized weight of $i{}^{th}$ factors and $r_{ij}$ is normalized decision matrix.

Thirdly, identify the negative ideal solution (NIS) and positive ideal solution (PIS). The other important thing in TOPSIS is to identify the positive ideal solution and negative ideal solution. These can be determined from weighted normalized decision matrix using Equations (9) and (10):

$$A^{*}=\left\{v_1^{*},v_2^{*},v_3^{*},\dots ,v_n^{*}\right\}\mathrm{maximum}\mathrm{values},\mathrm{where}{v}_i^{*}\left\{max\left(v_{ij}\right)ifj\in J\right\}$$

(9)

$$A^{-}=\left\{v_1^{-},v_2^{-},v_3^{-},\dots ,v_n^{-}\right\}\mathrm{maximum}\mathrm{values},\mathrm{where}{v}_i^{-}\left\{min\left(v_{ij}\right)ifj\in J\right\}.$$

(10)

where negative ideal solution (NIS) and positive ideal solution (PIS) denoted by $A^{-}$ and $A^{*}$, respectively.

Fourthly, determine the Euclidean distance of alternative. The Euclidean distance from the positive ideal solution (PIS) is represented by $d_i^{*}$ and the Euclidean distance from the negative ideal solution (NIS) is represented by $d_i^{-}$ can be determined by Equations (11) and (12):

$$d_i^{*}=\sqrt{{\displaystyle \sum }_{j=1}^n{(v_{ij}-v_j^{*})}^2}, j=1,2,3,\dots ,J$$

(11)

$$d_i^{-}=\sqrt{{{\displaystyle \sum }}_{j=1}^n{(v_{ij}-v_j^{-})}^2}, j=1,2,3,\dots ,J.$$

(12)

Finally, estimate closeness coefficient (CC). The risk level of delay determines based on closeness coefficient (CC) that deems to measure the influence level of the construction project lifecycle. The closeness coefficient (CC) expressed by Equation (13):

$$C{C}_i=\frac{d_i^{-}}{d_i^{*}+d_i^{-}},i=1,2,3,\dots J.$$

(13)

The closeness coefficient $\left(C{C}_i\right)$ ideal solution estimates one and the closeness coefficient $\left(C{C}_i\right)$ non-ideal solution estimates zero. Therefore, the risk level of schedule delay risk on the construction project lifecycle estimates based on the value of closeness coefficient $\left(C{C}_i\right)$ ideal solution.

4. Descriptive Case Study

The study demonstrated through an empirical analysis in the construction projects in Ethiopia. To gather data, participants were nominated based on the purposive sampling based on their experience in the different parts of the country. The participants were experienced and they serve as clients, contractors, consultants, managers, engineers, designers, surveyors, and other concerned positions. To minimize the subjectivity data were collected in discussion form, from 77 different groups in the participating construction projects and each group consists of at least five experts. For the questionnaire survey, the five-point Likert scale was employed, where each point corresponded to very small level risk (1), small level risk (2), medium level risk (3), high-level risk (4), and very high-level risk (5).

Based on the pairwise matrix the normalized weight of factors are computed, this used as a weight for comprehensive and multi-comprehensive evaluation in FCE and normalized weight for TOPSIS. The product of the normalized weight with a single fuzzy matrix can give the risk impact level of sub-criteria. The impact level of sub-criteria multiplied with the weight of criteria will give risk impact level of criteria. Then, the risk level of criteria multiplied with weight will give the level of risk for the construction lifecycle, as described from Formula 3 to 6. Whereas for TOPSIS, from the normalized weight of attributes and the normalized decision matrix, the weighted normalized decision matrix can be determined so based on the weighted normalized decision matrix the negative ideal solution (NIS), positive ideal solution (PIS), and Euclidian distance is estimated, then, finally, the closeness coefficient (CC) can be computed, as shown in formula 7 to 13.

The comprehensive evaluation of the sub-criteria such as client, contractor, consultant, and designer represented by {A1, A2, A3, A4}, respectively, under responsibility related criteria and the evaluation of sub-criteria, finance, material, labour, and equipment represented by {B1, B2, B3, B4} respectively under resource related criteria, computed in

Table 3. Comprehensive Evaluation of Sub-Criteria Risk on Construction Process.

Sub-Criteria	Pre-Construction					Construction						Post-Construction
	1	2	3	4	5	1		2	3	4	5	1	2	3	4	5
A1	0.11	0.24	0.31	0.21	0.13	0.09	0.24		0.30	0.26	0.11	0.09	0.21	0.35	0.17	0.18
A2	0.18	0.29	0.23	0.19	0.11	0.09	0.22		0.24	0.28	0.17	0.08	0.22	0.31	0.24	0.15
A3	0.10	0.28	0.29	0.19	0.14	0.09	0.23		0.24	0.27	0.17	0.14	0.30	0.30	0.15	0.11
A4	0.09	0.22	0.27	0.20	0.22	0.07	0.24		0.25	0.22	0.22	0.14	0.27	0.28	0.21	0.10
B1	0.08	0.22	0.30	0.20	0.20	0.05	0.22		0.28	0.23	0.22	0.13	0.24	0.28	0.21	0.14
B2	0.12	0.23	0.31	0.19	0.15	0.10	0.18		0.29	0.24	0.19	0.09	0.22	0.32	0.21	0.16
B3	0.13	0.25	0.27	0.19	0.16	0.10	0.22		0.29	0.24	0.15	0.09	0.31	0.30	0.17	0.13
B4	0.17	0.26	0.29	0.18	0.10	0.08	0.21		0.27	0.25	0.19	0.08	0.22	0.25	0.20	0.25

.

The multi-comprehensive evaluation results of delay risk on alternatives based on the criteria of {A, B, C, D} that represent responsibility, resource, contract condition, and external related, described in

Table 4. Multi-Comprehensive Evaluation of Criteria Risk on Construction Process.

Criteria	Pre-Construction					Construction						Post-Construction
	1	2	3	4	5	1		2	3	4	5	1	2	3	4	5
A	0.12	0.26	0.28	0.20	0.14	0.09	0.23		0.26	0.27	0.15	0.13	0.24	0.28	0.21	0.14
B	0.11	0.23	0.30	0.19	0.17	0.08	0.21		0.28	0.24	0.19	0.09	0.23	0.32	0.20	0.16
C	0.10	0.32	0.28	0.18	0.12	0.09	0.26		0.26	0.23	0.16	0.09	0.30	0.30	0.18	0.13
D	0.10	0.20	0.28	0.18	0.24	0.07	0.15		0.23	0.27	0.28	0.08	0.22	0.25	0.20	0.25

.

4.1. Evaluation of Schedule Delay Risk on Pre-Construction Stage

The pre-construction stage has the least risk alternative with 35% of a high and very high-risk level of schedule delay as described in

Table 5. Risk of Schedule Delay on Construction Process.

Alternatives	1	2	3	4	5
Pre-construction	0.11	0.25	0.29	0.19	0.16
Construction	0.08	0.22	0.26	0.25	0.19
Post-construction	0.10	0.25	0.28	0.20	0.17
Average schedule delay risk of Ethiopia construction projects	0.10	0.24	0.28	0.21	0.17

. The most influential criteria responsibility related is embraced by the substantial sub-criteria sequenced as designer, client, consultant, and contractor related (Table 3 and Table 4). The second important criteria external related include influential factors such as corruption and unavailability of utilities at a site (Table 4). The third critical criteria resource related has momentous sub-criteria ranked as material, finance, labour, and equipment related (Table 3 and Table 4). The least one is a contract condition related that has top contributing attributes of unrealistic cost and duration in the contract and insufficient details of the contract documents (Table 4).

4.2. Evaluation of Schedule Delay Risk on Construction Stage

The construction stage has the highest risk, which exposes 44% of the high and very high-risk level of schedule delay as denoted in Table 5. In the construction stage, the most influential criterion is responsibility related, with dominant sub-criteria sequenced as consultant, designer, contractor, and client related (Table 3 and Table 4). The second influential criterion is resource that has important sub-criteria ranked as finance, construction material, labour, and equipment related (Table 3 and Table 4). The third contract condition, which considerate influential attributes of unrealistic cost and duration in contract, and poor incentives and inadequate penalties in contract (Table 4). The external related is least one, counting the most contributing factors of corruption and unavailability of utilities at a site (Table 4).

4.3. Evaluation of Schedule Delay Risk on Post-Construction Stage

The second influenced by risk is the post-construction stage that covered 37% of the high and very high-risk level of schedule delay (Table 5). In this stage, the most persuasive criterion is responsibility related, with the extensive risk of sub-criteria sequenced as consultant, designer, contractor, and client related (Table 3 and Table 4). The second influential criteria external related include the dominant attributes of corruption and unavailability of utilities at a site (Table 4). Contract condition is the third noticeable criterion, with top contributing attributes of unrealistic cost and duration in contract, and poor incentives and inadequate penalties in contract (Table 4). The least contributing criteria resource related, containing influential sub-criteria ranked as finance, construction material, equipment, and labour (Table 3 and Table 4).

4.4. The Schedule Delay Risk Comparison at Each Construction Lifecycle

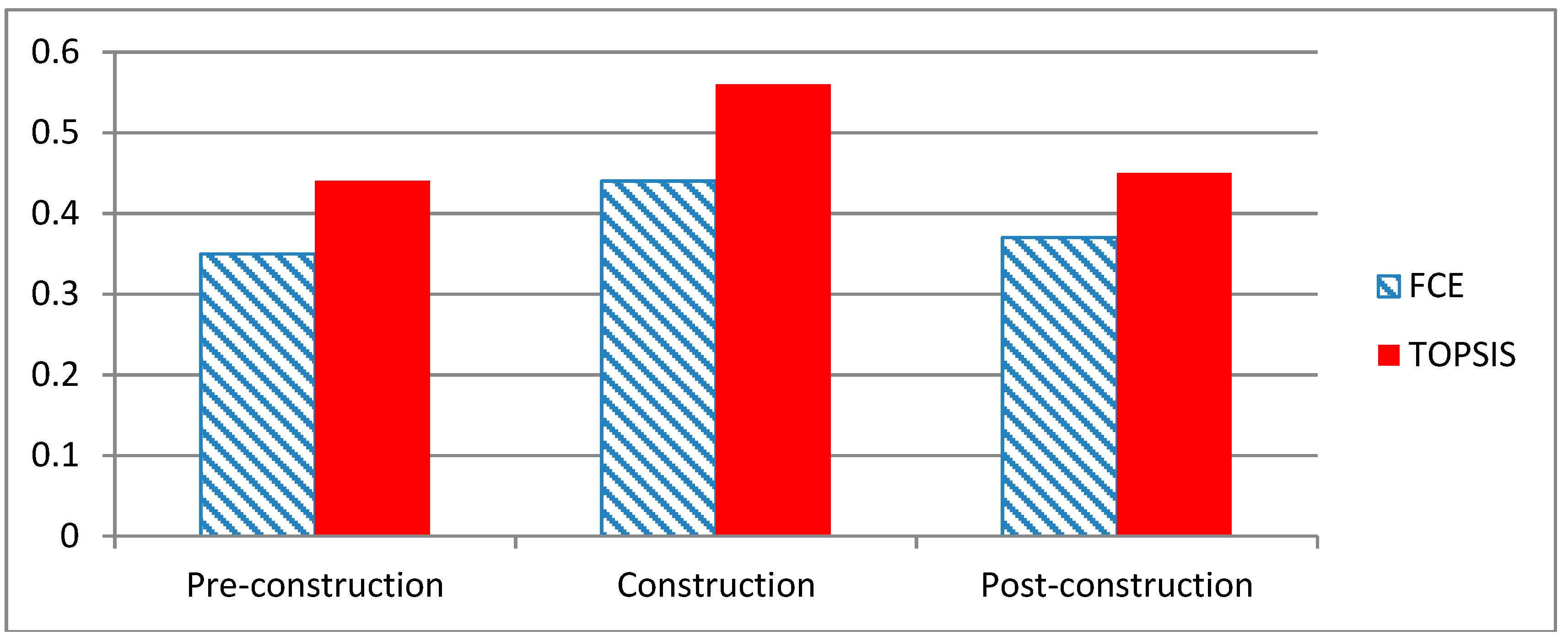
From multi-comprehensive evaluation matrix result of Table 5, the construction stage (44%) is high-risk, the second high-risk stage is post construction (37%), and the least risk stage is pre-construction (35%).

From the weighted normalized decision matrix, negative ideal solution, positive ideal solution, and Euclidean distance (

Table 6. Weighted Normalized Decision Matrix, positive ideal solution (PIS), negative ideal solution (NIS), and Euclidian Distance of Alternatives.

Factors	Pre-Construction	Construction	Post-Construction	PIS(A*)	NIS(A-)
A11	0.120	0.168	0.120	0.168	0.120
A12	0.149	0.106	0.064	0.149	0.064
A13	0.062	0.062	0.021	0.062	0.021
A14	0.162	0.116	0.116	0.162	0.116
A15	0.168	0.056	0.056	0.168	0.056
A16	0.056	0.019	0.019	0.056	0.019
A21	0.041	0.095	0.123	0.123	0.041
A22	0.109	0.140	0.140	0.140	0.109
A23	0.147	0.082	0.115	0.147	0.082
A24	0.043	0.099	0.043	0.099	0.043
A25	0.014	0.041	0.040	0.041	0.014
A26	0.042	0.099	0.099	0.099	0.042
A27	0.012	0.035	0.081	0.081	0.012
A31	0.122	0.073	0.073	0.122	0.073
A32	0.171	0.171	0.220	0.220	0.171
A33	0.121	0.121	0.170	0.170	0.121
A34	0.122	0.171	0.171	0.171	0.122
A41	0.197	0.154	0.110	0.197	0.110
A42	0.206	0.206	0.160	0.206	0.160
A43	0.197	0.154	0.110	0.197	0.110
A44	0.070	0.070	0.070	0.070	0.070
B11	0.136	0.136	0.136	0.136	0.136
B12	0.136	0.136	0.136	0.136	0.136
B13	0.104	0.104	0.074	0.104	0.074
B14	0.099	0.043	0.071	0.099	0.043
B15	0.136	0.136	0.136	0.136	0.136
B21	0.142	0.142	0.142	0.142	0.142
B22	0.137	0.098	0.176	0.176	0.098
B23	0.140	0.180	0.180	0.180	0.140
B24	0.099	0.139	0.139	0.139	0.099
B31	0.174	0.104	0.104	0.174	0.104
B32	0.102	0.170	0.102	0.170	0.102
B33	0.245	0.245	0.175	0.245	0.175
B34	0.036	0.036	0.036	0.036	0.036
B35	0.030	0.089	0.030	0.089	0.030
B41	0.181	0.325	0.253	0.325	0.181
B42	0.097	0.289	0.161	0.289	0.097
B43	0.040	0.040	0.040	0.040	0.040
B44	0.040	0.040	0.040	0.040	0.040
B45	0.040	0.040	0.040	0.040	0.040
C1	0.018	0.018	0.088	0.088	0.018
C2	0.025	0.02	0.025	0.025	0.025
C3	0.123	0.172	0.172	0.172	0.123
C4	0.069	0.115	0.161	0.161	0.069
C5	0.126	0.126	0.126	0.126	0.126
C6	0.125	0.075	0.075	0.125	0.075
D1	0.052	0.017	0.017	0.052	0.017
D2	0.055	0.018	0.055	0.055	0.018
D3	0.182	0.182	0.182	0.182	0.182
D4	0.020	0.020	0.020	0.020	0.020
D5	0.099	0.099	0.139	0.139	0.099
D6	0.182	0.182	0.182	0.182	0.182
d*	0.343	0.253	0.311
d-	0.264	0.325	0.250

) then the closeness coefficients (CC) is computed in

Table 7. Ranking of Risk Level of Schedule Delay on Construction Process.

Rank	Alternatives	Closeness Coefficient
1	Construction	0.563
2	Post construction	0.446
3	Pre-construction	0.435

. The higher value of closeness coefficient for a specific alternative denotes higher risk influence.

On the other hand, based on TOPSIS ideal solution of closeness coefficient rank in Table 7, construction stage (0.563) is high-risk, post construction stage (0.446) the second, and pre-construction stage (0.435) the least.

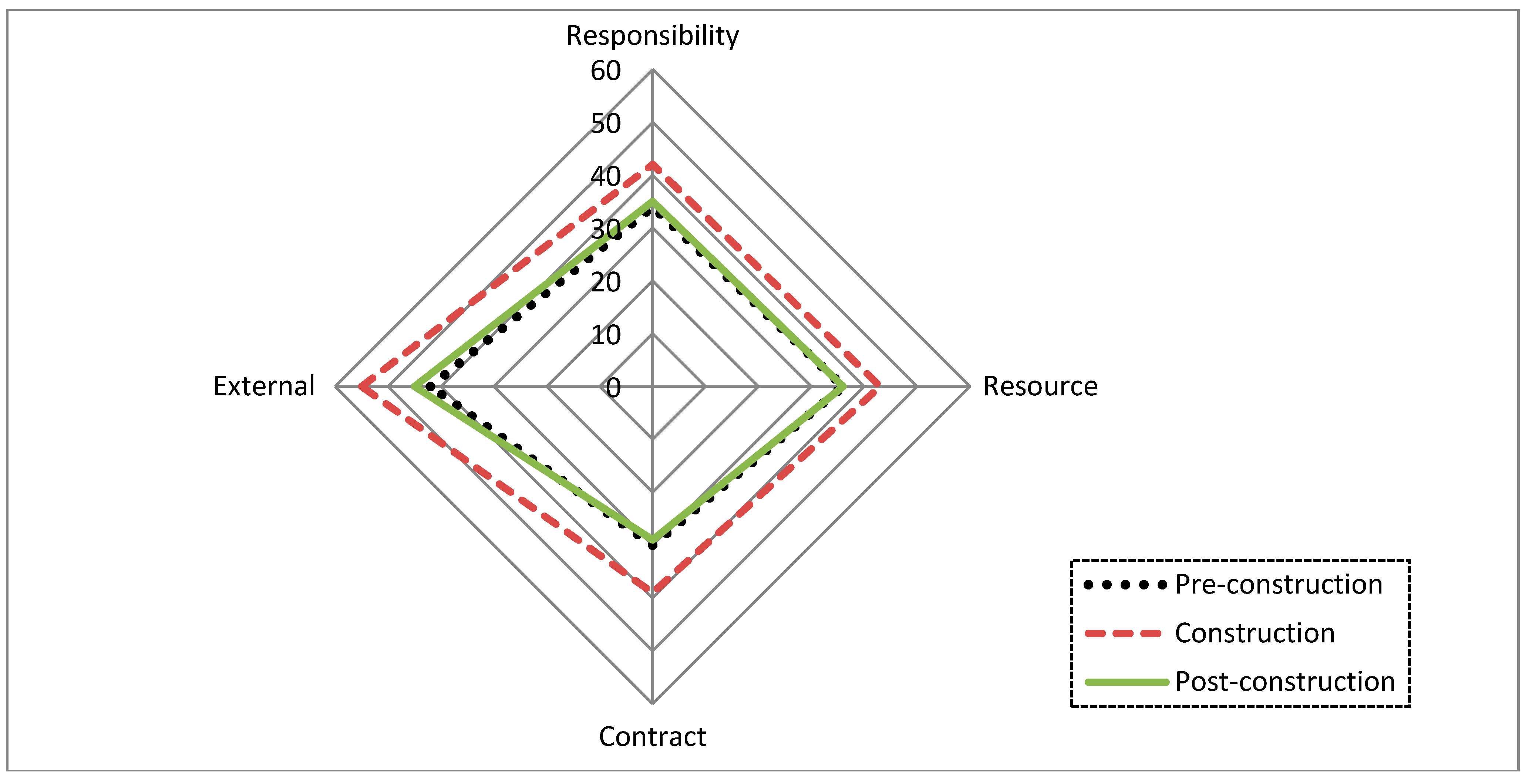
As a result, the risk of schedule delay at the different lifecycle of construction projects has a difference or the risk impact different either in level or in type. These differences are important to mitigation delay risk in the construction projects of Ethiopia by recognizing the exact influence level of risk at each activity for a better decision. Overall, Figure 2 shows the comparison of the risk of the major schedule delay risk factors, external, resource, responsibility, and contract condition related.

The study detects the influence of schedule delay risk in the construction projects of Ethiopia. The construction projects in Ethiopia have faced an average of 38% schedule delay risk at high and very high-risk level (Table 6). The rank, based on TOPSIS Closeness Coefficient and multi-comprehensive evaluations of risk at high and very high-risk level of alternatives are denoted in Figure 3.

5. Conclusions

Schedule delay risk was analyzed to provide a decision regarding the typical risk of delay in construction lifecycle to mitigate risk. This was achieved through the application of the hybrid model of FCE and TOPSIS. The application of this combined model can evaluate not only the typical risk of the schedule delay but also reflects the general risk of schedule delay. Based on the empirical study, the results identified that the risk level of the schedule delay varies at the construction projects lifecycle. The comparison on the empirical study shown that the construction stage (44%) is high risk, the second high-risk stage is post construction (37%), and the least risk is pre-construction (35%). The construction projects in Ethiopian have faced an average of 38% of schedule delay risk at the high and very high-risk level. This helps the construction managers to identify which schedule delay risk factor is highly influential and which construction lifecycle is highly risky and to make the right decision on how to mitigate the risk. The application of the integrated model of FCE and TOPSIS is a viable tool in delay risk management of construction project. The model can be applied at any time, with different project types by adapting the factors and evaluated weight.