1. Introduction
Marius Sophus Lie proposed a symmetry-based method for the analytical solution of differential equations using groups of continuous transformations known as Lie groups [
1,
2,
3,
4]. Amalie Emmy Noether later presented her remarkable theorem that relates variational symmetries with conservation laws or first integrals in Reference [
5]. In the literature, different methods are available to calculate first integrals of ordinary differential equations (ODEs), including the direct method, the characteristic or multiplier method, the Noether approach, and the partial Noether approach [
6,
7,
8,
9]. In this paper, we used the classical Noether approach to calculate the first integrals of a harmonic oscillator. We then applied the complex symmetry method in the restricted domain to find the first integrals of a system of harmonic oscillators by considering the Lagrangian in the complex variable domain [
10,
11,
12].
Concerning the numerical solutions of ODEs with quadratic first integrals, it is well known that symplectic numerical methods are a suitable candidate [
13]. These methods are a subclass of geometric integrators that preserve the geometric properties of the exact flow of ODEs. One class of symplectic methods with optimal order are the Gauss–Legendre Runge–Kutta methods. They are one-step numerical methods for ODEs and preserve all linear and quadratic first integrals of a dynamic system [
14]. If we intend to preserve cubic or higher-order first integrals, we do not have a general numerical scheme for such a purpose, but we can design a numerical method that has this as its specific goal, for example, with the splitting and discrete-gradient methods [
14]. In this paper, we present a way of constructing symplectic Runge–Kutta methods. We then take fourth-order Gauss–Legendre Runge–Kutta methods for the numerical integration of ODEs and report good preservation of first integrals by the numerical solution.
2. Symmetries and First Integrals
Consider a second-order ordinary differential equation,
which admits a Lagrangian
L satisfying the Euler–Lagrange equation,
To explain the invariance criteria for variational problems under a group of transformation, we consider the operator
where
X is the Noether symmetry generator for the Lagrangian
L with gauge function
, provided the following condition holds,
where
is a first-order prolongation of
X and
D represents total derivative,
According to the Noether theorem, for each Noether symmetry of a Euler–Lagrange equation, there corresponds a function
I
called the first integral or conserved quantity of Equation (
1) with respect to symmetry generator
X.
Complex Symmetry Analysis
We first discuss some important results related to complex Noether symmetries, complex Lagrangian, and the Noether theorem in the restricted complex domain. We use them to determine first integrals of second-order restricted complex ODEs [
15]. We then present expressions for Euler–Lagrange-like equations, conditions for Noether-like operators, and expressions for first integrals corresponding to these operators. For more details, see Reference [
10] and references therein.
Consider a system of two second-order ordinary differential equations of the form
Suppose we have a transformation
and
, which converts System (
7) to a second-order restricted complex ODE,
Assume that Equation (
8) admits a complex Lagrangian
, i.e.,
. Therefore, we have two Lagrangians,
and
, for System (
7) that satisfy Euler–Lagrange-like equations:
The operators
are called Noether-like operators for Lagrangians
and
such that:
where
and
are suitable gauge functions. The two first integrals corresponding to Noether-like operators
and
can be found as:
3. Runge–Kutta Methods
Runge–Kutta methods [
16] are one-step numerical methods for the approximate solution of IVPs:
These methods provide approximation
of the exact solution
at time
, where
and
h corresponds to the stepsize. The generalized form of an
s-stage Runge–Kutta method is
with
representing the weights and
, the nodes at which stages
are evaluated. A Runge–Kutta method can be represented by a Butcher tableau:
For explicit Runge–Kutta methods, we have for ; otherwise, they are implicit.
3.1. Symplectic Runge–Kutta Methods
If Equation (
13) has a quadratic first integral
where
S is a symmetric square matrix, then we have
We want to determine numerical solutions
such that first integral
is preserved numerically, i.e.,
It has been shown in References [
17,
18,
19] that only symplectic Runge–Kutta methods preserve quadratic first integrals while numerically integrating System (
13). Moreover, in this paper we are only considering implicit Runge–Kutta methods to check the numerical preservation of first integrals because explicit methods cannot be symplectic [
20]. A Runge–Kutta method is symplectic if its coefficients satisfy the following condition [
18,
19,
21]:
which can be derived as follows.
Firstly, apply the Runge–Kutta method (
14) to solve the IVP (
13). The stage values are
Moreover, for the output values, we have
Evidently from Systems (
16) and (
17), we have
provided that
3.2. Construction of Symplectic RK Methods
Although there exist several techniques to construct symplectic RK methods in the literature [
14,
22], here we constructed symplectic Runge–Kutta methods with the help of a Vandermonde transformation. This was first discussed in reference [
23].
A Vandermonde matrix is given as
Pre- and postmultiply, Vandermonde matrix
V with symplectic condition (
15) as
To construct methods with two stages (), we consider
The following order two conditions must be satisfied.
Using Equation (
24) in Equations (
20)–(
23), we have
If we take
and take summation of
i from 1 to 2, we get
Let us consider the shifted Legendre polynomials
on the interval
,
For Gauss methods, we choose abscissa as zeros of which have an order . For Radau methods, we choose either or , or both of them and then take for Radau I methods, the abscissa as the zeros of the polynomial of order . Similarly, for Radau II methods, we take the abscissa as the zeros of the polynomial of order . Moreover, for Lobatto III methods, we take the abscissa as the zeros of the polynomial of order . Thus, we have the following symplectic methods:
Similarly, we can construct methods with more stages and a higher order.
4. Construction of First Integrals and Their Numerical Preservation
We construct the first integrals of a system of harmonic oscillators (both coupled and uncoupled) determined by the second-order ODE:
We take different values of
k and
y, as follows:
Case I: ( and is real)
When
and
is real-valued, (
25) becomes a one-dimensional harmonic oscillator equation:
that possesses the standard Lagrangian
Taking the Lagrangian and inserting it in System (
4) yields the following determining system of equations:
Comparing different powers of
, we have a system of four partial differential equations whose solution gives rise to:
We thus obtain the following 5-Noether symmetry generators:
Using Symmetries (
30) and Lagrangian (
27) in Noether’s Theorem (
6), we obtain the following first integrals:
Among these five first integrals, only two are independent [
8]. We numerically integrate system (
26) using a fourth-order Gauss
symplectic Runge–Kutta method that we refer to from now on as Gauss2. We compare the results of the Gauss2 method with the famous symplectic Euler method [
14], given as:
for numerically integrating
and
. We take stepsize
, and
n = 10,000 number of steps. By employing symplectic integrators, we expect the first integrals of the system to be preserved by the numerical schemes, and this is what we have achieved. We look at the deviation of numerically evaluated first integral
from the actual value of first integral
. We calculate error by taking the difference of the first integral evaluated at initial value
with the value of the first integral evaluated at all subsequent numerically approximated values
given by the formula Error
.
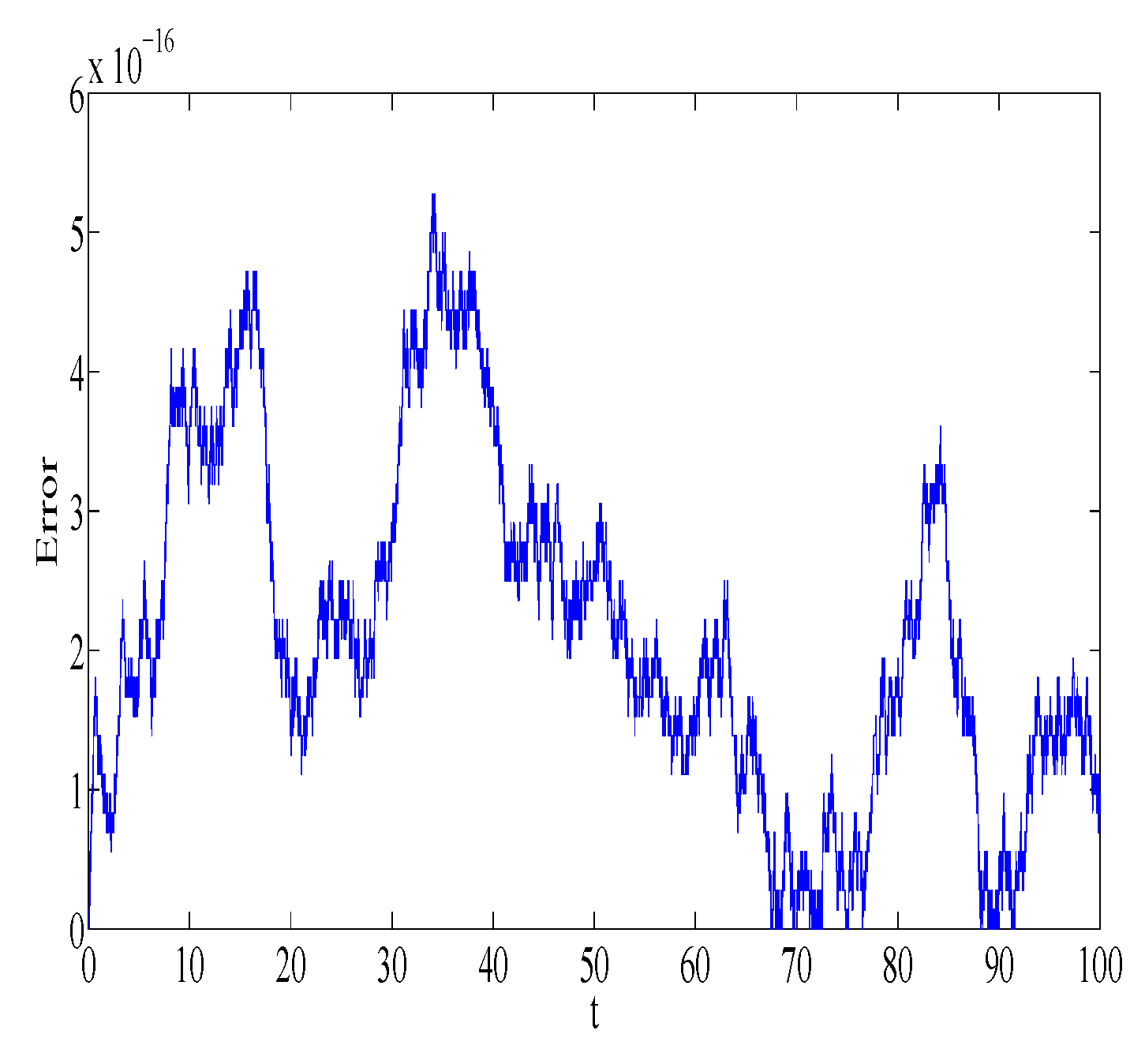
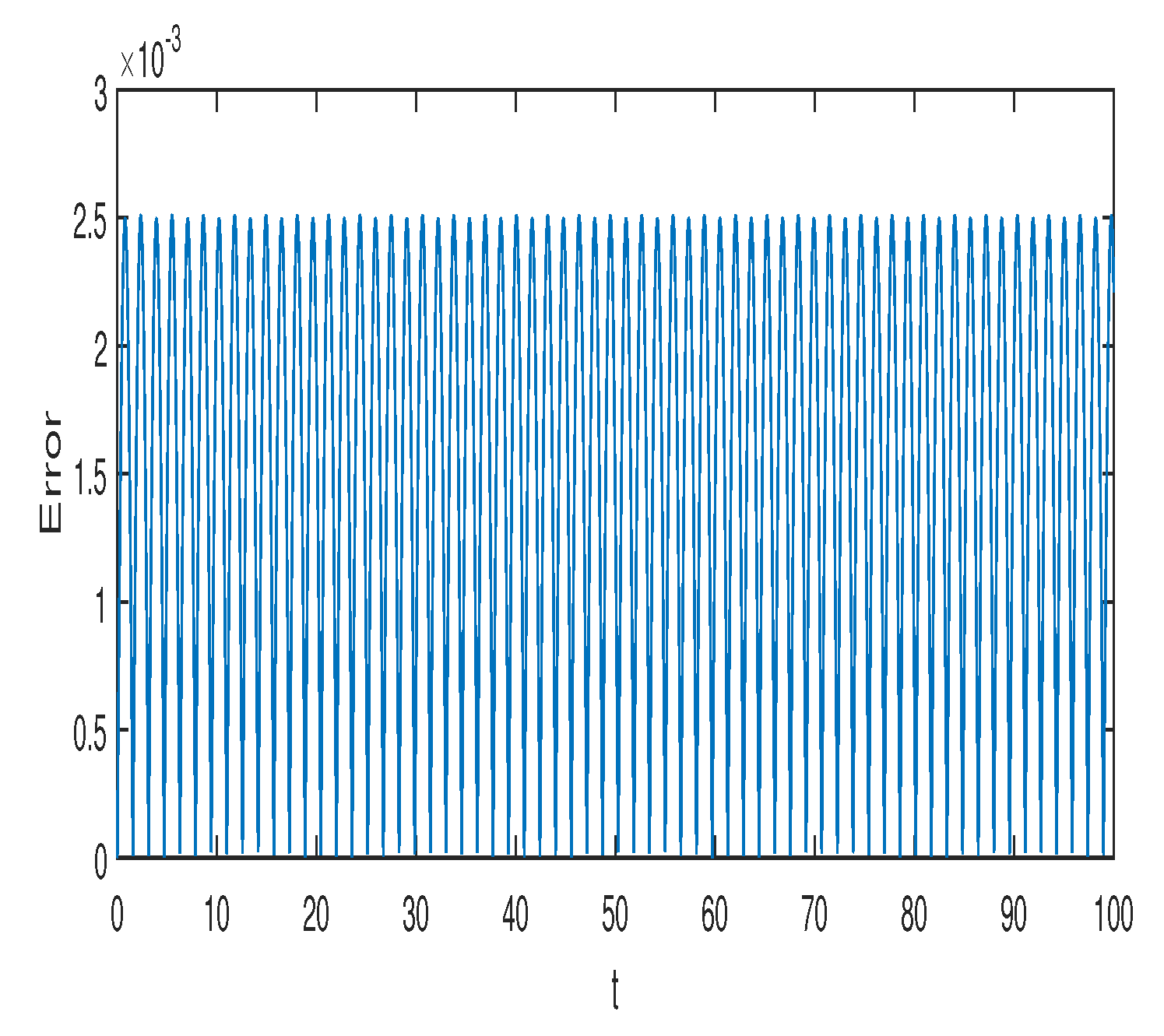
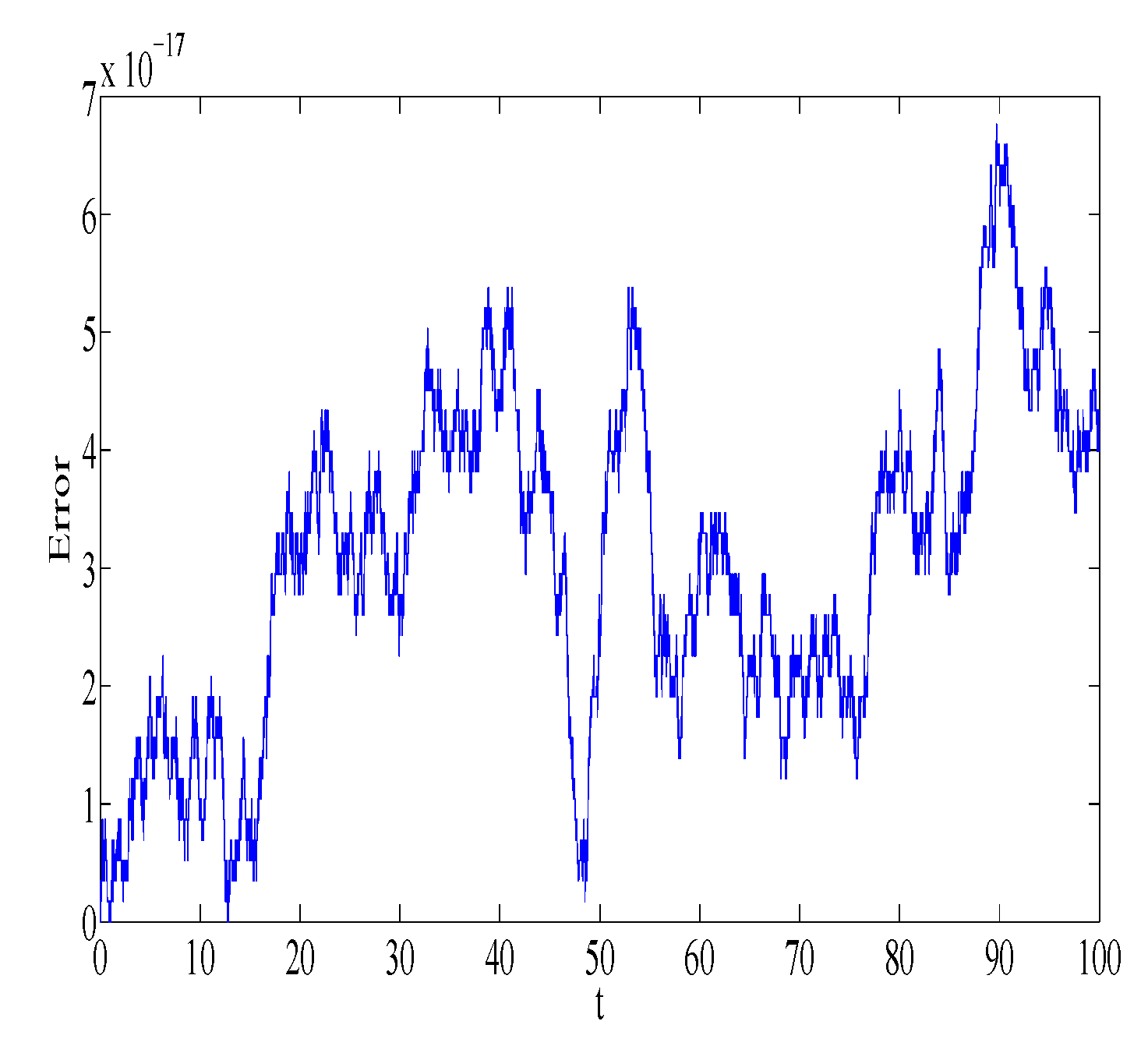
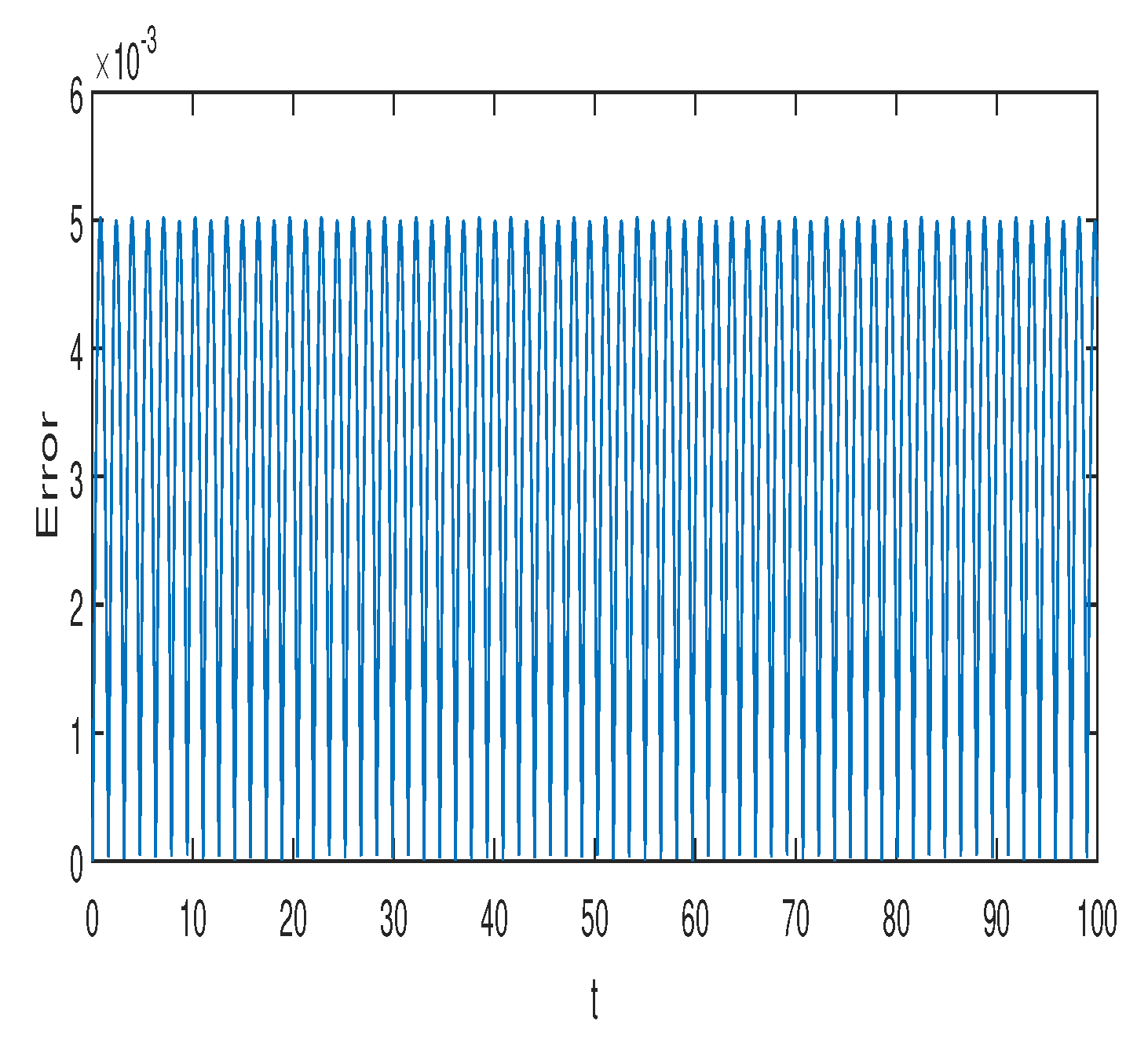
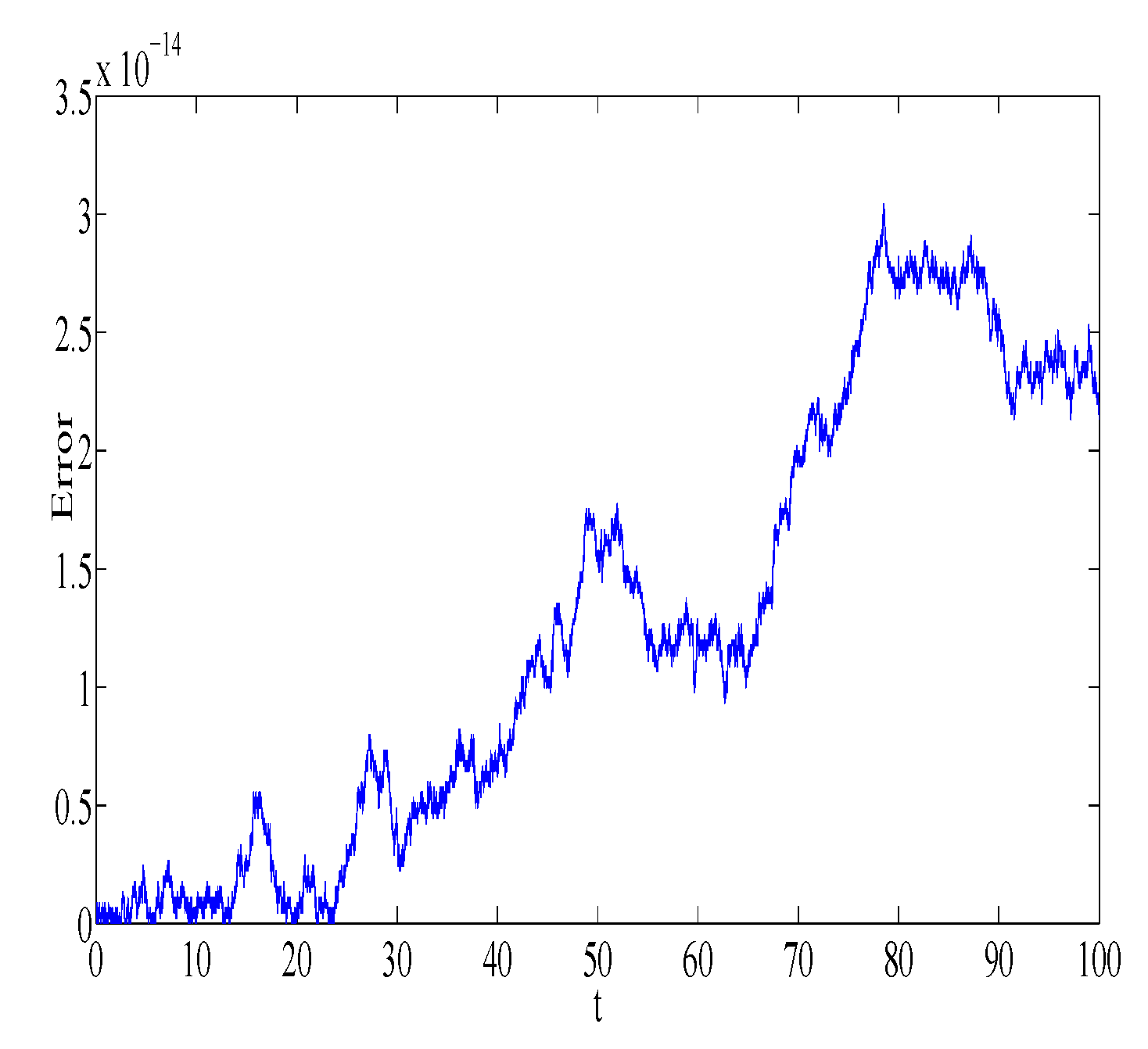
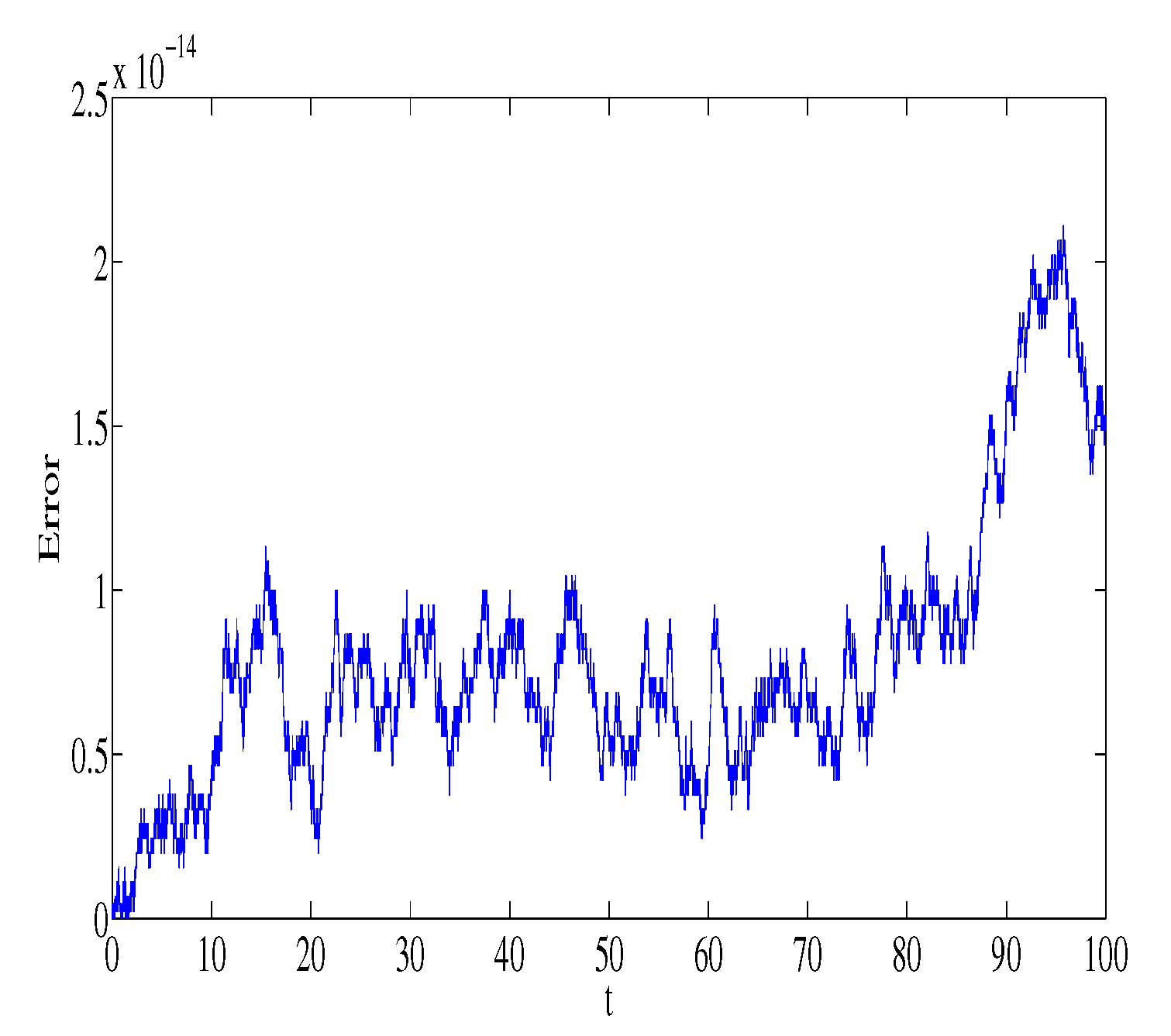
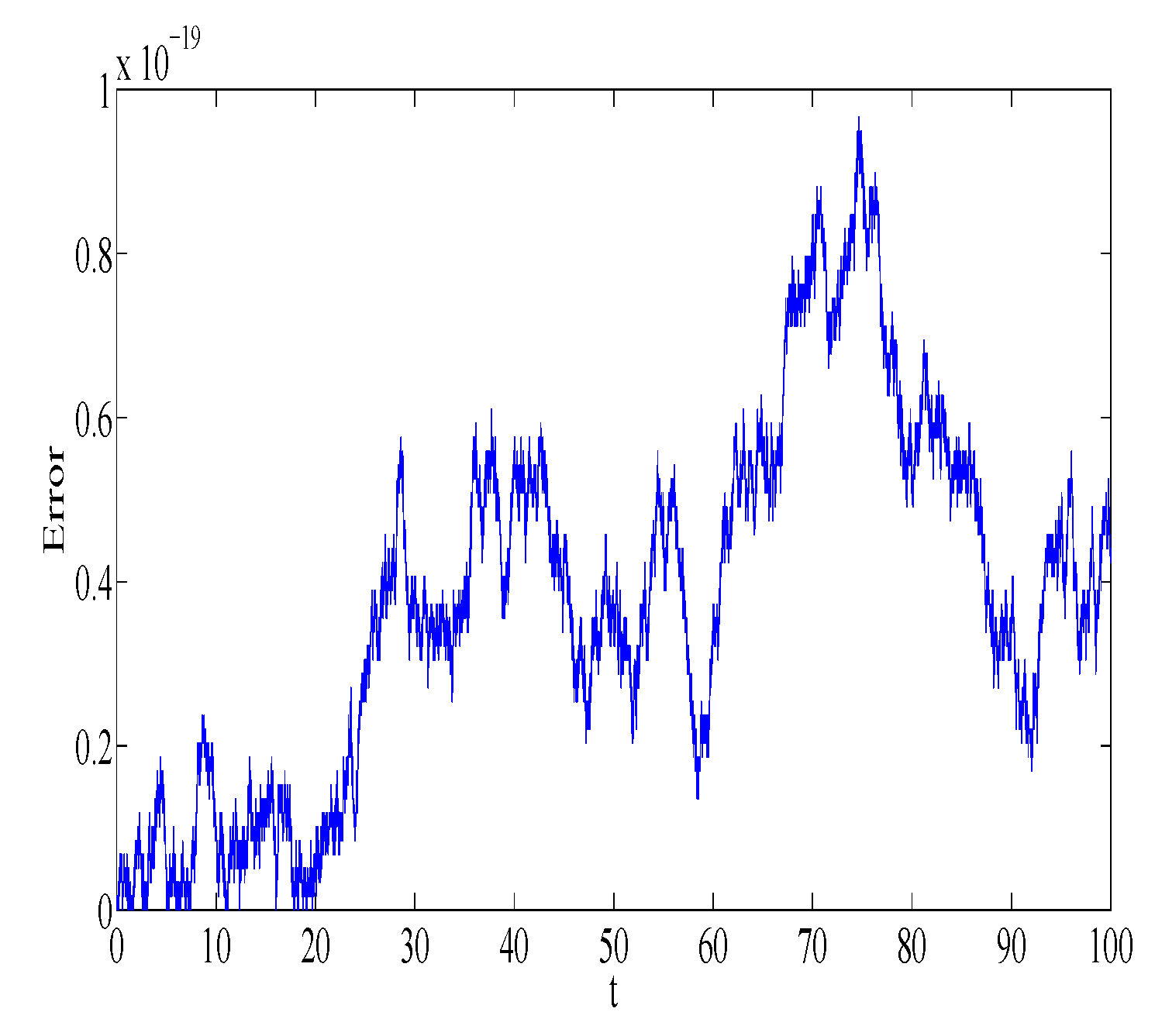
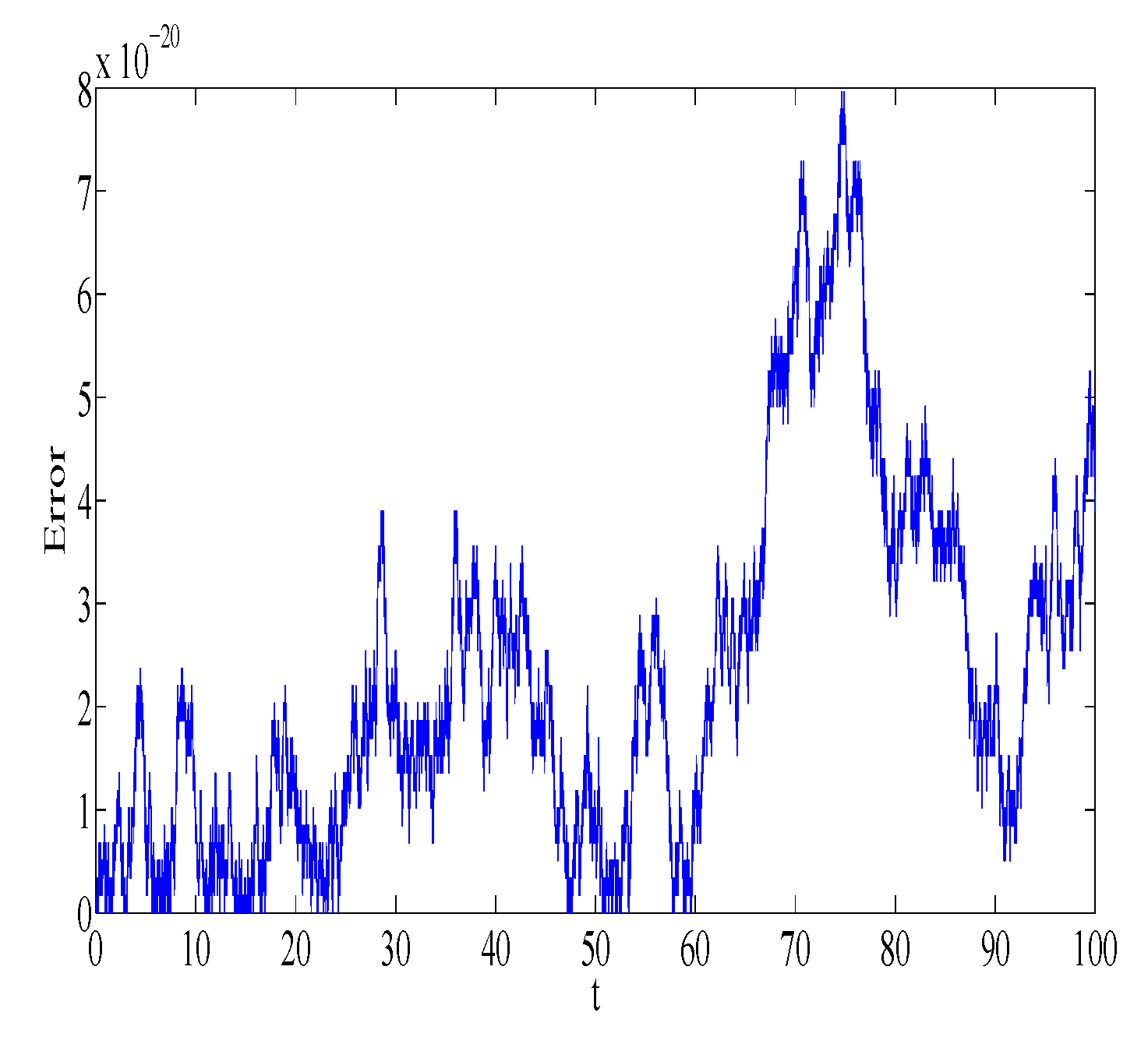
Figure 1 and
Figure 2 represent the absolute error in integral
using the Gauss2 and symplectic Euler method, respectively. Similarly,
Figure 3 and
Figure 4 represent the absolute error in integral
using the Gauss2 and symplectic Euler method, respectively. It is clear from the figures that the error is very small and bounded, depicting qualitatively correct numerical results. It is worth noting that the error of the Gauss2 method is much less compared to the error of the symplectic Euler method. The reason is that the Gauss2 method is fourth-order and more accurate compared to symplectic Euler method, which has order 1. Similar error behavior is obtained for other first integrals.
Case II: ( and is complex)
When
and
is a complex function
for
f and
g being real functions of
t, we get:
which admits the following Lagrangians:
Using Lagrangians (
33) in (
11), we obtain 9-Noether-like operators
Invoking Equation (
12), we obtain the following invariants:
associated with Noether-like operators (
34). System of Equation (
32) is integrated using the Gauss2 method with stepsize
and
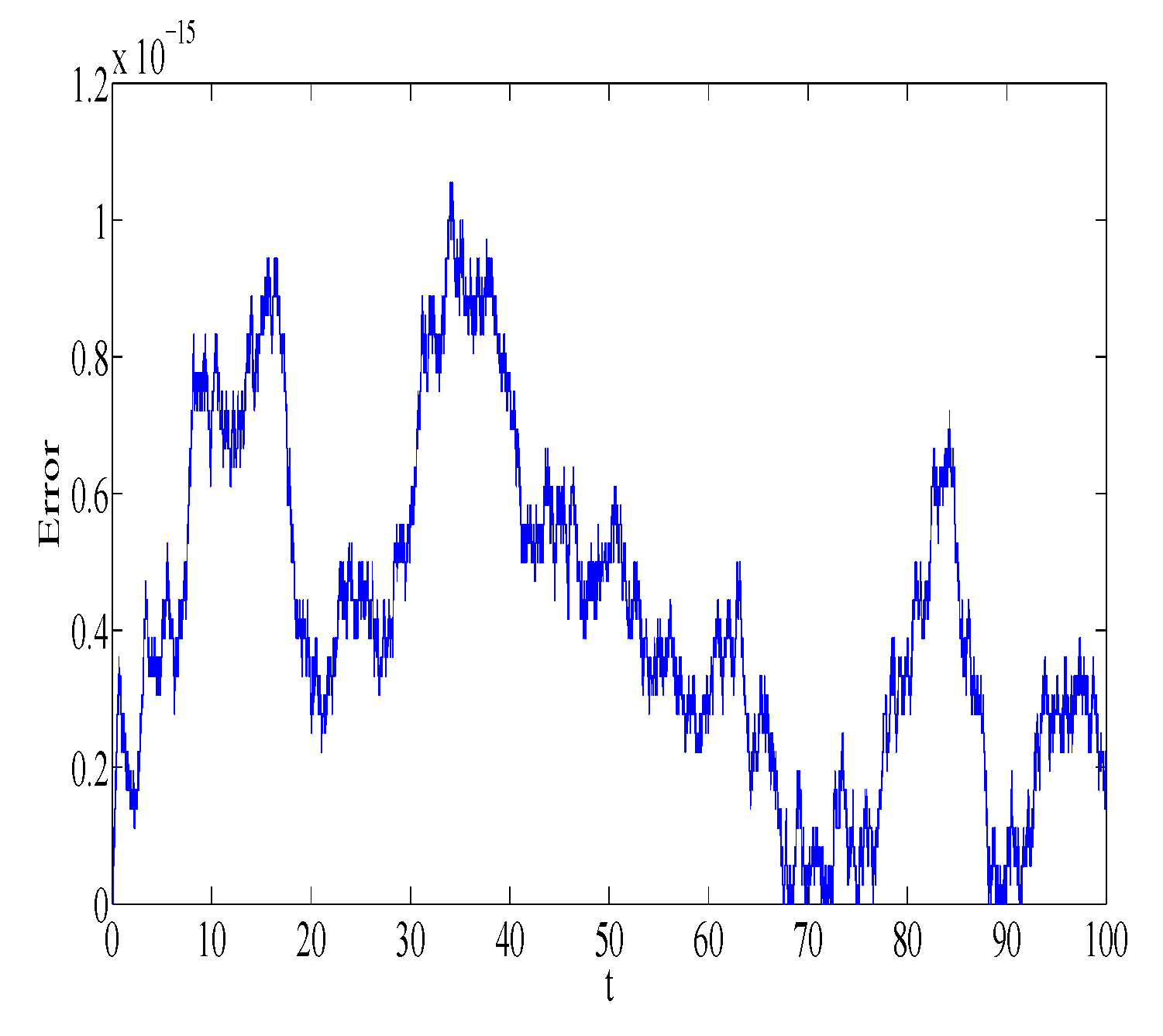
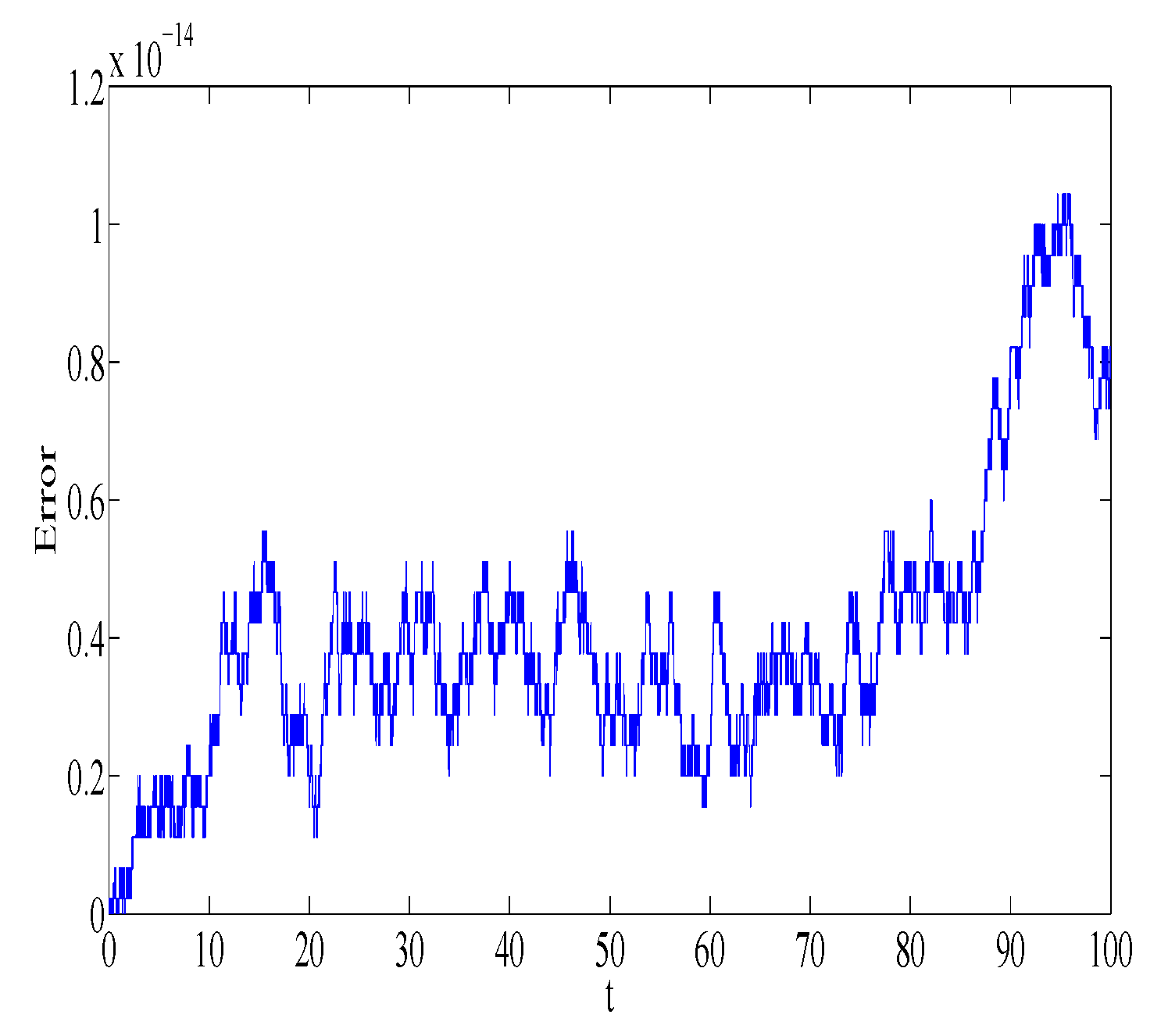
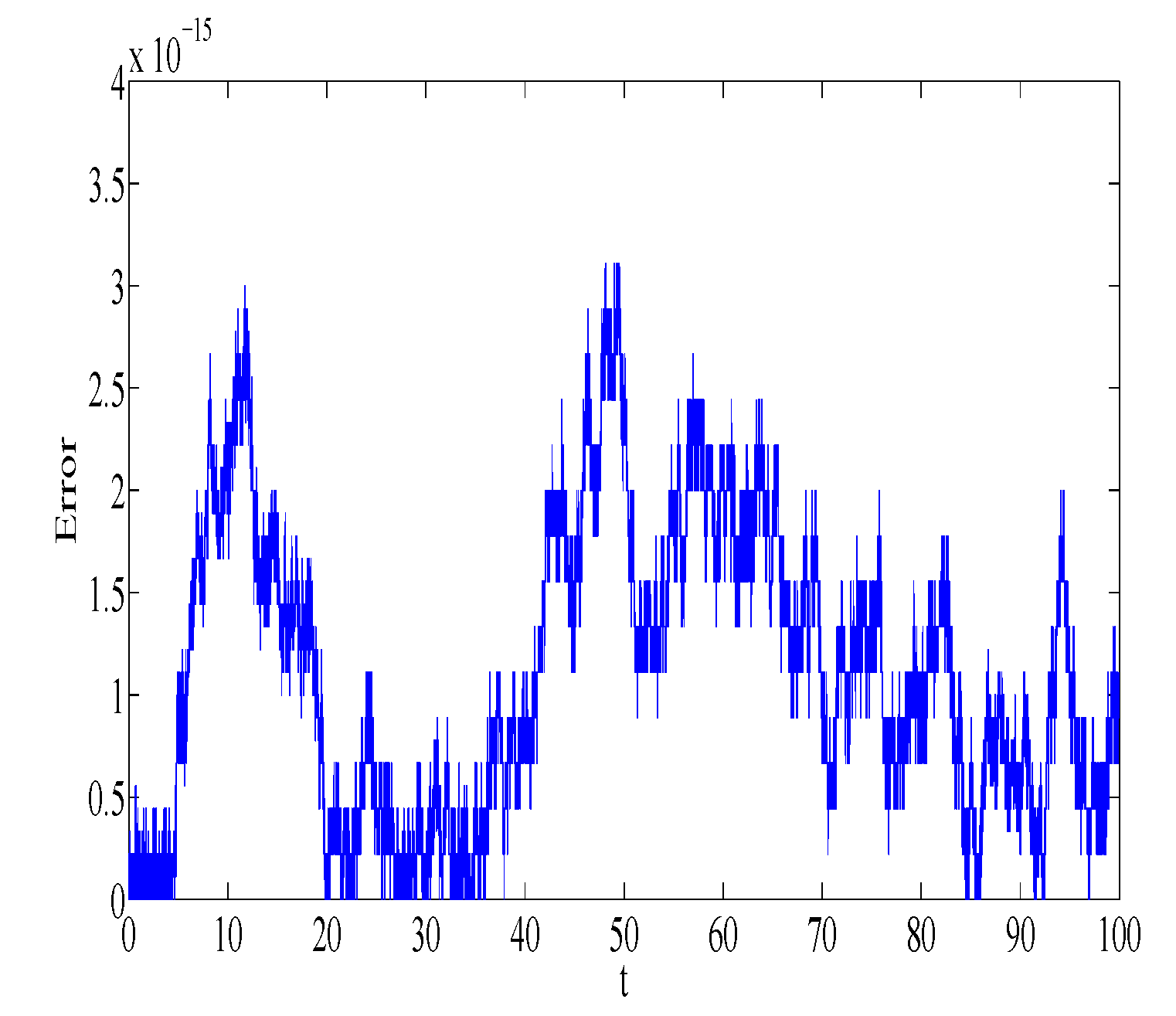
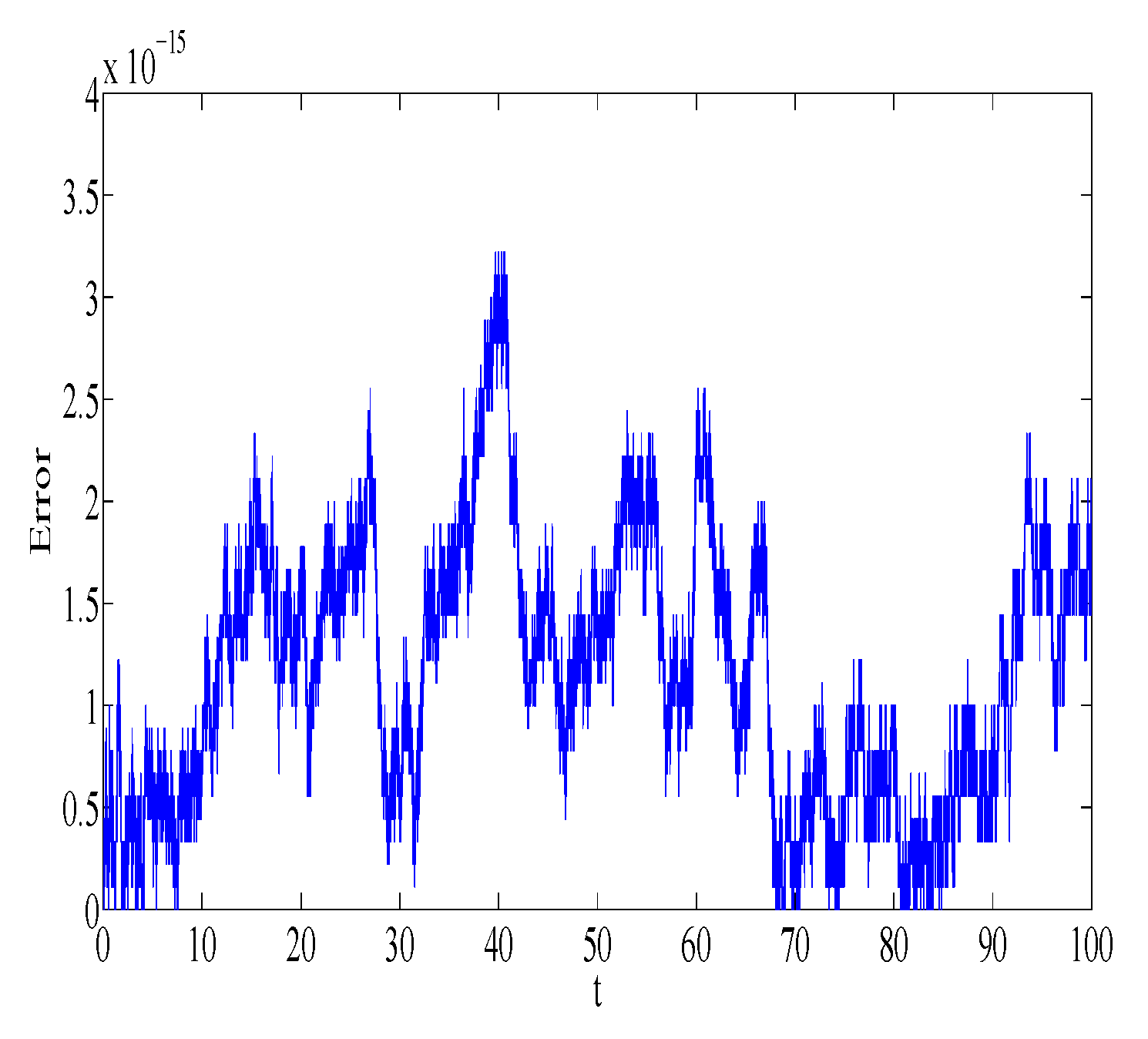
n = 10,000 number of steps. The absolute error in first integrals
,
,
, and
is plotted in
Figure 5,
Figure 6,
Figure 7 and
Figure 8, respectively. Similar error behavior is obtained for
,
,
,
,
, and
. We observe that the error does not grow out of bounds, which shows that the numerical method can mimic the true qualitative feature of the dynamical system.
Case III: ( and are complex)
When
k and
are both complex, i.e.,
and
for
f,
g,
, and
being real, the following coupled system of harmonic oscillators is obtained:
which admits a pair of Lagrangians [
11]:
System (
36) admits the following 9 Noether-like operators and first integrals:
The Gauss2 method is again used to integrate Equation (
36) with stepsize
and
n = 10,000 number of steps. The absolute error in the first integrals is calculated as before. The absolute error in integrals
,
,
and
is plotted in
Figure 9,
Figure 10,
Figure 11 and
Figure 12, respectively, which remains bounded for long time. Similar error behavior is obtained for
,
,
,
,
, and
. The symplectic Gauss2 method is able to preserve all first integrals obtained by performing complex symmetry analysis.