An Improved A* Algorithm Based on Hesitant Fuzzy Set Theory for Multi-Criteria Arctic Route Planning

Abstract

This paper presents a new route planning system for the purpose of evaluating the strategic prospects for future Arctic routes. The route planning problem can be regarded as a multi criteria decision making problem with large uncertainties originating from multi-climate models and experts’ knowledge and can be solved by a modified A* algorithm where the hesitant fuzzy set theory is incorporated. Compared to the traditional A* algorithm, the navigability of the Arctic route is firstly analyzed as a measure to determine the obstacle nodes and three key factors to the vessel navigation including sailing time, economic cost and risk are overall considered in the HFS-A* algorithm. A numerical experiment is presented to test the performance of the proposed algorithm.

1. Introduction

The dramatic variation of sea ice in the Arctic region, due to global warming, has attracted many researchers in science and engineering, where shipping in the Arctic water is one of the hottest issues. Compared to the traditional shipping routes, the Arctic routes have shorter distances linking Asia and North America, as well as linking Asia and Europe, and are a more open navigation environment, more access to the abundant oil and gas resources and lower piracy risk [1]. Therefore, navigation through Arctic routes is considered to be a money-making opportunity for shipping and oil gas companies.

Compared to the traditional ship path planning problem [2,3,4,5,6], sea ice condition becomes a key factor to the route planning in the Arctic region due to its impact on travel time and fuel consumption, as well as the risk of being stuck in the ice [7].

Reference [7] introduced a system for route optimization in ice-covered water, which consisted of an ice model, a ship transit model, and an end-user system. The system was operated on commercial vessels in the Baltic Sea, and its performance was tested. Reference [8] developed an ice navigation system combined with a sea ice model, transit model and a model for route planning which simulated the whole Arctic area. The system employed a modified transit model devised by [9], which integrated various parameters such as ice-breaking fee, port charge, capital cost, etc. Reference [10] developed another ice navigation system where the uncertainty of sea ice prediction and the extremely severe conditions were taken into consideration. The route optimization problem in ice-covered water was regarded as a dynamic stochastic path planning problem, and a heuristic route optimization model was proposed to solve it. Reference [11] devised an automatic ice navigation support system to find the safest- and- shortest routes in the Arctic area for different types of vessels with a geographic information system.

However, unlike the real-time path planning system, the model in this paper is mainly devised to evaluate the strategic prospects for future Arctic routes. Therefore, most data are incorporated for future prediction, where large uncertainties arise from the bias of current multi-climate models and the inconsistency of experts’ cognition. Additionally, for commercial navigating in the Arctic routes, sailing safety, as well as economic benefits, should be guaranteed according to the harsh weather conditions in the Arctic area. Therefore, sailing time, economic cost, and navigation safety are all key factors to influence the route planning, which makes the problem a multi-criteria decision making (MCDM) problem.

Owing to the MCDM problem with large uncertainties in the route optimization model, information on each grid has variation so that a new path planning method is required for the model to handle this uncertain decision problem. Many studies have examined that the hesitant fuzzy sets theory is a powerful tool to solve the mentioned kind of problem [12,13,14,15,16,17]. Therefore, this paper develops a new ice navigation system with a modified A* path planning algorithm called HFS-A* algorithm, where the hesitant fuzzy set theory is incorporated to improve the traditional A* algorithm. Three key factors, including sailing time, economic benefits, and navigation safety, are considered to the final decision-making in this system where multi-models of sea ice prediction and multiple experts’ knowledge are used as input. More details related to hesitant fuzzy set theory and A* algorithm can be seen in Section 2. Section 3 introduces the establishment of the HFS-A* algorithm. A numerical experiment has been used to examine the proposed model in Section 4, and the conclusion can be seen in Section 5.

2. Preliminaries

2.1. Traditional A* Algorithm

2.1.1. Basic Concepts

A* algorithm is a heuristic algorithm widely used for finding an optimal path in static road network presented by [18], which is derived from the Dijkstra algorithm [19] and the Greedy algorithm [20]. The Dijkstra algorithm can find the shortest path, but has to traverse the entire network with low efficiency, and the Greedy algorithm has fast search speed but cannot guarantee to find the best path. The A* algorithm can balance both search speed and global optimality by using the specific utility function $f\left(n\right)$, which consists of a kind of cost function $g\left(n\right)$ and a kind of cost function $q\left(n\right)$:

$$f\left(n\right)=g\left(n\right)+q\left(n\right)$$

(1)

where $g\left(n\right)$ represents the actual cost from initial node to the current node, and $q\left(n\right)$ is the estimated cost from the current node to the end node. When $q\left(n\right)=0$, only $q\left(n\right)$ works, then the A* algorithm degenerates to the Dijkstra algorithm, which can only guarantee finding the optimal route. When $h\left(n\right)\le q\left(n\right)$, then the A* algorithm can maintain the search speed and the global optimality, and the search speed will be slower when the value of $q\left(n\right)$ becomes smaller. When $h\left(n\right)\gg q\left(n\right)$, then the A* algorithm degenerates to the Greedy algorithm, which can run faster but may fall into local optimum.

2.1.2. Work Flow

The flow of the algorithm can be seen in Figure 1.

Step 1

Initiate two ordered lists called “OPEN” list and “CLOSE” list and generate two nodes called “START” node and “END” node.

Step 2

The utility function $f\left(n\right)$ is calculated by Equation (1) at “START” node and put the “START” node into “OPEN” list.

Where, $f\left(n\right)$ is the estimated value from the “START” node to the “END” node through the current node $n$; $g\left(n\right)$ is the actual value from the “START” node to the current node $n$; $g\left(n\right)$ is the estimated value from the current node $n$ to the “END” node.

Step 3

Take out the node of minimum utility from “OPEN” list and mark it as the current node $n$. This node will be saved in “CLOSE” list.

Step 4

If and only if the node $n$ is not the “END” node, continue the algorithm.

Step 5

Evaluate each adjacent node of node $n$ and skip the one which has already existed in “CLOSE” list. Then, compute the utility of this node if it is not in “OPEN” list and save it in “OPEN” list. If the node has already existed in “OPEN” list, recalculate the utility of this node and choose the smaller value by comparing the utility with the previous one. Finally, node $n$ is assigned as the parent node of the node.

Step 6

If “OPEN” list is not empty, back to Step 3. Otherwise, exit and report the failure of route search.

2.2. Basic Concepts of Hesitant Fuzzy Set

2.2.1. Hesitant Fuzzy Set

Hesitant fuzzy set, proposed by [21], is a more general fuzzy set. An HFS is defined in terms of a function that returns a set of membership values for each element in the domain [21].

Definition 1

([21]). A hesitant fuzzy set $A$ on $X$ is a function $h^A$ that when applied to $X$ returns a finite subset of [0,1], which can be represented as the following mathematical symbol:

$$A=\left\{\langle x,h_A\left(x\right)\rangle \right|x\in X\},$$

(2)

where $h_A\left(x\right)$ is a set of some values in [0,1], denoting the possible membership degrees of the element $x\in X$ to the set $A$. For convenience, $h_A\left(x\right)$ is named a hesitant fuzzy element (HFE) [22].

Definition 2

([21]). For a hesitant fuzzy set represented by its membership function $h=h_A\left(x\right)$, we define its complement as follows:

$$h^c={\cup }_{\gamma \in h}\left\{1-\gamma \right\}.$$

(3)

Definition 3

([22]). For an HFE $h$, $Sc\left(h\right)=\frac{1}{l_h}{\sum }_{\gamma \in h}\gamma$, is called the score function of $h$, where $l_h$ is the number of elements in $h$ and $Sc\left(h\right)\in \left[0,1\right]$. For two HFEs $h_1$ and $h_2$, if $Sc\left(h_1\right)>Sc\left(h_2\right)$, then $h_2\prec h_1$, if $Sc\left(h_1\right)=Sc\left(h_2\right)$, $h_2\approx h_1$.

Some operations on the HFEs ($h$, $h_1$ and $h_2$) and the scalar number $\lambda$ are defined by [22]:

$$h_1\oplus h_2={\cup }_{{\gamma }_1\in h_1,{\gamma }_2\in h_2}\left\{{\gamma }_1+{\gamma }_2\dot{-}{\gamma }_1{\gamma }_2\right\},$$

(4)

$$h_1\otimes h_2={\cup }_{{\gamma }_1\in h_1,{\gamma }_2\in h_2}\left\{{\gamma }_1{\gamma }_2\right\},$$

(5)

$$h^{\lambda }={\cup }_{\gamma \in h}\left\{{\gamma }^{\lambda }\right\},$$

(6)

$$h^{\lambda }={\cup }_{\gamma \in h}\left\{{\gamma }^{\lambda }\right\}.$$

(7)

2.2.2. The Aggregation Operators for Hesitant Fuzzy Information

Reference [23] proposed an aggregation principle for HFEs:

Definition 4

([23]). Let $A=\left\{h_1, h_2, \dots ,h_n\right\}$ be a set of $n$ HFEs, $\Theta$ be a function on $A$, $\Theta : {[0,1]}^N\to \left[0,1\right]$, then

$${\mathsf{\Theta }}_A={\cup }_{\gamma \in \left\{h_1\times h_2\times \dots \times h_n\right\}}\left\{\mathsf{\Theta }\left(\gamma \right)\right\}.$$

(8)

Based on Definition 4, some new aggregation operators for HFEs were given by [22]:

Definition 5

([22]). Let $h_i$ ($i=1,2,\dots ,n$) be a collection of HFEs, $w={(w_1, w_2,\dots , w_n)}^T$ be the weight vector of them, such that $w_i\in \left[0,1\right]$ and ${\sum }_{i=1}^n{w}_i=1$. A generalized hesitant fuzzy weighted averaging (GHFWA) operator is a mapping $H^n\to H$, and

$$GHFW{A}_{\lambda }\left(h_1,h_2,\dots ,h_n\right)={\left({\oplus }_{i=1}^n\left(w_i{h}_i{}^{\lambda }\right)\right)}^{\frac{1}{\lambda }}={\cup }_{{\gamma }_1\in h_1,{\gamma }_2\in h_2,\dots ,{\gamma }_n\in h_n}\left\{{\left(1-{\prod }_{i=1}^n{\left(1-{\gamma }_i^{\lambda }\right)}^{w_i}\right)}^{\frac{1}{\lambda }}\right\}.$$

(9)

Definition 6

([22]). Let $h_i$ ($i=1,2,\dots ,n$) be a collection of HFEs, $w={(w_1, w_2,\dots , w_n)}^T$ be the weight vector of them, such that $w_i\in \left[0,1\right]$ and ${\sum }_{i=1}^n{w}_i=1$. A generalized hesitant fuzzy weighted geometric (GHFWG) operator is a mapping $H^n\to H$, such that

$$\begin{array}{ll}GHFW{G}_{\lambda }\left(h_1,h_2,\dots ,h_n\right)& =\frac{1}{\lambda }\left({\otimes }_{i=1}^n{\left(\lambda h_i\right)}^{w_i}\right)\\ & ={\cup }_{{\gamma }_1\in h_1,{\gamma }_2\in h_2,\dots ,{\gamma }_n\in h_n}\left\{1-{\left(1-{\prod }_{i=1}^n{\left(1-{\left(1-{\gamma }_i\right)}^{\lambda }\right)}^{w_i}\right)}^{\frac{1}{\lambda }}\right\}.\end{array}$$

(10)

2.2.3. Decision Making Based on Hesitant Fuzzy Information

The decision method based on the above definitions can be derived as follows:

Step 1

The possible alternative $X_i$ of the attribute$A_i$ provided by decision makers or other sources are denoted by the hesitant fuzzy elements $h_i\left(i=1,2,\dots ,n\right)$.

Step 2

The aggregation operators mentioned above are utilized to obtain the hesitant fuzzy elements $h_i(i=1,2,\dots ,m$) for the possible alternative $X_i(i=1,2,\dots ,m$).

Step 3

The score values $Sc\left(h_i\right)$ of $h_i(j=1,2,\dots ,m$) are calculated by Definition 3.

Step 4

Choose the optimal alternative $X^{*}$ by the comparison of $Sc\left(h_i\right)$.

Example 1.

The vessel, which includes four directions$X_i(i=1,2,3,4$) to navigate, is planed to determine the optimal Arctic route for the following year. Suppose there are three factors$A_i\left(i=1,2,3\right)$that affect the decision making—$A_1$: navigation time;$A_2$: economic cost;$A_3$: navigation risk. It should be noted that all of them are of the minimization type. The weight vector of the attributes is$w={(0.3,0.4,0.3)}^T$.

Then, the optimal route can be determined by using the mentioned method.

Step 1

The decision matrix $H={(h_{ij})}_{n\times n}$ is presented in

Table 1. Hesitant fuzzy decision matrix.

	${\mathbf{A}}_1$	${\mathbf{A}}_2$	${\mathbf{A}}_3$
$X_1$	(0.1, 0.3, 0.5)	(0.2, 0.6, 0.8)	(0.3, 0.4, 0.5)
$X_2$	(0.2, 0.4, 0.7)	(0.1, 0.2, 0.4)	(0.3, 0.4, 0.6)
$X_3$	(0.3, 0.5, 0.6)	(0.2, 0.4, 0.5)	(0.3, 0.5, 0.7)
$X_4$	(0.3, 0.5, 0.6)	(0.4, 0.5, 0.6)	(0.2, 0.5, 0.6)

, where $h_{ij}\left(i=1,2,3,4;j=1,2,3\right)$ are in the form of HFEs.

Step 2

Two operators, GHFWA and GHFWG, are used to obtain the HFE $h_i\left(i=1,2,3,4\right)$ for the directions $X_i(i=1,2,3,4$). Take direction $X_1$ as an example and let $\mathsf{\lambda }=2$; we have

$$\begin{array}{c}{h}_1^A=GHFW{A}_2\left(h_{11},h_{12},h_{13}\right)={\left({\oplus }_{j=1}^3\left(w_j{h}_{1j}^2\right)\right)}^{\frac{1}{2}}\\ ={\cup }_{{\gamma }_{11}\in h_{11},{\gamma }_{12}\in h_{12},{\gamma }_{13}\in h_{13}}\left\{{\left(1-{\displaystyle \prod }_{j=1}^3{\left(1-{\gamma }_{1j}^2\right)}^{w_j}\right)}^{\frac{1}{2}}\right\}\\ =\{0.2157,0.2652,0.3503,0.4351,0.4577,0.5040,0.5966,0.6099,0.6383,0.2630,0.3039,\\ 0.3789,0.4566,0.4788,0.5213,0.6093,0.6220,0.6492,0.3166,0.3503,0.4149,0.4847,\\ 0.5040,0.5442,0.6263,0.6383,0.6639\}.\end{array}$$

$$\begin{array}{c}{h}_1^G=GHFW{G}_2\left(h_{11},h_{12},h_{13}\right)=\frac{1}{2}\left({\otimes }_{j=1}^3{\left(2h_{1j}\right)}^{w_j}\right)\\ ={\cup }_{{\gamma }_{11}\in h_{11},{\gamma }_{12}\in h_{12},{\gamma }_{13}\in h_{13}}\left\{1-{\left(1-{\displaystyle \prod }_{j=1}^3{\left(1-{\left(1-{\gamma }_{1j}\right)}^2\right)}^{w_j}\right)}^{\frac{1}{2}}\right\}\\ =\{0.1814,0.2541,0.2915,0.2672,0.3857,0.4514,0.2848,0.4142,0.4875,0.1958,0.2754,\\ 0.3168,0.2898,0.4226,0.4983,0.3092,0.4551,0.5411,0.2065,0.2915,0.3361,0.3071,\\ 0.4514,0.5361,0.3279,0.4875,0.5851\}.\end{array}$$

Step 3

The score values $\mathrm{Sc}\left(h_i\right),i=1,2,3,4$ are calculated by Definition 3, which can be seen in

Table 2. Score values obtained by the GHFWA operator and GHFWG operator and the rankings of alternatives ($\lambda =2$).

	$${\mathit{X}}_1$$	$${\mathit{X}}_2$$	$${\mathit{X}}_3$$	$${\mathit{X}}_4$$	Ranking
GHFWA2	0.4777	0.3993	0.4644	0.4887	$X_4>X_1>X_3>X_2$
GHFWG2	0.3649	0.3052	0.3052	0.3052	$X_4>X_3>X_1>X_2$

.

Step 4

From Table 2, $X_4$ will be chosen as the optimal direction based on both the GHFWA operator and GHFWG operator where $\lambda$ is set as 2.

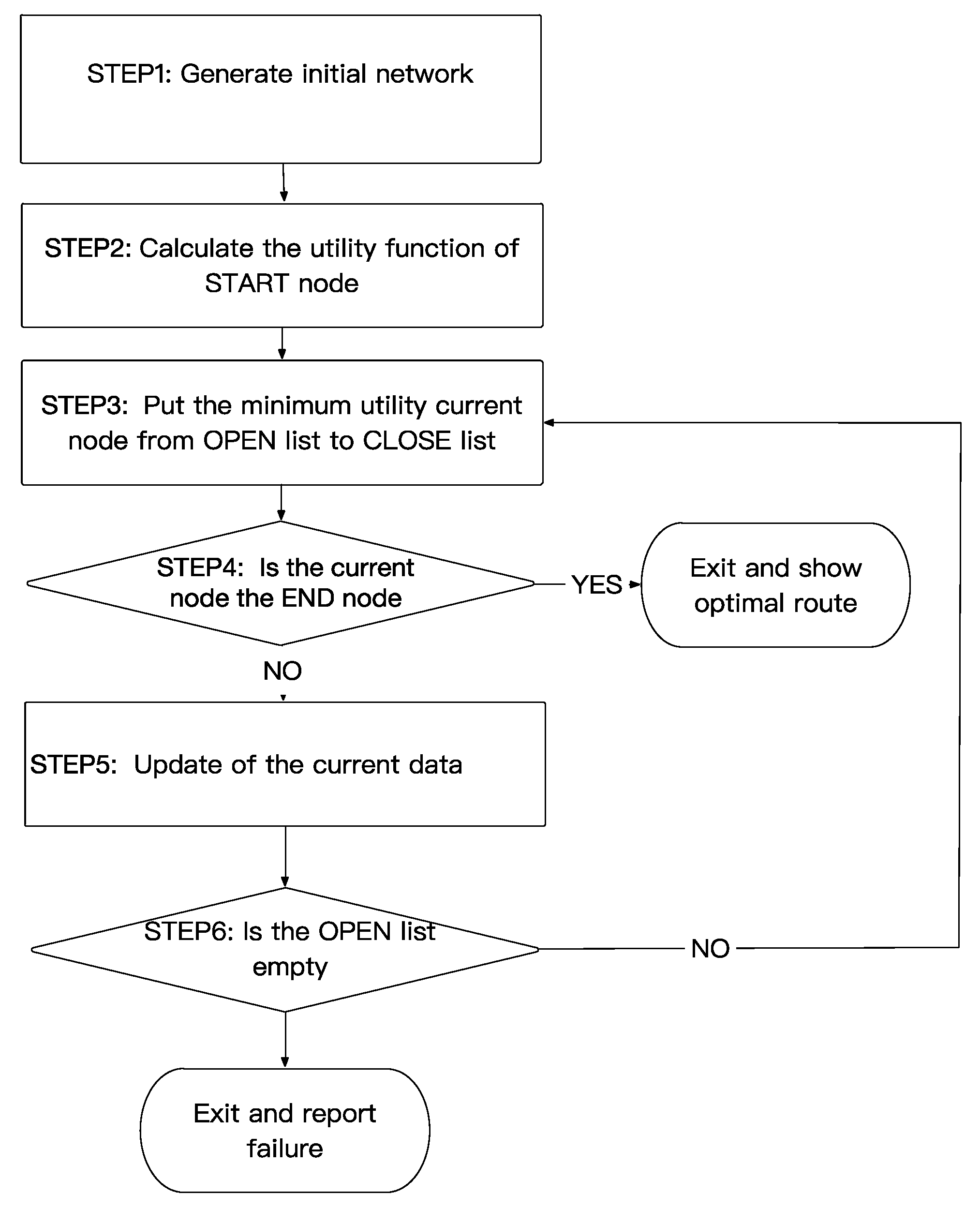
3. An Improved A* Algorithm (HFS-A*)

In light of the harsh weather conditions in the Arctic region, the primary task for route planning is to identify the obstacles (e.g., sea ice). The Coupled Model Intercomparison Project, phase 5 (CMIP5) provided 39 Global Climate Models (GCMs) to predict sea ice data, from history to 21st century, under different representative concentration pathways (RCPs) [23,24]. Unlike the route planning in other regions, for the current sea ice forecasts in the Arctic region, there exists large uncertainty among these GCMs [25,26], which leads to the uncertainty of the length of the navigation season and the economic risk of exploiting the Arctic routes [27]. Therefore, only treating the shortest distance as the optimal route in the Arctic region is not reasonable; more factors, including the navigation risk, the navigation time, and the economic cost during navigation should be considered. Compared to the traditional A* algorithm, the HFS-A* algorithm is used to tackle the multi-criteria decision-making (MCDM) problem with large uncertainty derived from multi-model outputs and expert knowledge. The improved parts mainly focus on t, the identification of obstacles, and the construction of utility function.

3.1. Navigability of the Arctic Routes

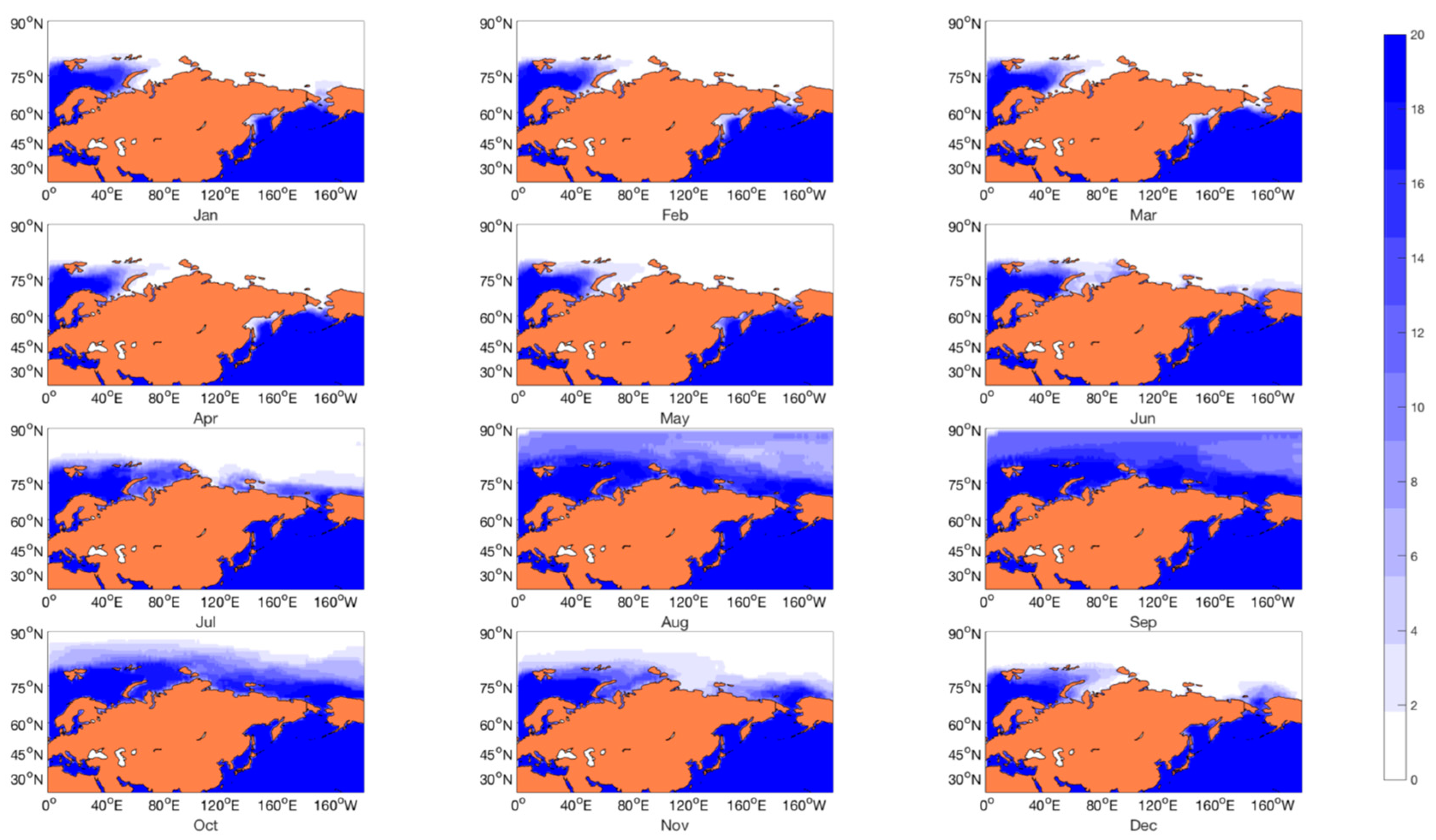
With the impact of global warming, the extent of Arctic sea ice continues to decline [27]. Human’s enthusiasm to explore and develop the Arctic routes are aroused by shorter sailing distance, longer navigation season and increased access to natural resources. There are three criteria related to sea ice conditions for evaluating the navigability in the Arctic area.

Criterion 1 (navigation uncertainty).

Sea ice concentration is considered only for no ice-breaking or ice-strengthening ships, and it is navigable when sea ice concentration is less than 15% [28,29,30,31].

Criterion 2 (navigation time).

Sea ice thickness derived from an empirical regression model is considered and for no ice-breaking or ice-strengthening ships, it is navigable when sea ice thickness is no more than 1.2 m [32,33].

Criterion 3 (navigation economic cost).

Both sea ice concentration and thickness are considered by computing the Ice Numeral (IN) index from the Arctic Ice Regime Shipping System (AIRSS) provided by the Canada Transport [34,35,36,37]. The Ice Numeral is given by

$$IN=C_{a}I{M}_a+C_{b}I{M}_b+\dots +C_{n}I{M}_n$$

(11)

where $C_n$ is the concentration in tenths of ice type $n$, and $I{M}_n$ is the Ice Multiplier for ice type $n$. Ice type describes the specific stage of development of ice, which is closely related to the ice age. Ice Multipliers, determined by ship class and ice type, are a series of integers, which are used to reflect the impact of sea ice type to the specific vessel. A negative $IM$ represents the obstacle effect of vessel sailing. Ice types are determined by [34,38], which are presented in Appendix A. For no ice-breaking or ice-strengthening ships, it is navigable when the IN index is larger than zero. Details about vessel type and IM can also be seen in Appendix A.

Additionally, geographical environment, including water depth and channel width, is also a key factor for ships to navigate, which is related to the vessel type and dimension.

Overall, various evaluation criteria will add to the uncertainty of the sea ice navigability projection. In this paper, we take all three criteria into consideration with geographical restriction to make sure the navigability of the Arctic region, in another words, for one region, can be defined as navigable if and only if the criteria mentioned above are all reached.

3.2. Route Planning Criterion 1: Uncertainty of Sea Ice Condition

In this paper, a series of GCMs have been chosen based on their reasonable projections for future sea ice conditions evaluated by literature studies [39,40,41,42] (see Appendix B). In order to obtain the uncertainty of each model, these model outputs were compared with the Pan-Arctic Ice Ocean Modeling and Assimilation System (PIOMAS) estimate data set, which is a reanalysis with good spatial and temporal consistency constrained by the quality of the assimilated observations [43,44,45,46].

Suppose we have $M$ GCMs, let each model data-set be ${\mathrm{X}}_i, i=1,2,\dots ,M$, the PIOMAS data set be $\tilde{X}$, then the uncertainty of each model can be obtained as follows:

$$\begin{array}{cc}{h}_{\mathrm{i}1}=0.5-0.5\times \frac{X_i·\tilde{X}}{\parallel X_i\parallel \times \parallel \tilde{X}\parallel },& i=1,2,\dots ,M\end{array}$$

(12)

where, $\frac{X_i·\tilde{X}}{\parallel X_i\parallel \times \parallel \tilde{X}\parallel }$ is called cosine similarity, which is a measure of similarity between two non-zero vectors introduced by [47]. $h_{\mathrm{i}1}, i=1,2,\dots ,M$ represents the bias from the model to the “real state”, which can also be regarded as model uncertainty. When $h_{\mathrm{i}1}$ is equal to zero, it represents that the model data sets can well reflect the “real state”, while when $h_{\mathrm{i}1}$ is equal to one, the model uncertainty reaches its maximum.

3.3. Route Planning Criterion 2: Time for Navigation on the Arctic Routes

The navigation time for each grid can be depicted as follows:

$$T_i=\frac{S_i}{V_i}, i=1,2,\dots , M,$$

(13)

where, $S_i$ is the distance of each grid, and $v_i$ is the velocity of the vessel on each grid. $h_{i2}$ is the normalization of $T_i$.

On the Northern Sea Route (NSR), the vessel speed is mainly impacted by sea ice conditions. A h-v curve presented by [48] can reflect, well, the relationship between sea ice thickness and vessel speed. In this h-v curve, the ice resistance and the net thrust of the engine to overcome the ice resistance should both be considered.

Step 1

The ice resistance can be presented as follows:

$$\begin{array}{c}{\mathrm{R}}_{\mathrm{ch}}=0.5{\mu }_B{\rho }_{\mathsf{\Delta }}{\mathrm{gH}}_F^2{K}_P{\left(\frac{1}{2}+\frac{H_M}{2H_F}\right)}^2\left[B+2H_F\left(cos\delta -1/tan\psi \right)\right]\left({\mu }_{h}cos\varphi +sin\psi sin\alpha \right)\\ +{\mu }_B{\rho }_{\mathsf{\Delta }}g{K}_0{\mu }_h{L}_{par}{H}_F^2+{\rho }_{\mathsf{\Delta }}g{\left(\frac{LT}{B^2}\right)}^3{H}_M{A}_{WF}{F}_n^2,\end{array}$$

(14)

where ${\mu }_B=0.5$ represents the ice porosity factor, ${\rho }_{\mathsf{\Delta }}=0.8$ is the density difference between ice and water. In this model, these two factors are considered to be constant for simple situations, e.g., when the temperature changes. Variables include the waterline area of the foreship $A_{WF}$, the Froude number $F_n$, the length $L$, the parallel midbody length at waterline $L_{par}$, the width B, the friction coefficient ${\mu }_h$ and the vessel draft $T$. $K_P$ and $K_0$ are mechanical factors of ice found by [49]. The thickness of the brash ice $H_F$ can be determined as follows:

$$H_F=H_M+\frac{B}{2}tan\gamma +\left(tan\gamma +tan\delta \right)\sqrt{B\left(\frac{H_M+\frac{B}{4}tan\gamma }{tan\gamma +tan\delta }\right)}.$$

(15)

Both γ and δ represent the slope angles of the brash ice.

The formula can be simplified by an approximation when $B>10\mathrm{m}$ and $H_M>4 \mathrm{m}$ [39]:

$$H_F=0.26+{\left(B{H}_M\right)}^{0.5}.$$

(16)

The flare angle ψ mentioned above can be obtained with the bow angles ϕ and α:

$$\psi =\arctan \left(\frac{tan\varphi }{sin\alpha }\right).$$

(17)

Step 2

The net thrust can be calculated by the following formula:

$$T_{tot}\left(v\right)\left(1-t\right)=R_{ow}\left(v\right)+R_i\left(v\right),$$

(18)

$$T_{tot}\left(v\right)\left(1-t\right)=R_{ow}\left(v\right)+R_i\left(v\right),$$

(19)

where $T_{tot}$ is the total thrust, $\left(1-t\right)$ represents the thrust deduction factor, and $R_i\left(v\right)$ and $R_{ow}\left(v\right)$ are the resistance in ice and in open water respectively.

The effect of vessel speed is approximated by a quadratic factor called bollard pull $T_B$ [50], with the maximum open water speed $v_{ow}$, and the net thrust can be rewritten as

$$T_{net}\left(v\right)=\left(1-\frac{\frac{1}{3}v}{v_{ow}}-\frac{2}{3}{\left(\frac{v}{v_{ow}}\right)}^2\right)T_B,$$

(20)

$$T_B=K_e{\left(P_D{D}_P\right)}^{\frac{2}{3}},$$

(21)

where v is the vessel speed in the ice, K_e is the bollard pull quality factor, $D_P$ is the propeller diameter and $P_D$ is the actual power delivered.

3.4. Route Planning Criterion 3: Economic Cost for Navigation on the Arctic Routes

The economic cost of navigation on the Arctic routes are consist of four parts, which are capital cost, fuel cost, operation cost, and transit cost:

$${\mathrm{Cos}\mathrm{t}}_{\mathrm{economic}}=Cos{t}_{capital}+Cos{t}_{fuel}+Cos{t}_{operation}+Cos{t}_{transit}$$

(22)

3.4.1. Model for Capital Cost

Capital cost is related to the price of new ship building or the cost of a ship with loans and depreciations [51]. Generally, the annual capital cost can be computed as follows [52]:

$$Cos{t}_{capital}=\left(P\times \left(1-eq\right)\times \frac{{\left(1+r\right)}^y\times r}{{\left(1+r\right)}^y-1}\right)+\left(eq\times C\right)/y$$

(23)

where $P$ is a new ship price, eq is the equity, r is the interest rate, and y is the term of loan. The former item is called annual interests, while the latter item is called cash price.

3.4.2. Model for Fuel Cost

Fuel cost is often depicted as the major cost on the marine transportation, which is the largest single cost factor to most related simulations, ranging from 36.7% to 61% [53].

Fuel cost is impacted by the rate of fuel consumption and the price of fuel, which can be descripted as follows:

$$Cos{t}_{fuel}=Fue{l}_{consumption}\times Fue{l}_{price}$$

(24)

The fuel consumption of a vessel can be influenced by ship dimensions (e.g., the ship size, hull design, engine profile, speed) and external factors (e.g., sea ice, wind, wave, current, foggy) [51]. The fuel consumption for a specific type of vessel is basically computed by multiplying SFOC (specific fuel oil consumption) (g/kWh), engine power (kw) and sailing hours (h) [54].

Most authors consider speed as the key factor impacting the fuel consumption when the type of a vessel is determined and a simple exponential law based on empirical data are derived: the fuel consumption per unit distance is proportional to the square of the speed [55,56,57], which can be presented as

$$\frac{V_1^2}{F_1}=\frac{V_2^2}{F_2},$$

(25)

where $F_1$ and $F_2$ are the fuel consumption rate under the velocity $V_1$ and $V_2$, respectively. Fuel price is affected by the fluctuation of the global economic market. Low fuel price indicates the depression of global economy, while high fuel price reflects the booming global market.

3.4.3. Model for Operation Cost

Operation cost mainly includes crew cost, insurance cost and maintenance fee which is presented as follows:

$$Cos{t}_{operation}=Cos{t}_{crew}+Cos{t}_{maintenance}+Cos{t}_{insurance}$$

(26)

1. Crew cost

Crew cost is determined by the vessel type, automation level and numerous other factors [51]. Compared to the open water, the crews in the Arctic region require additional ice navigation experience and the ability to cope with hash weather conditions, which may increase the crew cost [53]. The increased crew cost may come from the higher wage [58] for each member or the larger size of members [59].

2. Maintenance cost

For the purpose of preventing the occurrence of breakdowns and following the scheduled maintenance program, the cost of regular maintenance is needed for vessels.

3. Insurance cost

In face of the risk of Arctic navigation (e.g., collision, engine damage, propeller damage, local hull damage, grounding, etc.) analyzed IN some studies [60,61], maritime insurance is a good tool to mitigate the associated risks, which can be approximately separated into three major components: protection and indemnity (P&I), hull and machinery (H&M), and cargo insurance. The third-party liabilities encountered during the commercial operation of a ship are charged by P&I. H&M covers the cost of damage done to the ship or its equipment. Cargo insurance provides the payment for the damage to the cargo itself [62].

3.4.4. Model for Transit Cost

On the NSR, the transit fee based on vessel type and ice conditions mainly includes ice pilot fee and ice breaking fee and can be given as

$$Cos{t}_{transit}=Cos{t}_{icebreaking}\times Load\times Pa{y}_{load}+Cos{t}_{icepilot}$$

(27)

These services are mainly provided by the Russian icebreaking service provider, Atomflot, and are compulsively charged subject to the law of the Russian Federation, which is dependent on the vessel type (e.g., the size and the ice-class of a vessel), and the navigation length and pilotage distance [62]. In general, higher ice-classed vessels are charged with lower icebreaking fees.

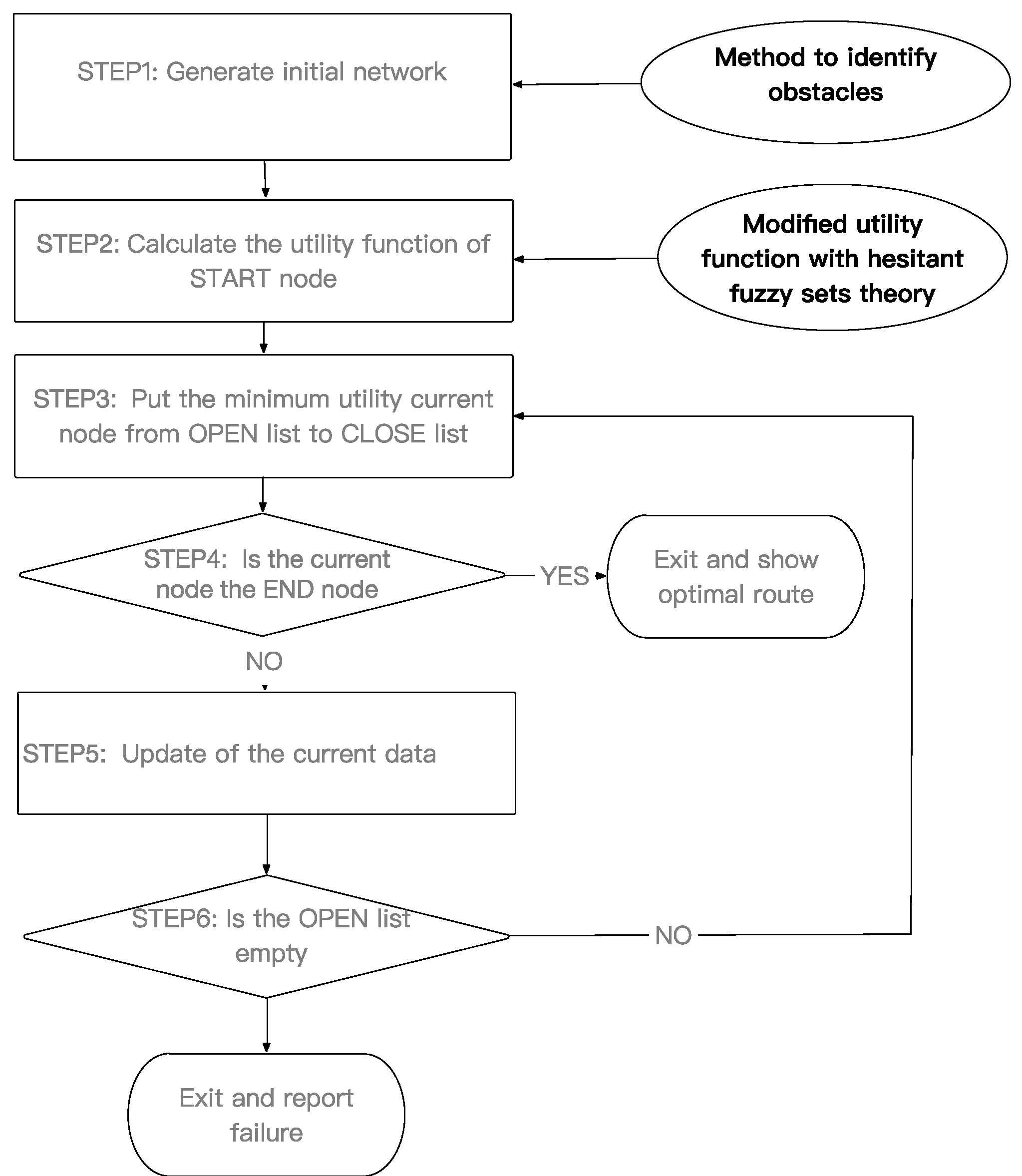
3.5. Work Flow of HFS-A* Algorithm

In this HFS-A* algorithm, the work flow can be seen in Figure 2. The method of obstacle identification has been discussed in Section 3.1 while the modified utility function can be described as follows:

$$f^{*}\left(i\right)=g^{*}\left(i\right)+q^{*}\left(i\right)$$

(28)

When the current node $i$ is determined, the actual cost $g^{*}\left(i\right)$ is equal to the score value $\mathrm{Sc}\left(h_i\right)$, which can be computed by Definition 3.

More specifically, we assume each selected node has three criteria $C_j\left(j=1,2,3\right)$ that affect the decision making—$C_1$: uncertainty of sea ice condition; $C_2$: navigation time; $C_3$: navigation economic cost. It should be noted that all of them are of the minimization type. The weight vector of the attributes is $w={(w_1,\dots ,w_j)}^T$.

The heuristic estimated cost function can be approximately evaluated:

$$q^{*}\left(i\right)=Sc\left(h_i\right)\times D$$

(29)

where, $D$ is the heuristic distance (Manhattan, Euclidean or Chebyshev) from the evaluated node to the END node [63].

Step 1 Map initialization

• Initialize map grid and interpolate the mentioned data into grid.
• Set the “START” node, “END” node, “OPEN” list and “CLOSE” list.
• Find the obstacle nodes in terms of the constrain conditions mentioned in Section 3.1.

Step 2 The construction of utility function

• Each time, compare all the adjacent nodes $i$ of the current node $n$ by

  $$f^{*}\left(i\right)=Sc\left(h_i\right)\times \left(D+1\right)$$

  (30)

  where, $Sc\left(h_i\right)=GHFW{G}_{\lambda }\left(h_{i1}, h_{i2},h_{i3}\right)$ or $Sc\left(h_i\right)=GHFW{A}_{\lambda }\left(h_{i1}, h_{i2},h_{i3}\right)$, $h_{i1}$ is the HFEs of navigation uncertainty (see Section 3.2), $h_{i2}$ is the HFEs of navigation time (see Section 3.3), and $h_{i3}$ is the HFEs of navigation economic cost (see Appendix D.2).

Step –6 The same as the traditional A* algorithm.

4. Case Study and Conclusion

4.1. Study Area and Data Description

This experiment is to find the optimal route on the Northern Sea Route (NSR) based on the proposed method from Shanghai to Bergen port for an IB-classed 3800TEU container vessel.

Data related to water depth is derived from a product called ETOPO1 provided by the National Geophysical Data Center (NGDC), with a resolution of 1 arc-minute [64]. Data related to AIRSS system can be seen in Appendix A. Data related to sea ice conditions (both sea ice thickness and sea ice concentration) can be seen in Appendix B. Data related to vessel information can be seen in Appendix C. Data related to economic cost can be seen in Appendix D. All the climate model outputs and data related to water depth are interpolated to the grid size of 360 × 120 for the comparison with PIOMAS estimate data set, which the spatial coverage is 45° N to 90$°$N and the temporal resolution is monthly.

4.2. Route Planning by HFS-A* Algorithm

4.2.1. Navigability of the NSR

The numerical simulation firstly examines the navigability of the IB-classed 3800 TEU container vessels on the NSR for each month in the year of 2050 (see Figure 3). According to the ensemble model predictions, the open time of the NSR for that vessel to access may last for 3 to 5 months in the year of 2050. Most model outputs show the navigable time starts from August to the October, while merely 2 to 4 models extend the navigable time (from July to November).

4.2.2. Selection of the Aggregation Operators and Route Optimization

Secondly, route planning criteria (uncertainty, time and economic cost) have been calculated based on the models mentioned in Section 3.2, Section 3.3 and Section 3.4, and the results can be seen in Appendix D. These factors can be normalized respectively between 0 and 1, which can be described as:

$$\frac{h_i-\min (h_i)}{max(h_i)-\min (h_i)}, i=1,2,\dots , M$$

(31)

Thirdly, the optimal routes for IB-classed 3800 TEU container vessels from Shanghai to Bergen port on the NSR in September of 2050 can be found by two kinds of the aggregation operators (${\mathrm{GHFHA}}_{\lambda }, \lambda =1, 2, 6$ and ${\mathrm{GHFHG}}_{\lambda }, \lambda =1, 2, 6$), which are used to aggregate the normalized results mentioned above. The detailed results can be seen in

Table 3. Results of route optimization for IB-classed 3800 TEU container vessels on the NSR from Shanghai to Bergen port in September of 2050 with different aggregation operators based on HFS-A* algorithm.

	Distance (Nautical Miles)	Sailing Time (day)	Economic Cost (Million USD)	Uncertainty (Mean)
GHFHA1	9900	25.99	1.20	0.5105
GHFHA2	10,110	26.53	1.21	0.5104
GHFHA6	10,142	26.98	1.23	0.5102
GHFHG1	8451	22.61	1.08	0.4700
GHFHG2	8513	22.78	1.09	0.4704
GHFHG6	8341	22.33	1.07	0.4901

. Compared these two kinds of aggregation operators, the performance of the ${\mathrm{GHFHG}}_{\lambda }, \lambda =1, 2, 6$ operators in the route optimization is better than the ${\mathrm{GHFHA}}_{\lambda }, \lambda =1, 2, 6$ operators from the view of total sailing distance, sailing time, economic cost and average uncertainty. In the light of the comparison of different $\lambda$ for each operator, the performance of the ${\mathrm{GHFHG}}_{\lambda }$ becomes better with the $\lambda$ increase, while the performance of the ${\mathrm{GHFHG}}_{\lambda }$ becomes better when $\lambda$ decreases. Therefore, the ${\mathrm{GHFHG}}_1$ operator has been examined as the best aggregation operator in this numerical study (The weights vectors for this experiment are assigned as 0.4, 0.3, and 0.3 for three criteria).

Finally, the optimal route determined by HFS-A* algorithm with the ${\mathrm{GHFHG}}_1$ operator can be seen in Figure 4. Three other routes according to simple single criterion (uncertainty, time, or economic cost) are also drawn in Figure 4. The detailed results can be seen in

Table 4. Results of route optimization for IB-classed 3800 TEU container vessels on the NSR from Shanghai to Bergen port in September of 2050 based on HFS-A* algorithm and simple A* algorithm (The percentages in brackets are compared with the values in GHFHG1).

	Distance (Nautical Miles)	Sailing Time (Day)	Economic Cost (Million USD)	Uncertainty (Mean)
GHFHG1	8451	22.61	1.08	0.4700
Uncertainty	10,674 (+26.0)	27.87 (+23.3%)	1.26 (+16.7%)	0.4404 (-6.3%)
Time	8603 (+1.7%)	21.97 (−2.8%)	1.07 (-0.9%)	0.5148 (+9.5%)
Economic cost	8167 (−3.4%)	21.07 (−6.8%)	1.04 (-3.7%)	0.5516 (+17.4%)

, where it can be found that path planning based on a single factor shows a slight advantage in its related aspect, but shows significant disadvantage in any other aspect compared with the optimal route. In other words, the optimal route can better balance these three key factors and show more realistic performance of the proposed route planning algorithm than the other three single factor route planning.

5. Conclusions

The opening of Arctic routes will be no longer a dream in the coming future with climate change; route planning is necessary for vessels to navigation on the Arctic region from different points of view (safe, economic cost, time etc.). This paper presents a modified A* algorithm where the hesitant fuzzy set theory is incorporated for the purpose of solving the MCDM problem in Arctic route planning with large uncertainties originating from multi-climate models and experts’ knowledge. Compared to the traditional A* algorithm, the navigability of the Arctic route is firstly analyzed as a measure to determine the obstacle nodes, and three key factors to vessel navigation, including sailing time, economic cost and risk are overall considered in the HFS-A* algorithm.

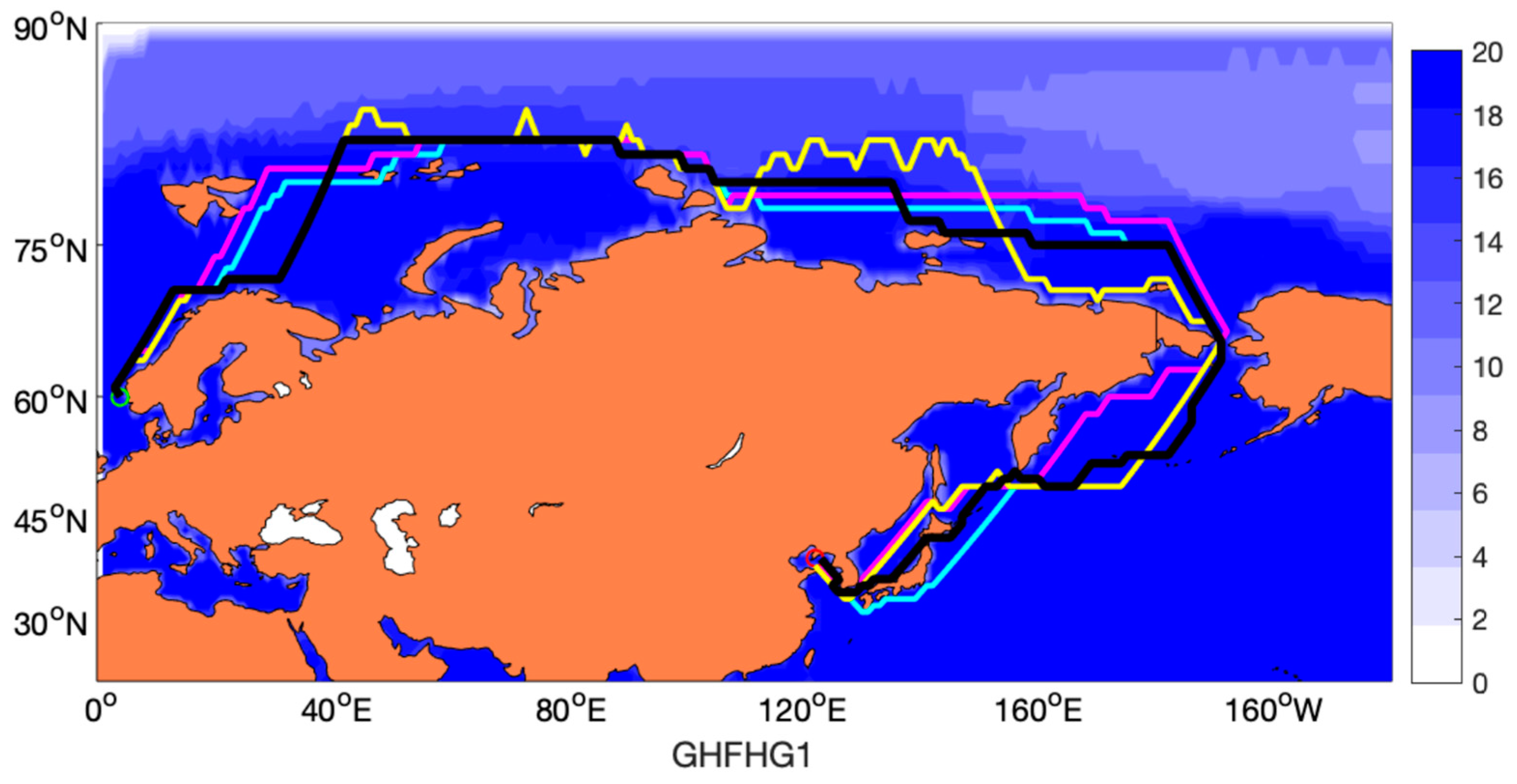
A numerical experiment, which is to find the optimal route between Bergen port and Shanghai port on the NSR, is presented to test the performance of the proposed algorithm. Multi-model ensemble forecast displays that the IB-class 3800 TEU container vessels can navigate on the NSR lasting for 3 to 5 months in the year of 2050. Most model outputs show the navigable time starts from August to October, while merely 2 to 4 models extend the navigable time (from July to November). The sensitivity analysis for the aggregation operators examines that the ${\mathrm{GHFHG}}_1$ operator has an advantage over other aggregation operators in route optimization, and its performance of integrating the three key factors in route planning is better than the performance of any other single factor.

In this paper, the improvement effects for this new approach have been evaluated theoretically and practically. Theoretically speaking, the simple A* algorithm cannot handle the Arctic path planning problem which has multi-criteria attribution with large uncertainties. Even if we can synthesize the time, economic and uncertainty factors by addition and multiplication, the uncertainties existing in climate model prediction and expert knowledge cannot be portrayed by a simple A* algorithm. Practically speaking, we compared the route planning result of HFS-A* algorithm and single factor route planning result (see Figure 4). It can be found that there is a more realistic performance of the HFS-A* route planning algorithm than compared with the simple A* route planning algorithm. Overall, this new HFS-A* algorithm can be well-applied to the Arctic region and to evaluate the strategic prospects for future Arctic routes.