1. Introduction
In comparison with empirical and random graphs, deterministic models have unique advantages in improving our comprehension in complex networks. For instance, we can obtain the solutions for a deterministic model by rigorous derivation, and the computation is only a small quantity of calculations. Deterministic models can be created by simple recursive operation [
1,
2,
3,
4], construction of fractal processes [
5], plane filling techniques [
6], the relationships between natural numbers [
7], or perspectives and methods from classical research of physical processes [
8,
9,
10,
11]. Recently, Zhang et al. introduced Farey graphs (FG) on the basis of classical Farey sequences. Farey graphs are simultaneously uniquely Hamiltonian, minimally three-colorable, maximally outer-planar, and perfect [
12,
13]. FG can be used as modules of multiple networks. The networks created by edge iterations [
14], or evolving graphs with geographical attachment preference [
15], coincide with the combination of three FG, while the merger of six FG generates graphs with multidimensional growth [
16]. Moreover, two new kinds of Farey-type graphs, the generalization of Farey graphs (GFG), and the extended Farey graphs (EFG) are deduced by generalizing the construction mechanism of FG, and they all are scale-free and small-world [
17,
18,
19].
Deterministic graphs also provide a new perspective and methodology for classical research of physical processes. For example, some important dynamical processes on the basis of Apollonian models [
20], a kind of deterministic matching graph, space-filling, Euclidean, small-world, and scale-free, has been researched extensively. Accurate analytical solutions are derived, including percolation [
21], electrical conduction [
20], Ising models [
20], quantum transport [
22], partially connected feedforward neural networks [
23], traffic gridlock [
24], Bose–Einstein condensation [
25], free-electron gas [
26], and so on. However, the study of physical processes using FG is still lacking, as the recursive relationships in FG are more complex than for Apollonian networks.
The label-based routing protocol for all shortest paths may also bridge Farey-type graphs with the fields below. The all-pairs shortest paths problem is frequently studied in textbooks and it has remained open to this day, the classical algorithms such as the A*, Bellman–Ford, Floyd–Warshall and Dijkstra algorithms all run in subcubic time
, where
[
27,
28,
29,
30,
31]. The
shortest path routing (KSPR) algorithm is an extension of the shortest path routing algorithm, in which
is the number of shortest paths to find [
32]. KSPR finds
K paths in order of increasing cost, including the shortest path. KSPR in Farey-type graphs will partly reduce to finding out all the shortest paths. Similar to the minimum spanning problem, the graph Steiner tree problem (GSTR) interconnects a set
of vertices by using a network of shortest length, and the length is the sum of the lengths of all edges [
33]. Most versions of GSTR are NP (non-deterministic polynomial) complete. Moreover, the bottleneck of many network analysis algorithms is the exorbitant computational complexity of calculating the shortest paths, so that scientists are forced to use approximation algorithms [
34].
Graph labeling is one active subject in graph theory. Graph labeling has a wide range of applications in many fields, such as communication design, circuit design, crystallography, and coding theory [
35]. Finding the shortest paths in graphs is an open problem, which has been well studied. Zhang and Camellas pioneered the relationship between the shortest paths and vertex labels [
35,
36,
37,
38,
39]. They can determine the shortest path just by applying simple rules and a few computations based only on their labels.
We propose an algorithm for labeling nodes—all of the shortest paths between any pair of vertices can be efficiently derived only on the basis of their labels. We found that the number of shortest paths between two vertices is huge, but the routing algorithm runs in logarithmic time O(logn).
Furthermore, the existence of symmetry in real-world graphs have been underlined by analyzing of over 1500 graph datasets [
40,
41,
42,
43]. It was found that over 70% of the empirical networks contain symmetries, independent of size and modularity. All the graphs we proposed here are symmetrically-structured on the basis of Farey-type graphs, and therefore our labeling and routing algorithms can provide a new viewpoint on empirical networks which are containing symmetries.
3. Labeling and Routing of
The labeling and routing protocol of GFG and EFG are extended from FG; the label-based routing algorithm was originally derived in [
33], but we redefine it here for completeness and clarity. In order to save space, we do not repeat the proofs of these properties in this section.
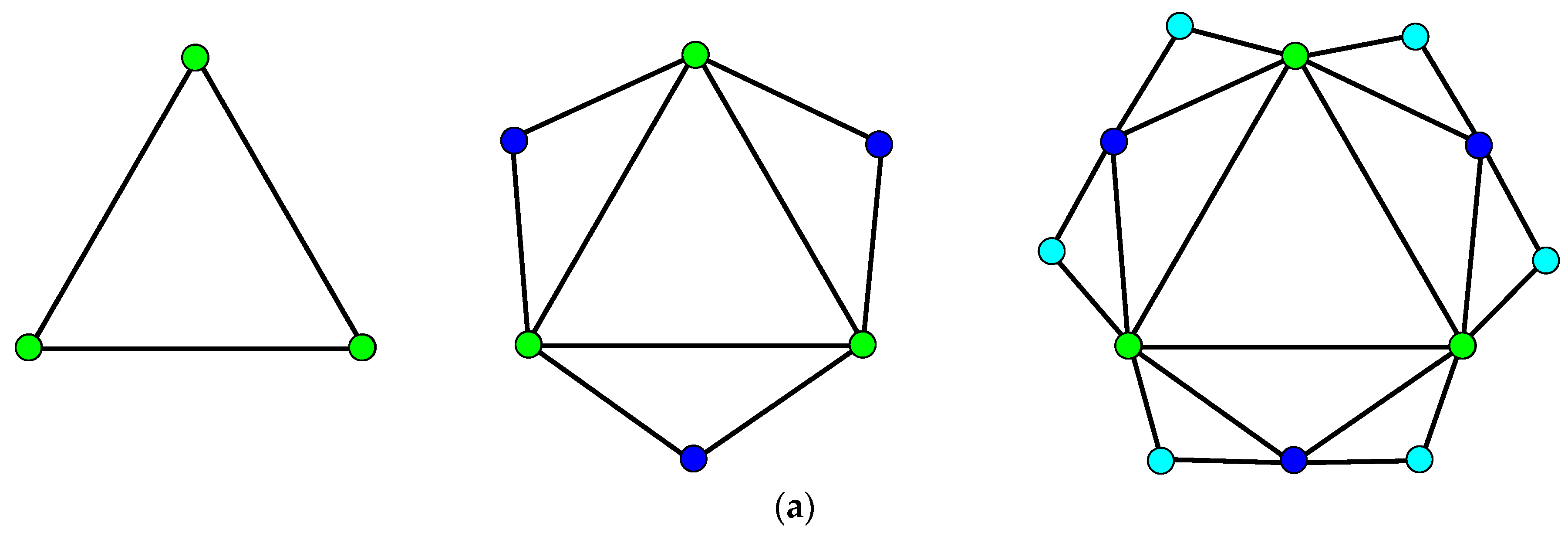
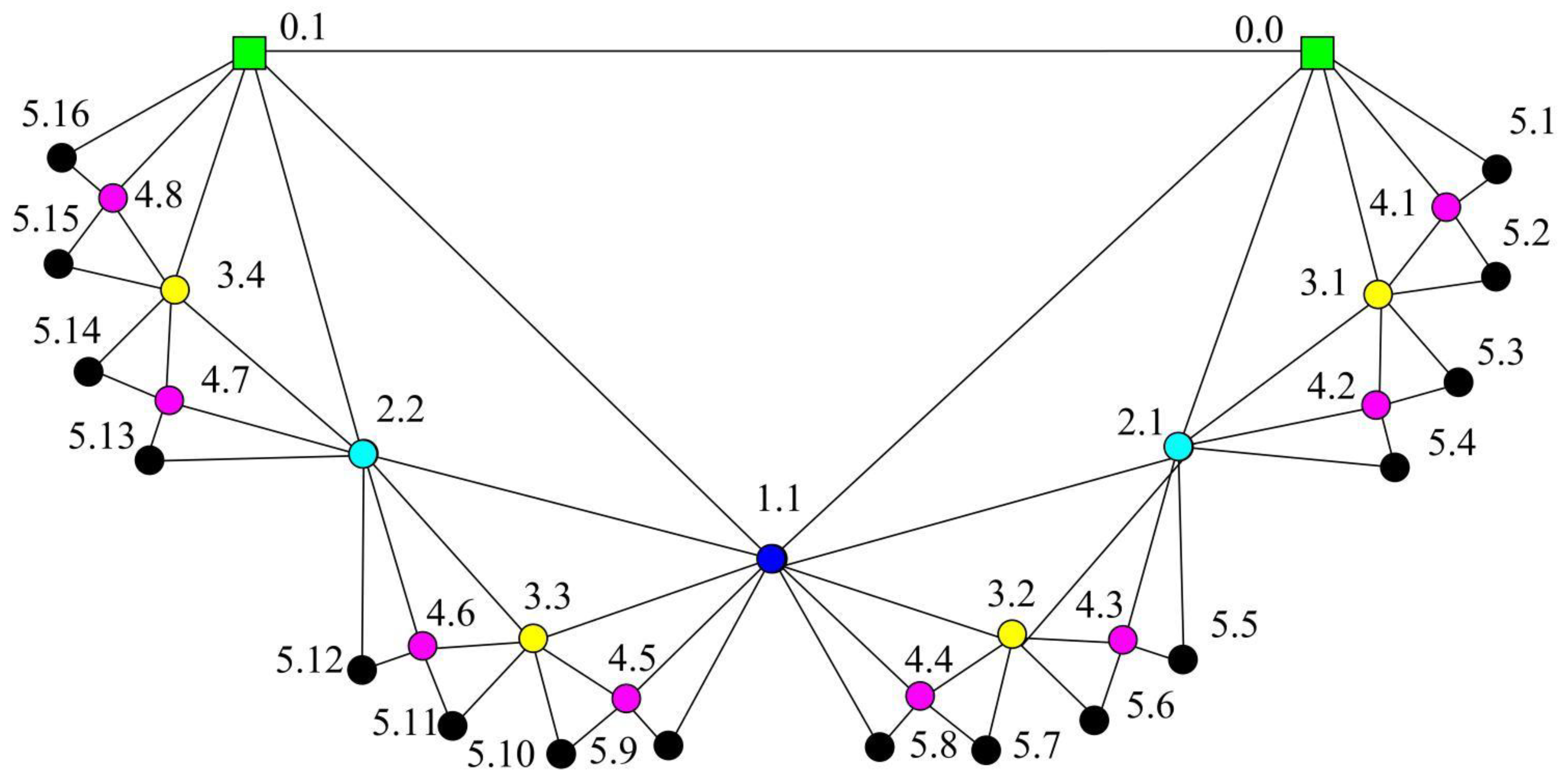
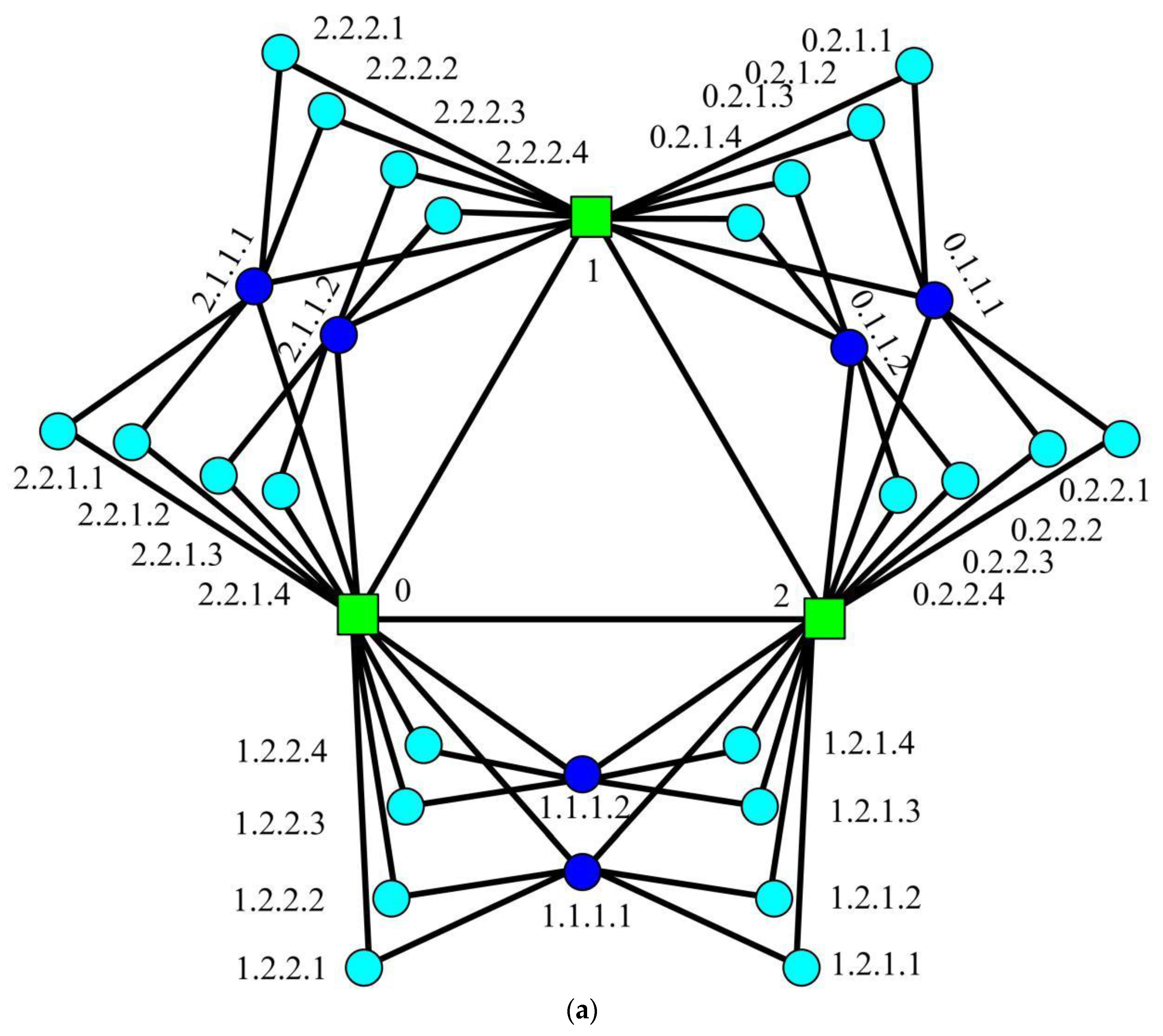
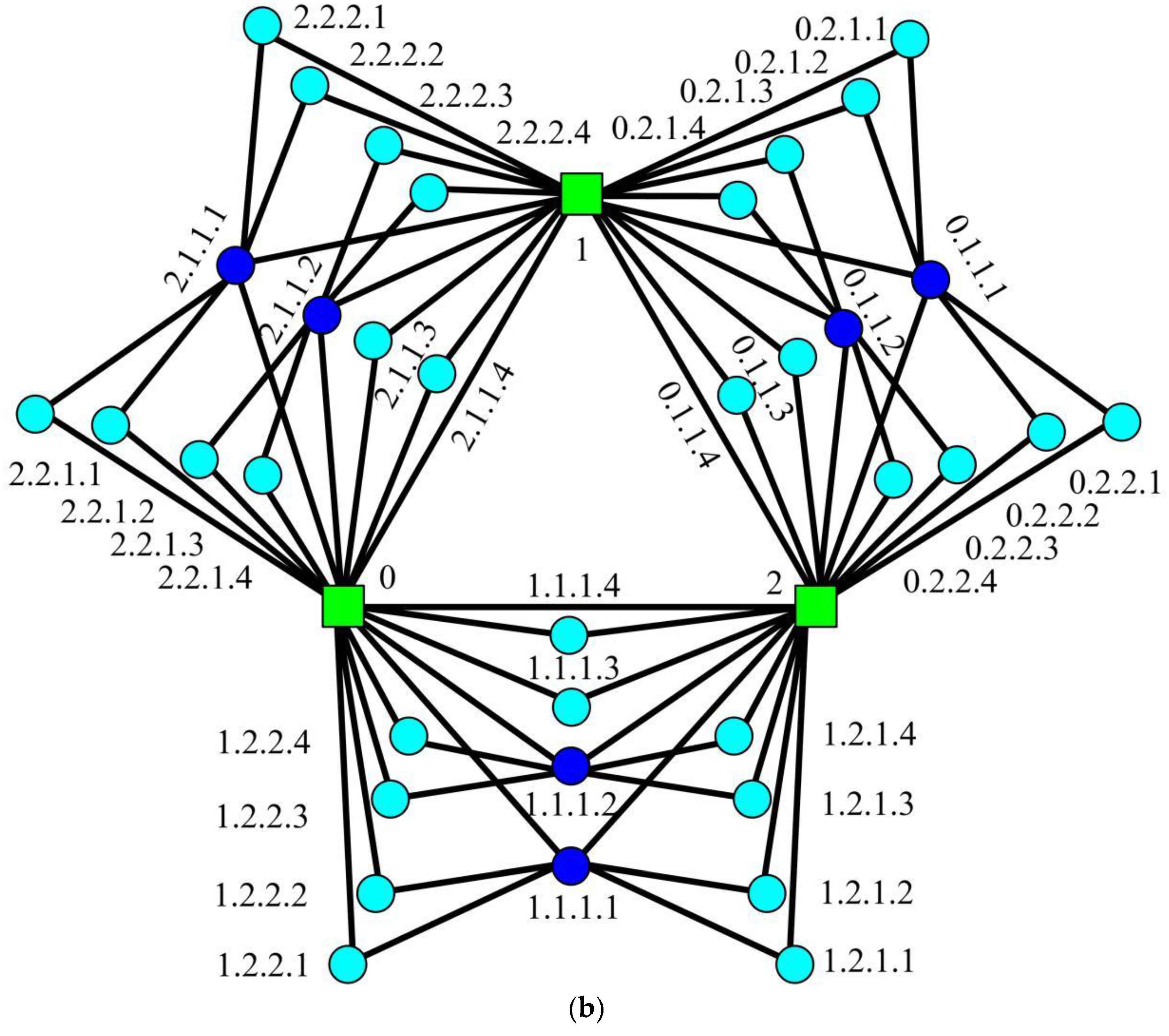
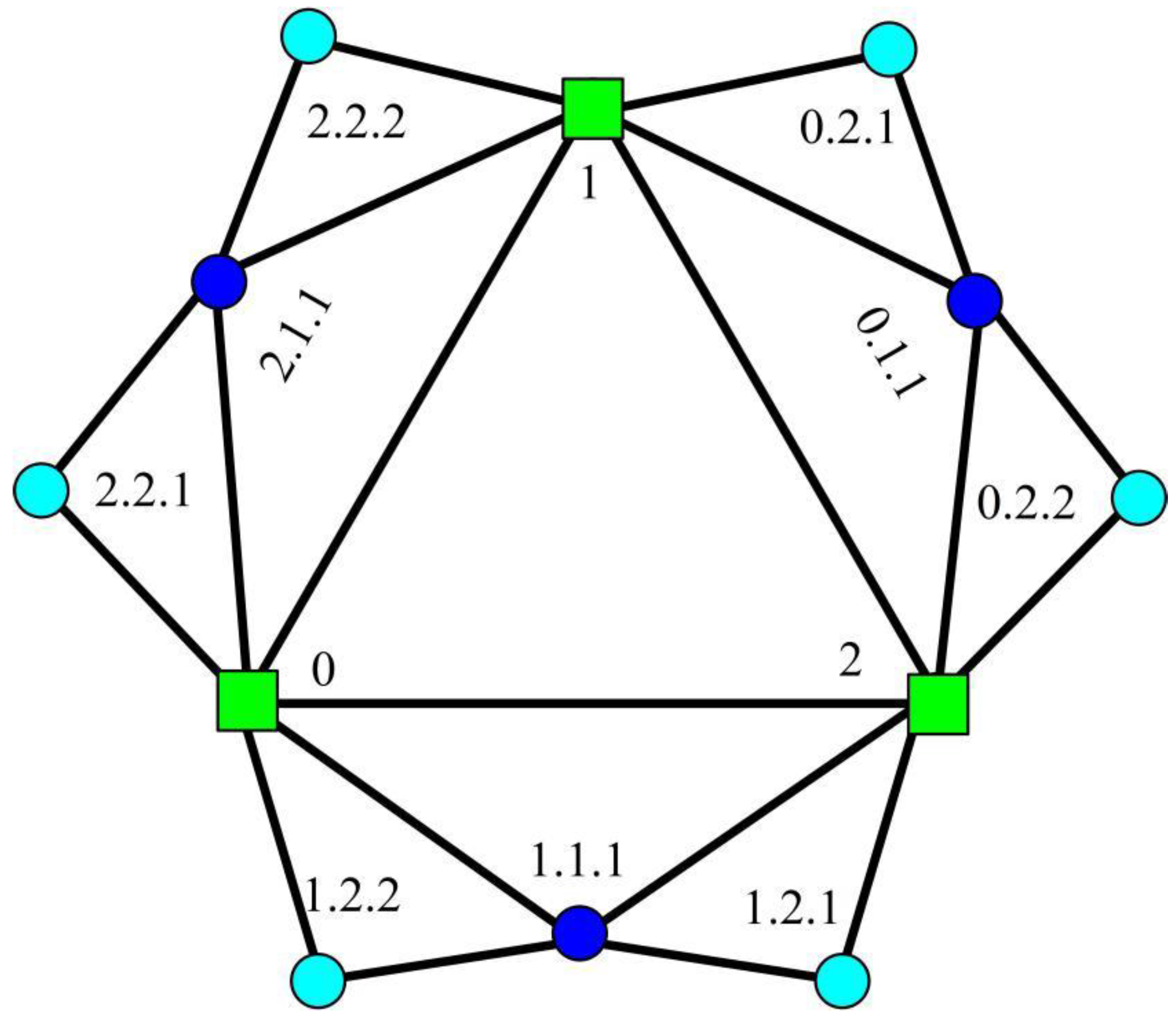
Definition 4. Labeling any vertex in FG as follow (see Figure 5): Label two initial vertices asandwhen t = 0.
When, the new vertices added at step t are marked with labels fromtoin a clockwise direction.
Supposing any two vertices are labeled with and , and . Then the mother vertex of added to the graph at step . Two vertices with same mother are brothers. The father is added to the graph at step or earlier. The following relationships between different vertices, are extracted with the help of their labels.
Property 1. (The family of )
Two children ofareandwhen.
When,The brother ofis(whenis odd) or(whenis even).
When,and its parents shapes a triangle. The mother isand the father is(in whichis the remainder ofdivided by 2,is a function rounding the real numberdown towards the nearest integer. The integeris the number of the continuous zeros from right to left in the binary sequence created by converting the value ofto base 2, plus one, that is, l = Function(k-rem (k,2)).
If, thegeneration of maternal ancestor ofis.
Property 2. (The neighbors of)
When, the neighbors ofis,, and the neighbors ofare,.
When, the neighbors ofare,.
When, the neighbors ofare,.
Property 3. When two vertices are located in different subgraphsandof, the hubofis on the shortest paths, if
(1)and,
(2) orand,
(3) orand,
(4)and. Two initial verticesandofare located on the shortest paths if
(1)and,
(2) orand.
Vertices,andlie on the shortest paths simultaneously if
(1)and,
(a) orand.
Property 4. All the shortest paths between any pair of vertices are located a minimum common subgraph (MCSG) denoted as . Moreover, one vertex is an initial vertex or alayer vertex in, the other is positioned in the outermost layer of.
Property 5. (The shortest paths routing algorithm of Farey graphs)
- 1.
Given a pair of vertices labeled withand.
- 2.
Determine whether the two vertices are neighbors or not.
Ifand, orand, by Property 1, the two vertices are in a mother-child or father-child relationship. Insert the two labels to the labels set of the shortest paths (). Noticing thatandis an integer increasing from one, go to step 6.
3. Find out MCSG when , namely, where is the generation of maternal ancestor of .
If, or, or ..., or, MCSG is the embedded subgraph fromto.is the initial vertexandis an outermost layer vertex in MCSG.
If, or, or ..., or, MCSG is also the embedded subgraph fromto, butis the other initial vertex. Go to step 5.
4. Find out MCSG when .
Ifis thegeneration of maternal ancestor of, then, in which. Go to step 5.
5. Determine whether , and of MCSG are on the shortest paths or not.
Map the labels ofonto labels ofand divide all the vertices ininto six sets as above:,and. Then, decide whether,andare on the shortest paths by Property 3 or not.
If only the nodeis on the paths, then insert the label of, assuming the label is, in the middle ofandin, and. Thereafter, go back to step 1 with two new pairs of labels:and,and.
If onlyandare on the paths, insert the labels ofand, beingandrespectively, in the middle ofandin, and. Get two new pairs of labels,and,and, and go back to step 1.
If,andare all on the paths at the same time, insertintoand, then insertandinto,. Go back to step 1 with four pairs of labels:and,and,and,and.
6. Ascertain the shortest paths routing.
The shortest paths are traversed over every element in every set ofin order, whereis the number of the shortest paths andis the distance betweenand.
Property 6. The shortest paths routing algorithm in Property 5 between any two vertices of a Farey graph runs in logarithmic time.
Proof. Each algorithm has its time complexity and space complexity.
The space complexity of the shortest paths routing algorithm in Property 5 is decided by the number of shortest paths. The number is exactly the product of two Fibonacci numbers. When
, the max number is
, increasing almost exponentially [
33]. The order and size of FG is
, so the space complexity increases almost linearly with O(
n).
However, the time complexity is determined by the maximum number of the vertices, which are located in the shortest paths in two Farey-type graphs. We can obtain that all the vertices on the shortest paths shape rhombuses which are zigzagged adjacent from the construction mechanism. The max number of rhombuses from to is . While from to is . That is to say, only at most vertices need to be ascertained in the routing algorithm. When determining a vertex of vertices, several operations of addition and multiplication are needed. For the order of FG is and , all the shortest paths can be determined in logarithmic time . ☐
4. Labeling of and
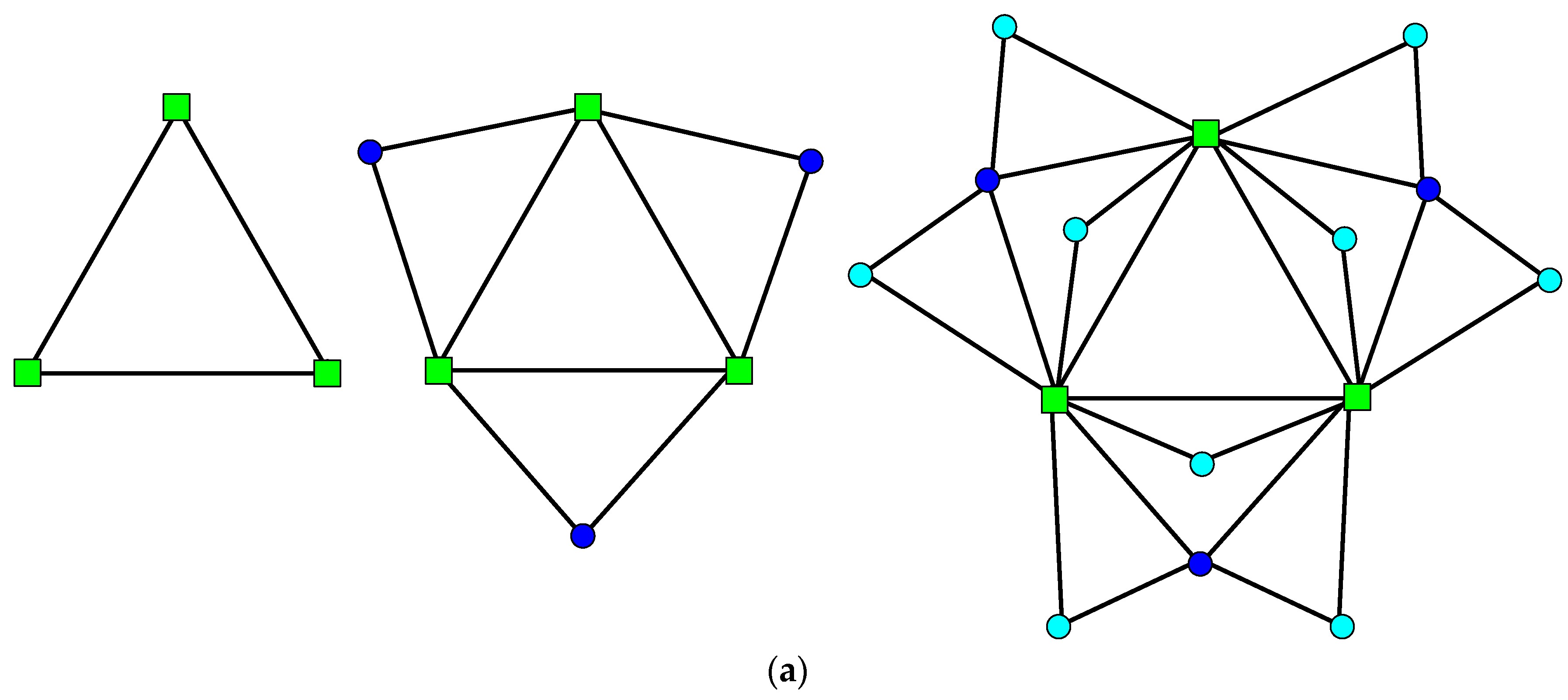
Definition 5. (The labeling of GFG) The labeling of any vertex in adheres to the following rules:
The three initial vertices are labeled with 0, 1 and 2.
At any step, a vertex inis marked withaccording to the group (), the subgroup () and the precise positions () from down to top in the same subgroup, in which,,and.
Definition 6. (The labeling of EFG) Vertices inare labeled as follows:
Label three initial vertices as 0, 1 and 2.
At step, a vertex is tagged with, in which,,and.
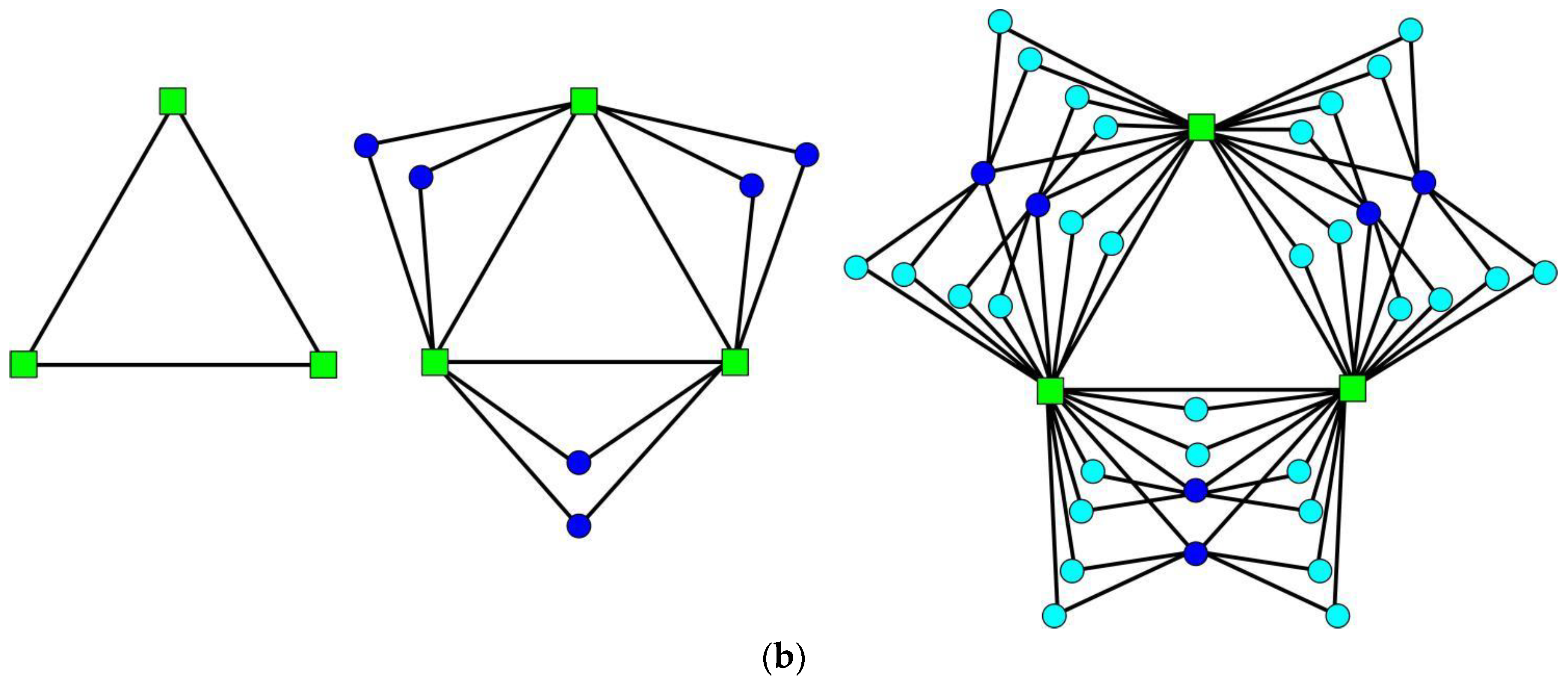
Labeling ofandare illustrated in Figure 6. Remark 4. A GFG has more petals than an EFG, such thatin EFG, whilein GFG.
When , any new vertex, added to GFG/EFG at step , links to two vertices: a mother and a father. The vertices added to graphs at the same time are siblings if they have the same parents. Supposing that two arbitrary vertices in GFG/EFG are labeled with and , in which , then, we give several properties satisfying GFG and EFG at once.
Property 7. (The family of )
When,belongs to a set of siblings {, }.
When,and its parents define a triangle, the mother is, the father is.
If, thegeneration of maternal ancestor ofis.
Proof. The above results are self-evident, with the exception of the formulation of the father’s label, which we shall now prove. If , let denotes the difference , thus, . When and with any , the fathers are all the initial vertexes. When is odd but excluding one, is one plus the number of the continuous zeros from right to left in the binary representation of , such that the father is labeled as . When is even, the time difference is one plus the number of the continuous zeros from right to left of the binary representation of , such that the father’s label is . In summary, the father of is when . ☐
Remark 5. The vertexhas two mothersand no father. The three initial vertices have no parents or siblings. Therefore, the neighbors ofare derived from Property 8.
Property 8. (The neighbors of )
When, the set of neighbors ofis,,, in which,.
The neighbors of initial vertexare, where,.
The neighbors ofareand, where,.
Property 9. (The projection of GFG/EFG) By merging vertices, which have the samebut a different, into a vertex labeling with,/is projected onto a graph which is exactly the combination of three Farey graphs starting from each edge of a triangle.
Proof. From the spatial relationship between vertices in different petals, all the vertices of are linked to common vertices up until two initial vertices are reached, so that all of can merged into a vertex of . By recursively using the spatial relationship, / is projected into a combination of three Farey graphs. ☐
Example 1. The projection graph of/is shown as Figure 7. Property 10. (The slice defined by ) For any vertex, the slice is obtained by recursively identifying all triangles, which are shaped by a vertex and its parents, up until two initial vertices are reached.
Proof. Any vertex has a father and a mother by Property 7, and the three vertices define a triangle. Then, the father’s mother, or the mother’s father, is obtained by recursively using Property 7. From the spatial relationship of vertices, and all these parents define a slice. ☐
5. Routing of and
Although the labels of the three initial vertices in GFG and EFG are slightly different from the labels of the two initial vertices in FG, the shortest paths protocol in GFG/EFG also benefit from the routing algorithm in FG. From the generation mechanism, GFG/EFG is divided into three groups by symmetry, and each group is consisted of or petals, and furthermore vertices in each group can also be divided into three sets by the differences in distance, similar to the equivalent division for FG: sets , and .
Property 11. (The characteristic of shortest paths when two vertices are located in different groups)
If, the initial vertexis on the shortest paths betweenandof GFG/EFG, if
(a)and,
(b) orand,
(c) orand,
(d) orand.
The two initial verticesandare on the shortest paths, if
(a)and,
(b) orand.
The shortest paths pass,andsimultaneously, if
(a)and,
(b) orand.
Proof. From Property 9, and are projected as and , which are located in different subgraphs and of Farey graphs . Following from the proof of Property 3, the conclusions can easily be deduced. ☐
Property 12. (The characteristic of shortest paths when two vertices lie in different slices of same group) Ifandare located in different petals, the shortest paths between them are positioned in two slices which are connected by two common vertices.
Proof. From the generating algorithm, if
and
are located in different petals or subpetals, then the neighbor sets of
and
are ascertained by Property 8. When two common neighbors are created during the same step, then
and
are positioned in different slices, and the two slices can be determined by Property 10. Supposing that the first two common neighbors are
and
, the two slices are rooted in them and belong to
and
. Compared with the construction schematic diagram in
Figure 2, the linking of
and
is slightly different. Name the initial vertices of
and
as
,
and
,
, respectively.
and
are linked exactly by merging
and
into
and linking
and
into
. The vertices of
and
can be divided into six parts similarly:
,
,
and
,
,
, by the distance between
or
to initial vertices
(i.e.,
) and
(i.e.,
), in which case then the shortest paths between
and
go via
, if
(a) and ,
(b) and ,
(c) or and .
The shortest paths go through and , if
(a) and ,
(b) or and ,
(c) and .
The shortest paths pass , if
(a) and ,
(b) and ,
(c) or and . ☐
Property 13. (The characteristic of shortest paths when two vertices are in same slice) Ifandare in the same slice of a petal or subpetal of same group, the shortest paths between them are determined by Property 5, as they have been projected onto a Farey graph.
Proof. If we obtained only one common neighbor vertex, labeled with , of vertices and at the same step, then and are located in same slice. Assuming , the projected Farey graph is with a hub vertex , in which case all the shortest paths are located in . So that all the shortest paths can be decided by Property 5. ☐
The detailed shortest routing algorithm in GFG/EFG is described as follows.
Property 14. (The shortest paths routing algorithm in GFG/EFG)
1. Given any two verticesand, insertandinto the labels set of the shortest paths (), .
2. If, and bothandare not initial vertices, then this is exactly the condition of two vertices being in different groups. Three initial vertices,andare ascertained as being on the shortest paths or not by property 11.
If onlyis on the paths, insert the labelin the middle ofandin,, and generate two new pairs of labels:and,and, respectively.
If onlyandare on the paths, insert the labelsandin the middle of two labelsand,, and get two new pairs of labels:and,and.
If,andare all on the paths, combine the two conditions above together.
Go back to step 1 with the new label pairs.
3. If, andoris an initial vertex, then it is the case of two vertices located in the same slice of a petal or subpetal in the same group. The common Farey graphsorare obtained by Property 13, in which case the shortest paths can be deduced by Property 5.
4. Ifandandare not initial vertices, find out the neighbors ofandby Property 8.
If two common neighbors are obtained at the same step, thenandare located in different slices. Whether the two common neighbors are positioned on the shortest paths or not are determined by Property 3. Assuming two common neighbors areand, if(or) is on the shortest paths, insert the label(or) in the middle ofand,, and generate two new pair labels ofand(or), and(or) and. Ifandare both on the shortest paths at the same time, insert the labelandin the set,,, and make up four new pair labels ofand,and,or,and. Go back to step 1 with the new label pairs.
If only one common neighbor is obtained at the same time, thenandare located in same slice. The shortest paths are projected into a Farey graph, and then all the shortest paths are derived by Property 5.
Remark 6. The expanded deterministic Apollonian networks, denoted by, are the generalization of Apollonian networks, being simultaneously small-world, scale-free and highly clustered. The label-based routing protocol for it is deduced in [35].(and) are constructed as follows.is a complete graph(or-clique).() is obtained fromby adding one new node and connecting it to all the nodes of each existing subgraph ofthat is isomorphic to a (d + 1)-clique and created at step. Apparently,is exactly the same as the special case of the generalization of Farey graphs, however, the algorithm in [35] can only get one of shortest paths in it. Recursive clique-trees,(,), have scale-free and small-world properties and allow a fine tuning of the power-law exponent of their discrete degree distribution and clustering [38].is the graph constructed as follows:is the complete graph(or q-clique).is obtained fromby adding to each of its existing subgraphs isomorphic to a q-clique a new vertex and then joining it to all the vertices of the subgraph. From the construction mechanisms used,is the same as the extended Farey graphs . Same as in Ref. [35], the protocol in [38] can only get one of shortest paths.