Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box
Abstract
1. Introduction
2. Description of the Original Encryption Algorithm
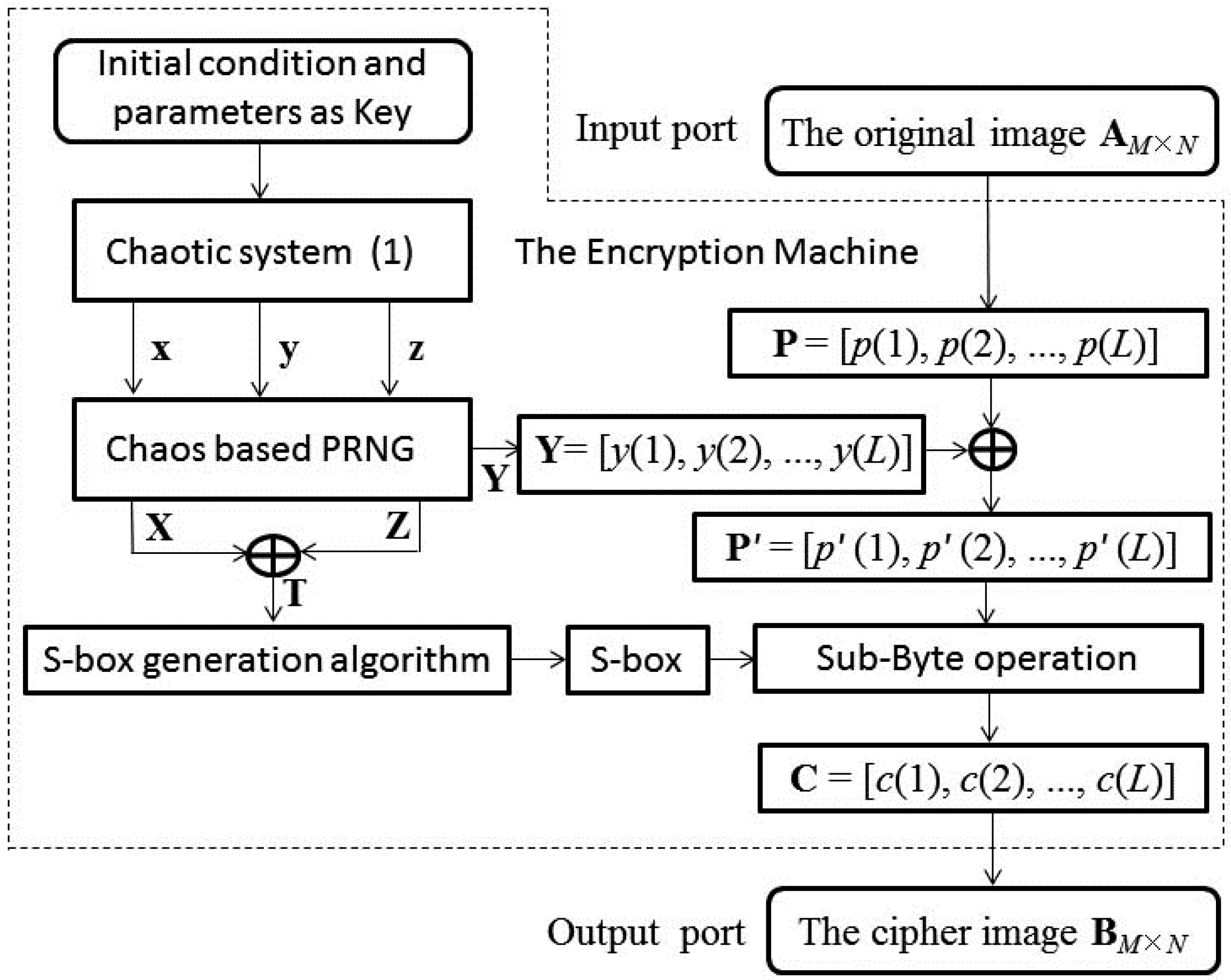
2.1. The Secret Keys and Flow Chart of IESB
2.2. Generating Chaotic Pseudo Random Number Sequences and S-Box
2.3. The Encryption Procedure
3. The Cryptanalysis and Chosen-Plaintext Attacks
3.1. The Algorithm of Cryptanalysis and Chosen-Plaintext Attacks
| Algorithm 1: The Matlab code of constructing P1 |
| 1. p1 = zeros(1, L); 2. j = 0; 3. for i = 1: L 4. if c0(i) = = m 5. p1(i) = j; 6. j = j + 1; 7. end 8. if j = = 256 9. break; 10. end 11. end |
| Algorithm 2: The Matlab code of constructing S |
| 1. s = zeros(1, 256); 2. j = 1; 3. for i = 1: L 4. if c0(i) = = m 5. s(j) = c1(i); 6. j = j + 1; 7. end 8. if j > 256 9. break; 10. end 11. end |
3.2. Examples of Chosen-Plaintext Attacks
3.2.1. The Secret Keys and S-Box
3.2.2. Breaking the Encrypted Test Image
3.2.3. A Simple Numerical Example
4. The Improved Image Encryption Scheme
4.1. Algorithm Description of the Improved Scheme
- Step 1. Set the initial conditions x0, y0, z0 system parameters a, b, c, d of system (1). Read the plain image I of size M × N and transform its 2D matrix into a 1D pixel sequence P = [p(1), p(2), ..., p(L)], where L = MN.
- Step 2. Iterate the chaotic system (1) with initial state values and system parameters for L0 times and obtain three chaotic pseudorandom sequences x = [x(i)], y = [y(i)], z = [z(i)], where i = 1, 2, ..., L0, L0 ≥ 65,536.
- Step 3. Convert the original chaotic sequences to 8-bit integer sequences {X, Y, Z} by using Equations (11)–(13).
- Step 4. Get sequence T by using X and Z: T = X ⨁ Z.
- Step 5. From the elements of T, select 256 different numbers to generate the S-box with size of 16 × 16, and transform the 2D matrix of S-box into an equivalent 1D sequence S = [s(1), s(2), ..., s(256)].
- Step 6. Perform the first round diffusion encryption with chaotic key sequence Y, and obtain the intermediate ciphertext image pixel sequence P′ = [p′(i)]. The operations are represented by the following formulas:p′(1) = mod(p(1) + y(1) + seed, 256);where, mod(x, y) returns the remainder after x is divided by y. p(i) is the i-th pixel value of the plaintext image and p′(i) is the i-th pixel value of the intermediate ciphertext image. seed is a new parameter used as a key. Here, the tilde notations represent variables.p′(i) = mod(p(i) + y(i) + p’(i − 1), 256); i = 2, 3, ..., L.
- Step 7. Perform the second round diffusion encryption with the equivalent of chaotic S-box, and obtain the final ciphertext image pixel sequence C= [c(i)]. The operations are represented by the following formulas:j = double(p′(L)) + 1; c(L) = mod(p’(L) + s(j) + seed, 256);J = double(p(i)) + 1; c(i) = mod(p’(i) + s(j) + c(i + 1), 256); i = L − 1, L − 2, ...,1.
- Step 8. Transform the 1D ciphertext image pixel sequence C into a 2D matrix CI, then the cipher image is obtained.
4.2. Performance Test and Analysis of the Improved Scheme
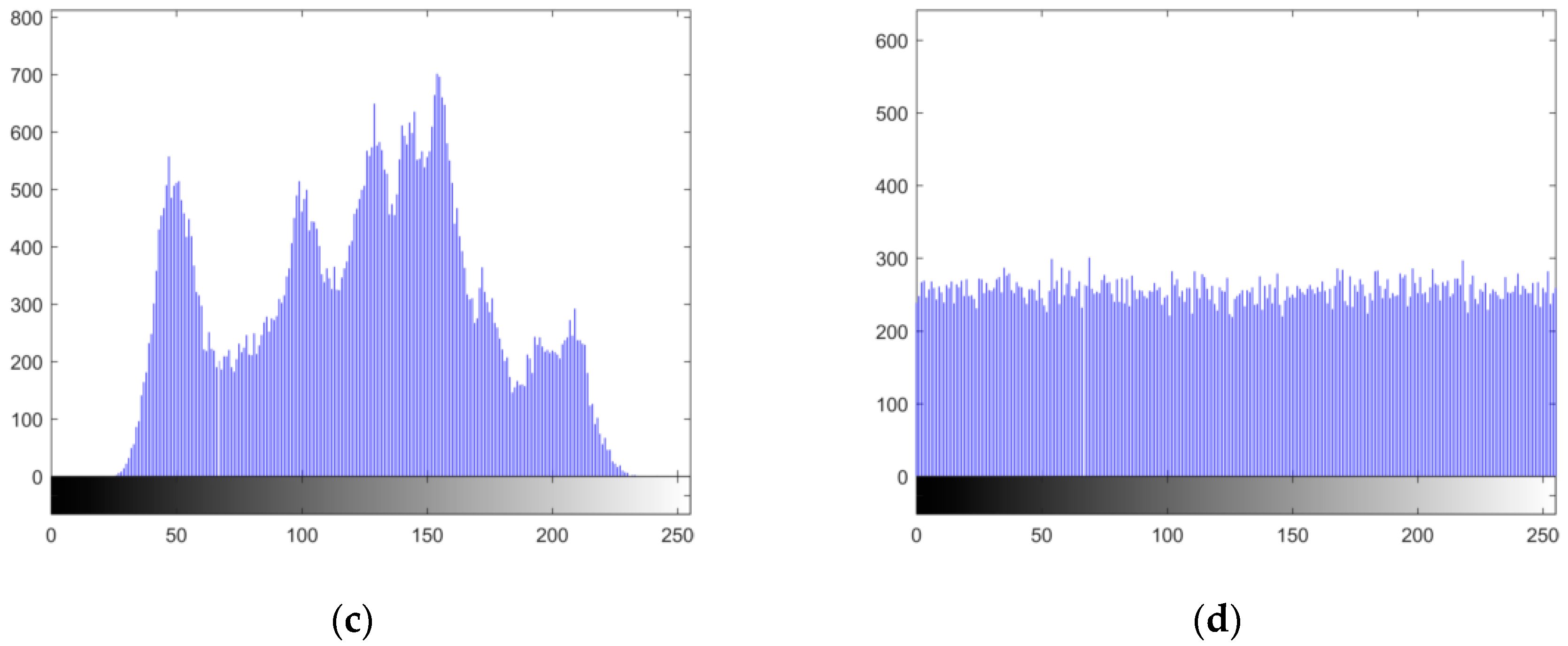
4.2.1. Histogram Analysis
4.2.2. Pixels Correlation Analysis
4.2.3. Information Entropy Analysis
4.2.4. Sensitivity Analysis
4.2.5. Key Space Analysis
4.2.6. Computation Efficiency
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Xiao, D.; Shu, Y.; Li, J. A novel image encryption scheme based on a linear hyperbolic chaotic system of partial differential equations. Signal Process. Image Commun. 2013, 28, 292–300. [Google Scholar] [CrossRef]
- Bashir, Z.; Watrobski, J.; Rashid, T.; Zafar, S.; Salabun, W. Chaotic dynamical state variables selection procedure based image encryption scheme. Symmetry 2017, 9, 312. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Zhang, H. An effective and fast image encryption algorithm based on chaos and interweaving of ranks. Nonlinear Dyn. 2016, 84, 1595–1607. [Google Scholar] [CrossRef]
- Ye, G.; Zhao, H.; Chai, H. Chaotic image encryption algorithm using wave-line permutation and block diffusion. Nonlinear Dyn. 2016, 83, 2067–2077. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. Double optical image encryption using discrete chirikov standard map and chaos-based fractional random transform. Opt. Lasers Eng. 2013, 51, 472–480. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Sun, X.; Li, Y. Chaos based adaptive double-image encryption scheme using hash function and s-boxes. Multimed. Tools Appl. 2018, 77, 1391–1407. [Google Scholar] [CrossRef]
- Zhu, C. A novel image encryption scheme based on improved hyperchaotic sequences. Opt. Commun. 2012, 285, 29–37. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q. A novel image encryption algorithm based on dynamic s-boxes constructed by chaos. Nonlinear Dyn. 2014, 75, 567–576. [Google Scholar] [CrossRef]
- Liu, Y.; Tong, X.; Ma, J. Image encryption algorithm based on hyper-chaotic system and dynamic s-box. Multimed. Tools Appl. 2016, 75, 7739–7759. [Google Scholar] [CrossRef]
- Khan, M.; Shah, T.; Batool, S.I. Construction of s-box based on chaotic boolean functions and its application in image encryption. Neural Comput. Appl. 2016, 27, 677–685. [Google Scholar] [CrossRef]
- Cavusoglu, U.; Zengin, A.; Pehlivan, I.; Kacar, S. A novel approach for strong s-box generation algorithm design based on chaotic scaled zhongtang system. Nonlinear Dyn. 2017, 87, 1081–1094. [Google Scholar] [CrossRef]
- Belazi, A.; Khan, M.; Abd El-Latif, A.A.; Belghith, S. Efficient cryptosystem approaches: S-boxes and permutation-substitution-based encryption. Nonlinear Dyn. 2017, 87, 337–361. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Fan, J.; Gong, L. Image encryption algorithm based on chaotic system and dynamic s-boxes composed of DNA sequences. Multimed. Tools Appl. 2016, 75, 4363–4382. [Google Scholar] [CrossRef]
- Devaraj, P.; Kavitha, C. An image encryption scheme using dynamic s-boxes. Nonlinear Dyn. 2016, 86, 927–940. [Google Scholar] [CrossRef]
- Cavusoglu, U.; Kacar, S.; Pehlivan, I.; Zengin, A. Secure image encryption algorithm design using a novel chaos based s-box. Chaos Solitons Fractals 2017, 95, 92–101. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lu, J. Cryptanalyzing an image-scrambling encryption algorithm of pixel bits. IEEE Multimed. 2017, 24, 64–71. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xie, T.; Chen, M.Z.Q. Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dyn. 2013, 73, 2083–2089. [Google Scholar] [CrossRef]
- Yap, W.-S.; Phan, R.C.W.; Yau, W.C.; Heng, S.H. Cryptanalysis of a new image alternate encryption algorithm based on chaotic map. Nonlinear Dyn. 2015, 80, 1483–1491. [Google Scholar] [CrossRef]
- Zhu, C.X.; Sun, K.H. Cryptanalysis and improvement of a class of hyperchaos based image encryption algorithms. Acta Phys. Sin. 2012, 61, 120503. [Google Scholar]
- Zhang, X.; Nie, W.; Ma, Y.; Tian, Q. Cryptanalysis and improvement of an image encryption algorithm based on hyper-chaotic system and dynamic s-box. Multimed. Tools Appl. 2017, 76, 15641–15659. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel color image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar]
- Zhu, C.; Sun, K. Cryptanalyzing and improving a novel color image encryption algorithm using rt-enhanced chaotic tent maps. IEEE Access 2018, 6, 18759–18770. [Google Scholar] [CrossRef]
- Wang, W.; Si, M.; Pang, Y.; Ran, P.; Wang, H.; Jiang, X.; Liu, Y.; Wu, J.; Wu, W.; Chilamkurti, N.; et al. An encryption algorithm based on combined chaos in body area networks. Comput. Electr. Eng. 2018, 65, 282–291. [Google Scholar] [CrossRef]
- Ahmad, M.; Al Solami, E.; Wang, X.Y.; Doja, M.; Beg, M.; Alzaidi, A. Cryptanalysis of an Image Encryption Algorithm Based on Combined Chaos for a Ban System, and Improved Scheme using SHA-512 and Hyperchaos. Symmetry 2018, 10, 266. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Mou, X. On the dynamical degradation of digital piecewise linear chaotic maps. Int. J. Bifurc. Chaos 2005, 15, 3119–3151. [Google Scholar] [CrossRef]
- Curiac, D.I.; Volosencu, C. Chaotic trajectory design for monitoring an arbitrary number of specified locations using points of interest. Math. Probl. Eng. 2012, 2012, 940276. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Wong, K.-W.; Mou, X.; Cai, Y. Baptista-type chaotic cryptosystems: Problems and countermeasures. Phys. Lett. A 2004, 332, 368–375. [Google Scholar] [CrossRef]
- Curiac, D.I.; Iercan, D.; Dranga, O.; Dragan, F.; Banias, O. Chaos-Based Cryptography: End of the Road? In Proceedings of the International Conference on Emerging Security Information, System and Technologies, Valencia, Spain, 14–20 October 2007; pp. 71–76. [Google Scholar]
- Zhang, S.; Wang, G.; Liu, Q.; Abawajy, J.H. A trajectory privacy-preserving scheme based on query exchange in mobile social networks. Soft Comput. 2018, 22, 6121–6133. [Google Scholar] [CrossRef]
- Bhuiyan, M.Z.A.; Wang, G.; Wu, J.; Cao, J.; Liu, X.; Wang, T. Dependable structural health monitoring using wireless sensor networks. IEEE Trans. Depend. Secur. Comput. 2017, 14, 363–376. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Q.; Wang, G. PRMS: A personalized mobile search over encrypted outsourced data. IEEE Access 2018, 6, 31541–31552. [Google Scholar] [CrossRef]


| 110 | 108 | 239 | 99 | 42 | 160 | 187 | 36 | 157 | 222 | 152 | 50 | 92 | 199 | 30 | 249 |
| 161 | 198 | 138 | 16 | 208 | 106 | 130 | 212 | 189 | 181 | 64 | 248 | 34 | 191 | 240 | 224 |
| 4 | 62 | 111 | 103 | 126 | 53 | 128 | 205 | 251 | 172 | 39 | 132 | 183 | 3 | 94 | 185 |
| 247 | 158 | 237 | 41 | 244 | 216 | 52 | 154 | 250 | 223 | 8 | 168 | 25 | 93 | 221 | 238 |
| 26 | 202 | 21 | 136 | 2 | 67 | 15 | 195 | 6 | 121 | 51 | 1 | 69 | 63 | 148 | 167 |
| 209 | 135 | 107 | 137 | 97 | 231 | 71 | 176 | 233 | 47 | 14 | 76 | 56 | 230 | 213 | 24 |
| 232 | 57 | 80 | 40 | 95 | 175 | 5 | 100 | 104 | 22 | 206 | 169 | 124 | 49 | 165 | 170 |
| 19 | 112 | 147 | 193 | 139 | 82 | 245 | 27 | 225 | 214 | 101 | 174 | 59 | 43 | 227 | 142 |
| 156 | 68 | 171 | 72 | 252 | 105 | 17 | 120 | 9 | 0 | 48 | 31 | 178 | 23 | 96 | 91 |
| 54 | 140 | 87 | 116 | 7 | 242 | 153 | 85 | 173 | 89 | 229 | 226 | 179 | 143 | 151 | 188 |
| 145 | 66 | 115 | 246 | 190 | 113 | 35 | 194 | 228 | 114 | 29 | 33 | 79 | 196 | 84 | 123 |
| 155 | 150 | 220 | 81 | 75 | 90 | 164 | 215 | 55 | 73 | 129 | 88 | 200 | 18 | 146 | 44 |
| 162 | 197 | 217 | 207 | 184 | 163 | 159 | 133 | 203 | 236 | 11 | 61 | 98 | 235 | 186 | 58 |
| 134 | 32 | 38 | 102 | 28 | 255 | 10 | 254 | 177 | 12 | 182 | 46 | 218 | 243 | 77 | 45 |
| 144 | 192 | 70 | 234 | 119 | 13 | 83 | 125 | 122 | 109 | 37 | 180 | 211 | 166 | 127 | 118 |
| 117 | 60 | 141 | 253 | 149 | 86 | 74 | 131 | 219 | 201 | 210 | 78 | 241 | 65 | 204 | 20 |
| Plain-Image | Cipher-Image | Cipher-Image Ref. [2] | Cipher-Image Ref. [15] | Cipher-Image Ref. [23] | Cipher-Image Ref. [24] |
|---|---|---|---|---|---|
| 0.924879 | 0.000249 | 0.005497 | 0.5310 | −0.00114 | 0.000329 |
| Proposed | Ref. [9] | Ref. [15] | Ref. [23] |
|---|---|---|---|
| 7.9977 | 7.993459 | 7.95667 | 7.9964 |
| Proposed | Ref. [15] | Ref. [24] | Ref. [2] | |
|---|---|---|---|---|
| NPCR (%) | 99.63226 | nearly 0 | 99.627 | 99.6002 |
| UACI (%) | 34.59600 | nearly 0 | 33.452 | 33.463 |
| x0 + 10−14 | y0 + 10−14 | z0 + 10−14 | a + 10−14 | b + 10−14 | c + 10−14 | d + 10−14 | seed + 1 | |
|---|---|---|---|---|---|---|---|---|
| NPCR (%) | 99.61 | 99.65 | 99.63 | 99.63 | 99.62 | 99.60 | 99.58 | 99.60 |
| UACI (%) | 34.20 | 33.63 | 32.93 | 32.39 | 33.93 | 34.49 | 33.11 | 33.56 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Wang, G.; Sun, K. Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box. Symmetry 2018, 10, 399. https://doi.org/10.3390/sym10090399
Zhu C, Wang G, Sun K. Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box. Symmetry. 2018; 10(9):399. https://doi.org/10.3390/sym10090399
Chicago/Turabian StyleZhu, Congxu, Guojun Wang, and Kehui Sun. 2018. "Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box" Symmetry 10, no. 9: 399. https://doi.org/10.3390/sym10090399
APA StyleZhu, C., Wang, G., & Sun, K. (2018). Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box. Symmetry, 10(9), 399. https://doi.org/10.3390/sym10090399







