Decaying Dark Energy in Light of the Latest Cosmological Dataset
Abstract
1. Introduction
2. Theoretical Framework
3. Methodology and Data
3.1. Supernovae Type Ia
3.2. Differential Ages,
3.3. Baryonic Acoustic Oscillation
3.4. Gamma Ray Burst
3.5. –Redshift Relation
3.6. PlanckTT + LowP
4. Results and Discussions
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BAO | Baryon Acoustic Oscillation |
| DE | Dark Energy |
| DM | Dark Matter |
| FRW | Friedman–Robertson–Walker |
| GR | General Relativity |
| GRB | Gamma Ray Burst |
| MCMC | Monte Carlo Markov Chain |
| SNIa | Supernovae Type Ia |
| SPT | South Pole Telescope |
References
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements of the Cosmological Parameters Omega and Lambda from the First Seven Supernovae at z ≥ 0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia Supernova Discoveries at z > 1 from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Astier, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.G.; Fabbro, S.; Fouchez, D.; et al. The Supernova Legacy Survey: Measurement of ΩM, ΩΛ and w from the first year data set. Astron. Astrophys. 2006, 447, 31–48. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Pope, A.C.; Matsubara, T.; Szalay, A.S.; Blanton, M.R.; Eisenstein, D.J.; Gray, J.; Jain, B.; Bahcall, N.A.; Brinkmann, J.; Budavari, T.; et al. Cosmological Parameters from Eigenmode Analysis of Sloan Digital Sky Survey Galaxy Redshifts. Astrophys. J. 2004, 607, 655. [Google Scholar] [CrossRef]
- Percival, W.J.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; Collins, C.; Couch, W.; Dalton, G.; et al. The 2dF Galaxy Redshift Survey: The power spectrum and the matter content of the Universe. Mon. Not. R. Astron. Soc. 2001, 327, 1297–1306. [Google Scholar] [CrossRef]
- Tegmark, M.; Blanton, M.R.; Strauss, M.A.; Hoyle, F.; Schlegel, D.; Scoccimarro, R.; Vogeley, M.S.; Weinberg, D.H.; Zehavi, I.; Berlind, M.S.; et al. The Three-Dimensional Power Spectrum of Galaxies from the Sloan Digital Sky Survey. Astrophys. J. 2004, 606, 702. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Not. R. Astron. Soc. 2011, 418, 1707. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv, 2018; arXiv:1807.06209. [Google Scholar]
- de Martino, I.; Génova-Santos, R.; Atrio-Barandela, F.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Constraining the Redshift Evolution of the Cosmic Microwave Background Blackbody Temperature with PLANCK Data. Astrophys. J. 2015, 808, 128. [Google Scholar] [CrossRef]
- De Martino, I.; Martins, C.J.A.P.; Ebeling, H.; Kocevski, D. Constraining spatial variations of the fine structure constant using clusters of galaxies and Planck data. Phys. Rev. D 2016, 94, 083008. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. Cosmology with a time-variable cosmological ’constant’. Astrophys. J. Lett. 1988, 325, L17. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a Positive Cosmological Λ-Term. Int. J. Mod. Phys. 2000, D9, 373. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant-the weight of the vacuum. Phys. Rep. 2003, 380, 235. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Rubano, C.; Tortora, C. Two viable quintessence models of the Universe: Confrontation of theoretical predictions with observational data. Astron. Astrophys. 2005, 431, 27. [Google Scholar] [CrossRef]
- Cardone, V.F.; Tortora, C.; Troisi, A.; Capozziello, S. Beyond the perfect fluid hypothesis for the dark energy equation of state. Phys. Rev. D 2006, 73, 043508. [Google Scholar] [CrossRef]
- Capolupo, A. Dark matter and dark energy induced by condensates. Adv. High Energy Phys. 2016, 2016. [Google Scholar] [CrossRef]
- Capolupo, A. Quantum vacuum, dark matter, dark energy and spontaneous supersymmetry breaking. Adv. High Energy Phys. 2018, 2018. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. A conventional approach to the dark energy concept. Astron. Astrophys. 2011, 529, A26. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. A conventional form of dark energy. J. Phys. Conf. Ser. 2011, 283, 012018. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. Polytropic dark matter flows illuminate dark energy and accelerated expansion. Astron. Astrophys. 2015, 576, A23. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. Dark energy: The shadowy reflection of dark matter? Entropy 2016, 18, 94. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. Cosmological perturbations in the ΛCDM-like limit of a polytropic dark matter model. Astron. Astrophys. 2017, 606, A116. [Google Scholar] [CrossRef]
- Caldwell, R.; Kamionkowski, M. The Physics of Cosmic Acceleration. Ann. Rev. Nuclear Part. Sci. 2009, 59, 397. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavón, D. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rep. Prog. Phys. 2016, 79, 9. [Google Scholar] [CrossRef] [PubMed]
- Capozziello, S.; de Laurentis, M.; Francaviglia, M.; Mercadante, S. From Dark Energy & Dark Matter to Dark Metric. Found. Phys. 2009, 39, 1161. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- de Martino, I.; De Laurentis, M.; Capozziello, S. Constraining f(R) gravity by the Large Scale Structure. Universe 2015, 1, 123. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Arraut, I. The graviton Higgs mechanism. Europhys. Letter 2015, 111, 61001. [Google Scholar] [CrossRef]
- Arraut, I.; Chelabi, K. Non-linear massive gravity as a gravitational σ-model. Europhys. Letter 2016, 115, 31001. [Google Scholar] [CrossRef]
- Arraut, I.; Chelabi, K. Vacuum degeneracy in massive gravity: Multiplicity of fundamental scales. Mod. Phys. Lett. A 2017, 32, 1750112. [Google Scholar] [CrossRef]
- Lima, J.A.S. Thermodynamics of decaying vacuum cosmologies. Phys. Rev. D 1996, 54, 2571. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Alcaniz, J.A.S. Flat Friedmann-Robertson-Walker cosmologies with adiabatic matter creation: kinematic tests. Astron. Astrophys. 1999, 348, 1. [Google Scholar]
- Lima, J.A.S.; Silva, A.I.; Viegas, S.M. Is the radiation temperature-redshift relation of the standard cosmology in accordance with the data? Mon. Not. R. Astron. Soc. 2000, 312, 747. [Google Scholar] [CrossRef]
- Puy, D. Thermal balance in decaying Λ cosmologies. Astron. Astrophys. 2004, 422, 1–9. [Google Scholar] [CrossRef]
- Ma, Y. Variable cosmological constant model: The reconstruction equations and constraints from current observational data. Nuclear Phys. B 2008, 804, 262. [Google Scholar] [CrossRef]
- Jetzer, P.; Puy, D.; Signore, M.; Tortora, C. Limits on decaying dark energy density models from the CMB temperature-redshift relation. Gen. Relat. Grav. 2011, 43, 1083. [Google Scholar] [CrossRef]
- Jetzer, P.; Tortora, C. Constraints from the CMB temperature and other common observational data sets on variable dark energy density models. Phys. Rev. D 2011, 84, 043517. [Google Scholar] [CrossRef]
- Fixsen, D.J. The Temperature of the Cosmic Microwave Background. Astrophys. J. 2009, 707, 916. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Wolf, R.A. Fine-Structure Transitions. Astrophys. J. 1968, 152, 701. [Google Scholar] [CrossRef]
- Fabbri, R.; Melchiorri, F.; Natale, V. The Sunyaev-Zel’dovich effect in the millimetric region. Astrophys. Space Sci. 1978, 59, 223. [Google Scholar] [CrossRef]
- Rephaeli, Y. On the determination of the degree of cosmological Compton distortions and the temperature of the cosmic blackbody radiation. Astrophys. J. 1980, 241, 858. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Observations of Relic Radiation as a Test of the Nature of X-Ray Radiation from the Clusters of Galaxies. Comment Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Avgoustidis, A.; Génova-Santos, R.T.; Luzzi, G.; Martins, C.J.A.P. Subpercent constraints on the cosmological temperature evolution. Phys. Rev. D 2016, 93, 043521. [Google Scholar] [CrossRef]
- Luzzi, G.; Shimon, M.; Lamagna, L.; Rephaeli, Y.; De Petris, M.; Conte, A.; De Gregori, S.; Battistelli, E.S. Redshift Dependence of the Cosmic Microwave Background Temperature from Sunyaev-Zeldovich Measurements. Astrophys. J. 2009, 705, 1122. [Google Scholar] [CrossRef]
- Luzzi, G.; Génova-Santos, R.T.; Martins, C.J.A.P.; De Petris, M.; Lamagna, L. Constraining the evolution of the CMB temperature with SZ measurements from Planck data. J. Cosmol. Astropart. Phys. 2015, 1509, 011. [Google Scholar] [CrossRef]
- Hurier, G.; Aghanim, N.; Douspis, M.; Pointecouteau, E. Measurement of the TCMB evolution from the Sunyaev-Zel’dovich effect. Astron. Astrophys. 2014, 561, A143. [Google Scholar] [CrossRef]
- Saro, A.; Liu, J.; Mohr, J.J.; Aird, K.A.; Ashby, M.L.N.; Bayliss, M.; Benson, B.A.; Bleem, L.E.; Bocquet, S.; Brodwin, M.; et al. Constraints on the CMB temperature evolution using multiband measurements of the Sunyaev-Zel’dovich effect with the South Pole Telescope. Mon. Not. R. Astron. Soc. 2014, 440, 2610. [Google Scholar] [CrossRef]
- De Martino, I.; Atrio-Barandela, F.; da Silva, A.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Measuring the Redshift Dependence of the Cosmic Microwave Background Monopole Temperature with Planck Data. Astrophys. J. 2012, 757, 144. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Hastings, W.K. Monte Carlo Sampling Methods using Markov Chains and their Applications. Biometrika 1970, 57, 97. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087. [Google Scholar] [CrossRef]
- Gelman, A.; Roberts, G.O.; Gilks, W.R. Efficient Metropolis jumping rule. Bayesian Stat. 1996, 5, 599. [Google Scholar]
- Roberts, G.O.; Gelman, A.; Gilks, W.R. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Probab. 1997, 7, 110. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716. [Google Scholar] [CrossRef]
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and Hubble Space Telescope Light Curves of Six Type Ia Supernovae at 0.511 < z < 1.12 and the Union2 Compilation. Astrophys. J. 2010, 716, 712. [Google Scholar]
- Di Pietro, E.; Claeskens, J.F. Future supernovae data and quintessence models. Mon. Not. R. Astron. Soc. 2003, 341, 1299. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Comparison of the Legacy and Gold SnIa Dataset Constraints on Dark Energy Models. Phys. Rev. D 2005, 72, 123519. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Constraints on linear negative potentials in quintessence and phantom models from recent supernova data. Phys. Rev. D 2005, 71, 063503. [Google Scholar] [CrossRef]
- Wei, H. Constraints on linear negative potentials in quintessence and phantom models from recent supernova data. Phys. Lett. B 2010, 687, 286. [Google Scholar] [CrossRef]
- Luković, V.V.; D’Agostino, R.; Vittorio, N. Is there a concordance value for H0? Astron. Astrophys. 2016, 595, A109. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2005, 573, 37. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Stanford, S.A.; Kamionkowski, M. Cosmic Chronometers: Constraining the Equation of State of Dark Energy. II. A Spectroscopic Catalog of Red Galaxies in Galaxy Clusters. Astrophys. J. Suppl. 2010, 188, 280. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Liu, S.; Zhang, T.J.; Sun, Y.C. Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 14, 1221. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. Mon. Not. R. Astron. Soc. 2015, 450, L16. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z∼1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 2012, 1112–1119. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Moresco, M.; Verde, L.; Pozzetti, L.; Jimenez, R.; Cimatti, A. New constraints on cosmological parameters and neutrino properties using the expansion rate of the Universe to z∼1.75. J. Cosmol. Astropart. Phys. 2012, 2012, 053. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Hu, W.; Tegmark, M. Cosmic Complementarity: H0 and Ωm from Combining Cosmic Microwave Background Experiments and Redshift Surveys. Astrophys. J. Lett. 1998, 504, L57. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample - I. A 4 per cent distance measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Busca, N.G.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.G.; Pieri, M.M.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Busca, N.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, E.; Bailey, S.; Bhardwaj, V.; et al. Quasar-Lyman α forest cross-correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 5, 27. [Google Scholar] [CrossRef]
- Wei, H. Observational constraints on cosmological models with the updated long gamma-ray bursts. J. Cosmol. Astropart. Phys. 2010, 1008, 020. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Luković, V.V.; D’Agostino, R.; Vittorio, N. Strong evidence for an accelerating Universe. Astron. Astrophys. 2017, 600, L1. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Guidorzi, C. Extremely energetic Fermi gamma-ray bursts obey spectral energy correlations. Astron. Astrophys. 2009, 508, 173. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; in’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81. [Google Scholar] [CrossRef]
- Amati, L.; Guidorzi, C.; Frontera, F.; Della Valle, M.; Finelli, F.; Landi, R.; Montanari, E. Measuring the cosmological parameters with the Ep,i − Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2008, 391, 577. [Google Scholar] [CrossRef]
- Kosowsky, A.; Milosavljevic, M.; Jimenez, R. Efficient cosmological parameter estimation from microwave background anisotropies. Phys. Rev. D 2002, 66, 063007. [Google Scholar] [CrossRef]
- Wang, Y.; Mukherjee, P. Observational Constraints on Dark Energy and Cosmic Curvature. Phys. Rev. D 2007, 76, 103533. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XIV. Dark energy and modified gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; MacKenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New Parallaxes of Galactic Cepheids from Spatially Scanning the Hubble Space Telescope: Implications for the Hubble Constant. arXiv, 2018; arXiv:1801.01120. [Google Scholar]
- Yu, H.; Ratra, B.; Wang, F.Y. Hubble Parameter and Baryon Acoustic Oscillation Measurement Constraints on the Hubble Constant, the Deviation from the Spatially Flat ΛCDM Model, the Deceleration-Acceleration Transition Redshift, and Spatial Curvature. Astrophys. J. 2018, 856, 3. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. J. Cosmol. Astropart. Phys. 2018, 2018, 051. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, W. Machine Learning Cosmic Expansion History. arXiv, 2018; arXiv:1712.09208. [Google Scholar]
- LSST Science Collaborations and LSST Project. LSST Science Book, 2nd ed.; LSST Science Collaborations and LSST Project: Tucson, AZ, USA, 2009. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguères, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report ESA/SRE(2011)12. arXiv, 2011; arXiv:1110.3193. [Google Scholar]
- Spergel, D.; Gehrels, N.; Baltay, C.; Bennett, D.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O.; et al. Wide-Field InfrarRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 Report. arXiv, 2015; arXiv:1503.03757. [Google Scholar]
- Kashlinsky, A.; Arendt, R.G.; Atrio-Barandela, F.; Helgason, K. Lyman-tomography of cosmic infrared background fluctuations with Euclid: Probing emissions and baryonic acoustic oscillations at z > 10. Astrophys. J. Lett. 2015, 813, L12. [Google Scholar] [CrossRef]
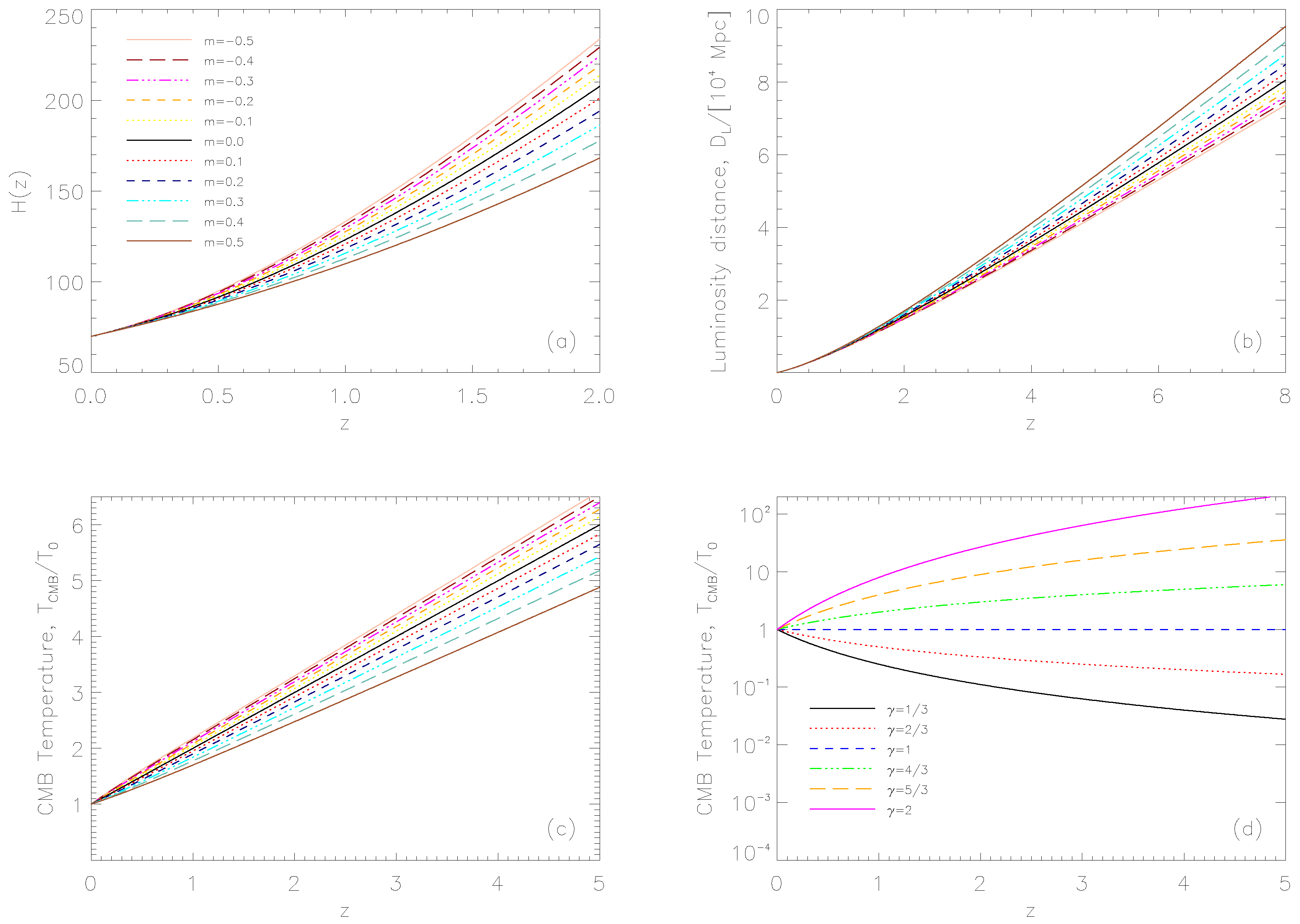
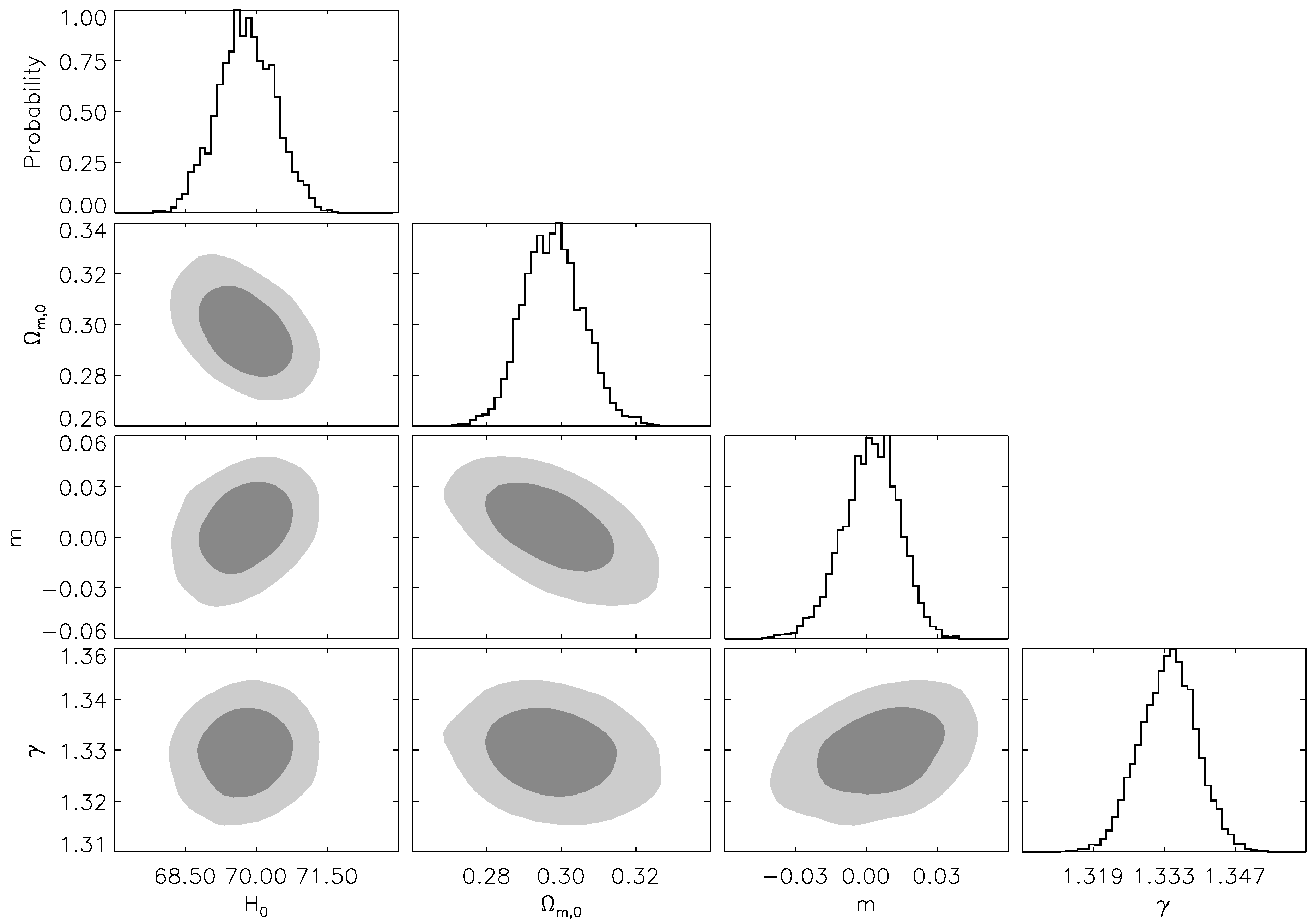
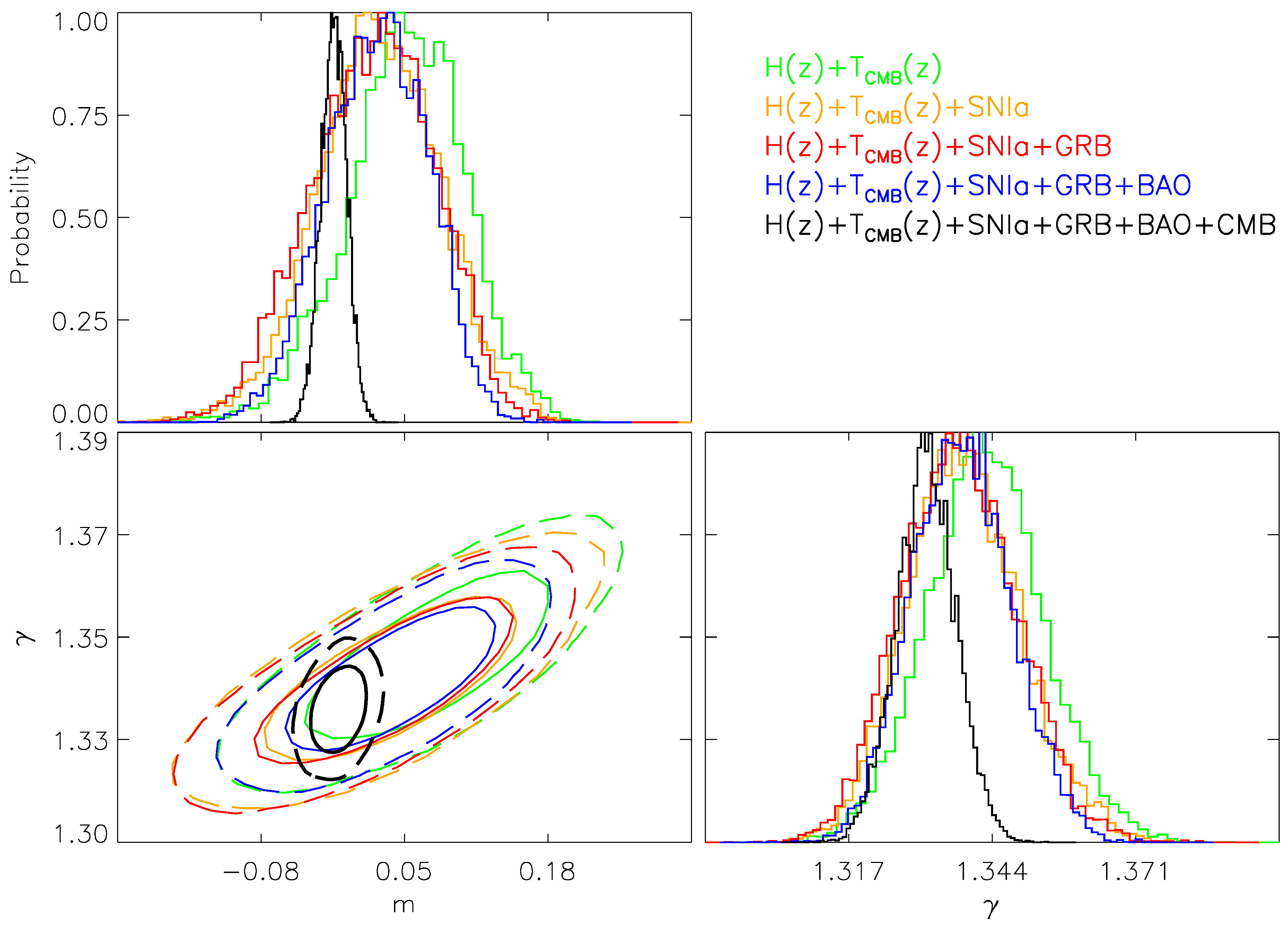
| Parameter | Priors |
|---|---|
| m | [−1, 1] |
| Dataset | Free | |||
|---|---|---|---|---|
| + | ||||
| SNIa++ | ||||
| SNIa+GRB++ | ||||
| SNIa+GRB++BAO+ | ||||
| SNIa+GRB++BAO++CMB | ||||
| + | ||||
| SNIa++ | ||||
| SNIa+GRB++ | ||||
| SNIa+GRB++BAO+ | ||||
| SNIa+GRB++BAO++CMB | ||||
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Martino, I. Decaying Dark Energy in Light of the Latest Cosmological Dataset. Symmetry 2018, 10, 372. https://doi.org/10.3390/sym10090372
De Martino I. Decaying Dark Energy in Light of the Latest Cosmological Dataset. Symmetry. 2018; 10(9):372. https://doi.org/10.3390/sym10090372
Chicago/Turabian StyleDe Martino, Ivan. 2018. "Decaying Dark Energy in Light of the Latest Cosmological Dataset" Symmetry 10, no. 9: 372. https://doi.org/10.3390/sym10090372
APA StyleDe Martino, I. (2018). Decaying Dark Energy in Light of the Latest Cosmological Dataset. Symmetry, 10(9), 372. https://doi.org/10.3390/sym10090372





