New Holographic Dark Energy Model in Brans-Dicke Theory
Abstract
1. Introduction
2. NHDE Model and BD Theory
2.1. Non-Interacting Case
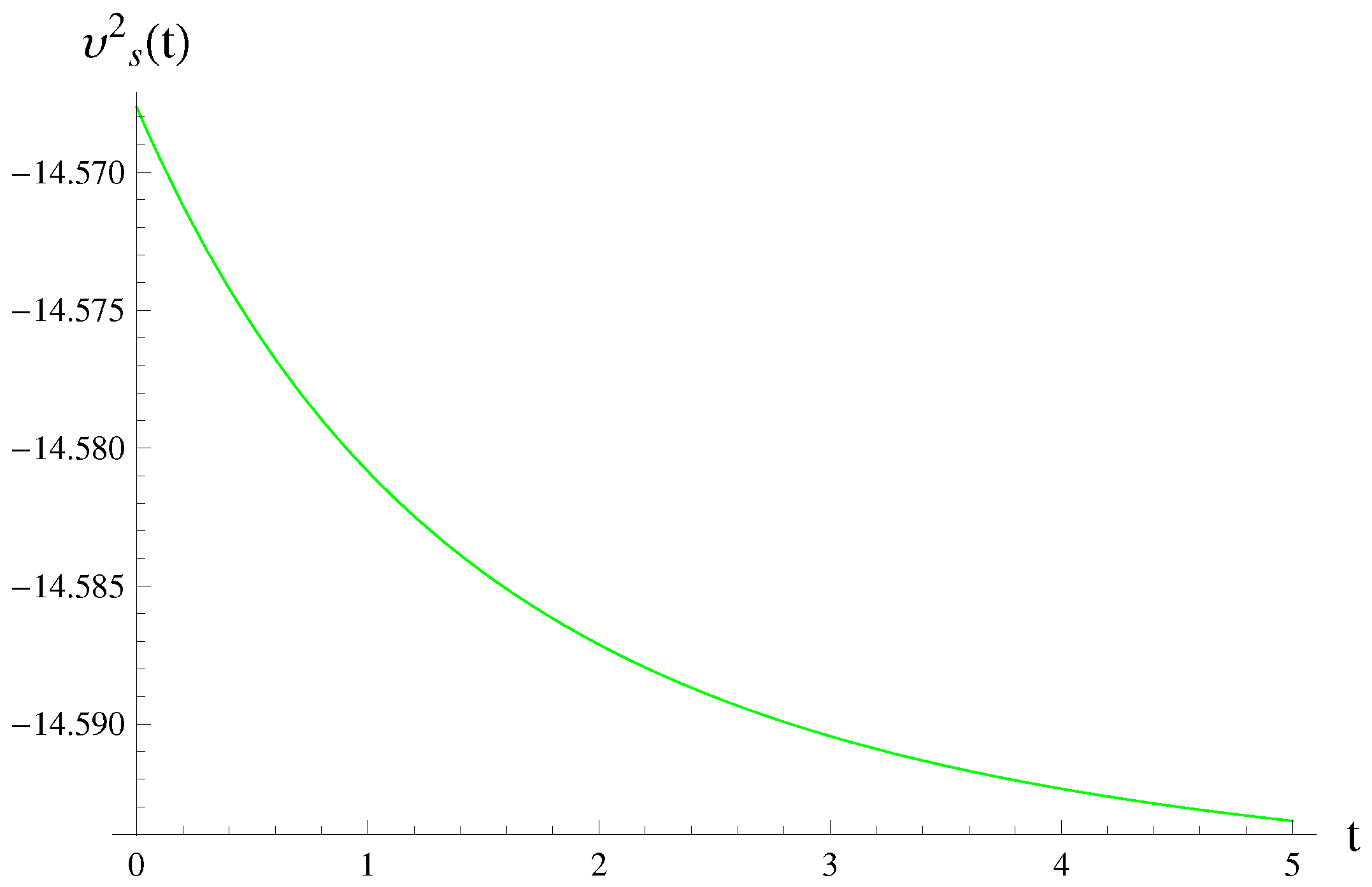
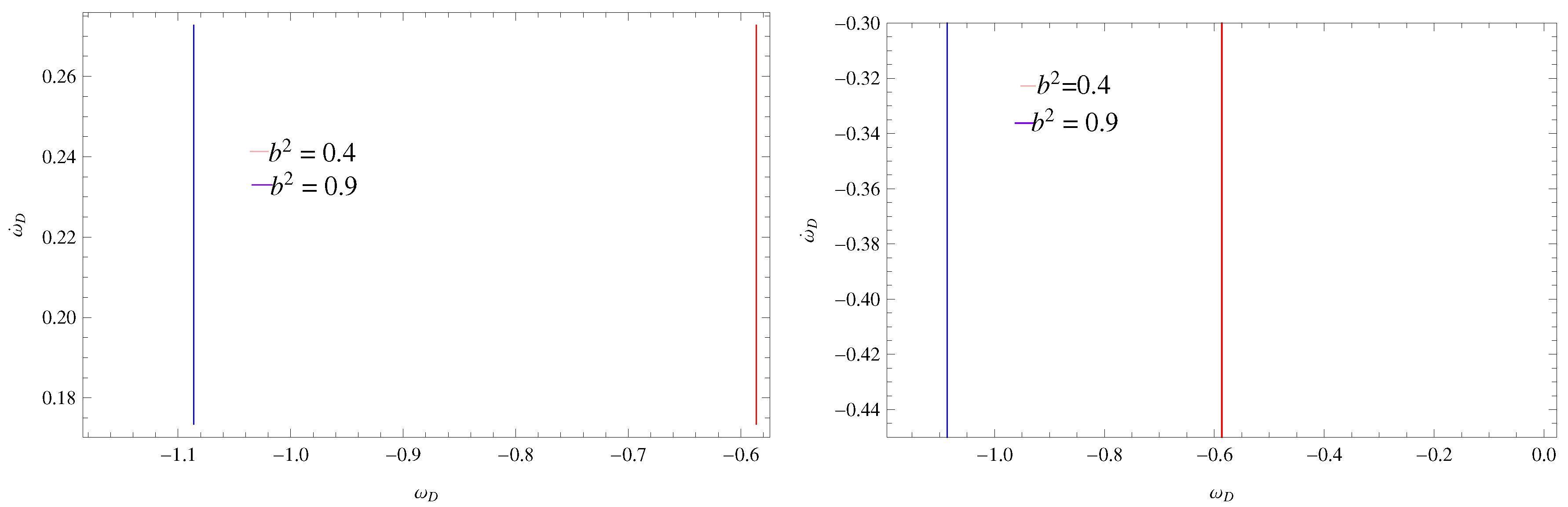
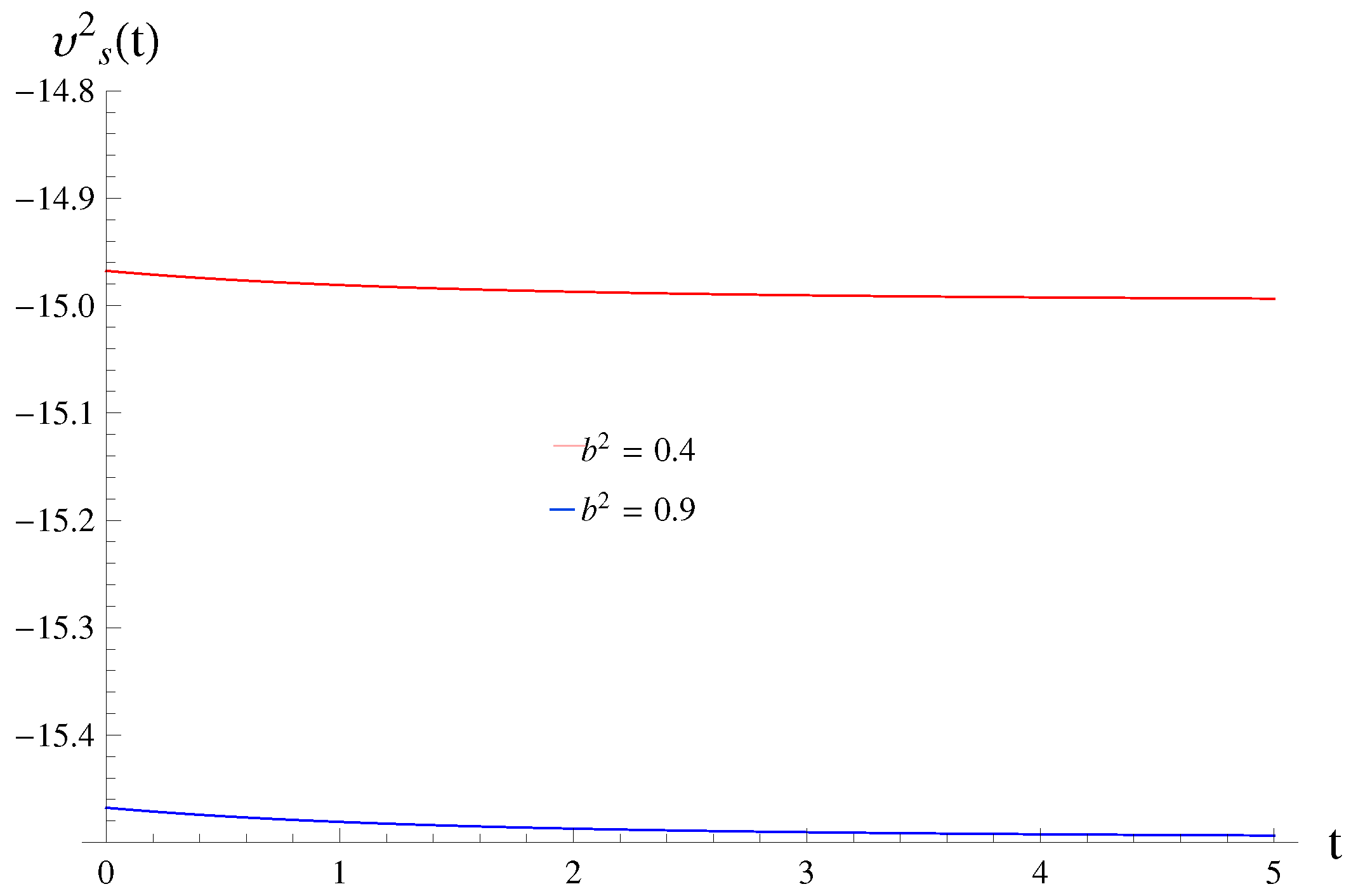
2.2. Interacting Case
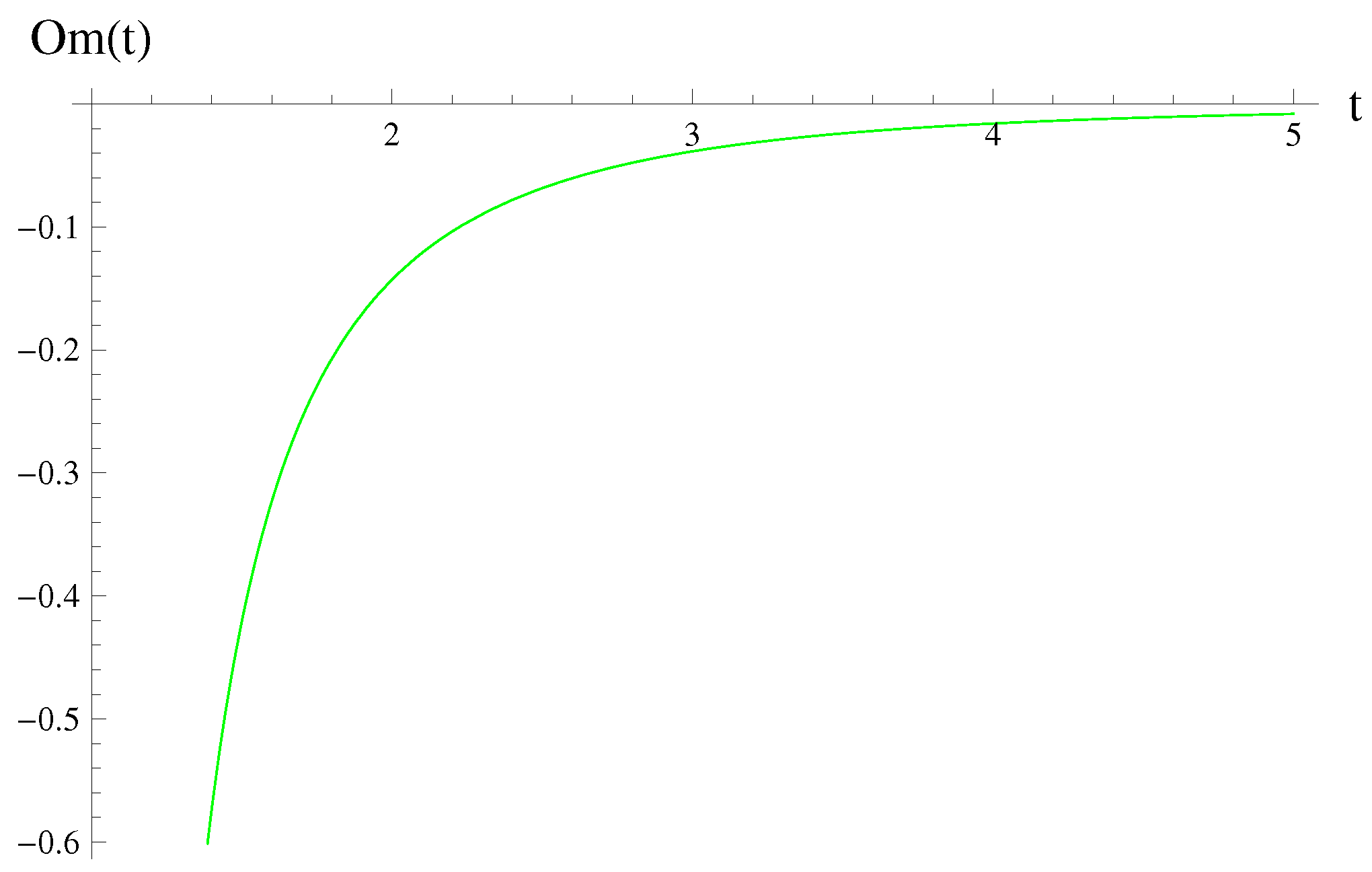
3. Om-Diagnostic
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From F (R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein gravity: A Survey of gravitational theories for cosmology and astrophysics. Fundam. Theor. Phys. 2010, 170. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.I.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Kleidis, K.; Spyrou, N.K. Dark Energy: The Shadowy Reflection of Dark Matter? Entropy 2016, 18, 94. [Google Scholar] [CrossRef]
- Li, M. A model of holographic dark energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Hsu, SD. Entropy bounds and dark energy. Phys. Lett. B 2004, 594, 13–16. [Google Scholar] [CrossRef]
- Xu, L.; Li, W.; Lu, J. Holographic dark energy in Brans–Dicke theory. Eur. Phys. J. C 2009, 60, 135–140. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in the (phantom) dark energy universe. Phys. Rev. D 2005, 71. [Google Scholar] [CrossRef]
- Kleidis, K.; Oikonomou, V.K. Effects of finite-time singularities on gravitational waves. Astrophys. Space Sci. 2016, 361, 326. [Google Scholar] [CrossRef]
- Granda, L.N.; Oliveros, A. Infrared cut-off proposal for the holographic density. Phys. Lett. B 2008, 669, 275–277. [Google Scholar] [CrossRef]
- Oliveros, A.; Acero, M.A. New holographic dark energy model with non-linear interaction. Astrophys. Space Sci. 2015, 357, 12. [Google Scholar] [CrossRef]
- Fayaz, V.; Hossienkhani, H.; Pasqua, A.; Amirabadi, M.; Ganji, M. f (T) theories from holographic dark energy models within Bianchi type I universe. Eur. Phys. J. Plus 2015, 130, 28. [Google Scholar] [CrossRef]
- Sadri, E.; Vakili, B. A new holographic dark energy model in Brans-Dicke theory with logarithmic scalar field. Astrophys. Space Sci. 2018, 363, 13. [Google Scholar] [CrossRef]
- Jahromi, A.S.; Moosavi, S.A.; Moradpour, H.; Graça, J.M.; Lobo, I.P.; Salako, I.G.; Jawad, A. Generalized entropy formalism and a new holographic dark energy model. Phys. Lett. B 2018, 780, 21–24. [Google Scholar] [CrossRef]
- Reddy, D.R.; Naidu, R.L.; Rao, V.U. A cosmological model with negative constant deceleration parameter in Brans-Dicke theory. Int. J. Theor. Phys. 2007, 46, 1443–1448. [Google Scholar] [CrossRef]
- Setare, M.R. The holographic dark energy in non-flat Brans–Dicke cosmology. Phys. Lett. B 2007, 644, 99–103. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, C.P. Exact bianchi type-I cosmological models in a scalar-tensor theory. Int. J. Theor. Phys. 2008, 47, 1722–1730. [Google Scholar] [CrossRef]
- Setare, M.R.; Vagenas, E.C. The cosmological dynamics of interacting holographic dark energy model. Int. J. Mod. Phys. D 2009, 18, 147–157. [Google Scholar] [CrossRef]
- Sharif, M.; Kausar, H.R. Anisotropic fluid and Bianchi type III model in f (R) gravity. Phys. Lett. B 2011, 697, 1–6. [Google Scholar] [CrossRef]
- Sharif, M.; Kausar, H.R. Non-vacuum solutions of Bianchi type VI 0 universe in f (R) gravity. Astrophys. Space Sci. 2011, 332, 463–471. [Google Scholar] [CrossRef]
- Sharif, M.; Waheed, S. Anisotropic universe models in Brans–Dicke theory. Eur. Phys. J. C 2012, 72, 1876. [Google Scholar] [CrossRef][Green Version]
- Srivastava, M.; Singh, C.P. Holographic Dark Energy Model in Brans-Dicke Theory with Future Event Horizon. arXiv, 2017; arXiv:1706.06777. [Google Scholar]
- Felegary, F.; Darabi, F.; Setare, M.R. Interacting holographic dark energy model in Brans–Dicke cosmology and coincidence problem. Int. J. Mod. Phys. D 2018, 27, 1850017. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom–non-phantom transition model and generalized holographic dark energy. Gen. Relativ. Gravit. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Covariant generalized holographic dark energy and accelerating universe. Eur. Phys. J. C 2017, 77, 528. [Google Scholar] [CrossRef]
- Sharif, M.; Jawad, A. Analysis of pilgrim dark energy models. Eur. Phys. J. C 2013, 73. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Linder, E.V. Limits of quintessence. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
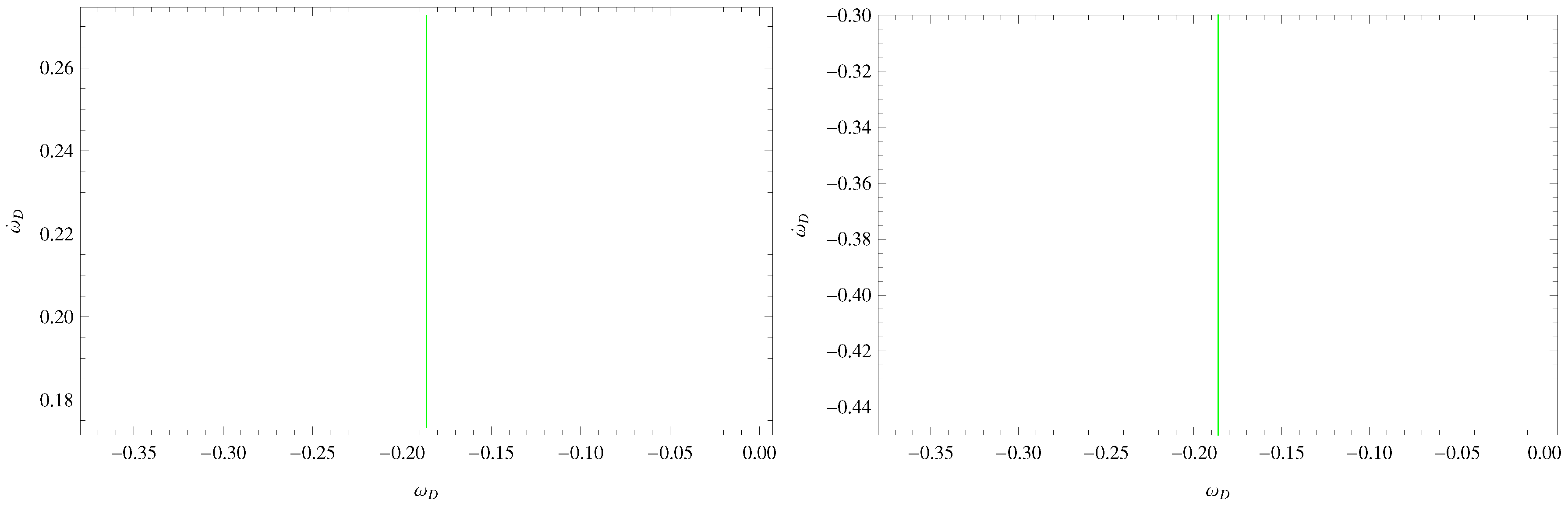
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharif, M.; Asif Ali Shah, S.; Bamba, K. New Holographic Dark Energy Model in Brans-Dicke Theory. Symmetry 2018, 10, 153. https://doi.org/10.3390/sym10050153
Sharif M, Asif Ali Shah S, Bamba K. New Holographic Dark Energy Model in Brans-Dicke Theory. Symmetry. 2018; 10(5):153. https://doi.org/10.3390/sym10050153
Chicago/Turabian StyleSharif, M., Syed Asif Ali Shah, and Kazuharu Bamba. 2018. "New Holographic Dark Energy Model in Brans-Dicke Theory" Symmetry 10, no. 5: 153. https://doi.org/10.3390/sym10050153
APA StyleSharif, M., Asif Ali Shah, S., & Bamba, K. (2018). New Holographic Dark Energy Model in Brans-Dicke Theory. Symmetry, 10(5), 153. https://doi.org/10.3390/sym10050153






