A Dynamic Adjusting Novel Global Harmony Search for Continuous Optimization Problems

Abstract

A novel global harmony search (NGHS) algorithm, as proposed in 2010, is an improved algorithm that combines the harmony search (HS), particle swarm optimization (PSO), and a genetic algorithm (GA). Moreover, the fixed parameter of mutation probability was used in the NGHS algorithm. However, appropriate parameters can enhance the searching ability of a metaheuristic algorithm, and their importance has been described in many studies. Inspired by the adjustment strategy of the improved harmony search (IHS) algorithm, a dynamic adjusting novel global harmony search (DANGHS) algorithm, which combines NGHS and dynamic adjustment strategies for genetic mutation probability, is introduced in this paper. Moreover, extensive computational experiments and comparisons are carried out for 14 benchmark continuous optimization problems. The results show that the proposed DANGHS algorithm has better performance in comparison with other HS algorithms in most problems. In addition, the proposed algorithm is more efficient than previous methods. Finally, different strategies are suitable for different situations. Among these strategies, the most interesting and exciting strategy is the periodic dynamic adjustment strategy. For a specific problem, the periodic dynamic adjustment strategy could have better performance in comparison with other decreasing or increasing strategies. These results inspire us to further investigate this kind of periodic dynamic adjustment strategy in future experiments.

1. Introduction

The last two decades have seen a significant increase in research into metaheuristic algorithms. The procedure of a metaheuristic algorithm can be divided into four steps: initialization, movement, replacement, and iteration [1]. The most popular metaheuristic algorithms to date are the particle swarm optimization (PSO) [2,3], genetic algorithm (GA) [4,5,6], and ant colony optimization (ACO) [7,8,9].

PSO was introduced by Kennedy and Eberhart in 1995 [10,11]. It imitates the foraging behavior of birds and fish, and provides a population-based search procedure, where each individual is abstracted as a “particle” that flies around in a multidimensional search space. The best positions encountered by a particle and its neighbors determine the particle’s trajectory, along with other PSO parameters. In other words, a PSO system attempts to balance exploration and exploitation by combining global and local search methods [12].

The GA has been widely investigated since Holland proposed it in 1960 [13,14]. The GA was developed from Darwinian evolution. Based on the concept of natural genetics and evolutionary principles, GA is a stochastic search technique that can search the near optimum solution in a large and complicated space. As Gordini [15] points out, “the GA differs from other non-linear optimization techniques in that it searches by maintaining a population of solutions from which better solutions are created, rather than making incremental changes to a single solution to a problem.” The GA is consisted of three operators: reproduction, crossover, and mutation [16]. Reproduction is a process of survival-of-the-fittest selection. Crossover is the partial swap between two parent strings in order to produce two offspring strings. Mutation is the occasional random inversion of bit values in order to generate a non-recursive offspring. One importance of the GA is that several metaheuristic algorithms have been developed from the GA, such as the honey-bee mating optimization (HBMO) algorithm [17] and the harmony search (HS) algorithm [16].

The harmony search (HS) algorithm is a modern metaheuristic intelligent evolution algorithm [18], and was inspired by the music improvisation process where musicians improvise their instruments’ pitches searching for a perfect state of harmony [19]. The HS algorithm simulates the principle of the music improvisation process in the same way that the GA simulates biological evolution, the simulated annealing algorithm (SA) [20] simulates physical annealing, and the PSO algorithm simulates the swarm behavior of birds and fish [18], etc. The HS algorithm has excellent exploitation capabilities. However, the HS algorithm suffers a very serious limitation of premature convergence if one or more initially generated harmonies are in the vicinity of local optimal [21]. As Assad and Deep [22] point out, “The efficiency of evolutionary algorithms depends on the extent of balance between diversification and intensification during the course of the search. Intensification, also called exploitation, is the ability of an algorithm to exploit the search space in the vicinity of the current good solution, whereas diversification, also called exploration, is the process of exploring the new regions of a large search space and thus allows dissemination of the new information into the population. Proper balance between these two contradicting characteristics is a must to enhance the performance of the algorithm.”

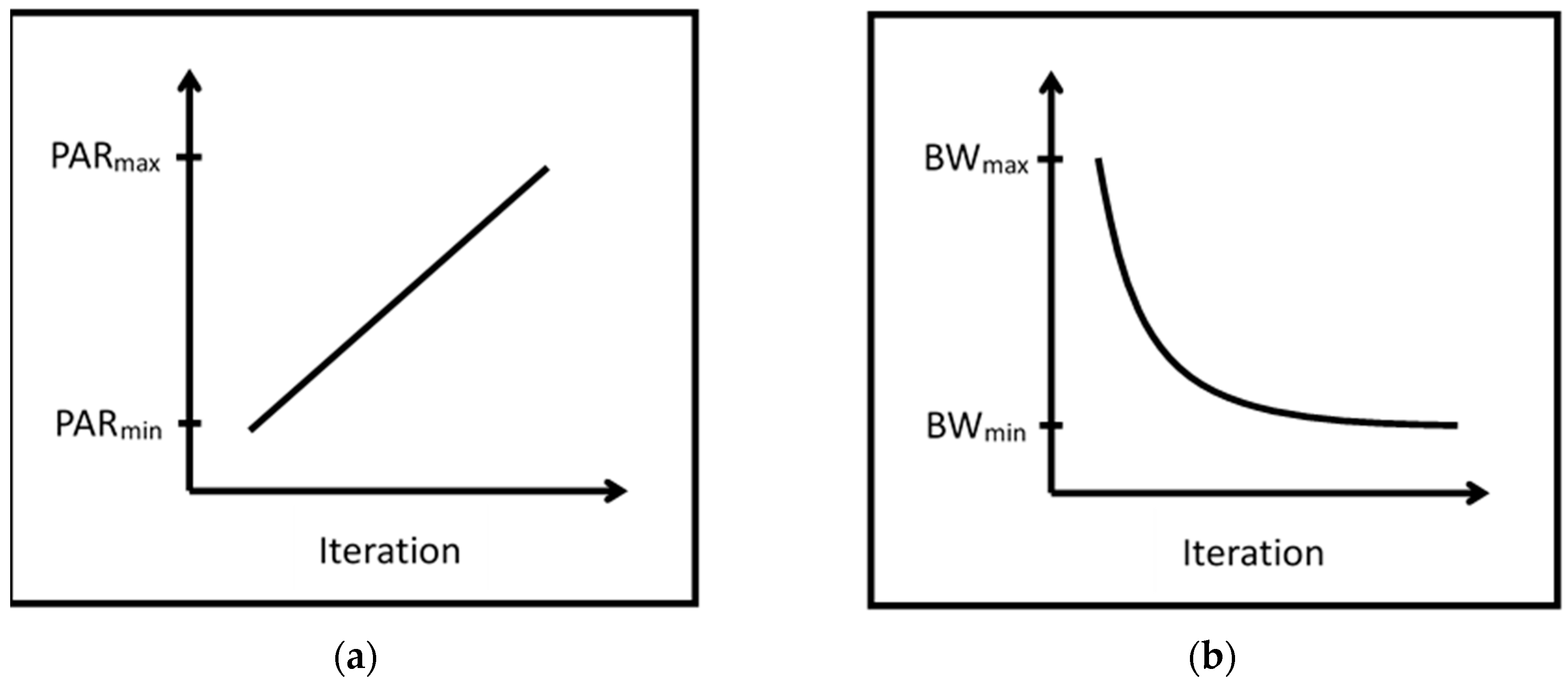
Therefore, in order to eradicate the aforementioned limitation, several improved HS algorithms have been proposed, such as the improved harmony search (IHS) algorithm [23], the self-adaptive global best harmony search (SHGS) [24], the novel global harmony search (NGHS) [25], the intelligent global harmony search (IGHS) algorithm [19], and so on. Of these algorithms, the IHS algorithm is the first to propose using the adjustment strategy to tune the pitch adjusting rate (PAR) and bandwidth (BW) parameters. In the HS algorithm, according to the value of PAR, the musicians will determine to adjust their instruments’ pitches or not. Besides, the musicians will adjust the pitches within the BW distance. The PAR and BW values change dynamically with generation number, as shown in Figure 1. In Mahdavi’s paper [23], the adjustment strategy was proofed; it can enhance the searching ability of the harmony search algorithm. In other words, the importance of the appropriate parameters was proofed in his paper.

Appropriate parameters can enhance the searching ability of a metaheuristic algorithm; their importance has been described in many studies. First, Pan et al. demonstrated that a good set of parameters can enhance an algorithm’s ability to search for the global optimum or near optimum region with a high convergence rate [19,24]. Second, in the NGHS algorithm, the new trial solutions are generated by the parameter $ste{p}_j$. Therefore, Zou et al. [25,26] showed that the most reasonable design for $ste{p}_j$ in the NGHS algorithm can guarantee that the proposed algorithm has strong global search ability in the early optimization stage, and strong local search ability in the late optimization stage. In addition, a dynamically adjusted $ste{p}_j$ maintains a balance between the global search and the local search. In another paper, Zou et al. [27] demonstrated that an appropriate harmony memory considering rate (HMCR) and PAR value in the SGHS algorithm can be gradually learned to suit the particular problem and the particular phases of the search process. In addition, there is no single choice for the genetic mutation probability ($p_m$) in the NGHS algorithm; it should be adjusted according to practical optimization problems. Last, Valian, Tavakoli, and Mohanna [28] observed that there can be no single choice for HMCR in the IGHS algorithm, and it should be adjusted according to the given optimization problems.

However, in the NGHS algorithm, the value of the genetic mutation probability ($p_m$) is a fixed value that is given in the initialization step. According to the result of Mahdavi’s paper [23], we supposed that the adjustment strategy could enhance the searching ability. Therefore, a dynamic adjusting novel global harmony search (DANGHS) algorithm was proposed in this paper. In the DANGHS algorithm, the mutation probability adjusts dynamically with the generation number by the adjustment strategy. However, we can adjust the mutation probability using different strategies. Therefore, this paper used 16 different strategies in the DANGHS algorithm in 14 well-known benchmark optimization problems. In other words, the performance of different strategies in the DANGHS algorithm for different problems was investigated. Besides, in general, one important characteristic of the metaheuristic algorithm is to be fast and efficient. A better metaheuristic algorithm cannot only search the more exact solution but also use less iterations than other algorithms. Therefore, we discuss the efficiency of the DANGHS algorithm in this paper. According to the numerical results, the DANGHS algorithm had better searching performance in comparison with other HS algorithms in most problems.

The remainder of this paper is arranged as follows. In Section 2, the HS, IHS, SGHS, and NGHS algorithms are introduced. Section 3 describes the DANGHS algorithm. A large number of experiments are carried out to test and compare the performance of 16 different strategies in the DANGHS algorithm in Section 4. Conclusions and suggestions for future research are given in Section 5.

2. HS, IHS, SGHS, and NGHS

In this section, the HS, the IHS, the SGHS, and the NGHS are reviewed.

2.1. Harmony Search Algorithm

The HS algorithm was proposed by Geem, Kim, and Loganathan in 2001 [16]. HS is similar in concept to other metaheuristic algorithms such as GA, PSO, and ACO in terms of combining the rules of randomness to imitate the process that inspired it. However, HS draws its inspiration not from biological or physical processes but from the improvisation process of musicians, such as that found in a Jazz trio [19,29].

In the musical improvisation process, each musician sounds any pitch within a possible range, and then together they make a single harmony. If all the pitches make a pleasing harmony, the experience is stored in each player’s memory, and the possibility of making a more pleasing harmony the next time is increased [30]. Similarly, in engineering optimization, each decision variable initially chooses any value within a possible range, together making one solution vector [27]. In the HS algorithm, each harmony, which means the trial solution for the problem, is represented by a D-dimension real vector, and a pleasing harmony means the good trial solution for the problem [19]. If all the decision variable values make a good solution, then that experience is stored in each variable’s memory, and the possibility of making a good solution the next time is also increased [27]. 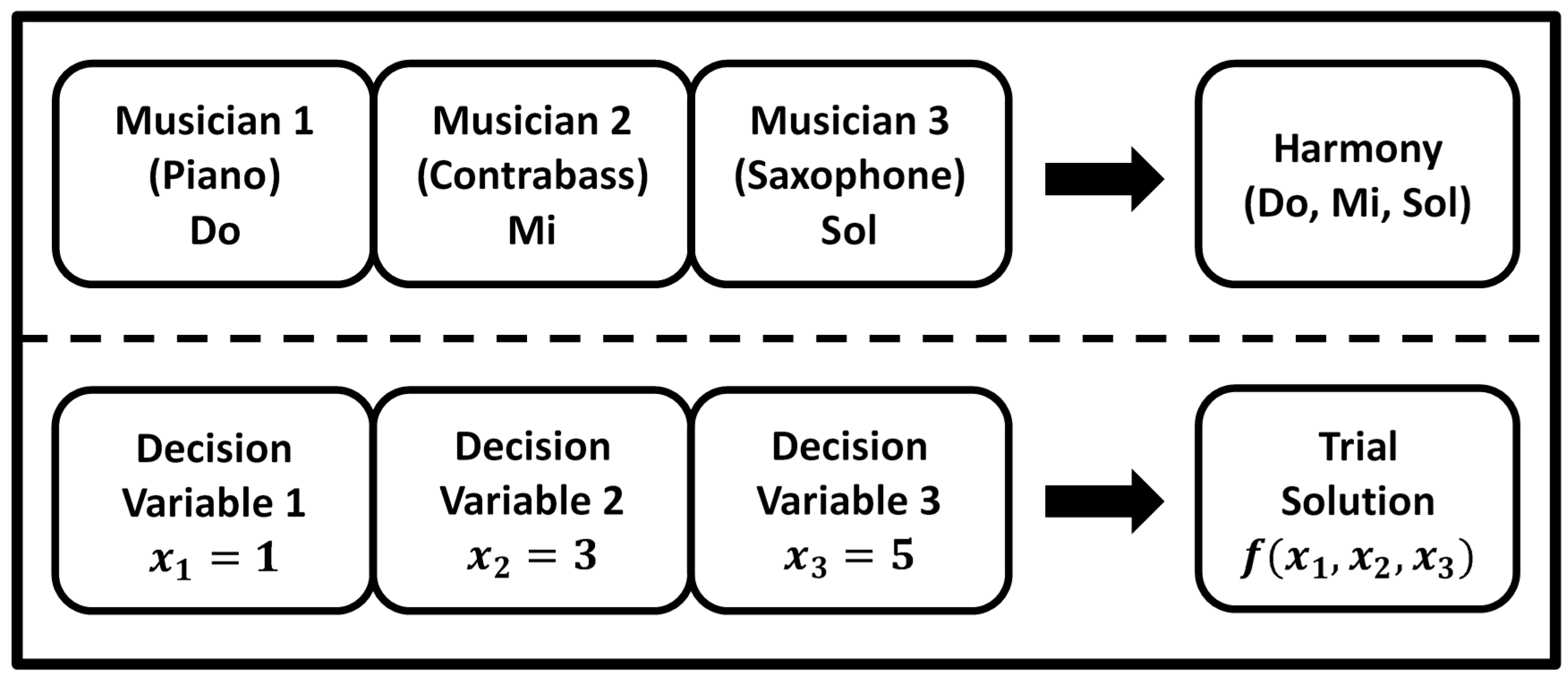Figure 2 shows the comparison between music improvisation and engineering optimization. In Figure 2, there is a Jazz trio consisting of three musicians. Each musician plays an instrument at the same time to make a single harmony. The pitches of the three instruments mean the values of the three decision variables.

In general, the HS algorithm works as follows [27]:

Step 1. Initialization: the algorithm and problem parameters

In this step, the parameters of the HS algorithm are determined. The parameters are the harmony memory size (m), the harmony memory considering rate (HMCR), the pitch adjusting rate (PAR), the bandwidth (BW), the current iteration (k = 1), and the maximum number of iterations (NI). Furthermore, the D-dimensional optimization problem is defined as Minimize f(x) subject to $x_{jL}\le x_j\le x_{jU}\left(j=1,2,\dots ,D\right)$. $x_{jL}$ and $x_{jU}$ are the lower and upper bounds for decision variables $x_j$.

Step 2. Initialization: the decision variable values and the harmony memory

The initial decision variable values $x_{ij}^{k=0}\left(\mathrm{i}=1,2,\dots ,\mathrm{m}\right)$ are generated by Equation (1). The harmony memory (HM) is as shown in Equation (2).

$$x_{ij}^0=x_{jL}+r\times \left(x_{jU}-x_{jL}\right)$$

(1)

$$\mathrm{HM}=\left[\begin{array}{cc}\begin{array}{cc}{x}_{11}^0& x_{12}^0\\ x_{21}^0& x_{22}^0\end{array}& \begin{array}{cc}\cdots & x_{1D}^0\\ \cdots & x_{2D}^0\end{array}\\ \begin{array}{cc}⋮& ⋮\\ x_{m1}^0& x_{m2}^0\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & x_{mD}^0\end{array}\end{array}\right]$$

(2)

In Equation (1), $r$ is the uniformly generated random numbers in the region of [0, 1].

Step 3. Movement: improvise a new harmony

Movement step is the most important step of any algorithm. The performance of global exploration and local exploitation are related to the design of the movement step. In the HS algorithm, the movement step is improvisation. The new harmony vector $x^{k+1}=\left(x_1^{k+1},x_2^{k+1},\dots ,x_D^{k+1}\right)$ is generated by memory consideration, pitch adjustment, and random selection mechanisms in this step. The HS movement steps (Pseudocode 1) are shown in Algorithm 1.

Algorithm 1 The Movement Steps of HS (Pseudocode 1)
1:	For $\mathrm{j}=1\mathrm{to}\mathrm{D}$ do
2:	If ${\mathrm{r}}_1\le \mathrm{H}\mathrm{M}\mathrm{C}\mathrm{R}$ then
3:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}$ % memory consideration
4:	If ${\mathrm{r}}_2\le \mathrm{P}\mathrm{A}\mathrm{R}$ then
5:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}-\mathrm{B}\mathrm{W}+{\mathrm{r}}_3\times 2\times \mathrm{B}\mathrm{W}$ % pitch adjustment
6:	If ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}>{\mathrm{x}}_{\mathrm{j}\mathrm{U}}$ then
7:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}\mathrm{U}}$
8:	Else if ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}<{\mathrm{x}}_{\mathrm{j}\mathrm{L}}$ then
9:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}\mathrm{L}}$
10:	End
11:	End
12:	Else
13:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{j}\mathrm{L}}+{\mathrm{r}}_4\times \left({\mathrm{x}}_{\mathrm{j}\mathrm{U}}-{\mathrm{x}}_{\mathrm{j}\mathrm{L}}\right)$ % random selection
14:	End
15:	End

Here, ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}$ is the j^th component of $x^{k+1}$. $i$ is an uniformly generated random number in [1, m], and $x_{ij}^k$ is the j^th component of the i^th candidate solution vector in the HM. $r_1$, $r_2$, $r_3$ and $r_4$ are the uniformly generated random numbers in the region of [0, 1], and BW is a given distance bandwidth.

Step 4. Replacement: update harmony memory

If the fitness value of the new harmony vector $x^{k+1}$ is better than that of the worst harmony in the HM, replace the worst harmony vector by $x^{k+1}$.

Step 5. Iteration: check the stopping criterion

If the stopping criterion (maximum number of iterations NI) is satisfied, the computation is terminated; otherwise, the current iteration k = k + 1 and go back to step 3.

2.2. Improved Harmony Search Algorithm

The IHS algorithm was proposed by Mahdavi, Fesanghary, and Damangir in 2007 for solving optimization problems [23]. In their paper, they noted that PAR and BW are very important parameters in the HS algorithm when fine-tuning optimized solution vectors, and can be potentially useful in adjusting the convergence rate of the algorithm to the optimal solution. Fine adjustment of these parameters is therefore of particular interest. The key difference between the IHS and the traditional HS method is thus in the way PAR and BW are adjusted in each iteration by Equations (3) and (4):

$$PA{R}^k=PA{R}_{min}+\frac{\left(PA{R}_{max}-PA{R}_{min}\right)}{NI}\times k$$

(3)

$$B{W}^k=B{W}_{max}\times e^{(\ln (\frac{B{W}_{min}}{B{W}_{max}})\times k/NI)}$$

(4)

In Equation (3), $PA{R}^k$ is the pitch adjustment rate in the current iteration k; $PA{R}_{min}$ and $PA{R}_{max}$ are the minimum and maximum adjustment rates, respectively. In Equation (4), $B{W}^k$ is the distance bandwidth in current iteration k, $B{W}_{min}$ is the minimum bandwidth, and $B{W}_{max}$ is the maximum bandwidth. Figure 1 shows that the PAR and BW values change dynamically with the iteration number.

2.3. Self-Adaptive Global Best Harmony Search Algorithm

The SGHS algorithm was presented by Pan et al. in 2010 for continuous optimization problems [24].

In the SGHS algorithm, the HMCR and PAR were dynamically adapted by the normal distribution and the BW was adjusted in each iteration. The value of $HMC{R}^k$ was generated by the mean $HMC{R}_m$ and the standard deviation. In the same way, the value of $PA{R}^k$ was generated by the mean $PA{R}_m$ and the standard deviation. Pan et al. assumed that the dynamic mean $HMC{R}_m$ is in the range of [0.9, 1.0] and the static standard deviation is 0.01; the dynamic mean $PA{R}_m$. is in the range of [0.0, 1.0] and the static standard deviation is 0.05. Furthermore, the $HMC{R}^k$ and $PA{R}^k$ were recorded by their historic values when the generated harmony successfully replaced the worst harmony in the harmony memory. After a specified learning period (LP), the $HMC{R}_m$ and $PA{R}_m$ were recalculated by averaging all the recorded $HMC{R}^k$ and $PA{R}^k$ values during this period respectively. In the subsequent iterations, new $HMC{R}^k$ and $PA{R}^k$ values were generated with the new mean $HMC{R}_m$ and $PA{R}_m$ and the given standard deviation. In addition, the $B{W}^k$ is decreased in each iteration by Equation (5).

$$B{W}^k=\{\begin{array}{cc}B{W}_{max}-\frac{B{W}_{max}-B{W}_{min}}{NI}\times 2k& ifk<NI/2,\\ B{W}_{min}& ifk\ge NI/2,\end{array}$$

(5)

In general, the SGHS algorithm works as follows:

Step 1. Initialization: the problem and algorithm parameters

Set parameters m, LP, NI, $B{W}_{max}$, $B{W}_{min}$, $HMC{R}_m$, $PA{R}_m$, the current iteration k = 1, and iteration counter lp = 1.

Step 2. Initialization: the decision variable values and the harmony memory

The initial decision variable values $x_{ij}^{k=0}\left(\mathrm{i}=1,2,\dots ,\mathrm{m}\right)$ is generated by Equation (1). The harmony memory (HM) is as shown in Equation (2).

Step 3. Movement: generate the algorithm parameters

Generate $HMC{R}^k$ and $PA{R}^k$ with $HMC{R}_m$ and $PA{R}_m$ by the normal distribution respectively. Generate $B{W}^k$ with $B{W}_{max}$ and $B{W}_{min}$ by Equation (5).

Step 4. Movement: improvise a new harmony

Improvise a new harmony $x^{k+1}$. The SGHS movement step (Pseudocode 2) is shown in Algorithm 2.

Algorithm 2 The Movement Steps of SGHS (Pseudocode 2) [24]
1:	For $\mathrm{j}=1\mathrm{to}\mathrm{D}$ do
2:	If ${\mathrm{r}}_1\le {\mathrm{HMCR}}^{\mathrm{k}}$ then
3:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}-\mathrm{B}{\mathrm{W}}^{\mathrm{k}}+{\mathrm{r}}_2\times 2\times \mathrm{B}{\mathrm{W}}^{\mathrm{k}}$
4:	If ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}>{\mathrm{x}}_{\mathrm{j}\mathrm{U}}$ then
5:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}\mathrm{U}}$
6:	Else if ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}<{\mathrm{x}}_{\mathrm{j}\mathrm{L}}$ then
7:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{i}\mathrm{L}}$
8:	End
9:	If ${\mathrm{r}}_3\le {\mathrm{PAR}}^{\mathrm{k}}$ then
10:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t},\mathrm{j}}^{\mathrm{k}}$
11:	End
12:	Else
13:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{j}\mathrm{L}}+{\mathrm{r}}_4\times \left({\mathrm{x}}_{\mathrm{j}\mathrm{U}}-{\mathrm{x}}_{\mathrm{j}\mathrm{L}}\right)$ % random selection
14:	End
15:	End

Here, $x_j^{k+1}$ is the j^th component of $x^{k+1}$. $i$ is an uniformly generated random number in [1, m], and $x_{ij}^k$ is the j^th component of the i^th candidate solution vector in the HM. $x_{best,j}^k$ is the j^th component of the best candidate solution vector in the HM. $r_1$, $r_2$, $r_3$ and $r_4$ are uniformly generated random numbers in [0, 1]. $r_1$ is used for position updating, $r_2$ determines the distance of the BW, $r_3$ is used for pitch adjustment, and $r_4$ is used for random selection.

Step 5. Replacement: update harmony memory

If the fitness value of the new harmony vector $x^{k+1}$ is better than that of the worst harmony in the HM, replace the worst harmony vector by $x^{k+1}$ and record the values of $HMC{R}^k$ and $PA{R}^k$.

Step 6. Replacement: update $HMC{R}_m$ and $PA{R}_m$

If lp = LP, recalculate $HMC{R}_m$ and $PA{R}_m$ by averaging all the recorded $HMC{R}^k$ and $PA{R}^k$ values respectively and reset lp = 1; otherwise, lp = lp +1.

Step 7. Iteration: check the stopping criterion

If NI is completed, return the best harmony vector $x_{best}$ in the HM; otherwise, the current iteration k = k + 1 and go back to step 3.

2.4. Novel Global Harmony Search Algorithm

The NGHS algorithm [25,26] is an improved algorithm that combines HS, PSO, and GA. A prominent characteristic of PSO is that individual particles attempt to imitate the social experience. It means the particles are affected by other better particles in the PSO algorithm. A prominent characteristic of GA is that it is possible for the trial solution to escape from the local optimum by mutation. In other words, NGHS tries to generate a new solution by moving the worst solution toward the best solution or by mutation.

Figure 3 is used to illustrate the principle of position updating. $ste{p}_j=\left|x_{best,j}^k-x_{worst,j}^k\right|$ is defined as an adaptive step of the j^th decision variable. This adaptive step can dynamically balance the performance of global exploration and local exploitation in the NGHS algorithm. As Zou et al. [26] points out, “In the early stage of optimization, all solution vectors are sporadic in the solution space, so most adaptive steps are large, and most trust regions are wide, which is beneficial to the global search of NGHS. However, in the late stage of optimization, all non-best solution vectors are inclined to move to the global best solution vector, so most solution vectors are close to each other. In this case, most adaptive steps are small and most trust regions are narrow, which is beneficial to the local search of NGHS.”

According to this prominent characteristic, NGHS modifies the movement step of HS therefore the NGHS algorithm can imitate the current best harmony in the HM. In general, the NGHS algorithm works as follows:

Step 1. Initialization: the algorithm and problem parameters

(1)

Set parameters m, NI, and the current iteration k = 1.

(2)

The genetic mutation probability ($p_m$) is included in NGHS, while the harmony memory considering rate (HMCR), pitch adjusting rate (PAR) and the bandwidth (BW) are excluded from NGHS.

Step 2. Initialization: the decision variable values and the harmony memory

The initial decision variable values $x_{ij}^{k=0}\left(\mathrm{i}=1,2,\dots ,\mathrm{m}\right)$ are generated by Equation (1). The HM is as shown in Equation (2).

Step 3. Movement: improvise a new harmony

NGHS modifies the movement step in HS. The NGHS movement step (Pseudocode 3) is shown in Algorithm 3.

Algorithm 3 The Movement Steps of NGHS (Pseudocode 3) [25,26,27].
1:	For $\mathrm{j}=1\mathrm{to}\mathrm{D}$ do
2:	${\mathrm{x}}_{\mathrm{R}}=2\times {\mathrm{x}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t},\mathrm{j}}^{\mathrm{k}}-{\mathrm{x}}_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t},\mathrm{j}}^{\mathrm{k}}$
3:	If ${\mathrm{x}}_{\mathrm{R}}>{\mathrm{x}}_{\mathrm{j}\mathrm{U}}$ then
4:	${\mathrm{x}}_{\mathrm{R}}={\mathrm{x}}_{\mathrm{j}\mathrm{U}}$
5:	Else if ${\mathrm{x}}_{\mathrm{R}}<{\mathrm{x}}_{\mathrm{j}\mathrm{L}}$ then
6:	${\mathrm{x}}_{\mathrm{R}}={\mathrm{x}}_{\mathrm{j}\mathrm{L}}$
7:	End
8:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t},\mathrm{j}}^{\mathrm{k}}+{\mathrm{r}}_1\times ({\mathrm{x}}_{\mathrm{R}}-{\mathrm{x}}_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t},\mathrm{j}}^{\mathrm{k}})$ % position updating
9:	If ${\mathrm{r}}_2\le {\mathrm{p}}_{\mathrm{m}}$ then
10:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{j}\mathrm{L}}+{\mathrm{r}}_3\times \left({\mathrm{x}}_{\mathrm{j}\mathrm{U}}-{\mathrm{x}}_{\mathrm{j}\mathrm{L}}\right)$  % genetic mutation
11:	End
12:	End

Here, $x_{best,j}^k$ and $x_{worst,j}^k$ are the best harmony and the worst harmony in the HM, respectively. $r_1$, $r_2$ and $r_3$ are uniformly generated random numbers in [0, 1]. $r_1$ is used for position updating, $r_2$ determines whether NGHS should carry out genetic mutation, and $r_3$ is used for genetic mutation.

Genetic mutation with a small probability is carried out for the current worst harmony in the HM after position updating [25,26,27].

Step 4. Replacement: update harmony memory

NGHS replaces the worst harmony $x_{worst,j}^k\left(\mathrm{j}=1,2,\dots ,\mathrm{D}\right)$ in the HM by the new harmony $x^{k+1}$, even if the new harmony is worse than the worst harmony.

Step 5. Iteration: check the stopping criterion

If the stopping criterion (maximum number of iterations NI) is satisfied, the computation is terminated; otherwise, the current iteration k = k + 1 and go back to step 3.

3. Dynamic Adjusting Novel Global Harmony Search (DANGHS) Algorithm

Appropriate parameters can enhance the searching ability of a metaheuristic algorithm. Inspired by this concept, a dynamic adjusting NGHS (DANGHS) is presented in this section. In the DANGHS, the genetic mutation probability ($p_m$) is dynamically adjusted in each iteration. However, we can enhance the searching ability of the NGHS algorithm by many kinds of dynamic adjustment strategies. Therefore, we introduced 16 dynamic adjustment strategies in this paper. All 16 strategies are shown as follows, and Figure 4, Figure 5 and Figure 6 are used to illustrate the 16 strategies.

(1)

Straight linear increasing strategy (Straight_1):

The genetic mutation probability is increased by Equation (6), which is a linear function.

$$p_m^k=p_{m\_min}+\frac{\left(p_{m\_max}-p_{m\_min}\right)}{NI}\times k.$$

(6)

Here, $p_{m\_min}$ is the minimum genetic mutation probability, and $p_{m\_max}$ is the maximum genetic mutation probability.

(2)

Straight linear decreasing strategy (Straight_2):

The genetic mutation probability is decreased by Equation (7), which is a linear function.

$$p_m^k=p_{m\_max}+\frac{\left(p_{m\_min}-p_{m\_max}\right)}{NI}\times k$$

(7)

(3)

Threshold linear prior increasing strategy (Threshold_1):

The genetic mutation probability is increased by Equation (8), which is a linear function with a threshold. The genetic mutation probability is raised before the threshold, but the genetic mutation probability is a fixed maximum value after the threshold.

$$p_m^k=\{\begin{array}{cc}{p}_{m\_min}+\frac{P_{m\_max}-P_{m\_min}}{NI}\times 2k& ifk<NI/2\\ p_{m\_max}& ifk\ge NI/2\end{array}$$

(8)

(4)

Threshold linear prior decreasing strategy (Threshold_2):

The genetic mutation probability is decreased by Equation (9), which is a linear function with a threshold. The genetic mutation probability is reduced before the threshold, but the genetic mutation probability is a fixed minimum value after the threshold.

$$p_m^k=\{\begin{array}{cc}{p}_{m\_max}+\frac{P_{m\_min}-P_{m\_max}}{NI}\times 2k& ifk<NI/2\\ p_{m\_min}& ifk\ge NI/2\end{array}$$

(9)

(5)

Threshold linear posterior increasing strategy (Threshold_3):

The genetic mutation probability is increased by Equation (10), which is a linear function with a threshold. The genetic mutation probability is a fixed minimum value before the threshold, but the genetic mutation probability is raised after the threshold.

$$p_m^k=\{\begin{array}{cc}{p}_{m\_min}& ifk<NI/2\\ p_{m\_min}+\frac{P_{m\_max}-P_{m\_min}}{NI}\times 2k& ifk\ge NI/2\end{array}$$

(10)

(6)

Threshold linear posterior decreasing strategy (Threshold_4):

The genetic mutation probability is decreased by Equation (11), which is a linear function with a threshold. The genetic mutation probability is a fixed maximum value before the threshold, but the genetic mutation probability is reduced after the threshold.

$$p_m^k=\{\begin{array}{cc}{p}_{m\_max}& ifk<NI/2\\ p_{m\_max}+\frac{P_{m\_min}-P_{m\_max}}{NI}\times 2k& ifk\ge NI/2\end{array}$$

(11)

(7)

Natural exponential increasing strategy (Exponential_1):

The genetic mutation probability is increased by Equation (12), which is a non-linear function.

$$p_m^k=p_{m\_min}\times e^{\left(\ln \left(\frac{p_{m\_max}}{p_{m\_min}}\right)\times k/NI\right)}$$

(12)

(8)

Natural exponential decreasing strategy (Exponential_2):

The genetic mutation probability is decreased by Equation (13), which is a non-linear function.

$$p_m^k=p_{m\_max}\times e^{(\ln (\frac{p_{m\_min}}{p_{m\_max}})\times k/NI)}$$

(13)

(9)

Exponential increasing strategy:

The genetic mutation probability is increased by Equation (14), which is a non-linear function. We can control the increasing rate by the modification rate ($mr$).

$$p_m^k=p_{m\_min}+\left(p_{m\_max}-p_{m\_min}\right)\times m{r}^{\left(NI-k\right)/NI}$$

(14)

In this paper, the $mr$ is equal to 0.01 or 0.001. Therefore, in this paper, the 9th strategy (Exponential_3) is the exponential increasing strategy with $mr=0.01$, and the 10th strategy (Exponential_5) is the exponential increasing strategy with $mr=0.001$.

(10)

Exponential decreasing strategy:

The genetic mutation probability is decreased by Equation (15), which is a non-linear function. We can control the decreasing rate by the modification rate ($mr$).

$$p_m^k=p_{m\_min}+\left(p_{m\_max}-p_{m\_min}\right)\times m{r}^{k/NI}$$

(15)

In this paper, the $mr$ is equal to 0.01 or 0.001. Therefore, in this paper, the 11th strategy (Exponential_4) is the exponential decreasing strategy with $mr=0.01$, and the 12th strategy (Exponential_6) is the exponential decreasing strategy with $mr=0.001$.

(11)

Concave cosine strategy:

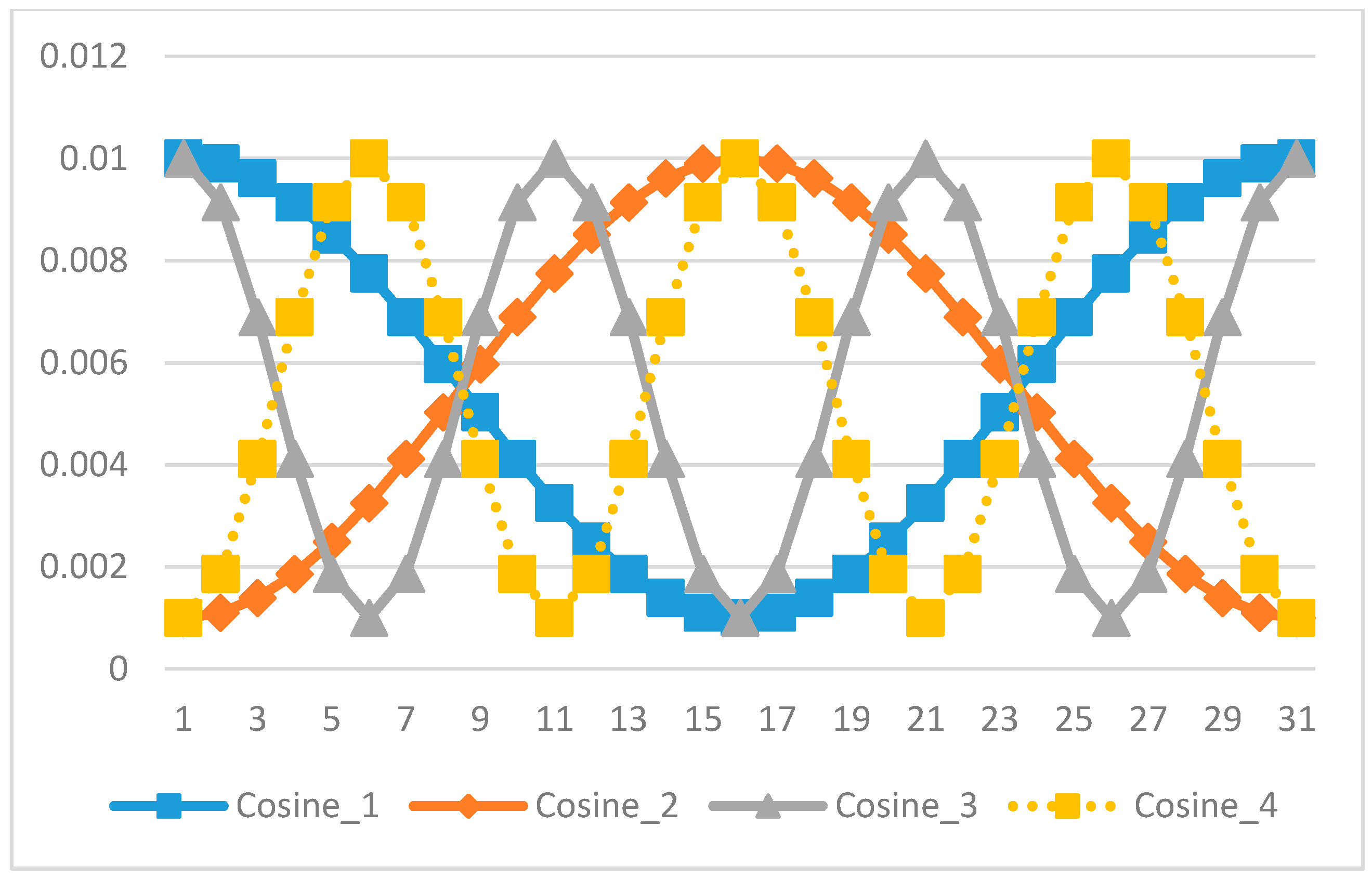
The genetic mutation probability is changed by Equation (16), which is a periodic function. The shape of this function is a concave, and we can control the cycle time of this function by the coefficient of cycle (cc).

$$p_m^k=\frac{p_{m\_max}+p_{m\_min}}{2}+\frac{p_{m\_max}-p_{m\_min}}{2}\times \cos \frac{k\times cc\times 2\pi }{NI}$$

(16)

In this paper, the $cc$ is equal to 1 or 3. Therefore, in this paper, the 13th strategy (Cosine_1) is the concave cosine strategy with $cc=1$, and the 14th strategy (Cosine_3) is the concave cosine strategy with $cc=3$.

(12)

Convex cosine strategy:

The genetic mutation probability is changed by Equation (17), which is a periodic function. The shape of this function is a convex, and we can control the cycle time of this function by the coefficient of cycle (cc).

$$p_m^k=\frac{p_{m\_max}+p_{m\_min}}{2}-\frac{p_{m\_max}-p_{m\_min}}{2}\times \cos \frac{k\times cc\times 2\pi }{NI}$$

(17)

In this paper, the $cc$ is equal to 1 or 3. Therefore, in this paper, the 15th strategy (Cosine_2) is the convex cosine strategy with $cc=1$, and the 16th strategy (Cosine_4) is the convex cosine strategy with $cc=3$.

In general, the DANGHS algorithm works as follows:

Step 1. Initialization: the problem and algorithm parameters

The parameters are the harmony memory size (m), the current iteration k = 1, and the maximum number of iterations (NI).

Step 2. Initialization: the decision variable values and the harmony memory

The initial decision variable values $x_{ij}^{k=0}\left(\mathrm{i}=1,2,\dots ,\mathrm{m}\right)$ is generated by Equation (1). The HM is as shown in Equation (2).

Step 3. Movement: generate the algorithm parameters

Generate the genetic mutation probability ($p_m^k$) in each iteration by dynamic adjustment strategies.

Step 4. Movement: improvise a new harmony

The DANGHS movement step (Pseudocode 4) is shown in Algorithm 4.

Algorithm 4 The Movement Steps of DANGHS (Pseudocode 4)
1:	For $\mathrm{j}=1\mathrm{to}\mathrm{D}$ do
2:	If ${\mathrm{r}}_1>{\mathrm{p}}_{\mathrm{m}}^{\mathrm{k}}$ then
3:	${\mathrm{x}}_{\mathrm{R}}=2\times {\mathrm{x}}_{\mathrm{best},\mathrm{j}}^{\mathrm{k}}-{\mathrm{x}}_{\mathrm{worst},\mathrm{j}}^{\mathrm{k}}$
4:	If ${\mathrm{x}}_{\mathrm{R}}>{\mathrm{x}}_{\mathrm{jU}}$ then
5:	${\mathrm{x}}_{\mathrm{R}}={\mathrm{x}}_{\mathrm{jU}}$
6:	Else if ${\mathrm{x}}_{\mathrm{R}}<{\mathrm{x}}_{\mathrm{jL}}$ then
7:	${\mathrm{x}}_{\mathrm{R}}={\mathrm{x}}_{\mathrm{jL}}$
8:	End
9:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{worst},\mathrm{j}}^{\mathrm{k}}+{\mathrm{r}}_2\times ({\mathrm{x}}_{\mathrm{R}}-{\mathrm{x}}_{\mathrm{worst},\mathrm{j}}^{\mathrm{k}})$ % position updating
10:	Else
11:	${\mathrm{x}}_{\mathrm{j}}^{\mathrm{k}+1}={\mathrm{x}}_{\mathrm{jL}}+{\mathrm{r}}_3\times \left({\mathrm{x}}_{\mathrm{jU}}-{\mathrm{x}}_{\mathrm{jL}}\right)$ % genetic mutation
12:	End
13:	End

Here, $x_{best,j}^k$ and $x_{worst,j}^k$ are the best harmony and the worst harmony in the HM, respectively. ${\mathrm{r}}_1$, ${\mathrm{r}}_2$ and ${\mathrm{r}}_3$ are uniformly generated random numbers in [0, 1]. ${\mathrm{r}}_1$ determines whether DANGHS should carry out genetic mutation, ${\mathrm{r}}_2$ is used for position updating, and ${\mathrm{r}}_3$ is used for genetic mutation.

Step 5. Replacement: update harmony memory

DANGHS replaces the worst harmony $x_{worst,j}^k\left(\mathrm{j}=1,2,\dots ,\mathrm{D}\right)$ in the HM by the new harmony $x^{k+1}$, even if the new harmony is worse than the worst harmony.

Step 6. Iteration: check the stopping criterion

If the stopping criterion (maximum number of iterations NI) is satisfied, terminate the computation and return the best harmony vector $x_{best}$ in the HM; otherwise, the current iteration k = k + 1 and go back to step 3.

4. Experiments and Analysis

In order to verify the performance of the 16 dynamic adjustment strategies in the DANGHS algorithm, 14 well-known benchmark optimization problems [24,28,31] are considered, as shown in

Table 1. 14 well-known benchmark optimization problems.

Name	Function	Search Space	Optimum
${\mathit{f}}_{\mathbf{1}}$ Sphere function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}{x}_i^2$	[−100, 100]n	0
${\mathit{f}}_{\mathbf{2}}$ Step function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}{\left(⎣x_i+0.5⎦\right)}^2$	[−100, 100]n	0
${\mathit{f}}_{\mathbf{3}}$ Schwefel’s problem 2.22	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}\left|x_i\right|+{\displaystyle {\displaystyle \prod }_{i=1}^N}\left|x_i\right|$	[−10, 10]n	0
${\mathit{f}}_{\mathbf{4}}$ Rotated hyper-ellipsoid function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}{({\displaystyle {\displaystyle \sum }_{j=1}^i}{x}_j)}^2$	[−100, 100]n	0
${\mathit{f}}_{\mathbf{5}}$ Griewank function	$\min f\left(x_i\right)=\frac{1}{4000}{\displaystyle {\displaystyle \sum }_{i=1}^N}{x}_i^2-{\displaystyle {\displaystyle \prod }_{i=1}^N}\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$	[−600, 600]n	0
${\mathit{f}}_{\mathbf{6}}$ Ackley’s function	$\min f\left(x_i\right)=20+\mathrm{e}-20\exp \left(-0.2\sqrt{{\displaystyle {\displaystyle \sum }_{i=1}^N}{x}_i^2/n}\right)-\exp \left({\displaystyle {\displaystyle \sum }_{i=1}^N}\cos \left(2\pi x_i\right)/n\right)$	[−32, 32]n	0
${\mathit{f}}_{\mathbf{7}}$ Rosenbrock function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^{N-1}}\left(100{\left(x_{i+1}-x_i^2\right)}^2+{\left(1-x_i\right)}^2\right)$	[−30, 30]n	0
${\mathit{f}}_{\mathbf{8}}$ Rastrigin function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}\left(x_i^2-10\cos \left(2\pi x_i\right)+10\right)$	[−5.12, 5.12]n	0
${\mathit{f}}_{\mathbf{9}}$ Schwefel’s problem 2.26	$\min f\left(x_i\right)=418.9829N-{\displaystyle {\displaystyle \sum }_{i=1}^N}\left(x_i\sin \left(\sqrt{\left|x_i\right|}\right)\right)$	[−500, 500]n	0
${\mathit{f}}_{\mathbf{10}}$ Shifted Sphere function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}{z}_i^2-450$	[−100, 100]n	−450
${\mathit{f}}_{\mathbf{11}}$ Shifted Rotated hyper-ellipsoid function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}{({\displaystyle {\displaystyle \sum }_{j=1}^i}{z}_i)}^2-450$	[−100, 100]n	−450
${\mathit{f}}_{\mathbf{12}}$ Shifted Rotated Griewank function	$\min f\left(x_i\right)=\frac{1}{4000}{\displaystyle {\displaystyle \sum }_{i=1}^N}{z}_i^2-{\displaystyle {\displaystyle \prod }_{i=1}^N}\cos \left(\frac{z_i}{\sqrt{i}}\right)+1-180$	[−600, 600]n	−180
${\mathit{f}}_{\mathbf{13}}$ Shifted Rosenbrock function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^{N-1}}\left(100{\left(z_{i+1}-z_i^2\right)}^2+{\left(1-z_i\right)}^2\right)+390$	[−30, 30]n	390
${\mathit{f}}_{\mathbf{14}}$ Shifted Rastrigin function	$\min f\left(x_i\right)={\displaystyle {\displaystyle \sum }_{i=1}^N}\left(z_i^2-10\cos \left(2\pi z_i\right)+10\right)-330$	[−5.12, 5.12]n	−330

. This study used Python 3.6.2 (64-bit) as the complier to write the program for finding the solution. The solution-finding equipment was an Intel Core (TM) i7-4720HQ (2.6 GHz) CPU, 8G of memory, and Windows 10 home edition (64-bit) OS.

Problems 1–4, 10 and 11, which are Sphere function, Step function, Schwefel’s problem 2.22, Rotated hyper-ellipsoid function, Shifted Sphere function, and Shifted Rotated hyper-ellipsoid function, are unimodal problems. Problems 5–9 and 12–14, which are Griewank function, Ackley’s function, Rosenbrock function, Rastrigin function, Schwefel’s problem 2.26, Shifted Rotated Griewank function, Shifted Rosenbrock function, and Shifted Rastrigin function, are difficult multimodal problems; i.e., there are several local optima in these problems and the number of local optima increases with the problem dimension (D) [24].

In order to verify the performance of the DANGHS algorithm, this paper compared the extensive experiment results of the DANGHS algorithm with other different HS algorithms. In the experiments, the parameters of the compared HS algorithms are shown in

Table 2. Parameters of compared harmony search (HS) algorithms.

Algorithm	m 1	HMCR 2	PAR 3	BW 4	LP 5	${\mathit{p}}_{\mathit{m}}$6
HS	5	0.9	0.3	0.01	–	–
IHS	5	0.9	$PA{R}_{min}=0.01$ $PA{R}_{max}=0.99$	$B{W}_{max}=\left(x_{jU}-x_{jL}\right)/20$ $B{W}_{min}=0.0001$	–	–
SGHS	5	$HMC{R}_m=0.98$	$PA{R}_m=0.9$	$B{W}_{max}=\left(x_{jU}-x_{jL}\right)/10$ $B{W}_{min}=0.0005$	100	–
NGHS	5	–	–	–	–	0.005
DANGHS	5	–	–	–	–	$P_{min}=0.001$ $P_{max}=0.010$.

¹ m: the harmony memory size; ² HMCR: the harmony memory considering rate; ³ PAR: the pitch adjusting rate; ⁴ BW: the bandwidth; ⁵ LP: the learning period; ⁶ $p_m$: the genetic mutation probability.

[28].

In all HS algorithms, the harmony memory size (m) is 5. For each problem, two different dimension sizes (D) are tested, and they are equal to 30 and 100. Therefore, the iteration number are equal to 60,000 and 150,000, respectively. Thirty independent experiments (n) are carried out for each problem. The experimental results obtained using the 16 proposed adjustment strategies in the DANGHS algorithms and those obtained using different HS algorithms are shown in

Table 3. Experimental results of 16 strategies in the DANGHS algorithms.

No.	Dimension (D) = 30					Dimension (D) = 100
	Adjustment strategy	Min	Max	Mean	SD	Adjustment strategy	Min	Max	Mean	SD
${\mathit{f}}_{\mathbf{1}}$	Straight_1	1.0461 × 10−17	4.3759 × 10−15	6.7177 × 10−16	1.1026 × 10−15	Straight_1	7.4075 × 10−6	3.1563 × 10−4	3.3196 × 10−5	5.3403 × 10−5
	Straight_2	3.1999 × 10−23	2.5783 × 10−18	3.6341 × 10−19	6.7121 × 10−19	Straight_2	1.0715 × 10−7	7.1045 × 10−6	8.4864 × 10−7	1.2362 × 10−6
	Threshold_1	1.5431 × 10−13	7.3069 × 10−11	6.6315 × 10−12	1.3094 × 10−11	Threshold_1	1.0024 × 10−3	9.1452 × 10−3	2.7025 × 10−3	1.6455 × 10−3
	Threshold_2	7.1381 × 10−39	2.0446 × 10−26	6.8264 × 10−28	3.6700 × 10−27	Threshold_2	3.9739 × 10−16	8.5814 × 10−14	1.7158 × 10−14	2.2275 × 10−14
	Threshold_3	1.5233 × 10−32	1.4639 × 10−22	4.9489 × 10−24	2.6266 × 10−23	Threshold_3	5.5110 × 10−15	4.3556 × 10−12	3.2639 × 10−13	7.8921 × 10−13
	Threshold_4	3.3374 × 10−18	4.3038 × 10−12	1.4919 × 10−13	7.7155 × 10−13	Threshold_4	3.2962 × 10−5	1.8976 × 10−4	8.5947 × 10−5	4.0524 × 10−5
	Exponential_1	1.5745 × 10−24	1.0309 × 10−18	4.3948 × 10−20	1.8663 × 10−19	Exponential_1	2.6917 × 10−9	4.3964 × 10−8	1.3508 × 10−8	9.5937 × 10−9
	Exponential_2	1.9177 × 10−30	9.0711 × 10−23	4.0772 × 10−24	1.6377 × 10−23	Exponential_2	3.3307 × 10−11	2.2886E × 10−9	4.9657 × 10−10	5.7327 × 10−10
	Exponential_3	1.4165 × 10−30	2.0068 × 10−23	9.8918 × 10−25	3.6255 × 10−24	Exponential_3	4.3579 × 10−12	9.8204 × 10−11	3.2054 × 10−11	2.5181 × 10−11
	Exponential_4	6.4644 × 10−35	4.5295 × 10−25	1.7018 × 10−26	8.1269 × 10−26	Exponential_4	9.8540 × 10−14	7.9844 × 10−12	1.7156 × 10−12	1.8932 × 10−12
	Exponential_5	2.5044 × 10−34	1.9318 × 10−25	6.4846 × 10−27	3.4669 × 10−26	Exponential_5	1.0612 × 10−14	6.4803 × 10−12	3.7018 × 10−13	1.1689 × 10−12
	Exponential_6	2.3735 × 10−38	3.7601 × 10−30	1.8344 × 10−31	7.0604 × 10−31	Exponential_6	1.6615 × 10−16	8.0332 × 10−14	1.2209 × 10−14	1.9706 × 10−14
	Cosine_1	1.0929 × 10−25	2.6839 × 10−19	1.2194 × 10−20	4.8268 × 10−20	Cosine_1	1.3660 × 10−9	8.8086 × 10−8	1.7253 × 10−8	2.0154 × 10−8
	Cosine_2	4.4254 × 10−21	3.5110 × 10−16	2.1719 × 10−17	7.1432 × 10−17	Cosine_2	5.6587 × 10−8	2.9214 × 10−6	5.8827 × 10−7	7.8914 × 10−7
	Cosine_3	1.2834 × 10−22	1.3530 × 10−17	7.1008 × 10−19	2.4622 × 10−18	Cosine_3	1.9881 × 10−9	2.8788 × 10−7	5.6503 × 10−8	6.6569 × 10−8
	Cosine_4	2.2000 × 10−22	6.3880 × 10−16	3.4309 × 10−17	1.1748 × 10−16	Cosine_4	1.7535 × 10−8	2.7122 × 10−6	2.0647 × 10−7	4.7558 × 10−7
${\mathit{f}}_{\mathbf{2}}$	Straight_1	0.0000	0.0000	0.0000	0.0000	Straight_1	0.0000	0.0000	0.0000	0.0000
	Straight_2	0.0000	0.0000	0.0000	0.0000	Straight_2	0.0000	0.0000	0.0000	0.0000
	Threshold_1	0.0000	0.0000	0.0000	0.0000	Threshold_1	0.0000	0.0000	0.0000	0.0000
	Threshold_2	0.0000	0.0000	0.0000	0.0000	Threshold_2	0.0000	0.0000	0.0000	0.0000
	Threshold_3	0.0000	0.0000	0.0000	0.0000	Threshold_3	0.0000	0.0000	0.0000	0.0000
	Threshold_4	0.0000	0.0000	0.0000	0.0000	Threshold_4	0.0000	0.0000	0.0000	0.0000
	Exponential_1	0.0000	0.0000	0.0000	0.0000	Exponential_1	0.0000	0.0000	0.0000	0.0000
	Exponential_2	0.0000	0.0000	0.0000	0.0000	Exponential_2	0.0000	0.0000	0.0000	0.0000
	Exponential_3	0.0000	0.0000	0.0000	0.0000	Exponential_3	0.0000	0.0000	0.0000	0.0000
	Exponential_4	0.0000	0.0000	0.0000	0.0000	Exponential_4	0.0000	0.0000	0.0000	0.0000
	Exponential_5	0.0000	0.0000	0.0000	0.0000	Exponential_5	0.0000	0.0000	0.0000	0.0000
	Exponential_6	0.0000	0.0000	0.0000	0.0000	Exponential_6	0.0000	0.0000	0.0000	0.0000
	Cosine_1	0.0000	0.0000	0.0000	0.0000	Cosine_1	0.0000	0.0000	0.0000	0.0000
	Cosine_2	0.0000	0.0000	0.0000	0.0000	Cosine_2	0.0000	0.0000	0.0000	0.0000
	Cosine_3	0.0000	0.0000	0.0000	0.0000	Cosine_3	0.0000	0.0000	0.0000	0.0000
	Cosine_4	0.0000	0.0000	0.0000	0.0000	Cosine_4	0.0000	0.0000	0.0000	0.0000
${\mathit{f}}_{\mathbf{3}}$	Straight_1	7.6101 × 10−11	2.1913 × 10−8	1.4051 × 10−9	3.9001 × 10−9	Straight_1	8.8188 × 10−4	2.8473 × 10−3	1.4467 × 10−3	4.5882 × 10−4
	Straight_2	6.3744 × 10−14	8.2891 × 10−10	5.6932 × 10−11	1.5070 × 10−10	Straight_2	1.0465 × 10−4	3.6867 × 10−4	2.0451 × 10−4	7.2735 × 10−5
	Threshold_1	4.6938 × 10−8	1.3461 × 10−6	2.1964 × 10−7	2.5585 × 10−7	Threshold_1	1.4060 × 10−2	3.5936 × 10−2	1.9850 × 10−2	4.3707 × 10−3
	Threshold_2	5.6623 × 10−23	8.2711 × 10−17	2.9440 × 10−18	1.4815 × 10−17	Threshold_2	2.5513 × 10−9	4.2922 × 10−8	1.0152 × 10−8	8.0648 × 10−9
	Threshold_3	4.7815 × 10−20	5.0811 × 10−11	1.7085 × 10−12	9.1183 × 10−12	Threshold_3	7.0365 × 10−9	1.3972 × 10−7	4.1610 × 10−8	3.3889 × 10−8
	Threshold_4	1.7455 × 10−10	1.3321 × 10−7	1.7945 × 10−8	3.2820 × 10−8	Threshold_4	1.3864 × 10−3	6.5341 × 10−3	3.0170 × 10−3	1.0805 × 10−3
	Exponential_1	9.8893 × 10−15	8.8305 × 10−11	6.3308 × 10−12	1.8435 × 10−11	Exponential_1	8.0177 × 10−6	7.4683 × 10−5	2.0822 × 10−5	1.1771 × 10−5
	Exponential_2	1.7782 × 10−17	6.9813 × 10−12	3.7142 × 10−13	1.4030 × 10−12	Exponential_2	7.3854 × 10−7	6.7228 × 10−6	3.3092 × 10−6	1.5847 × 10−6
	Exponential_3	7.5286 × 10−18	4.4195 × 10−13	2.0483 × 10−14	7.9637 × 10−14	Exponential_3	2.6791 × 10−7	1.9304 × 10−6	6.8633 × 10−7	3.3018 × 10−7
	Exponential_4	2.5827 × 10−20	1.1413 × 10−14	4.3303 × 10−16	2.0473 × 10−15	Exponential_4	3.1645 × 10−8	1.2139 × 10−6	2.0931 × 10−7	2.3506 × 10−7
	Exponential_5	1.5957 × 10−20	3.0055 × 10−15	1.1154 × 10−16	5.3828 × 10−16	Exponential_5	9.3641 × 10−9	1.3374 × 10−7	3.2879 × 10−8	2.5806 × 10−8
	Exponential_6	5.1270 × 10−23	2.5548 × 10−17	1.9511 × 10−18	5.5869 × 10−18	Exponential_6	1.7326 × 10−9	2.2346 × 10−8	7.9778 × 10−9	5.9706 × 10−9
	Cosine_1	8.2615 × 10−15	4.1648 × 10−10	1.9989 × 10−11	7.5562 × 10−11	Cosine_1	7.5681 × 10−6	9.0058 × 10−5	2.7007 × 10−5	1.7485 × 10−5
	Cosine_2	2.2087 × 10−12	1.3549 × 10−9	1.5788 × 10−10	2.9202 × 10−10	Cosine_2	5.0087 × 10−5	2.4876 × 10−4	1.1495 × 10−4	4.8700 × 10−5
	Cosine_3	8.7106 × 10−14	4.3784 × 10−11	6.6558 × 10−12	1.0409 × 10−11	Cosine_3	1.1137 × 10−5	1.2211 × 10−4	4.6150 × 10−5	2.7857 × 10−5
	Cosine_4	1.7511 × 10−13	4.2184 × 10−10	3.9035 × 10−11	8.5768 × 10−11	Cosine_4	1.6561 × 10−5	4.1825 × 10−4	8.5160 × 10−5	7.5082 × 10−5
${\mathit{f}}_{\mathbf{4}}$	Straight_1	3.8707 × 101	2.0746 × 102	9.2469 × 101	4.2467 × 101	Straight_1	7.4364 × 103	1.5798 × 104	1.2838 × 104	2.0788 × 103
	Straight_2	2.9107 × 101	2.9786 × 102	7.7546 × 101	5.2474 × 101	Straight_2	6.1981 × 103	1.2256 × 104	9.9557 × 103	1.5833 × 103
	Threshold_1	2.5223 × 101	2.4305 × 102	6.8420 × 101	4.2239 × 101	Threshold_1	1.2769 × 104	2.1277 × 104	1.6990 × 104	2.1766 × 103
	Threshold_2	8.2738 × 101	4.8897 × 102	2.4674 × 102	1.0081 × 102	Threshold_2	7.0477 × 103	1.6115 × 104	1.0330 × 104	1.9585 × 103
	Threshold_3	1.6962 × 102	7.4402 × 102	3.4890 × 102	1.5861 × 102	Threshold_3	7.9459 × 103	2.0032 × 104	1.3965 × 104	2.6464 × 103
	Threshold_4	1.5038 × 101	1.5980 × 102	6.0249 × 101	3.5686 × 101	Threshold_4	8.9389 × 103	1.9386 × 104	1.3070 × 104	2.9327 × 103
	Exponential_1	5.2571 × 101	3.3140 × 102	1.7427 × 102	7.7406 × 101	Exponential_1	7.8519 × 103	1.5283 × 104	1.1462 × 104	2.1096 × 103
	Exponential_2	3.7816 × 101	2.9649 × 102	1.4459 × 102	6.2181 × 101	Exponential_2	4.6763 × 103	1.3135 × 104	8.6301 × 103	1.9698 × 103
	Exponential_3	9.1368 × 101	7.9952 × 102	3.4719 × 102	1.6819 × 102	Exponential_3	8.0589 × 103	1.7800 × 104	1.1645 × 104	2.4428 × 103
	Exponential_4	5.2605 × 101	6.6496 × 102	2.5585 × 102	1.3827 × 102	Exponential_4	6.8390 × 103	1.4895 × 104	9.8522 × 103	1.6440 × 103
	Exponential_5	1.9773 × 102	1.0629 × 103	5.5626 × 102	2.1853 × 102	Exponential_5	7.2667 × 103	1.7819 × 104	1.2364 × 104	2.4484 × 103
	Exponential_6	1.1519 × 102	1.1733 × 103	5.4639 × 102	2.6598 × 102	Exponential_6	7.0572 × 103	1.4985 × 104	1.0313 × 104	1.8035 × 103
	Cosine_1	2.2677 × 101	1.6215 × 102	8.4233 × 101	3.8116 × 101	Cosine_1	8.5285 × 103	1.6216 × 104	1.1657 × 104	2.0568 × 103
	Cosine_2	3.5648 × 101	2.5791 × 102	1.0386 × 102	4.7531 × 101	Cosine_2	7.3675 × 103	1.6256 × 104	1.1952 × 104	2.1374 × 103
	Cosine_3	3.9845 × 101	2.5401 × 102	1.0903 × 102	5.1737 × 101	Cosine_3	8.7901 × 103	1.5058 × 104	1.2176 × 104	1.5990 × 103
	Cosine_4	4.0827 × 101	1.9696 × 102	9.1923 × 101	4.1878 × 101	Cosine_4	8.2399 × 103	1.4967 × 104	1.1576 × 104	1.6474 × 103
${\mathit{f}}_{\mathbf{5}}$	Straight_1	1.2321 × 10−2	2.7805 × 10−1	1.0051 × 10−1	6.7510 × 10−2	Straight_1	4.1360 × 10−6	3.5617 × 10−1	1.0453 × 10−1	9.3265 × 10−2
	Straight_2	0.0000	2.0030 × 10−1	4.1983 × 10−2	4.2581 × 10−2	Straight_2	5.1016 × 10−8	6.3390 × 10−2	1.1625 × 10−2	1.5055 × 10−2
	Threshold_1	1.7855 × 10−8	2.6377 × 10−1	9.8336 × 10−2	6.8880 × 10−2	Threshold_1	8.8364 × 10−4	2.8092 × 10−1	7.3770 × 10−2	6.8845 × 10−2
	Threshold_2	0.0000	1.8867 × 10−1	4.0923 × 10−2	4.6115 × 10−2	Threshold_2	1.4433 × 10−15	9.4723 × 10−2	1.7078 × 10−2	2.3582 × 10−2
	Threshold_3	3.6320 × 10−6	2.2197 × 10−1	1.1814 × 10−1	6.0107 × 10−2	Threshold_3	1.3545 × 10−14	3.6928 × 10−1	1.0457 × 10−1	9.8452 × 10−2
	Threshold_4	6.6613 × 10−16	8.0817 × 10−2	3.1209 × 10−2	2.3482 × 10−2	Threshold_4	1.7774 × 10−5	3.6827 × 10−2	9.0876 × 10−3	9.4618 × 10−3
	Exponential_1	0.0000	2.4379 × 10−1	7.9307 × 10−2	5.8015 × 10−2	Exponential_1	2.4888 × 10−9	4.4986 × 10−1	1.2518 × 10−1	9.4176 × 10−2
	Exponential_2	0.0000	1.7609 × 10−1	4.5556 × 10−2	4.1760 × 10−2	Exponential_2	3.5352 × 10−11	4.8906 × 10−2	6.4754 × 10−3	9.8313 × 10−3
	Exponential_3	4.2099 × 10−10	3.2955 × 10−1	1.1643 × 10−1	8.0421 × 10−2	Exponential_3	3.6280 × 10−12	3.2945 × 10−1	1.0033 × 10−1	9.5541 × 10−2
	Exponential_4	0.0000	2.0253 × 10−1	4.8723 × 10−2	4.6463 × 10−2	Exponential_4	8.5154 × 10−14	1.6488 × 10−1	1.2543 × 10−2	3.0277 × 10−2
	Exponential_5	8.8818 × 10−16	2.5708 × 10−1	8.4472 × 10−2	6.4674 × 10−2	Exponential_5	1.2990 × 10−14	4.9613 × 10−1	1.2331 × 10−1	1.0636 × 10−1
	Exponential_6	0.0000	1.6595 × 10−1	4.9137 × 10−2	3.9865 × 10−2	Exponential_6	2.2204 × 10−16	8.3124 × 10−2	1.2513 × 10−2	1.8702 × 10−2
	Cosine_1	0.0000	1.4149 × 10−1	4.2637 × 10−2	4.3674 × 10−2	Cosine_1	8.3748 × 10−10	5.4050 × 10−2	1.0821 × 10−2	1.5102 × 10−2
	Cosine_2	1.6653 × 10−15	3.3647 × 10−1	1.1985 × 10−1	8.0014 × 10−2	Cosine_2	6.3283 × 10−8	4.0323 × 10−1	9.7344 × 10−2	9.0742 × 10−2
	Cosine_3	0.0000	1.3191 × 10−1	5.2162 × 10−2	3.7768 × 10−2	Cosine_3	2.6663 × 10−9	1.7983 × 10−1	3.1360 × 10−2	4.5413 × 10−2
	Cosine_4	1.1102 × 10−16	2.7598 × 10−1	9.9773 × 10−2	6.7164 × 10−2	Cosine_4	1.6227 × 10−8	2.4487 × 10−1	5.5685 × 10−2	6.5963 × 10−2
${\mathit{f}}_{\mathbf{6}}$	Straight_1	4.4632 × 10−9	2.1372 × 10−7	3.9100 × 10−8	4.0940 × 10−8	Straight_1	9.1269 × 10−4	3.1804 × 10−3	1.6518 × 10−3	5.3523 × 10−4
	Straight_2	3.7761 × 10−12	8.6966 × 10−10	1.0236 × 10−10	2.0891 × 10−10	Straight_2	4.2112 × 10−5	3.8837 × 10−4	1.1886 × 10−4	7.9706 × 10−5
	Threshold_1	9.1029 × 10−7	8.0166 × 10−6	2.4129 × 10−6	1.5101 × 10−6	Threshold_1	1.2113 × 10−2	2.5585 × 10−2	1.9902 × 10−2	3.4669 × 10−3
	Threshold_2	7.4163 × 10−14	6.3549 × 10−13	1.6938 × 10−13	1.0610 × 10−13	Threshold_2	1.7921 × 10−9	6.5055 × 10−8	1.2631 × 10−8	1.2902 × 10−8
	Threshold_3	1.0014 × 10−12	5.2655 × 10−10	6.8025 × 10−11	1.2657 × 10−10	Threshold_3	2.5582 × 10−8	1.5023 × 10−6	2.2886 × 10−7	2.7137 × 10−7
	Threshold_4	1.4622 × 10−9	2.7494 × 10−7	3.1953 × 10−8	4.9739 × 10−8	Threshold_4	5.3312 × 10−4	3.8584 × 10−3	1.5894 × 10−3	7.9124 × 10−4
	Exponential_1	1.8744 × 10−11	4.9544 × 10−9	4.4463 × 10−10	8.7649 × 10−10	Exponential_1	1.7624 × 10−5	9.1723 × 10−5	4.3472 × 10−5	1.7983 × 10−5
	Exponential_2	1.1324 × 10−13	4.9805 × 10−12	9.3889 × 10−13	1.1256 × 10−12	Exponential_2	6.4716 × 10−7	6.8428 × 10−6	2.1846 × 10−6	1.3670 × 10−6
	Exponential_3	4.9338 × 10−13	5.5745 × 10−11	6.6129 × 10−12	1.1049 × 10−11	Exponential_3	6.0042 × 10−7	6.0591 × 10−6	2.4126 × 10−6	1.5002 × 10−6
	Exponential_4	7.4163 × 10−14	1.1862 × 10−12	1.7826 × 10−13	1.9564 × 10−13	Exponential_4	3.8729 × 10−8	3.1068 × 10−7	1.2811 × 10−7	6.7689 × 10−8
	Exponential_5	1.5588 × 10−13	4.0887 × 10−12	8.2758 × 10−13	8.0931 × 10−13	Exponential_5	3.9803 × 10−8	5.7158 × 10−7	1.4832 × 10−7	1.2402 × 10−7
	Exponential_6	4.9294 × 10−14	2.2338 × 10−13	9.6308 × 10−14	3.4392 × 10−14	Exponential_6	1.0897 × 10−9	2.9882 × 10−8	9.3030 × 10−9	7.9441 × 10−9
	Cosine_1	1.1506 × 10−12	9.2267 × 10−11	2.2030 × 10−11	2.6803 × 10−11	Cosine_1	2.3571 × 10−6	1.0218 × 10−4	1.8274 × 10−5	1.7509 × 10−5
	Cosine_2	1.7620 × 10−10	5.8307 × 10−8	6.5754 × 10−9	1.2324 × 10−8	Cosine_2	6.1209 × 10−5	5.0676 × 10−4	1.8226 × 10−4	1.1078 × 10−4
	Cosine_3	5.0302 × 10−12	7.4329 × 10−10	1.1653 × 10−10	1.6314 × 10−10	Cosine_3	8.4419 × 10−6	8.5649 × 10−5	2.7943 × 10−5	1.8587 × 10−5
	Cosine_4	7.7018 × 10−12	5.7757 × 10−9	5.7647 × 10−10	1.2234 × 10−9	Cosine_4	2.9068 × 10−5	1.9156 × 10−4	6.7917 × 10−5	4.2305 × 10−5
${\mathit{f}}_{\mathbf{7}}$	Straight_1	9.3515 × 10−3	2.2089 × 101	1.0089 × 101	8.7452	Straight_1	1.1325	5.6386 × 102	1.0620 × 102	1.2570 × 102
	Straight_2	8.6741 × 10−3	5.1406 × 102	4.4419 × 101	9.3454 × 101	Straight_2	1.0018 × 102	6.9565 × 102	2.6307 × 102	1.3802 × 102
	Threshold_1	7.9026 × 10−2	4.7147 × 102	2.5678 × 101	8.3161 × 101	Threshold_1	3.4344 × 101	2.3308 × 103	3.2695 × 102	5.9498 × 102
	Threshold_2	1.4559 × 10−3	6.1627 × 102	8.4192 × 101	1.6666 × 102	Threshold_2	1.1503 × 102	5.1947 × 102	2.3270 × 102	9.2809 × 101
	Threshold_3	4.4533 × 10−2	3.9917 × 102	3.9657 × 101	9.6881 × 101	Threshold_3	5.6804 × 10−2	1.1562 × 103	6.1559 × 101	2.0554 × 102
	Threshold_4	1.5343 × 10−3	1.6611 × 102	3.2721 × 101	4.3985 × 101	Threshold_4	1.8240 × 102	7.1746 × 102	2.8865 × 102	1.1583 × 102
	Exponential_1	8.0795 × 10−4	2.2094 × 101	1.2282 × 101	8.8145	Exponential_1	2.3784 × 10−1	1.2901 × 103	1.0700 × 102	2.5169 × 102
	Exponential_2	1.2988 × 10−2	2.2802 × 102	4.6231 × 101	5.4244 × 101	Exponential_2	1.1174 × 102	6.4584 × 102	2.2362 × 102	9.2963 × 101
	Exponential_3	5.6146 × 10−3	9.7058 × 102	5.8068 × 101	1.8542 × 102	Exponential_3	4.0212 × 10−2	1.0768 × 103	1.0022 × 102	2.1852 × 102
	Exponential_4	5.5288 × 10−3	9.3064 × 101	2.6240 × 101	3.2270 × 101	Exponential_4	7.6558 × 101	2.8626 × 102	2.0961 × 102	5.1587 × 101
	Exponential_5	2.7747 × 10−3	1.6422 × 103	1.3893 × 102	3.7163 × 102	Exponential_5	1.2275 × 10−3	1.5623 × 103	9.0305 × 101	2.8689 × 102
	Exponential_6	1.2831 × 10−5	4.9205 × 102	4.0422 × 101	9.0413 × 101	Exponential_6	5.8594 × 101	6.3056 × 102	2.1990 × 102	9.4453 × 101
	Cosine_1	1.8015 × 10−3	1.3748 × 102	2.9047 × 101	3.8603 × 101	Cosine_1	1.0997 × 102	1.2606 × 103	2.6362 × 102	2.0716 × 102
	Cosine_2	4.4398 × 10−3	5.3878 × 102	3.6644 × 101	1.0520 × 102	Cosine_2	8.8583 × 10−1	1.6674 × 103	1.5580 × 102	3.2284 × 102
	Cosine_3	1.1943 × 10−1	3.6476 × 102	3.5174 × 101	6.8477 × 101	Cosine_3	1.4076 × 102	1.7107 × 103	3.5751 × 102	3.8108 × 102
	Cosine_4	8.0777 × 10−3	8.0590 × 101	1.4814 × 101	1.8135 × 101	Cosine_4	1.0177	1.7477 × 103	1.9765 × 102	3.2461 × 102
${\mathit{f}}_{\mathbf{8}}$	Straight_1	3.1974 × 10−14	3.3089 × 10−7	1.1716 × 10−8	5.9285 × 10−8	Straight_1	2.0388 × 10−3	3.3216	6.6242 × 10−1	8.8988 × 10−1
	Straight_2	0.0000	3.5527 × 10−15	5.9212 × 10−16	1.1543 × 10−15	Straight_2	1.9115 × 10−7	2.9849	3.9804 × 10−1	7.9594 × 10−1
	Threshold_1	3.6512 × 10−10	2.1702 × 10−7	4.1154 × 10−8	6.3766 × 10−8	Threshold_1	2.2994	8.4160	5.4959	1.4385
	Threshold_2	0.0000	0.0000	0.0000	0.0000	Threshold_2	1.4211 × 10−14	1.9899	1.9909 × 10−1	4.7366 × 10−1
	Threshold_3	0.0000	9.9496 × 10−1	6.6407 × 10−2	2.4817 × 10−1	Threshold_3	3.2097 × 10−10	1.9918	4.5307 × 10−1	6.0607 × 10−1
	Threshold_4	0.0000	8.8285 × 10−13	1.0646 × 10−13	2.0045 × 10−13	Threshold_4	9.9507 × 10−1	7.9637	3.2612	1.7811
	Exponential_1	5.3291 × 10−15	7.1937 × 10−8	9.0557 × 10−9	2.0970 × 10−8	Exponential_1	6.3110 × 10−6	9.9714 × 10−1	1.4900 × 10−1	3.3483 × 10−1
	Exponential_2	0.0000	1.7764 × 10−15	1.7764 × 10−16	5.3291 × 10−16	Exponential_2	1.1186 × 10−10	9.9496 × 10−1	9.9549 × 10−2	2.9847 × 10−1
	Exponential_3	0.0000	6.4209 × 10−6	3.3419 × 10−7	1.2242 × 10−6	Exponential_3	3.5170 × 10−8	5.9362 × 10−1	2.7729 × 10−2	1.0943 × 10−1
	Exponential_4	0.0000	1.9899	9.9496 × 10−2	3.9382 × 10−1	Exponential_4	1.3145 × 10−13	9.9496 × 10−1	9.9497 × 10−2	2.9849 × 10−1
	Exponential_5	0.0000	9.9496 × 10−1	9.9534 × 10−2	2.9848 × 10−1	Exponential_5	1.9582 × 10−10	1.0029	1.3296 × 10−1	3.3892 × 10−1
	Exponential_6	0.0000	2.6645 × 10−14	1.0066 × 10−15	4.7815 × 10−15	Exponential_6	1.0658 × 10−14	1.9899	6.6332 × 10−2	3.5720 × 10−1
	Cosine_1	0.0000	4.7731 × 10−10	1.5911 × 10−11	8.5680 × 10−11	Cosine_1	4.0101 × 10−7	2.9978	6.8374 × 10−1	8.4558 × 10−1
	Cosine_2	0.0000	8.7041 × 10−14	1.0836 × 10−14	1.6641 × 10−14	Cosine_2	7.9506 × 10−7	1.9900	9.2880 × 10−1	7.2337 × 10−1
	Cosine_3	0.0000	4.4409 × 10−13	2.6053 × 10−14	8.0975 × 10−14	Cosine_3	9.6632 × 10−6	2.0318	6.9709 × 10−1	6.1734 × 10−1
	Cosine_4	0.0000	7.4181 × 10−9	3.8545 × 10−10	1.4870 × 10−9	Cosine_4	3.2724 × 10−5	2.9858	7.9728 × 10−1	8.2825 × 10−1
${\mathit{f}}_{\mathbf{9}}$	Straight_1	3.8183 × 10−4	3.8184 × 10−4	3.8184 × 10−4	2.3807 × 10−9	Straight_1	8.5055 × 10−3	2.7732 × 101	1.5810	5.5711
	Straight_2	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	1.5953 × 10−13	Straight_2	1.2731 × 10−3	1.3293 × 10−3	1.2773 × 10−3	1.0150 × 10−5
	Threshold_1	3.8183 × 10−4	3.8229 × 10−4	3.8190 × 10−4	9.3441 × 10−8	Threshold_1	6.0293 × 10−1	1.3343 × 102	1.6668 × 101	3.6662 × 101
	Threshold_2	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	1.3763 × 10−13	Threshold_2	1.2728 × 10−3	1.2728 × 10−3	1.2728 × 10−3	1.4537 × 10−9
	Threshold_3	3.8183 × 10−4	4.0474 × 10−4	3.8314 × 10−4	4.2676 × 10−6	Threshold_3	1.2728 × 10−3	1.1844 × 102	4.6076	2.1276 × 101
	Threshold_4	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	2.0629 × 10−12	Threshold_4	1.3933 × 10−3	1.1844 × 102	7.9095	2.9541 × 101
	Exponential_1	3.8183 × 10−4	1.5644 × 10−4	4.2241 × 10−4	2.1212 × 10−4	Exponential_1	1.2781 × 10−3	1.7045 × 10−2	2.7552 × 10−3	3.2908 × 10−3
	Exponential_2	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	1.4555 × 10−13	Exponential_2	1.2728 × 10−3	1.2728 × 10−3	1.2728 × 10−3	4.9514 × 10−9
	Exponential_3	3.8183 × 10−4	3.9497 × 10−4	3.8261 × 10−4	2.8259 × 10−6	Exponential_3	1.2728 × 10−3	4.6522 × 10−3	1.4855 × 10−3	6.7891 × 10−4
	Exponential_4	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	1.6171 × 10−13	Exponential_4	1.2728 × 10−3	1.3827 × 10−3	1.2764 × 10−3	1.9734 × 10−5
	Exponential_5	3.8183 × 10−4	4.2990 × 10−4	3.8366 × 10−4	8.6277 × 10−6	Exponential_5	1.2728 × 10−3	1.1844 × 102	6.9547	2.6270 × 101
	Exponential_6	3.8183 × 10−4	1.1844 × 102	3.9483	2.1260 × 101	Exponential_6	1.2728 × 10−3	1.2730 × 10−3	1.2728 × 10−3	4.1256 × 10−8
	Cosine_1	3.8183 × 10−4	3.8231 × 10−4	3.8184 × 10−4	8.6835 × 10−8	Cosine_1	1.2728 × 10−3	1.1844 × 102	4.1934	2.1251 × 101
	Cosine_2	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	5.5438 × 10−13	Cosine_2	1.2765 × 10−3	1.4798 × 10−3	1.3277 × 10−3	5.8337 × 10−5
	Cosine_3	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	8.8412 × 10−13	Cosine_3	1.2731 × 10−3	1.5879 × 10−3	1.3274 × 10−3	8.8845 × 10−5
	Cosine_4	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	3.6890 × 10−13	Cosine_4	1.2732 × 10−3	4.8779 × 10−2	3.7520 × 10−3	8.8272 × 10−3
${\mathit{f}}_{\mathbf{10}}$	Straight_1	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.0008 × 10−13	Straight_1	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.1952 × 10−5
	Straight_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	7.3385 × 10−14	Straight_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.4478 × 10−6
	Threshold_1	−4.5000 × 102	−4.4999 × 102	−4.4999 × 102	8.3459 × 10−12	Threshold_1	−4.5000 × 102	−4.4999 × 102	−4.4999 × 102	1.7050 × 10−3
	Threshold_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	6.3128 × 10−14	Threshold_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	2.4117 × 10−13
	Threshold_3	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	9.7356 × 10−14	Threshold_3	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	4.6932 × 10−13
	Threshold_4	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.9443 × 10−13	Threshold_4	−4.5000 × 102	−4.4999 × 102	−4.4999 × 102	9.0431 × 10−5
	Exponential_1	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	7.4115 × 10−14	Exponential_1	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.1789 × 10−8
	Exponential_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	5.4916 × 10−14	Exponential_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	4.2493 × 10−10
	Exponential_3	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	7.4838 × 10−14	Exponential_3	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	2.2269 × 10−10
	Exponential_4	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	6.8841 × 10−14	Exponential_4	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.5991 × 10−12
	Exponential_5	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	7.3385 × 10−14	Exponential_5	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	5.9672 × 10−13
	Exponential_6	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	7.1149 × 10−14	Exponential_6	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	2.8686 × 10−13
	Cosine_1	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	9.0475 × 10−14	Cosine_1	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.9650 × 10−8
	Cosine_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	9.0475 × 10−14	Cosine_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.1307 × 10−6
	Cosine_3	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	8.3025 × 10−14	Cosine_3	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	2.3531 × 10−7
	Cosine_4	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	8.5580 × 10−14	Cosine_4	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	1.5911 × 10−7
${\mathit{f}}_{\mathbf{11}}$	Straight_1	−4.2165 × 102	−1.3296 × 102	−3.0000 × 102	7.4536 × 101	Straight_1	1.1767 × 104	2.3516 × 104	1.6891 × 104	3.1744 × 103
	Straight_2	−4.3444 × 102	−1.0722 × 102	−3.2701 × 102	8.4417 × 101	Straight_2	8.4226 × 103	1.8619 × 104	1.2552 × 104	2.2028 × 103
	Threshold_1	−4.0106 × 102	−1.4896 × 102	−3.3088 × 102	5.8709 × 101	Threshold_1	1.5199 × 104	2.8379 × 104	2.1552 × 104	3.2507 × 103
	Threshold_2	−3.4901 × 102	2.5368 × 102	−6.2125 × 101	1.5696 × 102	Threshold_2	8.7977 × 103	1.7870 × 104	1.3695 × 104	2.2976 × 103
	Threshold_3	−3.3390 × 102	9.3989 × 102	1.2263 × 102	3.1892 × 102	Threshold_3	1.2026 × 104	3.1616 × 104	2.1121 × 104	4.5467 × 103
	Threshold_4	−4.4289 × 102	−2.5392 × 102	−3.7419 × 102	4.4269 × 101	Threshold_4	9.0435 × 103	2.5277 × 104	1.6287 × 104	3.1871 × 103
	Exponential_1	−3.1846 × 102	2.1908 × 102	−9.9376 × 101	1.4315 × 102	Exponential_1	1.0395 × 104	2.1639 × 104	1.5861 × 104	3.1550 × 103
	Exponential_2	−3.8982 × 102	3.1632 × 102	−1.6371 × 102	1.6523 × 102	Exponential_2	6.9718 × 103	1.7181 × 104	1.1471 × 104	2.4981 × 103
	Exponential_3	−3.0139 × 102	2.1120 × 103	1.5585 × 102	4.5585 × 102	Exponential_3	1.2034 × 104	2.4924 × 104	1.7356 × 104	2.6542 × 103
	Exponential_4	−3.3706 × 102	2.7787 × 102	−5.1714 × 101	1.6504 × 102	Exponential_4	8.1868 × 103	1.8387 × 104	1.2757 × 104	2.9393 × 103
	Exponential_5	−2.5225 × 102	1.5514 × 103	5.6252 × 102	4.1866 × 102	Exponential_5	1.2930 × 104	2.3952 × 104	1.8058 × 104	2.9540 × 103
	Exponential_6	−2.8287 × 102	9.9251 × 102	2.6238 × 102	3.3327 × 102	Exponential_6	9.7956 × 103	2.0311 × 104	1.3953 × 104	2.4149 × 103
	Cosine_1	−4.1764 × 102	−1.8561 × 101	−2.6591 × 102	9.4610 × 101	Cosine_1	9.0379 × 103	2.5832 × 104	1.5303 × 104	3.5867 × 103
	Cosine_2	−4.2366 × 102	−4.9167 × 101	−2.7333 × 102	9.0290 × 101	Cosine_2	1.2007 × 104	2.5142 × 104	1.7464 × 104	3.3184 × 103
	Cosine_3	−4.2193 × 102	8.5517 × 101	−2.2015 × 102	1.2019 × 102	Cosine_3	1.0444 × 104	2.0965 × 104	1.4526 × 104	2.5147 × 103
	Cosine_4	−4.0935 × 102	4.8281 × 101	−2.5462 × 102	1.2357 × 102	Cosine_4	1.0484 × 104	2.3679 × 104	1.6049 × 104	3.3138 × 103
${\mathit{f}}_{\mathbf{12}}$	Straight_1	−1.7895 × 102	−1.7527 × 102	−1.7807 × 102	9.8257 × 10−1	Straight_1	−1.5655 × 102	−9.8500 × 101	−1.3288 × 102	1.5417 × 101
	Straight_2	−1.7894 × 102	−1.7562 × 102	−1.7821 × 102	7.6813 × 10−1	Straight_2	−1.6750 × 102	−1.2621 × 102	−1.4904 × 102	1.1365 × 101
	Threshold_1	−1.7886 × 102	−1.7403 × 102	−1.7782 × 102	1.0687	Threshold_1	−1.3312 × 102	−5.8638 × 101	−9.9192 × 101	2.1166 × 101
	Threshold_2	−1.7891 × 102	−1.7361 × 102	−1.7769 × 102	1.0980	Threshold_2	−1.6995 × 102	−1.2583 × 102	−1.5366 × 102	1.0233 × 101
	Threshold_3	−1.7883 × 102	−1.7150 × 102	−1.7711 × 102	1.4020	Threshold_3	−1.6505 × 102	−1.2822 × 102	−1.4608 × 102	1.0842 × 101
	Threshold_4	−1.7888 × 102	−1.7563 × 102	−1.7812 × 102	7.7099 × 10−1	Threshold_4	−1.6802 × 102	−1.0750 × 102	−1.3614 × 102	1.5041 × 101
	Exponential_1	−1.7881 × 102	−1.7636 × 102	−1.7781 × 102	7.2018 × 10−1	Exponential_1	−1.6142 × 102	−1.1356 × 102	−1.4376 × 102	1.2858 × 101
	Exponential_2	−1.7883 × 102	−1.7565 × 102	−1.7788 × 102	9.6280 × 10−1	Exponential_2	−1.6950 × 102	−1.4032 × 102	−1.5798 × 102	6.6526
	Exponential_3	−1.7909 × 102	−1.7556 × 102	−1.7747 × 102	9.0208 × 10−1	Exponential_3	−1.6515 × 102	−1.2713 × 102	−1.5275 × 102	9.8056
	Exponential_4	−1.7890 × 102	−1.7505 × 102	−1.7780 × 102	8.8838 × 10−1	Exponential_4	−1.7101 × 102	−1.4042 × 102	−1.5931 × 102	7.7148
	Exponential_5	−1.7882 × 102	−1.7400 × 102	−1.7725 × 102	1.2914	Exponential_5	−1.7364 × 102	−1.2751 × 102	−1.5552 × 102	1.0491 × 101
	Exponential_6	−1.7892 × 102	−1.7468 × 102	−1.7757 × 102	1.0984	Exponential_6	−1.7066 × 102	−1.4082 × 102	−1.6037 × 102	6.8764
	Cosine_1	−1.7889 × 102	−1.7626 × 102	−1.7804 × 102	6.7941 × 10−1	Cosine_1	−1.7102 × 102	−9.7261 × 101	−1.4361 × 102	1.5506 × 101
	Cosine_2	−1.7888 × 102	−1.7610 × 102	−1.7807 × 102	6.4727 × 10−1	Cosine_2	−1.6466 × 102	−1.1821 × 102	−1.4021 × 102	1.3072 × 101
	Cosine_3	−1.7891 × 102	−1.7571 × 102	−1.7791 × 102	8.9066 × 10−1	Cosine_3	−1.6130 × 102	−1.1206 × 102	−1.4392 × 102	1.3861 × 101
	Cosine_4	−1.7873 × 102	−1.7465 × 102	−1.7780 × 102	8.3139 × 10−1	Cosine_4	−1.6327 × 102	−1.0337 × 102	−1.3840 × 102	1.5854 × 101
${\mathit{f}}_{\mathbf{13}}$	Straight_1	3.9000 × 102	4.5949 × 102	3.9958 × 102	1.3088 × 101	Straight_1	3.9280 × 102	3.6620 × 103	5.7871 × 102	5.8225 × 102
	Straight_2	3.9002 × 102	4.8656 × 102	4.0653 × 102	2.5520 × 101	Straight_2	5.5729 × 102	2.9468 × 103	8.3659 × 102	5.4759 × 102
	Threshold_1	3.9007 × 102	4.0876 × 102	3.9979 × 102	7.3298	Threshold_1	4.2763 × 102	3.9501 × 103	8.1099 × 102	8.3480 × 102
	Threshold_2	3.9000 × 102	7.9400 × 102	4.2759 × 102	7.5937 × 101	Threshold_2	4.9760 × 102	2.2597 × 103	6.9290 × 102	3.1747 × 102
	Threshold_3	3.9012 × 102	6.7882 × 102	4.0955 × 102	5.0771 × 101	Threshold_3	3.9002 × 102	2.8846 × 103	8.5966 × 102	7.8665 × 102
	Threshold_4	3.9000 × 102	4.7366 × 102	4.1236 × 102	3.1291 × 101	Threshold_4	4.8872 × 102	3.5299 × 103	9.3974 × 102	7.2954 × 102
	Exponential_1	3.9001 × 102	7.8965 × 102	4.1481 × 102	7.3227 × 101	Exponential_1	3.9200 × 102	2.8106 × 103	6.1515 × 102	4.9085 × 102
	Exponential_2	3.9007 × 102	7.3063 × 102	4.1744 × 102	6.3802 × 101	Exponential_2	4.7908 × 102	8.1095 × 102	6.1817 × 102	7.2382 × 101
	Exponential_3	3.9000 × 102	9.0772 × 102	4.2429 × 102	9.6564 × 101	Exponential_3	3.9006 × 102	2.9396 × 103	6.9200 × 102	6.6627 × 102
	Exponential_4	3.9013 × 102	5.4184 × 102	4.1655 × 102	3.5768 × 101	Exponential_4	4.8828 × 102	1.1518 × 103	6.4499 × 102	1.5060 × 102
	Exponential_5	3.9000 × 102	1.0517 × 103	4.4257 × 102	1.4997 × 102	Exponential_5	3.9001 × 102	2.7678 × 103	6.7424 × 102	6.4280 × 102
	Exponential_6	3.9004 × 102	4.7407 × 102	4.0836 × 102	2.6488 × 101	Exponential_6	4.6519 × 102	2.0147 × 103	6.5145 × 102	2.8388 × 102
	Cosine_1	3.9000 × 102	6.1903 × 102	4.2205 × 102	4.8758 × 101	Cosine_1	4.5850 × 102	2.3449 × 103	7.1282 × 102	3.4454 × 102
	Cosine_2	3.9002 × 102	8.5583 × 102	4.1202 × 102	8.2736 × 101	Cosine_2	3.9079 × 102	3.2281 × 103	7.6770 × 102	8.2332 × 102
	Cosine_3	3.9010 × 102	8.8341 × 102	4.2415 × 102	8.8994 × 101	Cosine_3	5.1242 × 102	1.8003 × 103	7.3318 × 102	2.8816 × 102
	Cosine_4	3.9001 × 102	4.0870 × 102	3.9875 × 102	7.7194	Cosine_4	3.9074 × 102	1.1216 × 103	5.3644 × 102	1.8263 × 102
${\mathit{f}}_{\mathbf{14}}$	Straight_1	−3.3000 × 102	−3.2999 × 102	−3.2999 × 102	2.3198 × 10−8	Straight_1	−3.2999 × 102	−3.2784 × 102	−3.2924 × 102	7.3617 × 10−1
	Straight_2	−3.3000 × 102	−3.3000 × 102	−3.3000 × 102	6.0514 × 10−14	Straight_2	−3.3000 × 102	−3.2801 × 102	−3.2962 × 102	5.9806 × 10−1
	Threshold_1	−3.3000 × 102	−3.2999 × 102	−3.2999 × 102	1.1729 × 10−7	Threshold_1	−3.2877 × 102	−3.2057 × 102	−3.2511 × 102	1.7985
	Threshold_2	−3.3000 × 102	−3.2901 × 102	−3.2997 × 102	1.7860 × 10−1	Threshold_2	−3.3000 × 102	−3.2901 × 102	−3.2977 × 102	4.2082 × 10−1
	Threshold_3	−3.3000 × 102	−3.2901 × 102	−3.2997 × 102	1.7859 × 10−1	Threshold_3	−3.3000 × 102	−3.2801 × 102	−3.2974 × 102	4.9350 × 10−1
	Threshold_4	−3.3000 × 102	−3.3000 × 102	−3.3000 × 102	1.4154 × 10−13	Threshold_4	−3.3000 × 102	−3.2303 × 102	−3.2718 × 102	1.5641
	Exponential_1	−3.3000 × 102	−3.2999 × 102	−3.2999 × 102	3.0646 × 10−8	Exponential_1	−3.3000 × 102	−3.2897 × 102	−3.2988 × 102	3.1104 × 10−1
	Exponential_2	−3.3000 × 102	−3.3000 × 102	−3.3000 × 102	1.0062 × 10−13	Exponential_2	−3.3000 × 102	−3.2901 × 102	−3.2983 × 102	3.7070 × 10−1
	Exponential_3	−3.3000 × 102	−3.2999 × 102	−3.2999 × 102	1.8858 × 10−6	Exponential_3	−3.3000 × 102	−3.2900 × 102	−3.2990 × 102	2.9728 × 10−1
	Exponential_4	−3.3000 × 102	−3.3000 × 102	−3.3000 × 102	1.0934 × 10−13	Exponential_4	−3.3000 × 102	−3.2901 × 102	−3.2997 × 102	1.7860 × 10−1
	Exponential_5	−3.3000 × 102	−3.2901 × 102	−3.2997 × 102	1.7852 × 10−1	Exponential_5	−3.3000 × 102	−3.2891 × 102	−3.2980 × 102	3.8883 × 10−1
	Exponential_6	−3.3000 × 102	−3.2901 × 102	−3.2997 × 102	1.7860 × 10−1	Exponential_6	−3.3000 × 102	−3.2901 × 102	−3.2987 × 102	3.3822 × 10−1
	Cosine_1	−3.3000 × 102	−3.2999 × 102	−3.2999 × 102	4.0641 × 10−9	Cosine_1	−3.3000 × 102	−3.2777 × 102	−3.2947 × 102	6.9220 × 10−1
	Cosine_2	−3.3000 × 102	−3.3000 × 102	−3.3000 × 102	2.9464 × 10−13	Cosine_2	−3.3000 × 102	−3.2702 × 102	−3.2920 × 102	1.0082
	Cosine_3	−3.3000 × 102	−3.2999 × 102	−3.2999 × 102	1.5012 × 10−11	Cosine_3	−3.3000 × 102	−3.2747 × 102	−3.2933 × 102	7.1582 × 10−1
	Cosine_4	−3.3000 × 102	−3.3000 × 102	−3.3000 × 102	2.0231 × 10−13	Cosine_4	−3.3000 × 102	−3.2701 × 102	−3.2924 × 102	9.1373 × 10−1

and

Table 4. Experimental results of difference HS algorithms.

No.	Dimension (D) = 30						Dimension (D) = 100
	Algorithm	Strategy	Min	Max	Mean	SD	Algorithm	Strategy	Min	Max	Mean	SD
1	HS	–	9.5152 × 10−1	7.2900	3.9526	1.8888	HS	–	9.8221 × 103	1.4318 × 104	1.2247 × 104	1.1304 × 103
	IHS	–	1.8017 × 10−7	4.5253 × 10−7	3.4508 × 10−7	6.9069 × 10−8	IHS	–	9.3279 × 103	1.5282 × 104	1.2496 × 104	1.2772 × 103
	SGHS	–	7.6930 × 10−10	1.5045 × 10−8	5.0535 × 10−9	3.1296 × 10−9	SGHS	–	6.6607 × 10−1	2.7569	1.5343	4.7765 × 10−1
	NGHS	–	1.7413 × 10−17	2.3048 × 10−15	3.4620 × 10−16	4.7004 × 10−16	NGHS	–	3.0447 × 10−4	1.3603 × 10−3	7.4741 × 10−4	2.1074 × 10−4
	DANGHS	Exponential_6	2.3735 × 10−38	3.7601 × 10−30	1.8344 × 10−31	7.0604 × 10−31	DANGHS	Exponential_6	1.6615 × 10−16	8.0332 × 10−14	1.2209 × 10−14	1.9706 × 10−14
2	HS	–	3.0000	1.7000 × 101	9.3000	3.7162	HS	–	8.4840 × 103	1.6381 × 104	1.2242 × 104	1.6586 × 103
	IHS	–	0.0000	3.0000	9.3333 × 10−1	1.0306	IHS	–	1.0060 × 104	1.5588 × 104	1.2560 × 104	1.3116 × 103
	SGHS	–	0.0000	0.0000	0.0000	0.0000	SGHS	–	3.0000	1.8000 × 101	8.7667	3.1271
	NGHS	–	0.0000	0.0000	0.0000	0.0000	NGHS	–	0.0000	0.0000	0.0000	0.0000
	DANGHS	Exponential_2	0.0000	0.0000	0.0000	0.0000	DANGHS	Exponential_2	0.0000	0.0000	0.0000	0.0000
3	HS	–	3.8826 × 10−2	2.1547 × 10−1	8.3000 × 10−2	3.9484 × 10−2	HS	–	5.2475 × 101	6.6253 × 101	6.0705 × 101	4.1892
	IHS	–	1.8454 × 10−3	2.7586 × 10−2	3.1832 × 10−3	4.5541 × 10−3	IHS	–	5.1429 × 101	6.9346 × 101	6.0238 × 101	4.2859
	SGHS	–	1.2406 × 10−4	2.3354 × 10−4	1.6844 × 10−4	2.7009 × 10−5	SGHS	–	6.9687 × 10−2	4.0539 × 10−1	2.2004 × 10−1	7.5524 × 10−2
	NGHS	–	2.8122 × 10−10	4.8894 × 10−9	1.3786 × 10−9	9.1666 × 10−10	NGHS	–	8.0120 × 10−3	1.8302 × 10−2	1.4477 × 10−2	2.3050 × 10−3
	DANGHS	Exponential_6	5.1270 × 10−23	2.5548 × 10−17	1.9511 × 10−18	5.5869 × 10−18	DANGHS	Exponential_6	1.7326 × 10−9	2.2346 × 10−8	7.9778 × 10−9	5.9706 × 10−9
4	HS	–	1.3615 × 103	8.1756 × 103	3.7966 × 103	1.4524 × 103	HS	–	1.2355 × 105	2.2504 × 105	1.8030 × 105	2.0587 × 104
	IHS	–	1.5474 × 103	6.0226 × 103	3.8475 × 103	1.1754 × 103	IHS	–	1.2992 × 105	2.3481 × 105	1.7522 × 105	2.7139 × 104
	SGHS	–	2.0150 × 101	1.0642 × 102	5.2245 × 101	2.2107 × 101	SGHS	–	1.7856 × 104	3.1133 × 104	2.2834 × 104	2.8349 × 103
	NGHS	-	2.8355 × 101	1.4013 × 102	6.5269 × 101	3.3421 × 101	NGHS	–	7.4976 × 103	1.2945 × 104	9.7007 × 103	1.6021 × 103
	DANGHS	Threshold_4	1.5038 × 101	1.5980 × 102	6.0249 × 101	3.5686 × 101	DANGHS	Exponential_2	4.6763 × 103	1.3135 × 104	8.6301 × 103	1.9698 × 103
5	HS	–	1.0212	1.1106	1.0591	2.2096 × 10−2	HS	–	9.5506 × 101	1.4758 × 102	1.1631 × 102	1.1240 × 101
	IHS	–	1.2959 × 10−7	3.4241 × 10−2	7.5274 × 10−3	9.2294 × 10−3	IHS	–	7.5548 × 101	1.4827 × 102	1.0997 × 102	1.4826 × 101
	SGHS	–	1.7833 × 10−2	2.3440 × 10−1	1.0043 × 10−1	5.1304 × 10−2	SGHS	–	4.4296 × 10−1	8.8847 × 10−1	6.8599 × 10−1	9.9379 × 10−2
	NGHS	–	3.3307 × 10−16	2.5387 × 10−1	6.1311 × 10−2	4.9633 × 10−2	NGHS	–	1.5343 × 10−4	9.9663 × 10−2	1.7168 × 10−2	2.2003 × 10−2
	DANGHS	Threshold_4	6.6613 × 10−16	8.0817 × 10−2	3.1209 × 10−2	2.3482 × 10−2	DANGHS	Exponential_2	3.5352 × 10−11	4.8906 × 10−2	6.4754 × 10−3	9.8313 × 10−3
6	HS	-	1.9421 × 10−2	1.3050	4.9617 × 10−1	4.2318 × 10−1	HS	–	1.0882 × 101	1.2567 × 101	1.1743 × 101	3.8517 × 10−1
	IHS	–	3.4980 × 10−4	1.3915	2.2199 × 10−1	3.4543 × 10−1	IHS	–	1.0987 × 101	1.2722 × 101	1.1852 × 101	4.3446 × 10−1
	SGHS	–	1.7703 × 10−5	4.5526 × 10−5	3.0830 × 10−5	6.1683 × 10−6	SGHS	–	6.3791 × 10−2	4.5729 × 10−1	2.4057 × 10−1	1.2018 × 10−1
	NGHS	–	7.7839 × 10−10	2.0025 × 10−8	5.7085 × 10−9	5.2959 × 10−9	NGHS	–	2.6973 × 10−3	5.3184 × 10−3	3.6500 × 10−3	5.4706 × 10−4
	DANGHS	Exponential_6	4.9294 × 10−14	2.2338 × 10−13	9.6308 × 10−14	3.4392 × 10−14	DANGHS	Exponential_6	1.0897 × 10−9	2.9882 × 10−8	9.3030 × 10−9	7.9441 × 10−9
7	HS	–	9.6358 × 101	3.9298 × 102	1.8204 × 102	5.9631 × 101	HS	–	3.2565 × 106	9.1894 × 106	5.9320 × 106	1.2941 × 106
	IHS	-	1.7586 × 101	2.1565 × 103	3.6705 × 102	5.5299 × 102	IHS	–	4.1100 × 106	8.2424 × 106	5.7186 × 106	1.0494 × 106
	SGHS	–	9.0932	2.0293 × 103	1.7534 × 102	3.7957 × 102	SGHS	–	1.0832 × 102	2.8592 × 103	5.1645 × 102	4.7866 × 102
	NGHS	–	6.6756 × 10−4	2.3003 × 102	1.4971 × 101	4.0757 × 101	NGHS	–	2.1179 × 101	1.4411 × 103	2.8501 × 102	2.8532 × 102
	DANGHS	Straight_1	9.3515 × 10−3	2.2089 × 101	1.0089 × 101	8.7452	DANGHS	Threshold_3	5.6804 × 10−2	1.1562 × 103	6.1559 × 101	2.0554 × 102
8	HS	–	3.0572 × 10−2	2.0546	4.6448 × 10−1	6.5390 × 10−1	HS	–	2.1874 × 102	2.8758 × 102	2.5192 × 102	1.6481 × 101
	IHS	–	4.1948 × 10−5	4.5484	1.2420	9.8291 × 10−1	IHS	–	2.0838 × 102	2.8193 × 102	2.4294 × 102	1.8844 × 101
	SGHS	–	3.7300 × 10−7	9.9498 × 10−1	1.3267 × 10−1	3.3822 × 10−1	SGHS	–	3.2260 × 10−2	9.1200	4.5553	2.2588
	NGHS	-	0.0000	1.6069 × 10−11	9.3241 × 10−13	3.2209 × 10−12	NGHS	–	1.2729 × 10−3	1.0102	2.1542 × 10−1	3.9474 × 10−1
	DANGHS	Threshold_2	0.0000	0.0000	0.0000	0.0000	DANGHS	Exponential_3	3.5170 × 10−8	5.9362 × 10−1	2.7729 × 10−2	1.0943 × 10−1
9	HS	–	6.9691	3.8058 × 101	1.8422 × 101	6.8471	HS	–	4.5568 × 103	6.9091 × 103	5.7964 × 103	5.5601 × 102
	IHS	–	3.8186 × 10−4	5.2695 × 10−1	1.7934 × 10−2	9.4522 × 10−2	IHS	–	4.2297 × 103	6.4098 × 103	5.4659 × 103	5.5784 × 102
	SGHS	–	2.3563 × 10−3	3.6545 × 10−2	1.3771 × 10−2	7.5711 × 10−3	SGHS	–	7.2936	3.8640 × 101	1.5981 × 101	7.4744
	NGHS	–	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	5.5493 × 10−13	NGHS	–	3.3819 × 10−3	6.8492 × 10−2	1.1069 × 10−2	1.3684 × 10−2
	DANGHS	Threshold_2	3.8183 × 10−4	3.8183 × 10−4	3.8183 × 10−4	1.3763 × 10−13	DANGHS	Threshold_2	1.2728 × 10−3	1.2728 × 10−3	1.2728 × 10−3	1.4537 × 10−9
10	HS	–	−4.4898 × 102	−4.3989 × 102	−4.4573 × 102	2.2745	HS	–	1.0055 × 104	1.6736 × 104	1.2963 × 104	1.7748 × 103
	IHS	–	−4.5000 × 102	−4.4999 × 102	−4.4999 × 102	1.1657 × 10−7	IHS	–	1.0425 × 104	1.4910 × 104	1.2856 × 104	1.2084 × 103
	SGHS	–	−4.5000 × 102	−4.4999 × 102	−4.4999 × 102	2.7913 × 10−9	SGHS	–	−4.4918 × 102	−4.4701 × 102	−4.4841 × 102	5.8573 × 10−1
	NGHS	–	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	6.9619 × 10−14	NGHS	–	−4.5000 × 102	−4.4999 × 102	−4.4999 × 102	3.0551 × 10−4
	DANGHS	Exponential_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	5.4916 × 10−14	DANGHS	Threshold_2	−4.5000 × 102	−4.5000 × 102	−4.5000 × 102	2.4117 × 10−13
11	HS	–	1.5142 × 103	7.6068 × 103	3.4157 × 103	1.2671 × 103	HS	–	1.4921 × 105	2.5525 × 105	1.9430 × 105	2.3256 × 104
	IHS	–	1.0412 × 103	7.3312 × 103	3.3180 × 103	1.3292 × 103	IHS	–	1.4941 × 105	2.7307 × 105	2.0189 × 105	2.7108 × 104
	SGHS	–	−4.3194 × 102	−3.2048 × 102	−3.9763 × 102	2.7006 × 101	SGHS	–	1.5646 × 104	3.5936 × 104	2.6350 × 104	4.0064 × 103
	NGHS	–	−4.2591 × 102	−1.9340 × 102	−3.3680 × 102	6.4820 × 101	NGHS	–	9.0685 × 103	1.7976 × 104	1.1950 × 104	2.0823 × 103
	DANGHS	Threshold_4	−4.4289 × 102	−2.5392 × 102	−3.7419 × 102	4.4269 × 101	DANGHS	Exponential_2	6.9718 × 103	1.7181 × 104	1.1471 × 104	2.4981 × 103
12	HS	–	−1.7016 × 102	−1.3324 × 102	−1.5876 × 102	9.4348	HS	–	3.2343 × 103	5.9684 × 103	4.7002 × 103	6.7476 × 102
	IHS	–	−1.7607 × 102	−1.3892 × 102	−1.5831 × 102	7.7527	IHS	–	3.4934 × 103	6.5826 × 103	4.8855 × 103	8.4393 × 102
	SGHS	–	−1.7830 × 102	−1.7149 × 102	−1.7583 × 102	1.6385	SGHS	–	−1.3057 × 102	−1.5099 × 101	−7.2944 × 101	2.8794 × 101
	NGHS	–	−1.7913 × 102	−1.7532 × 102	−1.7829 × 102	6.4615 × 10−1	NGHS	–	−1.5784 × 102	−1.1939 × 102	−1.4231 × 102	1.0814 × 101
	DANGHS	Straight_2	−1.7894 × 102	−1.7562 × 102	−1.7821 × 102	7.6813 × 10−1	DANGHS	Exponential_6	−1.7066 × 102	−1.4082 × 102	−1.6037 × 102	6.8764
13	HS	–	4.7650 × 102	2.5184 × 103	6.6765 × 102	3.6290 × 102	HS	–	4.0732 × 106	8.7806 × 106	6.0785 × 106	1.0919 × 106
	IHS	–	4.1262 × 102	1.7487 × 103	5.7845 × 102	2.3203 × 102	IHS	–	4.5479 × 106	8.5517 × 106	6.3527 × 106	1.2268 × 106
	SGHS	–	3.9001 × 102	5.6058 × 102	4.6408 × 102	4.0896 × 101	SGHS	–	6.4618 × 102	2.5249 × 103	9.7963 × 102	4.0336 × 102
	NGHS	–	3.9000 × 102	4.0874 × 102	3.9494 × 102	5.7399	NGHS	–	4.6424 × 102	1.6001 × 103	7.1517 × 102	2.9163 × 102
	DANGHS	Cosine_4	3.9001 × 102	4.0870 × 102	3.9875 × 102	7.7194	DANGHS	Cosine_4	3.9074 × 102	1.1216 × 103	5.3644 × 102	1.8263 × 102
14	HS	–	−3.2997 × 102	−3.2788 × 102	−3.2938 × 102	7.4966 × 10−1	HS	–	−9.3948 × 101	−6.2235	−5.1541 × 101	2.2413 × 101
	IHS	–	−3.2999 × 102	−3.2749 × 102	−3.2897 × 102	6.9697 × 10−1	IHS	–	−1.1215 × 102	−3.3592 × 101	−6.5372 × 101	1.6227 × 101
	SGHS	–	3.9000 × 102	−3.2901 × 102	−3.2993 × 102	2.4813 × 10−1	SGHS	–	−3.2900 × 102	−3.2101 × 102	−3.2614 × 102	2.2502
	NGHS	–	3.9000 × 102	−3.2999 × 102	−3.2999 × 102	1.1444 × 10−12	NGHS	–	3.9000 × 102	−3.2798 × 102	−3.2979 × 102	5.4096 × 10−1
	DANGHS	Straight_2	3.9000 × 102	3.9000 × 102	3.9000 × 102	6.0514 × 10−14	DANGHS	Exponential_4	3.9000 × 102	−3.2901 × 102	−3.2997 × 102	1.7860 × 10−1

, respectively. In the two tables, SD represents the standard deviation.

In Table 3, several experimental results are given. First of all, the best results given by the same strategy for different dimension sizes are obtained for problems 1, 3, 6, 9 and 13. Among these problems, the decreasing strategy can find the best objective function value for problems 1, 3, 6, and 9. According to the experimental results, the exponential decreasing strategy with mr = 0.001 (Exponential_6) can find the best objective function value for problems 1 (1.8344 × 10⁻³¹; 1.2209 × 10⁻¹⁴), 3 (1.9511 × 10⁻¹⁸ 7.9778 × 10⁻⁹) and 6 (9.6308 × 10⁻¹⁴; 9.3030 × 10⁻⁹); the threshold linear prior decreasing strategy (Threshold_2) can find the best objective function value for problem 9 (3.8183 × 10⁻⁴; 1.2728 × 10⁻³). More specifically, the convex cosine strategy with k = 3 (Cosine_4), which is the periodic strategy, can find the best objective function value for problem 13 (3.9875 × 10²; 5.3644 × 10²).

On the other hand, the best results given by different strategies for different dimension sizes are obtained for problems 4, 5, 7, 8, 10, 11, 12, and 14. Among these problems, the increasing strategy can find the best objective function value for problem 7. According to the experimental results, the straight linear increasing strategy (Straight_1) can find the best objective function value for problem 7 with D = 30 (1.0089 × 10¹). However, the threshold linear posterior increasing strategy (Threshold_3) can find the best objective function value for problem 7 with D = 100 (6.1559 × 10¹). Besides, the decreasing strategy can find the best objective function value for problems 4, 5, 10, 11, 12, and 14. According to the experimental results, the threshold linear posterior decreasing strategy (Threshold_4) can find the best objective function value for problems 4 (6.0249 × 10¹), 5 (3.1209 × 10⁻²) and 11 (−3.7419 × 10²) with D = 30. However, the natural exponential decreasing strategy (Exponential_2) can find the best objective function value for problems 4 (8.6301 × 10³), 5 (6.4754 × 10⁻³), and 11 (1.1471 × 10⁴) with D = 100. The natural exponential decreasing strategy (Exponential _2) can find the best objective function value for problem 10 with D = 30 (−4.5000 × 10²). However, the threshold linear prior decreasing strategy (Threshold_2) can find the best objective function value for problem 10 with D = 100 (−4.5000 × 10²). The straight linear decreasing strategy (Straight_2) can find the best objective function value for problem 12 with D = 30 (−1.7821 × 10²). However, the exponential decreasing strategy with $mr$ = 0.001 (Exponential_6) can find the best objective function value for problem 12 with D = 100 (−1.6037 × 10²). The straight linear decreasing strategy (Straight_2) can find the best objective function value for problem 14 with D = 30 (−3.3000 × 10²). However, the exponential decreasing strategy with $mr$ = 0.01 (Exponential_4) can find the best objective function value for problem 14 with D = 100 (−3.2997 × 10²).

Particularly, for problem 8, the decreasing strategy can find the best objective function value when D = 30, however the increasing strategy can find the best objective function value when D = 100. In other words, the threshold linear prior decreasing strategy (Threshold_2) can find the best objective function value for problem 8 with D = 30 (0.0000). However, the exponential increasing strategy with $mr$ = 0.01 (Exponential_3) can find the best objective function value for problem 8 with D = 100 (2.7729 × 10⁻²).

In Table 3, the best results are presented by the boldface type. For example, the Threshold_2 strategy had the best minimum objective function value for problems 1 with D = 30 (7.1381 × 10⁻³⁹). The Exponential_6 strategy had the best maximum objective function value (3.7601 × 10⁻³⁰) and had the minimum standard deviation value (7.0604 × 10⁻³¹) for problems 1 with D = 30.

In Table 4, among all problems for D = 30, the DANGHS algorithm can find the best objective function value for problems 1–3, 6–10, and 14. The SGHS algorithm can find the best objective function value for problems 2, 4, and 11. The NGHS algorithm can find the best objective function value for problems 2, 12, and 13. The IHS algorithm can find the best objective function value for problem 5. The best algorithms and the best results are presented by the boldface type in Table 4.

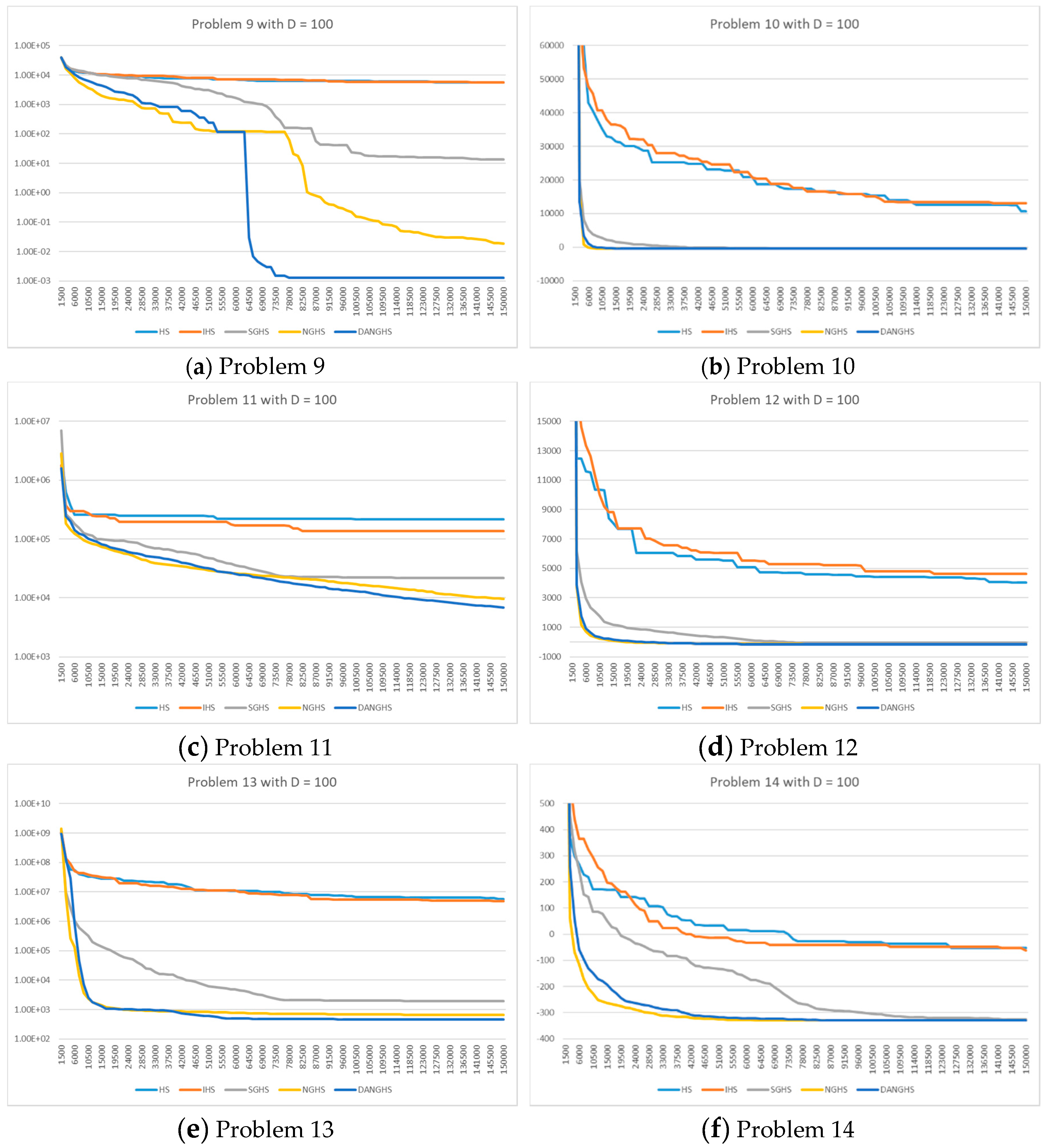
On the other hand, among all problems for D = 100, the DANGHS algorithm can find the best objective function value for problems 1–14. The NGHS algorithm can find the best objective function value for problem 2.

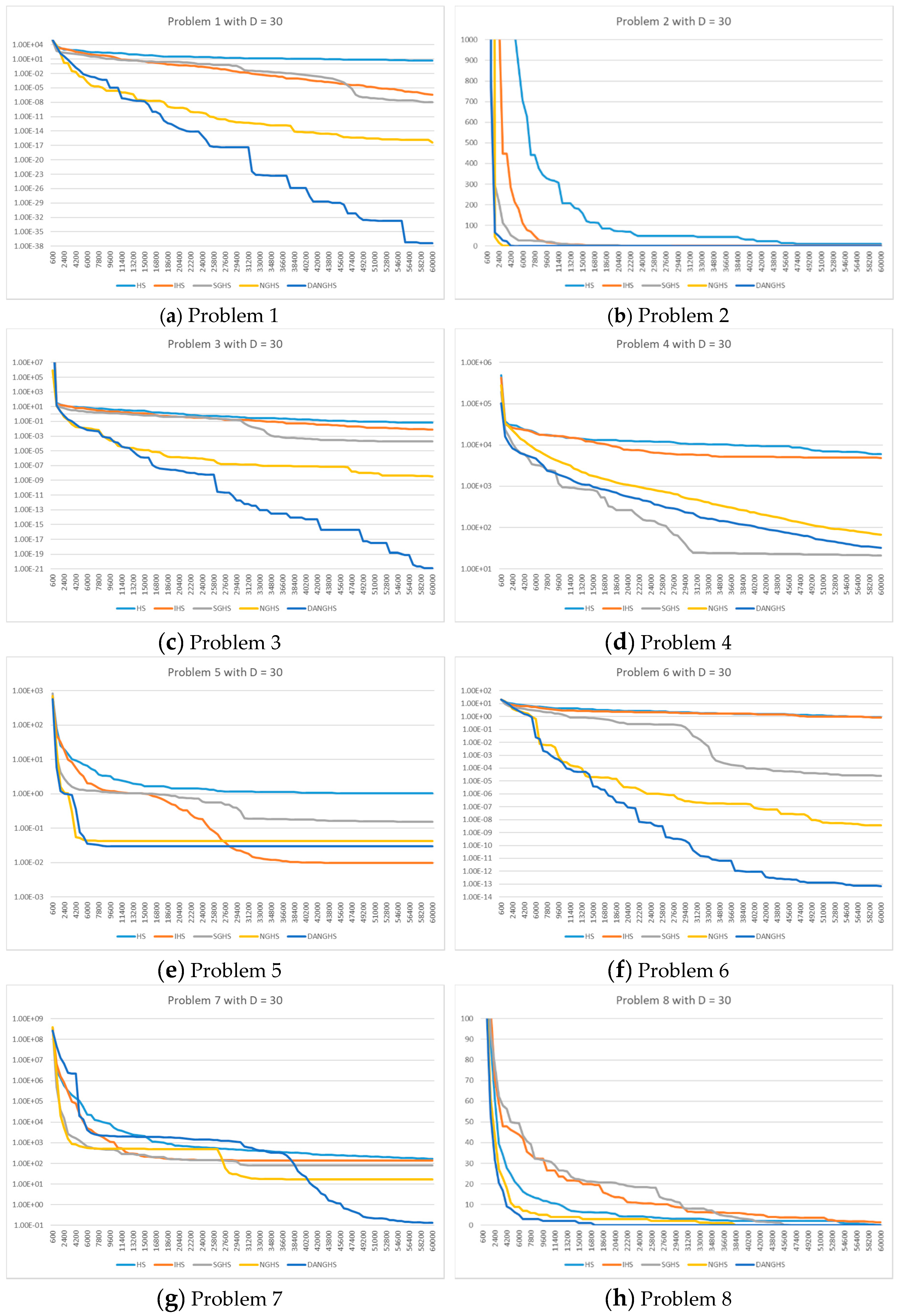
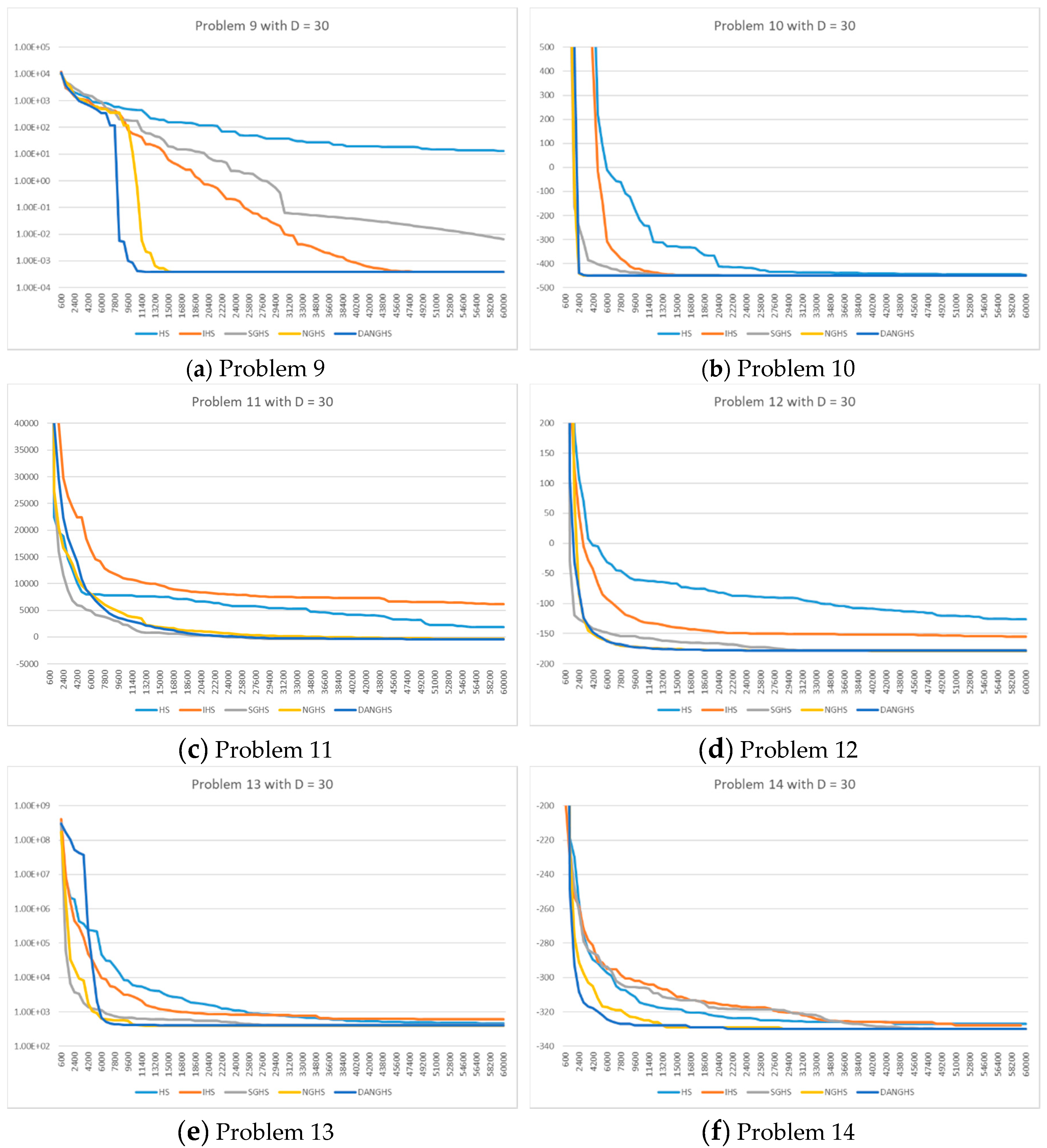
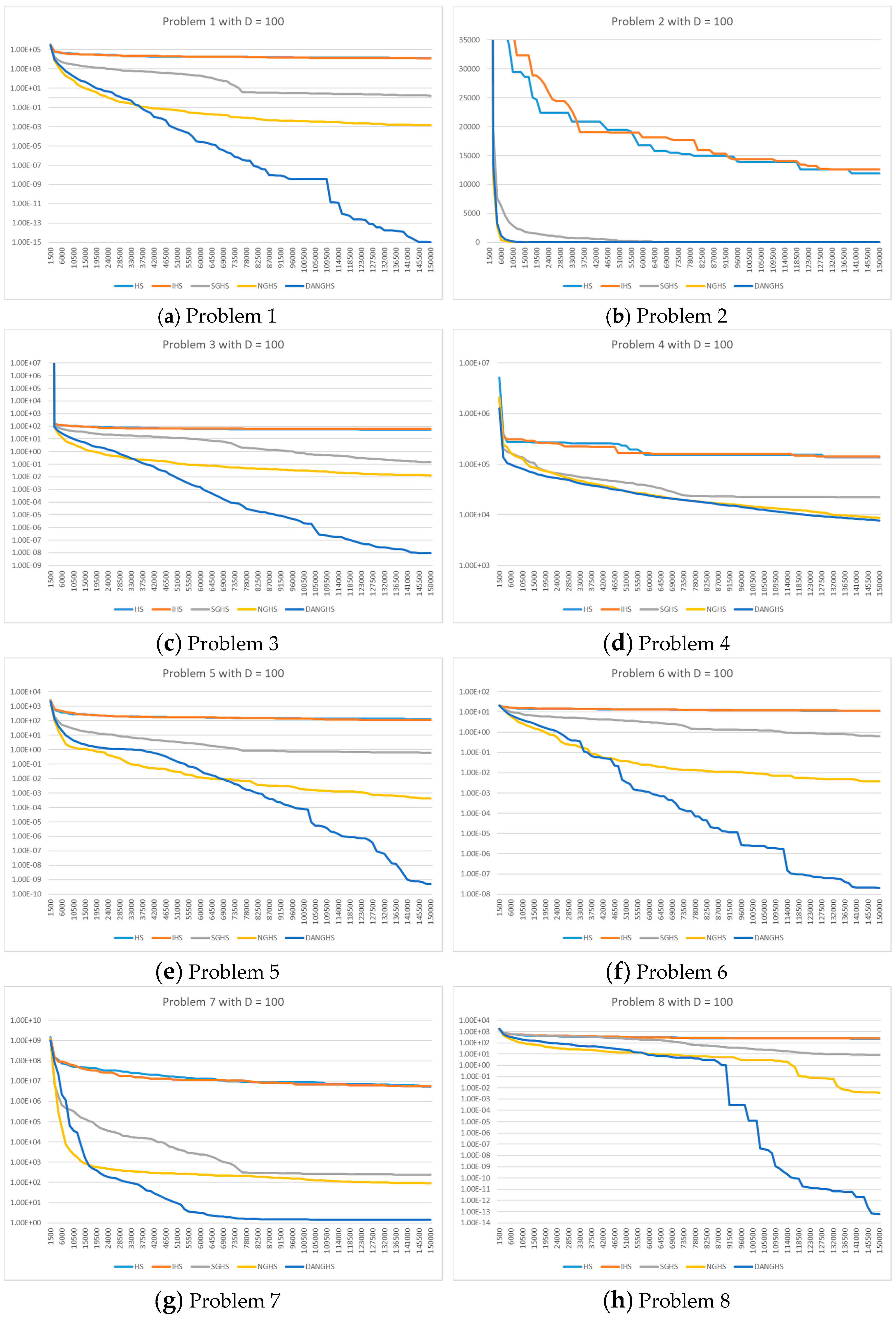
Figure 7 presents a typical solution history graph of five different algorithms along iterations for problems 1 to 8 with D = 30, and Figure 8 presents a typical solution history graph of five different algorithms along iterations for problems 9 to 14 with D = 30. Figure 9 presents a typical solution history graph of five different algorithms along iterations for problems 1 to 8 with D = 100, and Figure 10 presents a typical solution history graph of five different algorithms along iterations for problems 9 to 14 with D = 100.

Finally, we will discuss and analyze the efficiency of the DANGHS algorithm. In Figure 7, Figure 8, Figure 9 and Figure 10, we can easily find out that the DANGHS algorithm obviously had the better searching performance and convergence ability than other algorithms in most low-dimensional problems and in all high-dimensional problems. In other words, the DANGHS algorithm can use the less iterations to solve the problem and is more efficient than other HS algorithms. Besides, according to the experimental results, the DANGHS with Pseudocode 3 spent 603.5025 seconds to run 30 experiments; while the DANGHS with Pseudocode 4 spent 532.7705 seconds only to run 30 experiments. The DANGHS algorithm with Pseudocode 4 reduces 11.72% of the running time, as compared with Pseudocode 3. Therefore, the DANGHS algorithm with the proposed Pseudocode 4 is more efficient than with Pseudocode 3.

5. Conclusions

We presented a DANGHS algorithm, which combines NGHS and the dynamic adjustment strategy for genetic mutation probability. Moreover, the extensive computational experiments and comparisons were carried out for 14 benchmark continuous optimization problems. According to the extensive computational results, there are several findings in this paper worth summarizing.

First, different strategies are suitable for different problems.

• The decreasing dynamic adjustment strategies should be applied to some problems in which the DANGHS algorithm needs a larger, $p_m$, in the early iterations, in order to have a larger probability of finding a better trial solution around the current one.
• The increasing dynamic adjustment strategies should be applied to other problems. For these problems, if the current solution is trapped in a local optimum, the DANGHS algorithm requires a larger probability, $p_m$, in later iterations in order to avoid the local optima.
• The periodic dynamic adjustment strategy can find the best objective function value for problem 13. These particular results show that there are not only two kinds of adjustment strategies, decreasing and increasing strategies, which are suitable for all problems. This viewpoint is different from the common views: the adjustment strategy is as small as possible or as large as possible with a generation number. For a specific problem, the periodic dynamic adjustment strategy could have better performance in comparison with other decreasing or increasing strategies. Therefore, these results inspire us to further investigate this kind of periodic dynamic adjustment strategy in future experiments.

Second, the extensive experimental results showed that the DANGHS algorithm had better searching performance in comparison with other HS algorithms for D = 30 and 100 in most problems. Particularly for D = 100, the DANGHS algorithm could search the best objective function value in all 14 problems. In other words, the DANGHS had superior searching performance in high-dimensional problems. According to the numerical results, we proofed that algorithms with dynamic parameters, such as the DANGHS algorithm and the IHS algorithm, could have better searching performance than algorithms without dynamic parameters, such as the NGHS algorithm and the HS algorithm. Moreover, according to these results, we proofed that the viewpoint presented in previous studies is suitable for the NGHS algorithm. This viewpoint states that appropriate parameters can enhance the searching ability of a metaheuristic algorithm.

Finally, the DANGHS algorithm using Pseudocode 4 was more efficient than that using Pseudocode 3. In Pseudocode 3, the algorithm generates a new harmony, and then with $p_m$ probability, the algorithm abandoned it to generate a mutated harmony. Obviously, it was redundant and inefficient. Therefore, we modified the procedure in Pseudocode 3 and presented a more efficient Pseudocode 4 in this paper. In conclusion, the DANGHS algorithm is a more efficient and effective algorithm.