Abstract
In this paper, we introduce the concept of neutrosophic number from different viewpoints. We define different types of linear and non-linear generalized triangular neutrosophic numbers which are very important for uncertainty theory. We introduced the de-neutrosophication concept for neutrosophic number for triangular neutrosophic numbers. This concept helps us to convert a neutrosophic number into a crisp number. The concepts are followed by two application, namely in imprecise project evaluation review technique and route selection problem.
1. Introduction
1.1. Theory of Uncertainty and Uncertainty Quantification
Uncertainty theory playsanimportant role in modeling sciences and engineering problems. However, there is a basic question regarding how we can define or use the uncertainty concept in our mathematical modeling. Researchers around the globe defined many approaches to defining them, and give their various recommendations to using uncertainty theory. There are several literaturestudiesthatclassify some basic uncertain parameters. It should be noted that there is no unique reorientation of the uncertain parameter. For the problem’s purpose or decision makers’ choice, it can be varied and presented as a different application. We now, here, give some info about uncertain parameters, and show how they differ from eachother using the concept of uncertainty using some definition, flowcharts, and diagrams. In this paper, we recommend the researcher to take the uncertain parameter as a parametric interval valued neutrosophic number.
Some basic differences between some uncertain parameters:
If we take Interval number [1] then we can see,
- The information belongs to a certain interval
- There is no concept of membership function
If we take Fuzzy number [2,3], then we can see,
- The concept of belongingness of the elements comes
- The use of membership function is present
If we take Intuitionistic fuzzy number [4], then we can see,
- The concept of belongingness and non-belongingness of the elementscomes
- The use of membership and non-membership function is present
If we take Neutrosophic fuzzy number [5], then we can see,
- The concept of truthiness, falsity, and indeterminacy of the elements comes
- The use of membership function for truthiness, falsity, and indeterminacy is present
Please follow the idea given in the flowchart below, as shown in Figure 1:
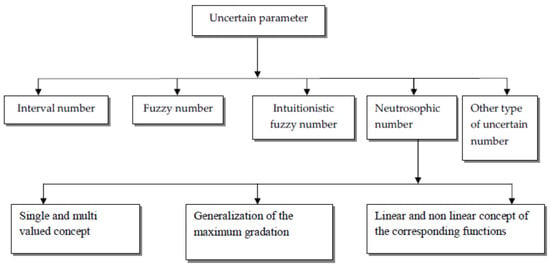
Figure 1.
Flowchart for different uncertain parameter.
1.2. Neutrosophic Number
Fuzzy systems (FSs) and Intuitionistic fuzzy systems (IFSs) cannot successfully deal with a situation where the conclusion is adequate, unacceptable, and decision-maker declaration is uncertain. Therefore, some novel theories are mandatory for solving the problem with uncertainty. The neutrosophic sets (NSs) [5] reflect on the truth membership, indeterminacy membership, and falsity membership concurrently, which is more practical and adequate than FSs and IFSs in commerce, which areuncertain, incomplete, and inconsistent in sequence. Single-valued neutrosophic sets are an extension of NSs which were introduced by Wang et al. [6]. Ye [7] introduced simplify neutrosophic sets, and Peng et al. [8,9] definite their novel operations and aggregation operators. Finally, there are different extensions of NSs, such as interval neutrosophic set [10], bipolar neutrosophic sets [11], and multi-valued neutrosophic sets [12,13]. The decision-making problem [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] is very important in study, when it is with uncertainty.
Although many researchers and scientists have worked in the recently developed neutrosophic method, and applied it in the field of decision making, there is, however, still some viewpoints regarding defining neutrosophic numbers in different forms, and their corresponding de-impreciseness is very important.
1.3. Ranking and De-Impreciseness
The ranking and de-impreciseness of the imprecise numbers are not a new concept.However, what is the basic concept of the above-said important results and what is the relation. Figure 2 shows the flowchart for de-impreciseness and ranking.
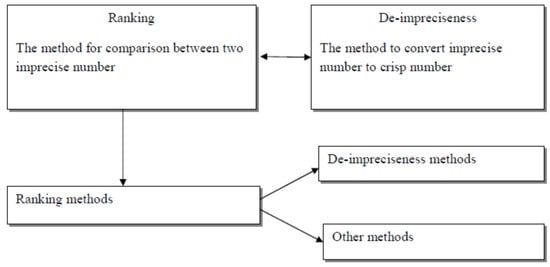
Figure 2.
Flowchart for de-impreciseness and ranking.
Ranking is a concept where we can compare two imprecise numbers, and de-impreciseness is a technique where the imprecise number is converted to a crisp number. Somewhere, the decision maker takes the two concepts as the same. In this case, they convert the imprecise number into crisp number, and compares them on the basis of crisp value.
1.4. Structure of the Paper
The paper is organized as follows. In Section 1, the basic concept on imprecise set theory and neutrosophic set theory are discussed. Section 2 contains the preliminaries section. Section 3 goes for the known definition of neutrosophic sets and numbers. Single valued linear neutrosophic number and its variation are showing in Section 3. In Section 4, we address the basic concept of neutrosophic non-linear number and generalized neutrosophic number. In Section 5, the de-neutrosophication of linear neutrosophic triangular fuzzy number is performed. The PERT problem is considered in Section 6. The application in assignment problem, considering aproblem, is taken in Section 7. The conclusions are written in Section 8.
2. Neutrosophic Number
Definition 1.
(Neutrosophic Set) A setin the universal discourse, which is denoted generically by, is said to be a neutrosophic set if, whereis called the truth membership function which represents the degree of confidence,is called the indeterminacy membership function which represents the degree of uncertainty, andis called the falsity membership function which represents the degree of scepticism on the decision given the decision maker.
exhibits the following relation:
Definition 2.
(Single Valued Neutrosophic Set) Neutrosophic setin the definition 2.3, is called a Single Valued Neutrosophic Setifis a single valued independent variable. Thus, whererepresents the truth, indeterminacy, and falsity membership function, respectively, as stated in definition 2.3, and also exhibits the same relationship as stated earlier.
If there exists three points, , for which , then the is called neut-normal.
A is said to be neut-convex, which implies that it is a subset of a real line, by satisfying the following conditions:
where, .
Definition 3.
(Single Valued Neutrosophic Number)Single Valued Neutrosophic Numberis defined aswhere, the truth membership function, the indeterminacy membership function, and the falsity membership functionis given as:
3. Single Valued Linear Neutrosophic Number
- Triangular Single Valued Neutrosophic number of Type 1: The quantity of the truth, indeterminacy and falsity are not dependent: A Triangular Single Valued Neutrosophic number of Type 1 is defined as whose truth membership, indeterminacy and falsity membership is defined as follows:andandwhere, , .
The parametric form of the above type number is , where,
here, , , and
Example 1.
Take.
The parametric representation is
Table 1 and Figure 3 show the value of , , , , , and and graphical representation of triangular single valued neutrosophic numbers (TrSVNNs) respectively.

Table 1.
Value of , , , , , and .
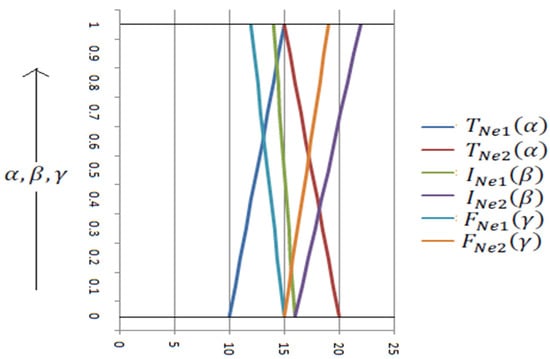
Figure 3.
Graphical representation of TrSVNNs.
- 2.
- Triangular Single Valued Neutrosophic Number of Type 2: The quantity of indeterminacy and falsity are dependent: A triangular single valued neutrosophic number (TrSVNN) of Type 2 is defined as whose truth membership, indeterminacy, and falsity membership are defined as follows:andandwhere, , .
The parametric form of the above type number is , where
Here, , , and and .
Example 2.
Take
The parametric representation is,
Table 2 and Figure 4 show the value of , , , , , and and graphical representation of type-2 TrSVNNs.

Table 2.
Value of , , , , , and .
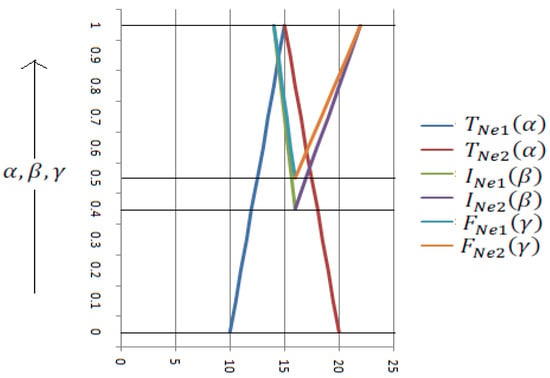
Figure 4.
Graphical representation of type-2 TrSVNNs.
- 3.
- Triangular Single Valued Neutrosophic number of Type 3: The quantity of the truth, indeterminacy, and falsity are dependent: A TrSVNN of Type 3 is defined as , whose truth membership, indeterminacy, and falsity membership are defined as follows:andandwhere, , .
The parametric form of the above type number is , where
Here, , , , and .
Example 3.
Take
The parametric representation is,

Table 3.
Value of , , , , and .
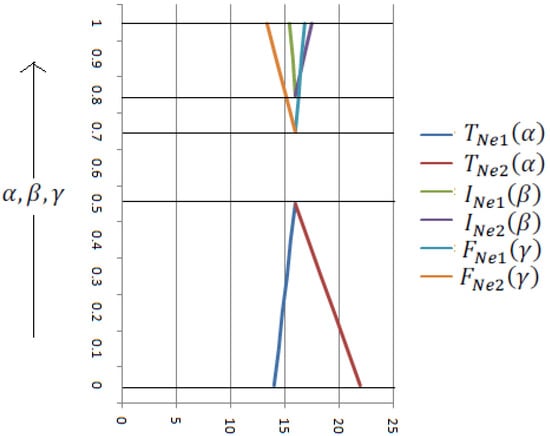
Figure 5.
Graphical representation of type-3 TrSVNNs.
Different Operational Laws of Two Triangular Neutrosophic Numbers: If and are two single valued neutrosophic numbers with nine components having truthmembership , indeterminacymembership , and falsitymembership , respectively, such as:
where a, band c are the scores given by the decision maker in the scale, ranging from lower limit Ll to upper limit Ul.
- Addition
- Negative of SVNNs
- Subtraction
- Multiplications
- Multiplication by a constant
- Inverse of SVNNs
- Divisions
Example 4.
Ifandare two single valued neutrosophic numbers with independent truth, indeterminate, and false values in the scale of 0 to 25, then find thewhere k = 3.
- Addition
- Subtraction
- Multiplication
- Division
- Multiplication by a constant
4. Neutrosophic Non-Linear Number and Generalized Neutrosophic Number
4.1. Single Valued Non-Linear Triangular Neutrosophic Number with Nine Components
A single valued non-linear triangular neutrosophic number with nine components is defined as , whose truth membership, indeterminacy, and falsity membership is defined as:
and
and
where, , .
Note. If , then single valued non-linear triangular neutrosophic number with nine components will be converted into single valued linear triangular neutrosophic number with nine components.
4.2. Single Valued Generalized Triangular Neutrosophic Number with Nine Components
A single valued triangular neutrosophic number with nine components is defined as , whose truth membership, indeterminacy, and falsity membership is defined as:
and
and
where, , .
4.3. Single Valued Generalized Non-Linear Triangular Neutrosophic Number with Nine Components
A single valued non-linear triangular neutrosophic number with nine components is defined as , whose truth membership, indeterminacy, and falsity membership is defined as:
and
and
where, , .
Note. if , then single valued generalized non-linear triangular neutrosophic number with nine components will be converted into single valued generalized linear triangular neutrosophic number with nine components.
5. De-Neutrosophication of Linear Neutrosophic Triangular Fuzzy Number
De-Neutrosophication Using Removal Area Method
Let us consider a linear neutrosophic triangular fuzzy number as follows:
whose pictorial representation is as follows.
Firstly, we consider the graphical representation of linear neutrosophic triangular fuzzy number in Figure 6.
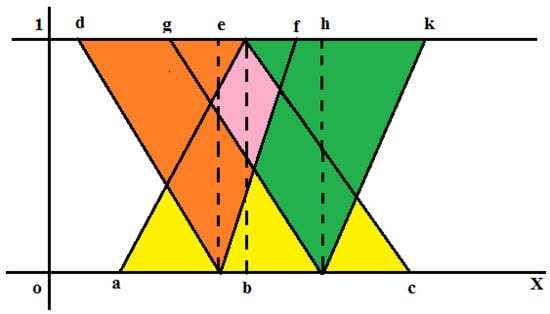
Figure 6.
Linear neutrosophic number.
We consider an ordinary number and a fuzzy number for the lower triangle, then left side removal of with respect to k is , defined as the area bounded by k and the left side of the fuzzy number Similarly, the right side removal of with respect to k is Also consider an ordinary number and a fuzzy number for the left most upper triangle(def), then the left side removal of with respect to k is , defined as the area bounded by k and the left side of the fuzzy number Similarly, the right side removal of with respect to k is . A fuzzy number for the right most upper triangle(ghk), then left side removal of with respect to k is , defined as the area bounded by k and the left side of the fuzzy number Similarly, the right side removal of with respect to k is
Mean is defined as , , .
Then, we defined the defuzzification of a linear neutrosophic triangular fuzzy as .
For ,
Then,
We take .
Figure 7 shows the pictorial representation of de-neutrosophication.
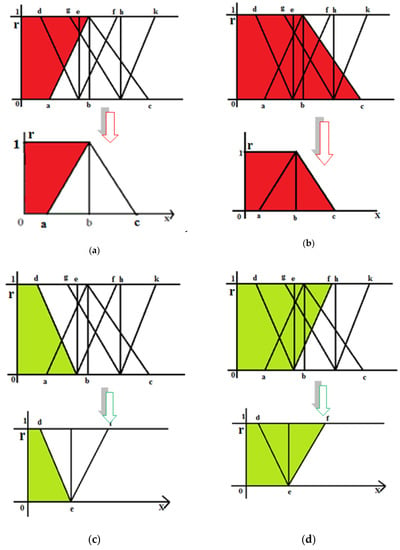
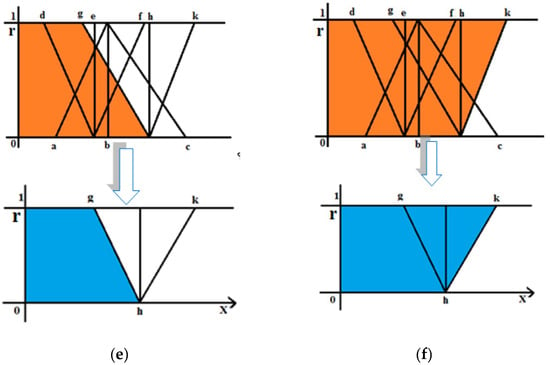
Figure 7.
Pictorial representation of de-neutrosophication. (a) Area of trapezium OABR; (b) Area of trapezium OABR; (c) Area of trapezium OEDR;(d) Area of trapezium OEFR; (e) Area of trapezium OHGR: (f) Area of trapezium OHKR.
Then,
Hence, , .
So, .
Example 5.
Finding De-neutrosophication value of Neutrosophic number.
Table 4 shows the de-neutrosophication value of Neutrosophic number.

Table 4.
De-neutrosophication value of Neutrosophic number.
6. PERT in Triangular Neutrosophic Environment and the Proposed Model
The full form of PERT method is project evaluation and review technique, which is a project management tool used to schedule, organize, and coordinate tasks within a project. It is basically a method to analyze the tasks involved in completing a given project, especially the time needed to complete each task, and to identify the minimum time needed to complete the total project.
PERT planning involves the following steps:
- Identify the specific activities and milestones.
- Determine the proper sequence of the activities.
- Construct a network diagram.
- Estimate the time required for each activity.
- Determine the critical path.
- Update the PERT chart as the project progresses.
The main objective of PERT is to facilitate decision making and to reduce both the time and cost required to complete a project. PERT is intended for very large-scale, one-time, non-routine, complex projects with a high degree of dependency, projects which require a series of activities, some of which must be performed sequentially, and others that can be performed in parallel with other activities. PERT has been mainly used in new projects which have large uncertainty with respect to design of a structure, technology, and networking system. To take care of associated uncertainties, we introduced triangular neutrosophic environment for PERT activity duration.
The three time estimates for activity duration are as follows:
Optimistic time : Generally, the shortest time in which the activity can be completed. It is common practice to specify optimistic time to be three standards deviations from the mean so that there is approximately a 1% chance that the activity will be completed within the optimistic time.
Pessimistic time : Generally, the longest time that an activity might require. Three standard deviations from the mean are commonly used for the pessimistic time.
Most likely time : Generally, it is the completion time, in normal circumstances, having the highest probability. Note that this time is different from the expected time.
Note 2. In Ref. [22], the authors introduced the concept of score and accuracy function to compute the crisp value of a trapezoidal neutrosophic number. In our proposed model, we choose all the three different times (optimistic, pessimistic, most likely) as triangular neutrosophic number.
To obtain the crisp value, we introduced the de-neutrosophication value of triangular neutrosophic number .
Now, the expected time and standard deviation can be calculated by the formula and , where o, p, and m are all crisp value of optimistic, pessimistic, and most likely time estimations, respectively.
Now, we use CPM method for further calculation of earliest/latest time, critical path, and float.
In forward pass, starting with a time of zero for the first event, the computation proceeds from left to right, up to the final event. For any activity , let denote the earliest time of event , then . If more than one activity enters an event, the earliest start time for that event is computed as for all activities emanating from node i entering into j.
In case of backward pass, starting with the final node, the computation proceeds from right to left, up to the initial event. For any activity , let denote the latest finished time of event i, then . If more than one activity enters an event, the latest finish time for that event is computed as for all activities emanating from node j entering into i.
After calculating the critical path, compute project length variance, which is the sum of the variances of all the critical activities. Next, calculate the standard normal variable , where is the scheduled time to complete the project, and is the normal expected project length duration. Using a normal curve, we can estimate the probability of completing the project within a specified time. The steps of the said method are shown in Figure 8. We also set the numerical value for the said problem to show the importance of our method in Table 5.
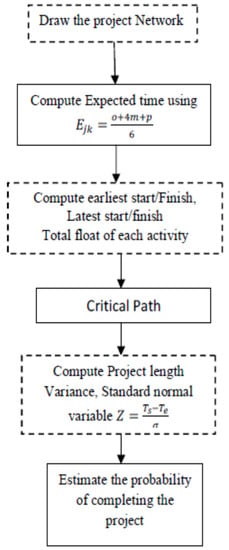
Figure 8.
Flowchart for the solution procedure.

Table 5.
Set of Neutrosophic value of the above problem.
Draw the project network and find the probability that the project is completed in 16 days.
Solution. Now, we solve the problem by the following steps, as shown in Table 6, Figure 9 and Figure 10.

Table 6.
The value of and for the above problem.
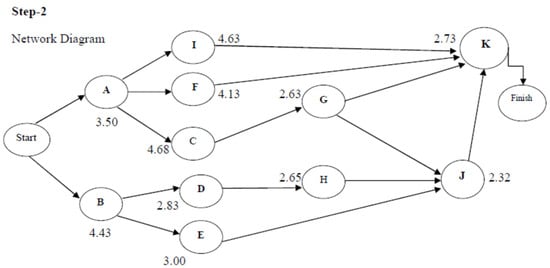
Figure 9.
The network diagram for the problem.
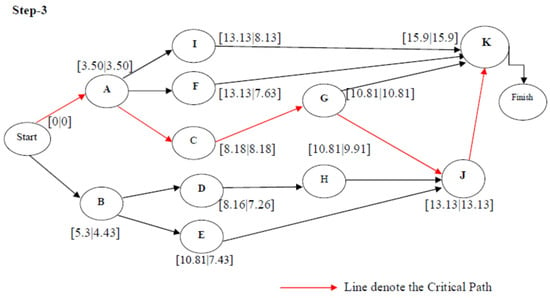
Figure 10.
Critical path analysis for the problem.
Step-1.
Therefore, the expected project duration is 15.9 days.
Critical path ACGJK.
Project length variance , standard deviation0.98.
Probability that the project will be finished within 16 days is
Area under the normal curve = 0.5398
The related normal curve is drawn in Figure 11.
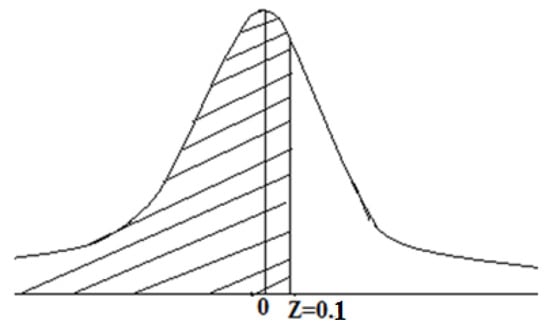
Figure 11.
The normal curve for the above problem.
7. Application of Triangular Neutrosophic Fuzzy Number in Assignment Problem Using De-Neutrosophic Value
The assignment problem is very important for transferring goods from one place to another place. In the assignment problem, if uncertainty occurs, then it is more complicated to solve. By the concept of impreciseness and its corresponding crispified value, we can easily handle the assignment problem. In this section, we take a route selection problem with neutrosophic cost data and solve the problem.
We consider a problem of assigning three different trucks to three different destinations. The assigning costs that are the travelling costs in rupees are given here. How should the trucks be dispatched so as to minimize the total travelling cost? Note, that all the costs are triangular neutrosophic numbers.
Let us consider that the transportation cost for the three trucks are neutrosophic in nature. For that viewpoint, we take that the cost of the three trucks are as follows in Table 1, in units of dollar. Each component represents the moneys in units of dollars.
Here, red car denotes Truck 1, yellow car denotes Truck 2, and green car denotes Truck 3 as shown in the Figure 12.
Figure 12.
Pictorial representation of the problem.
We apply the defuzzification result of triangular neutrosophic number from Table 7.

Table 7.
Neutrosophic value for the transportation costs.
to convert the numbers into a crisp number.
Then, we have the following Table 8.

Table 8.
De-neutrosophication value for the transportation costs.
Now, we consider row minimum from each row, and subtract it from the other element (row-wise). Thus, we get Table 9.

Table 9.
Row minimum from each row, and subtract it from the other element (row-wise).
Now, we consider column minimum from each column and subtract it from the other element (column-wise). Thus, we get Table 10.

Table 10.
Column minimum from each column and subtract it from the other element (column-wise).
Here, the minimum number of straight lines to cover all the zeros is 3 (which is also equal to the order of the matrix), as shown in Table 11.

Table 11.
Minimum number of straight lines to cover all the zeros.
From the Table 12, we see that if the Truck1 goes to Destination-3, Truck2 goes to Destination-2, and Truck3 goes to Destination-1, then the carrying is minimum.

Table 12.
Transformed table.
That means from the Figure 13 Truck-1Destination-3, Truck-2Destination-2, Truck-3Destination-1.
Figure 13.
Pictorial representation of the solution.
The corresponding Min cost = (3.92 + 1.71 + 2.92) = 8.55 units of dollar.
Then, we get Table 13.

Table 13.
Neutrosophic value of destinations.
Ye [21] built up the concept of score function and accuracy function. The score function S and the accuracy function H are applied to compare the grades of triangular fuzzy numbers (TFNS). These functions show that greater is the value, the greater is the TFNS, and by using these, concept paths can be ranked.
We apply the result of triangular neutrosophic number.
Let, be a triangular neutrosophic fuzzy number, then the score function is defined as , and accuracy function is defined as .
In order to make comparisons between two triangular neutrosophic values, Ye [21] presented the order relations between two triangular neutrosophic values.
Let and be two triangular neutrosophic values, then the ranking method is defined as follows.
- (i)
- if , then
- (ii)
- if and , then
We apply the score function result of triangular neutrosophic number to convert the numbers into a crisp number.
Then we have the following table, as shown in Table 14.

Table 14.
Converted the numbers into a crisp number.
Take the most negative cost (−1.42), add it with all the elements of the matrix we get Table 15.

Table 15.
Corrosponing positive value table.
Now, we consider row minimum from each row and subtract it from the other elements (row-wise). Thus, we get Table 16.

Table 16.
Row minimum from each row and subtract it from the other elements (row-wise).
Now, we consider column minimum from each column, and subtract it from the other elements (column-wise). Thus, we get Table 17.

Table 17.
Column minimum from each column, and subtract it from the other elements (column-wise).
Here, the minimum number of straight lines to cover all the zeros is 3(which is also equal to the order of the matrix), as shown in Table 18.

Table 18.
Minimum number of straight lines to cover all the zeros is 3.
From the Table 19, we see that if the Truck1 goes to Destination-1, Truck2 goes to Destination-3, and Truck3 goes to Destination-2, then the carrying is minimum.

Table 19.
Decision table.
That means from the Figure 14 the destination is as follows Truck1Destination-1, Truck2Destination-3, Truck3Destination-2.
Figure 14.
Pictorial representation of the solution.
The corresponding Min cost = (−0.92 − 1.42 − 0.08) = −2.42 units of dollar.
Note: Since, using de-neutrosophic value, we observe that min cost is 8.55 units of dollar, whereas using score function, we get min cost in negative quantity that is loss, hence de-neutrosophication gives us a better result than the score function.
8. Conclusions
The theory of uncertainty plays a key role in applied mathematical modeling. The concept of neutrosophic number is very popular nowadays. The formation and de-neutrosophication of the corresponding number can be very important for the researcher who deals with uncertainty and decision-making problems. In this paper, we construct the concept triangular neutrosophic number from different viewpoints, which is not defined earlier. We use the concept of linear and non-linear form with generalization of the pick value of truth, falsity, and indeterminacy functions by considering triangular neutrosophic numbers, which are very important for uncertainty theory. We introduced the de-neutrosophication concept for triangular neutrosophic numbers. This concept helps us to convert a neutrosophic number into a crisp number, which is surely helpful for decision-making problems. In future, we can extend the concept into different types of neutrosophic numbers, which can be more applicable in modeling with uncertainty.
Author Contributions
Conceptualization, A.C., S.P.M. and A.A.; Methodology, N.S. and S.S.; Vdation, S.A. and S.S.; Formal Analysis, A.C., S.P.M. and A.A.; Investigation, N.S. and S.A.
Acknowledgments
The authors acknowledge the financial support from Universiti Putra Malaysia under Putra-IPB grant: GP-IPB/2017/9542402.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moore, R.E. Methods and Applications of Interval Analysis; Society for Industrial and Applied Mathmatics: Philadelphia, PA, USA, 1979. [Google Scholar]
- Chang, S.S.; Zadeh, L.A. On Fuzzy Mappings and Control, Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 1996. [Google Scholar]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics Neutrosophy: Neutrosophic Probability, Set and Logic, 3rd ed.; American Research Press: Washington, DC, USA, 2003. [Google Scholar]
- Wang, H.B.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single Valued Neutrosophic Sets. Tech. Sci. Appl. Math. 2010. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.309.9470&rep=rep1&type=pdf (accessed on 31 July 2018).
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Int. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Zhang, H.Y.; Chen, X.H. The fuzzy cross-entropy for intuitionistic hesitant fuzzy sets and their applicationin multi-criteria decision-making. Int. J. Syst. Sci. 2015, 46, 2335–2350. [Google Scholar] [CrossRef]
- Wang, J.Q.; Peng, J.J.; Zhang, H.Y.; Liu, T.; Chen, X.H. An uncertain linguistic multi-criteria group decision-making method based on a cloud model. Group Decis. Negot. 2015, 24, 171–192. [Google Scholar] [CrossRef]
- Deli, I.; Ali, M.; Smarandache, F. Bipolar neutrosophic sets and their application based on multi-criteria decision making problems. arXiv, 2005; arXiv:1504.02773. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Wang, J.; Chen, X.H. Multi-valuedneutrosophic sets and power aggregation operators with their applications in multi-criteria group decision-making problems. Int. J. Comp. Int. Syst. 2015, 8, 345–363. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, X.E. The TODIM method with multi-valued neutrosophic sets. Control Decis. 2015, 30, 1139–1142. [Google Scholar]
- Ye, J. Trapezoidal fuzzy neutrosophic set and its application to multiple attribute decision making. Soft Computing. Neural Comp. Appl. 2015, 26, 1157–1166. [Google Scholar] [CrossRef]
- Mohamed, M.; Abdel-Basset, M.; Hussien, A.N.; Smarandache, F. Using Neutrosophic Sets to Obtain Pert Three-Times Estimates in Project Management, Neutrosophic Operational Research; Pons Publishing House: Bruxelles, Belgium, 2016; Volume 1, pp. 145–156. [Google Scholar]
- Karaa, S.S.; Cheikhrouhou, N. A multi criteria group decision making approach for collaborative software selection problem. J. Int. Fuzzy Syst. 2014, 26, 37–47. [Google Scholar]
- Wang, X.F.; Wang, J.Q.; Yang, W.E. Multi-criteria group decision making method based on intuitionistic linguistic aggregation operators. J. Int. Fuzzy Syst. 2014, 26, 115–125. [Google Scholar]
- Xiaohong, C.; Yang, L.; Wang, P.; Yue, W. A Fuzzy Multicriteria Group Decision-Making Method with New Entropy of Interval-Valued Intuitionistic Fuzzy Sets. J. Appl. Math. 2013, 2013, 1–8. [Google Scholar]
- Wang, J.Q.; Han, Z.Q.; Zhang, H.Y. Multi-criteria Group Decision-Making Method Based on Intuitionistic Interval Fuzzy Information. Group Decis. Negot. 2014, 23, 715–733. [Google Scholar] [CrossRef]
- Chaio, K.P. The multi-criteria group decision making methodology using type 2 fuzzy linguistic judgments. Appl. Soft Comput. 2016, 49, 189–211. [Google Scholar] [CrossRef]
- Wibowo, S.; Grandhi, S.; Deng, H. Multicriteria Group Decision Making for Selecting Human Resources Management Information Systems Projects. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications, Hefei, China, 5–7 June 2016; pp. 2158–2297. [Google Scholar]
- Hanine, M.; Boutkhoum, O.; Tikniouine, A.; Agouti, T. A new web-based framework development for fuzzy multi-criteria group decision-making. SpringerPlus 2016, 5, 601. [Google Scholar] [CrossRef] [PubMed]
- Büyüközkan, G.; Güleryüz, S. Multi Criteria Group Decision Making Approach for Smart Phone Selection Using Intuitionistic Fuzzy TOPSIS. Int. J. Comput. Int. Syst. 2016, 9, 709–725. [Google Scholar] [CrossRef]
- Efe, B. An Integrated Fuzzy Multi Criteria Group Decision Making Approach for ERP System Selection. Appl. Soft Comput. 2016, 38, 106–117. [Google Scholar] [CrossRef]
- Seddikia, M.; Anouchea, K.; Bennadjib, A.; Boatengba, P. A multi-criteria group decision-making method for the thermal enovation of masonry buildings: The case of Algeria. Energy Build. 2016, 129, 471–483. [Google Scholar] [CrossRef]
- Shen, F.; Xu, J.; Xu, Z. An outranking sorting method for multi-criteria group decision making using intuitionistic fuzzy sets. Inf. Sci. 2016, 334, 338–353. [Google Scholar] [CrossRef]
- You, X.; Chen, T.; Yang, Q. Approach to Multi-Criteria Group Decision-Making Problems Based on the Best-Worst-Method and ELECTRE Method. Symmetry 2016, 8, 95. [Google Scholar] [CrossRef]
- Bausys, R.; Juodagalviene, B. Garage location selection for residential house by WASPAS-SVNS method. J. Civ. Eng. Manag. 2017, 23, 421–429. [Google Scholar] [CrossRef]
- Chuu, S.J. Selecting the advanced manufacturing technology using fuzzy multiple attributes group decision making with multiple fuzzy information. Comput. Ind. Eng. 2009, 57, 1033–1042. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X. Multi attribute Group Decision Making Methods Based on Linguistic Intuitionistic Fuzzy Power Bonferroni Mean Operators. Complex 2017, 2017, 1–15. [Google Scholar]
- Ye, J. Exponential operations and aggregation operators of interval neutrosophic sets and their decision making methods. SpringerPlus 2016, 5, 1488. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Liu, C. Algorithms for neutrosophic soft decision making based on EDAS, new similarity measure and level soft set. J. Intell. Fuzzy Syst. 2017, 32, 955–968. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Bausys, R.; Juodagalviene, B.; Garnyte-Sapranaviciene, I. Model for residential house element and material selection by neutrosophic MULTIMOORA method. Eng. Appl. Artif. Intell. 2017, 64, 315–324. [Google Scholar] [CrossRef]
- Pouresmaeil, H.; Shivanian, E.; Khorram, E.; Fathabadi, H.S. An extended method using TOPSIS and VIKOR for multiple attribute decision making with multiple decision makers and single valued neutrosophic numbers. Adv. Appl. Stat. 2017, 50, 261–292. [Google Scholar] [CrossRef]
- Bausys, R.; Zavadskas, E.K. Multicriteria decision making approach by VIKOR under interval neutrosophic set environment. Econ. Comput. Econ. Cybern. Stud. Res. 2015, 49, 33–48. [Google Scholar]
- Zavadskas, E.K.; Bausys, R.; Kaklauskas, A.; Ubarte, I.; Kuzminske, A.; Gudiene, N. Sustainable market valuation of buildings by the single-valued neutrosophic MAMVA method. Appl. Soft Comput. 2017, 57, 74–87. [Google Scholar]
- Abdel-Basset, M.; Mohamed, M.; Hussien, A.N.; Sangaiah, A.K. A novel group decision-making model based on triangular neutrosophicnumbers. Soft Comput. 2017, 15, 1–15. [Google Scholar]
- Deli, I.; Şubaş, Y. A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. Int. J. Mach. Learn. Cybern. 2016, 8, 1309–1322. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).