Abstract
In this paper, the exact analytical solutions are developed for the thermodynamic behavior of an Euler-Bernoulli beam resting on an elastic foundation and exposed to a time decaying laser pulse that scans over the beam with a uniform velocity. The governing equations, namely the heat conduction equation and the vibration equation are solved using the Green’s function approach. The temporal and special distributions of temperature, deflection, strain, and the energy absorbed by the elastic foundation are calculated. The effects of the laser motion speed, the modulus of elastic foundation reaction, and the laser pulse duration time are studied in detail.
1. Introduction
Lasers are now widely utilized in engineering applications because of their super processing efficiency, adaptability to local treatment and high operation precision. Some companies have done a lot of researches and developments on laser manufacturing techniques. For example, HGTECH, a company of China, is now trying to develop high-efficiency intelligent laser hardening equipment, which is expected to be used in key components of railways and aircrafts. It is predicted that the service life of steel rails can be increased by 10 times, and the frequencies of rail replacement can be decreased by 50%. In some laser technique applications, such as laser marking, laser heat treating, and so on, the target object need to be put on a foundation, and the laser moves at a specific speed over the surface of the object.
Considerable studies have been carried out to obtain the solutions of workpieces irradiated by moving laser beams. Among them, in 1977, Cline and Anthony [1] presented a for heating and melting of materials subjected to a moving heat source. Mercier et al. [2] studied the thermoelastic stresses arising of a semi-infinite medium caused by a moving band source of heat on the surface by using the analytical temperature solutions and a numerical calculation of stress. Nguyen et al. [3] derived the theoretical solution of a semi-infinite body, which is exposed to a movable heat source with double-ellipsoidal power density. Van Elsen et al. [4] studied the temperature field of a semi-infinite structure irradiated by a uniform heating source. Sun et al. [5] investigated the thermoelastic response of a semi-infinite rod exposed to a time attenuating laser pulse.
The above literatures treated the infinite or semi-infinite structures. It is obvious that the thermoelastic problem of finite region is more complicated to be solved, for which the analytical solutions are less in existing literatures. Among them, Ootao and Tanigawa [6] derived the expression for the rectangular plate through adopting the Laplace and finite cosine transformations. Yang et al. [7] investigated the thermoslastic behavior of a clamped beam that is heated by a movable laser pulse. Sun et al. [8] studied the heating process of a circular plate composed of two layers by applying Green’s function approach. Abbas [9] investigated the generalized thermoelastic behavior of a thin slim strip by applying Green and Lindsay theory.
In geotechnical engineering, beams on elastic foundation are widely used. A lot of research has focused on the dynamic behaviors of beams induced by moving loads. In 1954, Kenney [10] first obtained the solution to an infinite beam on Winkler spring foundation applied to a concentrated force scanning at a uniform speed. Sun [11] and Kim [12] presented more works about the solutions of beams on viscoelastic foundation and on Winkler foundation. Basu and Rao [13] derived expressions for the static response of an infinite beam which is set on a visco-elastic foundation and applied to a concentrated force scanning at a uniform speed.
As a beam is irradiated by a laser pulse, its temperature will increase, and thermal strains will be generated at specific locations because of the thermal impulses. As a result, vibrations will be generated by the laser-induced thermal impulses which generate impulsive local thermal strains. For the beam set on a foundation, the vibration of the beam is restricted, and it shows behaviors different from a free beam. On the other hand, when the laser pulse moves, the induced strain also moves along the beam in the form of a strain wave. Many works have been done about wave propagations. For example, Brown et al. [14] studied the wave propagation in a viscoelastic medium. They considered both the classical and fractional differentiation of the Zener, Maxwell, and Voigt models, in which the coupling of different models inside the same medium are also covered.
The Green’s function approach is a helpful mathematical tool in solving partial differential equations. Many researchers have applied it in heat conduction problems and mechanics of structural members. The methods of obtaining of the specific diverse Green’s functions for structural members with homogeneous or nonhomogeneous material, uniform or non-uniform thickness, additional discrete elements, etc., have been reported. For example, Żur [15,16,17,18,19] presented a series of work over the free vibration analysis of thin circular plates and elastically supported functionally graded annular plates using the Green’s functions. Zhao et al. [20,21,22] analytically studied the vibration of a cracked Euler-Bernoulli beam induced by a heat flux or a harmonic force and that of Timoshenko beams due to a heat flux together with an external load. Chen et al. [23] studied the dynamic behavior of an axially forced Timoshenko beam under different boundary conditions. The Green’s functions were obtained by using the techniques of separation of variables and the Laplace transformation. Hozhabrossadati et al. [24] analyzed the Bernoulli beams under the resonant condition and they developed a Green’s function procedure by constructing the proper Green’s function and adopting the pertinent boundary conditions. Mohammad et al. [25] studied the thermoelastic static behaviors of a curved circular beam through Green’s function technique. Li and Yuan [26] applied the quasi-Green’s function technique to solve the free vibration problem of thin plates on the Winkler foundation. Sun et al. [27] studied the thermomechanical response of a beam induced by a movable laser pulse. They derived the Green’s function for the fourth-order vibration equation and derived the deflection of a heated beam. Ma et al. [28,29] utilized the Green’s function technique to present a general solution for the dual-phase-lag heat conduction equations of a two-dimensional square plate and a three-dimensional skin model.
In the work, a Bernoulli beam setting on an elastic foundation is considered, and its dynamic response is studied when it is exposed to a moving laser pulse. The nonhomogeneous heat conduction equation and vibration equation are solved analytically to derive the temperature, deflection and strain.
2. Basic Formulations of the Problem
Assume that a Bernoulli beam is exposed to a moving laser pulse which is decaying exponentially with time. Due to the irradiation of the laser pulse, the temperature of the beam will increase, and vibrations will be generated by thermal impulses generated by laser which generate impulsive local thermal strains. The beam is put on an elastic foundation and is simply supported on both ends. The Winkler model is selected to describe the vibration of the beam resting on the elastic foundation. The laser pulse moves on the top surface of the beam, which is illustrated in Figure 1. Assume that the beam material is isotropic and linear elastic and the deflection is small. The Cartesian coordinate is used to study the temperature rise and vibration of the beam. Then the laser pulse scans towards right from the left end at uniform speed . The dimensions of the beam are shown in Figure 1, that is, the length is , the width is , and the thickness is .
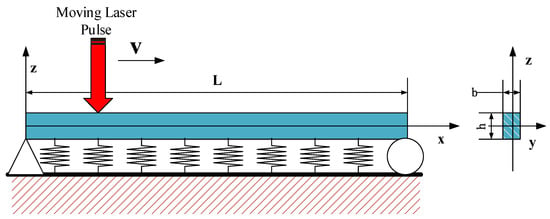
Figure 1.
Sketch map of the beam resting on elastic foundation.
The heat conduction is described by the following equation [30]:
where is time, the temperature rise, the thermal diffusivity, the thermal conductivity. And is the thermal source function as expressed by [7]
where, and are the power intensity and duration time of the laser, the energy absorption coefficient, the energy absorption depth, and the Dirac delta function.
The vibration equation of the beam on elastic foundation is [31,32]
where is the deflection, the modulus of elastic foundation reaction, the density, the Young’s modulus, the moment of inertial, the cross section area, the linear thermal expansion coefficient. is the thermal moment.
The beam is set to be isothermal on the two ends and the bottom surface, while adiabatic on the top surface, so the thermal boundary conditions are
Since the beam is simply supported on both ends, the supporting conditions are
And the initial conditions are
3. Derivation of Temperature Rise
The heat conduction equation is solved by adopting the Green’s function approach. Based on the approach of separation of variables, the following auxiliary problem for the same problem is considered [30]
and applied to the following condition
So, the proper Green’s function satisfying Equations (1), (2), (4) and (6) are obtained as
where, and and are the eigenfunctions of the homogeneous heat conduction equation related to the boundary conditions, which are given as
where , .
The temperature function can be obtained as [30]
Substitute Equations (2) and (10) into Equation (12), and the temperature can be obtained as
where
4. Solution of Vibration Equation
Substitution of Equation (12) into yields
where and .
It is obvious that , so . In such a case, the supporting conditions Equation (6) residues to
Equation (3) could be rearranged as
where, , and .
Substitution of Equation (16) into yields
The free transverse vibration of a beam setting on an elastic foundation is given by
The solution of this equation is gained through the approach of separation of variables. In this case, we assume a solution in the form
where depends on space and is a temporal function.
Consider the general case that the initial conditions are
The solution of Equation (20) for the homogeneous boundary conditions can be obtained as
where the vibration mode function satisfying the boundary conditions is
where (s = 1, 2, 3, …), , and .
The solution of Equation (20) by Green’s function approach is [33]
Comparison between Equations (23) and (25) gives
Since the above two expresses satisfy the following relationship:
the Green’s function for Equation (20) can be taken as .
The authors [27] have derived the Green’s function for the fourth-order vibration equation of a simple supported beam. Following the procedures of Ref. [27], the Green’s function of Equation (18) could be derived as , so the deflection of the beam can be expressed by [27]
The defection is achieved from Equations (19), (27) and (29) as
where,
One can find that
So only take the items of in Equation (30), and the expression of deflection could be simplified as
where
The total strain induced in the beam is
Substitute Equation (35) into Equation (37), and the expression of strain could be gained as
5. Results and Discussions
Take a copper beam as an example in the following calculations. The used parameters are [34]: , , , , , , , , , , .
5.1. Example Results of Temperature, Deflection and Strain
Figure 2 shows the time histories and spatial distributions of the temperature, deflection, and strain of the beam under the laser pulse velocity of 20 m/s. The other parameters in the calculation are and . The propagations of thermal wave and strain wave are obvious in the figures.
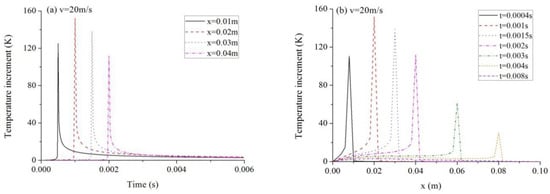
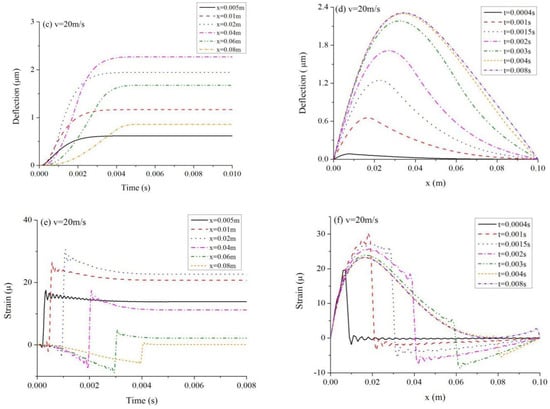
Figure 2.
Responses of the beam under the laser pulse velocity of 20 m/s. (a) Temperature increment vs. time; (b) Temperature increment vs. location; (c) Deflection vs. time; (d) Deflection vs. location; (e) Strain vs. time; (f) Strain vs. location.
Figure 2a shows the time histories of temperature increments on the top surface () at various axial locations and Figure 2b its spatial distribution at several moments. The temperature is zero at the beginning. It rises to the peak value soon and then declines to a steady value instantly. As the distance away from the left side enlarges, it needs a longer time for the temperature to begin rising. The steady value of temperature increment is almost the same at different locations, which is sure because the laser pulse decays after about and there is no heat input or loss under the condition of this problem. It could be found from Figure 2a,b that the peak temperature increment takes the maximum value at the location of and the highest value occurs at the moment of . This is because the power density of the laser pulse takes the maximum value at the moment of .
Figure 2c,d show the time histories and spatial distributions of deflection. Figure 2e,f show a the temporal and special distributions of strains on the top surface. It can be found that the deflection is not symmetric about the midspan of the beam. Instead, it takes the maximum deflection at a location near to the left end. This is the result of the motion of laser pulse. In addition, the propagation of the strain wave can be observed in Figure 2f. The vibrations are induced by thermal impulses which generate thermal strains at specific locations. Since the laser pulse, or the thermal impulse moves along the axis direction, the front of the strain wave propagates towards right as time passes.
In the following, the influences of the laser pulse speed, the modulus of elastic foundation reaction and the duration time of laser pulse on the thermal behaviors of the beam are evaluated.
5.2. Influence of Laser Pulse Speed
First of all, the effect of the laser speed is discussed. Four velocities are taken in the calculation, that is, 2, 5, 10, and 20 m/s, respectively. The values of and keep as and , respectively. Table 1 shows the maximum results of the temperature increment on the top surface () under the four laser speeds. It is obvious that when the velocity of laser pulse grows, the peak value of temperature increment drops.

Table 1.
Maximum temperature increment under different laser speed.
Figure 3 shows the maximum deflection of the beam and the corresponding location at which the maximum deflection occurs at several moments under the four laser velocities of 2, 5, 10, and 20 m/s, respectively. It can be seen that both the maximum deflection as well as the corresponding location enlarge with the rise of laser pulse speed. Under a low laser speed, the maximum deflection occurs at a location close to the left end. As the scanning speed rises, this location moves toward the right. These responses are because the deflection is induced by the thermal loading, which depends on the motion of the laser pulse.
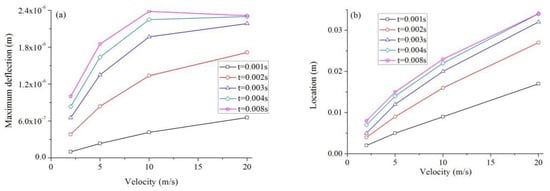
Figure 3.
Influences of laser speed on the deflection. (a) Maximum deflection vs. velocity; (b) Corresponding location vs. velocity.
Figure 4 shows the strain on the top surface along the axis of the beam when the motion velocities of laser pulse are 2, 5, and 10 m/s. Comparing with Figure 2f, it could be found that the velocity of laser pulse is important for the strain. The front of strain wave can be seen clearly in the figures. When the laser moves slowly, there is mainly tension stress close to the original point of the beam. However, as the laser pulse moves faster, the strain wave propagates a longer distance and the portion with positive strain becomes larger along the beam axis. Furthermore, the maximum value of strain drops as the laser velocity increases. At the same time, negative strain occurs, and its magnitude increases at the right part of the beam.
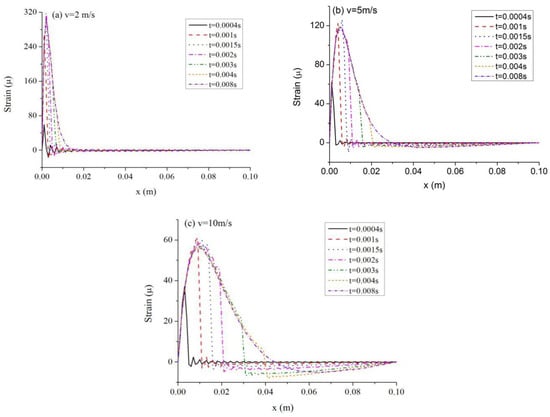
Figure 4.
Influences of laser speed on the strain. (a) ; (b) ; (c) .
Two parameters are used to describe the energy absorbed by the foundation: (a) Linear density of energy, defined as , which describes the energy density absorbed by the foundation along -axis; (b) Relative density of energy, defined as , which describes the percent of energy absorbed at each location to the total energy absorbed by the foundation over the beam span. The two parameters are defined as
where is the total energy absorbed by the foundation over the beam span.
To examine the influences of the laser velocity on and , the distribution of them along x-axis under four different laser speeds are calculated with the results shown in Figure 5. In the calculation, the time is . It can be found from Figure 5 that the scanning speed of laser pulse can affect the energy absorption properties greatly. As the scanning speed increases, the linear density of energy, , increases while the relative density of energy, , decreases. And the locations where the maximum values of and occur move towards right. This behavior is due to the laser motion. When the laser pulse moves slowly, only a small region of the beam is exposed to the laser pulse. So, the temperature of the small area can rise to a high level, but the other regions are hardly heated. As a result, the beam deflection is small, and the uniformity is low. However, when the speed of laser pulse increases, a larger region of the beam is heated, and the beam deflection increases. Meantime, the maximum value of temperature decreases, so the uniformity of deflection along the beam span increases. Consequently, we can find that increases while decreases with the increment of laser speed.
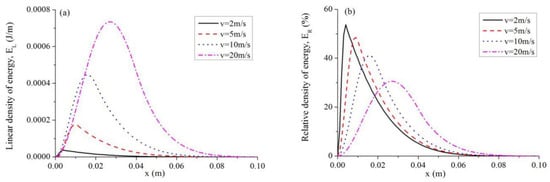
Figure 5.
Influence of scanning speed on energy absorption behaviors of foundation. (a) Linear density of energy vs. location; (b) Relative density of energy vs. location.
5.3. Influence of Modulus of Elastic Foundation Reaction
The influences of modulus of elastic foundation reaction, , on the thermoelastic responses are studied. Four values of are taken, namely 0, , , and . The values of and remain 20 m/s and 1 ms, respectively. Figure 6a shows the maximum deflection vs. at several moments. And the relationship between the corresponding location where the maximum deflection occurs and the value of is also shown in Figure 6b. The distribution of strain on the top surface of the beam for has been shown in Figure 2f, and the results for the other three values of are shown in Figure 7. It is known that a small means flexible foundation, while a large one stands for rigid foundation. As increases, more energy can be absorbed by the elastic foundation, so both the maximum deflection and the peak strain of the beam decrease. It is clear that the corresponding location of maximum deflection declines with the rise of . In addition, the vibration properties are quite different in the four cases. When is large, say , negative strain follows the peak value, and the absolute value of the negative strain first increases and then decreases as time passes. However, as is small, the negative strain also is small. Especially, when is 0, the strain is almost 0 after the wave front.
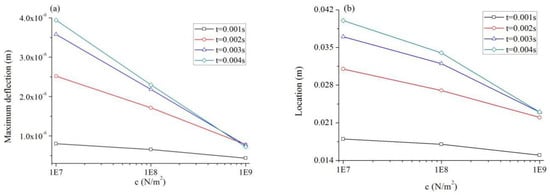
Figure 6.
Influence of on deflection. (a) Maximum deflection vs. ; (b) Corresponding location vs. .
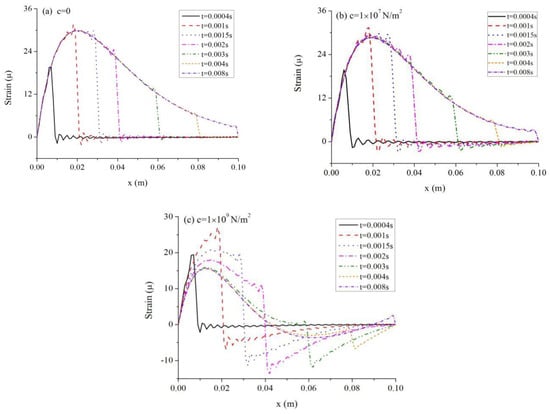
Figure 7.
Influence of on strain. (a) ; (b) ; (c) .
The influences of the modulus of elastic foundation reaction on and are shown in Figure 8. It is clear that as inclines, both and increase.
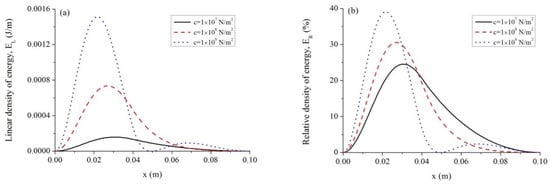
Figure 8.
Influence of modulus of elastic foundation reaction on energy absorption behaviors of foundation. (a) Linear density of energy vs. ; (b) Relative density of energy vs. .
It is easy to find in Figure 8 that there are two peaks in the curves when . This is because there is negative deflection in such a case. The deflection curves at the moment under three values of are shown in Figure 9.
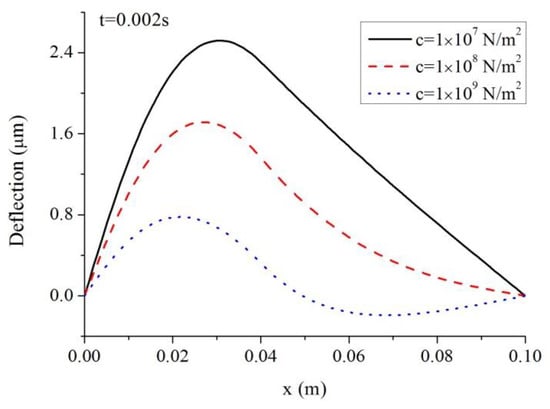
Figure 9.
Deflection vs. along the beam span ().
5.4. Influence of Duration Time of Laser Pulse
Three duration times of laser pulse are selected, namely, , and s. The laser velocity is and the other parameters are the same as those in Figure 2. Since the strain distribution is similar to that of Figure 2f, only the maximum strain, , and the corresponding location are given in Table 2. It is shown that decreases while the corresponding location moves toward the right when increases.

Table 2.
Influence of duration time on strain.
The energy absorption characteristics can vary with different duration time of laser pulse . The variations of and vs. are shown in Figure 10. Since the laser pulse disappears at the time of , the curves of and at the moment of are shown in Figure 10. It can be found that as increases, the peak value of first increases and then decreases, while continues decreasing. Furthermore, the locations where the peak values of and occur moves toward the right as increases.
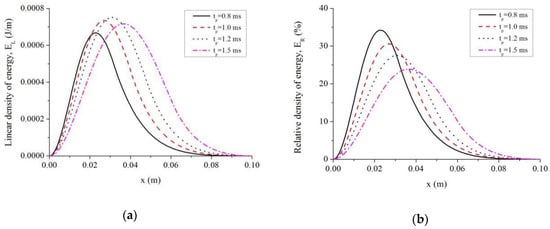
Figure 10.
Influence of tp on energy absorption behaviors of foundation. (a) Linear density of energy vs. location; (b) Relative density of energy vs. location.
6. Conclusions
The thermal behavior of a simply supported beam setting on an elastic foundation and irradiated by a moving laser pulse is studied. The analytical solutions of temperature, deflection, and strain were obtained through adopting the Green’s function technique.
The effects of the laser velocity, the modulus of elastic foundation reaction, and the duration time of the laser pulse are studied in detail. The following conclusions are drawn:
When the velocity of laser pulse rises, the peak values of temperature increment, strain, and the relative density of energy decrease, while the maximum deflection and the linear density of energy increases.
As the modulus of elastic foundation reaction increases, more energy can be absorbed by the elastic foundation, so the maximum deflection, the peak values of strain, the linear density of energy and the relative density of energy of the beam decrease. When is large enough, negative strain occurs following the wave front.
As rises, the maximum strain declines, and the corresponding location moves toward the right. Meanwhile, the peak value of first increases and then decreases, while continues decreasing.
Author Contributions
Methodology, S.L.; Investigation, Z.R. and Y.L.; Writing—Original Draft Preparation, Y.S.; Supervision, J.Y.
Acknowledgments
This work is financially supported by the National Natural Science Foundation of China under grant number 11002017.
Conflicts of Interest
The authors declare they have no conflict of interest.
References
- Cline, H.E.; Anthony, T.R. Heat treating and melting material with a scanning laser or electron beam. J. Appl. Phys. 1977, 48, 3895–3900. [Google Scholar] [CrossRef]
- Mercier, R.J.; Malkin, S.; Mollendorf, J.C. Thermal stresses from a moving band source of heat on the surface of a semi-infinite solid. J. Eng. Ind. 1978, 100, 43–48. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Ohta, A.; Matsuoka, K.; Suzuki, N.; Maeda, Y. Analytic solutions for transient temperature of semi-infinite body subjected to 3-D moving heat sources. Weld. Res. 1999, 8, 265–274. [Google Scholar]
- Elsen, M.V.; Baelmans, M.; Mercelis, P.; Kruth, J.P. Solutions for modelling moving heat sources in a semi-infinite medium and applications to laser material processing. Int. J. Heat Mass Trans. 2007, 50, 4872–4882. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ma, J.X.; Wang, X.; Soh, A.K.; Yang, J.L. Thermoelastic response of a one-dimensional semi-infinite rod heated by a moving laser pulse. Can. J. Phys. 2016, 94, 953–959. [Google Scholar] [CrossRef]
- Ootao, Y.; Tanigawa, Y. Three-dimensional solution for transient thermal stresses offunctionally graded rectangular plate due to nonuniform heat supply. Int. J. Mech. Sci. 2005, 47, 1769–1788. [Google Scholar] [CrossRef]
- Yang, X.F.; Ma, J.X.; Liu, S.B.; Xing, Y.; Yang, J.L.; Sun, Y.X. Exact analytical solution for thermoelastic response of clamped beams subjected to a movable laser pulse. Symmetry 2018, 10, 139. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ma, J.X.; Liu, S.B.; Yang, J.L. Analytical solution of transient heat conduction in a bi-layered circular plate irradiated by laser pulse. Can. J. Phys. 2017, 95, 322–330. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Kenney, J.T. Steady-state vibrations of beam on elastic foundation for moving load. J. Appl. Mech. 1954, 21, 359–364. [Google Scholar]
- Sun, L. A closed-form solution of beam on viscoelastic subgrade subjected to moving loads. Comput. Struct. 2002, 80, 1–8. [Google Scholar] [CrossRef]
- Kim, S.M. Vibration and stability of axial loaded beams on elastic foundation under moving harmonic loads. Eng. Struct. 2004, 26, 95–105. [Google Scholar] [CrossRef]
- Basu, D.; Rao, V.K. Analytical solutions for Euler–Bernoulli beam on visco-elastic foundation subjected to moving load. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 945–960. [Google Scholar] [CrossRef]
- Brown, T.; Du, S.K.; Eruslu, H.; Sayas, F.J. Analysis of models for viscoelastic wave propagation. Appl. Math. Nonlinear Sci. 2018, 3, 55–96. [Google Scholar]
- .Żur, K.K. Green’s function approach to frequency analysis of thin circular plates. Bull. Polish Acad. Sci. Tech. Sci. 2016, 64, 181–188. [Google Scholar]
- Żur, K.K. Free vibration analysis of elastically supported functionally graded annular plates via quasi-Green’s function method. Comp. Part B Eng. 2018, 144, 37–55. [Google Scholar] [CrossRef]
- Żur, K.K. Green’s function for frequency analysis of thin annular plates with nonlinear variable thickness. Appl. Math. Model. 2016, 40, 3601–3619. [Google Scholar] [CrossRef]
- Żur, K.K. Green’s function in frequency analysis of circular thin plates of variable thickness. J. Theor. Appl. Mech. 2015, 53, 873–884. [Google Scholar] [CrossRef]
- Żur, K.K. Quasi-Green’s function approach to free vibration analysis of elastically supported functionally graded circular plates. Comput. Struct. 2018, 183, 600–610. [Google Scholar] [CrossRef]
- Zhao, X.; Hu, Q.J.; Crossley, W.; Du, C.C.; Li, Y.H. Analytical solutions for the coupled thermoelastic vibrations of the cracked Euler-Bernoulli beams by means of Green’s functions. Int. J. Mech. Sci. 2017, 128–129, 37–53. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, E.C.; Li, Y.H. Analytical solutions for the coupled thermoelastic vibrations of Timoshenko beams by means of Green’s functions. Int. J. Mech. Sci. 2017, 128, 37–53. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Y.R.; Gao, X.Z.; Li, X.Y.; Li, Y.H. Green’s functions for the forced vibrations of cracked Euler–Bernoulli beams. Mech. Syst. Signal Process. 2016, 68–69, 155–175. [Google Scholar] [CrossRef]
- Chen, T.; Su, G.Y.; Shen, Y.S.; Gao, B.; Li, X.Y.; Müller, R. Unified Green’s functions of forced vibration of axially loaded Timoshenko beam: Transition parameter. Int. J. Mech. Sci. 2016, 113, 211–220. [Google Scholar] [CrossRef]
- Hozhabrossadati, S.M.; Sani, A.A.; Mehri, B.; Mofid, M. Green’s function for uniform Euler–Bernoulli beams at resonant condition: introduction of Fredholm alternative theorem. Appl. Math. Model. 2015, 39, 3366–3379. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Rajabzadeh-Safaei, N.; Hozhabrossadati, S.M. Three-dimensional deformations of a curved circular beam subjected to thermo-mechanical loading using green’s function method. Int. J. Mech. Sci. 2018, 142, 163–175. [Google Scholar] [CrossRef]
- Li, S.Q.; Yuan, H. Quasi-Green’s function method for free vibration of clamped thin plates on Winkler foundation. Appl. Math. Mech. Engl. Ed. 2011, 32, 265–276. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ma, J.X.; Yang, X.F.; Liu, S.B.; Yang, J.L. Thermoelastic response of a simply supported beam irradiated by a movable laser pulse. Can. J. Phys. 2017, 95, 1012–1022. [Google Scholar] [CrossRef]
- Ma, J.X.; Sun, Y.X.; Yang, J.L. Analytical solution of dual-phase-lag heat conduction in a finite medium subjected to a moving heat source. Int. J. Therm. Sci. 2018, 125, 34–43. [Google Scholar] [CrossRef]
- Ma, J.X.; Yang, X.F.; Liu, S.B.; Sun, Y.X.; Yang, J.L. Exact solution of thermal response in a three-dimensional living bio-tissue subjected to a scanning laser beam. Int. J. Heat Mass Trans. 2018, 124, 1107–1116. [Google Scholar] [CrossRef]
- Ozisik, M.N. Heat Conduction, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Warburton, G.B. The Dynamical Behavior of Structures, 2nd ed.; Pergamon Press Ltd.: Oxford, UK, 1976. [Google Scholar]
- Zhou, H.F.; Jiang, J.Q.; Zhang, T.Q. Steady-state response of infinite beam on Kelvin foundation under moving loads. J. Zhejiang Univ. (Eng. Sci.) 2004, 38, 1328–1333. (In Chinese) [Google Scholar]
- Stakgold, I. Green’s Functions and Boundary Value Problems, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1997. [Google Scholar]
- Sun, Y.X.; Jiang, Y.; Yang, J.L. Thermoelastic damping of the axisymmetric vibration of laminated trilayered circular plate resonators. Can. J. Phys. 2014, 92, 1026–1032. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).