Abstract
In classical group theory, homomorphism and isomorphism are significant to study the relation between two algebraic systems. Through this article, we propose neutro-homomorphism and neutro-isomorphism for the neutrosophic extended triplet group (NETG) which plays a significant role in the theory of neutrosophic triplet algebraic structures. Then, we define neutro-monomorphism, neutro-epimorphism, and neutro-automorphism. We give and prove some theorems related to these structures. Furthermore, the Fundamental homomorphism theorem for the NETG is given and some special cases are discussed. First and second neutro-isomorphism theorems are stated. Finally, by applying homomorphism theorems to neutrosophic extended triplet algebraic structures, we have examined how closely different systems are related.
1. Introduction
Groups are finite or infinite set of elements which are vital to modern algebra equipped with an operation (such as multiplication, addition, or composition) that satisfies the four basic axioms of closure, associativity, the identity property, and the inverse property. Groups can be found in geometry studied by “Felix klein in 1872” [1], characterizing phenomenality like symmetry and certain types of transformations. Group theory, firstly introduced by “Galois” [2], with the study of polynomials has applications in physics, chemistry, and computer science, and also puzzles like the Rubik’s cube as it may be expressed utilizing group theory. Homomorphism is both a monomorphism and an epimorphism maintaining a map between two algebraic structures of the same type (such as two groups, two rings, two fields, two vector spaces) and isomorphism is a bijective homomorphism defined as a morphism, which has an inverse that is also morphism. Accordingly, homomorphisms are effective in analyzing and calculating algebraic systems as they enable one to recognize how intently distinct systems are associated. Similar to the classical one, neuro-homomorphism is the transform between two neutrosophic triplet algebraic objects N and H. That is, if elements in N satisfy some algebraic equation involving binary operation “*”, their images in H satisfy the same algebraic equation. A neutro-isomorphism identifies two algebraic objects with one another. The most common use of neutro-homomorphisms and neutro-isomorphisms in this study is to deal with homomorphism theorems which allow for the identification of some neutrosophic triplet quotient objects with certain other neutrosophic triplet subgroups, and so on.
The neutrosophic logic and a neutrosophic set, firstly made known by Florentin Smarandache [3] in 1995, has been widely applied to several scientific fields. This study leads to a new direction, exploration, path of thinking to mathematicians, engineers, computer scientists, and many other researchers, so the area of study grew extremely and applications were found in many areas of neutrosophic logic and sets such as computational modelling [4], artificial intelligence [5], data mining [6], decision making problems [7], practical achievements [8], and so forth. Florentin Smarandache and Mumtazi Ali investigated the neutrosophic triplet group and neutrosophic triplet as expansion of matter plasma, nonmatter plasma, and antimatter plasma [9,10]. By using the concept of neutrosophic theory Vasantha and Smarandache introduced neutrosophic algebraic systems and N-algebraic structures [11] and this was the first neutrosofication of algerbraic structures. The characterization of cancellable weak neutrosophic duplet semi-groups and cancellable NTG are investigated [12] in 2017. Florentin Smarandache and Mumtaz Ali examined the applications of the neutrosophic triplet field and neutrosophic triplet ring [13,14] in 2017. Şahin Mehmet and Abdullah Kargın developed the neutrosophic triplet normed space and neutrosophic triplet inner product [15,16]. The neutrosophic triplet G-module and fixed point theorem for NT partial metric space are given in literature [17,18]. Similarity measures of bipolar neutrosophic sets and single valued triangular neutrosophic numbers and their appliance to multi-attribute group decision making investigated in [19,20]. By utilizing distance-based similarity measures, refined neutrosophic hierchical clustering methods are achieved in [21]. Single valued neutrosophic sets to deal with pattern recognition problems are given with their application in [22]. Neutrosophic soft lattices and neutrosophic soft expert sets are analyzed in [23,24]. Centroid single valued neutrosophic numbers and their applications in MCDM is considered in [25]. Bal Mikail, Moges Mekonnen Shalla, and Necati Olgun reviewed neutrosophic triplet cosets and quotient groups [26] by using the concept of NET in 2018. The concepts concerning neutrosophic sets and neutrosophic modules are described in [27,28], respectively. A method to handle MCDM problems under the SVNSs are introduced in [29]. Bipolar neutrosophic soft expert set theory and its basic operations are defined in [30].
The other parts of a paper is coordinated thusly. Subsequently, through the literature analysis in the first section and preliminaries in the second section, we investigated neutro-monomorphism, neutro-epimorphism, neutro-isomorphism, and neutro-automorphism in Section 3 and a fundamental homomorphism theorem for NETG in Section 4. We give and prove the first neutro-isomorphism theorem for NETG in Section 5, and then the second neutro-isomorphism theorem for NETG is given in Section 6. Finally, results are given in Section 7.
2. Preliminaries
In this section, we provide basic definitions, notations and facts which are significant to develop the paper.
2.1. Neutrosophic Extended Triplet
Let U be a universe of discourse, and (N, ∗) a set included in it, endowed with a well-defined binary law ∗.
Definition 1
([3]).The set N is called a neutrosophic extended triplet set if for any x ∈ N there exist eneut(x) ∈ N and eanti(x) ∈ N. Thus, a neutrosophic extended triplet is an object of the form (x, eneut(x), eanti(x)) where eneut(x) is extended neutral of x, which can be equal or different from the classical algebraic unitary element if any, such that
and eanti(x) ∈ N is the extended opposite of x such that
In general, for each x ∈ N there are many existing and .
Theorem 1
([11]).Let (N, ∗) be a commutative NET with respect to ∗ and a, b ∈ N;
- (i)
- (ii)
Theorem 2
([11]).Let (N, ∗) be a commutative NET with respect to ∗ and a ∈ N;
- (i)
- (ii)
2.2. NETG
Definition 2
([3]).Let (N, ∗) be a neutrosophic extended triplet set. Then (N, ∗) is called a NETG, if the following classical axioms are satisfied.
- (a)
- (N, ∗) is well defined, i.e., for any one has
- (b)
- (N, ∗) is associative, i.e., for anyone has
We consider, that the extended neutral elements replace the classical unitary element as well the extended opposite elements replace the inverse element of classical group. Therefore, NETGs are not a group in classical way. In the case when NETG enriches the structure of a classical group, since there may be elements with more extended opposites.
2.3. Neutrosophic Extended Triplet Subgroup
Definition 3
([26]).Given a NETG (N, ∗), a neutrosophic triplet subset H is called a neutrosophic extended triplet subgroup of N if it itself forms a neutrosophic extended triplet group under ∗. Explicity this means
- (1)
- The extended neutral element lies in H.
- (2)
- For any
- (3)
- If then
In general, we can show and then
Definition 4.
Suppose that N is NETG and are called neutrosophic triplet conjugates of N if thereby
2.4. Neutro-Homomorphism
Definition 5
([26]).Let (N1, ∗) and (N2, ∘) be two NETGs. A mapping is called a neutro-homomorphism if
- (a)
- For any we have
- (b)
- If is a neutrosophic extended triplet from N1, thenand
Definition 6
([26]).Let f: N1→N2 be a neutro-homomorphism from a NETG (N1, ∗) to a NETG (N2, ∘). The neutrosophic triplet image of f is
Definition 7
([26]).Let f: N1→N2 be a neutro-homomorphism from a NETG (N1, ∗) to a NETG (N2, ∘) and B ⊆ N2. Then
is the neutrosophic triplet inverse image of B under f.
Definition 8
([26]).Let be a neutro-homomorphism from a NETG (N1, ∗) to a NETG (N2, ∘). The neutrosophic triplet kernel of f is a subset
where neut(x) denotes the neutral element of N2.
Definition 9.
The neutrosophic triplet kernel of φ is called the neutrosophic triplet center of NETG N and it is denoted by Z(N). Explicitly,
Hence Z(N) is the neutrosophic triplet set of elements in N that commute with all elements in N. Note that obviously Z(N) is a neutrosophic triplet. We have in the case that N is abelian.
Definition 10
([26]).Let N be a NETG and the set is called neutrosophic triplet coset denoted by xH. Analogously,
and
When is called the left neutrosophic triplet coset of H in N containing x, and Hx is called the right neutrosophic triplet coset of H in N containing x. are used to denote the number of elements in respectively.
2.5. Neutrosophic Triplet Normal Subgroup and Quotient Group
Definition 11
([26]).A neutrosophic extended triplet subgroup H of a NETG of N is called a neutrosophic triplet normal subgroup of N if and we denote it as
Example 1.
Let N be NETG. {neut} ⊲ N and N ⊴ N.
Definition 12
([26]).If N is a NETG and H ⊴ N is a neutrosophic triplet normal subgroup, then the neutrosophic triplet quotient group N/H has elements the neutrosophic triplet cosets of H in N, and operation
3. Neutro-Monomorphism, Neutro-Epimorphism, Neutro-Isomorphism, Neutro-Automorphism
In this section, we define neutro-monomorphism, neutro-epimorphism, neutro-isomorphism, and neutro-automorphism. Then, we give and some important theorems related to them.
3.1. Neutro-Monomorphism
Definition 13.
Assume that (N1, ∗) and (N2, ∘) be two NETG’s. If a mapping of NETG is only one to one (injective) f is called neutro-monomorphism.
Theorem 3.
Let (N1, ∗) and (N2, ∘) be two NETG’s. is a neutro-monomorphism of NETG if and only if
Proof.
Assume φ is injective. If a ∈ kerφ, then
and hence by injectivity a = neutN1. Conversely, assume kerφ = φ(neutN1). Let a,b ∈ N1 such that φ(a) = φ(b). We need to show that a = b.
Thus and hence, by assumption We conclude that ☐
Definition 14.
Let (N1, ∗) and (N2, ∘) be two NETG’s. If a mapping is only onto (surjective) f is called neutro-epimorphism.
Theorem 4.
Let N and H be two NETG’s. If is a neutro-homomorphism of NETG, then so is φ−1: H → N.
Proof.
Let and So Now
☐
Theorem 5.
Let N be NETG and The map is a neutro-homomorphism.
Proof.
For any fixed we have
It is in fact has anti-neutral element i.e., Since and so φn is injective. ☐
Theorem 6.
Let be a neutro-homomorphism of NETG N and H. For and
Proof.
- (1)
- Let’s show thatIf then and then If then:For at least If then,
- (2)
- Let’s show that Let For at leastIf and thenby (1) and (2), we obtain ☐
Theorem 7.
Let be a neutro-homomorphism of NETG N1 and N2.
- (1)
- (2)
Proof.
- (1)
- If and then and so . Since H2 is neutrosophic triplet normal subgroup. We conclude
- (2)
- Since H1 is neutrosophic triplet normal subgroup, we have Since we assume φ is surjective, every can be written as Therefore, ☐
Theorem 8
([26]).Let be a neutro-homomorphism from a NETG N to a NETG H.
Theorem 9.
Let N be NETG and H ⊴ N. The map is a neutro-homomorphism with neutrosophic triplet kernel
Proof.
We have so φ is a neutro-homomorphism. As to the neutrosophic triplet kernel, (since H is neutral in N/H) (by definition of φ) ☐
Theorem 10.
Let N be NETG and be a non-empty neutrosophic extended triplet subset. Then if and only if there exists a neutro-homomorphism
Proof.
Its straight forward. ☐
3.2. Neutro-Isomorphism
Definition 15.
Let (N1, ∗) and (N2, ∘) be two NETGs. If a mapping neutro-homomorphism is one to one and onto f is called neutro-isomorphism. Here, N1 and N2 are called neutro-isomorphic and denoted as
Theorem 11.
Let (N1, ∗) and (N2, ∘) be two NETG’s. If is a neutro-isomorphism of NETG’s, then so is
Proof.
It is obvious to show that f is one to one and onto. Now let’s show that f is neutro-homomorphism. Let and so, Now ☐
3.3. Neutro-Automorphism.
Definition 16.
Let (N1, ∗) and (N2, ∘) be two NETG’S. If a mapping is one to one and onto f is called neutro-automorphism.
Definition 17.
Let N be NETG. is called a neutro-inner automorphism if there is a such that
Proposition 1.
Let N be a NETG. For such that is a neutro-automorphism
Proof.
- (1)
- we have to show thatTherefore, f is one to one.
- (2)
- we have to show thatSo, f is onto. Therefore, fa is a neutro-automorphism. ☐
Lemma 1.
Let a be an element of NETG N such that Then
Proof.
We have
☐
Theorem 12.
Let N be NETG and Then the neutrosophic extended triplet set is a neutrosophic extended triplet subgroup in the case that
Proof.
Suppose H1H2 is a neutrosophic extended triplet subgroup. Then, for all we have But also for we find thereby and then So , that’s, On the other hand, assume that Then we have Furthermore, we have ☐
4. Fundamental Theorem of Neutro-Homomorphism
The fundamental theorem of neutro-homomorphism relates the structure of two objects between which a neutrosophic kernel and image of the neutro-homomorphism is given. It is also significant to prove neutro-isomorphism theorems. In this section, we give and prove the fundamental theorem of neutro-homomorphism. Then, we discuss a few special cases. Finally, we give examples by using NETG.
Theorem 13.
Let N1, N2 be NETG’s and be a neutro-homomorphism. Then, Furthermore if ϕ is neutro-epimorphism, then
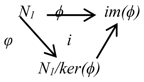
N1/kerϕ ≅ N2.
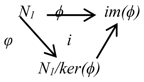
Proof.
We will construct an explicit map and prove that it is a neutro-isomorphism and well defined. Since ker(ϕ) is neutrosophic triplet normal subgroup of N1. Let and recall that Define Thus, we need to check the following conditions.
- (1)
- i is well defined
- (2)
- i is injective
- (3)
- i is surjective
- (4)
- i is a neutro-homomorphism
- (1)
- We must show that if then Suppose We haveHere, Hence, Therefore, it is well defined.
- (2)
- We must show that Suppose that ThenThus, i is injective.
- (3)
- We must show that for any element in the domain (N1/K) gets mapped to it by i. let’s pick any element By definition, hence i is surjective.
- (4)
- We must show that Thus, i is a neutro-homomorphism.
In summary, since is a well-defined neutro-homomorphism that is injective and surjective. Therefore, it is a neutro-isomorphism. and the fundamental theorem of neutro-homomorphism is proven. ☐
Corollary 1 (A Few Special Cases of Fundamental Theorem of Neutro-homomorphism).
- Let N = (1, 1, 1) be a trivial neutrosophic extended triplet. If ϕ: N1→N2 is an embedding, then neutrosophic ker(ϕ) = {neut(1) = 1N1}. The Theorem 12 says that im(ϕ) ≅ {N1/1N1} ≅ N1.
- If ϕ: N1→N2 is a map ϕ(n) = neut(1) = 1N2 for all n2 ∈ N1, then neutrosophic ker(ϕ) = N1, so Theorem 13 says that 1N2 = im(ϕ) ≅ N1/N1.
Example 2.
The neutrosophic extended triplet alternating group An (the neutrosophic extended triplet subgroup of even permutation in NETG Sn) has index 2 in Sn.
Solution.
To prove that [Sn:An] = 2. We will construct a surjective neutro-homomorphism φ: Sn→Z2 with neutrosophic triplet . Here the neutrosophic extended triplets of Z2 are (0, 0, 0) and (1, 1, 1). If this is achieved, it would follow that so |Sn/An| = |Z2| = 2, and therefore [Sn:An] = |Sn/An| = 2, as desired. Define φ: Sn→Z2 by φ(f) =
By construction φ is surjective. To prove that φ is a neutro-homomorphism we need to show that φ(x) + φ(y) = φ(xy), ∀x, y ∈ Sn. Here if x and y are both even or both odd, then xy is even. If x is even and y is odd, or if x is odd and y is even, then xy is odd. Let us see these four different cases as follows:
- (1)
- x and y are both even. Then xy is also even. So, φ(x) = φ(y) = φ(xy) = [0]. Since [0] + [0] = [0] holds.
- (2)
- x is even, and y is odd. Then xy is odd. So, φ(x) + φ(y) = [0] + [1] = [1] = φ(xy).
- (3)
- x is odd, and y is even. This case is analogous to case 2.
- (4)
- x and y are both odd. Then xy is even, so φ(x) + φ(y) = [1] + [1] = [0] = φ(xy). Thus, we verified that φ is a neutro-homomorphism. Finally, neutrosophic trplet kerφ = {x ∈ Sn: φ(x) = [0]2} is the neutrosophic extended triplet set of all even permutations, so neutrosophic triet
5. First Neutro-Isomorphism Theorem
The first neutro-isomorphism theorem relates two neutrosophic triplet quotient groups involving products and intersections of neutrosophic extended triplet subgroups. In this section, we give and prove the first neutro-isomorphism theorem. Finally, we give an example by using NETG.
Theorem 14.
Let N be NETG and H, K be two neutrosophic extended triplet subgroup of N and H is a neutrosophic triplet normal in K. Then
- (a)
- is neutrosophic triplet subgroup of N.
- (b)
- is neutrosophic triplet normal subgroup in K.
- (c)
Proof.
- (a)
- Let If and and Consider
- (b)
- We have to prove is neutrosophic triplet normal subgroup in k or Let and If and then because and because Thus, Since
- (c)
- . Let H ⋂ K = D, so = . Now let’s define a mapping ϕ: HK→ by
- ϕ is well defined
- ϕ is neutro-homomorphism.
- ϕ is onto.
Since for every under ϕ such that Hence, ϕ is onto.
Now by Theorem 13,
Now it is enough to prove that Let Thus
Conversly, where and If then
by (1) . ☐
Example 3.
Let N be NETG. Neutro-isomorphism theorems are for instance useful in the calculation of NETG orders, since neutro-isomorphic groups have the same order. If H ≤ N and K ⊴ N so that HK is finite, then Lagrange’s theorem [26] in neutrosophic triplet with theorem 13 yield
|HK|/|K| = |HK : K|
= |HK/K|
= |H/H ⋂ K|
= |H : H ⋂ K|
= |H|/|H ⋂ K|, that is
|HK| = |H||K|/|H ⋂ K|
= |HK/K|
= |H/H ⋂ K|
= |H : H ⋂ K|
= |H|/|H ⋂ K|, that is
|HK| = |H||K|/|H ⋂ K|
6. Second Neutro-Isomorphism Theorem
The second neutro- isomorphism theorem is extremely useful in analyzing the neutrosophic extended normal subgroups of a neutrosophic triplet quotient group. In this section, we give and prove the second neutro-homomorphism theorem for NETG.
Theorem 15.
Let N be a NETG. Let H and K be neutrosophic triplet normal subgroup of N with Then and
Proof.
Consider the natural map Ѱ:N→N/H. The neutrosophic triplet kernel, H contains K. Thus, by the universal property of , it follows that there is a neutro-homomorphism This map is clearly surjective. In fact, it sends the neutrosophic triplet left coset to the neutrosophic triplet left coset Now suppose that nK is in the neutrosophic triplet kernel. Then the neutrosophic triplet left coset nH is the neutral neutrosophic triplet coset, that is, so that Thus the neutrosophic triplet kernel consists of those neutrosophic triplet left cosets of the form nK, for that is,
- Ѱ is well defined. Let
- Ѱ is neutro-homomorphism
- Ѱ is ontoFor all Ѱ
- kerѰ = H/KThe neutral element of is H. ThereforeBy Theorem 13 ☐
7. Conclusions
This paper is mainly focused on fundamental homomorphism theorems for neutrosophic extended triplet groups. We gave and proved the fundamental theorem of neutro-homomorphism, as well as first and second neutro-isomorphism theorems explained for NETG. Furthermore, we define neutro-monomorphism, neutro-epimorphism, neutro-automorphism, inner neutro-automorphism, and center for neutrosophic extended triplets. Finally, by applying them to neutrosophic algebraic structures, we have examined how closely different systems are related. By using the concept of a fundamental theorem of neutro-homomorphism and neutro-isomorphism theorems, the relation between neutrosophic algebraic structures (neutrosophic triplet ring, neutrosophic triplet field, neutrosophic triplet vector space, neutrosophic triplet normed space, neutrosophic modules, etc.) can be studied and the field of study in neutrosophic algebraic structures will be extended.
Author Contributions
M.Ç. defined and studied preliminaries and the fundamental theorem of neutro-homomorphism theorem with examples and wrote part of the paper. M.M.S. defined and studied first and second neutro-isomorphism theorems with example. The revision and submission of the paper was completed by N.O.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klein, F. His “Erlanger Programm”. In History and Philosophy of Modern Mathematics; University of Minnesota Press: Minneapolis, MN, USA, 1988; Volume 11, p. 145. [Google Scholar]
- Schneps, L.; Lochak, P. (Eds.) Around Grothendieck’s Esquisse D’un Programme; Cambridge University Press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis; American Research Press: Santa Fe, NM, USA, 1998. [Google Scholar]
- Solis, A.R.; Panoutsos, G. Granular computing neural-fuzzy modelling: A neutrosophic approach. Appl. Soft Comput. 2013, 13, 4010–4021. [Google Scholar] [CrossRef]
- Khatibi, V.; Montazer, G.A. Intuitionistic fuzzy set vs. fuzzy set application in medical pattern recognition. Artif. Intell. Med. 2009, 47, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Ye, J. Single-valued neutrosophic minimum spanning tree and its clustering method. Int. J. Intell. Syst. 2014, 23, 311–324. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria decision-making method using the correlation coefficient under single-valued neutrosophic environment. Int. J. Gen. Syst. 2013, 42, 386–394. [Google Scholar] [CrossRef]
- Smarandache, F.; Ye, J. Summary of the Special Issue “Neutrosophic Information Theory and Applications” at “Information” Journal. Information 2018, 9, 49. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2018, 29, 595–601. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic triplet as extension of matter plasma, unmatter plasma, and antimatter plasma. Available online: http://adsabs.harvard.edu/abs/2016APS..GECHT6110S (accessed on 1 August 2018).
- Kandasamy, W.B.; Smarandache, F. Some Neutrosophic Algebraic Structures and Neutrosophic N-Algebraic structures. Available online: https://books.google.com.tr/books/about/Some_Neutrosophic_Algebraic_Structures_a.html?id=ICTeBAAAQBAJ&redir_esc=y (accessed on 1 August 2018).
- Zhang, X.; Smarandache, F.; Liang, X. Neutrosophic Duplet Semi-Group and Cancellable Neutrosophic Triplet Groups. Symmetry 2017, 9, 275. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic Triplet Field used in Physical Applications. Bull. Am. Phys. Soc. 2017, 7, 62. [Google Scholar]
- Smarandache, F.; Ali, M. Neutrosophic Triplet Ring and its Applications (Log Number: NWS17-2017-000062). In Proceedings of the 18th Annual Meeting of the APS Northwest Section, Pacific University, Forest Grove, OR, USA, 1–3 June 2017. [Google Scholar]
- Şahin, M.; Kargın, A. Neutrosophic triplet normed space. Open Phys. 2017, 15, 697–704. [Google Scholar] [CrossRef]
- Şahin, M.; Kargın, A. Neutrosophic triplet inner product space. Neutrosophic Oper. Res. 2017, 2, 193–215. [Google Scholar]
- Smarandache, F.; Şahin, M.; Kargın, A. Neutrosophic Triplet G-Module. Mathematics 2018, 6, 53. [Google Scholar] [CrossRef]
- Şahin, M.; Kargın, A.; Çoban, M.A. Fixed Point Theorem for Neutrosophic Triplet Partial Metric Space. Symmetry 2018, 7, 240. [Google Scholar] [CrossRef]
- Uluçay, V.; Deli, I.; Şahin, M. Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making. Neural Comput. Appl. 2018, 29, 739–748. [Google Scholar] [CrossRef]
- Şahin, M.; Kargın, A.; Smarandache, F. Generalized Single Valued Triangular Neutrosophic Numbers and Aggregation Operators for Application to Multi-attribute Group Decision Making. In New Trends in Neutrosophic Theory and Applications; International Knowledge Press: Manchester, UK, 2017. [Google Scholar]
- Memet, S.; Orhan, E.; Vakkas, U.; Harun, D. Refined Neutrosophic Hierchical Clustering Methods. Asian J. Math. Comput. Res. 2017, 15, 283–295. [Google Scholar]
- Sahin, M.; Olgun, N.; Uluçay, V.; Kargın, A.; Smarandache, F. A New Similarity Measure Based on Falsity Value between Single Valued Neutrosophic Sets Based on the Centroid Points of Transformed Single Valued Neutrosophic Numbers with Applications to Pattern Recognition. Neutrosophics Sets Syst. 2017, 15, 35–52. [Google Scholar]
- Uluçay, V.; Şahin, M.; Olgun, N.; Kilicman, A. On neutrosophic soft lattices. Afr. Matematika 2017, 28, 379–388. [Google Scholar] [CrossRef]
- Sahin, M.; Alkhazaleh, S.; Ulucay, V. Neutrosophic soft expert sets. Appl. Math. 2015, 6, 116–127. [Google Scholar] [CrossRef]
- Sahin, M.; Ecemis, O.; Uluçay, V.; Kargın, A. Some New Generalized Aggregation Operators Based on Centroid Single Valued Triangular Neutrosophic Numbers and Their Applications in Multi-Attribute Decision Making. Asian J. Math. Comput. Res. 2017, 16, 63–84. [Google Scholar]
- Bal, M.; Shalla, M.M.; Olgun, N. Neutrosophic Triplet Cosets and Quotient Groups. Symmetry 2018, 10, 126. [Google Scholar] [CrossRef]
- Olgun, N.; Bal, M. Neutrosophic Modules. In Neutrosophic Operational Research; Pons Publishing House: Brussels, Belgium, 2017; Volume 2, pp. 181–192. [Google Scholar]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Uluçay, V.; Sahin, M.; Dey, A.; Dhar, M.; Tan, R.P.; Bahnasse, A.; et al. Neutrosophic Sets: An Overview. Available online: http://www.rxiv.org/pdf/1805.0007v1.pdf (accessed on 1 August 2018).
- Şahin, M.; Uluçay, V.; Acıoglu, H. Some weighted arithmetic operators and geometric operators with SVNSs and their application to multi-criteria decision making problems. Available online: https://zenodo.org/record/1237954#.W2M2u9IzbIU (accessed on 1 August 2018).
- Şahin, M.; Uluçay, V.; Broumi, S. Bipolar Neutrosophic Soft Expert Set Theory. Available online: https://books.google.com.tr/books/about/Bipolar_Neutrosophic_Soft_Expert_Set_The.html?id=aAhZDwAAQBAJ&redir_esc=y (accessed on 1 August 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).