1. Introduction
In a complex network, one is always interested to uniquely identify the location of nodes by assigning an address with reference to a particular set. Such a particular set with minimum possible nodes is known as the metric basis and its cardinality is known as the metric dimension.
These facts have been efficiently utilized in drug design to attack on particular nodes. Some computational aspects of carbon and boron nanotubes have been summed up in [
1]. Similarly, a moving point in a graph may be located by finding the distance from the point to the collection of sonar stations, which have been properly positioned in the graph [
2]. Thus, finding a minimal sufficiently large set of labeled vertices, such that a robot can find its position, is a problem known as robot navigation, already well-studied in [
3]. This sufficiently large set of labeled vertices is a resolving set of the graph space and the cardinality of such a set with minimum possible elements is the metric dimension. Similarly, on another node, a real-world problem is the study of networks whose structure has not been imposed by a central authority but is also brought into light from local and distributed processes. Obtaining a map of all nodes and the links between them is difficult as well as expensive. To have a good approximation of the real network, a frequently used technique is to attain a local view of network from multiple dimensions and join them. The metric dimension also has some applications in this respect as well.
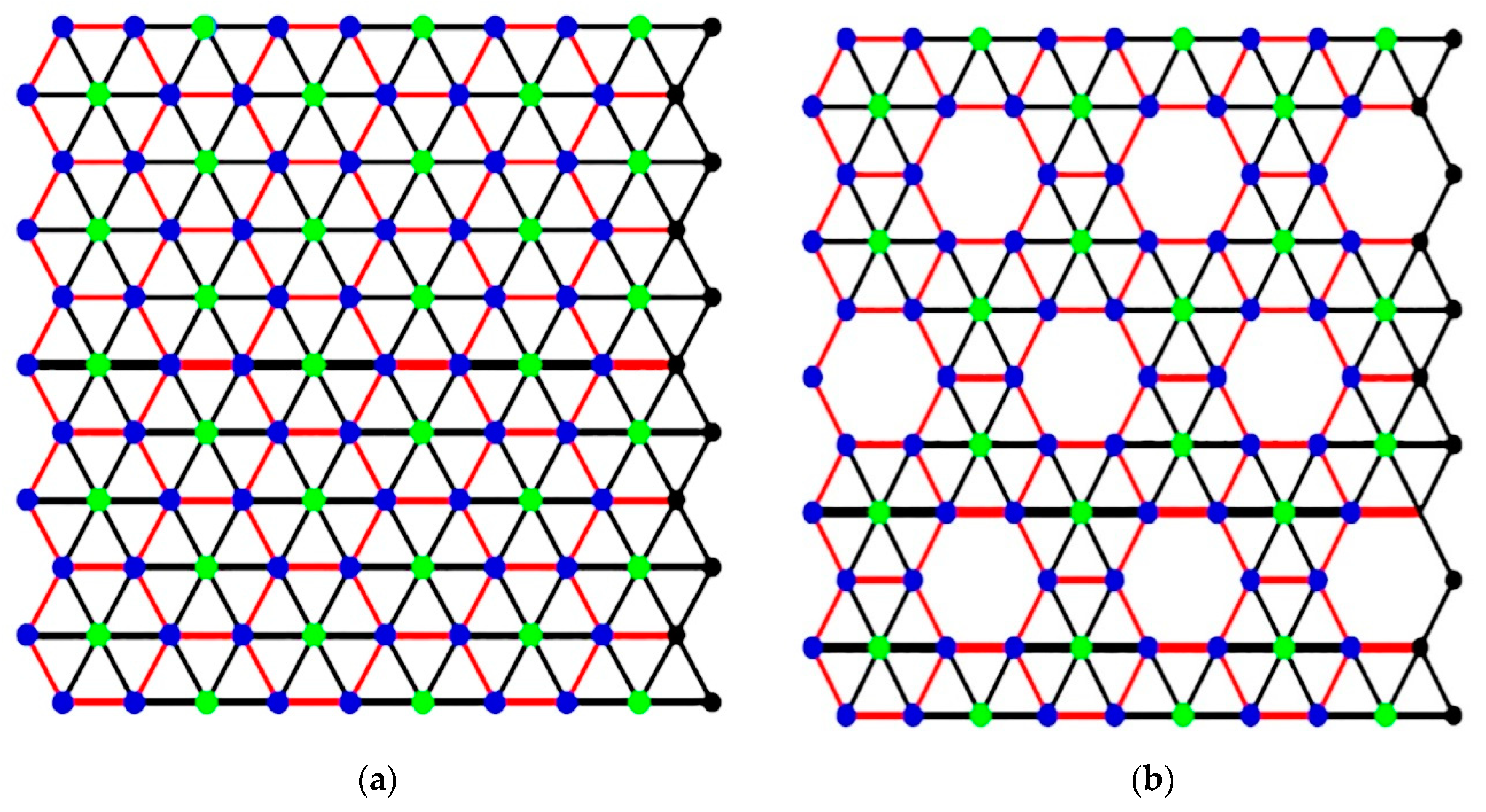
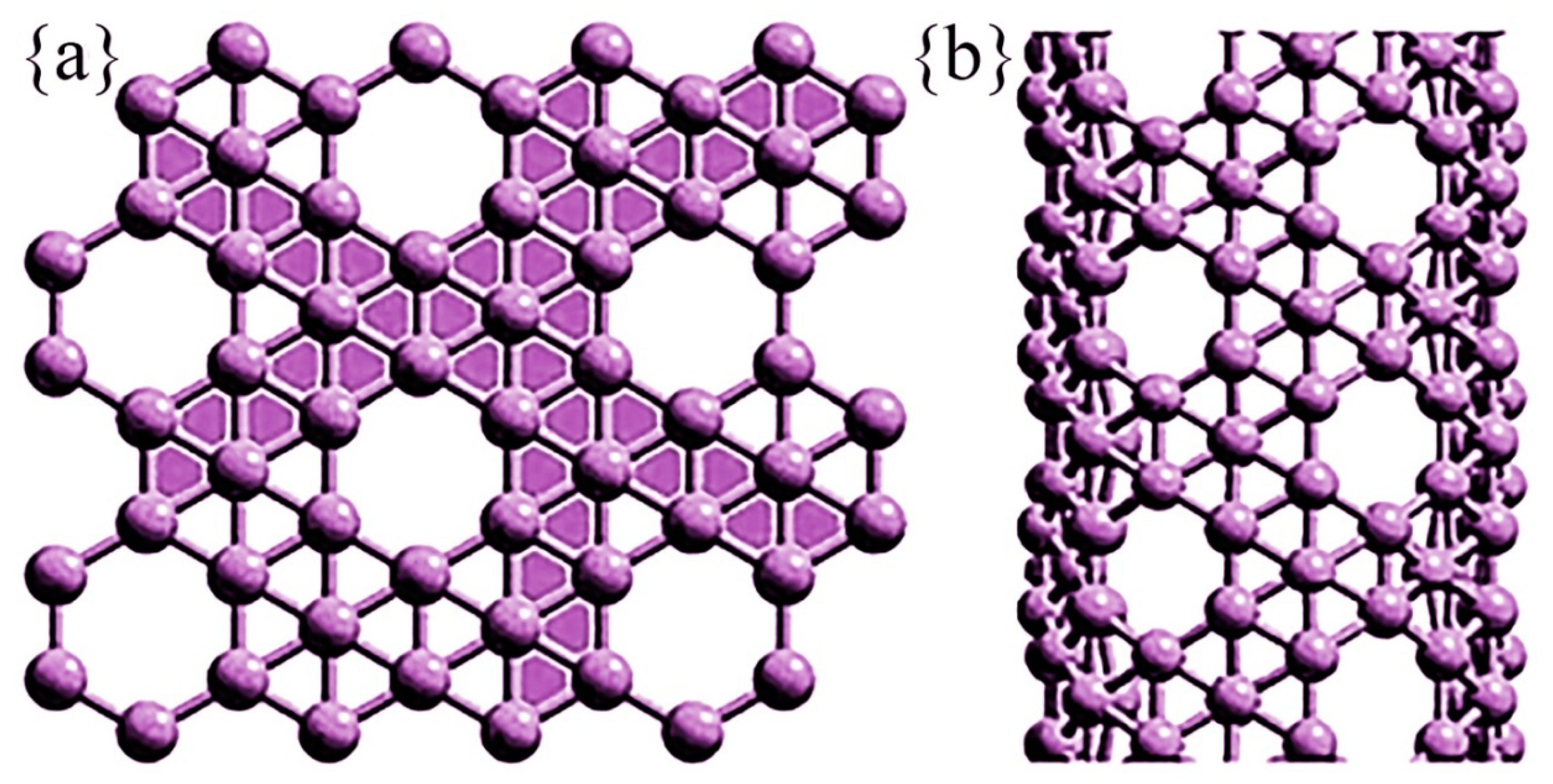
In nanomaterials, nanowires, nanocrystals, and nanotubes formulate three main classes. Boron nanotubes are becoming highly attractive due to their extraordinary features, including work function, transport properties, electronic structure, and structural stability, [
3,
4]. Triangular boron and α-boron are deduced from a triangular sheet and an α-sheet as shown in
Figure 1 below.
The first boron nanotubes were made, in 2004, from a buckled triangular latticework [
4]. The other famous type, alpha-boron, is constructed from an α-sheet. Both types are more conductive than carbon nanotubes regardless of their structure and chiralities. Due to an additional atom at the center of some of the hexagons, alpha-boron nanotubes have a more complex structure than triangular boron nanotubes [
4]. This structure is the most stable known theoretical structure for boron nanotubes. With this specimen, boron nanotubes should have variable electrical properties, where wider ones should be metallic conductors, but narrower ones should be semiconductors. These tubes will replace carbon nanotubes in Nano devices like diodes and transistors. The following figure represents alpha-boron nanotubes.
The subject matter of the present article is the metric dimension of the 2D-lattices of alpha-boron nanotubes. An elementary problem in chemistry is to provide a distinct mathematical representation for the set of atoms, molecules, or compounds in a big structure. Consequently, the huge structure of a chemical compound under discussion can be represented by a labeled graph whose vertex and edge labels specify the atom and bond types, respectively. So, a graph-theoretic interpretation of this problem is to provide unique mathematical representations for the vertices of a graph in such a way that distinct vertices have distinct representations [
5]. Going with a similar idea, we associate a 2D planar graph corresponding to the structure where nodes or vertices are represented for atoms, and where edges are actually the bonds between them. For the basics of graph theory, we refer to [
6].
Let G be a connected graph and
u,
w be any two vertices of G. The length of the shortest path between
u and
w is called the distance between
u and
w and the number of edges between
u and
v in this shortest path is denoted by
. Let
be an ordered set of vertices of G and v
V(G). The k-vector
is called the representation
of
with respect to
. If the distinct vertices of G have a distinct representation with respect to
, then
is called a resolving set of G (see [
7,
8,
9,
10]). A resolving set of minimum cardinality is called a basis of G and this minimum cardinality is the metric dimension of G, denoted by dim(G).
The concept of the metric dimension was first crafted for metric spaces of a continuous nature but later on, these concepts were used for graphs. In fact, Slater initiated the concepts of metric dimension and resolving sets and these concepts were also studied by Melter and Harary independently in [
11,
12]. Resolving sets have been analyzed a lot since then. The resolving sets have applications in many fields including network discovery and verification [
13], connected joins in graphs, strategies for the mastermind games [
14], applications to problems of pattern recognition, image processing, combinatorial optimization, pharmaceutical chemistry, and game theory. In [
8,
10], authors computed metric dimension of some graphs and proved that it is 1 if and only if graph is the path
. The metric dimension of complete graph
is
for
and the metric dimension of cycle graph
is 2 for
[
8]. In [
7], authors computed the metric dimension of the Cartesian products of some graphs. In [
9], Imran et al. computed the metric dimension of the generalized Peterson graph. Also, generalized Petersen graphs
, antiprisms
, and circulant graphs
are families of graphs with a constant metric dimension [
15]. In [
16], Imran et. al. discussed some families of graphs with a constant metric dimension. Ali et al. computed partial results about the metrics dimension of classical Mobius Ladders in [
17], whereas Munir et al. computed the exact and full results for this family in [
18]. In [
19], authors computed the metric dimension of a generalized wheel graph and ant-web gear graph. Authors also gave a new family of convex polytopes with an unbounded metric dimension [
19]. Recently authors in [
20] computed metric dimension of some families of Gear graphs. Manuel et. al. computed the metric dimension of a honey-comb network in [
21]. In [
22], the authors computed the metric dimension of circulant graphs. In [
23], authors computed explicit formula for the metric dimension of a regular bipartite graph. Imran et al. computed the metric dimension of a Jahangir graph in [
24]. Authors discussed the metric dimension of the circulant and Harary graph in [
25].
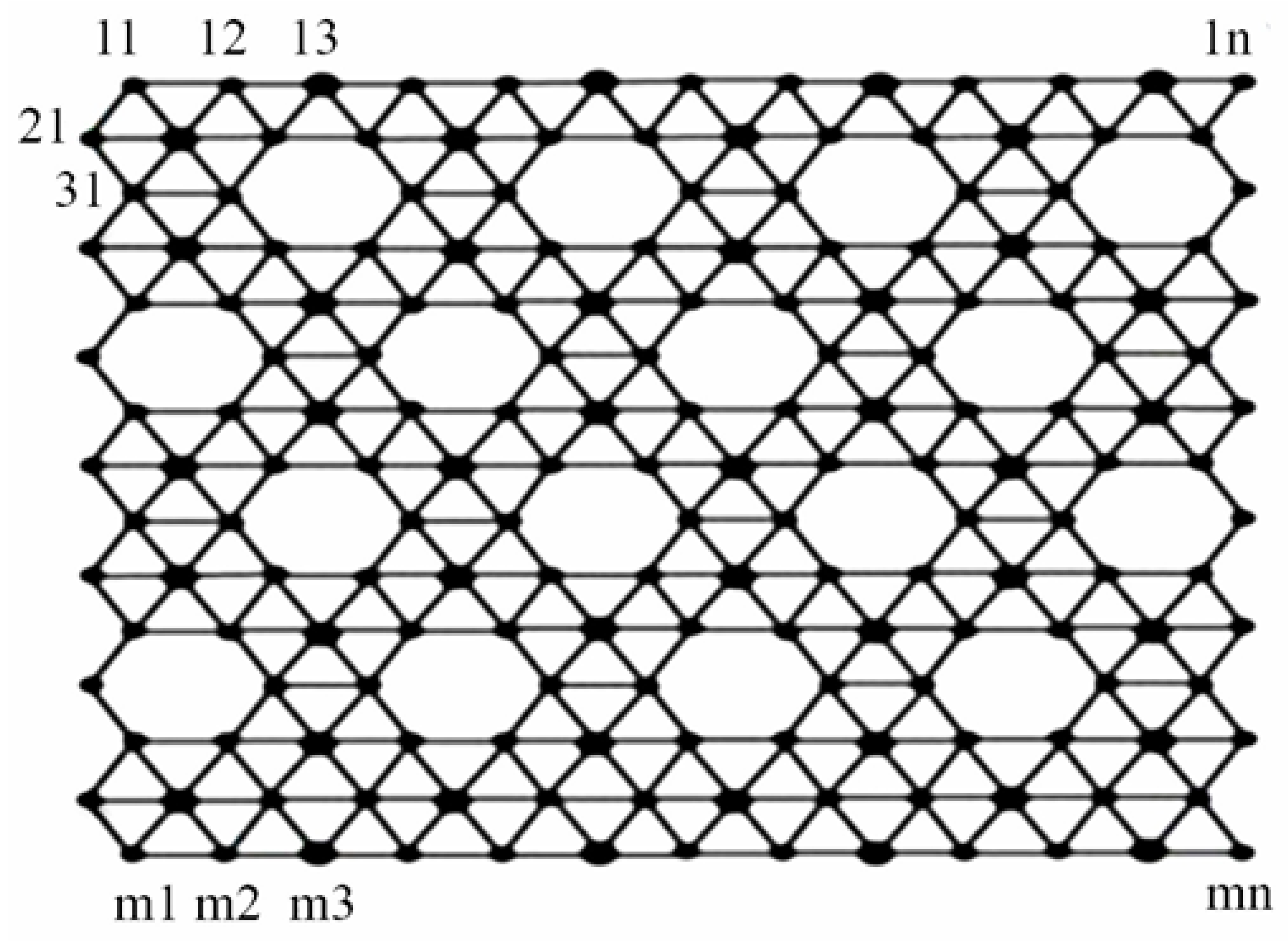
In the present article, we intend to compute the metric dimension of 2D lattices of an α-boron Nanotube. For the rest of this article, we reserve the symbol
for the 2D lattice of the α-boron Nanotube of dimensions m and n. We use the term lattice only to denote the 2D sheet of the alpha-boron tubes. The vertices of the alpha-boron sheet in the first row are
, in second row
, in third row
, etc. The representation of vertices is
, where
is the row number and
is the column number. For the sake of simplicity, we label the vertices in
Figure 2 as 11, 12, 13 etc. instead of
etc. Please see below,
Figure 2.
In the tubes, m1 and 1n are connected with each other, whereas in the 2D-lattice these vertices are at
distance apart, see
Figure 3.
2. Main Results
Theorem 1. For all and , we have .
Proof. We consider the following labelling of vertices of 2D-lattice of alpha-boron tubes as depicted in the above figure. Consider
2D-lattice of
nanotubes. The vertex set of G is partitioned as
If m < nLet
. We prove that
is a resolving set for
. The representations of different vertices of
are
In general, for 3 <
i ≤
m where
i is odd and
i ≠ 3
kIn general, for 4 ≤
i ≤
m where
i is even and
i ≠ 3
kThese representations are distinct. So is a resolving set for and the dim() ≤ 2. Since is not a path so dim() ≥ 2. Hence the dim() = 2 in this case. ☐
Theorem 2. For all and , we have
Proof. Let . We prove that is a resolving set. The representations of vertices with respect to W are
Case I:m is odd with
and
m ≠ 6
k + 1
If i is odd and i ≠ 3k then
If i is even and i ≠ 3k then
If m = 6k + 1 with i ≠ 3k and i is odd
If m = 6k + 1 with i ≠ 3k and i is even
If and is odd
If and is even
Case II: If is even and
For i is odd and
If is even
If with and is odd
If with and is even
If and is odd
If and is odd
If m is odd, and
For i = rn + k where
If
If m is even, and
For i = rn + k where
These representations are distinct. So, is a resolving set for . Therefore, the metric dimension of is ≤3. Now we prove that the metric dimension of is greater than 2. For this we shall prove that any set of cardinality two does not resolve. ☐
Theorem 3. For all and , we have
Proof. Let be a resolving set for . We consider all possibilities and come up with a contradistinction in each case. The following three possibilities arise
Possibility 1: If lie on the same row then i = p.
If then if n is even and , if n is odd so both cases result in contradiction. In all remaining possibilities, we denote instead of where no confusion arises.
- (i)
If and and then , a contradiction.
- (ii)
If and , i = 3k and then or , a contradiction.
- (iii)
If and and then , a contradiction.
- (iv)
If and then or , a contradiction.
- (v)
If and then , a contradiction.
- (vi)
If and then , a contradiction.
- (vii)
If and then , a contradiction.
Possibility 2: If lie on the same column then j = q.
- (i)
If then , a contradiction.
- (ii)
If and then or , a contradiction.
- (iii)
If and then or , a contradiction.
- (iv)
If , then or , a contradiction.
- (v)
If , then or , a contradiction.
- (vi)
If , then , a contradiction.
- (vii)
If and then or , a contradiction.
- (viii)
If then either or , a contradiction.
Possibility 3: If lie neither on the same row nor the same column so i p and j q.
Let . Since i p so let i < p.
- (i)
If j < q then or , a contradiction
- (ii)
If j > q then or , a contradiction
- (iii)
If i = 1 and p = m then or or , a contradiction.
So any set with cardinality 2 does not resolve . So, the metric dimension of is greater than 2. Hence metric dimension of is 3 if m > n. ☐