A Study on Neutrosophic Cubic Graphs with Real Life Applications in Industries

Abstract

Neutrosophic cubic sets are the more generalized tool by which one can handle imprecise information in a more effective way as compared to fuzzy sets and all other versions of fuzzy sets. Neutrosophic cubic sets have the more flexibility, precision and compatibility to the system as compared to previous existing fuzzy models. On the other hand the graphs represent a problem physically in the form of diagrams, matrices etc. which is very easy to understand and handle. So the authors applied the Neutrosophic cubic sets to graph theory in order to develop a more general approach where they can model imprecise information through graphs. We develop this model by introducing the idea of neutrosophic cubic graphs and introduce many fundamental binary operations like cartesian product, composition, union, join of neutrosophic cubic graphs, degree and order of neutrosophic cubic graphs and some results related with neutrosophic cubic graphs. One of very important futures of two neutrosophic cubic sets is the R-union that R-union of two neutrosophic cubic sets is again a neutrosophic cubic set, but here in our case we observe that R-union of two neutrosophic cubic graphs need not be a neutrosophic cubic graph. Since the purpose of this new model is to capture the uncertainty, so we provide applications in industries to test the applicability of our defined model based on present time and future prediction which is the main advantage of neutrosophic cubic sets.

1. Introduction

In 1965, Zadeh [1] published his seminal paper “Fuzzy Sets” which described fuzzy set theory and consequently fuzzy logic. The purpose of Zadeh’s paper was to develop a theory which could deal with ambiguity and imprecision of certain classes or sets in human thinking, particularly in the domains of pattern recognition, communication of information and abstraction. This theory proposed making the grade of membership of an element in a subset of a universal set a value in the closed interval $[0,1]$ of real numbers. Zadeh’s ideas have found applications in computer sciences, artificial intelligence, decision analysis, information sciences, system sciences, control engineering, expert systems, pattern recognition, management sciences, operations research and robotics. Theoretical mathematics has also been touched by fuzzy set theory. The ideas of fuzzy set theory have been introduced into topology, abstract algebra, geometry, graph theory and analysis. Further, he made the extension of fuzzy set to interval-valued fuzzy sets in 1975, where one is not bound to give a specific membership to a certain element. In 1975, Rosenfeld [2] discussed the concept of fuzzy graphs whose basic idea was introduced by Kauffmann [3] in 1973. The fuzzy relations between fuzzy sets were also considered by Rosenfeld and he developed the structure of fuzzy graphs obtaining analogs of several graph theoretical concepts [4]. Bhattacharya provided further studies on fuzzy graphs [5]. Akram and Dudek gave the idea of interval valued fuzzy graphs in 2011 where they used interval membership for an element in the vertex set [6]. Akram further extended the idea of interval valued fuzzy graphs to Interval-valued fuzzy line graphs in 2012. More detail of fuzzy graphs, we refer the reader to [7,8,9,10,11,12]. In 1986, Atanassov [13] use the notion of membership and non-membership of an element in a set X and gave the idea of intuitionistic fuzzy sets. He extended this idea to intuitionistic fuzzy graphs and for more detail in this direction, we refer the reader to [14,15,16,17,18,19,20]. Akram and Davvaz [21] introduced the notion of strong intuitionistic fuzzy graphs and investigated some of their properties. They discussed some propositions of self complementary and self weak complementary strong intuitionistic fuzzy graphs. In 1994, Zhang [22] started the theory of bipolar fuzzy sets as a generality of fuzzy sets. Bipolar fuzzy sets are postponement of fuzzy sets whose membership degree range is $[-1,1]$. Akram [23,24] introduced the concepts of bipolar fuzzy graphs, where he introduced the notion of bipolar fuzzy graphs, described various methods of their construction, discussed the concept of isomorphisms of these graphs and investigated some of their important properties. He then introduced the notion of strong bipolar fuzzy graphs and studied some of their properties. He also discussed some propositions of self complementary and self weak complementary strong bipolar fuzzy graphs and applications, for example see [25]. Smarandache [26,27,28] extended the concept of Atanassov and gave the idea of neutrosophic sets. He proposed the term “neutrosophic” because “neutrosophic” etymologically comes from “neutrosophy” This comes from the French neutre < Latin neuter, neutral, and Greek sophia, skill/wisdom, which means knowledge of neutral thought, and this third/neutral represents the main distinction between “fuzzy” and “intuitionistic fuzzy” logic/set, i.e., the included middle component (Lupasco-Nicolescu’s logic in philosophy), i.e., the neutral/indeterminate/unknown part (besides the “truth”/“membership” and “falsehood”/“non-membership” components that both appear in fuzzy logic/set). See the Proceedings of the First International Conference on Neutrosophic Logic, The University of New Mexico, Gallup Campus, 1–3 December 2001, at http://www.gallup.unm.edu/~smarandache/FirstNeutConf.htm.

After that, many researchers used the idea of neutrosophic sets in different directions. The idea of neutrosophic graphs is provided by Kandasamy et al. in the book title as Neutrosophic graphs, where they introduce idea of neutrosophic graphs [29]. This study reveals that these neutrosophic graphs give a new dimension to graph theory. An important feature of this book is that it contains over 200 neutrosophic graphs to provide better understandings of these concepts. Akram and others discussed different aspects of neutrosophic graphs [30,31,32,33]. Further Jun et al. [34] gave the idea of cubic set and it was characterized by interval valued fuzzy set and fuzzy set, which is more general tool to capture uncertainty and vagueness, while fuzzy set deals with single value membership and interval valued fuzzy set ranges the membership in the form of interval. The hybrid platform provided by the cubic set is the main advantage, in that it contains more information then a fuzzy set and interval valued fuzzy set. By using this concept, we can solve different problems arising in several areas and can pick finest choice by means of cubic sets in various decision making problems. This hybrid nature of the cubic set attracted these researchers to work in this field. For more detail about cubic sets and their applications in different research areas, we refer the reader to [35,36,37]. Recently, Rashid et al. [38] introduced the notion of cubic graphs where they introduced many new types of graphs and provided their application. More recently Jun et al. [39,40] combined neutrosophic set with cubic sets and gave the idea of Neutrosophic cubic set and defined different operations.

Therefore, the need was felt to develop a model for neutrosophic cubic graphs which is a more generalized tool to handle uncertainty. In this paper, we introduce the idea of neutrosophic cubic graphs and introduce the fundamental binary operations, such as the cartesian product, composition, union, join of neutrosophic cubic graphs, degree, order of neutrosophic cubic graphs and some results related to neutrosophic cubic graphs. We observe that R-union of two neutrosophic cubic graphs need not to be a neutrosophic cubic graph. At the end, we provide applications of neutrosophic cubic graphs in industries to test the applicability of our presented model.

2. Preliminaries

We recall some basic definitions related to graphs, fuzzy graphs and neutrosophic cubic sets.

Definition 1.

A graph is an ordered pair $G^{\ast }=(V,E)$, where V is the set of vertices of $G^{\ast }$ and E is the set of edges of $G^{\ast }$.

Definition 2.

A fuzzy graph [2,3,4] with an underlying set V is defined to be a pair $G=(\mu ,\nu )$ where μ is a fuzzy function in V and ν is a fuzzy function in $E\subseteq V\times V$ such that $\nu (\{x,y\})\le min(\mu (x),\mu (y))$ for all $\{x,y\}\in E$.

We call $\mu$ the fuzzy vertex function of V, $\nu$ the fuzzy edge function of $E,$ respectively. Please note that $\nu$ is a symmetric fuzzy relation on $\mu$. We use the notation $xy$ for an element $\{x,y\}$ of E. Thus, $G=(\mu ,\nu )$ is a fuzzy graph of $G^{\ast }=(V,E)$ if $\nu (xy)\le min(\mu (x),\mu (y))$ for all $xy\in E$.

Definition 3.

Let $G=(\mu ,\nu )$ be a fuzzy graph. The order of a fuzzy graph [2,3,4] is defined by $O(G)={\sum }_{x\in V}\mu (x).$ The degree of a vertex x in G is defined by $deg(x)={\sum }_{xy\in E}\nu (xy).$

Definition 4.

Let ${\mu }_1$ and ${\mu }_2$ be two fuzzy functions of $V_1$ and $V_2$ and let ${\nu }_1$ and ${\nu }_2$ be fuzzy functions of $E_1$ and $E_2$, respectively. The Cartesian product of two fuzzy graphs $G_1$ and $G_2$ [2,3,4] of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ is denoted by $G_1\times G_2=({\mu }_1\times {\mu }_2,{\nu }_1\times {\nu }_2)$ and is defined as follows:

(i) 

$({\mu }_1\times {\mu }_2)(x_1,x_2)=min({\mu }_1(x_1),{\mu }_2(x_2)),$ for all $(x_1,x_2)\in V.$

(ii) 

$({\nu }_1\times {\nu }_2)((x,x_2)(x,y_2))=min({\mu }_1(x),{\nu }_2(x_2{y}_2)),$ for all $x\in V_1$, for all $x_2{y}_2\in E_2$.

(iii) 

$({\nu }_1\times {\nu }_2)((x_1,z)(y_1,z))=min({\nu }_1(x_1{y}_1),{\mu }_2(z)),$ for all $z\in V_2$, for all $x_1{y}_1\in E_1.$

Definition 5.

Let ${\mu }_1$ and ${\mu }_2$ be fuzzy functions of $V_1$ and $V_2$ and let ${\nu }_1$ and ${\nu }_2$ be fuzzy functions of $E_1$ and $E_2$, respectively. The composition of two fuzzy graphs $G_1$ and $G_2$ of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ [2,3,4] is denoted by $G_1\left[G_2\right]=({\mu }_1\circ {\mu }_2,{\nu }_1\circ {\nu }_2)$ and is defined as follows:

(i) 

$({\mu }_1\circ {\mu }_2)(x_1,x_2)=min({\mu }_1(x_1),{\mu }_2(x_2)),$ for all $(x_1,x_2)\in V$.

(ii) 

$({\nu }_1\circ {\nu }_2)((x,x_2)(x,y_2))=min({\mu }_1(x),{\nu }_2(x_2{y}_2)),$ for all $x\in V_1,$ for all $x_2{y}_2\in E_2.$

(iii) 

$({\nu }_1\circ {\nu }_2)((x_1,z)(y_1,z))=min({\nu }_1(x_1{y}_1),{\mu }_2(z)),$ for all $z\in V_2,$ for all $x_1{y}_1\in E_1.$

(iv) 

$({\nu }_1\circ {\nu }_2)((x_1,x_2)(y_1,y_2))=min({\mu }_2(x_2),{\mu }_2(y_2),{\nu }_1(x_1{y}_1)),$ for all $z\in V_2,$ for all$(x_1,x_2)(y_1,y_2)\in E^0-E.$

Definition 6.

Let ${\mu }_1$ and ${\mu }_2$ be fuzzy functions of $V_1$ and $V_2$ and let ${\nu }_1$ and ${\nu }_2$ be fuzzy functions of $E_1$ and $E_2$, respectively. Then union of two fuzzy graphs $G_1$ and $G_2$ of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ [2,3,4] is denoted by $G_1\cup G_2=({\mu }_1\cup {\mu }_2,{\nu }_1\cup {\nu }_2)$ and is defined as follows:

(i) 

$({\mu }_1\cup {\mu }_2)(x)={\mu }_1(x)$ if $x\in V_1\cap V_2,$

(ii) 

$({\mu }_1\cup {\mu }_2)(x)={\mu }_2(x)$ if $x\in V_2\cap V_1,$

(iii) 

$({\mu }_1\cup {\mu }_2)(x)=max({\mu }_1(x),{\mu }_2(x))$ if $x\in V_1\cap V_2,$

(iv) 

$({\nu }_1\cup {\nu }_2)(xy)={\nu }_1(xy)$ if $xy\in E_1\cap E_2,$

(v) 

$({\nu }_1\cup {\nu }_2)(xy)={\nu }_2(xy)$ if $xy\in E_2\cap E_1,$

(vi) 

(${\nu }_1\cup {\nu }_2)(xy)=max($${\nu }_1(xy),$${\nu }_2(xy))$ if $xy\in E_1\cap E_2$.

Definition 7.

Let ${\mu }_1$ and ${\mu }_2$ be fuzzy functions of $V_1$ and $V_2$ and let ${\nu }_1$ and ${\nu }_2$ be fuzzy functions of $E_1$ and $E_2$, respectively. Then join of two fuzzy graphs $G_1$ and $G_2$ of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ [2,3,4] is denoted by $G_1+G_2=({\mu }_1+{\mu }_2,{\nu }_1+{\nu }_2)$ and is defined as follows:

(i) 

$({\mu }_1+{\mu }_2)(x)=({\mu }_1\cup {\mu }_2)(x)$ if $x\in V_1\cup V_2,$

(ii) 

$({\nu }_1+{\nu }_2)(xy)=({\nu }_1\cup {\nu }_2)(xy)={\nu }_1(xy)$ if $xy\in E_1\cup E_2,$

(iii) 

$({\nu }_1+{\nu }_2)(xy)=min({\mu }_1(x),{\mu }_2(y))$ if $xy\in E^{\prime }$.

Definition 8.

Let X be a non-empty set. A neutrosophic cubic set (NCS) in X [39] is a pair $\mathit{A}=(\mathbf{A},\Lambda )$ where $\mathbf{A}=\left\{〈x,A_T(x),A_I(x),A_F(x)〉\right|x\in X\}$ is an interval neutrosophic set in X and $\Lambda =\left\{〈x,{\lambda }_T(x),{\lambda }_I(x),{\lambda }_F(x)〉\right|x\in X\}$ is a neutrosophic set in X.

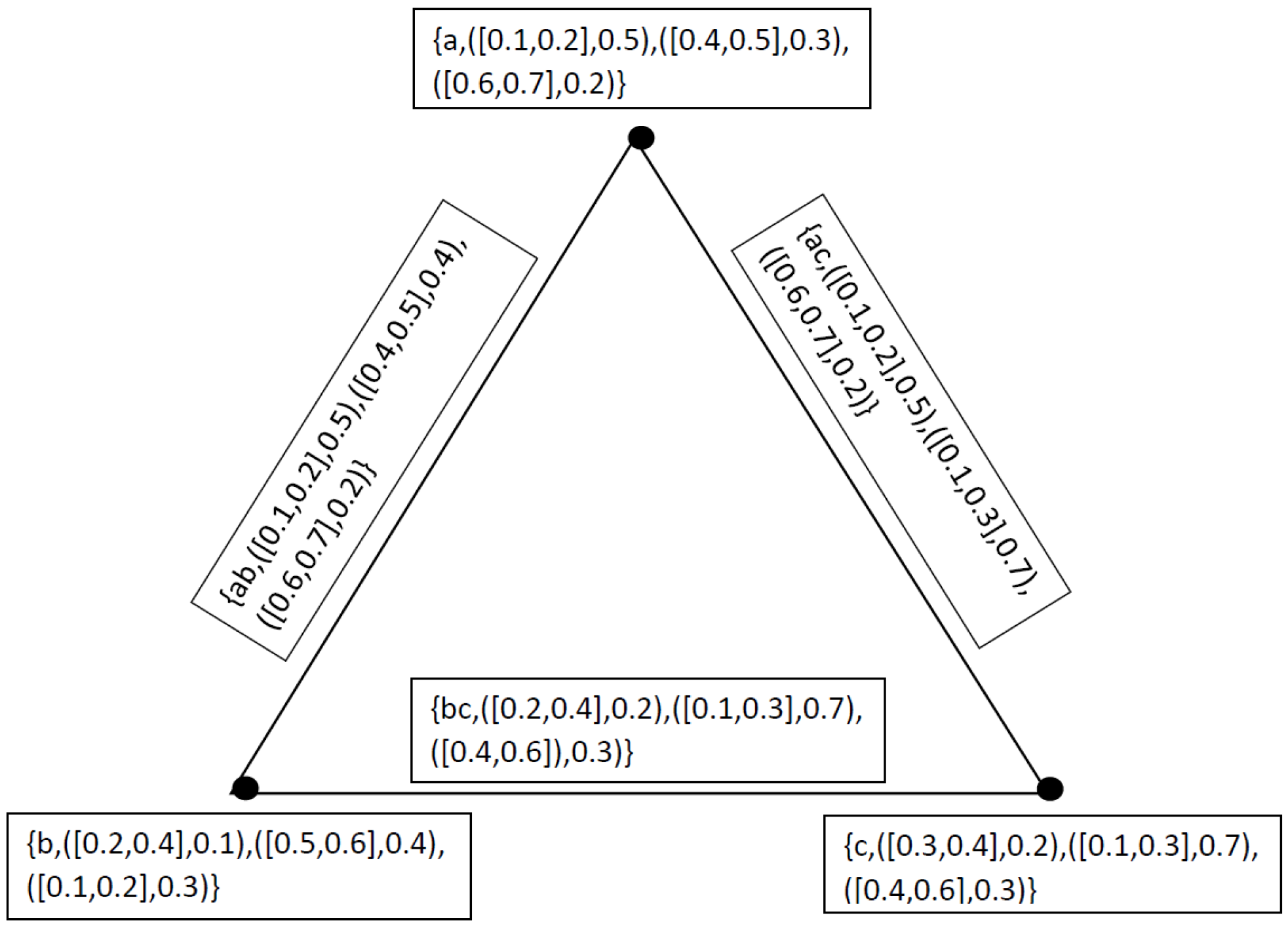
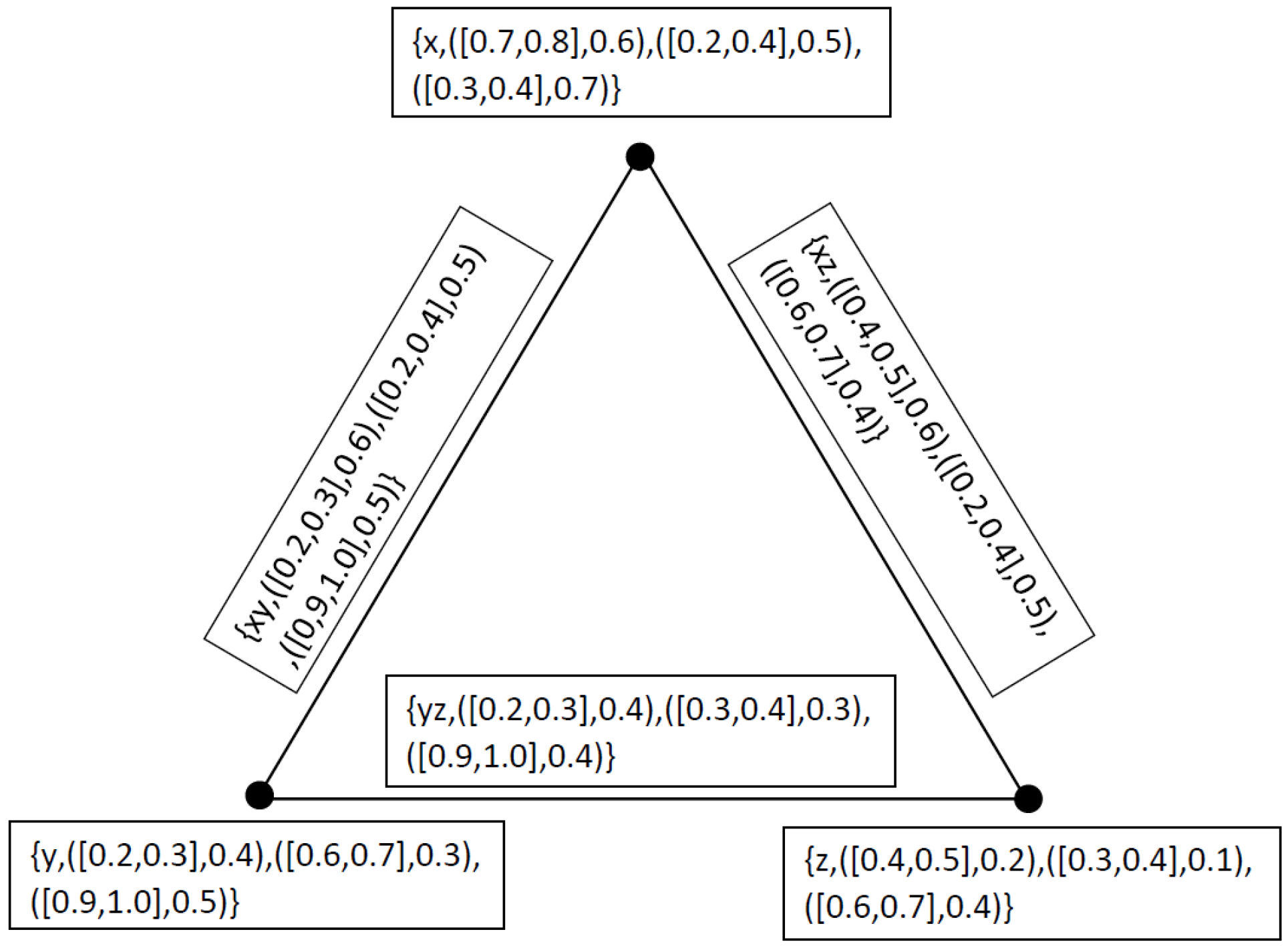
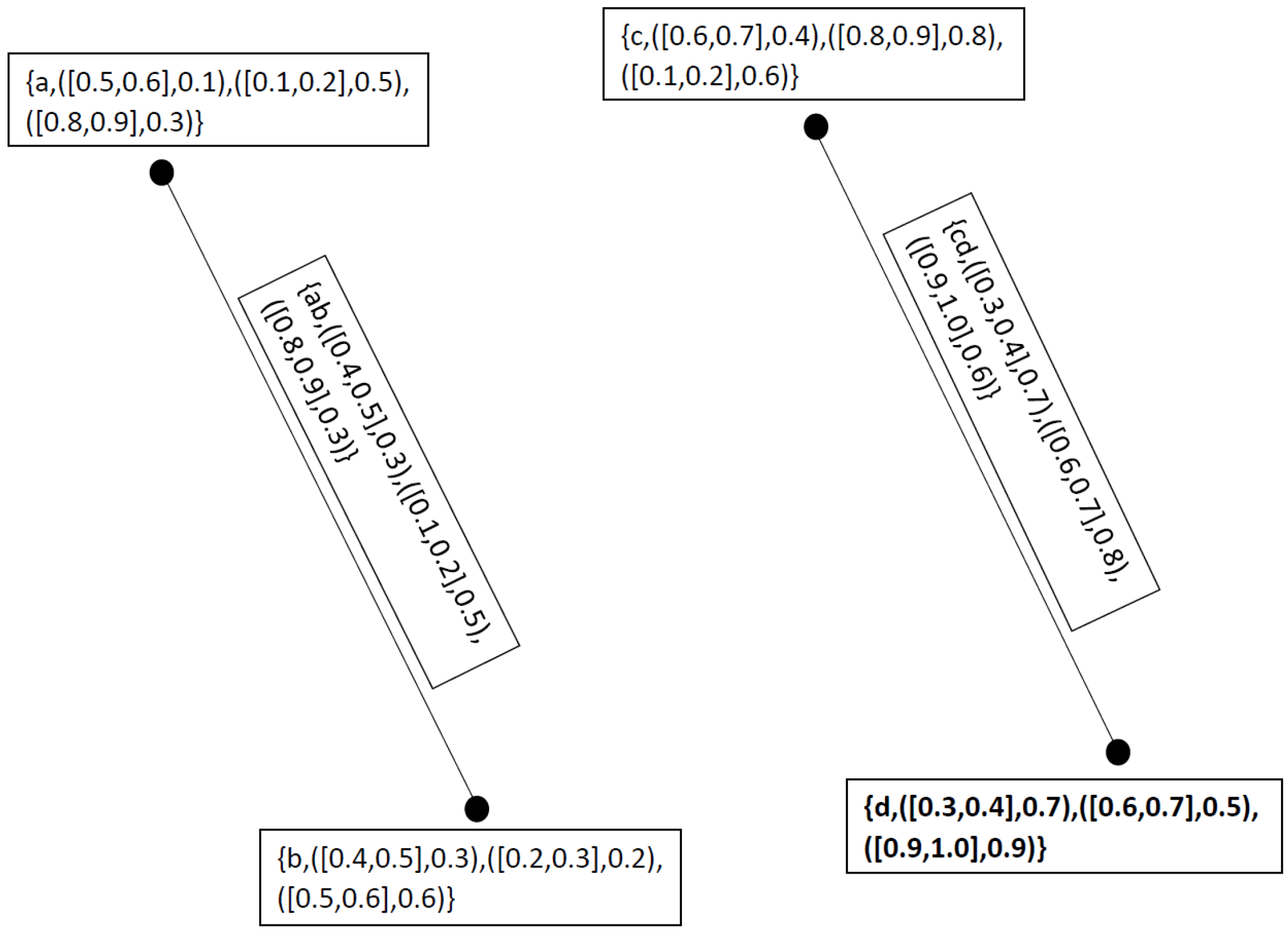
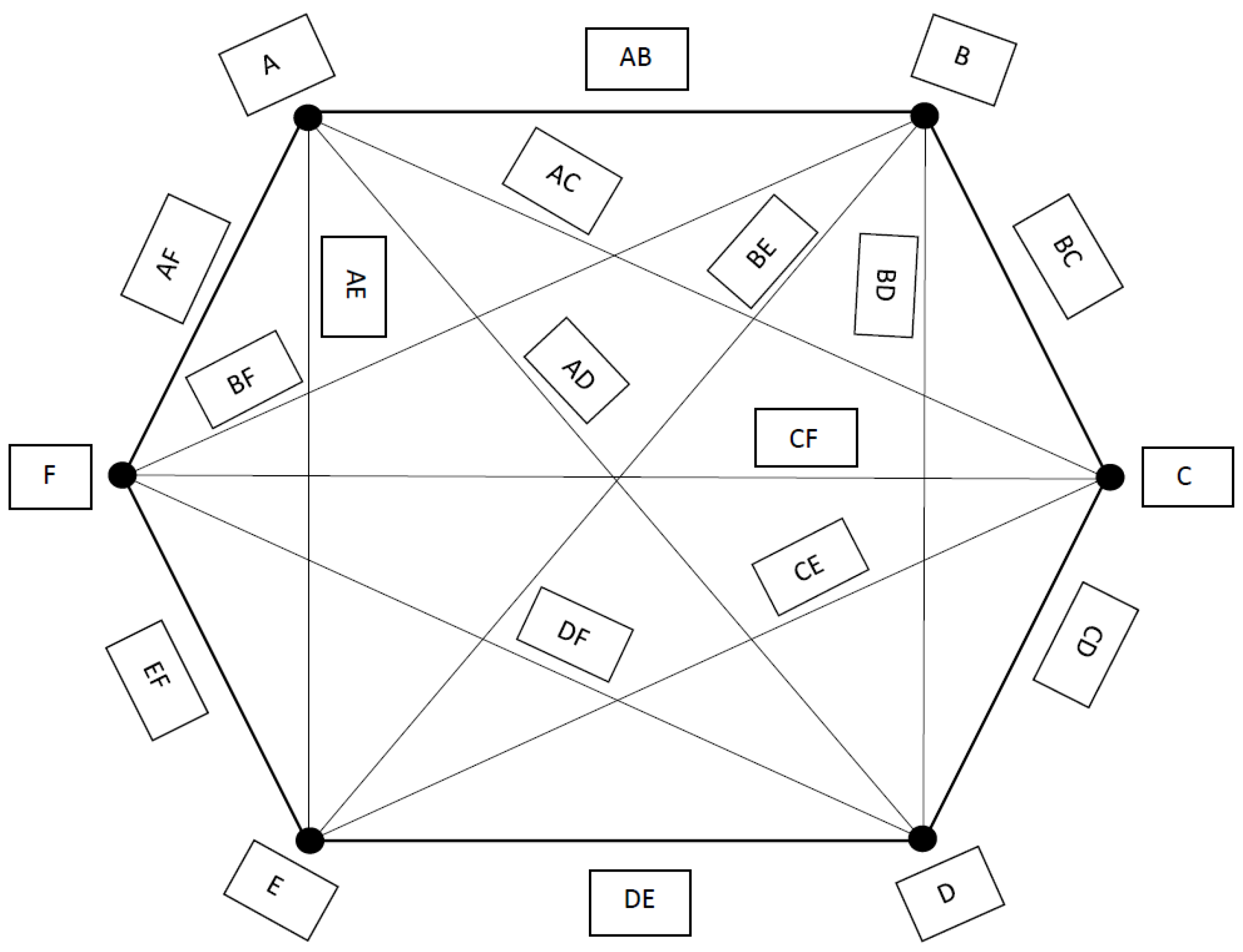
3. Neutrosophic Cubic Graphs

The motivation behind this section is to combine the concept of neutrosophic cubic sets with graphs theory. We introduce the concept of neutrosophic cubic graphs, order and degree of neutrosophic cubic graph and different fundamental operations on neutrosophic cubic graphs with examples.

Definition 9.

Let $G^{\ast }=(V,E)$ be a graph. By neutrosophic cubic graph of $G^{\ast }$, we mean a pair $G=(M,N)$ where $M=(A,B)=(({\tilde{T}}_A,T_B),({\tilde{I}}_A,I_B),({\tilde{F}}_A,F_B))$ is the neutrosophic cubic set representation of vertex set V and $N=(C,D)=(({\tilde{T}}_C,T_D),({\tilde{I}}_C,I_D),({\tilde{F}}_C,F_D))$ is the neutrosophic cubic set representation of edges set E such that;

(i) 

$\left({\tilde{T}}_C(u_i{v}_i)⪯rmin\{{\tilde{T}}_A(u_i),{\tilde{T}}_A(v_i)\},T_D(u_i{v}_i)\le max\{T_B(u_i),T_B(v_i)\}\right),$

(ii) 

$\left({\tilde{I}}_C(u_i{v}_i)⪯rmin\{{\tilde{I}}_A(u_i),{\tilde{I}}_A(v_i)\},I_D(u_i{v}_i)\le max\{I_B(u_i),I_B(v_i)\}\right),$

(iii) 

$\left({\tilde{F}}_C(u_i{v}_i)⪯rmax\{{\tilde{F}}_A(u_i),{\tilde{F}}_A(v_i)\},F_D(u_i{v}_i)\le min\{F_B(u_i),F_B(v_i)\}\right).$

Example 1.

Let $G^{\ast }=(V,E)$ be a graph where $V=\{a,b,c,d\}$ and $E=\{ab,bc,ac,ad,cd\}$, where

$$\begin{array}{ccc}\hfill M& =& 〈\begin{array}{c}\{a,([0.2,0.3],0.5),([0.1,0.4],0.6),([0.5,0.6],0.3)\},\\ \{b,([0.1,0.2],0.4),([0.4,0.5],0.6),([0.7,0.8],0.4)\},\\ \{c,([0.4,0.7],0.1),([0.7,0.8],0.9),([0.3,0.4]),0.5)\},\\ \{d,([0.3,0.5],0.2),([0.9,1],0.5),([0.2,0.4],0.1)\}\end{array}〉\hfill \\ \hfill N& =& 〈\begin{array}{c}\{ab,([0.1,0.2],0.5),([0.1,0.4],0.6),([0.7,0.8],0.3)\},\\ \{ac,([0.2,0.3],0.5),([0.1,0.4],0.9),([0.5,0.6],0.3)\},\\ \{ad,([0.2,0.3],0.5),([0.1,0.4],0.6),([0.5,0.6]),0.1)\},\\ \{bc,([0.1,0.2],0.4),([0.4,0.5],0.9),([0.7,0.8],0.4)\},\\ \{bd,([0.1,0.2],0.4),([0.4,0.5],0.6),([0.7,0.8],0.1)\},\\ \{cd,([0.3,0.5],0.2),([0.7,0.8],0.9),([0.3,0.4],0.1)\}\end{array}〉\hfill \end{array}$$

Then clearly $G=(M,N)$ is a neutrosophic cubic graph of $G^{\ast }=(V,E)$ as showin in Figure 1.

Remark 1.

1. 

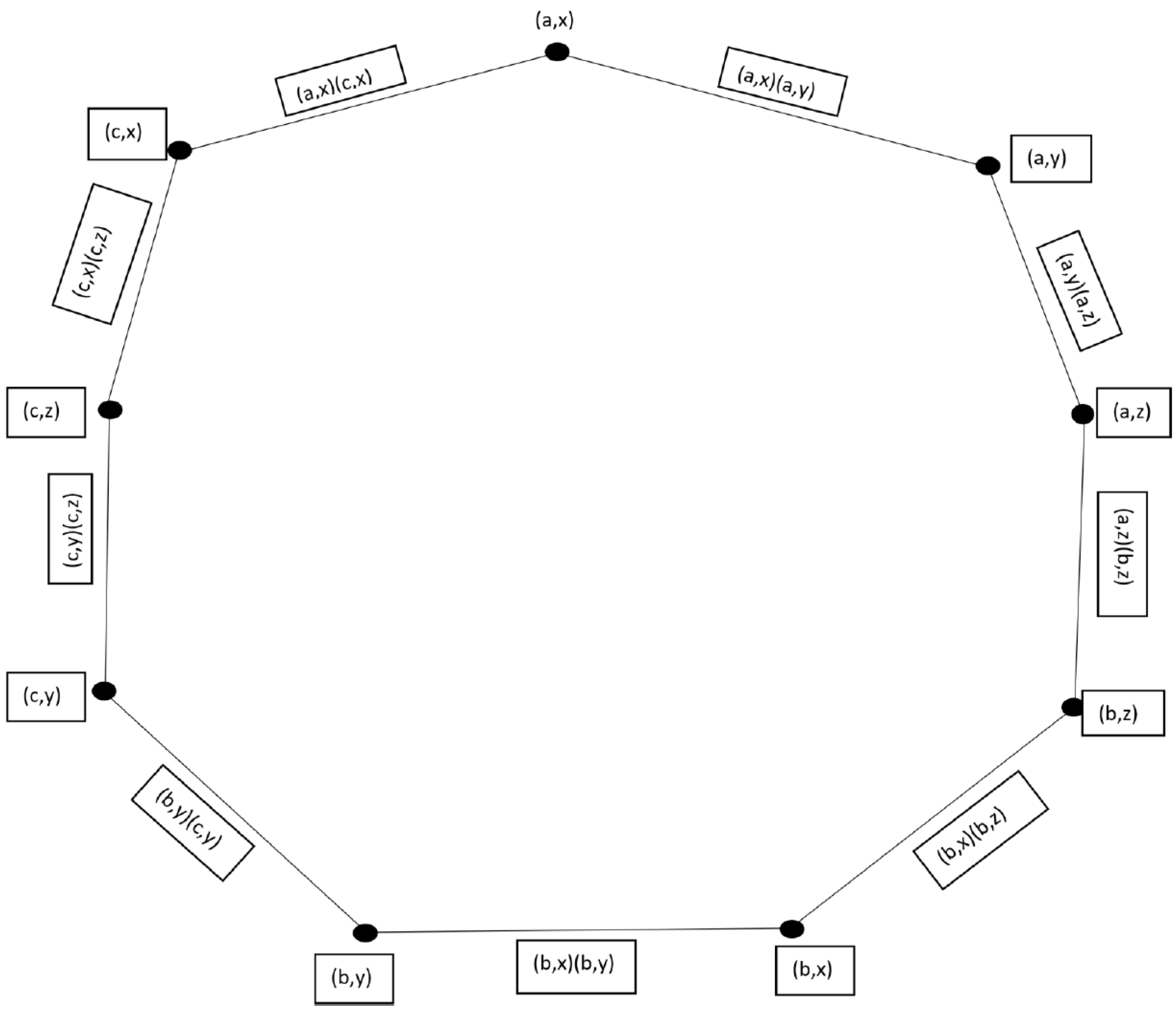
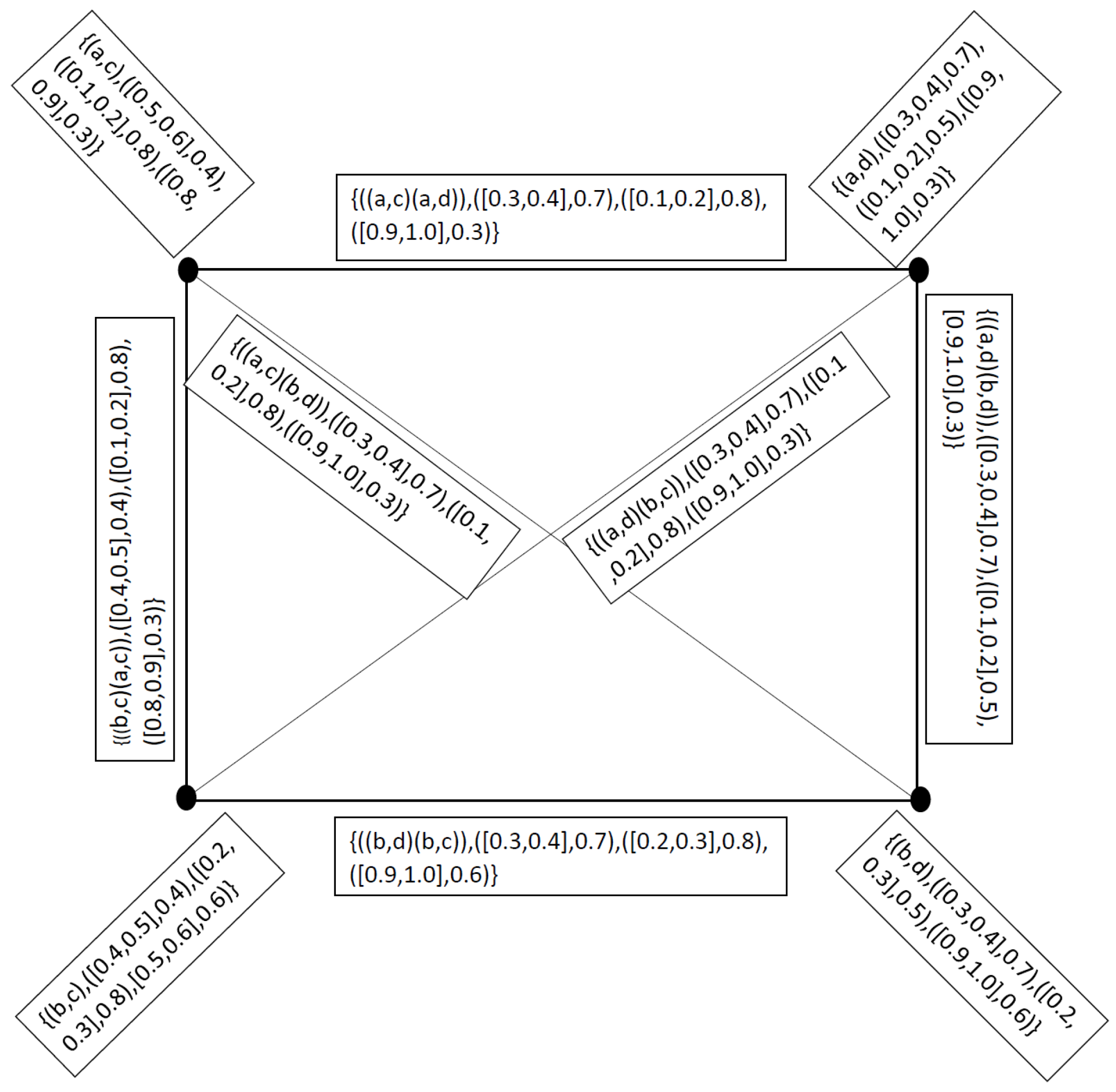
If $n\ge 3$ in the vertex set and $n\ge 3$ in the set of edges then the graphs is a neutrosophic cubic polygon only when we join each vertex to the corresponding vertex through an edge.

2. 

If we have infinite elements in the vertex set and by joining the each and every edge with each other we get a neutrosophic cubic curve.

Definition 10.

Let $G=(M,N)$ be a neutrosophic cubic graph. The order of neutrosophic cubic graph is defined by $O(G)={\Sigma }_{xϵV}\{({\tilde{T}}_A,T_B)(x),({\tilde{I}}_A,I_B)(x),({\tilde{F}}_A,F_B)(x)\}$ and degree of a vertex x in G is defined by $deg(x)={\Sigma }_{xyϵE}\{({\tilde{T}}_C,T_D)(xy),({\tilde{I}}_C,I_D)(xy),({\tilde{F}}_C,F_D)(xy))\}$.

Example 2.

In Example 1, Order of a neutrosophic cubic graph is

$$O(G)=\{([1.0,1.7],1.2),([2.1,1.8],2.6),([1.7,2.2],1.3)\}$$

and degree of each vertex in G is

$$\begin{array}{c}deg(a)=\{([0.5,0.8],1.5),([0.3,1.2],2.1),([1.7,2.0],0.7)\}\\ deg(b)=\{([0.3,0.6],1.3),([0.9,1.4],2.1),([2.1,2.4],0.8)\}\\ deg(c)=\{([0.6,1.0],1.1),([1.2,1.7],2.7),([1.5,1.8],0.8)\}\\ deg(d)=\{([0.6,1.0],1.1),([1.2,1.7],2.1),([1.5,1.8],0.3)\}\end{array}$$

Definition 11.

Let $G_1=(M_1,N_1)$ be a neutrosophic cubic graph of $G_1^{\ast }=(V_1,E_1),$ and $G_2=(M_2,N_2)$ be a neutrosophic cubic graph of $G_2^{\ast }=(V_2,E_2)$. Then Cartesian product of $G_1$ and $G_2$ is denoted by

$$\begin{array}{ccc}\hfill G_1\times G_2& =& (M_1\times M_2,N_1\times N_2)=((A_1,B_1)\times (A_2,B_2),(C_1,D_1)\times (C_2,D_2))\hfill \\ & =& ((A_1\times A_2,B_1\times B_2),(C_1\times C_2,D_1\times D_2))\hfill \\ & =& 〈\begin{array}{c}(({\tilde{T}}_{A_1\times A_2},T_{B_1\times B_2}),({\tilde{I}}_{A_1\times A_2},I_{B_1\times B_2}),({\tilde{F}}_{A_1\times A_2},F_{B_1\times B_2})),\\ (({\tilde{T}}_{C_1\times C_2},T_{D_1\times D_2}),({\tilde{I}}_{C_1\times C_2},I_{D_1\times D_2}),({\tilde{F}}_{C_1\times C_2},F_{D_1\times D_2}))\end{array}〉\hfill \end{array}$$

and is defined as follow

(i) 

$\left({\tilde{T}}_{A_1\times A_2}(x,y)=rmin({\tilde{T}}_{A_1}(x),{\tilde{T}}_{A_2}(y)),T_{B_1\times B_2}(x,y)=max(T_{B_1}(x),T_{B_2}(y))\right),$

(ii) 

$\left({\tilde{I}}_{A_1\times A_2}(x,y)=rmin({\tilde{I}}_{A_1}(x),{\tilde{I}}_{A_2}(y)),I_{B_1\times B_2}(x,y)=max(I_{B_1}(x),I_{B_2}(y))\right),$

(iii) 

$\left({\tilde{F}}_{A_1\times A_2}(x,y)=rmax({\tilde{F}}_{A_1}(x),{\tilde{F}}_{A_2}(y)),F_{B_1\times B_2}(x,y)=min(F_{B_1}(x),F_{B_2}(y))\right),$

(iv) 

$\left(\begin{array}{c}{\tilde{T}}_{C_1\times C_2}((x,y_1)(x,y_2))=rmin({\tilde{T}}_{A_1}(x),{\tilde{T}}_{C_2}(y_1{y}_2)),\\ T_{D_1\times D_2}((x,y_1)(x,y_2))=max(T_{B_1}(x),T_{D_2}(y_1{y}_2))\end{array}\right),$

(v) 

$\left(\begin{array}{c}{\tilde{I}}_{C_1\times C_2}((x,y_1)(x,y_2))=rmin({\tilde{I}}_{A_1}(x),{\tilde{I}}_{C_2}(y_1{y}_2)),\\ I_{D_1\times D_2}((x,y_1)(x,y_2))=max(I_{B_1}(x),I_{D_2}(y_1{y}_2))\end{array}\right),$

(vi) 

$\left(\begin{array}{c}{\tilde{F}}_{C_1\times C_2}((x,y_1)(x,y_2))=rmax({\tilde{F}}_{A_1}(x),{\tilde{F}}_{C_2}(y_1{y}_2)),\\ F_{D_1\times D_2}((x,y_1)(x,y_2))=min(F_{B_1}(x),F_{D_2}(y_1{y}_2))\end{array}\right),$

(vii) 

$\left(\begin{array}{c}{\tilde{T}}_{C_1\times C_2}((x_1,y)(x_2,y))=rmin({\tilde{T}}_{C_1}(x_1{x}_2),{\tilde{T}}_{A_2}(y)),\\ T_{D_1\times D_2}((x_1,y)(x_2,y))=max(T_{D_1}(x_1{x}_2),T_{B_2}(y))\end{array}\right),$

(viii) 

$\left(\begin{array}{c}{\tilde{I}}_{C_1\times C_2}((x_1,y)(x_2,y))=rmin({\tilde{I}}_{C_1}(x_1{x}_2),{\tilde{I}}_{A_2}(y)),\\ I_{D_1\times D_2}((x_1,y)(x_2,y))=max(I_{D_1}(x_1{x}_2),I_{B_2}(y))\end{array}\right),$

(ix) 

$\left(\begin{array}{c}{\tilde{F}}_{C_1\times C_2}((x_1,y)(x_2,y))=rmax({\tilde{F}}_{C_1}(x_1{x}_2),{\tilde{F}}_{A_2}(y)),\\ F_{D_1\times D_2}((x_1,y)(x_2,y))=min(F_{D_1}(x_1{x}_2),F_{B_2}(y))\end{array}\right),$∀$(x,y)\in (V_1,V_2)=V$ for $(i)-(iii),\forall x\in V_1$ and $y_1{y}_2\in E_2$ for $(iv)-(vi),\forall y\in V_2$ and $x_1{x}_2\in E_1$ for $(vi)-(ix)$.

Example 3.

Let $G_1=(M_1,N_1)$ be a neutrosophic cubic graph of $G_1^{\ast }=(V_1,E_1)$ as showin in Figure 2, where $V_1=\{a,b,c\},$$E_1=\{ab,bc,ac\}$

$$\begin{array}{ccc}\hfill M_1& =& 〈\begin{array}{c}\{a,([0.1,0.2],0.5),([0.4,0.5],0.3),([0.6,0.7],0.2)\},\\ \{b,([0.2,0.4],0.1),([0.5,0.6],0.4),([0.1,0.2],0.3)\},\\ \{c,([0.3,0.4],0.2),([0.1,0.3],0.7),([0.4,0.6],0.3)\}\end{array}〉\hfill \\ \hfill N_1& =& 〈\begin{array}{c}\{ab,([0.1,0.2],0.5),([0.4,0.5],0.4),([0.6,0.7],0.2)\},\\ \{bc,([0.2,0.4],0.2),([0.1,0.3],0.7),([0.4,0.6]),0.3)\},\\ \{ac,([0.1,0.2],0.5),([0.1,0.3],0.7),([0.6,0.7],0.2)\}\end{array}〉\hfill \end{array}$$

and $G_2=(M_2,N_2)$ be a neutrosophic cubic graph of $G_2^{\ast }=(V_2,E_2)$ as showin in Figure 3, where $V_2=\{x,y,z\}$ and $E_2=\{xy,yz,xz\}$

$$\begin{array}{ccc}\hfill M_2& =& 〈\begin{array}{c}\{x,([0.7,0.8],0.6),([0.2,0.4],0.5),([0.3,0.4],0.7)\},\\ \{y,([0.2,0.3],0.4),([0.6,0.7],0.3),([0.9,1.0],0.5)\},\\ \{z,([0.4,0.5],0.2),([0.3,0.4],0.1),([0.6,0.7],0.4)\}\end{array}〉\hfill \\ \hfill N_2& =& 〈\begin{array}{c}\{xy,([0.2,0.3],0.6),([0.2,0.4],0.5),([0,9,1.0],0.5)\},\\ \{yz,([0.2,0.3],0.4),([0.3,0.4],0.3),([0.9,1.0],0.4)\},\\ \{xz,([0.4,0.5],0.6),([0.2,0.4],0.5),([0.6,0.7],0.4)\}\end{array}〉\hfill \end{array}$$

then $G_1\times G_2$ is a neutrosophic cubic graph of $G_1^{\ast }\times G_2^{\ast }$, as showin in Figure 4, where $V_1\times V_2=\{(a,x),(a,y),(a,z),(b,x),(b,y),(b,z),(c,x),(c,y),(c,z)\}$ and

$$\begin{array}{ccc}\hfill M_1\times M_2& =& 〈\begin{array}{c}\{(a,x),([0.1,0.2],0.6),([0.2,0.4],0.5),([0.6,0.7],0.2)\},\\ \{(a,y),([0.1,0.2],0.5),([0.4,0.5],0.3),([0.9,1.0],0.2)\},\\ \{(a,z),([0.1,0.2],0.5),([0.3,0.4],0.3),([0.6,0.7],0.2)\},\\ \{(b,x),([0.2,0.4],0.6),([0.2,0.4],0.5),([0.3,0.4],0.3)\},\\ \{(b,y),([0.2,0.3],0.4),([0.5,0.6],0.4),([0.9,1.0],0.3)\},\\ \{(b,z),([0.2,0.4],0.2),([0.3,0.4],0.4),([0.6,0.7],0.3)\},\\ \{(c,x),([0.3,0.4],0.6),([0.1,0.3],0.7),([0.4,0.6]),0.3)\},\\ \{(c,y),([0.2,0.3],0.4),([0.1,0.3],0.7),([0.9,1.0],0.3)\},\\ \{(c,z),([0.3,0.4],0.2),([0.1,0.3],0.7),([0.6,0.7],0.3)\}\end{array}〉\hfill \\ \hfill N_1\times N_2& =& 〈\begin{array}{c}\{((a,x)(a,y)),([0.1,0.2],0.6),([0.2,0.4],0.5),([0.9,1.0],0.2)\},\\ \{((a,y)(a,z)),([0.1,0.2],0.5),([0.3,0.4],0.3),([0.9,1.0],0.2)\},\\ \{((a,z)(b,z)),([0.1,0.2],0.5),([0.3,0.4],0.4),([0.6,0.7],0.2)\},\\ \{((b,x)(b,z)),([0.2,0.4],0.6),([0.2,0.4],0.5),([0.6,0.7],0.3)\},\\ \{((b,x)(b,y)),([0.2,0.3],0.6),([0.2,0.4],0.5),([0.9,1.0],0.3)\},\\ \{((b,y)(c,y)),([0.2,0.3],0.4),([0.1,0.3],0.7),([0.9,1.0],0.3)\},\\ \{((c,y)(c,z)),([0.2,0.3],0.4),([0.1,0.3],0.7),([0.9,1.0],0.3)\},\\ \{((c,x)(c,z)),([0.3,0.4],0.6),([0.1,0.3],0.7),([0.6,0.7],0.3)\},\\ \{((a,x)(c,x)),([0.1,0.2],0.6),([0.1,0.3],0.7),([0.6,0.7],0.2)\}\end{array}〉\hfill \end{array}$$

Proposition 1.

The cartesian product of two neutrosophic cubic graphs is again a neutrosophic cubic graph.

Proof. 

Condition is obvious for $M_1\times M_2$. Therefore we verify conditions only for $N_1\times N_2,$ where $N_1\times N_2=\left\{(({\tilde{T}}_{C_1\times C_2},T_{D_1\times D_2}),({\tilde{I}}_{C_1\times C_2},I_{D_1\times D_2}),({\tilde{F}}_{C_1\times C_2},F_{D_1\times D_2}))\right\}.$ Let $x\in V_1$ and $x_2{y}_2\in E_2$. Then

$$\begin{array}{ccc}\hfill {\tilde{T}}_{C_1\times C_2}((x,x_2)(x,y_2))& =& rmin\left\{({\tilde{T}}_{A_1}(x),{\tilde{T}}_{C_2}(x_2{y}_2))\right\}\hfill \\ & ⪯& rmin\{({\tilde{T}}_{A_1}(x),rmin(({\tilde{T}}_{A_2}(x_2),({\tilde{T}}_{A_2}(y_2))\}\hfill \\ & =& rmin\{rmin(({\tilde{T}}_{A_1}(x),({\tilde{T}}_{A_2}(x_2)),rmin(({\tilde{T}}_{A_1}(x),({\tilde{T}}_{A_2}(y_2))\}\hfill \\ & =& rmin\{({\tilde{T}}_{A_1}\times {\tilde{T}}_{A_2})(x,x_2),(({\tilde{T}}_{A_1}\times {\tilde{T}}_{A_2})(x,y_2)\}\hfill \\ \hfill T_{D_1\times D_2}((x,x_2)(x,y_2))& =& max\left\{(T_{B_1}(x),T_{D_2}(x_2{y}_2))\right\}\hfill \\ & \le & max\{(T_{B_1}(x),max((T_{B_2}(x_2),(T_{B_2}(y_2))\}\hfill \\ & =& max\{max((T_{B_1}(x),(T_{B_2}(x_2)),max((T_{B_1}(x),(T_{B_2}(y_2))\}\hfill \\ & =& max\{(T_{B_1}\times T_{B_2})(x,x_2),((T_{B_1}\times T_{B_2})(x,y_2)\}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\tilde{I}}_{C_1\times C_2}((x,x_2)(x,y_2))& =& rmin\left\{({\tilde{I}}_{A_1}(x),{\tilde{I}}_{C_2}(x_2{y}_2))\right\}\hfill \\ & ⪯& rmin\{({\tilde{I}}_{A_1}(x),rmin(({\tilde{I}}_{A_2}(x_2),({\tilde{I}}_{A_2}(y_2))\}\hfill \\ & =& rmin\{rmin(({\tilde{I}}_{A_1}(x),({\tilde{I}}_{A_2}(x_2)),rmin(({\tilde{I}}_{A_1}(x),({\tilde{I}}_{A_2}(y_2))\}\hfill \\ & =& rmin\{({\tilde{I}}_{A_1}\times {\tilde{I}}_{A_2})(x,x_2),(({\tilde{I}}_{A_1}\times {\tilde{I}}_{A_2})(x,y_2)\}\hfill \\ \hfill I_{D_1\times D_2}((x,x_2)(x,y_2))& =& max\left\{(I_{B_1}(x),I_{D_2}(x_2{y}_2))\right\}\hfill \\ & \le & max\{(I_{B_1}(x),max((I_{B_2}(x_2),(I_{B_2}(y_2))\}\hfill \\ & =& max\{max((I_{B_1}(x),(I_{B_2}(x_2)),max((I_{B_1}(x),(I_{B_2}(y_2))\}\hfill \\ & =& max\{(I_{B_1}\times I_{B_2})(x,x_2),((I_{B_1}\times I_{B_2})(x,y_2)\}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\tilde{F}}_{C_1\times C_2}((x,x_2)(x,y_2))& =& rmax\left\{({\tilde{F}}_{A_1}(x),{\tilde{F}}_{C_2}(x_2{y}_2))\right\}\hfill \\ & ⪯& rmax\{({\tilde{F}}_{A_1}(x),rmax(({\tilde{F}}_{A_2}(x_2),({\tilde{F}}_{A_2}(y_2))\}\hfill \\ & =& rmax\{rmax(({\tilde{F}}_{A_1}(x),({\tilde{F}}_{A_2}(x_2)),rmax(({\tilde{F}}_{A_1}(x),({\tilde{F}}_{A_2}(y_2))\}\hfill \\ & =& rmax\{({\tilde{F}}_{A_1}\times {\tilde{F}}_{A_2})(x,x_2),(({\tilde{F}}_{A_1}\times {\tilde{F}}_{A_2})(x,y_2)\}\hfill \\ \hfill F_{D_1\times D_2}((x,x_2)(x,y_2))& =& min\left\{(F_{B_1}(x),F_{D_2}(x_2{y}_2))\right\}\hfill \\ & \le & min\{(F_{B_1}(x),min((F_{B_2}(x_2),(F_{B_2}(y_2))\}\hfill \\ & =& min\{min((F_{B_1}(x),(F_{B_2}(x_2)),min((F_{B_1}(x),(F_{B_2}(y_2))\}\hfill \\ & =& min\{(F_{B_1}\times F_{B_2})(x,x_2),(F_{B_1}\times F_{B_2})(x,y_2)\}\hfill \end{array}$$

similarly we can prove it for $z\in V_2$ and $x_1{y}_1\in E_1$. ☐

Definition 12.

Let $G_1=(M_1,N_1)$ and $G_2=(M_2,N_2)$ be two neutrosophic cubic graphs. The degree of a vertex in $G_1\times G_2$ can be defined as follows, for any $(x_1,x_2)\in V_1\times V_2$

$$\begin{array}{ccc}\hfill deg({\tilde{T}}_{A_1}\times {\tilde{T}}_{A_2})(x_1,x_2)& =& {\Sigma }_{(x_1,x_2)\left(y_1,y_2\right)\in E_2}rmax({\tilde{T}}_{C_1}\times {\tilde{T}}_{C_2})((x_1,x_2)(y_1,y_2))\hfill \\ & =& {\Sigma }_{x_1=y_1=x,x_2{y}_2\in E_2}rmax({\tilde{T}}_{A_1}(x),{\tilde{T}}_{C_2}(x_2{y}_2))\hfill \\ & & +{\Sigma }_{x_2=y_2=z,x_1{y}_1\in E}rmax({\tilde{T}}_{A_2}(z),{\tilde{T}}_{C_1}(x_1{y}_1))\hfill \\ & & +{\Sigma }_{x_1{y}_1\in E_1,x_2{y}_2\in E_2}rmax({\tilde{T}}_{C_1}(x_1{y}_1),{\tilde{T}}_{C_2}(x_2{y}_2))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill deg(T_{B_1}\times T_{B_2})(x_1,x_2)& =& {\Sigma }_{(x_1,x_2)\left(y_1,y_2\right)\in E_2}min(T_{D_1}\times T_{D_2})((x_1,x_2)(y_1,y_2))\hfill \\ & =& {\Sigma }_{x_1=y_1=x,x_2{y}_2\in E_2}min(T_{B_1}(x),T_{D_2}(x_2{y}_2))\hfill \\ & & +{\Sigma }_{x_2=y_2=z,x_1{y}_1\in E}min(T_{B_2}(z),T_{D_1}(x_1{y}_1))\hfill \\ & & +{\Sigma }_{x_1{y}_1\in E_1,x_2{y}_2\in E_2}min(T_{D_1}(x_1{y}_1),T_{D_2}(x_2{y}_2))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill deg({\tilde{I}}_{A_1}\times {\tilde{I}}_{A_2})(x_1,x_2)& =& {\Sigma }_{(x_1,x_2)\left(y_1,y_2\right)\in E_2}rmax({\tilde{I}}_{C_1}\times {\tilde{I}}_{C_2})((x_1,x_2)(y_1,y_2))\hfill \\ & =& {\Sigma }_{x_1=y_1=x,x_2{y}_2\in E_2}rmax({\tilde{I}}_{A_1}(x),{\tilde{I}}_{C_2}(x_2{y}_2))\hfill \\ & & +{\Sigma }_{x_2=y_2=z,x_1{y}_1\in E}rmax({\tilde{I}}_{A_2}(z),{\tilde{I}}_{C_1}(x_1{y}_1))\hfill \\ & & +{\Sigma }_{x_1{y}_1\in E_1,x_2{y}_2\in E_2}rmax({\tilde{I}}_{C_1}(x_1{y}_1),{\tilde{I}}_{C_2}(x_2{y}_2))\hfill \\ \hfill deg(I_{B_1}\times I_{B_2})(x_1,x_2)& =& {\Sigma }_{(x_1,x_2)\left(y_1,y_2\right)\in E_2}min(I_{D_1}\times I_{D_2})((x_1,x_2)(y_1,y_2))\hfill \\ & =& {\Sigma }_{x_1=y_1=x,x_2{y}_2\in E_2}min(I_{B_1}(x),I_{D_2}(x_2{y}_2))\hfill \\ & & +{\Sigma }_{x_2=y_2=z,x_1{y}_1\in E}min(I_{B_2}(z),I_{D_1}(x_1{y}_1))\hfill \\ & & +{\Sigma }_{x_1{y}_1\in E_1,x_2{y}_2\in E_2}min(I_{D_1}(x_1{y}_1),I_{D_2}(x_2{y}_2))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill deg({\tilde{F}}_{A_1}\times {\tilde{F}}_{A_2})(x_1,x_2)& =& {\Sigma }_{(x_1,x_2)\left(y_1,y_2\right)\in E_2}rmin({\tilde{F}}_{C_1}\times {\tilde{F}}_{C_2})((x_1,x_2)(y_1,y_2))\hfill \\ & =& {\Sigma }_{x_1=y_1=x,x_2{y}_2\in E_2}rmin(F_{B_1}(x),F_{D_2}(x_2{y}_2))\hfill \\ & & +{\Sigma }_{x_2=y_2=z,x_1{y}_1\in E}rmin(F_{B_2}(z),F_{D_1}(x_1{y}_1))\hfill \\ & & +{\Sigma }_{x_1{y}_1\in E_1,x_2{y}_2\in E_2}rmin(F_{D_1}(x_1{y}_1),F_{D_2}(x_2{y}_2))\hfill \\ \hfill deg(F_{B_1}\times F_{B_2})(x_1,x_2)& =& {\Sigma }_{(x_1,x_2)\left(y_1,y_2\right)\in E_2}max(F_{D_1}\times F_{D_2})((x_1,x_2)(y_1,y_2))\hfill \\ & =& {\Sigma }_{x_1=y_1=x,x_2{y}_2\in E_2}max(F_{B_1}(x),F_{D_2}(x_2{y}_2))\hfill \\ & & +{\Sigma }_{x_2=y_2=z,x_1{y}_1\in E}max(F_{B_2}(z),F_{D_1}(x_1{y}_1))\hfill \\ & & +{\Sigma }_{x_1{y}_1\in E_1,x_2{y}_2\in E_2}max(F_{D_1}(x_1{y}_1),F_{D_2}(x_2{y}_2))\hfill \end{array}$$

Example 4.

In Example 3

$$\begin{array}{c}\hfill d_{G_1\times G_2}(a,x)=\{([0.9,1.1],1.0),([0.6,0.9],0.8),([0.9,1.1],1.2)\}\\ \hfill d_{G_1\times G_2}(a,y)=\{([0.4,0.6],0.9),([0.8,1.0],0.6),([1.2,1.4],0.9)\}\\ \hfill d_{G_1\times G_2}(a,z)=\{([0.6,0.8],0.6),([0.8,1.0],0.4),([1.2,1.4],0.8)\}\\ \hfill d_{G_1\times G_2}(b,z)=\{([0.8,1.0],0.3),([0.9,1.1],0.5),([0.7,0.9],1.1)\}\\ \hfill d_{G_1\times G_2}(b,x)=\{([0.6,0.9],0.6),([1.0,1.2],0.7),([0.2,0.4],1.2)\}\\ \hfill d_{G_1\times G_2}(b,y)=\{([0.4,0.8],0.7),([1.1,1.3],0.6),([0.5,0.8],1.0)\}\\ \hfill d_{G_1\times G_2}(c,y)=\{([0.5,0.8],0.4),([0.9,1.1],0.6),([0.8,1.2],0.9)\}\\ \hfill d_{G_1\times G_2}(c,z)=\{([0.7,0.9],0.4),([0.5,0.8],0.8),([0.8,1.2],1.1)\}\\ \hfill d_{G_1\times G_2}(c,x)=\{([1.1,1.3],0.7),([0.4,0.8],1.0),([0.7,1.0],1.4)\}\end{array}$$

Definition 13.

Let $G_1=(M_1,N_1)$ be a neutrosophic cubic graph of $G_1^{\ast }=(V_1,E_1)$ and $G_2=(M_2,N_2)$ be a neutrosophic cubic graph of $G_2^{\ast }=(V_2,E_2).$ Then composition of $G_1$ and $G_2$ is denoted by $G_1\left[G_2\right]$ and defined as follow

$$\begin{array}{ccc}\hfill G_1\left[G_2\right]& =& (M_1,N_1)\left[(M_2,N_2)\right]=\{M_1\left[M_2\right],N_1\left[N_2\right]\}=\{(A_1,B_1)\left[(A_2,B_2)\right],(C_1,D_1)\left[(C_2,D_2)\right]\}\hfill \\ & =& \{(A_1\left[A_2\right],B_1\left[B_2\right]),(C_1\left[C_2\right],D_1\left[D_2\right])\}\hfill \\ & =& \left\{\begin{array}{c}〈(({\tilde{T}}_{A_1}\circ {\tilde{T}}_{A_2}),(T_{B_1}\circ T_{B_2})),(({\tilde{I}}_{A_1}\circ {\tilde{I}}_{A_2}),(I_{B_1}\circ I_{B_2})),(({\tilde{F}}_{A_1}\circ {\tilde{F}}_{A_2}),(F_{B_1}\circ F_{B_2}))〉,\\ 〈(({\tilde{T}}_{C_1}\circ {\tilde{T}}_{C_2}),(T_{D_1}\circ T_{D_2})),(({\tilde{I}}_{C_1}\circ {\tilde{I}}_{C_2}),(I_{D_1}\circ I_{D_2})),({\tilde{F}}_{C_1}\circ {\tilde{F}}_{C_2})),(F_{D_1}\circ F_{D_2}))〉\end{array}\right\}\hfill \end{array}$$

where

(i) 

$\forall (x,y)\in (V_1,V_2)=V,$

$$({\tilde{T}}_{A_1}\circ {\tilde{T}}_{A_2})(x,y)=rmin({\tilde{T}}_{A_1}(x),{\tilde{T}}_{A_2}(y)),(T_{B_1}\circ T_{B_2})(x,y)=max(T_{B_1}(x),T_{B_2}(y))$$

$$({\tilde{I}}_{A_1}\circ {\tilde{I}}_{A_2})(x,y)=rmin({\tilde{I}}_{A_1}(x),{\tilde{I}}_{A_2}(y)),(I_{B_1}\circ I_{B_2})(x,y)=max(I_{B_1}(x),I_{B_2}(y))$$

$$({\tilde{F}}_{A_1}\circ {\tilde{F}}_{A_2})(x,y)=rmax({\tilde{F}}_{A_1}(x),{\tilde{F}}_{A_2}(y)),(F_{B_1}\circ F_{B_2})(x,y)=min(F_{B_1}(x),F_{B_{F_2}}(y))$$

(ii) 

$\forall x\in V_1$ and $y_1{y}_2\in E$

$$({\tilde{T}}_{C_1}\circ {\tilde{T}}_{C_2})((x,y_1)(x,y_2))=rmin({\tilde{T}}_{A_1}(x),{\tilde{T}}_{C_2}(y_1{y}_2)),(T_{D_1}\circ T_{D_2})((x,y_1)(x,y_2))=max(T_{B_1}(x),T_{D_2}(y_1{y}_2))$$

$$({\tilde{I}}_{C_1}\circ {\tilde{I}}_{C_2})((x,y_1)(x,y_2))=rmin({\tilde{I}}_{A_1}(x),{\tilde{I}}_{C_2}(y_1{y}_2)),(I_{D_1}\circ I_{D_2})((x,y_1)(x,y_2))=max(I_{B_1}(x),I_{D_2}(y_1{y}_2))$$

$$({\tilde{F}}_{C_1}\circ {\tilde{F}}_{C_2})((x,y_1)(x,y_2))=rmax({\tilde{F}}_{A_1}(x),{\tilde{F}}_{C_2}(y_1{y}_2)),(F_{D_1}\circ F_{D_2})((x,y_1)(x,y_2))=min(F_{B_1}(x),F_{D_2}(y_1{y}_2))$$

(iii) 

$\forall y\in V_2$ and $x_1{x}_2\in E_1$

$$({\tilde{T}}_{C_1}\circ {\tilde{T}}_{C_2})((x_1,y)(x_2,y))=rmin({\tilde{T}}_{C_1}(x_1{x}_2),{\tilde{T}}_{A_2}(y)),(T_{D_1}\circ T_{D_2})((x_1,y)(x_2,y))=max(T_{D_1}(x_1{x}_2),T_{B_2}(y))$$

$$({\tilde{I}}_{C_1}\circ {\tilde{I}}_{C_2})((x_1,y)(x_2,y))=rmin({\tilde{I}}_{C_1}(x_1{x}_2),{\tilde{I}}_{A_2}(y)),(I_{D_1}\circ I_{D_2})((x_1,y)(x_2,y))=max(I_{D_1}(x_1{x}_2),I_{B_2}(y))$$

$$({\tilde{F}}_{C_1}\circ {\tilde{F}}_{C_2})((x_1,y)(x_2,y))=rmax({\tilde{F}}_{C_1}(x_1{x}_2),{\tilde{F}}_{A_2}(y)),(F_{D_1}\circ F_{D_2})((x_1,y)(x_2,y))=min(F_{D_1}(x_1{x}_2),F_{B_2}(y))$$

(iv) 

$\forall (x_1,y_1)(x_2,y_2)\in E^0-E$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{C_1}\circ {\tilde{T}}_{C_2})((x_1,y_1)(x_2,y_2))& =& rmin({\tilde{T}}_{A_2}(y_1),{\tilde{T}}_{A_2}(y_2),{\tilde{T}}_{C_1}(x_1{x}_2)),(T_{D_1}\circ T_{D_2})((x_1,y_1)(x_2,y_2))\hfill \\ & =& max(T_{B_2}(y_1),T_{B_2}(y_2),T_{D_1}(x_1{x}_2))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{I}}_{C_1}\circ {\tilde{I}}_{C_2})((x_1,y_1)(x_2,y_2))& =& rmin({\tilde{I}}_{A_2}(y_1),{\tilde{I}}_{A_2}(y_2),{\tilde{I}}_{C_1}(x_1{x}_2)),(I_{D_1}\circ I_{D_2})((x_1,y_1)(x_2,y_2))\hfill \\ & =& max(I_{B_2}(y_1),I_{B_2}(y_2),I_{D_1}(x_1{x}_2))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{F}}_{C_1}\circ {\tilde{F}}_{C_2})((x_1,y_1)(x_2,y_2))& =& rmax({\tilde{F}}_{A_2}(y_1),{\tilde{F}}_{A_2}(y_2),{\tilde{F}}_{C_1}(x_1{x}_2)),(F_{D_1}\circ F_{D_2})((x_1,y_1)(x_2,y_2))\hfill \\ & =& min(F_{B_2}(y_1),F_{B_2}(y_2),F_{D_1}(x_1{x}_2))\hfill \end{array}$$

Example 5.

Let $G_1^{\ast }=(V_1,E_1)$ and $G_1^{\ast }=(V_2,E_2)$ be two graphs as showin in Figure 5, where $V_1=(a,b)$ and $V_2=(c,d)$. Suppose $M_1$ and $M_2$ be the neutrosophic cubic set representations of $V_1$ and $V_2.$ Also $N_1$ and $N_2$ be the neutrosophic cubic set representations of $E_1$ and $E_2$ defined as

$$\begin{array}{ccc}\hfill M_1& =& 〈\begin{array}{c}\{a,([0.5,0.6],0.1),([0.1,0.2],0.5),([0.8,0.9],0.3)\},\\ \{b,([0.4,0.5],0.3),([0.2,0.3],0.2),([0.5,0.6],0.6)\}\end{array}〉\hfill \\ \hfill N_1& =& 〈\begin{array}{c}\left\{ab,([0.4,0.5],0.3),([0.1,0.2],0.5),([0.8,0.9],0.3)\right\}\end{array}〉\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill M_2& =& 〈\begin{array}{c}\{c,([0.6,0.7],0.4),([0.8,0.9],0.8),([0.1,0.2],0.6)\},\\ \{d,([0.3,0.4],0.7),([0.6,0.7],0.5),([0.9,1.0],0.9)\}\end{array}〉\hfill \\ \hfill N_2& =& 〈\begin{array}{c}\left\{cd,([0.3,0.4],0.7),([0.6,0.7],0.8),([0.9,1.0],0.6)\right\}\end{array}〉\hfill \end{array}$$

Clearly $G_1=(M_1,N_1)$ and $G_2=(M_2,N_2)$ are neutrosophic cubic graphs. So, the composition of two neutrosophic cubic graphs $G-1$ and $G-2$ is again a neutrosophic cubic graph as shown in Figure 6, where

$$\begin{array}{ccc}\hfill M_1\left[M_2\right]& =& 〈\begin{array}{c}\{(a,c),([0.5,0.6],0.4),([0.1,0.2],0.8),([0.8,0.9],0.3)\},\\ \{(a,d),([0.3,0.4],0.7),([0.1,0.2],0.5),([0.9,1.0],0.3)\},\\ \{(b,c),([0.4,0.5],0.4),([0.2,0.3],0.8),[0.5,0.6],0.6)\},\\ \{(b,d),([0.3,0.4],0.7),([0.2,0.3],0.5),([0.9,1.0],0.6)\}\end{array}〉\hfill \\ \hfill N_1\left[N_2\right]& =& 〈\begin{array}{c}\{((a,c)(a,d)),([0.3,0.4],0.7),([0.1,0.2],0.8),([0.9,1.0],0.3)\},\\ \{((a,d)(b,d)),([0.3,0.4],0.7),([0.1,0.2],0.5),[0.9,1.0],0.3)\},\\ \{((b,d)(b,c)),([0.3,0.4],0.7),([0.2,0.3],0.8),([0.9,1.0],0.6)\},\\ \{((b,c)(a,c)),([0.4,0.5],0.4),([0.1,0.2],0.8),([0.8,0.9],0.3)\},\\ \{((a,c)(b,d)),([0.3,0.4],0.7),([0.1,0.2],0.8),([0.9,1.0],0.3)\},\\ \{((a,d)(b,c)),([0.3,0.4],0.7),([0.1,0.2],0.8),([0.9,1.0],0.3)\}\end{array}〉\hfill \end{array}$$

Proposition 2.

The composition of two neutrosophic cubic graphs is again a neutrosophic cubic graph.

Definition 14.

Let $G_1=(M_1,N_1)$ and $G_2=(M_2,N_2)$ be two neutrosophic cubic graphs of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ respectively. Then P-union is denoted by $G_1{\cup }_P{G}_2$ and is defined as

$$\begin{array}{ccc}\hfill G_1{\cup }_P{G}_2& =& \left\{(M_1,N_1){\cup }_P(M_2,N_2)\right\}=\{M_1{\cup }_P{M}_2,N_1{\cup }_P{N}_2\}\hfill \\ & =& \{〈(({\tilde{T}}_{A_1}{\cup }_p{\tilde{T}}_{A_2}),(T_{B_1}{\cup }_p{T}_{B_2})),(({\tilde{I}}_{A_1}{\cup }_p{\tilde{I}}_{A_2}),(I_{B_1}{\cup }_p{I}_{B_2})),(({\tilde{F}}_{A_1}{\cup }_p{\tilde{F}}_{A_2}),(F_{B_1}{\cup }_p{F}_{B_2}))〉,\hfill \\ & & 〈(({\tilde{T}}_{C_1}{\cup }_p{\tilde{T}}_{C_2}),(T_{D_1}{\cup }_p{T}_{D_2})),(({\tilde{I}}_{C_1}{\cup }_p{\tilde{I}}_{C_2}),(I_{D_1}{\cup }_p{I}_{D_2})),(({\tilde{F}}_{C_1}{\cup }_p{\tilde{F}}_{C_2}),(F_{D_1}{\cup }_p{F}_{D_2}))〉\}\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{A_1}{\cup }_p{\tilde{T}}_{A_2})(x)& =& \left\{\begin{array}{cc}{\tilde{T}}_{A_1}(x)& ifx\in V_1-V_2\\ {\tilde{T}}_{A_2}(x)& ifx\in V_2-V_1\\ rmax\{{\tilde{T}}_{A_1}(x),{\tilde{T}}_{A_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \\ \hfill (T_{B_1}{\cup }_p{T}_{B_2})(x)& =& \left\{\begin{array}{cc}{T}_{B_1}(x)& ifx\in V_1-V_2\\ T_{B_2}(x)& ifx\in V_2-V_1\\ max\{T_{B_1}(x),T_{B_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{I}}_{A_1}{\cup }_p{\tilde{I}}_{A_2})(x)& =& \left\{\begin{array}{cc}{\tilde{I}}_{A_1}(x)& ifx\in V_1-V_2\\ {\tilde{I}}_{A_2}(x)& ifx\in V_2-V_1\\ rmax\{{\tilde{I}}_{A_1}(x),{\tilde{I}}_{A_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \\ \hfill (I_{B_1}{\cup }_p{I}_{B_2})(x)& =& \left\{\begin{array}{cc}{I}_{B_1}(x)& ifx\in V_1-V_2\\ I_{B_2}(x)& ifx\in V_2-V_1\\ max\{I_{B_1}(x),I_{B_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{F}}_{A_1}{\cup }_p{\tilde{F}}_{A_2})(x)& =& \left\{\begin{array}{cc}{\tilde{F}}_{A_1}(x)& ifx\in V_1-V_2\\ {\tilde{F}}_{A_2}(x)& ifx\in V_2-V_1\\ rmax\{{\tilde{F}}_{A_1}(x),{\tilde{F}}_{A_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \\ \hfill (F_{B_1}{\cup }_p{F}_{B_2})(x)& =& \left\{\begin{array}{cc}{F}_{B_1}(x)& ifx\in V_1-V_2\\ F_{B_2}(x)& ifx\in V_2-V_1\\ max\{F_{B_1}(x),F_{B_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{C_1}{\cup }_p{\tilde{T}}_{C_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{\tilde{T}}_{C_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ {\tilde{T}}_{C_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ rmax\{{\tilde{T}}_{C_1}(x_2{y}_2),{\tilde{T}}_{C_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \\ \hfill (T_{D_1}{\cup }_p{T}_{D_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{T}_{D_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ T_{D_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ max\{T_{D_1}(x_2{y}_2),T_{D_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{I}}_{C_1}{\cup }_p{\tilde{I}}_{C_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{\tilde{I}}_{C_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ {\tilde{I}}_{C_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ rmax\{{\tilde{I}}_{C_1}(x_2{y}_2),{\tilde{I}}_{C_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \\ \hfill (I_{D_1}{\cup }_p{I}_{D_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{I}_{D_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ I_{D_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ max\{I_{D_1}(x_2{y}_2),I_{D_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{F}}_{C_1}{\cup }_p{\tilde{F}}_{C_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{\tilde{F}}_{C_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ {\tilde{F}}_{C_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ rmax\{{\tilde{F}}_{C_1}(x_2{y}_2),{\tilde{F}}_{C_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \\ \hfill (F_{D_1}{\cup }_p{F}_{D_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{F}_{D_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ F_{D_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ max\{F_{D_1}(x_2{y}_2),F_{D_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \end{array}$$

and R-union is denoted by $G_1{\cup }_R{G}_2$ and is defined by

$$\begin{array}{ccc}\hfill G_1{\cup }_R{G}_2& =& \left\{(M_1,N_1){\cup }_R(M_2,N_2)\right\}=\{M_1{\cup }_R{M}_2,N_1{\cup }_R{N}_2\}\hfill \\ & =& \{〈(({\tilde{T}}_{A_1}{\cup }_R{\tilde{T}}_{A_2}),(T_{B_1}{\cup }_R{T}_{B_2})),(({\tilde{I}}_{A_1}{\cup }_R{\tilde{I}}_{A_2}),(I_{B_1}{\cup }_R{I}_{B_2})),(({\tilde{F}}_{A_1}{\cup }_R{\tilde{F}}_{A_2}),(F_{B_1}{\cup }_R{F}_{B_2}))〉,\hfill \\ & & 〈(({\tilde{T}}_{C_1}{\cup }_R{\tilde{T}}_{C_2}),(T_{D_1}{\cup }_R{T}_{D_2})),(({\tilde{I}}_{C_1}{\cup }_R{\tilde{I}}_{C_2}),(I_{D_1}{\cup }_R{I}_{D_2})),(({\tilde{F}}_{C_1}{\cup }_R{\tilde{F}}_{C_2}),(F_{D_1}{\cup }_R{F}_{D_2}))〉\}\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{A_1}{\cup }_R{\tilde{T}}_{A_2})(x)& =& \left\{\begin{array}{cc}{\tilde{T}}_{A_1}(x)& ifx\in V_1-V_2\\ {\tilde{T}}_{A_2}(x)& ifx\in V_2-V_1\\ rmax\{{\tilde{T}}_{A_1}(x),{\tilde{T}}_{A_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \\ \hfill (T_{B_1}{\cup }_R{T}_{B_2})(x)& =& \left\{\begin{array}{cc}{T}_{B_1}(x)& ifx\in V_1-V_2\\ T_{B_2}(x)& ifx\in V_2-V_1\\ min\{T_{B_1}(x),T_{B_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{I}}_{A_1}{\cup }_R{\tilde{I}}_{A_2})(x)& =& \left\{\begin{array}{cc}{\tilde{I}}_{A_1}(x)& ifx\in V_1-V_2\\ {\tilde{I}}_{A_2}(x)& ifx\in V_2-V_1\\ rmax\{{\tilde{I}}_{A_1}(x),{\tilde{I}}_{A_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \\ \hfill (I_{B_1}{\cup }_R{I}_{B_2})(x)& =& \left\{\begin{array}{cc}{I}_{B_1}(x)& ifx\in V_1-V_2\\ I_{B_2}(x)& ifx\in V_2-V_1\\ min\{I_{B_1}(x),I_{B_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{F}}_{A_1}{\cup }_R{M}_{T_{F_2}})(x)& =& \left\{\begin{array}{cc}{\tilde{F}}_{A_1}(x)& ifx\in V_1-V_2\\ {\tilde{F}}_{A_2}(x)& ifx\in V_2-V_1\\ rmax\{{\tilde{F}}_{A_1}(x),{\tilde{F}}_{A_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \\ \hfill (F_{B_1}{\cup }_R{F}_{B_2})(x)& =& \left\{\begin{array}{cc}{F}_{B_1}(x)& ifx\in V_1-V_2\\ F_{B_2}(x)& ifx\in V_2-V_1\\ min\{F_{B_1}(x),F_{B_2}(x)\}& ifx\in V_1\cap V_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{C_1}{\cup }_R{\tilde{T}}_{C_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{\tilde{T}}_{C_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ {\tilde{T}}_{C_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ rmax\{{\tilde{T}}_{C_1}(x_2{y}_2),{\tilde{T}}_{C_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \\ \hfill (T_{D_1}{\cup }_R{N}_{D_{{}_2}})(x_2{y}_2)& =& \left\{\begin{array}{cc}{T}_{D_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ T_{D_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ min\{T_{D_1}(x_2{y}_2),T_{D_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ({\tilde{F}}_{C_1}{\cup }_R{\tilde{F}}_{C_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{\tilde{F}}_{C_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ {\tilde{F}}_{C_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ rmax\{{\tilde{F}}_{C_1}(x_2{y}_2),{\tilde{F}}_{C_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \\ \hfill (F_{D_1}{\cup }_R{F}_{D_2})(x_2{y}_2)& =& \left\{\begin{array}{cc}{F}_{D_1}(x_2{y}_2)& if{x}_2{y}_2\in V_1-V_2\\ F_{D_2}(x_2{y}_2)& if{x}_2{y}_2\in V_2-V_1\\ min\{F_{D_1}(x_2{y}_2),F_{D_2}(x_2{y}_2)\}& if{x}_2{y}_2\in E_1\cap E_2\end{array}\right.\hfill \end{array}$$

Example 6.

Let $G_1$ and $G_2$ be two neutrosophic cubic graphs as represented by Figure 7 and Figure 8, where

$$\begin{array}{ccc}\hfill M_1& =& 〈\begin{array}{c}\left\{a,([0.2,0.3],0.5),([0.4,0.5],0.9),([0.1,0.3],0.2)\right\},\\ \{b,([0.3,0.4],0.2),[0.1,0.2],0.1),[0.4,0.6],0.5)\},\\ \{c,([0.2,0.4],0.6),([0.7,0.8],0.8),([0.3,0.5],0.7)\}\end{array}〉\hfill \\ \hfill N_1& =& 〈\begin{array}{c}\left\{ab,([0.2,0.3],0.5),([0.1,0.2],0.9),([0.4,0.6],0.2)\right\},\\ \left\{bc,([0.2,0.4],0.6),([0.1,0.2],0.8),([0.4,0.6],0.5)\right\},\\ \{ac,([0.2,0.3],0.6),([0.4,0.5],0.9),([0.3,0.5],0.2)\}\end{array}〉\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill M_2& =& 〈\begin{array}{c}\left\{a,([0.5,0.6],0.3),([0.1,0.2],0.6),([0.3,0.4],0.5)\right\},\\ \left\{b,([0.6,0.7],0.6),([0.7,0.8],0.4),([0.1,0.2],0.5)\right\},\\ \{c,([0.4,0.5],0.1),([0.2,0.5],0.5),([0.5,0.6],0.3)\}\end{array}〉\hfill \\ \hfill N_2& =& 〈\begin{array}{c}\left\{ab,([0.5,0.6],0.6),([0.1,0.2],0.6),([0.3,0.4],0.5)\right\},\\ \left\{bc,([0.4,0.5],0.6),([0.2,0.5],0.5),([0.5,0.6],0.3)\right\},\\ \{ac,([0.4,0.5],0.3),([0.1,0.2],0.6),([0.5,0.6],0.3)\}\end{array}〉\hfill \end{array}$$

then $G_1{\cup }_p{G}_2$ will be a neutrosophic cubic graph as shown in Figure 9, where

$$\begin{array}{ccc}\hfill M_1{\cup }_p{M}_2& =& 〈\begin{array}{c}\left\{a,([0.5,0.6],0.5),([0.4,0.5],0.9),([0.3,0.4],0.5)\right\},\\ \left\{b,([0.6,0.7],0.6),([0.7,0.8],0.4),([0.4,0.6],0.5)\right\},\\ \left\{c,([0.4,0.5],0.6),([0.7,0.8],0.8),([0.5,0.6],0.7)\right\}\end{array}〉\hfill \\ \hfill N_1{\cup }_P{N}_2& =& 〈\begin{array}{c}\left\{ab,([0.5,0.6],0.6),([0.1,0.2],0.9),([0.4,0.6],0.5)\right\},\\ \left\{bc,([0.4,0.5],0.6),([0.2,0.5],0.8),[0.5,0.6],0.5)\right\},\\ \left\{ac,([0.4,0.5],0.6),([0.4,0.5],0.9),([0.5,0.6],0.3)\right\}\end{array}〉\hfill \end{array}$$

and $G_1{\cup }_R{G}_2$ will be a neutrosophic cubic graph as shown in Figure 10, where

$$\begin{array}{ccc}\hfill M_1{\cup }_R{M}_2& =& \begin{array}{c}\left\{a,([0.5,0.6],0.3),([0.4,0.5],0.6),([0.3,0.4],0.2)\right\},\\ \left\{b,([0.6,0.7],0.2),([0.7,0.8],0.1),[0.4,0.6],0.5)\right\},\\ \left\{c,([0.4,0.5],0.1),([0.7,0.8],0.5),([0.5,0.6],0.3)\right\}\end{array}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill N_1{\cup }_R{N}_2& =& \begin{array}{c}\left\{ab,\left(\right[0.5,0.6],0.5),\left(\right[0.1,0.2],0.6),\left(\right[0.4,0.6],0.2)\right\},\\ \left\{bc,\left(\right[0.4,0.5],0.6),\left(\right[0.2,0.5],0.5),\left(\right[0.5,0.6],0.3)\right\},\\ \left\{ac,\left(\right[0.4,0.5],0.3),\left(\right[0.4,0.5],0.6),\left(\right[0.5,0.6],0.2)\right\}\end{array}\hfill \end{array}$$

Proposition 3.

The P-union of two neutrosophic cubic graphs is again a neutrosophic cubic graph.

Remark 2.

The R-union of two neutrosophic cubic graphs may or may not be a neutrosophic cubic graph as in the Example 6 we see that

$$T_{D_1{\cup }_R{D}_2}(ab)=0.5\nleqq max\{0.3,0.2\}=0.3=max\{T_{D_1{\cup }_R{D}_2}(a),T_{D_1{\cup }_R{D}_2}(b)\}$$

Definition 15.

Let $G_1=(M_1,N_1)$ and $G_2=(M_2,N_2)$ be two neutrosophic cubic graphs of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ respectively then P-join is denoted by $G_1{+}_P{G}_2$ and is defined by

$$\begin{array}{ccc}\hfill G_1{+}_P{G}_2& =& (M_1,N_1){+}_P(M_2,N_2)=(M_1{+}_P{M}_2,N_1{+}_P{N}_2)\hfill \\ & =& \{〈(({\tilde{T}}_{A_1}{+}_P{\tilde{T}}_{A_2}),(T_{B_1}{+}_P{T}_{B_2})),(({\tilde{I}}_{A_1}{+}_P{\tilde{I}}_{A_2}),(I_{B_1}{+}_P{I}_{B_2})),(({\tilde{F}}_{A_1}{+}_P{\tilde{F}}_{A_2}),(F_{B_1}{+}_P{F}_{B_2}))〉,\hfill \\ & & 〈(({\tilde{T}}_{C_1}{+}_P{\tilde{T}}_{C_2}),(T_{D_1}{+}_P{T}_{D_2})),(({\tilde{I}}_{C_1}{+}_P{\tilde{I}}_{C_2}),(I_{D_1}{+}_P{I}_{D_2})),(({\tilde{F}}_{C_1}{+}_P{\tilde{F}}_{C_2}),(F_{D_1}{+}_P{F}_{D_2}))〉\}\hfill \end{array}$$

where

(i) 

if $x\in V_1\cup V_2$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{A_1}{+}_P{\tilde{T}}_{A_2})(x)& =& ({\tilde{T}}_{A_1}{\cup }_P{\tilde{T}}_{A_2})(x),(T_{B_1}{+}_P{T}_{B_2})(x)=(T_{B_1}{\cup }_P{T}_{B_2})(x)\hfill \\ \hfill ({\tilde{I}}_{A_1}{+}_P{\tilde{I}}_{A_2})(x)& =& ({\tilde{I}}_{A_1}{\cup }_P{\tilde{I}}_{A_2})(x),(I_{B_1}{+}_P{I}_{B_2})(x)=(I_{B_1}{\cup }_P{I}_{B_2})(x)\hfill \\ \hfill ({\tilde{F}}_{A_1}{+}_P{\tilde{F}}_{A_2})(x)& =& ({\tilde{F}}_{A_1}{\cup }_P{\tilde{F}}_{A_2})(x),(F_{B_1}{+}_P{F}_{B_2})(x)=(F_{B_1}{\cup }_P{F}_{B_2})(x)\hfill \end{array}$$

(ii) 

if $xy\in E_1\cup E_2$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{C_1}{+}_P{\tilde{T}}_{C_2})(xy)& =& ({\tilde{T}}_{C_1}{\cup }_P{\tilde{T}}_{C_2})(xy),(T_{D_1}{+}_P{T}_{D_2})(xy)=(T_{D_1}{\cup }_P{T}_{D_2})(xy)\hfill \\ \hfill ({\tilde{I}}_{C_1}{+}_P{\tilde{I}}_{C_2})(xy)& =& ({\tilde{I}}_{C_1}{\cup }_P{\tilde{I}}_{C_2})(xy),(I_{D_1}{+}_P{I}_{D_2})(xy)=(I_{D_1}{\cup }_P{I}_{D_2})(xy)\hfill \\ \hfill ({\tilde{F}}_{C_1}{+}_P{\tilde{F}}_{C_2})(xy)& =& ({\tilde{F}}_{C_1}{\cup }_P{\tilde{F}}_{C_2})(xy),(F_{D_1}{+}_P{F}_{D_2})(xy)=(F_{D_1}{\cup }_P{F}_{D_2})(xy)\hfill \end{array}$$

(iii) 

if $xy\in E^{\ast }$, where $E^{\ast }$ is the set of all edges joining the vertices of $V_1$ and $V_2$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{C_1}{+}_P{\tilde{T}}_{C_2})(xy)& =& rmin\{{\tilde{T}}_{A_1}(x),{\tilde{T}}_{A_2}(y)\},(T_{D_1}{+}_P{T}_{D_2})(xy)=min\{T_{B_1}(x),T_{B_2}(y)\}\hfill \\ \hfill ({\tilde{I}}_{C_1}{+}_P{\tilde{I}}_{C_2})(xy)& =& rmin\{{\tilde{I}}_{A_1}(x),{\tilde{I}}_{A_2}(y)\},(I_{D_1}{+}_P{I}_{D_2})(xy)=min\{I_{B_1}(x),I_{B_2}(y)\}\hfill \\ \hfill ({\tilde{F}}_{C_1}{+}_P{\tilde{F}}_{C_2})(xy)& =& rmin\{{\tilde{F}}_{A_1}(x),{\tilde{F}}_{A_2}(y)\},(F_{D_1}{+}_P{F}_{D_2})(xy)=min\{F_{B_1}(x),F_{B_2}(y)\}\hfill \end{array}$$

Definition 16.

Let $G_1=(M_1,N_1)$ and $G_2=(M_2,N_2)$ be two neutrosophic cubic graphs of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ respectively then R-join is denoted by $G_1{+}_R{G}_2$ and is defined by

$$\begin{array}{ccc}\hfill G_1{+}_R{G}_2& =& (M_1,N_1){+}_R(M_2,N_2)=(M_1{+}_R{M}_2,N_1{+}_R{N}_2)\hfill \\ & =& \{〈(({\tilde{T}}_{A_1}{+}_R{\tilde{T}}_{A_2}),(T_{B_1}{+}_R{T}_{B_2})),(({\tilde{I}}_{A_1}{+}_R{\tilde{I}}_{A_2}),(I_{B_1}{+}_R{I}_{B_2})),(({\tilde{F}}_{A_1}{+}_R{\tilde{F}}_{A_2}),(F_{B_1}{+}_R{F}_{B_2}))〉,\hfill \\ & & 〈(({\tilde{T}}_{C_1}{+}_R{\tilde{T}}_{C_2}),(T_{D_1}{+}_R{T}_{D_2})),(({\tilde{I}}_{C_1}{+}_R{\tilde{I}}_{C_2}),(I_{D_1}{+}_R{I}_{D_2})),(({\tilde{F}}_{C_1}{+}_R{\tilde{F}}_{C_2}),(F_{D_1}{+}_R{F}_{D_2}))〉\}\hfill \end{array}$$

where

(i) 

if $x\in V_1\cup V_2$

$$\begin{array}{ccc}\hfill ({\tilde{T}}_{A_1}{+}_R{\tilde{T}}_{A_2})(x)& =& ({\tilde{T}}_{A_1}{\cup }_R{\tilde{T}}_{A_2})(x),(T_{B_1}{+}_R{T}_{B_2})(x)=(T_{B_1}{\cup }_R{T}_{B_2})(x)\hfill \\ \hfill ({\tilde{I}}_{A_1}{+}_R{\tilde{I}}_{A_2})(x)& =& ({\tilde{I}}_{A_1}{\cup }_R{\tilde{I}}_{A_2})(x),(I_{B_1}{+}_R{I}_{B_2})(x)=(I_{B_1}{\cup }_R{I}_{B_2})(x)\hfill \\ \hfill ({\tilde{F}}_{A_1}{+}_R{\tilde{F}}_{A_2})(x)& =& ({\tilde{F}}_{A_1}{\cup }_R{\tilde{F}}_{A_2})(x),(F_{B_1}{+}_R{F}_{B_2})(x)=(F_{B_1}{\cup }_R{F}_{B_2})(x)\hfill \end{array}$$

(ii) 

if $xy\in E_1\cup E_2$

$$\begin{array}{c}2a.\left\{({\tilde{T}}_{C_1}{+}_R{\tilde{T}}_{C_2})(xy)=({\tilde{T}}_{C_1}{\cup }_R{\tilde{T}}_{C_2})(xy),(T_{D_1}{+}_R{T}_{D_2})(xy)=(T_{D_1}{\cup }_R{T}_{D_2})(xy)\right.\hfill \\ 2b.\left\{({\tilde{I}}_{C_1}{+}_R{\tilde{I}}_{C_2})(xy)=({\tilde{I}}_{C_1}{\cup }_R{\tilde{I}}_{C_2})(xy),(I_{D_1}{+}_R{I}_{D_2})(xy)=(I_{D_1}{\cup }_R{I}_{D_2})(xy)\right.\hfill \\ 2c.\left\{({\tilde{F}}_{C_1}{+}_R{\tilde{F}}_{C_2})(xy)=({\tilde{F}}_{C_1}{\cup }_R{\tilde{F}}_{C_2})(xy),(F_{D_1}{+}_R{F}_{D_2})(xy)=(F_{D_1}{\cup }_R{F}_{D_2})(xy)\right.\hfill \end{array}$$

(iii) 

if $xy\in E^{\ast }$, where $E^{\ast }$ is the set of all edges joining the vertices of $V_1$ and $V_2$

$$\begin{array}{c}3a.\left\{\begin{array}{c}({\tilde{T}}_{C_1}{+}_R{\tilde{T}}_{C_2})(xy)=rmin\{{\tilde{T}}_{A_1}(x),{\tilde{T}}_{A_2}(y)\},\\ (T_{D_1}{+}_R{T}_{D_2})(xy)=max\{T_{B_1}(x),T_{B_2}(y)\}\end{array}\right.\hfill \\ 3b.\left\{\begin{array}{c}({\tilde{I}}_{C_1}{+}_R{\tilde{I}}_{C_2})(xy)=rmin\{{\tilde{I}}_{A_1}(x),{\tilde{I}}_{A_2}(y)\},\\ (I_{D_1}{+}_R{I}_{D_2})(xy)=max\{I_{B_1}(x),I_{B_2}(y)\}\end{array}\right.\hfill \\ 3c.\left\{\begin{array}{c}({\tilde{F}}_{C_1}{+}_R{\tilde{F}}_{C_2})(xy)=rmin\{{\tilde{F}}_{A_1}(x),{\tilde{F}}_{A_2}(y)\},\\ (F_{D_1}{+}_R{F}_{D_2})(xy)=max\{F_{B_1}(x),F_{B_2}(y)\}\end{array}\right.\hfill \end{array}$$

Proposition 4.

The P-join and R-join of two neutrosophic cubic graphs is again a neutrosophic cubic graph.

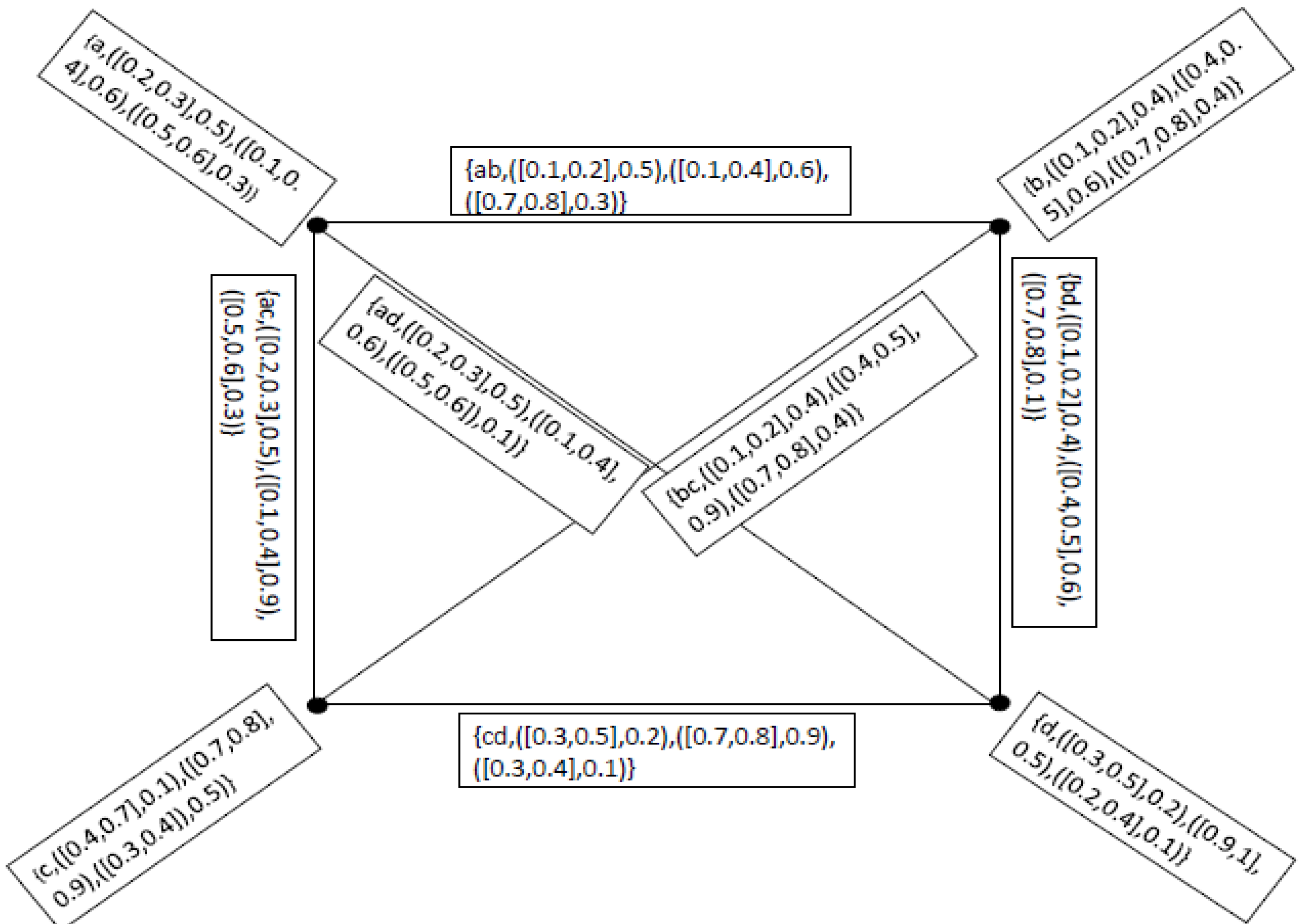
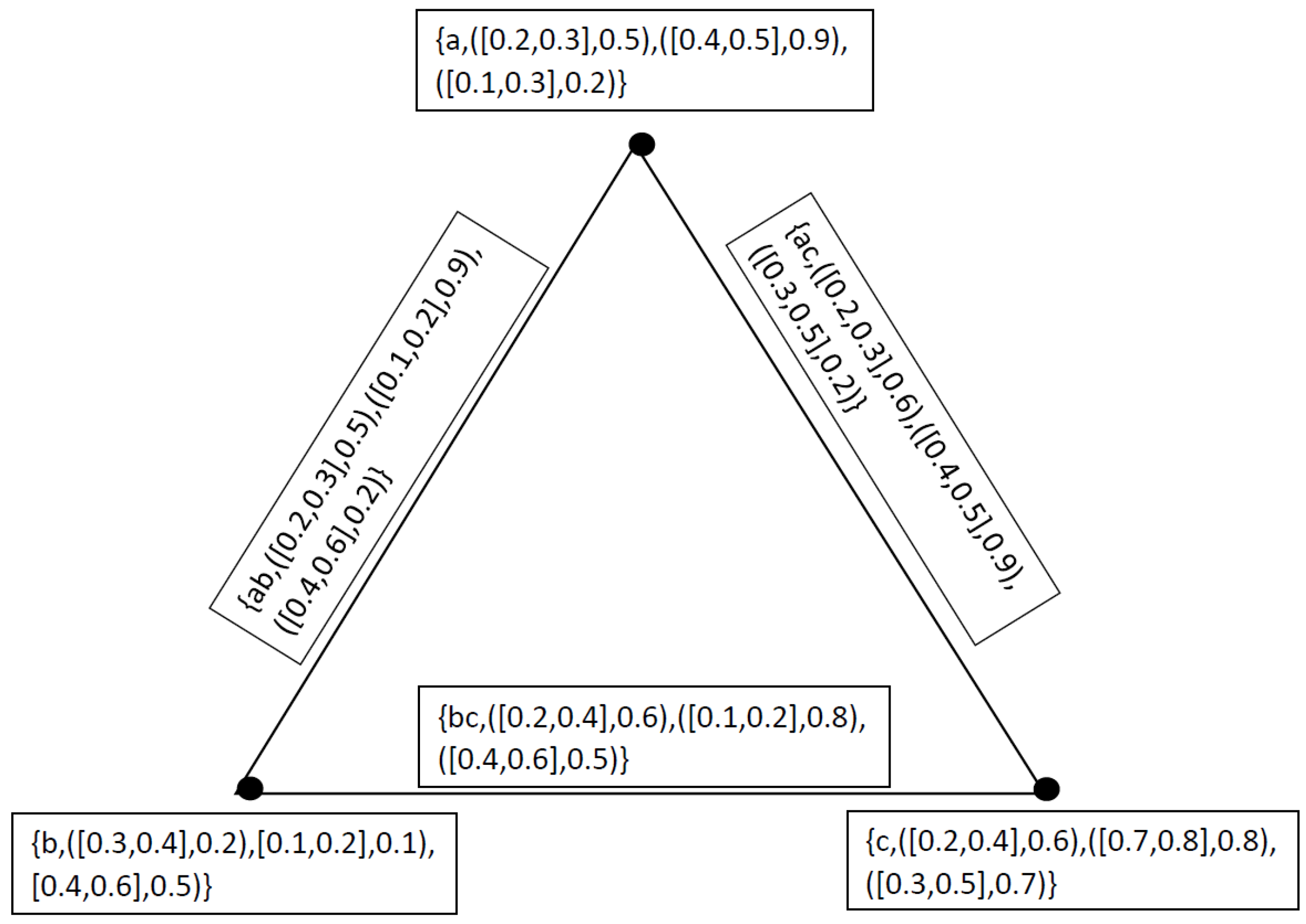
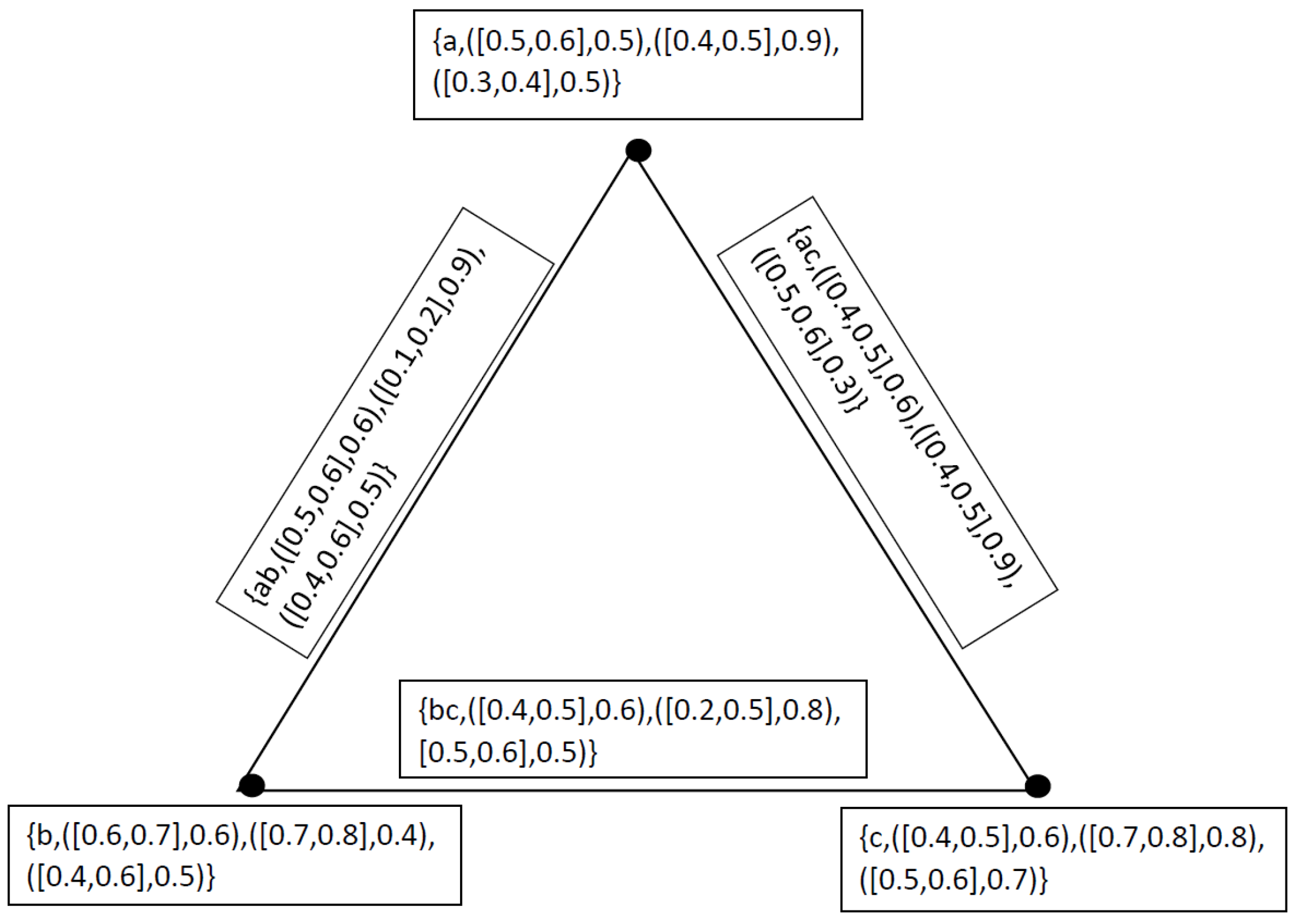
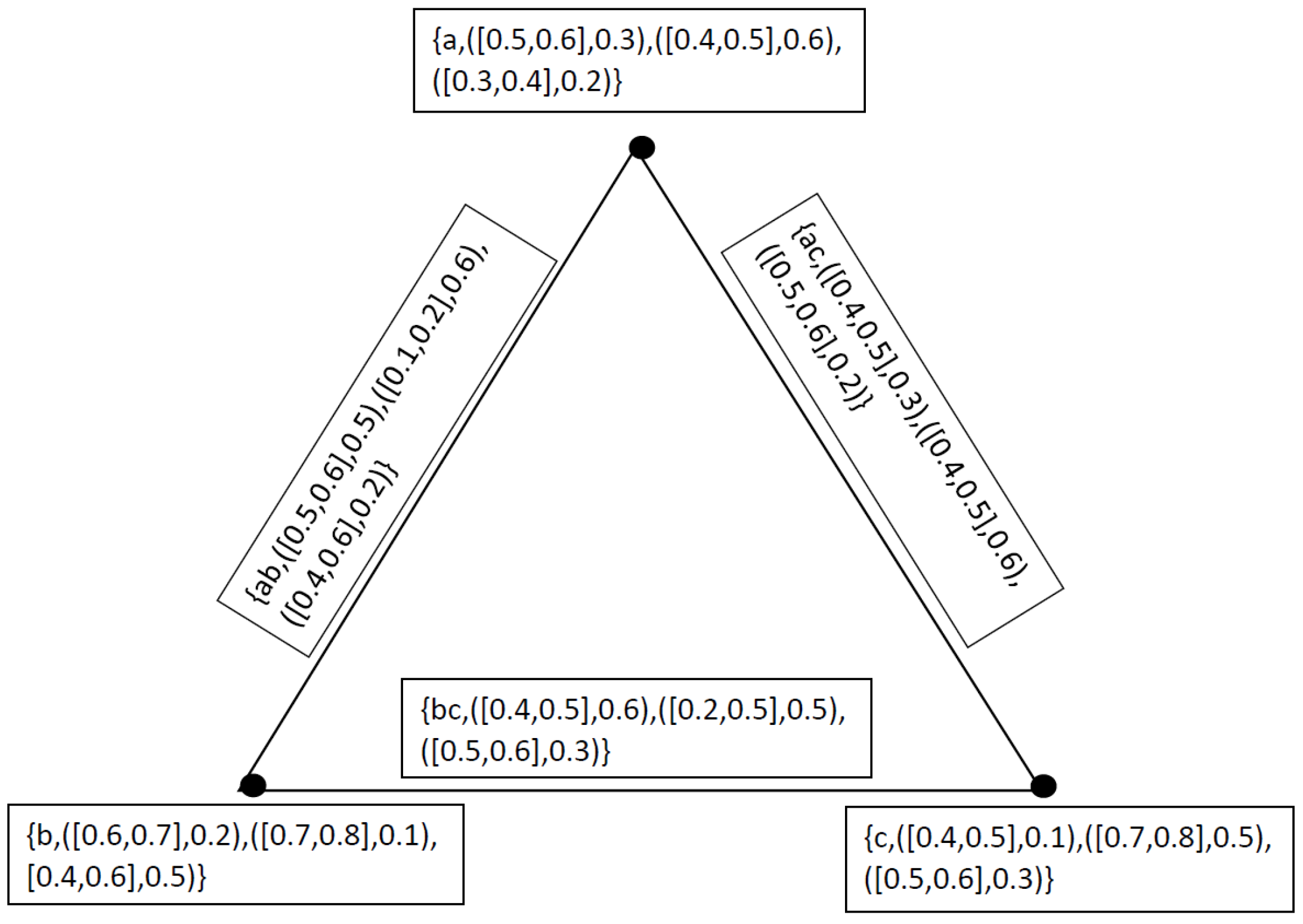
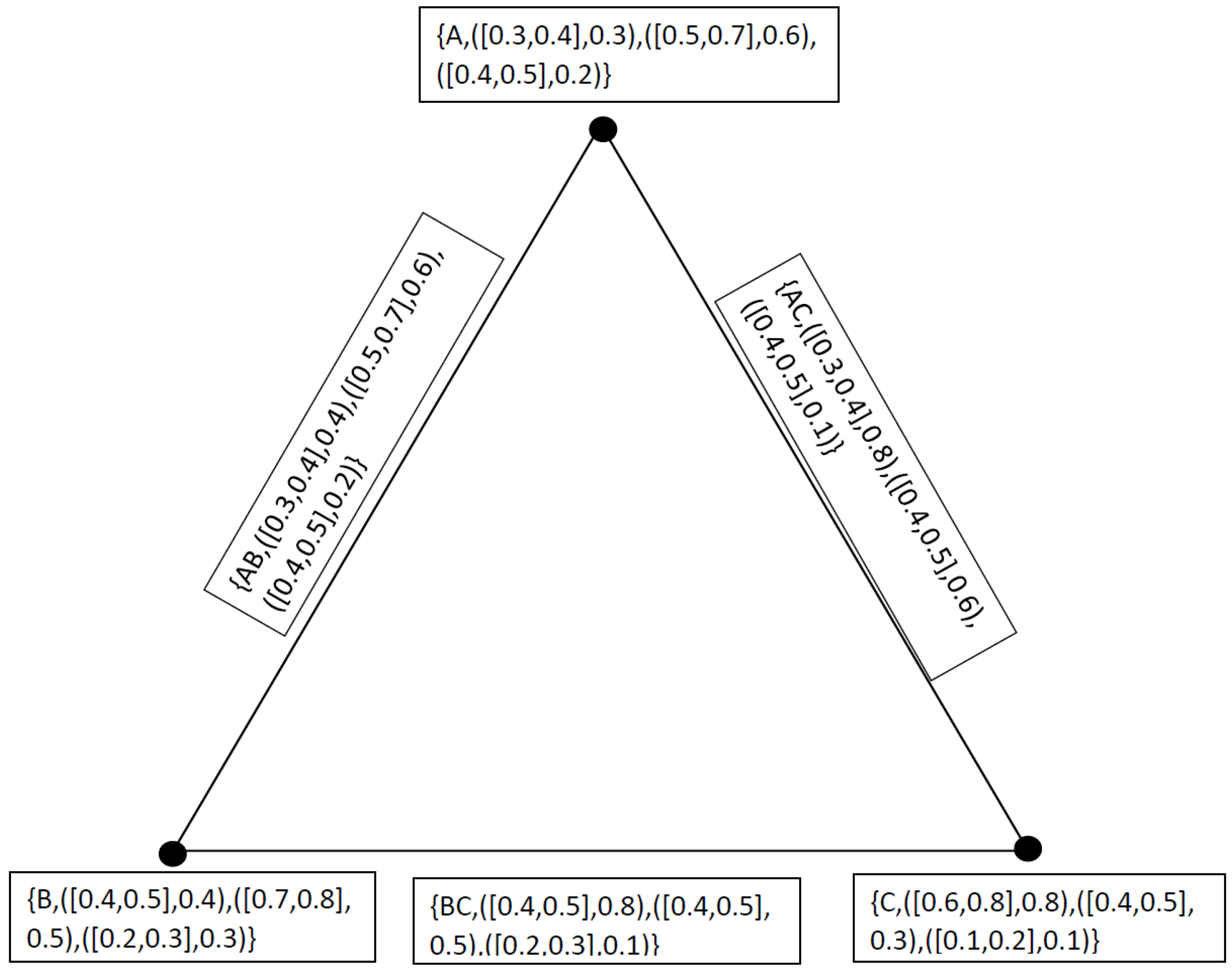
4. Applications

Fuzzy graph theory is an effective field having a vast range of applications in Mathematics. Neutrosophic cubic graphs are more general and effective approach used in daily life very effectively.

Here in this section we test the applicability of our proposed model by providing applications in industries.

Example 7.

Let us suppose a set of three industries representing a vertex set $V=\{A,B,C\}$ and let the truth-membership of each vertex in V denotes “win win” situation of industry, where they do not harm each other and do not capture other’s customers. Indetermined-membership of members of vertex set represents the situation in which industry works in a diplomatic and social way, that is, they are ally being social and competitive being industry. Falsity-membership shows a brutal competition where price war starts among industries. We want to observe the effect of one industry on other industry with respect to their business power and strategies. Let we have a neutrosophic cubic graph for industries having the following data with respect to business strategies

$$M=〈\begin{array}{c}\{A,([0.3,0.4],0.3),([0.5,0.7],0.6),([0.4,0.5],0.2)\},\hfill \\ \{B,([0.4,0.5],0.4),([0.7,0.8],0.5),([0.2,0.3],0.3)\},\hfill \\ \{C,([0.6,0.8],0.8),([0.4,0.5],0.3),([0.1,0.2],0.1)\}\hfill \end{array}〉$$

where interval memberships indicate the business strength and strategies of industries for the present time while fixed membership indicates the business strength and strategies of industries for future based on given information. So on the basis of M we get a set of edges defined as

$$N=〈\begin{array}{c}\{AB,([0.3,0.4],0.4),([0.5,0.7],0.6),([0.4,0.5],0.2)\},\hfill \\ \{BC,([0.4,0.5],0.8),([0.4,0.5],0.5),([0.2,0.3],0.1)\},\hfill \\ \{AC,([0.3,0.4],0.8),([0.4,0.5],0.6),([0.4,0.5],0.1)\}\hfill \end{array}〉$$

where interval memberships indicate the business strength and strategies of industries for the present time while fixed membership indicate the business strength and strategies of industries for future when it will be the time of more competition. It is represented in Figure 11.

Finally we see that the business strategies of one industry strongly affect its business with other industries. Here

$$order(G)=\{([1.3,1.7],1.5),([1.6,2.0],1.4),([0.7,1.0],0.6)\}$$

and

$$\begin{array}{ccc}\hfill deg(A)& =& \{([0.6,0.8],1.2),([0.9,1.2],1.2),([0.8,1.0],0.3)\}\hfill \\ \hfill deg(B)& =& \{([0.7,0.9],1.2),([0.9,1.2],1.1),([0.6,0.8],0.3)\}\hfill \\ \hfill deg(C)& =& \{([0.7,0.9],1.6),([0.8,1.0],1.1),([0.6,0.8],0.2)\}\hfill \end{array}$$

Order of G represents the overall effect on market of above given industries A, B and C. Degree of A represents the effect of other industries on A link through an edge with the industry A. The minimum degree of A is 0 when it has no link with any other.

Example 8.

Let us take an industry and we want to evaluate its overall performance. There are a lot of factors affecting it. However, some of the important factors influencing industrial productivity are with neutrosophic cubic sets as under, where the data is provided in the form of interval based on future prediction and data given in the form of a number from the unit interval $[0,1]$ is dependent on the present time after a careful testing of different models as a sample in each case,

1. 

Technological Development $A=(({\tilde{T}}_A,T_A),({\tilde{I}}_A,I_A),({\tilde{F}}_A,F_A))=(($degree of mechanization), (technical know-how), (product design$))=\{A,([0.3,0.4],0.3),([0.5,0.7],0.6),([0.4,0.5],0.2)\},$

2. 

Quality of Human Resources $B=(({\tilde{T}}_B,T_B),({\tilde{I}}_B,I_B),({\tilde{F}}_B,F_B))=(($ability of the worker), (willingness of the worker), (the environment under which he has to work$))=\{B,([0.4,0.5],0.4),([0.7,0.8],0.5),([0.2,0.3],0.3)\},$

3. 

Availability of Finance $C=(({\tilde{T}}_C,T_C),({\tilde{I}}_C,I_C),({\tilde{F}}_C,F_C))=(($advertisement campaign), (better working conditions to the workers), (up-keep of plant and machinery$))=\{C,([0.6,0.8],0.8),([0.4,0.5],0.3),([0.1,0.2],0.1)\}$,

4. 

Managerial Talent $D=(({\tilde{T}}_D,T_D),({\tilde{I}}_D,I_D),({\tilde{F}}_D,F_D))=(($devoted towards their profession), (Links with workers, customers and suppliers), (conceptual, human relations and technical skills$))$ $=\{D,([0.3,0.6],0.4),([0.2,0.7],0.9),([0.3,0.5],0.6)\},$

5. 

Government Policy $=E=(({\tilde{T}}_E,T_E),({\tilde{I}}_E,I_E),({\tilde{F}}_E,F_E))=$ Government Policy $=(($favorable conditions for saving), (investment), (flow of capital from one industrial sector to another$))$ $=\{E,([0.2,0.4],0.5),([0.5,0.6],0.1),([0.4,0.5],0.2)\},$

6. 

Natural Factors $=F=(({\tilde{T}}_F,T_F),({\tilde{I}}_F,I_F),({\tilde{F}}_F,F_F))=(($physical), (geographical$),$(climatic exercise$))=\{F,([0.1,0.4],0.8),([0.5,0.7],0.2),([0.4,0.5],0.2)\}$. As these factors affecting industrial productivity are inter-related and inter-dependent, it is a difficult task to evaluate the influence of each individual factor on the overall productivity of industrial units. The use of neutrosophic cubic graphs give us a more reliable information as under. Let $X=\{A,B,C,D,F,E\}$ we have a neutrosophic cubic set for the vertex set as under

$$M=〈\begin{array}{c}\{A,([0.3,0.4],0.3),([0.5,0.7],0.6),([0.4,0.5],0.2)\},\hfill \\ \{B,([0.4,0.5],0.4),([0.7,0.8],0.5),([0.2,0.3],0.3)\},\hfill \\ \{C,([0.6,0.8],0.8),([0.4,0.5],0.3),([0.1,0.2],0.1)\},\hfill \\ \{D,([0.3,0.6],0.4),([0.2,0.7],0.9),([0.3,0.5],0.6)\},\hfill \\ \{E,([0.2,0.4],0.5),([0.5,0.6],0.1),([0.4,0.5],0.2)\},\hfill \\ \{F,([0.1,0.4],0.8),([0.5,0.7],0.2),([0.4,0.5],0.2)\}\hfill \end{array}〉$$

Now, in order to find the combined effect of all these factors we need to use neutrosophic cubic sets for edges as under

$$N=〈\begin{array}{c}\{AB,([0.3,0.4],0.4),([0.5,0.7],0.6),([0.4,0.5],0.2)\},\hfill \\ \{AC,([0.3,0.4],0.8),([0.4,0.5],0.6),([0.4,0.5],0.1)\},\hfill \\ \{AD,([0.3,0.4],0.4),([0.2,0.7],0.9),([0.4,0.5],0.2)\},\hfill \\ \{AE,([0.2,0.4],0.5),([0.5,0.6],0.6),([0.4,0.5],0.2)\},\hfill \\ \{AF,([0.1,0.4],0.8),([0.5,0.7],0.6),([0.4,0.5],0.2)\},\hfill \\ \{BC,([0.4,0.5],0.8),([0.4,0.5],0.5),([0.2,0.3],0.1)\},\hfill \\ \{BD,([0.3,0.5],0.4),([0.2,0.7],0.9),([0.3,0.5],0.3)\},\hfill \\ \{BE,([0.2,0.4],0.5),([0.5,0.6],0.5),([0.4,0.5],0.2)\},\hfill \\ \{BF,([0.1,0.4],0.8),([0.5,0.7],0.5),([0.4,0.5],0.2)\},\hfill \\ \{CD,([0.3,0.6],0.8),([0.2,0.5],0.9),([0.3,0.5],0.1)\},\hfill \\ \{CE,([0.2,0.4],0.8),([0.4,0.5],0.3),([0.4,0.5],0.1)\},\hfill \\ \{CF,([0.1,0.4],0.8),([0.4,0.5],0.3),([0.4,0.5],0.1)\},\hfill \\ \{DE,([0.2,0.4],0.5),([0.2,0.6],0.9),([0.4,0.5],0.2)\},\hfill \\ \{DF,([0.1,0.4],0.8),([0.2,0.7],0.9),([0.4,0.5],0.2)\},\hfill \\ \{EF,([0.1,0.4],0.8),([0.5,0.6],0.2),([0.4,0.5],0.2)\}\hfill \end{array}〉$$

where the edge $\{AB,([0.3,0.4],0.4),([0.5,0.7],0.6),([0.4,0.5],0.2)\}$ denotes the combined effect of technological development and quality of human resources on the productivity of the industry. Now, if we are interested to find which factors are more effective to the productivity of the industry, we may use the score and accuracy of the neutrosophic cubic sets, which will give us a closer view of the factors. It is represented in Figure 12.

Remark. We used degree and order of the neutrosophic cubic graphs in an application see Example 7 and if we have two different sets of industries having finite number of elements, we can easily find the applications of cartesian product, composition, union, join, order and degree of neutrosophic cubic graphs.

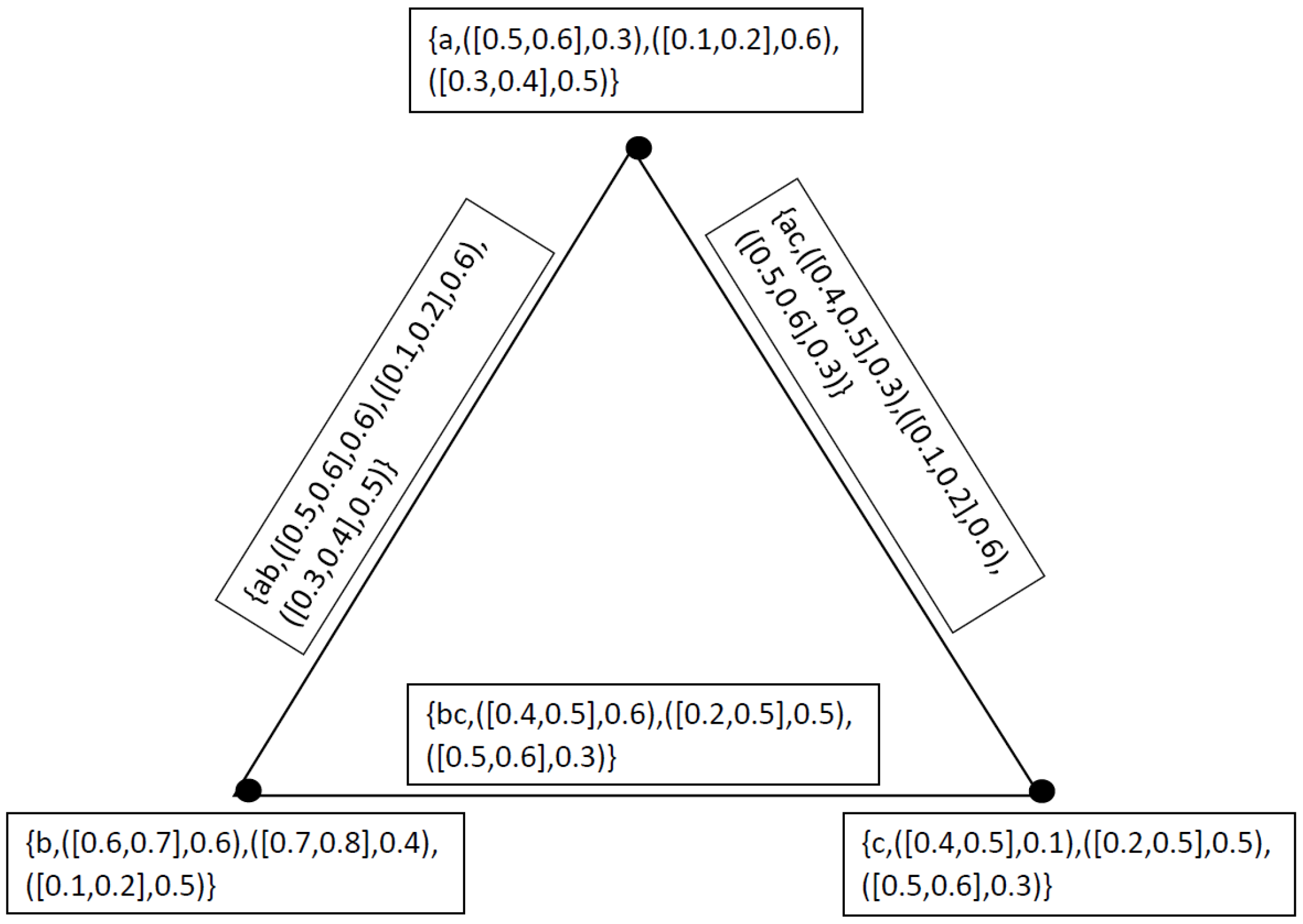
5. Comparison Analysis

In 1975, Rosenfeld discussed the concept of fuzzy graphs whose basic idea was introduced by [3] Kauffmann in 1973. Atanassov extended this idea to intuitionistic fuzzy graphs [14] in 1995. The idea of neutrosophic graphs provided by Kandasamy et al. in the book [29]. [38] Recently Rashid et al., introduced the notion of cubic graphs. In this paper, we introduced the study of neutrosophic cubic graphs. We claim that our model is more generalized from the previous models, as if we both indeterminacy and falsity part of neutrosophic cubic graphs $G=(M,N)$ where $M=(A,B)=(({\tilde{T}}_A,T_B),({\tilde{I}}_A,I_B),({\tilde{F}}_A,F_B))$ is the neutrosophic cubic set representation of vertex set V and $N=(C,D)=(({\tilde{T}}_C,T_D),({\tilde{I}}_C,I_D),({\tilde{F}}_C,F_D))$ is the neutrosophic cubic set representation of edges set E vanishes we get a cubic graph provided by Rashid et al., in [38]. Similarly, by imposing certain conditions on cubic graphs, we may obtain intuitionistic fuzzy graphs provided by Atanassov in 1995 and after that fuzzy graphs provided by Rosenfeld in 1975. So our proposed model is a generalized model and it has the ability to capture the uncertainty in a better way.

6. Conclusions

A generalization of the old concepts is the main motive of research. So in this paper, we proposed a generalized model of neutrosophic cubic graphs with different binary operations. We also provided applications of neutrosophic cubic graphs in industries. We also discussed conditions under which our model reduces to the previous models. In future, we will try to discuss different types of neutrosophic cubic graphs such as internal neutrosophic cubic graphs, external neutrosophic cubic graphs and many more with applications.