Intrinsic Metrics on Sierpinski-Like Triangles and Their Geometric Properties

Abstract

The classical Sierpinski Gasket defined on the equilateral triangle is a typical example of fractals. Sierpinski-like triangles can also be constructed on isosceles or scalene triangles. An explicit formula for the intrinsic metric on the classical Sierpinski Gasket via code representation of its points is given. The aim of this paper is to generalize this formula to the Sierpinski-like triangles. We also investigate geometrical properties of these triangles with respect to the intrinsic metric. Moreover, we describe certain properties of the classical Sierpinski gasket which are not shared by all of its analogues.

1. Introduction

Fractals are popular research subjects not only in mathematics but also in physics, chemistry, biology, social science, computer science, engineering and economics. There have been many studies on fractals in the last decade (for details see [1,2,3,4]). Most classic fractals have two basic features: the first one is self-similarity, and the second one is that their Hausdorff dimensions are larger than their topological dimensions. The Sierpinski Gasket, which is named after Waclaw Sierpinski, is one of the leading examples of fractals. The basic characteristics of the Sierpinski Gasket, S, are given as follows:

This fractal is the attractor of an iterated function system (IFS). An IFS on a metric space X is a finite family $\{f_0,f_1,\dots ,f_n\}$ of contracting maps $f_i:X\to X$ whose contracting factors are $r_i$ for $i=0,1,2,\dots ,n$. It is well-known that if $\{f_0,f_1,\dots ,f_n\}$ is an IFS on a complete metric space X, then there is unique non-empty compact subset K of X such that

$$K=\bigcup _{i=0}^n{f}_i\left(K\right).$$

The set K is called the attractor associated with the IFS (for the construction of S as the attractor of an IFS see Equation (1)).

The area of the Sierpinski Gasket is zero and its fractal dimension is non-integer. The topological dimension of this fractal is one. It satisfies the open set condition and thus its fractal dimension, the unique real solution of the Moran equation

$${\displaystyle \sum _{i=0}^2{r}_i^s=\frac{1}{2^s}+\frac{1}{2^s}+\frac{1}{2^s}=\frac{3}{2^s}=1,}$$

is $\frac{ln3}{ln2}$.

That is, Hausdorff dimension of the Sierpinski Gasket is larger than its topological dimension. Therefore, this set exhibits all of the classical properties of fractals.

However, none of the above listed features depend on whether the Sierpinski Gasket is constructed on the equilateral, isosceles, scalene triangles or not. The only difference that will occur is the coefficients of the functions with respect to IFS. In other words, S, which is constructed with the vertices $P=(p_0,p_1),Q=(q_0,q_1)$ and $R=(r_0,r_1)$, is the attractor of the iterated function system $\{{\mathbb{R}}^2;f_0,f_1,f_2\}$ such that

$${\displaystyle \begin{array}{ccc}{f}_0(x,y)& =& {\displaystyle \left(\frac{x}{2}+\frac{p_0}{2},\frac{y}{2}+\frac{p_1}{2}\right),}\\ f_1(x,y)& =& {\displaystyle \left(\frac{x}{2}+\frac{q_0}{2},\frac{y}{2}+\frac{q_1}{2}\right),}\\ f_2(x,y)& =& {\displaystyle \left(\frac{x}{2}+\frac{r_0}{2},\frac{y}{2}+\frac{r_1}{2}\right).}\end{array}}$$

(1)

It is obvious that if we choose $p_0=p_1=q_1=0,q_0=1,r_0=\frac{1}{2}$ and $r_1=\frac{\sqrt{3}}{2}$, then we get the classical Sierpinski Gasket as the attractor of the IFS. If these coefficients are taken as $p_0=p_1=q_1=r_0=0,q_0=1$ and $r_1=1$, then the right angled Sierpinski Gasket becomes the attractor of the IFS (see Figure 1).

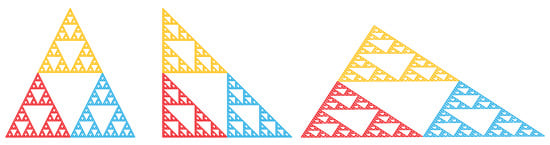
Figure 1. The Sierpinski Gaskets constructed on the equilateral, isosceles and scalene triangles respectively.

Besides these characteristics, different geometric properties can be examined by defining the intrinsic metrics on the equilateral, isosceles and scalene Sierpinski triangles. It is well-known that there are different ways to define the Sierpinski Gasket apart from the notion of IFS. By using these alternative definitions, various different properties of this fractal can be obtained. As one of them, the construction of the intrinsic metric on S can be given in several ways (for details see [5,6,7,8,9,10]).

The general definition of the intrinsic metric on S is expressed as follows:

$$d(x,y)=min\left\{\delta \right|\delta \mathrm{is}\mathrm{the}\mathrm{length}\mathrm{of}\mathrm{a}\mathrm{rectifiable}\mathrm{curve}\mathrm{in}\mathrm{S}\mathrm{joining}x\mathrm{and}y\},$$

(2)

for $x,y\in S$ (for details see [11]). Throughout this paper, we will only deal with the intrinsic metric obtained from the code representations of points on S. In [12], the intrinsic metric on the equilateral Sierpinski Gasket is explicitly formulated as follows:

Definition 1.

Let $a_1{a}_2\dots a_{k-1}{a}_k{a}_{k+1}\dots$ and $b_1{b}_2\dots b_{k-1}{b}_k{b}_{k+1}\dots$ be two representations respectively of the points A and B on the equilateral Sierpinski Gasket such that $a_i=b_i$ for $i=1,2,\dots ,k-1$ and $a_k\ne b_k.$ The distance $d(A,B)$ between A and B is determined by the following formula:

$$d(A,B)=min\left\{\sum _{i=k+1}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i},\frac{1}{2^k}+\sum _{i=k+1}^{\infty }\frac{{\gamma }_i+{\delta }_i}{2^i}\right\},$$

(3)

where

$$\begin{array}{ccc}{\alpha }_i=\left\{\begin{array}{cc}0,& a_i=b_k\\ 1,& a_i\ne b_k\end{array}\right.,& & {\beta }_i=\left\{\begin{array}{cc}0,& b_i=a_k\\ 1,& b_i\ne a_k\end{array}\right.,\end{array}$$

$$\begin{array}{ccc}{\gamma }_i=\left\{\begin{array}{cc}0,& a_i\ne a_{k}and{a}_i\ne b_k\hfill \\ 1,& otherwise\hfill \end{array}\right.,& & {\delta }_i=\left\{\begin{array}{cc}0,& b_i\ne b_{k}and{b}_i\ne a_k\hfill \\ 1,& otherwise\hfill \end{array}\right..\end{array}$$

Note that, since there exists at least one shortest path between any two points, the metric d defined in Equation (3) is a strictly intrinsic metric on the code set of S ([12]). Moreover, in [13], we classify geodesics of the Sierpinski Gasket by using this metric.

In this paper, we give a general formula for the case of different edge lengths of the triangle. That is, we obtain a formula for the intrinsic metric on the code set of the scalene Sierpinski Gasket in Theorem 1. Afterwards, we show the relationship between the coefficients of formulas computed for the equilateral, isosceles and scalene Sierpinski Gasket. Finally, in Propositions 3 and 4, we get some important geometrical properties by using these formulas.

In the following section, we express some basic concepts that are needed to describe the metric given in Equation (4).

2. Preliminaries

Let us fix $w_1,w_2,\dots ,w_n$ where $w_i\in \{0,1,2\}$ for $i=1,2,\dots ,n$. The bottom-left part, the bottom-right part and the upper part of $S_{w_1{w}_2\dots w_n}$ are denoted by $S_{w_1{w}_2\dots w_{n}0}$, $S_{w_1{w}_2\dots w_{n}1}$ and $S_{w_1{w}_2\dots w_{n}2}$ respectively. Thus, we have the sub-triangle

$$S_{w_1\dots w_{n}0}=\left\{w_1\dots w_{n}0a_{n+2}{a}_{n+3}\dots \right|a_i\in \{0,1,2\}\mathrm{and}i=n+2,n+3,\dots \},$$

$$S_{w_1\dots w_{n}1}=\left\{w_1\dots w_{n}1a_{n+2}{a}_{n+3}\dots \right|a_i\in \{0,1,2\}\mathrm{and}i=n+2,n+3,\dots \},$$

$$S_{w_1\dots w_{n}2}=\left\{w_1\dots w_{n}2a_{n+2}{a}_{n+3}\dots \right|a_i\in \{0,1,2\}\mathrm{and}i=n+2,n+3,\dots \}.$$

Hence, the code set of S is the union of the code sets $S_0,S_1$ and $S_2$ (see Figure 2).

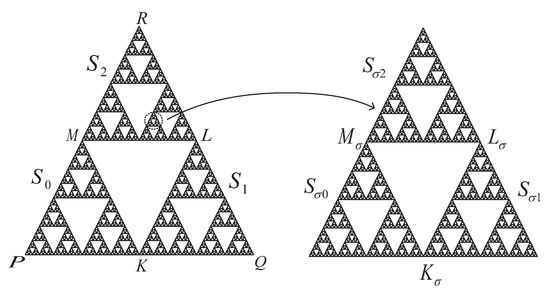
Figure 2. The equilateral Sierpinski Gasket and the sub-triangle $S_{\sigma }$ where $\sigma =w_1{w}_2\dots w_n$.

From now on, we will define the code representation of a point on S by using these code sets. The construction above shows that

$$S_{a_1},S_{a_1{a}_2},S_{a_1{a}_2{a}_3},\dots ,S_{a_1{a}_2\dots a_n},\dots$$

is a nested sequence of sets such that

$$S_{a_1}\supset S_{a_1{a}_2}\supset S_{a_1{a}_2{a}_3}\supset \dots \supset S_{a_1{a}_2\dots a_n}\supset \dots .$$

The Cantor intersection theorem states that the infinite intersection

$$\bigcap _{n=1}^{\infty }{S}_{a_1{a}_2\dots a_n}$$

is a point on S, which we denote by A. A code representation of A is the infinite word $a_1{a}_2\dots a_n\dots$ where $a_n\in \{0,1,2\},n\in \mathbb{N}$. Note that, if $A\in S$ is the intersection point of any two sub-triangles of $S_{a_1{a}_2\dots a_k}$, then A is called a junction point of S. In such a case, A has two different code representations of forms $a_1{a}_2\dots a_k\beta \alpha \alpha \alpha \dots$ and $a_1{a}_2\dots a_k\alpha \beta \beta \beta \dots$ where $\alpha ,\beta \in \{0,1,2\}$ and $\alpha \ne \beta$. (If a point is not in this form, then it has a unique code representation. For example, the vertices $P,Q$ and R have the code representations $000\dots$$111\dots$ and $222\dots$ respectively). Let $S_0\cap S_1=\left\{K\right\}$, $S_1\cap S_2=\left\{L\right\}$ and $S_0\cap S_2=\left\{M\right\}$. $0111\dots$ and $1000\dots$ are different code representations of K, $1222\dots$ and $2111\dots$ are different code representations of L, $0222\dots$ and $2000\dots$ are different code representations of M. Moreover, the code set of all points on the line segment connecting the vertices P and Q is

$$PQ=\left\{a_1{a}_2{a}_3\dots \right|a_i\in \{0,1\}\},$$

the code set of all points on the line segment connecting the vertices P and R is

$$PR=\left\{a_1{a}_2{a}_3\dots \right|a_i\in \{0,2\}\},$$

and the code set of all points on the line segment connecting the vertices Q and R is

$$QR=\left\{a_1{a}_2{a}_3\dots \right|a_i\in \{1,2\}\}.$$

For the general case, let us fix $\sigma =a_1{a}_2{a}_3\dots a_{k-1}$ where $a_i\in \{0,1,2\}$ for $i=1,2,\dots ,k-1$. We now consider the sub-triangles $S_{\sigma 0},S_{\sigma 1}$ and $S_{\sigma 2}$. Let $S_{\sigma 0}\cap S_{\sigma 1}=\left\{K_{\sigma }\right\}$, $S_{\sigma 1}\cap S_{\sigma 2}=\left\{L_{\sigma }\right\}$ and $S_{\sigma 0}\cap S_{\sigma 2}=\left\{M_{\sigma }\right\}$. Similarly, $\sigma 0111\dots$ and $\sigma 1000\dots$ are different code representations of $K_{\sigma }$, $\sigma 1222\dots$ and $\sigma 2111\dots$ are different code representations of $L_{\sigma }$, $\sigma 0222\dots$ and $\sigma 2000\dots$ are different code representations of $M_{\sigma }$. Furthermore, the code set of all points on the line segment connecting the vertices $K_{\sigma }$ and $L_{\sigma }$ is

$$K_{\sigma }{L}_{\sigma }=\left\{\sigma 1a_{k+1}{a}_{k+2}{a}_{k+3}\dots \right|a_i\in \{0,2\}\mathrm{for}i=k+1,k+2,\dots \},$$

the code set of all points on the line segment connecting the vertices $K_{\sigma }$ and $M_{\sigma }$ is

$$K_{\sigma }{M}_{\sigma }=\left\{\sigma 0a_{k+1}{a}_{k+2}{a}_{k+3}\dots \right|a_i\in \{1,2\}\mathrm{for}i=k+1,k+2,\dots \},$$

and the code set of all points on the line segment connecting the vertices $L_{\sigma }$ and $M_{\sigma }$ is

$$L_{\sigma }{M}_{\sigma }=\left\{\sigma 2a_{k+1}{a}_{k+2}{a}_{k+3}\dots \right|a_i\in \{0,1\}\mathrm{for}i=k+1,k+2,\dots \}.$$

Moreover, it can be easily seen that

$$|K_{\sigma }{L}_{\sigma }|=\frac{\left|PR\right|}{2^k}=\frac{d_{eucl}(P,R)}{2^k},$$

$$|K_{\sigma }{M}_{\sigma }|=\frac{\left|QR\right|}{2^k}=\frac{d_{eucl}(Q,R)}{2^k},$$

$$|L_{\sigma }{M}_{\sigma }|=\frac{\left|PQ\right|}{2^k}=\frac{d_{eucl}(P,Q)}{2^k},$$

owing to the fact that $PR\parallel K_{\sigma }{L}_{\sigma }$, $QR\parallel K_{\sigma }{M}_{\sigma }$, $PQ\parallel L_{\sigma }{M}_{\sigma }$ and $\mid \sigma \mid =k-1$.

3. The Intrinsic Metric on the Scalene Sierpinski Gasket

Consider a scalene Sierpinski Gasket with vertices $P=(p_0,p_1),Q=(q_0,q_1)$ and $R=(r_0,r_1)$. In the following proposition, we formulate the distance between two different points on a scalene Sierpinski Gasket by using the code representations of these points. Then a special case of this formula will be given on the isosceles Sierpinski Gasket and it will be associated with the formula given in Definition 1 on the equilateral Sierpinski Gasket.

Theorem 1.

Suppose that the points A and B on the scalene Sierpinski Gasket have two representations $a_1{a}_2\dots a_{k-1}{a}_k{a}_{k+1}\dots$ and $b_1{b}_2\dots b_{k-1}{b}_k{b}_{k+1}\dots$ respectively such that $a_i=b_i$ for $i=1,2,\dots ,k-1$ and $a_k\ne b_k.$ Then the distance $d(A,B)$ between A and B is determined by the following formula;

$${\displaystyle \begin{array}{c}{\displaystyle d(A,B)=min\left\{\sum _{i=k+1}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i},\frac{\kappa }{2^k}+\sum _{i=k+1}^{\infty }\frac{{\gamma }_i+{\delta }_i}{2^i}\right\}}\end{array}}$$

(4)

such that

$${\alpha }_i=\left\{\begin{array}{cc}0,& a_i=b_k\hfill \\ \left|PQ\right|,& (a_i=0,b_k=1)\mathrm{or}(a_i=1,b_k=0)\hfill \\ \left|PR\right|,& (a_i=0,b_k=2)\mathrm{or}(a_i=2,b_k=0)\hfill \\ \left|QR\right|,& (a_i=1,b_k=2)\mathrm{or}(a_i=2,b_k=1)\hfill \end{array}\right.,$$

$${\beta }_i=\left\{\begin{array}{cc}0,& b_i=a_k\hfill \\ \left|PQ\right|,& (b_i=0,a_k=1)\mathrm{or}(b_i=1,a_k=0)\hfill \\ \left|PR\right|,& (b_i=0,a_k=2)\mathrm{or}(b_i=2,a_k=0)\hfill \\ \left|QR\right|,& (b_i=1,a_k=2)\mathrm{or}(b_i=2,a_k=1)\hfill \end{array}\right.,$$

$${\gamma }_i=\left\{\begin{array}{cc}0,& a_i=c_k\hfill \\ \left|PQ\right|,& (a_i=0,c_k=1)\mathrm{or}(a_i=1,c_k=0)\hfill \\ \left|PR\right|,& (a_i=0,c_k=2)\mathrm{or}(a_i=2,c_k=0)\hfill \\ \left|QR\right|,& (a_i=1,c_k=2)\mathrm{or}(a_i=2,c_k=1)\hfill \end{array}\right.,$$

$${\delta }_i=\left\{\begin{array}{cc}0,& b_i=c_k\hfill \\ \left|PQ\right|,& (b_i=0,c_k=1)\mathrm{or}(b_i=1,c_k=0)\hfill \\ \left|PR\right|,& (b_i=0,c_k=2)\mathrm{or}(b_i=2,c_k=0)\hfill \\ \left|QR\right|,& (b_i=1,c_k=2)\mathrm{or}(b_i=2,c_k=1)\hfill \end{array}\right.,$$

where

$$\begin{array}{c}\kappa =\left\{\begin{array}{cc}\left|PQ\right|,& (a_k=0,b_k=1)\mathrm{or}(a_k=1,b_k=0)\hfill \\ \left|PR\right|,& (a_k=0,b_k=2)\mathrm{or}(a_k=2,b_k=0)\hfill \\ \left|QR\right|,& (a_k=1,b_k=2)\mathrm{or}(a_k=2,b_k=1)\hfill \end{array}\right.,\end{array}$$

and $a_k\ne c_k\ne b_k$ and $c_k\in \{0,1,2\}$.

Note that we only give a sketch proof since it is long and tedious to show all the cases. However, different cases can be shown in a similar way.

Proof. 

Suppose that A and B, which are two different points of the scalene Sierpinski, have the code representations $a_1{a}_2\dots a_n\dots$ and $b_1{b}_2\dots b_n\dots$ respectively. It is obvious that there exists at least one natural number s such that $a_s\ne b_s$. Thus, we have $A\in S_{\sigma a_k}$ and $B\in S_{\sigma b_k}$ where $k=min\left\{s\right|a_s\ne b_s,s=1,2,3,\dots \}.$ Let $a_k=0$ and $b_k=1$ (or $a_k=1$ and $b_k=0$). In this case, the shortest paths between A and B must pass through either the point $K_{\sigma }$ or the line $L_{\sigma }{M}_{\sigma }$. If $a_k=0$ and $b_k=2$ (or $a_k=2$ and $b_k=0$), then the shortest paths between a and b must pass through either the point $M_{\sigma }$ or the line $K_{\sigma }{L}_{\sigma }$. If $a_k=1$ and $b_k=2$ (or $a_k=2$ and $b_k=1$), then the shortest paths between a and b must pass through either the point $L_{\sigma }$ or the line $K_{\sigma }{M}_{\sigma }$.

Case 1.

Firstly, we will deal with the shortest paths that pass through the point $K_{\sigma }$. We thus have $a_k=0$ and $b_k=1$ or $a_k=1$ and $b_k=0$. Let us only investigate $a_k=0$ and $b_k=1$ because the proof is the same for $a_k=1$ and $b_k=0$. The union of a path between A and $K_{\sigma }$ and a path between $K_{\sigma }$ and B gives a path between A and B. If we compute the length of the shortest paths between A and $K_{\sigma }$, then the paths between $K_{\sigma }$ and B can be obtained using a similar argument.

Given $A\in S_{\sigma 00}$ and let $S_{{\sigma }^{\prime }0}\cap S_{{\sigma }^{\prime }1}=\left\{K_{{\sigma }^{\prime }}\right\}$ where ${\sigma }^{\prime }=\sigma 0$. Then we must compute the length of the line segment $K_{\sigma }{K}_{{\sigma }^{\prime }}$. Thus, the length of the shortest paths between A and $K_{\sigma }$ is ${\displaystyle \mu =\frac{\left|PQ\right|}{2^{k+1}}+\epsilon }$ for some $\epsilon \ge 0$. (For the case $a_{k+1}=0$ and $b_k=1$, we actually get ${\alpha }_{k+1}=\left|PQ\right|$).

If $A\in S_{\sigma 02}$, then we must compute the length of the line $K_{\sigma }{L}_{{\sigma }^{\prime }}$ where $S_{{\sigma }^{\prime }1}\cap S_{{\sigma }^{\prime }2}=\left\{L_{{\sigma }^{\prime }}\right\}$ to obtain the length of the shortest path between A and $K_{\sigma }$. Hence, this length equals to ${\displaystyle \mu =\frac{\left|QR\right|}{2^{k+1}}+\epsilon }$ for some $\epsilon \ge 0$ (that is, if $a_{k+1}=2$ and $b_k=1$, then ${\alpha }_{k+1}=\left|QR\right|$).

If $A=M_{{\sigma }^{\prime }}$ where $M_{{\sigma }^{\prime }}$ is the intersection point of the sub-triangles $S_{{\sigma }^{\prime }0}$ and $S_{{\sigma }^{\prime }2}$, then there are two shortest paths between A and $K_{\sigma }$. These paths are the union of the line segments $M_{{\sigma }^{\prime }}{K}_{{\sigma }^{\prime }}$ and $K_{{\sigma }^{\prime }}{K}_{\sigma }$ or the union of the line segments $L_{{\sigma }^{\prime }}{M}_{{\sigma }^{\prime }}$ and $L_{{\sigma }^{\prime }}{K}_{\sigma }$. So, the length of these paths are exactly obtained as

$$\mu =\frac{\left|QR\right|}{2^{k+1}}+\frac{\left|PQ\right|}{2^{k+1}}.$$

(In this case, a has the code representations $\sigma 00222\dots$ or $\sigma 02000\dots$. For $i=2,3,4,\dots$, if $a_{k+1}=0$ and $a_{k+i}=2$, then we obtain ${\alpha }_{k+1}=\left|PQ\right|$ and ${\alpha }_{k+i}=\left|QR\right|$ or similarly if $a_{k+1}=2$ and $a_{k+i}=0$, then we get ${\alpha }_{k+1}=\left|QR\right|$ and ${\alpha }_{k+i}=\left|PQ\right|$).

Let us now consider $A\in S_{\sigma 01}$. Notice that, the multiplier $\frac{1}{2^{k+1}}$ is not included in the computation of the length of the shortest paths between A and $K_{\sigma }$ since $K_{\sigma }\in S_{\sigma 01}$. If $A\in S_{\sigma 010}$ or $A\in S_{\sigma 012}$, then we must compute the length of the line segment $K_{{\sigma }^{″}}{K}_{\sigma }$ or the length of the line segment $L_{{\sigma }^{″}}{K}_{\sigma }$ to get the shortest distance such that $K_{{\sigma }^{″}}=S_{{\sigma }^{″}0}\cap S_{{\sigma }^{″}1}$, $L_{{\sigma }^{″}}=S_{{\sigma }^{″}1}\cap S_{{\sigma }^{″}2}$ where ${\sigma }^{″}=\sigma 01$. In this case, we get

$$\mu =\frac{\left|PQ\right|}{2^{k+2}}+\epsilon$$

or

$$\mu =\frac{\left|QR\right|}{2^{k+2}}+\epsilon$$

respectively for some $\epsilon \ge 0$.

For the case $A=M_{{\sigma }^{″}}$, where $M_{{\sigma }^{\prime \prime }}$ is the intersection point of the sub-triangles $S_{{\sigma }^{″}0}$ and $S_{{\sigma }^{″}2}$, there are two paths to obtain the shortest distance between A and $K_{\sigma }$ as before. These paths are the union of the line segments $M_{{\sigma }^{″}}{K}_{{\sigma }^{″}}$ and $K_{{\sigma }^{″}}{K}_{\sigma }$ or the union of the line segments $M_{{\sigma }^{″}}{L}_{{\sigma }^{″}}$ and $L_{{\sigma }^{″}}{K}_{\sigma }$. The length of these two paths is

$$\mu =\frac{\left|PQ\right|}{2^{k+2}}+\frac{\left|QR\right|}{2^{k+2}}.$$

This procedure also continues for smaller triangles. By splicing these shortest paths between “A and $K_{\sigma }$” and “$K_{\sigma }$ and B”, we can determine the length of the shortest paths between A and B passing through the point $K_{\sigma }$.

Case 2.

Now, we will investigate the length of the shortest paths passing through the line segment $L_{\sigma }{M}_{\sigma }$. In this case, we must figure out the shortest paths between “A and $M_{\sigma }$” and between “B and $L_{\sigma }$”. Note that we can compute the lengths of these shortest paths in the same way as the Case 1. As we add $\frac{\left|PQ\right|}{2^k}$ (the length of the path $L_{\sigma }{M}_{\sigma }$) to these lengths, we obtain the length of the shortest path passing through $L_{\sigma }{M}_{\sigma }$.

We now consider the shortest paths passing through the line segment $K_{\sigma }{L}_{\sigma }$. The shortest paths (thus the corresponding length) between “A and $K_{\sigma }$” and between “B and $L_{\sigma }$” can be obtained similarly. We get the length of the shortest path passing through $K_{\sigma }{L}_{\sigma }$ by adding the length of the path $K_{\sigma }{L}_{\sigma }$, which equals to $\frac{\left|PR\right|}{2^k}$, to these lengths.

Also, we can compute the length of the shortest paths passing through the line segment $K_{\sigma }{M}_{\sigma }$. In this sense, this length is obtained by adding $\frac{\left|QR\right|}{2^k}$ to the length of the shortest paths between “A and $K_{\sigma }$” and between “B and $M_{\sigma }$”.

As a result, the minimum of the lengths obtained from Case 1 and 2 gives us the length of the shortest paths between A and B. □

Remark 1.

The length of the shortest paths passing through one of the points $K_{\sigma }$, $L_{\sigma }$ and $M_{\sigma }$ is the first sum in Equation (4), $\mu ={\displaystyle \sum _{i=k+1}^{\infty }}\frac{{\alpha }_i+{\beta }_i}{2^i}$. And the second value in Equation (4), $\nu =\frac{\kappa }{2^k}+{\displaystyle \sum _{i=k+1}^{\infty }}\frac{{\gamma }_i+{\delta }_i}{2^i}$, gives us the length of the shortest paths passing through one of the line segment $K_{\sigma }{L}_{\sigma }$, $L_{\sigma }{M}_{\sigma }$ and $K_{\sigma }{M}_{\sigma }$ where $\frac{\kappa }{2^k}$ is the length of the line segment $K_{\sigma }{M}_{\sigma }$, $L_{\sigma }{M}_{\sigma }$ and $K_{\sigma }{M}_{\sigma }$ respectively.

The metric given in Theorem 1 is equivalent to the metric given in Equation (2) due to the fact that the metric d is defined as the minimum of the lengths of the admissible paths connecting the points A and B of the scalene Sierpinski Gasket.

The proof of the following proposition is similar to the proof in [12]. Thus the proof here will be omitted.

Proposition 1.

The metric d defined in Theorem 1 does not depend on the choice of the code representations of the points.

Suppose that the points A and B on the isosceles Sierpinski Gasket have the code representations $a_1{a}_2\dots a_{k-1}{a}_k{a}_{k+1}\dots$ and $b_1{b}_2\dots b_{k-1}{b}_k{b}_{k+1}\dots$ respectively where $a_i=b_i$ for $i=1,2,\dots ,k-1$ and $a_k\ne b_k.$ In Theorem 1, if we choose $P_0=(0,0),P_1=(1,0)$ and $P_2=(0,1)$, then the distance formula on isosceles Sierpinski Gasket will be as follows:

Corollary 1.

The distance between A and B is defined by the following formula:

$$\begin{array}{c}{\displaystyle d(A,B)=min\left\{\sum _{i=k+1}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i},\frac{\kappa }{2^k}+\sum _{i=k+1}^{\infty }\frac{{\gamma }_i+{\delta }_i}{2^i}\right\}}\end{array}$$

such that

$${\alpha }_i=\left\{\begin{array}{cc}0,& a_i=b_k\hfill \\ \sqrt{2},& (a_i=1,b_k=2)\mathrm{or}(a_i=2,b_k=1)\hfill \\ 1,& \mathit{otherwise}\hfill \end{array}\right.,$$

$${\beta }_i=\left\{\begin{array}{cc}0,& b_i=a_k\hfill \\ \sqrt{2},& (b_i=1,a_k=2)\mathrm{or}(b_i=2,a_k=1)\hfill \\ 1,& \mathit{otherwise}\hfill \end{array}\right.,$$

$${\gamma }_i=\left\{\begin{array}{cc}0,& a_i=c_k\hfill \\ \sqrt{2},& (a_i=1,c_k=2)\mathrm{or}(a_i=2,c_k=1)\hfill \\ 1,& \mathit{otherwise}\hfill \end{array}\right.,$$

$${\delta }_i=\left\{\begin{array}{cc}0,& b_i=c_k\hfill \\ \sqrt{2},& (b_i=1,c_k=2)\mathrm{or}(b_i=2,c_k=1)\hfill \\ 1,& \mathit{otherwise}\hfill \end{array}\right.,$$

where

$$\begin{array}{c}\kappa =\left\{\begin{array}{cc}\sqrt{2},& (a_k=1,b_k=2)\mathrm{or}(a_k=2,b_k=1)\hfill \\ 1,& \mathit{otherwise}\hfill \end{array}\right.,\end{array}$$

and $a_k\ne c_k\ne b_k$ and $c_k\in \{0,1,2\}$.

Note that if we take $P_0=(0,0),P_1=(1,0)$ and $P_2=(\frac{1}{2},\frac{\sqrt{3}}{2})$, then the distance formula on equilateral Sierpinski Gasket is obtained as Definition 1. Hence, Theorem 1 is very useful since it gives us the general case.

We now give an illustrative example which shows the computation of the distance between any two points on an isosceles Sierpinski triangle.

Example 1.

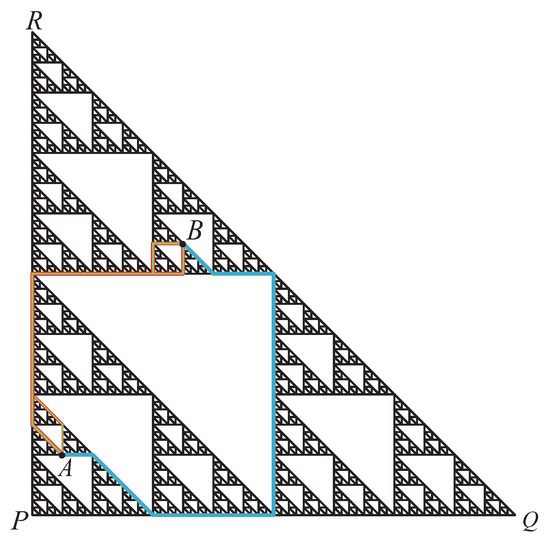
Consider an isosceles triangle with vertices $P=(0,0),Q=(1,0)$ and $R=(0,1)$. Let A and B be the points of S whose code representations are $0020\overline{1}=0020111\cdots$ and $2101\overline{2}=2101222\cdots$ respectively.

We get $k=1$ since the first terms of the code representations of A and B are different. By using Corollary 1, we compute

$${\alpha }_2=1,{\alpha }_3=0,{\alpha }_4=1,{\alpha }_i=\sqrt{2}\mathrm{for}i=5,6,7,\dots ,$$

$${\beta }_2=1,{\beta }_3=0,{\beta }_i=1\mathrm{for}i=4,5,6,\dots ,$$

and

$${\gamma }_2=1,{\gamma }_3=\sqrt{2},{\gamma }_4=1,{\gamma }_i=0\mathrm{for}i=5,6,7\dots ,$$

$${\delta }_2=0,{\delta }_3=1,{\delta }_4=0,{\delta }_i=\sqrt{2}\mathrm{for}i=5,6,7\dots .$$

It follows that

$$\begin{array}{ccc}{\displaystyle \mu =\sum _{i=2}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i}}\hfill & =\hfill & \frac{1+1}{2^2}+\frac{0+0}{2^3}+\frac{1+1}{2^4}+\sum _{k=5}^{\infty }\frac{\sqrt{2}+1}{2^k}\hfill \\ & =\hfill & \frac{1}{2}+\frac{1}{2^3}+\frac{\sqrt{2}+1}{2^4}\hfill \\ & =\hfill & \frac{11+\sqrt{2}}{2^4},\hfill \end{array}$$

and

$$\begin{array}{ccc}{\displaystyle \nu =\frac{1}{2}+\sum _{i=2}^{\infty }\frac{{\gamma }_i+{\delta }_i}{2^i}}\hfill & =\hfill & \frac{1+0}{2^2}+\frac{\sqrt{2}+1}{2^3}+\frac{1+0}{2^4}+\sum _{k=5}^{\infty }\frac{0+\sqrt{2}}{2^k}\hfill \\ & =\hfill & \frac{1}{2}+\frac{1}{2^2}+\frac{\sqrt{2}+1}{2^3}+\frac{1}{2^4}+\frac{\sqrt{2}}{2^4}\hfill \\ & =\hfill & \frac{15+2\sqrt{2}}{2^4},\hfill \end{array}$$

which shows $d(A,B)=\frac{11+\sqrt{2}}{2^4}$ (see Figure 3).

Figure 3. The shortest paths between the points A and B of the isosceles Sierpinski Gasket.

4. Some Interesting Properties of the Equilateral, Isosceles and Scalene Sierpinski Gaskets

In this section, we give some important geometrical properties with the intrinsic metric on the equilateral, scalene and isosceles Sierpinski Gaskets via the code representations of their points. We first begin with a proposition related to the equilateral Sierpinski Gasket whose proof is given in [12] as follows:

Proposition 2 ([12]).

Let $S_{\sigma }$ be a sub-triangle of the equilateral Sierpinski Gasket with edge length 1 and let $P_{\sigma }$, $Q_{\sigma }$ and $R_{\sigma }$ be vertices of $S_{\sigma }$. If $A_{\sigma }$ is an arbitrary point of $S_{\sigma }$ then

$$d(A_{\sigma },P_{\sigma 0})+d(A_{\sigma },P_{\sigma 1})+d(A_{\sigma },P_{\sigma 2})=\frac{1}{2^{k-2}},$$

where $\sigma =a_1{a}_2{a}_3\dots a_{k-1}$.

Proposition 2 does not hold for scalene and isosceles Sierpinski Gaskets. That is, there are points A and B such that

$$d(A,P)+d(A,Q)+d(A,R)\ne d(B,P)+d(B,Q)+d(B,R),$$

(5)

as shown the following example:

Example 2.

Let us consider the scalene Sierpinski Gasket with vertices $P=(0,0),Q=(6,0)$ and $R=(0,8)$. Let A and B be the points of S such that their code representations are $0\overline{1}=0111\dots$ and $1\overline{2}=1222\dots$ respectively. It is clear that $P,Q$ and R have the code representations $000\dots$, $111\dots$, $222\dots$ respectively. For the computation of the shortest distance between A and P, we obtain $k=2$, ${\alpha }_i=6$, ${\beta }_i=6$, ${\gamma }_i=10$ and ${\delta }_i=8$ for $i=3,4,5\dots$ and thus $d(A,P)=min\{3,\frac{19}{4}\}=3$. Since $k=1$, ${\alpha }_i=0$, ${\beta }_i=6$, ${\gamma }_i=10$ and ${\delta }_i=10$ for $i=2,3,4\dots$, we compute $d(A,Q)=min\{3,13\}=3$. Due to the fact that $k=1$, ${\alpha }_i=0$, ${\beta }_i=10$, ${\gamma }_i=0$ and ${\delta }_i=10$ for $i=2,3,4\dots$, we get $\mu =\nu =9$ and thus $d(A,R)=9$. By using the formula given in Theorem 1, we have

$$d(A,P)+d(A,Q)+d(A,R)=15.$$

Moreover, $d(B,P)=7$ since we have $k=1$, ${\alpha }_i=8$, ${\beta }_i=6$, ${\gamma }_i=0$ and ${\delta }_i=8$ for $i=2,3,4\dots$. Owing to the fact that $k=2$, ${\alpha }_i=10$, ${\beta }_i=10$, ${\gamma }_i=10$ and ${\delta }_i=10$ for $i=3,4,5\dots$, we compute $d(B,Q)=min\{5,6\}=5$. Given $k=1$, ${\alpha }_i=0$, ${\beta }_i=10$, ${\gamma }_i=8$ and ${\delta }_i=8$ for $i=2,3,4,\dots$, we get $d(B,R)=min\{5,13\}=5$. This shows that

$$d(B,P)+d(B,Q)+d(B,R)=17.$$

By the code representations of points, we will demonstrate another property that is obtained on the equilateral Sierpinski Gasket but not on the isosceles and scalene Sierpinski Gaskets. We first recall the definition of the distance of a point to a set:

Definition 2.

Let $(\mathbb{X},\tilde{d})$ is a metric space and let B be a point of $\mathbb{X}$ and $\mathbb{A}\subseteq \mathbb{X}$. Then the distance of B to $\mathbb{A}$ is determined by

$$\tilde{d}(B,\mathbb{A})=inf\left\{\tilde{d}(B,A)\right|A\in \mathbb{A}\}.$$

Obviously, if $B\in \mathbb{A}$, then we get $\tilde{d}(B,\mathbb{A})=0$.

Remark 2.

It is well-known that the sum of the shortest distances of an arbitrary point on one edge of an equilateral triangle to the other two edges is fixed, and this number is equal to the height of the triangle. In the following proposition, we apply this property to the equilateral Sierpinski Gasket with the intrinsic metric and obtain a remarkable result.

Proposition 3.

Let $S_{\sigma }$ be a sub-triangle of the equilateral Sierpinski Gasket with edge length 1 and let $P_{\sigma }$, $Q_{\sigma }$ and $R_{\sigma }$ be vertices of $S_{\sigma }$. If $A_{\sigma }$ with code representation $\sigma a_k{a}_{k+1}{a}_{k+2}\dots$ is an arbitrary point on the edge $P_{\sigma }{Q}_{\sigma }$ of $S_{\sigma }$, then

$$d(A_{\sigma },P_{\sigma }{R}_{\sigma })+d(A_{\sigma },Q_{\sigma }{R}_{\sigma })=\frac{1}{2^{k-1}}=\left|P_{\sigma }{Q}_{\sigma }\right|.$$

(6)

Proof. 

Firstly, assume that $A_{\sigma }=P_{\sigma }$. In such a case, the code representation of $A_{\sigma }$ is $\sigma 000\dots$. Thus, $d(A_{\sigma },P_{\sigma }{R}_{\sigma })=0$ since $A_{\sigma }\in P_{\sigma }{Q}_{\sigma }$. We will compute $d(A_{\sigma },Q_{\sigma }{R}_{\sigma })$. Let X be any point on $Q_{\sigma }{R}_{\sigma }$ which is the closest points to $A_{\sigma }$. It is clear that X has the code representation $\sigma x_k{x}_{k+1}{x}_{k+2}\dots$ where $x_i\in \{1,2\}$. Because $a_k\ne x_k$, $x_i\ne a_k$ and $a_i\ne x_k$ for $i=k+1,k+2,k+3,\dots$, we have

$$\mu =\sum _{i=k+1}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i}=\sum _{i=k+1}^{\infty }\frac{1+1}{2^i}=\frac{1}{2^{k-1}}.$$

We now show $\nu =\frac{1}{2^{k-1}}.$ Let us consider cases $x_k=1$ and $x_k=2$ separately. If $x_k=1$, then we obtain $c_k=2$. Due to the fact that $a_i=0$, we have ${\gamma }_i=1$ for $i=k+1,k+2,k+3,\dots$. In order to get the closest distance, $x_i$ must be 2 and thus ${\delta }_i=0$ for $i=k+1,k+2,k+3,\dots$. Therefore, we get

$${\displaystyle \nu =\frac{1}{2^k}+\sum _{i=k+1}^{\infty }\frac{{\gamma }_i+{\gamma }_i}{2^i}=\frac{1}{2^k}+\sum _{i=k+1}^{\infty }\frac{0+1}{2^i}=\frac{1}{2^{k-1}}.}$$

Similarly, $\nu$ equals to $\frac{1}{2^{k-1}}$ for the case $x_k=2$. Following the similar way, the same result is acquired if $A_{\sigma }=Q_{\sigma }$. Hence, the proof is completed for the special cases $A_{\sigma }=P_{\sigma }$ and $A_{\sigma }=Q_{\sigma }$.

We now consider $A_{\sigma }\ne P_{\sigma }$ and $A_{\sigma }\ne Q_{\sigma }$. There exist $m\in \mathbb{N}$ and $n\in \mathbb{N}$ such that $a_m=0$ and $a_n=1$. We choose m and n as the first index such that $m\ge k$ and $n\ge k$. Let $n>m$ (the other case is done analogously). As $A_{\sigma }$ is on the edge $P_{\sigma }{Q}_{\sigma }$ of $S_{\sigma }$, we get $a_k=0$. Hence, we have $a_i=0$ for $i=k+1,k+2,\dots ,n-1$ and $a_n=1$. Consider any point X with code representation $\sigma x_k{x}_{k+1}{x}_{k+2}\dots$ on $P_{\sigma }{R}_{\sigma }$ and any point Y with code representation $\sigma y_k{y}_{k+1}{y}_{k+2}\dots$ on $Q_{\sigma }{R}_{\sigma }$ which are the closest points to $A_{\sigma }$. In that case, $x_i$ must be 0 for $i=k,k+1,\dots ,n-1$. There are only two options for $x_n$ which are 0 or 2. In the case of $x_n=2$, it is obtained ${\alpha }_i=1$ for $i=n+1,n+2,\dots$. So, $x_n$ must be equal to 0 for the computation of the closest distance. In addition, we attain ${\beta }_i=1$ since $x_i\ne 1$ for $i=n+1,n+2,\dots$. Moreover, we get $y_i\ne a_k$ for $i=k,k+1,k+2\dots$ because Y is on the edge $Q_{\sigma }{R}_{\sigma }$ (that is, $y_i\in \{1,2\}$ for $i=k,k+1,k+2\dots$). We thus have ${\beta }_i^{\prime }=1$ for $i=k+1,k+2,k+3\dots$. Furthermore, for $i=k+1,k+2,\dots ,n-1$, we obtain ${\alpha }_i^{\prime }=1$ and ${\alpha }_n^{\prime }=0$ since $a_i=0$ and $a_n=1$. (Note that, $y_k$ must be equal to 1). For any $i=n+1,n+2,n+3\dots$, if $a_i=0$, then ${\alpha }_i=0$ and ${\alpha }_i^{\prime }=1$ and if $a_i=1$, then ${\alpha }_i=1$, ${\alpha }_i^{\prime }=0$. It follows that

$$\begin{array}{ccc}{\displaystyle \mu +{\mu }^{\prime }}& =& {\displaystyle \sum _{i=k+1}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i}+\sum _{i=k+1}^{\infty }\frac{{\alpha }_i^{\prime }+{\beta }_i^{\prime }}{2^i}}\hfill \\ & =& {\displaystyle \sum _{i=n+1}^{\infty }\frac{{\alpha }_i+{\beta }_i}{2^i}+\sum _{i=k+1}^{\infty }\frac{{\alpha }_i^{\prime }+{\beta }_i^{\prime }}{2^i}}\hfill \\ & =& {\displaystyle \sum _{i=n+1}^{\infty }\frac{{\alpha }_i+1}{2^i}+\sum _{i=k+1}^{\infty }\frac{{\alpha }_i^{\prime }+1}{2^i}}\hfill \\ & =& {\displaystyle \frac{1}{2^n}+\frac{1}{2^k}+\sum _{i=k+1}^{n-1}\frac{{\alpha }_i^{\prime }}{2^i}+\sum _{i=n+1}^{\infty }\frac{{\alpha }_i+{\alpha }_i^{\prime }}{2^i}}\hfill \\ & =& {\displaystyle \frac{1}{2^n}+\frac{1}{2^k}+\sum _{i=k+1}^{n-1}\frac{1}{2^i}+\sum _{i=n+1}^{\infty }\frac{1}{2^i}}\hfill \\ & =& {\displaystyle \frac{1}{2^n}+\frac{1}{2^k}+\sum _{i=k+1}^{n-1}\frac{1}{2^i}+\sum _{i=n+1}^{\infty }\frac{1}{2^i}}\hfill \\ & =& {\displaystyle \frac{1}{2^{k-1}}.}\hfill \end{array}$$

(7)

A similar computation shows $\nu +{\nu }^{\prime }\ge \frac{1}{2^{k-1}}.$ This concludes the proof. □

Remark 3.

If $B_{\sigma }$ and $C_{\sigma }$ are on the sides $Q_{\sigma }{R}_{\sigma }$ and $P_{\sigma }{R}_{\sigma }$ of the equilateral Sierpinski Gasket with edge length 1 respectively, then we have

$$d(B_{\sigma },P_{\sigma }{Q}_{\sigma })+d(B_{\sigma },P_{\sigma }{R}_{\sigma })=\frac{1}{2^{k-1}}=\left|Q_{\sigma }{R}_{\sigma }\right|,$$

(8)

and

$$d(C_{\sigma },P_{\sigma }{Q}_{\sigma })+d(C_{\sigma },Q_{\sigma }{R}_{\sigma })=\frac{1}{2^{k-1}}=\left|P_{\sigma }{R}_{\sigma }\right|.$$

(9)

However, Proposition 3 does not hold for every edges of scalene and isosceles Sierpinski Gaskets.

Example 3.

Consider the scalene Sierpinski Gasket with vertices $P=(0,0),Q=(0,8)$ and $R=(6,0)$. Let A with code representation $1\overline{0}=1000\dots$ be a point on the edge $PQ$ of the scalene Sierpinski Gasket. By using the formula given in Theorem 1, we first compute the distance $d(100\dots ,PR)$. The code representation of any point on $PR$ must be in the form $x_1{x}_2{x}_3\dots$ where $x_i\in \{0,2\}.$ In order to obtain ${\alpha }_i$ as 0, $x_1$ must be 0 since the term $a_i$ of A equals to zero for $i=2,3,4\dots$. Moreover, we have to take $x_i$ as 0 for $i=2,3,4\dots$ owing to the fact that $a_1=1$, $\left|PQ\right|=8$ and $\left|QR\right|=10$. We thus obtain

$$d(100\dots ,PR)=d(100\dots ,000\dots )=\frac{\left|PQ\right|}{2^2+2^3+2^4+\cdots }=4.$$

We now compute the distance $d(100\dots ,RQ)$. The code representation of any point on $RQ$ must be in the form $y_1{y}_2{y}_3\dots$ where $y_i\in \{1,2\}.$ To get the shortest distance, we must choose $y_1$ as $a_1$ (if we take $y_1$=2, then we obtain $y_1{y}_2{y}_3\dots =2111\dots$ for computation of shortest distance). Furthermore, $y_i$ must be 2 for $i=2,3,4\dots$ because $a_2=0$, $\left|PQ\right|=8$ and $\left|PR\right|=6$. Thus we have $y_1{y}_2{y}_3\dots =1222\dots$. So, we have

$$d(100\dots ,RQ)=d(100\dots ,1222\dots )=\frac{\left|PR\right|+\left|PR\right|}{2^3+2^4+2^5+\cdots }=3,$$

which shows

$$d(100\dots ,PR)+d(100\dots ,PR)=7\ne 8=\left|PQ\right|.$$

By similar calculations, the following result can be given.

Corollary 2.

Let S be a scalene or an isosceles Sierpinski Gasket. If A is a point on the shortest edge of S, then the sum of the distances of point A to the other two edges is fixed and this distance equals to the length of the shortest edge.

Proposition 4.

Let S be an equilateral Sierpinski Gasket with vertices P, Q and R. Suppose that A is a point on the edge $PQ$ with the code representation $a_1{a}_2{a}_3\dots$ where $A\ne P$. Then there are many points on $PR$ that determine the shortest distance of the point A to the line $PR$. Additionally, if n is the first index such that $a_i\ne 0$, then the set of points on $PR$ which determines this shortest distance is

$$\left\{a_1{a}_2{a}_3\dots a_{n-1}{x}_n{x}_{n+1}{x}_{n+2}{x}_{n+3}\dots \right|x_i\in \{0,2\}\mathrm{for}i=n,n+1,n+2,\dots \}.$$

Proof. 

Let A be a point on the edge $PQ$ with the code representation $a_1{a}_2{a}_3\dots$ where $A\ne P$ and let n be the first index such that $a_i\ne 0$. Consider any point X on $PR$ with the code representation $x_1{x}_2{x}_3\dots$ where $x_i\in \{0,2\}.$

Firstly, suppose that $a_i=1$ for $i=n+1,n+2,n+3,\dots$. In this case, $x_i$ must be 0 for $i=1,2,\dots ,n-1$ to obtain the shortest distance between X and A. We can choose $x_n$ as 0 or 2 since $a_i=1$ for $i=n+1,n+2,n+3,\dots$, and thus ${\alpha }_i=1$ for $i=n+1,n+2,n+3,\dots$. Additionally, $x_i$ can be taken 0 or 2 for $i=n+1,n+2,n+3,\dots$ because $a_i=1$, and so ${\beta }_i=1$ for $i=n+1,n+2,n+3,\dots$. This shows that the set of points X is

$$\left\{a_1{a}_2{a}_3\dots a_{n-1}{x}_n{x}_{n+1}{x}_{n+2}{x}_{n+3}\dots \right|x_i\in \{0,2\}\mathrm{for}i=n+1,n+2,n+3,\dots \}.$$

We now assume that there exists at least one $a_s=0$ for $s\in \{n+1,n+2,n+3,\dots \}$. Obviously, $x_i$ must be 0 for $i=1,2,\dots ,n-1$. Note that there are two options for $x_n$ such as 0 and 2. However, in order to obtain the shortest distance between X and A, $x_n$ has to be 0 since at least one $a_s$ is 0 for $s\in \{n+1,n+2,n+3,\dots \}$. Hence, at least one ${\alpha }_s$ must be 0. Moreover, $x_i$ can be taken 0 or 2 for $i=n+1,n+2,n+3,\dots$ as $a_i=1$, and thus ${\beta }_i=1$ for $i=n+1,n+2,n+3,\dots$. Consequently, the set of points X are

$$\left\{a_1{a}_2{a}_3\dots a_{n-1}0x_{n+1}{x}_{n+2}{x}_{n+3}\dots \right|x_i\in \{0,2\}\mathrm{for}i=n+1,n+2,n+3,\dots \}.$$

□

5. Conclusions

In this paper, we define code metrics on the code sets of Sierpinski-like triangles and then we give some interesting geometrical properties by using these metric formulas. These metric formulas can be also used in different computational works associated with the Sierpinski triangle.