Abstract
This article is based on new developments on a neutrosophic triplet group (NTG) and applications earlier introduced in 2016 by Smarandache and Ali. NTG sprang up from neutrosophic triplet set X: a collection of triplets for an that obeys certain axioms (existence of neutral(s) and opposite(s)). Some results that are true in classical groups were investigated in NTG and were shown to be either universally true in NTG or true in some peculiar types of NTG. Distinguishing features between an NTG and some other algebraic structures such as: generalized group (GG), quasigroup, loop and group were investigated. Some neutrosophic triplet subgroups (NTSGs) of a neutrosophic triplet group were studied. In particular, for any arbitrarily fixed , the subsets and of X, where is a neutrosophic triplet group homomorphism, were shown to be NTSG and normal NTSG, respectively. Both and were shown to be a-normal NTSGs and found to partition X. Consequently, a Lagrange-like formula was found for a finite NTG based on the fact that . The first isomorphism theorem was established for NTGs. Using an arbitrary non-abelian NTG X and its NTSG , a Bol structure was constructed. Applications of the neutrosophic triplet set, and our results on NTG in relation to management and sports, are highlighted and discussed.
MSC:
Primary 20N02; Secondary 20N05
1. Introduction
1.1. Generalized Group
Unified gauge theory has the algebraic structure of a generalized group abstrusely, in its physical background. It has been a challenge for physicists and mathematicians to find a desirable unified theory for twistor theory, isotopies theory, and so on. Generalized groups are instruments for constructions in unified geometric theory and electroweak theory. Completely simple semigroups are precisely generalized groups (Araujo et al. [1]). As recorded in Adeniran et al. [2], studies on the properties and structures of generalized groups have been carried out in the past, and these have been extended to smooth generalized groups and smooth generalized subgroups by Agboola [3,4], topological generalized groups by Molaei [5], Molaei and Tahmoresi [6], and quotient space of generalized groups by Maleki and Molaei [7].
Definition 1 (Generalized Group(GG)).
A generalized group X is a non-void set with a binary operation called multiplication obeying the set of rules given below.
- (i)
- for all .
- (ii)
- For each there is a unique such that (existence and uniqueness of identity element).
- (iii)
- For each , there is such that (existence of inverse element).
Definition 2.
Let X be a non-void set. Let (·) be a binary operation on X. Whenever for all , then is called a groupoid.
Whenever the equation (or ) have unique solution with respect to x (or y) i.e., satisfies the left (or right) cancellation law, then is called a left (or right) quasigroup. If a groupoid is both a left quasigroup and right quasigroup, then it is called a quasigroup. If there is an element called the identity element such that for all , , then a quasigroup is called a loop.
Definition 3.
A loop is called a Bol loop whenever it satisfies the identity
Remark 1.
One of the most studied classes of loops is the Bol loop.
For more on quasigroups and loops, interested readers can check [8,9,10,11,12,13,14,15].
A generalized group X has the following properties:
- (i)
- For each , there is a unique .
- (ii)
- and if .
- (iii)
- If X is commutative, then X is a group.
1.2. Neutrosophic Triplet Group
Neutrosophy is a novel subdivision of philosophy that studies the nature, origination, and ambit of neutralities, including their interaction with ideational spectra. Florentin Smarandache [16] introduced the notion of neutrosophic logic and neutrosophic sets for the first time in 1995. As a matter of fact, the neutrosophic set is the generalization of classical sets [17], fuzzy sets [18], intuitionistic fuzzy sets [17,19], and interval valued fuzzy sets [17], to cite a few. The growth process of neutrosophic sets, fuzzy sets, and intuitionistic fuzzy sets are still evolving, with diverse applications. Some recent research findings in these directions are [20,21,22,23,24,25,26,27].
Smarandache and Ali [28] were the first to introduce the notion of the neutrosophic triplet, which they had earlier talked about at a conference. These neutrosophic triplets were used by them to introduce the neutrosophic triplet group, which differs from the classical group both in fundamental and structural properties. The distinction and comparison of the neutrosophic triplet group with the classical generalized group were given. They also drew a brief outline of the potential applications of the neutrosophic triplet group in other research fields. For discussions of results on neutrosophic triplet groups, neutrosophic quadruples, and neutrosophic duplets of algebraic structures, as well as new applications of neutrosophy, see Jaiyéọlá and Smarandache [29]. Jaiyéọlá and Smarandache [29] were the first to introduce and study inverse property neutrosophic triplet loops with applications to cryptography for the first time.
Definition 4 (Neutrosophic Triplet Set-NTS).
Let X be a non-void set together with a binary operation ★ defined on it. Then X is called a neutrosophic triplet set if, for any , there is a neutral of ‘a’ denoted by (not necessarily the identity element) and an opposite of ‘a’ denoted by , with such that
The elements and are together called neutrosophic triplet, and represented by .
Remark 2.
For an , each of and may not be unique. In a neutrosophic triplet set , an element b (or c) is the second (or third) component of a neutrosophic triplet if () such that and . Thus, is a neutrosophic triplet.
Example 1
(Smarandache and Ali [28]). Consider such that and is multiplication in modulo 6. , and are neutrosophic triplets, but 3 will not give rise to a neutrosophic triplet.
Definition 5 (Neutrosophic Triplet Group—NTG).
Let be a neutrosophic triplet set. Then is referred to as a neutrosophic triplet group if is a semigroup. Furthermore, if obeys the commutativity law, then is referred to as a commutative neutrosophic triplet group.
Let be a neutrosophic triplet group. Whenever for all , then X is referred to as a normal neutrosophic triplet group.
Let be a neutrosophic triplet group and let . H is referred to as a neutrosophic triplet subgroup (NTSG) of X if is a neutrosophic triplet group. Whence, for any fixed , H is called a-normal NTSG of X, written if for all .
Remark 3.
An NTG is not necessarily a group. However, a group is an NTG where , the general identity element for all , and is unique for each .
Example 2
(Smarandache and Ali [28]). Consider such that . is a commutative NTG but neither a GG nor a classical group.
Example 3
(Smarandache and Ali [28]). Consider such that . is a non-commutative NTG but not a classical group.
Definition 6 (Neutrosophic Triplet Group Homomorphism).
Let be a mapping such that X and Y are two neutrosophic triplet groups. Then f is referred to as a neutrosophic triplet group homomorphism if for all . The kernel of f at is defined by
The Kernel of f is defined by
such that , where .
Remark 4.
The definition of neutrosophic triplet group homomorphism above is more general than that in Smarandache and Ali [28]. In Theorem 5, it is shown that, for an NTG homomorphism , and for all .
The present work is a continuation of the study of a neutrosophic triplet group (NTG) and its applications, which was introduced by Smarandache and Ali [28]. Some results that are true in classical groups were investigated in NTG and will be proved to be either generally true in NTG or true in some classes of NTG. Some applications of the neutrosophic triplet set, and our results on NTG in relation to management and sports will be discussed.
The first section introduces GG and NTG and highlights existing results that are relevant to the present study. Section 2 establishes new results on algebraic properties of NTGs and NTG homomorphisms, among which are Lagrange’s Theorem and the first isomorphism theorem, and presents a method of the construction of Bol algebraic structures using an NTG. The third section describes applications of NTGs to human management and sports.
2. Main Results
We shall first establish the relationship among generalized groups, quasigroups, and loops with a neutrosophic triplet group assumed.
Lemma 1.
Let X be a neutrosophic triplet group.
- 1.
- X is a generalized group if it satisfies the left (or right) cancellation law or X is a left (or right) quasigroup.
- 2.
- X is a generalized group if and only if each element has a unique .
- 3.
- Whenever X has the cancellation laws (or is a quasigroup), then X is a loop and group.
Proof.
- Let x have at least two neutral elements, say . Then . Therefore, X is a generalized group. Similarly, X is a generalized group if it is has the right cancellation law or if it is a right quasigroup.
- This follows by definition.
- This is straightforward because every associative quasigroup is a loop and group.
☐
2.1. Algebraic Properties of Neutrosophic Triplet Group
We now establish some new algebraic properties of NTGs.
Theorem 1.
Let X be a neutrosophic triplet group. For any , .
Proof.
by Theorem 1 ([29]). After multiplying by a, we obtain
Theorem 2.
Let X be a neutrosophic triplet group such that the left cancellation law is satisfied, and if and only if . Then X is an idempotent neutrosophic triplet group if and only if .
Proof.
.
Theorem 3.
Let X be a normal neutrosophic triplet group in which . Then, .
Proof.
Since , then by multiplying both sides of the equation on the right by , we obtain
Going by Theorem 1([29]),
It is worth characterizing the neutrosophic triplet subgroup of a given neutrosophic triplet group to see how a new NTG can be obtained from existing NTGs.
Lemma 2.
Let H be a non-void subset of a neutrosophic triplet group X. The following are equivalent.
- (i)
- H is a neutrosophic triplet subgroup of X.
- (ii)
- For all , .
- (iii)
- For all , , and .
Proof.
- (i)⇒ (ii)
- If H is an NTSG of X and , then . Therefore, by closure property, .
- (ii)⇒ (iii)
- If , and , then we have , , and , i.e., .
- (iii)⇒ (i)
- , so H is associative since X is associative. Obviously, for any , . Let , then . Therefore, . Thus, H is an NTSG of X.
☐
Theorem 4.
Let G and H be neutrosophic triplet groups. The direct product of G and H defined by
is a neutrosophic triplet group under the binary operation ∘ defined by
Proof.
This is simply done by checking the axioms of neutrosophic triplet group for the pair , in which case and . ☐
Lemma 3.
Let be a family of neutrosophic triplet subgroups of a neutrosophic triplet group X such that . Then is a neutrosophic triplet subgroup of X.
Proof.
This is a routine verification using Lemma 2. ☐
2.2. Neutrosophic Triplet Group Homomorphism
Let us now establish results on NTG homomorphisms, its kernels, and images, as well as a Lagrange-like formula and the First Isomorphism Theorem for NTGs.
Theorem 5.
Let be a homomorphism where X and Y are two neutrosophic triplet groups.
- 1.
- for all .
- 2.
- for all .
- 3.
- If H is a neutrosophic triplet subgroup of X, then is a neutrosophic triplet subgroup of Y.
- 4.
- If K is a neutrosophic triplet subgroup of Y, then is a neutrosophic triplet subgroup of X.
- 5.
- If X is a normal neutrosophic triplet group and the set with the productis a neutrosophic triplet group.
Proof.
Since f is an homomorphism, for all .
- Place in to obtain . Additionally, place in to obtain . Thus, for all .
- Place in to obtain . Additionally, place in to obtain . Thus, for all .
- If H is an NTSG of G, then . We shall prove that is an NTSG of Y by Lemma 2.Since for , . Let . Then and . Thus, . Therefore, is an NTSG of Y.
- If K is a neutrosophic triplet subgroup of Y, then . We shall prove that is an NTSG of Y by Lemma 2.Let . Then such that and . Thus, . Therefore, is an NTSG of X.
- Given the neutrosophic triplet group X and the set with the product . is a groupoid.For let . Then . Additionally, let . Then .Thus, and similarly, .On the other hand, , and similarly, .Therefore, is a neutrosophic triplet group. ☐
Theorem 6.
Let be a neutrosophic triplet group homomorphism.
- 1.
- .
- 2.
- .
- 3.
- is a normal neutrosophic triplet group.
- 4.
- .
- 5.
- for all .
- 6.
- If X is finite, for all where is the index of in , i.e., the number of distinct left cosets of in .
- 7.
- .
- 8.
- If X is finite, .
Proof.
- . Let , then . We shall use Lemma 2..Thus, is a neutrosophic triplet subgroup of X. For the a-normality, let , then . Therefore, for all . Therefore, .
- . . Therefore, . Let . Then . , and . Therefore, .. Thus, is a neutrosophic triplet subgroup of X.. Therefore, , and . Thus, . Therefore, .
- Let . Then . Therefore, . Thus, is a normal NTG.
- For all , . Therefore, based on Point 3 and Theorem 3, .
- Define a relation ≍ on as follows: if for all . . Therefore, ≍ is reflexive.. Therefore, ≍ is symmetric.. Therefore, ≍ is transitive and ≍ is an equivalence relation.The equivalence class . Therefore, .Thus, for all .
- If X is finite, then for all . Thus, for all where is the index of in , i.e., the number of distinct left cosets of in .
- Define a relation ∼ on X: if . ∼ is an equivalence relation on X, so and, therefore, .
- Hence, based on Point 7, if X is finite, then
☐
Theorem 7.
Let and be a neutrosophic triplet group homomorphism. Then
- 1.
- f is a monomorphism if and only if for all ;
- 2.
- the factor set is a neutrosophic triplet group (neutrosophic triplet factor group) under the operation defined by
Proof.
- Let and let . If , this implies thatSimilarly,Conversely, if f is mono, then . Let . Then . Therefore, for all .
- Let .
- Groupoid:
- Based on the multiplication , the factor set is a groupoid.
- Semigroup:
- .
- Neutrality:
- Let . Then and similarly, .
- Opposite:
- Let . Then . Similarly, .
is an NTG. ☐
Theorem 8.
Let be a neutrosophic triplet group homomorphism. Then .
Proof.
Based on Theorem 6(7), . Similarly, define a relation ≈ on : if . ≈ is an equivalence relation on , so and . It should be noted that in Theorem 6(2).
Let given by . It should be noted that, by Theorem 6(1), . Therefore, . Thus, is well defined.
. This means that is 1-1. is obviously onto. Thus, is bijective.
Now, based on the above and Theorem 7(2), we have a bijection
defined by . Thus, if , then
. ☐
2.3. Construction of Bol Algebraic Structures
We now present a method of constructing Bol algebraic structures using an NTG.
Theorem 9.
Let X be a non-abelian neutrosophic triplet group and let for any fixed . For , define ∘ on A as follows:
Then is a Bol groupoid.
Proof.
Let . By checking, it is true that . Therefore, is non-associative. is a normal neutrosophic triplet group by Theorem 6(3). A is a groupoid.
Let us now verify the Bol identity:
Following Theorem 6(4),
Therefore, LHS = RHS. Hence, is a Bol groupoid. ☐
Corollary 1.
Let H be a subgroup of a non-abelian neutrosophic triplet group X, and let . For , define ∘ on A as follows:
Then is a Bol groupoid.
Proof.
A subgroup H is a normal neutrosophic triplet group. The rest of the claim follows from Theorem 9. ☐
Corollary 2.
Let H be a neutrosophic triplet subgroup (which obeys the cancellation law) of a non-abelian neutrosophic triplet group X, and let . For , define ∘ on A as follows:
Then is a Bol groupoid.
Proof.
By Theorem 1(3), H is a subgroup of X. Hence, following Corollary 1, is a Bol groupoid. ☐
Corollary 3.
Let H be a neutrosophic triplet subgroup of a non-abelian neutrosophic triplet group X that has the cancellation law and let . For , define ∘ on A as follows:
Then is a Bol loop.
Proof.
By Theorem 1(3), X is a non-abelian group and H is a subgroup of X. Hence, is a loop and a Bol loop by Theorem 9. ☐
3. Applications in Management and Sports
3.1. One-Way Management and Division of Labor
Consider a company or work place consisting of a set of people X with number of people. A working unit or subgroup with a leader ‘a’ is denoted by .
for any represents a co-worker (or co-workers) who has (have) a good (non-critical) working relationship with x, while represents a co-worker (or co-workers) whom x considers as his/her personal critic(s) at work.
Hence, can be said to include both critics and non-critics of each worker x. It should be noted that in , for all . This means that every worker in has a good relationship with the leader ‘a’.
Thus, by Theorem 6(7)— and —the company or work place X can be said to have a good division of labor for effective performance and maximum output based on the composition of its various units (). See Figure 1.
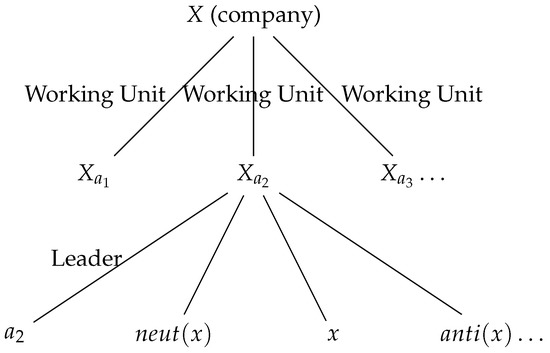
Figure 1.
One-way management and division of labor.
3.2. Two-Way Management Division of Labor
Consider a company or work place consisting of a set of people X with number of people at a location A and another company or work place consisting of people Y with number of people at another location B. Assume that both companies are owned by the same person f. Hence, can be considered as a movement (transfer) or working interaction between workers at A and at B. The fact that f is a neutrosophic triplet group homomorphism indicates that the working interaction between X and Y is preserved.
Let ‘a’ be a unit leader at A whose work correlates to another leader at B. Then represents the set of workers x in a unit at A under the leadership of ‘a’ such that there are other, corresponding workers at B under the leadership of . Here, means that workers at B under the leadership of are loyal and in a good working relationship. The mapping shows that the operation of a subgroup leader (the operation is denoted by ‘a’) is subject to the modus operandi of the owner of the two companies, where the owner is denoted by f.
The final formula in Theorem 6(8) shows that the overall performance of the set of people X is determined by how the unit leaders ‘a’ at A properly harmonize with the unit leaders at B in the effective administration of and (Figure 2).
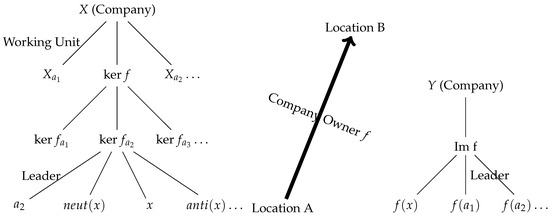
Figure 2.
Two-way management division of labor.
3.3. Sports
In the composition of a team, a coach can take as the set of players who play in a particular department (e.g., forward, middle field, or defence), where a is the leader of that department. Let represent player(s) whose performance is the same as that of player x, and let represent player(s) that can perform better than player x. It should be noted that the condition for all means that the department has player(s) who are equal in performance; i.e., those whose performance are equal to that of the departmental leader a. Hence, a neutrosophic triplet is a triple from which a coach can make a choice of his/her starting player and make a substitution. The neutrosophic triplet can also help a coach to make the best alternative choice when injuries arise. For instance, in the goal keeping department (for soccer/football), three goal keepers often make up the team for any international competition. Imagine an incomplete triplet , i.e., no player is found to be better than x, which reduces to a duplet.
can also be used for grouping teams in competitions in the preliminaries. If , then that can beat x and that can play draw with x. Therefore, neutrosophic triplet is a triplet with which competition organizers can draw teams into groups for a balanced competition. The Fédération Internationale de Football Association (FIFA) often uses this template in drawing national teams into groups for its competitions. Club teams from various national leagues, to qualify for continental competitions (e.g., Union of European Football Associations (UEFA) Champions League and Confederation of African Football (CAF) Champions League), have to be among the five. This implies the application of duplets, triplets, quadruples, etc. (Figure 3).
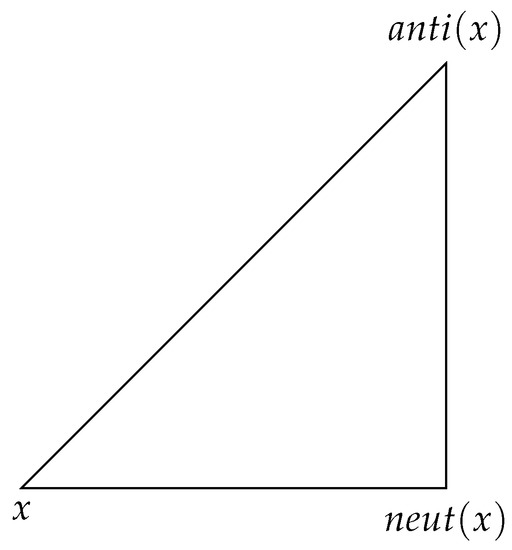
Figure 3.
Sports.
Author Contributions
T.G.J. established new properties of neutrosophic triplet groups. He further presented applications of the neutrosophic triplet sets and groups to management and sports. F.S. cointroduced the neutrosophic triplet set and group, as well as their properties. He confirmed the relevance of the neutrosophic duplet and the quadruple in the applications of neutrosophic triplet set.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Araujo, J.; Konieczny, J. Molaei’s Generalized Groups are Completely Simple Semigroups. Bul. Inst. Polytech. Jassy Sect. I Mat. Mec. Teor. Fiz. 2002, 48, 1–5. [Google Scholar]
- Adeniran, J.O.; Akinmoyewa, J.T.; Solarin, A.R.T.; Jaiyeola, T.G. On some algebraic properties of generalized groups. Acta Math. Acad. Paedagog. Nyhazi. 2011, 27, 23–30. [Google Scholar]
- Agboola, A.A.A. Smooth generalized groups. J. Niger. Math. Soc. 2004, 23, 6–76. [Google Scholar]
- Agboola, A.A.A. Smooth generalized subgroups and homomorphisms. Adv. Stud. Contemp. Math. 2004, 9, 183–193. [Google Scholar]
- Molaei, M.R. Topological generalized groups. Int. J. Appl. Math. 2000, 2, 1055–1060. [Google Scholar]
- Molaei, M.R.; Tahmoresi, A. Connected topological generalized groups. Gen. Math. 2004, 12, 13–22. [Google Scholar]
- Maleki, H.; Molaei, H. On the quotient space of a generalized action of a generalized group. arXiv, 2014; arXiv:1402.3408. [Google Scholar]
- Jaiyéọlá, T.G. A Study of New Concepts in Smarandache Quasigroups and Loops; Books on Demand, ProQuest Information and Learning: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Shcherbacov, V. Elements of Quasigroup Theory and Applications; Monographs and Research Notes in Mathematics; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4987-2155-4. [Google Scholar]
- Chein, O.; Pflugfelder, H.O.; Smith, J.D.H. Quasigroups and Loops: Theory and Applications; Sigma Series in Pure Mathematics 8; Heldermann: Berlin, Germany, 1990; ISBN 3-88538-008-0. [Google Scholar]
- Pflugfelder, H.O. Quasigroups and Loops: Introduction; Sigma Series in Pure Math. 7; Heldermann: Berlin, Germany, 1990. [Google Scholar]
- Smith, J.D.H. An introduction to Quasigroups and Their Representations; Studies in Advanced Mathematics; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; ISBN 978-1-58488-537-5, 1-58488-537-8. [Google Scholar]
- Smith, J.D.H. Poset Loops. Order 2017, 34, 265–285. [Google Scholar] [CrossRef]
- Glukhov, M.M. On the multiplicative groups of free and free commutative quasigroups. J. Math. Sci. (New York) 2017, 223, 508–517. [Google Scholar] [CrossRef]
- Greer, M. Semiautomorphic inverse property loops. Comm. Algebra 2017, 45, 2222–2237. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press (ARP): Rehoboth, NM, USA, 2003; ISBN 1-879585-76-6. [Google Scholar]
- Smarandache, F. Neutrosophic set, a generalization of the intuitionistic fuzzy set. In Proceedings of the 2006 IEEE International Conference on Granular Computing, Atlanta, GA, USA, 10–12 May 2006; pp. 38–42. [Google Scholar] [CrossRef]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Atanassov, A.K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, P.; Liu, J.; Chen, S.M. Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 2018, 69, 1–24. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.M. Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans. Cybern. 2017, 47, 2514–2530. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Chen, S.M. Multiattribute Group Decision Making Based on Intuitionistic 2-Tuple Linguistic Information. Inf. Sci. 2018, 430–431, 599–619. [Google Scholar] [CrossRef]
- Liu, P. Multiple attribute group decision making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput. Ind. Eng. 2017, 108, 199–212. [Google Scholar] [CrossRef]
- Liu, P.; Li, H. Interval-valued intuitionistic fuzzy power Bonferroni aggregation operators and their application to group decision making. Cognit. Comput. 2017, 9, 494–512. [Google Scholar] [CrossRef]
- Liu, P.; Liu, J.; Merigo, J.M. Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl. Soft Comput. 2018, 62, 395–422. [Google Scholar] [CrossRef]
- Liu, P.; Shi, L. Some Neutrosophic uncertain linguistic number Heronian mean operators and their application to multi-attribute group decision making. Neural Comput. Appl. 2017, 28, 1079–1093. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, L.; Liu, X.; Wang, P. Multi-valued Neutrosophic number Bonferroni mean operators and their application in multiple attribute group decision making. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 1181–1210. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Jaiyéọlá, T.G.; Smarandache, F. Inverse Properties in Neutrosophic Triplet Loop and their Application to Cryptography. Algorithms 2018, 11, 32. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).