Towards Generalized Noise-Level Dependent Crystallographic Symmetry Classifications of More or Less Periodic Crystal Patterns
Abstract
1. Introduction and Background
2. Kanatani’s Comments on Symmetry as a Continuous and Hierarchic Feature
3. Kanatani’s Dictum
4. Geometric Akaike Information Criteria (G-AICs)
4.1. General Considerations
4.2. G-AIC for Plane and Frieze Symmetry Groups
4.3. G-AIC for 2D Laue Classes
4.4. G-AIC for 2D Bravais Lattice Types
4.5. When is a Noise Level Estimate Mandatory?
5. Utilizing Geometric Akaike Information Criteria
5.1. Highlights of the Underlying Information Theory
5.2. Updated Bayesian Posterior Model Probabilities and Confidence Sets for Crystallographic Symmetry Classifications
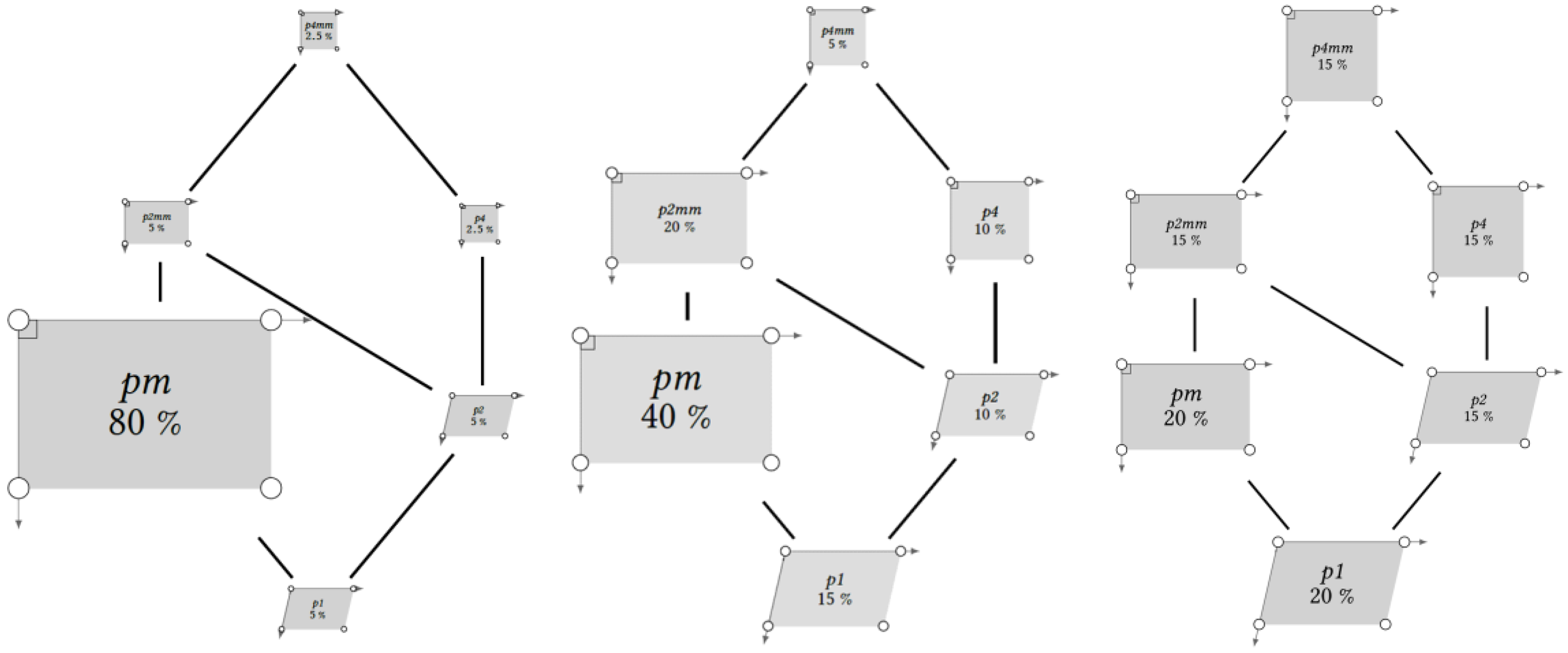
5.2.1. Illustration of the Updated Bayesian Posterior Model Probabilities Idea
5.2.2. Illustration of the Idea of Rescaled Confidence Sets over Stretches of Crystallographic Symmetry Hierarchy Branches
5.3. Multi-Model Averaging for Better Predictions and Safer Conclusions
5.4. Acknowledging Model Selection Uncertainties in Qualitative Ways
 2mg with a comparatively small model selection uncertainty.
2mg with a comparatively small model selection uncertainty. 2mg and
2mg and  2mm [135] are nearly equal to each other, signifying a large model selection uncertainty. The reason for this could well be the simultaneous existence of genuine pseudo-symmetries in the form a glide-line and a horizontal mirror-line in the recorded time series data; see Appendix E for further discussions.
2mm [135] are nearly equal to each other, signifying a large model selection uncertainty. The reason for this could well be the simultaneous existence of genuine pseudo-symmetries in the form a glide-line and a horizontal mirror-line in the recorded time series data; see Appendix E for further discussions.6. Summary and Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Opportunities and Background in the Context of 1D Periodic 2D Images as Obtained from Plane Edge-On Projected 3D Grain Boundaries
Appendix B. Pseudo-Symmetries
Appendix C. Pseudo-Symmetries and Other Problems in Mainstream 3D Crystallography that Have Led to Misclassified Entries in Major Crystallographic Databases
Appendix C.1. Space Group Symmetry Misclassifications in Major Crystallographic Databases
Appendix C.2. Reasons Why R Values and Similar “Pure Distance Measures” Are Not Helpful in Crystallographic Symmetry Classifications
Appendix C.3. Suspected Pseudo-Symmetry Mediated Space Group Symmetry Misclassification of a Highly Topical Material
Appendix D. Standard Statistical Descriptors and Utility of Contemporary Null Hypothesis Tests in Mainstream 3D Crystallography
Appendix E. Comments on the Experimental Studies of Liu and Co-Workers
 2mg) possessing a smaller least-squares residual than one of its translationengleiche subgroups (
2mg) possessing a smaller least-squares residual than one of its translationengleiche subgroups ( 211). As Inequality (1) shows, this can never happen with good data that are processed correctly because kmore > kless, both variables are positive integers, and kless > 1.
211). As Inequality (1) shows, this can never happen with good data that are processed correctly because kmore > kless, both variables are positive integers, and kless > 1. 2mg and
2mg and  2mm possess, for the walking human being, least-squares residuals that seem to be too large to allow for the conclusion that either of these two groups can serve as the Kullback-Leibler best model on the basis of Inequality (1) even without having the benefit of a generalized noise level estimate [5]. This could, again, be the result of ignoring the crystallographic origin convention [35] for frieze symmetry groups.
2mm possess, for the walking human being, least-squares residuals that seem to be too large to allow for the conclusion that either of these two groups can serve as the Kullback-Leibler best model on the basis of Inequality (1) even without having the benefit of a generalized noise level estimate [5]. This could, again, be the result of ignoring the crystallographic origin convention [35] for frieze symmetry groups.  11g, where there are no site symmetries other than the identity rotation. A time series of a walking human being can, however, only possess this frieze symmetry when the recording camera has been oriented so that its axis is perpendicular to the approximate mirror plane of the still-standing person. In all other orientations, the camera will record a time series with frieze symmetry
11g, where there are no site symmetries other than the identity rotation. A time series of a walking human being can, however, only possess this frieze symmetry when the recording camera has been oriented so that its axis is perpendicular to the approximate mirror plane of the still-standing person. In all other orientations, the camera will record a time series with frieze symmetry  111, i.e. the equivalent of pure translation periodicity only. All point symmetries of the walking human being motif higher than 1 that are implied by frieze symmetry classifications higher than
111, i.e. the equivalent of pure translation periodicity only. All point symmetries of the walking human being motif higher than 1 that are implied by frieze symmetry classifications higher than  111 and
111 and  11g in the results of Liu and coworkers [4,5] are, therefore, actually genuine pseudo-symmetries [50].
11g in the results of Liu and coworkers [4,5] are, therefore, actually genuine pseudo-symmetries [50]. 11g symmetry is reduced to pure translation symmetry.
11g symmetry is reduced to pure translation symmetry. 111 and
111 and  11g result.
11g result.References and Notes
- Liu, Y.; Hel-Or, H.; Kaplan, C.S.; Van Gool, L. Computational Symmetry in Computer Vision and Computer Graphics. Found. Trends Comput. Graph. Vis. 2009, 5, 1–195. [Google Scholar] [CrossRef]
- Albert, F.; Gómis, J.M.; Blasco, J.; Valiente, J.M.; Aleixos, N. A new method to analyse mosaics based on symmetry group theory applied to Islamic geometric patterns. Comput. Vis. Image Underst. 2015, 130, 54–70. [Google Scholar] [CrossRef]
- Kanatani, K. Comments on “Symmetry as a Continuous Feature”. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 246–247. [Google Scholar] [CrossRef]
- Liu, Y.; Collins, R.T.; Tsin, Y. A computational model for periodic pattern perception based on frieze and wallpaper groups. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 354–371. [Google Scholar] [PubMed]
- Liu, Y.; Collins, R.T.; Tsin, Y. A Computational Model for Periodic Pattern Perception Based on Frieze and Wallpaper Groups. (Longer and More Detailed 2002/2003 Version of [4]). Available online: http://www.cs.cmu.edu/~yanxi/images/Bio2003/2002PAMIwallpaper.pdf (accessed on 5 May 2017).
- Liu, Y.; Collins, R.T.; Tsin, Y. Gait Sequence Analysis using Frieze Patterns. In Proceedings ECCV 2002; Lecture Notes in Computer Science; Heyden, A., Sparr, G., Nielsen, M., Johansen, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2351, pp. 657–671. [Google Scholar] [CrossRef]
- Moeck, P. Advances in Crystallographic Image Processing for Scanning Probe Microscopy. In Microscopy Book Series; Méndez-Vilas, A., Ed.; Formatex: Badajoz, Spain, 2017; pp. 503–514. Available online: http://www.microscopy7.org/book/503-514.pdf (accessed on 5 May 2017).
- Authier, A.; Chapius, G. (Eds.) Online Dictionary of Crystallography of the IUCr. In A Little Dictionary of Crystallography; International Union of Crystallography: Chester, UK, 2014; p. 49. Available online: http://reference.iucr.org/dictionary/Crystal_pattern (accessed on 5 May 2017).
- Kanatani, K. For geometric inference from images, what kind of statistical model is necessary? Syst. Comput. Jpn. 2004, 35, 1–9. [Google Scholar] [CrossRef]
- Kanatani, K. Uncertainty Modeling and Geometric Inference. In Handbook of Geometric Computing, Applications in Pattern Recognition, Computer Vision, Neuralcomputing, and Robotics; Corrochano, E.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Chapter 14; pp. 462–491. [Google Scholar]
- Kanatani, K. Geometric Information Criterion for Model Selection. Int. J. Comput. Vis. 1998, 26, 171–189. [Google Scholar] [CrossRef]
- Kanatani, K. Statistical Optimization for Geometric Computation: Theory and Practice, 2nd ed.; Dover: Mineola, NY, USA, 2005; Chapter 13; pp. 415–450. ISBN 0-486-44308-6. [Google Scholar]
- Anderson, D.R. Model Based Inference in the Life Sciences: A Primer on Evidence; Springer: New York, NY, USA, 2008; ISBN 978-0-387-74073-7. [Google Scholar]
- Johnson, J.B.; Omland, K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2004, 19, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002; ISBN 978-0-387-22456-5. [Google Scholar]
- Burnham, K.P.; Anderson, D.R.; Huyvaert, K.P. AIC model selection and multimodel inference in behavioral ecology: Some background, observations, and comparisons. Behav. Ecol. Sociobiol. 2011, 65, 23–35. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R.; Huyvaert, K.P. Erratum to: AIC model selection and multimodel inference in behavioral ecology: Some background, observations, and comparisons. Behav. Ecol. Sociobiol. 2011, 65, 415. [Google Scholar] [CrossRef]
- Kalinin, S.V.; Sumpter, B.G.; Archibald, R.K. Big-deep-smart data in imaging for guiding materials design. Nat. Mater. 2015, 14, 973–980. [Google Scholar] [CrossRef] [PubMed]
- Straton, J.C.; Bilyeu, T.T.; Moon, B.; Moeck, P. Double-tip effects on Scanning Tunneling Microscopy imaging of 2D periodic objects: Unambiguous detection and limits of their removal by crystallographic averaging in the spatial frequency domain. Cryst. Res. Technol. 2014, 49, 663–680. [Google Scholar] [CrossRef]
- Straton, J.C.; Moon, B.; Bilyeu, T.T.; Moeck, P. Removal of multiple-tips artifacts from scanning tunneling microscope images by crystallographic averaging. Adv. Struct. Chem. Imaging 2015, 1, 14. [Google Scholar] [CrossRef][Green Version]
- Moeck, P. Crystallographic image processing for scanning probe and transmission electron microscopy. In Proceedings of the 11th IEEE International Conference Nanotechnology, Portland, OR, USA, 15–18 August 2011; pp. 520–525. [Google Scholar] [CrossRef]
- Moeck, P. Crystallographic image processing for scanning probe microscopy. In Microscopy Book Series; Méndez-Vilas, A., Diaz, J., Eds.; Formatex: Badajoz, Spain, 2010; Volume 3, pp. 1951–1962. Available online: http://www.formatex.info/microscopy4/1951-1962.pdf (accessed on 5 May 2017).
- Hahn, T. (Ed.) International Tables for Crystallography, Brief Teaching Edition of Volume A, Space-Group Symmetry, 5th ed.; Wiley & Sons: Chichester, UK, 2010; ISBN 978-0-470-68911-0. [Google Scholar]
- Aroyo, M.I. (Ed.) International Tables for Crystallography, Volume A, Space-Group Symmetry, 6th ed.; Wiley & Sons: Chichester, UK, 2016; ISBN 978-0-470-97423-0. [Google Scholar]
- Klug, A. Image analysis and reconstruction in the electron microscopy of biological macromolecules. Chem. Scr. 1978–1979, 14, 245–256. [Google Scholar]
- Van Aert, S. Statistical Parameter Estimation Theory—A Tool for Quantitative Electron Microscopy. In Handbook of Nanoscopy, 1st ed.; Van Tendeloo, G., Van Dyck, D., Pennycook, S.J., Eds.; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2012; pp. 281–308. [Google Scholar]
- De Backer, A. Quantitative Atomic Resolution Electron Microscopy Using Advanced Statistical Techniques. Ph.D. Thesis, Department of Physics, University of Antwerp, Antwerp, Belgium, 2015. [Google Scholar]
- Van Aert, S.; De Backer, A.; Martinez, G.T.; Den Dekker, A.J.; Van Dyck, D.; Bals, S.; Van Tendeloo, G. Advanced electron crystallography through model-based imaging. IUCrJ 2016, 3, 71–83. [Google Scholar] [CrossRef] [PubMed]
- De Backer, A.; Van den Bos, K.H.W.; Van den Broek, W.; Sijbers, J.; Van Aert, S. StatSTEM: An efficient approach for accurate and precise model-based quantification of atomic resolution electron microscopy images. Ultramicroscopy 2016, 171, 104–116. [Google Scholar] [CrossRef] [PubMed]
- De Backer, A.; Jones, L.; Lobato, I.; Altantzis, T.; Goris, B.; Nellist, P.D.; Bals, S.; Van Aert, S. Three-dimensional atomic models from a single projection using Z-contrast imaging: Verification by electron tomography and opportunities. Nanoscale 2017, 9, 8791–8798. [Google Scholar] [CrossRef] [PubMed]
- Vasudevan, R.K.; Ziatdinov, M.; Jesse, S.; Kalinin, S.V. Phases and Interfaces from Real Space Atomically Resolved Data: Physics-Based Deep Data Image Analysis. Nano Lett. 2016, 16, 5574–5581. [Google Scholar] [CrossRef] [PubMed]
- Pólya, G. Über die Analogie der Kristallsymmetrie in der Ebene. Z. Kristallogr. 1924, 60, 278–282. (In German) [Google Scholar] [CrossRef]
- Fedorov, E. Симметрія на плоскости (La symétrie sur un plan). Proc. Imp. Petersb. Mineral. Soc. 1891, 28, 345–390. (In Russian) [Google Scholar]
- Julian, M.M. Foundations of Crystallography: With Computer Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2015; ISBN 978-1-4665-5291-3. [Google Scholar]
- Kopský, V.; Litvin, D.B. (Eds.) International Tables for Crystallography, Volume E, Subperiodic Groups, 2nd ed.; Wiley & Sons: Chichester, UK, 2010; ISBN 978-0-470-68672-0. [Google Scholar]
- Tong, W.; Yang, H.; Moeck, P.; Nandasiri, M.I.; Browning, N.D. General Schema for [001] Tilt Grain Boundaries in Dense Packing Cubic Crystals. Acta Mater. 2013, 61, 3392–3398. [Google Scholar] [CrossRef]
- Yang, H.; Lee, H.S.; Sarahan, M.C.; Sato, Y.; Chi, M.; Ikuhara, Y.; Moeck, P.; Browning, N.D. Statistical analysis of atomic resolution images to quantify stoichiometry induced variations in grain boundary structure and energy in SrTiO3. Philos. Mag. 2013, 93, 1219–1229. [Google Scholar] [CrossRef]
- Inoue, K.; Saito, M.; Wang, Z.; Kotani, M.; Ikuhara, Y. On the periodicity of <001> symmetrical tilt grain boundaries. Mater. Trans. 2015, 56, 281–287. [Google Scholar] [CrossRef]
- Inoue, K.; Saito, M.; Chen, C.; Kotani, M.; Ikuhara, Y. Mathematical analysis and STEM observations of arrangement of structural units in <001> symmetrical tilt grain boundaries. Microscopy 2016, 65, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Kozak, R.; Kurdzesau, F.; Prieto, I.; Skibitzki, O.; Schroeder, T.; Dasilva, Y.A.R.; Erni, R.; von Känel, H.; Rossell, M.D. A tool for automatic recognition of [110] tilt grain boundaries in zincblende-type crystals. J. Appl. Crystallogr. 2017, 50, 1299–1306. [Google Scholar] [CrossRef]
- Moeck, P.; York, B.W.; Browning, N.D. Symmetries of migration related segments of all [001] CSL tilt boundaries in (001) projection for all holohedral cubic materials. Cryst. Res. Technol. 2014, 49, 708–720. [Google Scholar] [CrossRef]
- Pond, R.C.; Vlachavas, D. Bicrystallography. Proc. R. Soc. Lond. Ser. 1983, 386, 95–143. [Google Scholar] [CrossRef]
- Kalonji, G. A roadmap for the use of interfacial symmetry groups. J. Phys. Colloq. 1985, 46, C4-249–C4-256. [Google Scholar] [CrossRef]
- Kalonji, G.L. Symmetry Principles in the Physics of Crystalline Interfaces. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge University, Cambridge, MA, USA, 1982. [Google Scholar]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Materials; Oxford University Press: Oxford, UK, 1995; ISBN 978-0-19-921106-7. [Google Scholar]
- Romeu, D. Interfaces and quasicrystals as competing crystal lattice: Towards a crystallographic theory of interfaces. Phys. Rev. B 2003, 67, 024202-1–024202-12. [Google Scholar] [CrossRef]
- Runnels, B. A projection-based reformulation of the coincident site lattice Σ for arbitrary bicrystals at finite temperature. Acta Crystallogr. A 2017, 73, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Priester, L. Grain Boundaries, From Theory to Engineering, 1st ed.; Springer Series in Materials Science; Springer: Dordrecht, The Netherlands, 2013; Volume 172, Chapter 1; pp. 3–47. ISBN 978-2-7598-0769-7. [Google Scholar] [CrossRef]
- Litvin, D.B. Scanning of two-dimensional space groups. Acta Crystallogr. A 2015, 71, 111–113. [Google Scholar] [CrossRef] [PubMed]
- Online Dictionary of Crystallography of the IUCr. Available online: http://reference.iucr.org/dictionary/Pseudo_symmetry (accessed on 19 May 2017).
- Herbst-Irmer, R. Twinning. Oxford Scholarship Online, 2010. Available online: www.oxfordscholarship.com (accessed on 19 May 2017). [CrossRef]
- Müller, P.; Herbst-Irmer, R.; Spek, A.L.; Schneider, T.R.; Sawaya, M.R. Crystal Structure Refinement: A Crystallographer’s Guide to SHELXL; IUCr Texts on Crystallography 8; Oxford University Press: Oxford, UK, 2006; Chapter 7; pp. 106–149. ISBN 9780198570769. [Google Scholar]
- Zwart, P.H.; Grosse-Kunstleve, R.W.; Lebedev, A.A.; Murshudov, G.N.; Adams, P.D. Surprises and pitfalls arising from (pseudo) symmetry. Acta Crystallogr. D 2008, 64, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Poon, B.K.; Grosse-Kunstleve, R.W.; Zwart, P.H.; Sauter, N.K. Detection and correction of underassigned rotational symmetry prior to structure deposition. Acta Crystallogr. D 2010, 66, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. On the validation of crystallographic symmetry and the quality of structures. Prot. Sci. 2015, 24, 621–632. [Google Scholar] [CrossRef] [PubMed]
- Brünger, A.T. Free R value: A novel statistical quantity for assessing the accuracy of crystal structures. Nature 1992, 355, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Baur, W.H.; Kassner, D. The perils of Cc: Comparing the frequencies of falsely assigned space groups with their general population. Acta Crystallogr. B 1992, 48, 356–369. [Google Scholar] [CrossRef]
- Dauter, Z.; Wlodawer, A.; Minor, W.; Jaskolskih, M.; Rupp, B. Avoidable errors in deposited macromolecular structures: An impediment to efficient data mining. IUCrJ 2014, 1, 179–193. [Google Scholar] [CrossRef] [PubMed]
- Lebedev, A.A.; Isupov, M.N. Space-group and origin ambiguity in macromolecular structures with pseudo-symmetry and its treatment with the program Zanuda. Acta Crystallogr. D 2014, 70, 2430–2443. [Google Scholar] [CrossRef] [PubMed]
- Marsh, R.E.; Herbstein, F.H. More space-group changes. Acta Crystallogr. B 1988, 44, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Baur, W.H.; Tillmanns, E. How to avoid unnecessarily low symmetry in crystal structure determinations. Acta Crystallogr. B 1986, 42, 95–111. [Google Scholar] [CrossRef]
- Somov, N.V.; Chuprunov, E.V. The translational and inversion pseudosymmetry of the atomic crystal structure of organic and organometallic compounds. Crystallogr. Rep. 2009, 54, 727–733. [Google Scholar] [CrossRef]
- Clemente, D.A. A study of the 8466 structures reported in Inorganica Chimica Acta: 52 space group changes and their chemical consequences. Inorg. Chim. Acta 2005, 358, 1725–1748. [Google Scholar] [CrossRef]
- Marsh, R.E. Some thoughts on choosing the correct space group. Acta Crystallogr. B 1995, 51, 897–907. [Google Scholar] [CrossRef]
- Donohue, J. Incorrect Crystal Structures: Can they be avoided? In Critical Evaluation of Chemical and Physical Structural Information, Proceedings of the a Conference with the Same Name at Dartmouth College, Hanover, New Hampshire, 24–29 June 1973; Lide, D.R., Paul, M.A., Eds.; National Academy of Sciences: Washington, DC, USA, 1974; pp. 199–218. ISBN 0-309-02146-4. [Google Scholar]
- Brown, E.N.; Ramaswamy, S. Quality of protein crystal structures. Acta Crystallogr. D 2007, 63, 941–950. [Google Scholar] [CrossRef] [PubMed]
- Borman, S. Structure quality, crystal structures in ‘hotter’ journals tend to have more errors. Chem. Eng. News 2007, 85, 11–12. [Google Scholar] [CrossRef]
- Ibers, J.A. Problem Crystal Structures. In Critical Evaluation of Chemical and Physical Structural Information, Proceedings of the a Conference with the Same Name at Dartmouth College, Hanover, New Hampshire, 24–29 June 1973; Lide, D.R., Paul, M.A., Eds.; National Academy of Sciences: Washington, DC, USA, 1974; pp. 186–198. ISBN 0-309-02146-4. [Google Scholar]
- Marsh, R.E. P1 or P1? Or something else? Acta Crystallogr. B 1999, 55, 931–936. [Google Scholar] [CrossRef] [PubMed]
- Chook, M.; Lipscomb, W.N.; Ke, H. Detection and use of pseudo-translation in determination of protein structures. Acta Crystallogr. D 1998, 54, 822–827. [Google Scholar] [CrossRef] [PubMed]
- Ruck, M. Kristallographische Konsequenzen von Pseudosymmetrie in Kristallstrukturen. Z. Kristallogr. 2000, 215, 148–156. (In German) [Google Scholar] [CrossRef]
- Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Brock, C.P.; Dunitz, J.D. Towards a Grammer of Crystal Packing. Chem. Mater. 1994, 6, 1118–1127. [Google Scholar] [CrossRef]
- Kuleshova, L.N.; Antipin, M.Y.; Komkov, I.V. The role of molecular association in the formation of crystals with Z’ > 1 of some hydroxy-containing compounds. J. Mol. Struct. 2003, 647, 41–51. [Google Scholar] [CrossRef]
- Anderson, K.M.; Goeta, A.E.; Hancock, K.S.B.; Steed, J.W. Unusual variations in the incidence of Z’ > 1 in oxo-anion structures. Chem. Commun. 2006, 2138–2140. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R. On the presence of multiple molecules in the crystal asymmetric unit (Z’ > 1). CrystEngComm 2007, 9, 91–92. [Google Scholar] [CrossRef]
- Anderson, K.M.; Steed, J.W. Comment on “On the presence of multiple molecules in the crystal asymmetric unit (Z’ > 1)” by Gautam R. Desiraju. CrystEngComm 2007, 9, 328–330. [Google Scholar] [CrossRef]
- Steed, J.W. Should solid-state molecular packing have to obey the rules of crystallographic symmetry? CrystEngComm 2003, 5, 159–178. [Google Scholar] [CrossRef]
- Müller, P. Pseudo-Symmetry. Oxford Scholarship Online, 2010. Available online: www.oxfordscholarship.com (accessed on 24 February 2018). [CrossRef]
- Müller, P.; Herbst-Irmer, R.; Spek, A.L.; Schneider, T.R.; Sawaya, M.R. Crystal Structure Refinement: A Crystallographer’s Guide to SHELXL; IUCr Texts on Crystallography 8; Oxford University Press: Oxford, UK, 2006; Chapter 6; pp. 97–105. ISBN 9780198570769. [Google Scholar]
- Harlow, R.L. Troublesome Crystal Structures: Prevention, Detection, and Resolution. J. Res. Natl. Inst. Stand. Technol. 1996, 101, 327–339. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Kleywegt, G.J.; Nakamura, H.; Markley, J.L. The Protein Data Bank archive as an open data resource. J. Comput. Aided Mol. Des. 2014, 28, 1009–1014. [Google Scholar] [CrossRef] [PubMed]
- Gore, S.; Velankar, S.; Kleywegt, G.J. Implementing an X-ray validation pipeline for the Protein Data Bank. Acta Crystallogr. D 2012, 68, 478–483. [Google Scholar] [CrossRef] [PubMed]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Gražulis, S.; Chateigner, D.; Downs, R.T.; Yokochi, A.F.T.; Quirós, M.; Lutterotti, L.; Manakova, E.; Butkus, J.; Moeck, P.; Le Bail, A. Crystallography Open Database—An open access collection of crystal structures. J. Appl. Crystallogr. 2009, 42, 726–729. [Google Scholar] [CrossRef] [PubMed]
- Gražulis, S.; Daškevič, A.; Merkys, A.; Chateigner, D.; Lutterotti, L.; Quirós, M.; Serebryanaya, N.; Moeck, P.; Downs, R.T.; Le Bail, A. Crystallography Open Database (COD): An open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res. 2011, 40, D420–D427. [Google Scholar] [CrossRef] [PubMed]
- Wlodawer, A.; Dauter, Z. ‘Atomic resolution’: A badly abused term in structural biology. Acta Crystallogr. D 2017, 73, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Brändén, C.-I.; Jones, T.A. Between objectivity and subjectivity. Nature 1990, 343, 687–689. [Google Scholar] [CrossRef]
- Jones, P.G. Crystal Structure Determination: A Critical Review. Chem. Soc. Rev. 1984, 13, 157–172. [Google Scholar] [CrossRef]
- Schwarzenbach, D.; Abrahams, S.C.; Flack, H.D.; Gonschorek, W.; Hahn, T.; Huml, K.; Marsh, R.E.; Prince, E.; Robertson, B.E.; Rollett, J.S.; et al. Statistical descriptors in crystallography, Report of the International Union of Crystallography Subcommittee on Statistical Descriptors. Acta Crystallogr. A 1989, 45, 63–75. [Google Scholar] [CrossRef]
- Schwarzenbach, D.; Abrahams, S.C.; Flack, H.; Prince, E.; Wilson, A.J.C. Statistical descriptions in crystallography. II: Report of a Working Group on Expression of Uncertainty in Measurement. Acta Crystallogr. A 1995, 51, 565–569. [Google Scholar] [CrossRef]
- Online Dictionary of Crystallography of the IUCr. Available online: http://reference.iucr.org/dictionary/Statistical_descriptors (accessed on 24 February 2018).
- Prince, E.; Spiegelman, C.H. Statistical significance tests. In International Tables for Crystallography, Vol. C: Mathematical, Physical and Chemical Tables, 3rd ed.; Prince, E., Ed.; International Union for Crystallography: Chester, UK, 2004; pp. 702–706. ISBN 978-1-4020-1900-5. [Google Scholar]
- Cruickshank, D.W.J. Remarks about protein structure precision. Acta Crystallogr. D 1999, 55, 583–601. [Google Scholar] [CrossRef] [PubMed]
- Cruickshank, D.W.J. Remarks about protein structure precision, Erratum. Acta Crystallogr. D 1999, 55, 1108. [Google Scholar] [CrossRef] [PubMed]
- Cruickshank, D.W.J.; Robertson, A.P. The comparison of theoretical and experimental determinations of molecular structures, with applications to naphthalene and anthracene. Acta Crystallogr. 1953, 6, 698–705. [Google Scholar] [CrossRef]
- Hamilton, W.C. Significance tests on the crystallographic R factor. Acta Crystallogr. 1965, 18, 502–510. [Google Scholar] [CrossRef]
- Hamilton, W.C. Tests for statistical significance. In International Tables for X-ray Crystallography, Vol. IV Revised and Supplementary Tables to Vol. II and III; Ibers, J.A., Hamilton, W.C., Eds.; Kynoch Press: Birmingham, UK, 1974; pp. 285–310. [Google Scholar]
- Prince, E. Comparison of the fits of two models to the same data set. Acta Crystallogr. B 1982, 38, 1099–1100. [Google Scholar] [CrossRef]
- Mondloch, J.E.; Bury, W.; Fairen-Jimenez, D.; Kwon, S.; DeMarco, E.J.; Weston, M.H.; Sarjeant, A.A.; Nguyen, S.T.; Stair, P.C.; Snurr, R.Q.; et al. Vapor-Phase Metalation by Atomic Layer Deposition in a Metal–Organic Framework. J. Am. Chem. Soc. 2013, 135, 10294–10297. [Google Scholar] [CrossRef] [PubMed]
- Sarjeant, A.A. personal and several e-mail communications at and after the 24th World Congress and General Assembly of the International Union of Crystallography, Hyderabad, India, August 2017; Sir Stoddart, J.F. personal communication October 2017; and Farha, O.K. several email communications between November 2017 and February 2018 (on the advice of Sarjeant and Sir Stoddart).
- Wang, T.C.; Wang, T.C.; Vermeulen, N.A.; Kim, I.S.; Martinson, A.B.; Stoddart, J.F.; Hupp, J.T.; Farha, O.K. Scalable synthesis and post-modification of a mesoporous metal-organic framework called NU-1000. Nat. Protoc. 2016, 11, 149–162. [Google Scholar] [CrossRef] [PubMed]
- McGonigal, P.R.; Deria, P.; Hod, I.; Peyman, Z.; Moghadam, P.Z.; Avestro, A.-J.; Horwitz, N.E.; Gibbs-Hall, I.C.; Blackburn, A.K.; Chen, D.; et al. Electrochemically addressable trisradical rotaxanes organized within a metal–organic framework. Proc. Natl. Acad. Sci. USA 2015, 112, 11161–11168. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Sun, J.; Li, P.; Hod, I.; Moghadam, P.Z.; Kean, Z.S.; Snurr, R.Q.; Hupp, J.T.; Farha, O.K.; Stoddart, J.F. A Redox-Active Bistable Molecular Switch Mounted inside a Metal–Organic Framework. J. Am. Chem. Soc. 2016, 138, 14242–14245. [Google Scholar] [CrossRef] [PubMed]
- Howarth, A.J.; Buru, C.T.; Liu, Y.; Ploskonka, A.M.; Hartlieb, K.J.; McEntee, M.; Mahle, J.J.; Buchanan, J.H.; Durke, E.M.; Al-Juaid, S.S.; et al. Postsynthetic Incorporation of a Singlet Oxygen Photosensitizer in a Metal–Organic Framework for Fast and Selective Oxidative Detoxification of Sulfur Mustard. Chem. Eur. J. 2017, 23, 214–218. [Google Scholar] [CrossRef] [PubMed]
- Spek, A.L. PLATON SQUEEZE: A tool for the calculation of the disordered solvent contribution to the calculated structure factors. Acta Crystallogr. C 2015, 71, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Moeck, P.; Mehdi, B.L.; Stevens, A.; DeStefano, P.; Browning, N. Scanning transmission electron microscopy assessment of a metal-organic framework compound. Acta Crystallogr. A 2017, 73, C596, (In Proceedings of the 24th World Congress and General Assembly of the International Union of Crystallography, Hyderabad, India, 21–28 August 2017). [Google Scholar] [CrossRef]
- Platero-Prats, A.E.; League, A.B.; Bernales, V.; Ye, J.; Gallington, L.C.; Vjunov, A.; Schweitzer, N.M.; Li, Z.; Zheng, J.; Mehdi, B.L.; et al. Bridging Zirconia Nodes within a Metal–Organic Framework via Catalytic Ni-Hydroxo Clusters to Form Heterobimetallic Nanowires. J. Am. Chem. Soc. 2017, 139, 10410–10418. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.-G.; Truhlar, D.G. Computational linker design for highly crystalline metal-organic framework NU-1000. Chem. Mater. 2017, 29, 8073–8081. [Google Scholar] [CrossRef]
- Hindeleh, A.M.; Hosemann, R. Microparacrystals: The intermediate stage between crystalline and amorphous. J. Mater. Sci. 1991, 26, 5127–5133. [Google Scholar] [CrossRef]
- Webber, T.E.; Liu, W.-G.; Desai, S.P.; Lu, C.C.; Truhlar, D.G.; Penn, R.L. Role of a modulator in the synthesis of phase-pure NU-1000. Appl. Mater. Interfaces 2017, 9, 39342–39346. [Google Scholar] [CrossRef] [PubMed]
- Moeck, P.; DeStefano, P. Accurate lattice parameters from 2D periodic images for subsequent Bravais lattice type assignments. Adv. Struct. Chem. Imaging 2018, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Mevenkamp, N.; Berkels, B. Unsupervised and accurate extraction of primitive unit cells from crystal images. Lect. Notes Comput. Sci. 2015, 9358, 105–116. [Google Scholar] [CrossRef]
- Klinger, M.; Jäger, A.J. Crystallographic Tool Box (CrysTBox): Automated tools for transmission electron microscopists and crystallographers. J. Appl. Crystallogr. 2015, 48, 2012–2018. [Google Scholar] [CrossRef] [PubMed]
- Hovmöller, S. CRISP: Crystallographic image processing on a personal computer. Ultramicroscopy 1992, 41, 121–135. [Google Scholar] [CrossRef]
- Fan, H.-F.; Zhong, Z.-Y.; Zheng, C.-D.; Li, F.-H. Image processing in high-resolution electron microscopy using the direct method. I. Phase Extension. Acta Crystallogr. A 1985, 41, 163–165. [Google Scholar] [CrossRef]
- Han, F.-S.; Fan, H.-F.; Li, F.-H. Image processing in high-resolution electron microscopy using the direct method. II. Image deconvolution. Acta Crystallogr. A 1986, 42, 353–356. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Fan, H.-F.; Zheng, C.-D. Image processing in high-resolution electron microscopy using the direct method. III. Structure-factor extrapolation. Acta Crystallogr. A 1988, 44, 61–63. [Google Scholar] [CrossRef]
- Zou, X.; Hovmöller, S.; Oleynikov, P. Electron Crystallography: Electron Microscopy and Electron Diffraction; IUCr Texts on Crystallography 16; Oxford University Press: Oxford, UK, 2011; ISBN 978-0-19-958020-0. [Google Scholar]
- Unit Cell Extraction. Available online: https://nmevenkamp.github.io/UnitCellExtraction/ (accessed on 5 May 2017).
- Chuprunov, E.V. Fedorov Pseudosymmetry of Crystals: Review. Crystallogr. Rep. 2007, 52, 1–11. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Akaike, H. A Bayesian analysis of the minimum AIC procedure. Ann. Inst. Stat. Math. A 1978, 30, 9–14. [Google Scholar] [CrossRef]
- Verberck, B. Symmetry-Adapted Fourier Series for the Wallpaper Groups. Symmetry 2012, 4, 379–426. [Google Scholar] [CrossRef]
- Cochran, W. The Fourier Method of Crystal-Structure Analysis. Acta Crystallogr. 1948, 1, 138–142. [Google Scholar] [CrossRef]
- Cochran, W. The Fourier Method of Crystal Structure Analysis. Nature 1948, 161, 765. [Google Scholar] [CrossRef]
- Booth, A.D. A New Fourier Refinement Technique. Nature 1948, 161, 765–766. [Google Scholar] [CrossRef]
- Cruickshank, D.W.J. The convergence of the least-squares and Fourier refinement methods. Acta Crystallogr. 1950, 3, 10–13. [Google Scholar] [CrossRef]
- Cruickshank, D.W.J. On the relations between Fourier and least-squares methods of structure determination. Acta Crystallogr. 1952, 5, 511–518. [Google Scholar] [CrossRef]
- Cruickshank, D.W.J.; Rollett, J.S. Electron-Density Errors at Special Positions. Acta Crystallogr. 1953, 6, 705–707. [Google Scholar] [CrossRef]
- Cruickshank, D.W.J. Errors in Fourier series. In Computing Methods in Crystallography; Rollett, J.S., Ed.; Pergamon Press: Oxford, UK, 1965; Chapter 14; pp. 107–111. [Google Scholar]
- Cruickshank, D.W.J. Errors in least squares methods. In Computing Methods in Crystallography; Rollett, J.S., Ed.; Pergamon Press: Oxford, UK, 1965; Chapter 14; pp. 112–116. [Google Scholar]
- Note that frieze symmetries
2mg and
2mm are disjoint in the translationengleiche sense only [35]. Since
2mm is a type II minimal non-isomorphic supergroup of
2mg, the latter group is also a type IIa maximal non-isomorphic subgroup of the former when the transformation is employed.
- Curie, P. Sur la symmétrie des phénomènes physiques: Symmétrie d’un champ électrique et d’un champ magnétique. J. Phys. 1894, 3, 393–415. (In French) [Google Scholar]
- Allen, S.M.; Thomas, E.L. The Structure of Materials; The MIT Series in Materials Science & Engineering; John Wiley & Sons Inc.: New York, NY, USA, 1999; pp. 188–189. ISBN 0-471-00082-5. [Google Scholar]
- Lombardo, G.M.; Punzo, F. False symmetry, pseudosymmetry, disorder, polymorphism and atomic displacement parameters. J. Mol. Struct. 2014, 1078, 158–164. [Google Scholar] [CrossRef]
- Online Dictionary of Crystallography of the IUCr. Available online: http://reference.iucr.org/dictionary/Noncrystallographic_symmetry (accessed on 19 May 2017).
- Nespolo, M.; Souvignier, B.; Litvin, D.B. About the definition of “noncrystallographic symmetry”. Z. Kristallogr. 2008, 223, 605–606. [Google Scholar] [CrossRef]
- Katkova, M.R.; Krutov, A.I.; Chuprunov, E.V. On pseudosymmetry in structure types. Crystallogr. Rep. 1995, 40, 62–65. [Google Scholar]
- Mackay, A.L. The Development of Electron Crystallography. Crystallogr. Rep. 2001, 46, 901–908. [Google Scholar] [CrossRef]
- Moeck, P.; Qin, W.; Fraundorf, P.B. Towards 3D image-based nanocrystallography by means of transmission electron goniometry. Mater. Res. Soc. Symp. Proc. 2005, 839, P4.3.1–P4.3.6. [Google Scholar] [CrossRef]
- Fraundorf, P.; Qin, W.; Moeck, P.; Mandell, E. Making sense of nanocrystal lattice fringes. J. Appl. Phys. 2005, 98, 114308. [Google Scholar] [CrossRef]
- Moeck, P.; Fraundorf, P. Transmission electron goniometry and its relation to electron tomography for materials science applications. arXiv, 2006; arXiv:cond-mat/0611345. [Google Scholar]
- Merritt, E.A. To B or not to B: A question of resolution? Acta Crystallogr. D 2012, 68, 468–477. [Google Scholar] [CrossRef] [PubMed]
- Krebs, F.C. How the R factor changes as the molecules become larger. J. Appl. Crystallogr. 2000, 33, 392–393. [Google Scholar] [CrossRef]
- Wondratschek, H.; Müller, U. (Eds.) International Tables for Crystallography, Volume A1, Symmetry Relations between Space Groups, 1st ed.; Kluwer Academic Publishers: Dortrecht, The Netherlands; Boston, MA, USA; London, UK, 2004; ISBN 1-4020-2355-3. [Google Scholar]
- Authier, A.; Chapius, G. (Eds.) Online Dictionary of Crystallography of the IUCr. In A Little Dictionary of Crystallography; International Union of Crystallography: Chester, UK, 2014; pp. 167–168. Available online: http://reference.iucr.org/dictionary/R_factor (accessed on 31 December 2017).
- Müller, U. Symmetry Relationships between Crystal Structures, Applications of Crystallographic Group Theory in Crystal Chemistry; IUCr Texts on Crystallography 18; Oxford University Press: Oxford, UK, 2013; ISBN 978-0-19-966995-0. [Google Scholar]
- Cruickshank, D.W.J.; Lynton, H.; Barclay, G.A. A reinvestigation of the crystal structure of thortveitite Sc2Si2O7. Acta Crystallogr. 1962, 15, 491–498. [Google Scholar] [CrossRef]
- Kleywegt, G.J.; Hoier, H.; Jones, T.A. A re-evaluation of the crystal structure of chloromuconate cycloisomerase. Acta Crystallogr. 1996, 52, 858–863. [Google Scholar] [CrossRef] [PubMed]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Ferraris, G.; Gilli, G.; Zanotti, G.; Catti, M. Fundamentals of Crystallography, 2nd ed.; IUCr Texts on Crystallography 7; Oxford University Press: Oxford, UK, 2002; ISBN 0-19-850958-8. [Google Scholar]
- Shoemaker, D.P. Well-behaved crystal structure determinations. In Critical Evaluation of Chemical and Physical Structural Information, Proceedings of a Conference with the Same Name at Dartmouth College, Hanover, New Hampshire, 24-29 June 1973; Lide, D.R., Paul, M.A., Eds.; National Academy of Sciences: Washington, DC, USA, 1974; pp. 157–185. ISBN 0-309-02146-4. [Google Scholar]
- Taper, M.L.; Lele, S.R. (Eds.) The Nature of Scientific Evidence, Statistical, Philosophical, and Empirical Considerations; Chicago University Press: Chicago, IL, USA, 2004; ISBN 0-226-78957-8. [Google Scholar]
- Hodges, J.L., Jr.; Lehmann, E.L. Testing the approximate validity of statistical hypotheses. J. R. Stat. Soc. Ser. B 1954, 16, 261–268. [Google Scholar]
- Serlin, R.C.; Lapsley, D.K. Rationality in psychological research: The good-enough principle. Am. Psychol. 1985, 40, 73–83. [Google Scholar] [CrossRef]
- Lakatos, I. The Methodology of Scientific Research Programs; Philosophical Papers; Cambridge University Press: Cambridge, UK, 1980; Volume 1, ISBN 0521280311. [Google Scholar]
- Rao, C.R.; Lovric, M.M. Testing Point Null Hypothesis of a Normal Mean and the Truth: 21st Century Perspective. J. Mod. Appl. Stat. Methods 2016, 15, 2–21. [Google Scholar] [CrossRef]
- Zumbo, B.D.; Kroc, E. Some Remarks on Rao and Lovric’s ‘Testing Point Null Hypothesis of a Normal Mean and the Truth: 21st Century Perspective’. J. Mod. Appl. Stat. Methods 2016, 15, 33–40. [Google Scholar] [CrossRef]
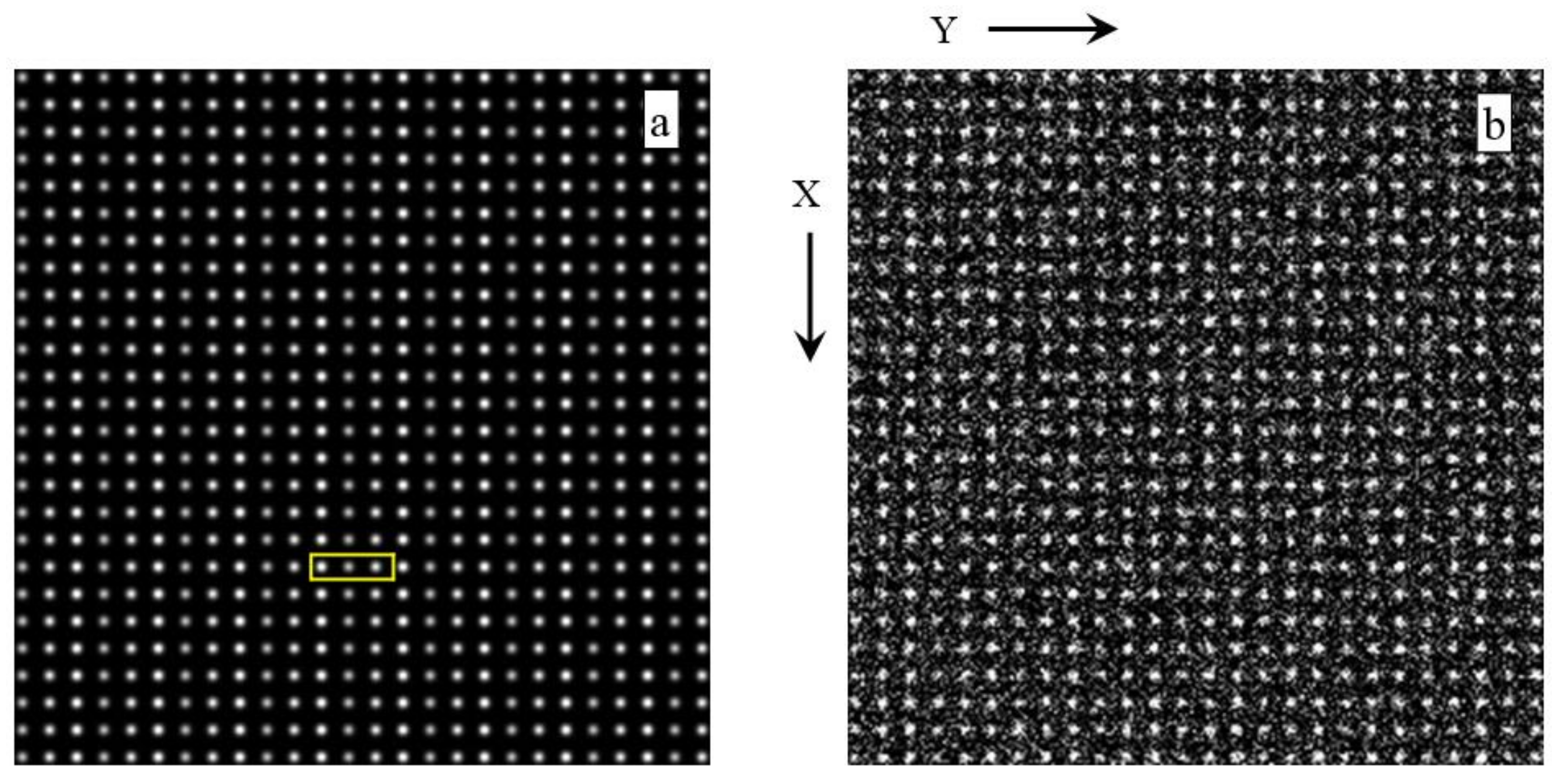
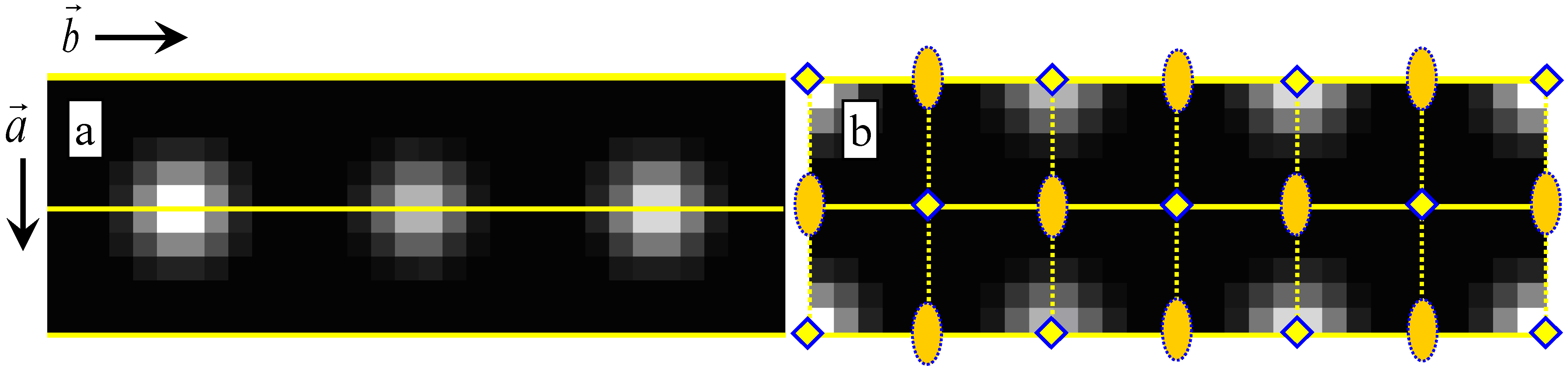
| Algorithm’s Number in the Final Reference Section | Algorithm’s Letter Reference in this Review |
|---|---|
| [115] | A |
| [116] | B |
| [117] | C |
| Algorithm’s Reference Letter | a/b | γ in ° | Unit Cell Area in Square Pixels |
|---|---|---|---|
| A | 0.333 ± 0.06 | 90.0 ± 0.4 | 300.0 ± 2.0 |
| B | 1.004 ± 0.01 | 90.0 ± 0.05 | 99.4 ± 1.0 |
| C | 0.998 ± 0.01 | 90.0 ± 0.05 | 99.8 ± 1.0 |
| Algorithm’s Reference Letter | a/b | γ in ° | Unit Cell Area in Square Pixels |
|---|---|---|---|
| B | 0.335 ± 0.01 | 90.0 ± 0.05 | 298.2 ± 3.0 |
| C | 0.333 ± 0.02 | 90.0 ± 0.05 | 300.0 ± 2.0 |
| Algorithm’s Reference Letter | a/b | γ in ° | Unit Cell Area in Square Pixels |
|---|---|---|---|
| A | 1.414 ± 0.07 | 135.8 ± 0.6 | 98.6 ± 1.5 |
| B | 0.995 ± 0.01 | 90.2 ± 0.05 | 99.1 ± 1.0 |
| C | 1.000 ± 0.01 | 90.0 ± 0.05 | 100.0 ± 1.0 |
| Algorithm’s Reference Letter | a/b | γ in ° | Unit Cell Area in Square Pixels |
|---|---|---|---|
| B | 0.332 ± 0.01 | 90.2 ± 0.05 | 297.3 ± 3.0 |
| C | 0.333 ± 0.02 | 90.0 ± 0.05 | 300.0 ± 2.0 |
| Parallelogram | Rectangle | General Rhombus | Square | Hexagonal Rhombus |
|---|---|---|---|---|
| 2 | 3 | 3 | 4 | 4 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moeck, P. Towards Generalized Noise-Level Dependent Crystallographic Symmetry Classifications of More or Less Periodic Crystal Patterns. Symmetry 2018, 10, 133. https://doi.org/10.3390/sym10050133
Moeck P. Towards Generalized Noise-Level Dependent Crystallographic Symmetry Classifications of More or Less Periodic Crystal Patterns. Symmetry. 2018; 10(5):133. https://doi.org/10.3390/sym10050133
Chicago/Turabian StyleMoeck, Peter. 2018. "Towards Generalized Noise-Level Dependent Crystallographic Symmetry Classifications of More or Less Periodic Crystal Patterns" Symmetry 10, no. 5: 133. https://doi.org/10.3390/sym10050133
APA StyleMoeck, P. (2018). Towards Generalized Noise-Level Dependent Crystallographic Symmetry Classifications of More or Less Periodic Crystal Patterns. Symmetry, 10(5), 133. https://doi.org/10.3390/sym10050133





