A Novel Multimodal Biometrics Recognition Model Based on Stacked ELM and CCA Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Related Work
2.1.1. The ELM Method
| Algorithm 1. The extreme learning machine (ELM) algorithm. |
| Input: training set , activation function and hidden-layer node number n |
| Output: the output weight β |
| Step 1: Randomly assign input weight and bias |
| Step 2: Calculate the hidden-layer output matrix . |
| Step 3: Calculate the output weight β. where |
2.1.2. The CCA Method
| Algorithm 2. The canonical correlation analysis (CCA) algorithm. |
| Input: |
| Output: —the correlation coefficient of output: X, Y; |
| Step 1: calculate the variance of X and Y: and covariance of X and Y, and Y and X: ; |
| Step 2: calculate the matrix ; |
| Step 3: make singular value decomposition for matrix M, obtain the largest singular value and its corresponding left and right singular vectors and ; |
| Step 4: calculate the linear coefficient vectors of X and Y: ; |
2.2. Proposed Method
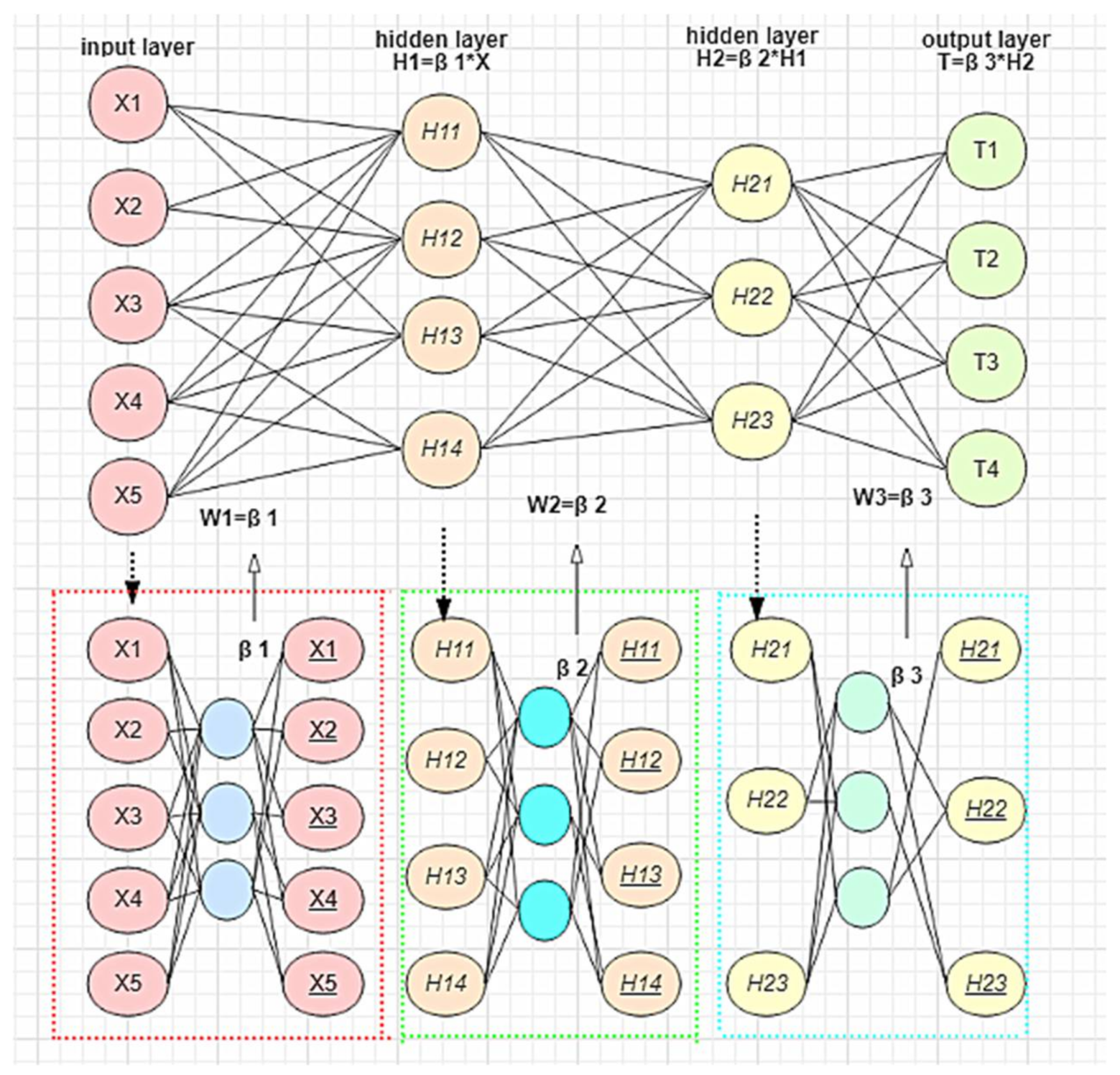
2.2.1. The Stacked ELM Model
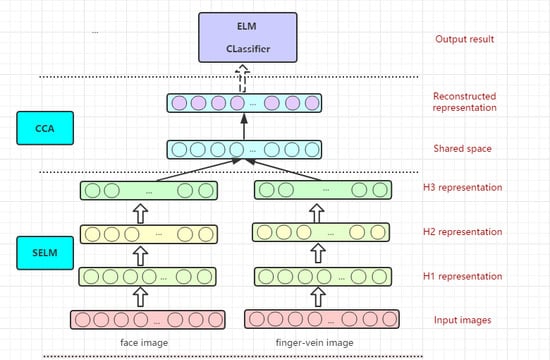
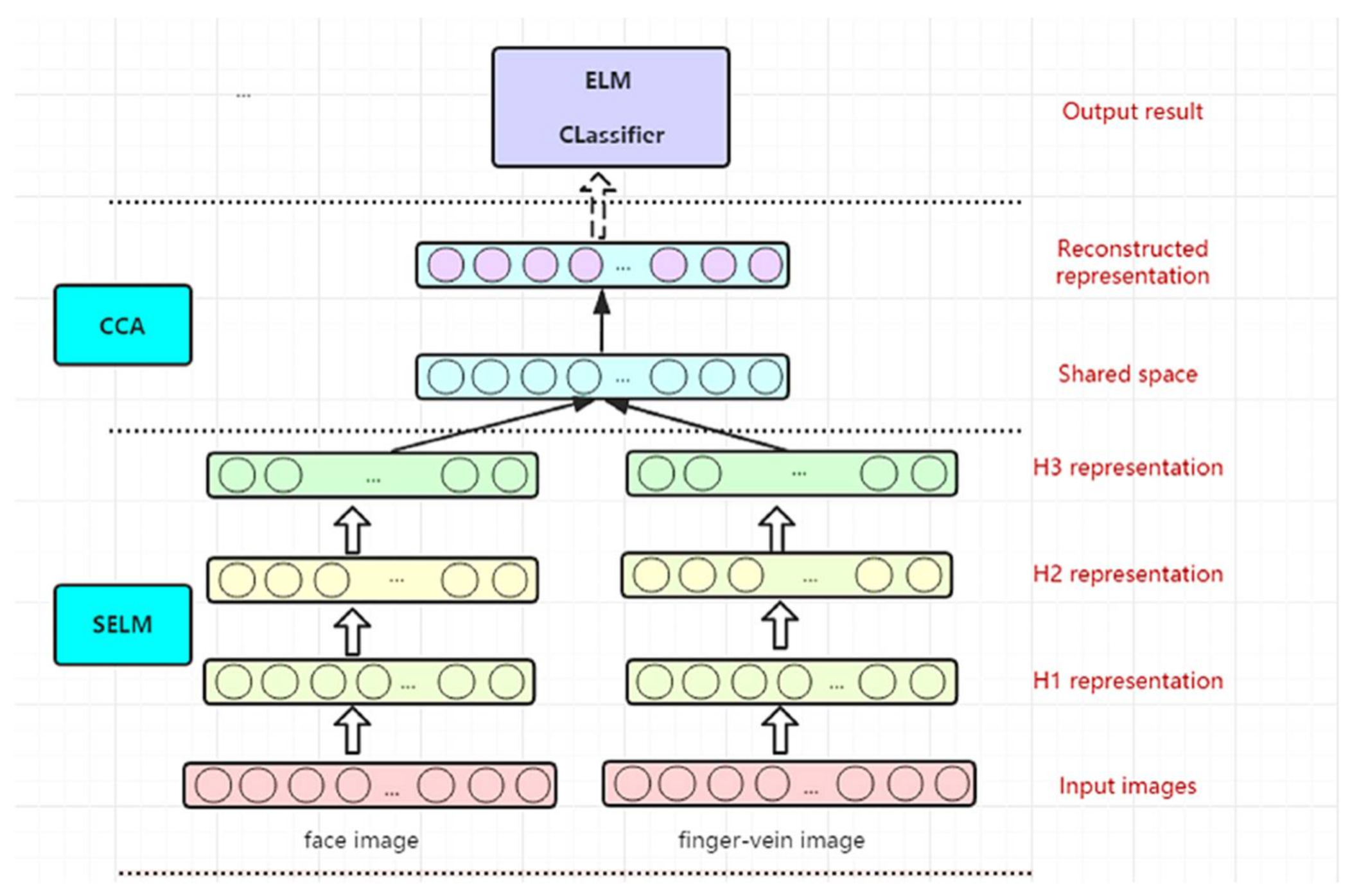
2.2.2. The S-E-C Model for Multi-Biometrics Recognition
| Algorithm 3. The S-E-C algorithm description. |
| Input: face feature matrix , finger-vein face vector and label matrix . |
| Output: weight matrix |
| Initialize: choose the depth of the model for each modality and hidden-layer node . |
| for j = 1 to 2 do |
| for i = 1 to k do |
| (1) Randomly generating hidden-layer input weighting matrix and Bias matrix ; |
| (2) Calculating hidden-layer output: ; |
| (3) Computing using Equations (3) or (4) under the condition |
| ; |
| (4) calculating , ; |
| (5) update the hidden-layer output: ; |
| end for |
| end for |
| Canonical correlation analysis: |
| (1) Calculate the variance of and : , and |
| (2) Calculate the matrix M: ; |
| (3) Make singular value decomposition for matrix M, obtain the largest singular value and its corresponding left and right singular vectors and : ; |
| (4) Calculate the linear coefficient vectors of , : ; |
| (5) Construct feature representation: . |
| Supervised training and testing: |
| Applying simple ELM to a new dataset |
| Computing using Equation (3) or (4) under the condition : |
3. Results
3.1. Database
3.1.1. The Olivetti Research Laboratory (ORL) Face Dataset
3.1.2. The Face Recognition Technology (FERET) Face Dataset
3.1.3. The MMCBNU-6000 Finger-Vein Dataset
- (a)
- ORL+MMCBNU: total of 400 groups with each group taking 10 face images and 60 finger-vein images;
- (b)
- FERET+MMCBNU: total of 1000 groups with each group taking 7 face images and 60 finger-vein images.
3.2. Experimental Environment
3.3. Experiment Results and Analysis
3.3.1. Ability to Represent Hidden-Layer Features of Stacked ELM
3.3.2. Comparison of the Classification Effect of the CCA Fusion Method
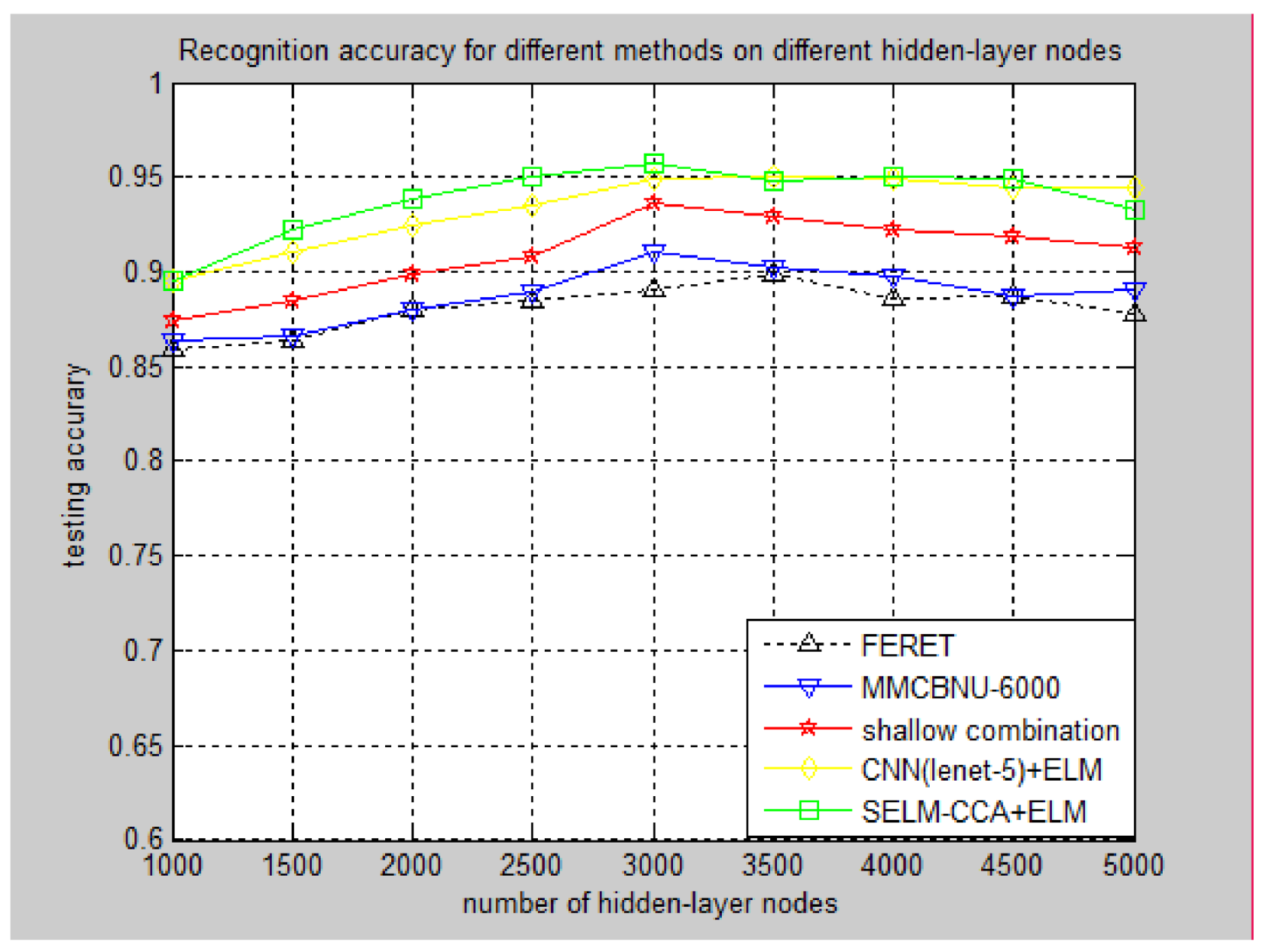
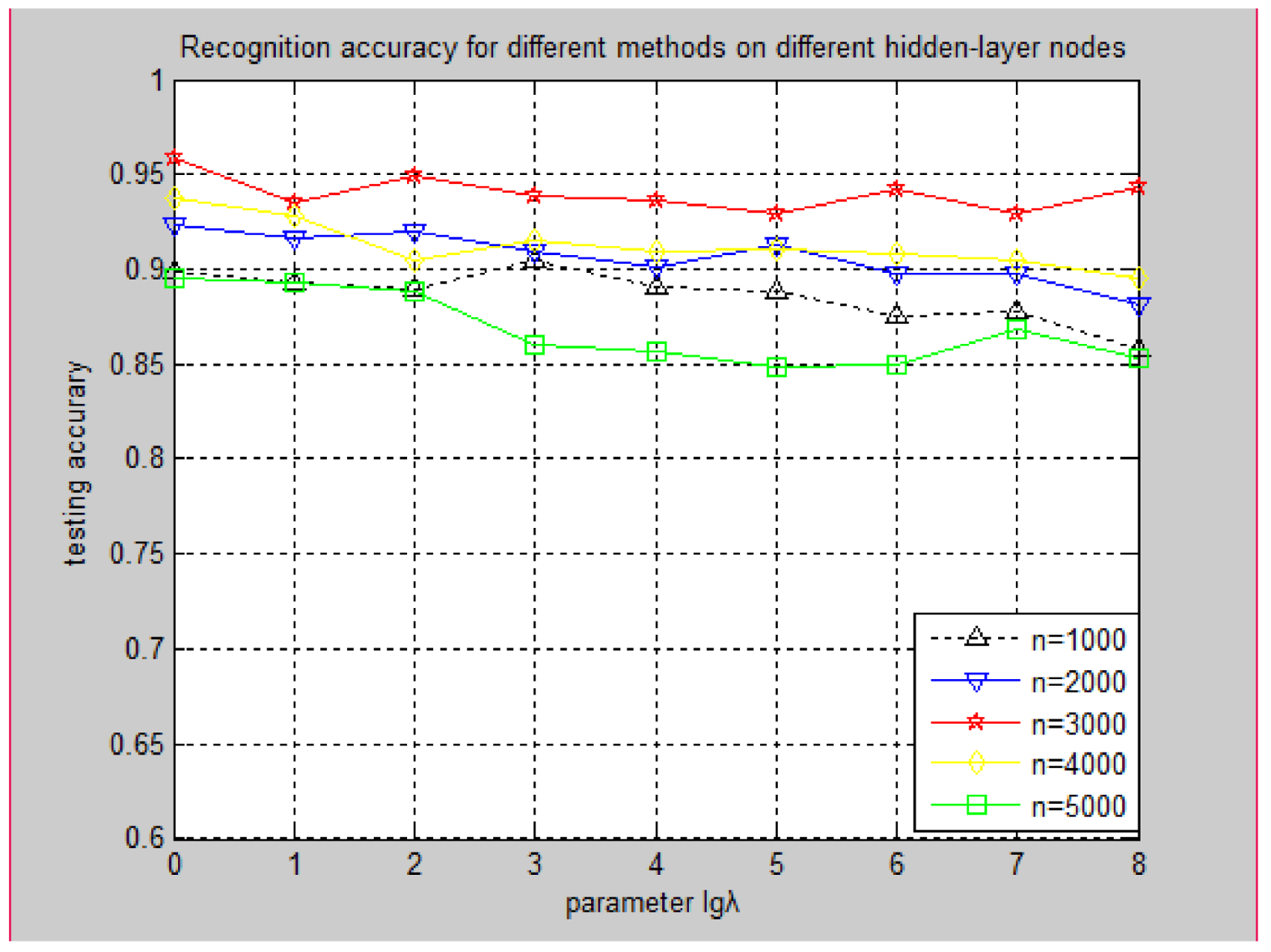
3.3.3. Experiment Performance for Different Methods on Different Hidden-Layer Nodes
3.3.4. Effect of Parameters for Recognition Accuracy
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Parkavi, R.; Babu, K.R.C.; Kumar, J.A. Multimodal Biometrics for user authentication. In Proceedings of the International Conference on Intelligent Systems and Control, Coimbatore, India, 5–6 January 2017; pp. 501–505. [Google Scholar]
- Oquab, M.; Bottou, L.; Laptev, I.; Sivic, J. Learning and Transferring Mid-Level Image Representations using Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1717–1724. [Google Scholar]
- Liu, Y.; Feng, X.; Zhou, Z. Multimodal video classification with stacked contractive auto-encoders. Signal Process. 2016, 120, 761–766. [Google Scholar] [CrossRef]
- Ngiam, J.; Khosla, A.; Kim, M. Multimodal deep learning. In Proceedings of the 28th International Conference on International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 689–696. [Google Scholar]
- Srivastava, N.; Salakhutdinov, R. Learning representations for multi-modal data with deep belief nets. In Proceedings of the International Conference on Machine Learning Workshop, Edinburgh, UK, 26 June–1 July 2012. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neural Comput. 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Paul, P.P.; Gavrilova, M.L.; Alhajj, R. Decision Fusion for Multimodal Biometrics Using Social Network Analysis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 44, 1522–1533. [Google Scholar] [CrossRef]
- Haghighat, M.; Abdel-Mottaleb, M.; Alhalabi, W. Discriminant correlation analysis of feature level fusion with application to multimodal biometrics. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 20–25 March 2016; pp. 1984–1996. [Google Scholar]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme learning machines: A survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Xie, Z.; Xu, K.; Shan, W. Projective Feature Learning for 3D Shapes with Multi-View Depth Images. In Computer Graphics Forum; John Wiley & Sons, Ltd.: Chichester, UK, 2015; Volume 34, pp. 1–11. [Google Scholar]
- Akusok, A.; Bjork, K.M.; Miche, Y. High-Performance Extreme Learning Machines: A Complete Toolbox for Big Data Applications. IEEE Access 2015, 3, 1011–1025. [Google Scholar] [CrossRef]
- Hoteling, H. Relations between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Borga, M. Canonical Correlation a Tutorial. 2011. Available online: https://web.cs.hacettepe.edu.tr/~aykut/classes/spring2013/bil682/supplemental/CCA_tutorial.pdf (accessed on 10 February 2018).
- Hardoon, D.R.; Szedmak, S.; Shawe-Taylor, J. Canonical correlation analysis: An overview with application to learning methods. Neural Comput. 2014, 16, 2639–2664. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Sun, Q.; Yang, J. MRCCA: A Novel CCA Based Method and Its Application in Feature Extraction and Fusion for Matrix Data. Appl. Soft Comput. 2017, 62, 45–56. [Google Scholar] [CrossRef]
- Yang, X.; Liu, W.; Tao, D. Canonical Correlation Analysis Networks for Two-view Image Recognition. Inf. Sci. 2017, 385, 338–352. [Google Scholar] [CrossRef]
- Ouyang, W.; Chu, X.; Wang, X. Multi-source deep learning for human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2329–2336. [Google Scholar]




| Experiment Methods | ORL | FERET | MMCBNU | |||
|---|---|---|---|---|---|---|
| Time (s) | Accuracy | Time (s) | Accuracy | Time (s) | Accuracy | |
| BP | 8.2459 | 88.45% | 9.9887 | 89.96% | 12.7864 | 91.73% |
| SVM | 6.7680 | 90.32% | 8.7869 | 91.92% | 10.3670 | 93.02% |
| ELM | 1.3786 | 89.38% | 2.0679 | 90.87% | 2.8568 | 92.62% |
| CNN (lenet5) | 28.8769 | 92.48% | 34.8979 | 93.06% | 45.3478 | 94.84% |
| SAE | 36.7842 | 93.64% | 42.2985 | 94.46% | 69.3587 | 95.24% |
| DBN | 30.3478 | 90.82% | 38.8876 | 92.34% | 60.5874 | 94.48% |
| Stacked ELM (H3) | 10.2714 | 93.62% | 14.3224 | 94.58% | 17.6368 | 95.58% |
| Biometrics | Performance (Accuracy %) |
|---|---|
| ORL | 89.38% |
| FERET | 89.87% |
| MMCBNU-6000 | 92.62% |
| ORL+MMCBNU (cascade) | 93.51% |
| FERET+MMCBNU (cascade) | 93.67% |
| ORL+MMCBNU (CCA) | 94.46% |
| FERET+MMCBNU (CCA) | 94.97% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Sun, W.; Liu, N.; Chen, Y.; Wang, Y.; Han, S. A Novel Multimodal Biometrics Recognition Model Based on Stacked ELM and CCA Methods. Symmetry 2018, 10, 96. https://doi.org/10.3390/sym10040096
Yang J, Sun W, Liu N, Chen Y, Wang Y, Han S. A Novel Multimodal Biometrics Recognition Model Based on Stacked ELM and CCA Methods. Symmetry. 2018; 10(4):96. https://doi.org/10.3390/sym10040096
Chicago/Turabian StyleYang, Jucheng, Wenhui Sun, Na Liu, Yarui Chen, Yuan Wang, and Shujie Han. 2018. "A Novel Multimodal Biometrics Recognition Model Based on Stacked ELM and CCA Methods" Symmetry 10, no. 4: 96. https://doi.org/10.3390/sym10040096
APA StyleYang, J., Sun, W., Liu, N., Chen, Y., Wang, Y., & Han, S. (2018). A Novel Multimodal Biometrics Recognition Model Based on Stacked ELM and CCA Methods. Symmetry, 10(4), 96. https://doi.org/10.3390/sym10040096