Abstract
Nowadays, 3D printing is widely used in many areas of life. This leads to 3D printing models often being used illegally without any payment to the original providers. Therefore, providers need a solution to identify and protect the copyright of 3D printing. This paper presents a novel watermarking method for the copyright protection of 3D printing based on the Menger facet curvature and K-mean clustering. The facets of the 3D printing model are classified into groups based on the value of Menger curvature and the K-mean clustering, and the mean Menger curvature of each group will then be computed for embedding the watermark data. The watermark data are embedded into the groups of facets by changing the mean Menger curvature of each group according to the bit of watermark data. In each group, we select a facet that has the Menger curvature closest to the changed mean Menger curvature, and we then transform the vertices of the selected facet according to the changed Menger curvature for the watermarked 3D printing model generation. Watermark data are extracted from 3D-printed objects, which are printed from the watermarked 3D printing models by the 3D printer. Experimental results after embedding the watermark verified that the proposed method is invisible and robust to geometric attacks such as rotation, scaling and translation. In experiments with an XYZ Printing Pro 3D printer and 3D scanner, the accuracy and performance of the proposed method was higher than the two previous methods in the 3D printing watermarking domain. The proposed method provides a better solution for the copyright protection of 3D printing.
1. Introduction
Three-dimensional (3D) printing, also known as additive manufacturing, makes directly physical solid objects from digital models by the layer adding process [1,2]. Due to the flexibility and ease of production, 3D printing is applied to many areas, such as healthcare systems, industry, aerospace and automotive production [3,4,5]. Due to the fact that the benefit of 3D printing is great, the products of 3D printing are widely used. However, the products of 3D printing are often illegally used in many cases. This means manufacturers cannot protect their copyright and cannot receive fees from users. Besides, manufacturers also desire to track the ownership of their products in commercial transactions. Thus, a watermarking method is suitable and necessary to protect the ownership and copyright of 3D printing [6].
Previously, there were many watermarking methods for 3D models that have been extensively researched. 3D watermarking schemes generally focus on both the geospatial and frequency domains [7,8,9,10,11,12]. Overall, the main content of 3D model watermarking is to embed watermark data into the 3D model to obtain the watermarked 3D model. The watermark data are then extracted from the watermarked 3D model. This means 3D model watermarking methods only extract the embedded watermark from the watermarked 3D models, which is not the output of 3D printing, while the target of 3D printing watermarking is to extract the embedded watermark from the 3D-printed object of the watermarked 3D printing model. Thus, these methods could not extract the embedded watermark from physical 3D-printed objects. Consequently, the watermarking methods for the 3D model could not be applied to the purpose of 3D printing watermarking because the output of 3D printing is a physical 3D-printed object. Moreover, the accuracy of current watermarking methods for 3D printing [13,14] is very low and not flexible. There is even a method [14] that requires a complex system for the experiments. Therefore, the watermarking methods for 3D printing should have high accuracy, be flexible and reduce the complexity of the experiments.
To replace the unsuitability of 3D model watermarking methods for the purpose of 3D printing watermarking and to respond to the risks of the previous watermarking methods for 3D printing, we would like to propose a novel watermarking method for 3D printing in this paper. The main content of the proposed method is to classify the facets of the 3D printing model into groups based on the Menger facet curvature before embedding watermark data. The watermark data are embedded by changing the value of the mean Menger curvature of each group based on the reference of a special value. After the watermark embedding process, the watermarked 3D printing model will be used to print the physical 3D object by a 3D printer. The watermark data are then extracted from the scanned 3D triangle mesh of the 3D-printed object. The proposed method is valid for the copyright protection of 3D printing, because it could extract the embedded watermark data into a 3D printing model from a physical 3D-printed object. That is what 3D model watermarking methods could not do. Moreover, the proposed method is more flexible than the two previously proposed methods for 3D printing watermarking because the length of the watermark bits is flexible, while the length of watermark bits in the two previous methods was fixed. It does not require a complex system, as did one of the previous method [14]. Finally, the accuracy of the proposed method is also higher than the two previously proposed methods. To clarify the proposed method, in Section 2, we look into previous watermarking techniques for the 3D model and 3D printing and explain the relation of the Menger curvature to the proposed method. In Section 3, we show the proposed method in detail. Experimental results and the evaluation of the proposed method will be shown in Section 4. Section 5 provides the conclusion.
2. Related Works
2.1. 3D Model Watermarking
Currently, the watermarking schemes for the 3D model are implemented both in the geospatial domain and the frequency domain. In the spatial domain, watermarking methods embed watermark data in the 3D model by modifying the value of the vertices or geometric features of the 3D model, such as the length or area. In the frequency domain, watermarking schemes embed watermark data in the spectrum coefficients of the discrete Fourier transform, or discrete wavelet transform, or discrete cosine transform of a sequence of vertices of the 3D model. The embedded watermark is then extracted from the watermarked 3D models. This means that this work is not related to 3D printing, because watermark data are extracted from a virtual 3D model. while the output of 3D printing is a physical 3D-printed object. Therefore, the watermarking schemes for 3D models are not suitable for the purpose of 3D printing watermarking.
2.2. 3D Printing Watermarking
Until now, there have been two methods proposed and related to 3D printing watermarking. Yamazaki et al. [13] proposed a method of extracting watermark from physical 3D-printed objects that is created from 3D mesh data. The watermark is embedded into the spread spectrum of 3D meshes and then extracted from physical 3D-printed objects via the scanned 3D triangle meshes of 3D-printed objects. This method has low accuracy because the scanned 3D triangle meshes have many errors in the 3D scanning process, and after transformation to the frequency domain, the spread spectrum of 3D meshes was changed greatly. Moreover, the length of the embedded watermark bits is fixed at 256 bits. Therefore, this method is not flexible. Suzuki et al. [14] proposed a technique to protect the copyright of the digital content for 3D printers. This method considers the copyright information as a watermark and inserts the copyright information into solid objects in the 3D printing process. This technique requires a complex hardware system of halogen and laser lights for the watermark embedding process. This technique is also not flexible and is expensive. Moreover, this method did not show how to extract the embedded watermark from 3D-printed objects. Previously, we (Giao et al. [15]) introduced a simple idea for 3D printing watermarking. However, in that paper, we just mentioned the main concept of the idea for 3D printing watermarking based on Menger curvature and experimented on our idea based on a virtual environment. We only tested the watermark embedding ability into Menger curvature and evaluated the invisibility of the proposed method in that paper. We did not experiment with a 3D printer or 3D scanner and evaluated the robustness and performance of the proposed method. In this paper, we improved our idea by experimenting with a 3D printer and 3D scanners, applying a correction method to construct the scanned 3D models from 3D-printed objects. Finally, we analyze, evaluate and compare the robustness and performance of the proposed method to the conventional works and two previous methods of 3D printing watermarking.
2.3. Menger Curvature-Based 3D Printing Watermarking
The input of 3D printing is a 3D triangle mesh [16,17], which is designed by CAD software. A 3D triangle mesh contains a set of facets. Each facet includes three vertices and a normal vector (see Figure 1a). Each vertex is presented by three coordinates x, y and z. The Menger curvature is the curvature of a triple of points in n-dimensional Euclidean space [18,19]; thus, the Menger curvature of a facet is computed by Equation (1) as below:
with the Menger facet curvature, A the area of the facet, R the circumscribed circle radius of the facet and a, b and c the edges of the facet, respectively (see Figure 1b). Based on Equation (1), we can conclude that the Menger curvature of a facet is dependent on the circumscribed circle radius of that facet or the length of the edges of that facet.
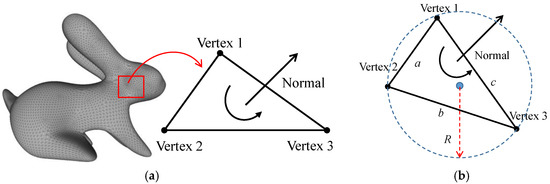
Figure 1.
(a) Structure of a facet and (b) circumscribed circle of a facet.
Due to the fact that the output of 3D printing is a physical 3D-printed object, to extract the embedded watermark, we have to extract them from the scanned 3D triangle mesh of physical 3D-printed objects after the 3D scanning and reconstructing process. Because the 3D scanning process is affected by noise, the coordinates of the vertices of each triangle in the scanned 3D triangle mesh are not the same as the coordinates of the vertices in the original 3D triangle mesh, but the overall shape of the 3D triangle mesh is not changed. This leads to the mean Menger curvature of each group remining unchanged or being changed very little. Moreover, the Menger curvature of a facet is robust to geometric attacks, such as rotation and translation, because if we rotate or translate a facet, the area or length of the edges of that facet is not changed. Therefore, we used the Menger facet curvature for the purpose of 3D printing watermarking.
3. The Proposed Algorithm
3.1. Overview
The proposed method is described in Figure 2. Facets are firstly extracted from the 3D printing model (3D triangle mesh) to compute their Menger curvatures. These facets are then classified into groups by the K-mean clustering algorithm [20] based on the value of the Menger curvatures. The watermark key is the number of groups into which we want to classify facets. This means the watermark key is secret and used to determine the number of groups and the length of watermark bits that are generated to embed into the 3D triangle mesh. The watermark key is defined or chosen by the users. The watermark key is re-used in the watermark extraction process (see Figure 2). With each group of facets, we compute the mean Menger curvature of that group and then embed a watermark bit into that mean Menger curvature by changing the value of mean Menger curvature based on the reference of a special value. Finally, the watermarked 3D triangle mesh is generated according to the watermarked mean Menger curvatures. The watermarked 3D triangle mesh is the input of a 3D printer. After the 3D printing process, the 3D-printed object will be used for the 3D scanning and reconstruction process to obtain the scanned 3D triangle mesh. The facets of the scanned 3D triangle mesh are then extracted to compute their Menger curvatures. Next, the facets of the scanned 3D triangle mesh are also divided into groups based on the value of Menger curvatures. After the facet clustering step, we have to calculate the mean Menger curvature of each group. The watermark data will be extracted from the mean Menger curvature of each group. The detailed watermark embedding and extraction processes are described in Section 3.2 and Section 3.3.
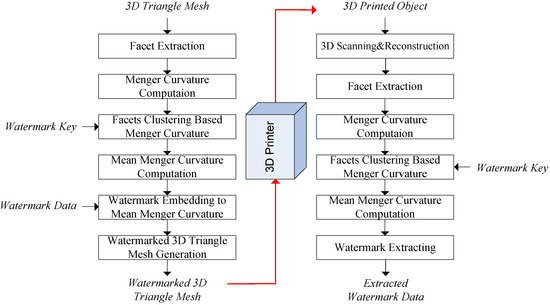
Figure 2.
The proposed algorithm.
3.2. Watermark Embedding
A 3D printing model (3D triangle mesh) contains a number of facets, . Here, |M| is the number of facets in a 3D triangle mesh M, and is the facet. Each facet contains three vertices (three points), and a normal vector . The Menger curvature of each facet is computed by its vertices and corresponding area as shown in Equation (2).
Therein, is the area of the facet. The |M| facets in the 3D triangle mesh M are divided into G groups; based on the value of the Menger curvature. Figure 3 shows the result of the facet clustering of the bunny triangle mesh based on Menger curvature. Facets in the same group will have the same color.
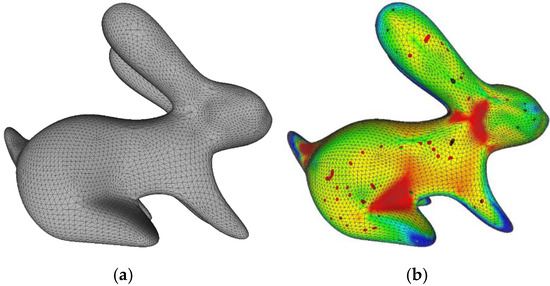
Figure 3.
(a) Original bunny triangle mesh and (b) facet clustering based on Menger curvature.
After classifying |M| facets into G groups, we find the maximum Menger curvature and minimum Menger curvature of each group and calculate the mean Menger curvature of each group. Assume that are the maximum Menger curvature, minimum Menger curvature and mean Menger curvature of the group , respectively. The mean Menger curvature of the group is the average value of all Menger curvatures in the group and calculated as shown in Equation (3) with the number of facets in the group .
Next, we define as the average value of as shown in Equation (4). is the special value mentioned in Section 3.1 and used to change the value of the mean Menger curvature
Each group is embedded in a watermark bit by changing the value of the mean Menger curvature of the group on the reference of the average value . This means if , will be transformed into that is smaller than . If , will be transformed into that is greater than :
To satisfy the above embedding condition, the watermarked mean curvature will be changed as shown in Equations (6) and (7).
Figure 4 shows the change of the mean Menger curvature of the group to according to the watermark bit . The mean Menger curvature is represented by the blue point. The watermarked mean Menger curvature is represented by the red point. When will become less than if it is equal or greater than . When will become greater than if it is less than .
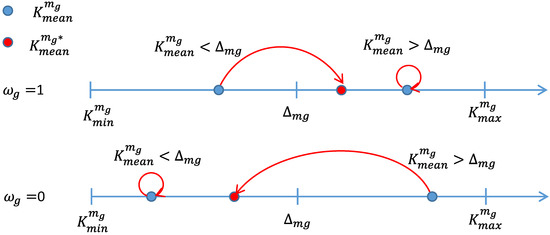
Figure 4.
Watermark bit embedding by changing the mean Menger curvature.
After embedding the watermark bit into the mean Menger curvature of the group , we compute the change rate between the watermarked mean Menger curvature and the reference value as shown in Equation (8):
The change rate is used to generate the watermarked 3D triangle mesh in the watermarked 3D triangle mesh generation process according to the watermarked mean Menger curvature of each group . To generate the watermarked 3D triangle mesh, in each group we select a facet that has the Menger curvature value closest to the watermarked mean Menger curvature , and change the selected facet according to the change rate . Assume that, in the group , we found that the facet , has the Menger curvature value closest to the watermarked mean Menger curvature , so the facet will be transformed into the facet in the watermarked 3D triangle mesh as shown in Equation (9). Therein, are three vertices of the facet .
3.3. Watermark Extracting
The watermark extraction process is similar to the embedding process. Firstly, we also extract facets from the scanned 3D triangle mesh M’ to compute the Menger facet curvatures. After that, we classify them into groups by the K-mean clustering algorithm based on the value of Menger curvatures. The watermark key is re-used for the clustering process. For each group , we find the maximum Menger curvature and the minimum Menger curvature and calculate the mean Menger curvature similar to Equation (3). is the average value of . Finally, the watermark bit can be extracted by comparing the mean Menger curvature with the average value as described in Equation (10).
4. Experimental Results and Analysis
We experimented on the proposed method with test models as shown in Figure 5. The format of the 3D triangle mesh is STL and VRML files. We used the K-mean algorithm to cluster facets into groups. The watermark key is used to determine the number of groups and defined by the user. Each model will correspond to a watermark key. These watermark keys are then stored in a database file and will be queried in the watermark extraction as shown in Figure 2. The number of groups must always be smaller than half the number of facets. To satisfy the above condition, in our experiments, we defined the number of groups G (the watermark key) according to the number of facets |M| as shown in Equation (11).
with the number of digits of |M|. For example, if , then . To evaluate the proposed method, we evaluate the invisibility, robustness and performance of the proposed method. Section 4.1 shows the invisibility evaluation of the proposed method. The robustness of the proposed method is described in Section 4.2, and the performance of the proposed method is shown in Section 4.3.
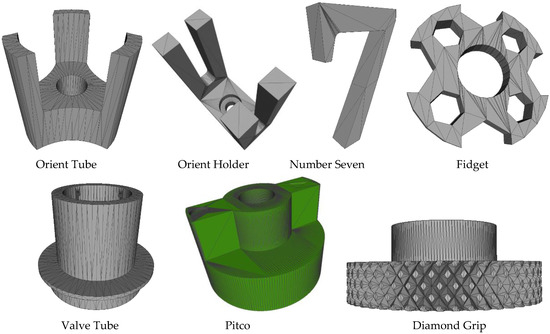

Figure 5.
Test 3D triangle meshes.
4.1. Invisibility Evaluation
We embedded differential watermarks into test models according to the number of groups. This means each test model will be embedded into a watermark where the length of the watermark bits is equal to the number of groups corresponding to that model. Each watermark is randomly generated. In order to evaluate the invisibility of the proposed method, we computed the mean distance error between the original 3D triangle mesh and the watermarked 3D triangle mesh. The mean distance error is calculated by Equation (12). Therein, v, v’ are the vertices of the original 3D triangle mesh and the vertices of the watermarked 3D triangle mesh, respectively.
The computation result of the mean distance error between the watermarked 3D triangle mesh and the original 3D triangle mesh for test models in Figure 5 is shown in Table 1. Overall, the mean distance error between the watermarked 3D triangle mesh and the original 3D triangle mesh is very small. With the test models in Figure 5 divided into 19–887 groups according to the number of facets, the mean distance error is formed from 2.4931 × 10−6 to 4.113 × 10−6. This proves that the difference between the watermarked 3D triangle mesh and the original 3D triangle mesh is very small. Therefore, it proves that the invisibility of the proposed method is very high. Based on Equation (12), we concluded that the mean distance error is dependent on the number of watermarked vertices and the number of vertices. The number of watermarked vertices is dependent on the number of groups and the mean Menger curvature of each group. Therefore, we concluded that the mean distance error (the invisibility of the proposed method) is dependent on the number of groups. From Table 1, we concluded that the mean distance error is decreased according to the number of groups. Figure 6 shows the mean distance error according to the number of groups.

Table 1.
Mean distance error.
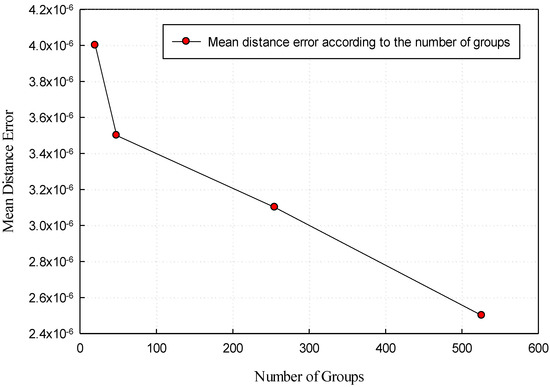
Figure 6.
Mean distance error according to the number of groups.
4.2. Robustness Evaluation and Analysis
The security of watermarking methods is due to their robustness. If a watermarking method is robust, it is difficult to remove the watermark embedded into objects. This means the original provider easily protects the copyright of their products. To evaluate the robustness of the proposed method, we would like to analyze two aspects. The first aspect is the robustness of the watermarked 3D triangle meshes with geometric attacks, such as rotation, translation and scaling. As we explained in Section 2.3, the Menger curvature of a facet is robust to rotation and translation because these attacks only change the spatial location of 3D triangle meshes. With scaling attack, it changes the size of 3D triangle meshes. To re-scale, we only find the highest vertex and the lowest vertex on the original 3D triangle mesh and then calculate the distance between these vertices. With the scaled 3D triangle mesh, we also perform a similar calculation. Finally, we compare the distances to find the scale-ratio for the rescaling process. Regarding the second aspect, we evaluate and analyze the accuracy of the extracted watermark from 3D-printed objects comparing it to the original watermark. If the accuracy of the extracted watermark from 3D-printed objects is high, the robustness of the proposed method is high and otherwise low. To extract the watermark data from 3D-printed objects, we have to use a 3D scanner to scan 3D-printed objects and extract the watermark data from the scanned 3D triangle meshes. Due to the fact that geometric attacks, such as translation, rotation and scaling, do not affect the 3D scanning process and we always receive the scanned 3D triangle meshes, which are the same size as 3D-printed objects, we concluded that geometric attacks do not affect the scanned 3D triangle mesh. Moreover, the Menger curvature is robust to translation and rotation attacks. Because these attacks only change the spatial location of the 3D printing model, they do not change the shape of the 3D printing model. Consequently, the proposed method is robust to geometric attacks. Here, we used the XYZ Printing Pro 3in1 3D printer [21] to print test models in Figure 5. Figure 7 shows the 3D-printed objects from test models. After the 3D printing process, we used the XYZ 3D Scanner [21] to scan 3D-printed objects and to construct the scanned 3D triangle meshes as shown in Figure 8. Due to the fact that the scanned 3D triangle mesh is affected by noise in the 3D scanning process, it is not perfectly the same as the original 3D triangle mesh. This means the number of facets in the scanned 3D triangle mesh is always different with the number of facets in the original 3D triangle mesh (see Table 1 and Table 2). Therefore, to calculate the accuracy between the extracted watermark from 3D-printed objects and the original watermark, we used an expression as shown in Equation (13).


Figure 7.
3D-printed objects with the 3D printer.

Figure 8.
Scanned 3D triangle meshes from 3D-printed objects.

Table 2.
Accuracy of the extracted watermark.
Here, we would like to explain one more time the difference between 3D model watermarking and 3D printing watermarking to show the novelty. In 3D model watermarking, watermark data are extracted from the watermarked 3D model. In 3D printing watermarking, watermark data are extracted from 3D-printed objects via the scanned 3D triangle mesh of 3D-printed objects. Table 2 shows the accuracy of the proposed method with test models. It is formed from 50.00%–74.42% with the 3D-printed objects in Figure 7. Overall, we can see that the accuracy of the proposed method is higher than 55%. The accuracy of the proposed method is very much dependent on the scanned 3D triangle meshes. However, the scanned 3D triangle meshes are dependent on the resolution of the 3D-printed object and the quality of the 3D scanner. Thus, we concluded that the accuracy of the proposed method is dependent on the quality of the 3D printer and 3D scanner. This means the robustness of the proposed method is dependent on the quality of the 3D printer and 3D scanner. In our experiments, the XYZ Printing 3D printer and 3D scanner are low quality, so the average accuracy of the proposed method being greater than 55% is not bad and understandable. In addition, we used a Maker-Bot 3D scanner [22] to scan 3D-printed objects. The quality of this 3D scanner is lower than the quality of our 3D scanner. The result of the 3D scanning process is very low. We cannot extract watermark data from the scanned 3D triangle meshes. Therefore, we conclude that with a high quality 3D printer and 3D scanner, the accuracy of the proposed method will be higher.
4.3. Performance Evaluation
In order to evaluate the performance of the proposed method, we compare the flexibility and the accuracy of the proposed method to the recent watermarking methods for 3D printing (Yamazaki’s method and Suzuki’s method). However, to prove the superiority of the proposed method to the conventional works and the previous methods of 3D printing watermarking, we will firstly compare the proposed method to two previous methods of 3D printing watermarking. Secondly, we will compare the proposed method to the conventional works of 3D model watermarking. This comparison is to prove that our method can be applied to both 3D model watermarking and 3D printing watermarking.
To compare the proposed method to the two previously-proposed methods for 3D printing watermarking, we compare the flexibility and the accuracy between the methods. This accuracy is the accuracy of the extracted watermark from the 3D-printed objects, because two previous methods also experimented with 3D-printed objects. In Yamazaki’s method [13], the watermark data are embedded in the frequency domain based on spectrum decomposition and modulation. Watermark data are extracted from the scanned 3D triangle mesh of 3D-printed objects. His experiments are divided in two parts. In the first part, he experimented on the watermark detection from the simulated scans. This experiment is performed in a virtual environment, and the length of watermark is 256 bits for all experiments. He discussed that the percentage that is precise for a casting object is improved significantly compared to the method of Obbuchi et al. [23]. The percentage of Obbuchi’s method that is precise for a casting object is 12.8% (approximate 10−1). In the second part, he experimented on three 3D triangle meshes: bunny, casting and hand with a 3D printer. He discussed that the percentage that is precise for a casting object is smaller than 10−5. Therefore, we concluded that the accuracy of Yamazaki’s method is approximate 40%. In addition, the risk of Yamazaki’s method is the length of the watermark bits is fixed and equal to 256 bits for all test models. As a result, there is a limitation of watermark bits in this method, and attackers can remove the embedded watermark more easily. In Suzuki’s method [14], the watermark data are embedded in the printed objects in the 3D printing process by a complex system of laser and halogen lights. This requires a complex hardware system, but it could not embed all expected watermark bits inside 3D-printed objects. Suzuki experimented on his method with two 3D triangle meshes. Following the experimental results of Suzuki, the maximum length of the embedded watermark bits was 64 bits. In addition, Suzuki did not describe how to extract the embedded watermark data from the 3D-printed objects. Therefore, we considered the accuracy of Suzuki’s method to be approximately 0%. In our method, the length of watermark bits is flexible and can be changed by the user based on the number of facets in each model (see Table 1 and refer to Section 4, Paragraph 1, and Equation (1)). This helps the users change the content of watermark bits according to their purpose. As we explained in Section 4.2, the accuracy of our method is dependent on the quality of the 3D printer and 3D scanner. The maximum accuracy of our method is 74.42% with the test models shown in Table 2. Table 3 describes the comparison between the proposed method and two previous methods. Figure 9 shows the performance of the proposed method compared to the two previous methods of 3D printing watermarking. Consequently, the proposed method is better than the two methods of Yamazaki and Suzuki.

Table 3.
Comparison between methods.
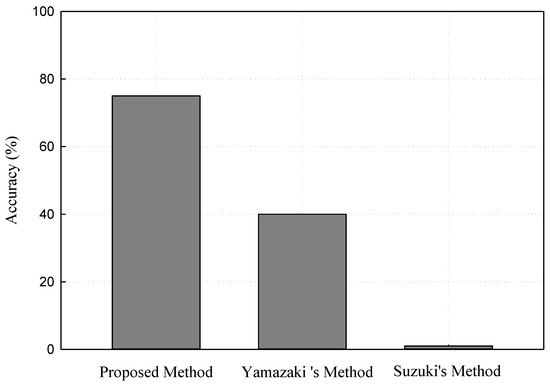
Figure 9.
Performance of the proposed method compared to the two previous methods.
To compare the proposed method with the conventional works of 3D triangle mesh model watermarking, we also compare the accuracy between the methods. This accuracy is the accuracy of the extracted watermark from the watermarked 3D triangle mesh. In Liu’s method [9], he embedded the watermark by modifying the selected vertices based on the topology of the 3D triangle mesh. He experimented with two 3D models and explained that his method can extract the embedded watermark when the watermarked 3D model is simplified by less than 5%. This means the maximum accuracy of Liu’s method is 95%. The robustness of Liu’s method is affected by geometric attacks (rotation, translation and scaling) and the perturbation of the order of facets, because it used vertices to embed watermark bits. In Rolland’s method [10], he also embedded watermark bits by modifying the vertex positions along the radial directions. He experimented on 13 models with noise of 0.1%, 1% and 5%, respectively. This method is also affected by geometric attacks and the perturbation of the order of facets. The maximum accuracy of Rolland’s method is 98%. In Hou’s method [12], he performed the watermark embedding process by modifying the input model according to the changes of the histogram of the x-y plane projected face normal vector from the input model. He experimented with four 3D triangle meshes, and the average bit error rate (BER) is approximate 4%. This means the average accuracy of Hou’s method is 96%. Hou’s method is affected by rotation, scaling and the perturbation of the order of facets. In our method, the watermark embedding process is based on changing the mean Menger curvature of groups of facets in the 3D triangle mesh. The Menger curvature of a facet is robust to geometric attacks and independent of the order of facets. This means the perturbation of facets does not affect the Menger facet curvatures. This leads to the clustering process not being affected by the perturbation of facets. Thus, the embedded watermark is robust to the perturbation. Here, we conclude that our method is robust to geometric attacks and perturbation. To compare to the conventional works of 3D model watermarking, we extracted the embedded watermark from the watermarked 3D triangle meshes after the watermark embedding process (refer to Figure 2). The average accuracy of the extracted watermark from the watermarked 3D triangle meshes is greater than 98.5%. This means the accuracy of our method is better than the accuracy of the conventional works of 3D model watermarking. Figure 10 shows the performance of the proposed method compared to the conventional works of 3D model watermarking. Consequently, the proposed method is better than the conventional methods of 3D model watermarking in both aspects: accuracy and robustness.
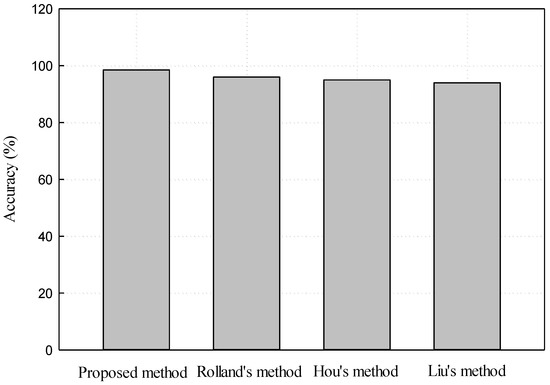
Figure 10.
Performance of the proposed method compared to the conventional works.
5. Conclusions
In this paper, we proposed a novel watermarking method for 3D printing. It is based on the Menger facet curvature and the K-mean clustering algorithm. We experiment on the proposed method using the XYZ Printing Pro 3D printer and XYZ 3D scanner. Experimental results showed that the proposed method is invisible and robust to geometric attacks, such as rotation, translation and scaling. Experimental results with the XYZ Printing Pro 3D printer and 3D scanner also verified that the accuracy of the proposed method is moderate and higher than the accuracy of the two previous methods in the 3D printing domain. Compared to the conventional works for 3D model watermarking, the accuracy of the proposed method is also higher. Therefore, the proposed method can be applied to both 3D printing watermarking and 3D model watermarking. As future works, we will consider some correction methods in the 3D scanning process or after the 3D scanning process to increase the accuracy of the proposed method. Moreover, we will improve the proposed method and experiment on it with other 3D printers and 3D scanners. We will consider applying the proposed method to some contexts or real applications.
Acknowledgments
This research is supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (No. 2016R1D1A3B03931003, No. 2017R1A2B2012456), the MSIP (Ministry of Science and ICT), Korea, under the Grand Information Technology Research Center support program (IITP-2017-2016-0-00318) supervised by the IITP (Institute for Information & communications Technology Promotion), the Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government (MSIT) (No. 2015-0-00225) and the Brain Busan 21 (BB21) project in 2017.
Author Contributions
In this research activity, all of the authors participated in the data analysis and preprocessing phases, the simulation, the results’ analysis and discussion, as well as the manuscript’s preparation. All of the authors have approved the submitted manuscript. All of the authors equally contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- How 3D Printing Works: The Vision, Innovation and Technologies Behind Inkjet 3D Printing. 3D Systems: Rock Hill, CA, USA, 2012. Available online: http://www.officeproductnews.net/sites/default/files/3dWP_0.pdf (accessed on 14 March 2018).
- How Paper-Based 3D Printing Works: The Technology and Advantages. Mcor Technologies Ltd. 2013. Available online: http://rapid3dparts.co.za/how-paper-based-3d-printing-works.pdf (accessed on 14 March 2018).
- Ramya, A.; Vanapalli, S. 3D Printing Technology in Various Applications. Int. J. Mech. Eng. Technol. 2016, 7, 396–409. [Google Scholar]
- Rulania, T. Impact and Applications of 3D Printing Technology. SSRG Int. J. Comput. Sci. Eng. 2016, 3, 79–82. [Google Scholar]
- Helena, D. Applications of 3D printing in healthcare. Kardiochir. iTorakochirurgia Polska 2016, 13, 283–293. [Google Scholar] [CrossRef]
- Ira, S.; Parker, S. Copyright Issues in 3D Printing. In Proceedings of the International Technology Law Conference, Paris, France, 30–31 October 2014; pp. 1–14. [Google Scholar]
- Feng, X.; Liu, Y.; Fang, L. Digital Watermark of 3D CAD Product Model. Int. J. Secur. Its Appl. 2015, 9, 305–320. [Google Scholar] [CrossRef]
- Hu, Q.; Lang, Z. The Study of 3D Digital Watermarking Algorithm Which is based on a Set of Complete System of Legendre Orthogonal Function. Open Autom. Control Syst. J. 2014, 6, 1710–1716. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; He, W.; Li, Y. A New Watermarking Method of 3D Mesh Model. Indones. J. Electr. Eng. 2014, 12, 1610–1617. [Google Scholar] [CrossRef]
- Rolland, X.; Do, D.; Pierre, A. Triangle Surface Mesh Watermarking based on a Constrained Optimization Framework. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1491–1501. [Google Scholar] [CrossRef]
- Ho, J.U.; Kim, D.G.; Choi, S.H.; Lee, H.K. 3D Print-Scan Resilient Watermarking Using a Histogram-Based Circular Shift Coding Structure. In Proceedings of the 3rd ACM Workshop on Information Hiding and Multimedia Security, Portland, OR, USA, 17–19 June 2015; pp. 115–121. [Google Scholar]
- Hou, J.U.; Kim, D.G.; Lee, H.K. Blind 3D Mesh Watermarking for 3D Printed Model by Analyzing Layering Artifact. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2712–2725. [Google Scholar] [CrossRef]
- Yamazaki, S.; Satoshi, K.; Masaaki, M. Extracting Watermark from 3D Prints. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 4576–4581. [Google Scholar]
- Suzuki, M.; Piyarat, S.; Kazutake, U.; Hiroshi, U.; Takashima, Y. Copyright Protection for 3D Printing by Embedding Information inside Real Fabricated Objects. In Proceedings of the 10th International Conference on Computer Vision Theory and Applications, Berlin, Germany, 11–14 March 2015; pp. 180–185. [Google Scholar]
- Giao, N.P.; Song, H.J.; Lee, S.H.; Kwon, K.R. 3D Printing Watermarking Method Based on Radius Curvature of 3D Triangle. J. Korea Multimedia Soc. 2017, 20, 1951–1959. [Google Scholar] [CrossRef]
- STL Format in 3D Printing. Available online: https://all3dp.com/what-is-stl-file-format-extension-3d-printing/ (accessed on 16 February 2018).
- The Virtual Reality Modeling Language. Available online: http://www.cacr.caltech.edu/~slombey/asci/vrml/ (accessed on 16 February 2018).
- Lecture Notes in Mathematics. Analytic Capacity, Rectifiability, Menger Curvature and the Cauchy Integral. Available online: https://www.springer.com/la/book/9783540000013 (accessed on 16 February 2018).
- Leymarie, F. Notes on Menger Curvature. 2007. Available online: https://web.archive.org/web/20070821103738/http://www.lems.brown.edu/vision/people/leymarie/Notes/CurvSurf/MengerCurv/index.html (accessed on 3 April 2018).
- Mac Queen. K-means Clustering Algorithm. In Some Methods for Classification and Analysis of Multivariate Observations; Chapter 1; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- XYZ Printing Printer Pro 3in1. Available online: http://eu.xyzprinting.com/eu_en/Product/da-Vinci-1.0-Professional3in1 (accessed on 16 February 2018).
- MakerBot Digitizer Desktop 3D Scanner. Available online: https://www.makerbot.com/media-center/2013/08/22/makerbot-digitizer-desktop-3d-scanner-order-today (accessed on 14 March 2018).
- Ohbuchi, R.; Takahashi, S.; Miyazawa, T.; Mukaiyama, A. Watermarking 3D Polygonal Meshes in the Mesh Spectral Domain. In Proceedings of the Graphics Interface, Ottawa, ON, Canada, 7–9 June 2001; pp. 9–18. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).