Abstract
The beginning of the 21st-century resulted in a more developed multi-attribute decision-making (MADM) tool and inspired new application areas that have resulted in discoveries in sustainable construction and building life cycle analysis. Construction and civil engineering stand for the central axis of a body consisting of a multidisciplinary (multi-dimensional) world with ties to disciplines constituting the surface, and with the disciplines, as a consequence, tied to each other. When dealing with multi-attribute decision-making problems generally multiple solutions exist, especially when there is a large number of attributes, and the concept of Pareto-optimality is inefficient. The symmetry and structural regularity are essential concepts in many natural and man-made objects and play a crucial role in the design, engineering, and development of the world. The complexity and risks inherent in projects along with different effective indicators for success and failure may contribute to the difficulties in performance evaluation. In such situations, increasing the importance of uncertainty is observed. This paper proposes a novel integrated tool to find a balance between sustainable development, environmental impact and human well-being, i.e., to find symmetry axe with respect to goals, risks, and constraints (attributes) to cope with the complicated problems. The concept of “optimal solution” as the maximum degree of implemented goals (attributes) is very important. The model is built using the most relevant variables cited in the reviewed project literature and integrates two methods: the Step-Wise Weight Assessment Ratio Analysis (SWARA) method and a novel interval-valued fuzzy extension of the Additive Ratio Assessment (ARAS) method. This model was used to solve real case study of oil and gas well drilling projects evaluation. Despite the importance of oil and gas well drilling projects, there is lack of literature that describes and evaluates performance in this field projects. On the other hand, no structured assessment methodology has been presented for these types of projects. Given the limited research on performance evaluation in oil & gas well-drilling projects, the research identifies a set of performance criteria and proposes an evaluation model using fuzzy Delphi method. An illustrative example shows that the proposed method is a useful and alternative decision-making method.
1. Introduction
Today, projects have a significant role to play in the success of any company and the integration of activities leading to new products or services can improve its performance [1]. That is why many companies consider the use of project management as a key strategy for their survival in a competitive environment as well as for increasing the possibility of value creation in their businesses [2]. A project is a temporary attempt to produce a unique product or service and project management refers to the application of knowledge, skills, tools and techniques to carry out all activities of the project [3] as well as, project is a complex effort involving interconnected activities, with the purpose of achieving an objective [1]. A project performance evaluation dealing with evaluating and rating all tasks [4] help Decision Makers (‘DM’) through determining the status of the project and its weaknesses and strengths [5] and will help establish benchmarks of high performance projects for cross-learning and identify inefficiencies of low performance projects for potential improvement [6]. Therefore, the importance of project performance evaluation is inevitable and has long been confirmed by practitioners and academics from a variety of functional disciplines [7]. As a result, several project performance evaluation approach has been advanced that MCDM models is one of them. In a business environment, evaluation of the “best” project can be done by a decision committee, instead of a single DMs. Different DMs can bring their own points of view and knowledge, which must be resolved within a framework of understanding and mutual concessions [8,9]. In such situations, MCDM can help in finding a sufficiently good solution from a collection of alternatives and can address complex problems that involve high uncertainty, conflicting objectives, different forms of information, multiple interests and different perspectives [8]. MCDM methods solve a complex problem by converting it into several small problems and as smaller processes are weighted and re-aggregated, a general picture of decision makers is provided [10]. Therefore, given the inherent complexity, risks and uncertainties of projects and the diversity of success/failure criteria, this paper aims to introduce a novel assessment framework for projects using Interval-Valued Fuzzy Additive Ratio Assessment as a recent MADM approach dealing with uncertainties in decision making. In many practical situations, there exists information which is incomplete and uncertain so that decision makers cannot easily express their judgments on the candidates with exact and crisp values. As well as there are many real-life complex problems that need to involve a wide domain of knowledge. Therefore, fuzzy sets provide generally more adequate description to model real-life decision problems than real numbers [11]. However, it became apparent that the fuzzy sets are not sufficient for uncertain MCDM. Therefore, Zadeh (1975) [12] and Gorzałczany (1987) [13] developed the concept of interval-valued fuzzy sets, whereas Atanassov (1986) [14] proposed intuitionistic fuzzy sets [15]. Consequently, interval-valued fuzzy sets allow us to achieve a better imagination from environmental ambiguity and uncertainty [16].
On the other hand, Over the past two decades, infrastructure projects as an important category of projects have accounted for 3.8% of global GDP and this number is expected to rise to 1.4% by 2030 [5]. These type of projects include general fields of energy, transport, water, communications and social infrastructure such as hospitals [17]. Infrastructure projects are defined as long-term, large-scale and difficult-to-implement projects that can hardly be valued; therefore, evaluation of these projects is a complex and specialized activity [17].
Further, oil and gas well drilling projects are of great importance among major infrastructure projects because of a large volume of investment and the economic benefits of their proper implementation [4,18]. Difficulty in predicting operational costs due to inherent uncertainties in the economic evaluation of oil and gas exploration and development projects [19], costs of renting drilling rigs as well as drilling services required by these projects [20] are major parameters resulting in the need for high-volume investments. Like any costly projects for the highest quality and lowest cost and time, oil and gas drilling projects require appropriate decision-making procedures to face upcoming challenges and achieve the desired level of productivity [21]. A fast, continuous, timely and data-based decision-making process can lead to improved productivity; particularly as today’s global demand for energy and environmental constraints have forced oil and gas projects to enhance their activities in terms of efficiency and effectiveness [18]. In addition, similar to other projects, oil and gas well-drilling projects deal with inherent uncertainties [22] that are generally arisen from environmental factors, organizational complexities, as well as changes, deviations and events occurring in a project [23]. Accordingly, oil and gas projects face various risks and complexities that make the decision-making process so difficult [18].
However, a brief review of the literature shows a limited portion of structured performance evaluation models in these field and though a variety of project evaluation approaches like multi-criteria decision-making (MCDM) methods have been applied in other project fields [6] but there is a necessity for structured assessment methodology in the field of oil and gas well drilling projects. Therefore, we choised oil and gas well drilling projects as a case study and tried to identify an initial list of performance criteria based on review of literature and propose an evaluation model using Delphi method.
According to the above discussion, the purpose of this study is to provide an interval-valued MADM-based framework as a novel approach for evaluating the performance of projects that oil and gas well drilling projects was considered in order to remove the limitations noted in this type of projects. To this end, a review on the literature is provided and an initial list of evaluation criteria is extracted. Due to the research limitations in this context, the Fuzzy Delphi technique and expert panels are used to develop a more complete list of effective criteria. Next, the identified criteria are weighted by the SWARA method and finally the Interval-Valued Fuzzy Additive Ratio Assessment is employed to assess and rank active projects of a certain company in the field of oil and gas drilling.
The structure of this paper will be as follows. Section 2 presents the literature review and the initial list of criteria. Section 3 describes the research methodology, while Section 4 provides an experimental example using data from a set of seven oil and gas well drilling projects from a subsidiary of the National Iranian Oil Company (NIOC) in Iran. Finally, Section 5 concludes the study.
2. Literature Review
Decision making in a project context is a complex undertaking. The term complexity is an increasingly important point of reference when we are trying to understand the managerial demands of modern projects in general, and of the various situations encountered in projects [24,25]. On the one hand, a project is a temporary and transient organization surrounded by inherent uncertainty [24,26]. When complexity becomes too great, the possibilities and interrelations become so fuzzy that the system has to be assisted by appropriate tools and skills. Consequently, managers facing complex project need access to a decision-making aid model based on relevant performance evaluation [24]. Therefore the project performance evaluation is inevitable and necessary issue. So far, several decsion approach has been used to help project evaluation such as economic models, mathematical programming, artificial intelligence optimization methods, integrated models, data envelopment analysis (DEA) method, integrated the balanced scorecard (BSC) approach and MCDM models [27]. among these, MCDM models can help in finding a sufficiently good solution from a collection of alternatives and can address complex problems that involve high uncertainty, conflicting objectives, different forms of information, multiple interests and different perspectives [8]. In measuring the overall performance of projects, MCDM models have been used to aggregate multiple performance measures under various application contexts [6] and incidentally are widely used for energy projects [8]. Analytical Hierarchy Process (AHP) [28,29], Analytic Network Process (ANP) [29,30], TOPSIS [31], DEMATEL [32], ELECTRE [33] and some hybrid methods [4,8,34] are number of MCDM methods applied to projects evaluation.
On the other hand in many projects in practical situations, there exists information which is incomplete and uncertain so that decision makers cannot easily express their judgments on the candidates with exact and crisp values. As well as there are many real-life complex problems that need to involve a wide domain of knowledge. These conditions in which decisions are based on obscure and unreliable information or lake of knowledge and personal preferences of the experts can create difficulties in the decision-making process. These difficulties can lead to deceptive and uncertain decisions. Therefore, solving decision-making problems existing in real life and modeling them in the form of multi-criteria decision-making problems is still considered as a challenging topic [35,36,37] and fuzzy sets provide generally more adequate description to model real-life decision problems than real numbers [11] and presented to fix these challenges and provided a basis for development of a variety of fuzzy decision-making models. The development of the fuzzy concept has led to the provision of models which have the flexibility to control and display uncertainty and low accuracy due to lack of knowledge of experts and inadequate data [38,39]. Many developments have been made to better address inadequate and inaccurate data [14,40]. Atanassov developed intuitive fuzzy sets [14]. These sets included the membership function, the non-membership function and the hesitancy function [41]. Zadeh [12] introduced a type-2 fuzzy set which allowed expressing the membership of the components in the form of a fuzzy set. Further, the type-n fuzzy numbers were defined [42] which were the generalized form of type-2 fuzzy numbers and allowed the membership of elements to be in the form of a type-(n − 1) fuzzy set. Since the concept of fuzzy numbers with interval values has been presented, there has been an increasing interest of researchers in this field [43] so that it was successfully used in numerous decision-making issues in conditions of uncertainty. Briefly, there are two approaches to classify studies in this area: (1) Content Approach; (2) Applied Approach [44]. In the content approach, two main steps are considered for decision-making issues: aggregation of opinions [45,46,47] and method exploitation. In the applied approach, researches on fuzzy numbers with interval values can be classified into five main domains [48]: (1) basic operators in fuzzy space with interval values [49]; (2) group decision [50,51]; (3) combining decision making with linguistic variables [52,53]; (4) matrix of judgment based on priority relations [54] and (5) development of the model of dual interval-valued fuzzy sets [55]. In recent years, researches have been a growing trend in two domains; decision making with linguistic variables and development of basic operators in fuzzy space with interval values.
Given that this paper aims to prioritize the projects, it is related to the method exploitation step. In this category of methods, it is tried to find priority relations in non-preferred alternatives so that a set of options is ranked based on them. So far, various decision-making methods have been combined with fuzzy numbers with interval values [56] including the VIKOR method [57,58], the TOPSIS method [59], the MULTIMOORA method [15] and the TODIM method [60]. In this paper, we tried to use Additive Ratio Assessment (ARAS) method combined with fuzzy numbers with interval values which is addressed when we introduce fuzzy numbers with interval values and combined method steps.
In addition to the performance evaluation methodology, it is also necessary to define the performance evaluation criteria for each project. Evaluation criteria are quantitative or qualitative variables that measure the performances and the impacts of the analyzed alternatives [61]. Through a literature review, this section also seeks to develop an initial list of criteria as inputs for the fuzzy Delphi process. As discussed before, despite the importance of oil and gas well drilling projects, there is a limited research available on performance evaluation of these projects, by using some measures of these criteria. Below provides further details of some relevant research studies:
Dachyar and Pratama (2014) evaluated the efficiency of oil and gas well drilling projects using the MACBETH method [22]. The author introduced criteria such as implementation methods, time, cost, quality, risk and safety. Ahari and Niaki (2014) used a neuro-fuzzy network to assess the quality of oil and gas well drilling projects for a contractor selection problem [4,21]. The authors defined three criteria of time, cost and quality as the basic assessment objectives. Also, a set of five parameters were introduced as inputs; (1) the cost compliance percentage with plans; (2) the time compliance percentage with plans; (3) the percentage of quality failure in all operational failures; (4) the number of HSE incidences; and (5) the number of quality failures without non-productive time. The quality of work measure was defined as the model output. The authors followed the size of drilled holes as an important factor in the work package plan. Exploring the design of drilling contracts, Osmundsen et al. (2006) suggested safety and associated risks from the important indicators of a drilling project [20]. In other study (2010), the authors examined new incentive schemes in offshore drilling contracts to improve project performance. They highlighted higher cost and its rapid growth in drilling activity, especially for renting and drilling services, as well as the need to carefully examine effective criteria in drilling projects [62]. Liu et al. (2013) considered risks in drilling projects [63]. They identified a set of 25 risk factors in six categories of natural risks, R & D risks, management risks, drilling risks, equipment risks and security risk and environmental factors.
In addition to the related studies referred to above, in general, three main traditional criteria have always been considered; including time, cost, and quality. A project would be succeeded when it is implemented at a reasonable cost and quality during a planned period time, and meet stakeholders’ satisfaction [1]. This traditional approach—referred as the “Iron Triangle” [4]—merely deals with the economic dimension of projects, while ignoring other major aspects [64]. Further, these criteria are less flexible in evaluating project performance [65]. In order to overcome limitations of the traditional criteria, academic researchers suggest a variety of criteria for project performance evaluations. Some examples are safety of the project site [66,67,68], geographic location of projects [69], environmental impacts [70] and satisfaction of community, client or customer [71,72]. Moreover, the quality and variety of materials and goods used in a project [73,74], number of active labor force and salaries [75,76,77] and experience and scientific levels of employees in the project [78,79] are amongst other effective measures of project performance. Risks and operational risks, in particular, are also important indicators that many researchers have taken into account [23,63,80]. In addition, research and development (R & D) and related costs are identified as influential parameters in improving project performance [81,82].
Considering the generality of criteria mentioned above, these can be used in oil and gas wells drilling projects. As noted, there is a limited research available on performance evaluation of oil and gas well-drilling projects, however, a list of initial criteria for evaluating oil and gas well drilling projects can be found by reviewing the literature (Table 1). Obviously, these criteria are precisely related to the drilling of oil and gas wells and do not include all the relevant criteria in the entire oil and gas industry. This list will be completed in Section 4 using the Fuzzy Delphi method.

Table 1.
Primary Criteria from Literature Review.
3. Research Methodology
First, a list of assessment criteria is derived from the literature available on the research subject. Then by using the Fuzzy Delphi method and expert opinions, the criteria are extended and the final list is obtained for oil and gas well-drilling proje cts (Table 4). The Step-Wise Weight Assessment Ratio Analysis (SWARA) method is employed to determine final criteria weights. According to the interval-values fuzzy Additive Ratio Assessment and the decision Table developed for a set of oil and gas projects, project performance is evaluated. Figure 1 presents the flowchart of the research.
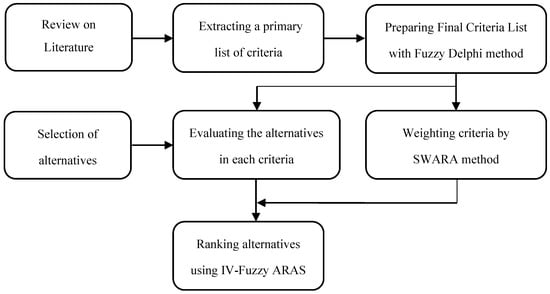
Figure 1.
Schematic diagram of research design.
3.1. Fuzzy Delphi Method
The traditional “Project DELPHI” was originally developed by Dalkey and Helmer (1963) to achieve the most reliable consensus among experts on a particular topic [83]; a theoretical consensus obtained through several rounds of extensive consultations through expert interviews [84]. The most important advantage of this method is to avoid direct confrontation of participants [85]. However, the Delphi method has been criticized for higher operational costs, lower degree of convergence and the possibility to remove some key ideas by organizers. Therefore, Murray et al. (1985) proposed the integration of the traditional Delphi method and fuzzy set theory to improve ambiguity and inconsistency in requirements [86,87]. A variety of techniques have been developed to determine metrics by using Delphi method. Here, based on the approach presented by Hsu and Yang (2000) and Kuo and Chen (2008), triangular fuzzy numbers are used to incorporate expert opinions and to implement the fuzzy Delphi technique. Maximum and minimum values obtained based on expert opinions are defined as two endpoints of triangular fuzzy numbers, while the geometric mean is expressed as the membership degree in triangular fuzzy numbers in order to avoid the portion of terminal values [86,88]. Kuo and Chen believed that this method enables decision-makers to achieve a better solution for the selection [86].
Further, the authors highlighted the simplicity and the lack of survey repetition, as well as the use of all expert opinions. Each fuzzy number (TA) is defined as follows (1):
where, is the proposed value of the i-th decision-maker in terms of the critical factor A; (i = 1,2…). , and represent the values of lower bound, upper bound and geometric mean for the critical factor A, respectively. In the next step, the Center of Area (COA) defuzzification process is performed using the model developed by Zheng and Teng (1993) [89]. The formula is presented as follows (2):
where, the index k represents the number of criteria and , and represent the values of lower bound, upper bound and geometric mean for the critical factor k.
The final step is to determine the threshold value for accepting or rejecting the criteria. To this end, the score of 0.7 is determined based on expert opinions. Finally, those criteria with a number less than the threshold value are removed from the list and the final list provides the necessary evaluation criteria.
3.2. SWARA Method
For a large number of multi-attribute decision-making problems, weighting indicators are included among the most important procedures in problem solution [90]. Accordingly, experts play a vital role in criteria evaluation and weighting and form inevitable part of the decision-making process. The Step-Wise Weight Assessment Ratio Analysis (SWARA) method newly proposed by Krešulienė et al. (2010) allows decision-makers to select, evaluate and weight the criteria [91]. The most important advantage of this approach is its potential for evaluating the accuracy of expert opinions about weights allocated by the process [91]. Further, expert consultations can yield more accurate results than other common methods of multi-criteria decision-making (MCDM) [92]. The main steps of determining the criteria weights based on the SWARA method are described below:
- -
- Step 1: Rank Criteria—First, the criteria determined by decision-makers are selected as the final criteria and then all the criteria are ranked in order of their importance. Accordingly, the most/least important criteria take the highest/lowest position of ranking.
- -
- Step 2: Determine Relative Importance for Criteria ()—Now, the relative importance of each criterion is measured against the most important criterion. This value is represented by .
- -
- Step 3: Calculate Coefficient Value of —As a function of the relative importance for each criterion, the coefficient is determined using Equation (3).
- -
- Step 4: Calculate Initial Weights for Criteria—In this step, the initial weights of each criterion are calculated by Equation (4). Note that the initial weight for the first—i.e., the most important—criterion is generally considered equal to 1 ().
- -
- Step 5: Calculate Final Normalized Weights—As the final step of SWARA, the final weights which is also known as the normalized weights are determined by Equation (5).
As mentioned before, SWARA is a newly established method for weighting which has been recently used by different studies [93].
3.3. Interval-Valued Fuzzy Additive Ratio Assessment
3.3.1. Generalized Fuzzy Numbers
A generalized fuzzy number à defined as (6),
It is a fuzzy subset of the real line Ʀ with the membership function () which has the following features [94]:
- is a continuous mapping from Ʀ to the closed interval [0, 1].
- is strictly increasing on [a, b].
- for all , where ω is a constant on [0, 1], .
- is strictly decreasing on [c, d].
- for all .
If is linear on the intervals [a, b] and [c, d], then a generalized fuzzy number is called a generalized trapezoidal fuzzy number. Figure 2 shows a relationship between the generalized fuzzy number, and the normalized trapezoidal fuzzy number, Ã.
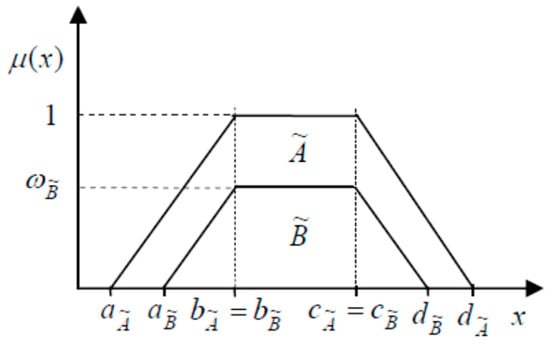
Figure 2.
Generalized fuzzy number.
As seen from Figure 2, the normalized trapezoidal fuzzy numbers demonstrate certain cases of generalized fuzzy numbers, where ω = 1. Also, if b = c, then the trapezoidal fuzzy number becomes a triangular fuzzy number.
3.3.2. Interval-Valued Fuzzy Numbers
The interval-valued fuzzy numbers are special forms of generalized fuzzy numbers. Similar to generalized fuzzy numbers, these numbers can find a trapezoidal shape. Moreover, interval-valued triangular fuzzy numbers have a triangular shape. Figure 3 shows a graphical representation of an interval-valued triangular fuzzy number.
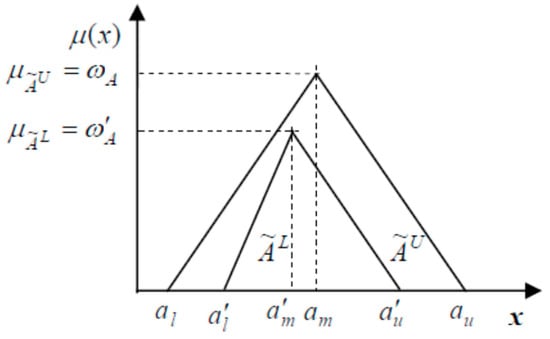
Figure 3.
Interval-valued triangular fuzzy number.
An interval-valued triangular fuzzy number can be defined as (7) [95]:
where ÃL and ÃU are the lower and upper triangular fuzzy numbers, ÃL ÃU and are their membership functions. However, and denote the lower and upper membership functions.
Suppose and are two interval-valued triangular fuzzy numbers. Then, the basic arithmetic operations on these fuzzy numbers can be represented as (8) to (11):
Figure 4 shows a certain case of generalized interval-valued fuzzy numbers, normalized with the same mode and it can be represented as (12)
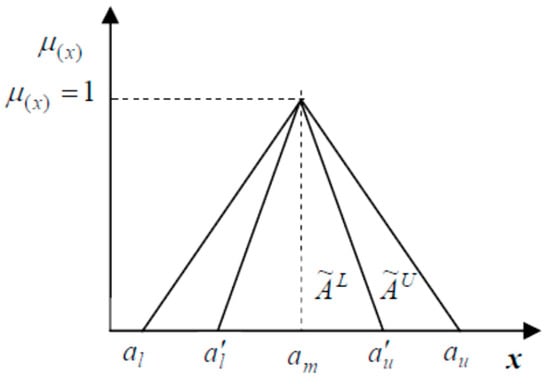
Figure 4.
Normalized interval-valued triangular fuzzy number with the same mode.
Suppose and denote two normalized interval-valued triangular fuzzy numbers with the same mode. Then, the basic arithmetic operations on these fuzzy numbers can be defined as (13) to (16) [96]:
In addition, the following unary operation defined on interval-valued triangular fuzzy numbers is of great importance. It is denoted as (17):
3.3.3. Linguistic Variables
The linguistic variables refer to variables whose values correspond to words or sentences in a natural or artificial language. A linguistic variable has a practical potential for dealing with many real-world decision-making problems, which are usually complex and relatively uncertain. A wide range of research studies have reported different linguistic variables with triangular fuzzy numbers [97,98,99]. Also, the literature provides linguistic variables based on the use of interval-valued fuzzy numbers. Wei and Chen (2009), for example, developed a scale of nine level linguistic terms using interval-valued trapezoidal fuzzy numbers [100]. Ashtiani et al. (2009) presented a seven-level linguistic terms scale based on interval-valued triangular fuzzy numbers. Table 2 and Table 3 show the linguistic variables for the weights of criteria and performance ratings, based on the use of triangular fuzzy numbers and interval-valued triangular fuzzy numbers [57].

Table 2.
Linguistic variables for the weights of criteria.

Table 3.
Linguistic variables for the performance ratings.
Since interval-valued fuzzy numbers are more complex than ordinary fuzzy numbers, the transformation of the ordinary fuzzy numbers into the corresponding interval-valued fuzzy numbers can raise some advantages. To transform their weights and performance ratings, the following equations are given:
is the corresponding interval-valued triangular fuzzy number, while is the triangular fuzzy number obtained on the basis of opinion of kth decision maker. The parameters l and u denote the smallest and the greatest performance ratings among all stakeholders, respectively; which reflect the extreme attitudes provided by the experts. Unlike these parameters, other parameters of the interval-valued triangular fuzzy number reflect the expert opinions much more effectively. The reason is that these numbers are obtained as the geometric mean of attitudes from all experts.
3.3.4. Defuzzification of Interval-Valued Triangular Fuzzy Numbers
Since the results of arithmetic operations will be fuzzy numbers, they can be transformed into non-fuzzy numbers in order to rank and compare alternatives. Different procedures have been proposed for ranking fuzzy numbers and for their defuzzification but these procedures concern mainly the trapezoidal or triangular fuzzy numbers. By small changes, however, the same procedures can be used for the defuzzification of interval-valued triangular fuzzy numbers. Equations (23) and (24) are two general defuzzification equations for triangular fuzzy numbers (λ is a coefficient on [0, 1]):
Moreover, (25) and (26) are proposed for defuzzification of interval-valued triangular fuzzy numbers:
where represents ordinary triangular fuzzy numbers, whereas presents interval-valued fuzzy numbers. λ is a coefficient on [0, 1]. Equation (25) is a simple extension of (24), providing an effective way for the defuzzification of known interval-valued fuzzy numbers, represented as the Best Non-Fuzzy Performance (BNP). In contrast, Equation (25) is relatively more complex but it has some advantages. For instance, varying the coefficient λ makes a greater importance to the parameters and against l and u and vice versa.
3.3.5. Additive Ratio Assessment (ARAS) Method
As a relatively new tool for MCDM, the ARAS method has received significant interested recently, still based on the theory that complex phenomena of the world could be accurately perceived trough simple relative comparisons [101,102,103]. The ARAS method uses the concept of optimality degree to find a ranking. It is the sum of normalized weighted values of the criteria with respect to each alternative divided by the sum of normalized weighted values of the best alternative.
- Step 1: First, a decision matrix is assembled as , where m denotes alternatives and n denotes criteria.
is the performance measure of the i-th alternative on the j-th criterion. Also, shows the optimum value for the j-th criterion. If the optimum value of the variable j is undetermined, then it can be determined as follows:
In general, the evaluation values of alternatives with respect to criteria and the weights for each criterion () are given as the inputs in the decision matrix. Note that each criterion reflects its certain dimensions; therefore, a comparative analysis and preventing potential consequences from different dimensions require derive dimensionless quantities. To do this, the weighted values are simply divided by optimum obtained as (28). Numerous methods are available for deriving dimensionless useful dimensionless values which will be described below. Through normalization, the values of an original decision matrix are converted into the values on [0, 1] or on [0, ∞].
- Step 2: The primary inputs are normalized for all criteria, represented by and formed the matrix elements.
Since there are benefit type and cost type criteria, then the normalization is processed positively or negatively by using (30) and (31), respectively.
The achievement of dimensionless quantities provides a framework for comparing each criterion against all others.
- Step 3: Here, the weighted normalized decision matrix, , is calculated by applying the weight values on the normalized decision matrix . The weights are determined by expert panels and should meet the following requirements:
Again, denotes the weight value for the jth criterion and represents the normalized value for the ith alternative. Therefore, the value of an optimal function can be calculated as follows:
According to the logic of ARAS, the best alternative is the only one with the greatest value for an optimal function. Clearly, the worst alternative obtains the value of minimum for the optimal function. To put it differently, the alternative ranking is determined based on the value of .
The degree of utility can be measured by comparing each alternative against the best/optimal one with the best value, represented by . The degree of utility, , of the alternative follows Equation (35):
where, and are derived from Equation (34). Clearly, places on the interval [0, 1] and its value is used for ranking all alternatives.
3.3.6. An Extension of ARAS Method Based on Interval-Valued Triangular Fuzzy Numbers
- Step 1: Determine the optimal performance rating for each criterion
The first point to be considered is that the optimal performance rating for each criterion should be calculated as an interval-valued fuzzy number. Therefore, optimal interval-valued fuzzy performance ratings can be determined as follows:
where, represents the optimal interval-valued fuzzy performance rating of the jth criterion. Also, other criteria are defined as follows:
denotes the benefit criteria, i.e., the higher the values are, the better it is; and denotes the set of cost criteria, i.e., the lower the values are, the better it is.
- Step 2: Calculate the normalized decision matrix
To enable the use of these interval-valued fuzzy numbers, the normalization process requires some modifications. So, (34) can be replaced by (42):
Here, is the optimal interval-valued fuzzy performance rating for the ith alternative on the jth criterion. Further,
- Step 3: Calculate the normalized weighted interval-valued decision matrix
This is principally similar to the third step in the original ARAS method. The difference is that fuzzy numbers are to be now multiplied by using the multiplication operation on interval-valued triangular fuzzy numbers. Therefore, this can be expressed as follow:
where, is the normalized weighted interval-valued fuzzy performance rating for the i-th alternative on the j-th criterion.
- Step 4: Compute the overall interval-valued fuzzy performance ratings
This step can be expressed using (44):
where, is the overall interval-valued fuzzy performance rating for the ith alternative.
- Step 5: Measure the degree of utility for each alternative
Since the result obtained from the previous step is provided as an interval-valued fuzzy numbers, the calculation process is often more complex with the overall degree of utility. Obviously, it should be transformed into a non-fuzzy number. The degree of utility can be calculated as follow:
Again, as the products of (45) are still interval-valued fuzzy numbers, these typically need to be defuzzified. The defuzzification process must be initiated prior of determining the degree of utility. There are a wide range of defuzzification methods with a variety of impacts on resultant outputs. Therefore, it is important how to choose an appropriate defuzzification technique.
- Step 6: Rank alternatives and select the most efficient one
This step follows the similar process as the original Additive Ratio Assessment method.
4. Results: A Case Study of Well-Drilling Projects
The case study of this research includes a company active in the Iranian drilling industry, implementing seven oil and gas well drilling projects. The locations of these projects are Iranian oil reservoirs which have a major portion of the country’s oil production. Concerns about environmental issues show other challenges related to such projects. Based on the opinion of the senior management, a group of three experienced professionals in the field of Iranian oil and gas drilling industry was established as the expert team to provide expertized views in different stages. In the first step, the initial questionnaire obtained from Table 1 was distributed among 15 experts in Iran’s oil and gas wells projects who were introduced by the expert team. The questionnaire consisted of two main parts: The first part included the importance evaluation of the criteria derived from previous studies (Table 1) based on a Likert scale. In the second part, the expert was asked to propose some measures important in the project evaluation but not included in the first part. As the first round of survey completed, a total of 13 criteria were confirmed by the Delphi method, while 14 new criteria were suggested by experts. Based on these results, the second questionnaire was formulated and its results were also analyzed as in the first stage. Finally, a list of 20 criteria was developed and categorized for evaluating oil and gas well drilling projects using the Fuzzy Delphi method. According to the expert opinions, these criteria were classified in six main criteria (Table 4).

Table 4.
Evaluation Criteria in Oil & Gas Well-Drilling Projects using Fuzzy Delphi method.
Next, the SWARA technique was implemented to determine weights of all criteria and sub-criteria based on the opinion of each expert. Also, the obtained values were integrated to calculate the final weights. Table 5 shows the results.

Table 5.
Calculation of Criteria Weights for Expert #1.
As seen in Table 5, based on the first step of the SWARA method, the expert was asked to rank the criteria in a descending order of importance. The results are displayed in the second column of Table 5. Also, the second, third and fourth steps of the SWARA method are presented in the columns 3, 4 and 5 of Table 5, respectively. By implementing the final step of the SWARA method to normalize the weights of criteria, the final weighting values are shown in the column 6 of Table 5. A similar procedure was carried out for the second and third experts. Moreover, for comparative analysis of the weights of all criteria according to expert opinions and the geometric means, the weights and the geometric means obtained from each expert are presented in Figure 5. The same was carried out for the sub-criteria. According to the results, the most important sub-criteria for the materials and equipment, human resource, planning and the quality criteria are types of drilling rigs, experience of drilling specialists working in project, cost spent for drilling project and actual cost compliance percentage with planned cost. Now, to determine the final weights of the sub-criteria, the weights of one sub-criterion obtained from each expert multiplied by the weights of the criteria corresponding to that sub-criterion. In order to aggregate expert opinions, the geometric means for the weights obtained for each sub-criterion from three experts were calculated, shown in the last column of Table 6. Finally, each element of the column was divided by the sum of all its elements to determine the normalized final weight of each sub-criterion. The results are shown in the last column of Table 6.
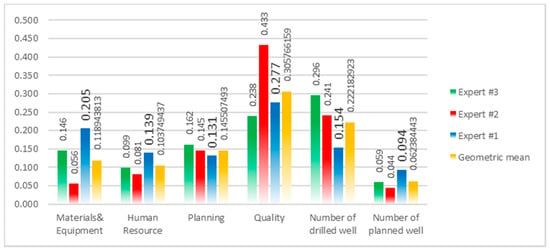
Figure 5.
Comparative Analysis of Criteria Weights based on Expert Opinions.

Table 6.
Calculation of Sub-Criteria Weights for individual Experts and Normalized Final Weights.
As found, some criteria such as the number of drilled wells and the sub-criteria such as the actual cost compliance percentage with planned costs and the percentage of waiting time to total well drilling time have been identified as the most important sub-criteria. Table 7 shows the ranking of the criteria in terms of importance.

Table 7.
Rankings of Sub-criteria in order of importance.
Now, as the weight and importance of the criteria determined, the evaluation of each alternative in terms of all criteria was carried out by the experts using the linguistic variables in Table 2. The results are presented in Table 8.

Table 8.
Initial Decision Matrix on Linguistic Variables.
Then, the qualitative values were converted into quantitative values using Table 2, in order to establish the initial decision-making tables for the three experts. Table 9, Table 10 and Table 11 provide the quantitative values for the experts.

Table 9.
Initial Decision Matrix for Expert #1 with Quantitative Values.

Table 10.
Initial Decision Matrix for Expert #2 with Quantitative Values.

Table 11.
Initial Decision Matrix for Expert #3 with Quantitative Values.
Next, using Equations (18)–(22), the fuzzy values in the decision matrix of three experts were converted into fuzzy numbers with interval values, as shown in Table 12.

Table 12.
Aggregated Decision Matrix as Fuzzy Numbers with Interval Values.
Table 12 presents the ideal alternative using Equations (35)–(40). In the next step using Equation (41), the interval valued fuzzy decision matrix (Table 12) was normalized. The normalized matrix is shown in Table 13.

Table 13.
Normalized Decision Matrix as Fuzzy Numbers with Interval Values.
Here, the weighting values obtained from the SWARA method normalized and aggregated in the final column of Table 6 and also Equation (43) were applied to achieve the normalized decision matrix with fuzzy intervals, as shown in Table 14.

Table 14.
Normalized weighted Decision Matrix with Interval-valued Fuzzy Numbers.
Following the fourth step of the ARAS method and using Equation (44), the values of S, presented as interval-valued fuzzy numbers, were calculated. To perform the fifth step of the ARAS method and compute the Q values, we have to convert the interval-valued fuzzy numbers of S to Crisp numbers by using Equations (23)–(26). The conversion and calculations for each alternative are displayed for different values of λ in Table 15.

Table 15.
Final ARAS calculations with interval values and Alternative rankings.
As seen, for different values of λ, Project #2 can be selected as the ideal alternative. The analytical discussion confirms its higher score for the criteria such as the quality of materials and goods used, scientific levels of drilling specialists working in the project, as well as the actual cost compliance percentage with planned cost.
5. Conclusions and Recommendations
The necessity of project performance evaluation is crucial and undeniable which helps projects identify weaknesses and strengths as well as recognize and improve inefficiencies. Therefore several project performance evaluation approach has been used and advanced over the years that MCDM models is one of them. As a result, due to the complexity of the projects, and in order to achieve a better imagination of environmental ambiguities and overcome the inherent uncertainty of the projects, in this study, an Interval-Valued Fuzzy Additive Ratio Assessment (ARAS) Method proposed as a novel MCDM approach for evaluating the projects. On the other hand, despite the importance and certain position of oil and gas well drilling projects as well as its impact on the economies of countries, no structured assessment methodology has been presented for these types of projects and research works show the lack of literature in this field. So, the oil and gas well drilling projects selected as a case study. Given the limited research on performance evaluation in the context of such operations, the initial list of criteria and sub-criteria of evaluation obtained from available literature, was improved using the Fuzzy Delphi method. In order to determine criteria weights, the importance value of each final criterion was calculated through SWARA method based on expert opinions. As the performance scores of projects were determined with respect to defined criteria, a set of seven Iranian oil and gas projects were ranked by using interval-valued fuzzy ARAS method. The results revealed six general assessment criteria for oil and gas well-drilling projects including: number of planned wells, number of drilled wells, materials & equipment, Human resource, quality and planning. However, the third to sixth criteria consist of several sub-criteria among which the number of drilled wells, actual cost compliance percentage with planned costs and percentage of waiting time to total well drilling time were defined as the most important sub-criteria. From the projects being studied, Project #2 was defined as the best alternative due to its distinguished performance in terms of sub-criteria of type of drilling rigs, number of operational experts working on the project, scientific levels of drilling specialists working in the project, type of drilled wells in terms of operational risk and actual cost compliance percentage with planned cost. Rather, Project #3 was considered as the weakest alternative. The managerial investigation of Project #2 showed that management stability, along with the use of new methods for employee assessment, as well as the implementation of knowledge management methods had significant role in the success of that project, while Project #3 presented frequently-changed management. The innovations of this study include the development of a comprehensive list of criteria and sub-criteria in performance evaluation of oil and gas well-drilling projects by using Fuzzy Delphi, SWARA and interval-valued fuzzy ARAS methods.
As mentioned before, there are unpredictable issues in the process of conducting research that are one of the sources of uncertainties having been emphasized in the literature. It seems that stochastic MADM methods which have been considered in the recent year’s literature can be used in future researches. On the other hand, performing drilling projects is time-consuming and the evaluation of options and the criteria weights may change over time due to changes in both the macro environment and the preferences and the priorities of the experts. Hence, the use of the prospective MADM method is recommended to better cover possible changes. Also, in future researches, we can use aggregate operators to integrate experts’ opinions and hesitant fuzzy sets to further investigate the sensitive analysis of decisions which are taken.
Finally, we assumed that identified criteria are independent from each other. Future research can examine the existence of this dependency and in case of confirmation of the relationship between criteria; they can use appropriate methods (Like ANP, DEMATEL and ISM).
Author Contributions
Each author has participated and contributed sufficiently to take public responsibility for appropriate portions of the content. (Jalil Heidary Dahooie and Edmundas Kazimieras Zavadskas developed the methodology; Amirsalar Vanaki analyzed the results of case study; Mahdi Abolhasani wrote the paper; Zenonas Turskis revised and improved the paper.)
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salazar-Aramayo, J.L.; Rodrigues-da-Silveira, R.; Rodrigues-de-Almeida, M.; de Castro-Dantas, T.N. A conceptual model for project management of exploration and production in the oil and gas industry: The case of a Brazilian company. Int. J. Proj. Manag. 2013, 31, 589–601. [Google Scholar] [CrossRef]
- Lewis, J.P. The Project Manager’s Desk Reference: A Comprehensive Guide to Project Planning, Scheduling, Evaluation, Control and Systems; McGraw-Hill Inc.: Chicago, IL, USA, 1999. [Google Scholar]
- Institute, P.M.; Staff, P.M.I. A Guide to The Project Management Body of Knowledge (PMBOK Guide), 3rd ed.; An American National Standard, ANSI/PMI 99-001-2004; Project Management Institute: Sydney, Australia, 2004. [Google Scholar]
- Ahari, R.M.; Niaki, S.T.A. A hybrid approach based on locally linear neuro-fuzzy modeling and TOPSIS to determine the quality grade of gas well-drilling projects. J. Pet. Sci. Eng. 2014, 114, 99–106. [Google Scholar] [CrossRef]
- Butt, A.; Naaranoja, M.; Savolainen, J. Project change stakeholder communication. Int. J. Proj. Manag. 2016, 34, 1579–1595. [Google Scholar] [CrossRef]
- Xu, Y.; Yeh, C.-H. A performance-based approach to project assignment and performance evaluation. Int. J. Proj. Manag. 2014, 32, 218–228. [Google Scholar] [CrossRef]
- Cao, Q.; Hoffman, J.J. A case study approach for developing a project performance evaluation system. Int. J. Proj. Manag. 2011, 29, 155–164. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Karabulut, Y. Energy project performance evaluation with sustainability perspective. Energy 2017, 119, 549–560. [Google Scholar] [CrossRef]
- Haralambopoulos, D.; Polatidis, H. Renewable energy projects: Structuring a multi-criteria group decision-making framework. Renew. Energy 2003, 28, 961–973. [Google Scholar] [CrossRef]
- Barfod, M.B. An MCDA approach for the selection of bike projects based on structuring and appraising activities. Eur. J. Oper. Res. 2012, 218, 810–818. [Google Scholar] [CrossRef]
- Wei, G.; Zhao, X. Induced hesitant interval-valued fuzzy Einstein aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2013, 24, 789–803. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Gorzałczany, M.B. A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Baležentis, T.; Zeng, S. Group multi-criteria decision making based upon interval-valued fuzzy numbers: An extension of the MULTIMOORA method. Expert Syst. Appl. 2013, 40, 543–550. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Hajiagha, S.H.R.; Hashemi, S.S. Extension of weighted aggregated sum product assessment with interval-valued intuitionistic fuzzy numbers (WASPAS-IVIF). Appl. Soft Comput. 2014, 24, 1013–1021. [Google Scholar] [CrossRef]
- Grimsey, D.; Lewis, M.K. Evaluating the risks of public private partnerships for infrastructure projects. Int. J. Proj. Manag. 2002, 20, 107–118. [Google Scholar] [CrossRef]
- Castillo, L.; Dorao, C.A. Decision-making in the oil and gas projects based on game theory: Conceptual process design. Energy Convers. Manag. 2013, 66, 48–55. [Google Scholar] [CrossRef]
- Luo, D.; Zhao, X. Modeling the operating costs for petroleum exploration and development projects. Energy 2012, 40, 189–195. [Google Scholar] [CrossRef]
- Osmundsen, P.; Toft, A.; Agnar Dragvik, K. Design of drilling contracts—Economic incentives and safety issues. Energy Policy 2006, 34, 2324–2329. [Google Scholar] [CrossRef]
- Ahari, R.M.; Niaki, S.T.A. Contractor selection in gas well-drilling projects with quality evaluation using Neuro-fuzzy networks. IERI Procedia 2014, 10, 274–279. [Google Scholar] [CrossRef]
- Dachyar, M.; Pratama, N.R. Performance evaluation of a drilling project in oil and gas service company in Indonesia by MACBETH method. J. Phys. Conf. Ser. 2014, 495, 012012. [Google Scholar] [CrossRef]
- Martinsuo, M.; Korhonen, T.; Laine, T. Identifying, framing and managing uncertainties in project portfolios. Int. J. Proj. Manag. 2014, 32, 732–746. [Google Scholar] [CrossRef]
- Marques, G.; Gourc, D.; Lauras, M. Multi-criteria performance analysis for decision making in project management. Int. J. Proj. Manag. 2011, 29, 1057–1069. [Google Scholar] [CrossRef]
- Kähkönen, K. Level of complexity in projects and its impacts on managerial solutions. Int. Proj. Manag. Assoc. 2008, XXIX, 3. [Google Scholar]
- Turner, J.R.; Müller, R. On the nature of the project as a temporary organization. Int. J. Proj. Manag. 2003, 21, 1–8. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Liou, J.J.; Chiu, C.-Y. A Consistent Fuzzy Preference Relations Based ANP Model for R&D Project Selection. Sustainability 2017, 9, 1352. [Google Scholar]
- Strojny, J.; Szulc, J.; Baran, M. Applying the AHP Method into the Assessment of Project Attitudes. In Eurasian Business Perspectives; Springer: New York, NY, USA, 2018; pp. 183–197. [Google Scholar]
- Aragonés-Beltrán, P.; Chaparro-González, F.; Pastor-Ferrando, J.-P.; Pla-Rubio, A. An AHP (Analytic Hierarchy Process)/ANP (Analytic Network Process)-based multi-criteria decision approach for the selection of solar-thermal power plant investment projects. Energy 2014, 66, 222–238. [Google Scholar] [CrossRef]
- He, Q.; Luo, L.; Hu, Y.; Chan, A.P. Measuring the complexity of mega construction projects in China—A fuzzy analytic network process analysis. Int. J. Proj. Manag. 2015, 33, 549–563. [Google Scholar] [CrossRef]
- Ozcan, U.; Dogan, A.; Soylemez, I. Evaluation of Research Projects of Undergraduate Students in an Engineering Department Using Topsis Method. Eurasia Proc. Educ. Soc. Sci. 2016, 5, 420–424. [Google Scholar]
- Altuntas, S.; Dereli, T. A novel approach based on DEMATEL method and patent citation analysis for prioritizing a portfolio of investment projects. Expert Syst. Appl. 2015, 42, 1003–1012. [Google Scholar] [CrossRef]
- Beccali, M.; Cellura, M.; Mistretta, M. Decision-making in energy planning. Application of the Electre method at regional level for the diffusion of renewable energy technology. Renew. Energy 2003, 28, 2063–2087. [Google Scholar] [CrossRef]
- Çolak, M.; Kaya, İ. Prioritization of renewable energy alternatives by using an integrated fuzzy MCDM model: A real case application for Turkey. Renew. Sustain. Energy Rev. 2017, 80, 840–853. [Google Scholar] [CrossRef]
- Anagnostopoulos, K.; Doukas, H.; Psarras, J. A linguistic multicriteria analysis system combining fuzzy sets theory, ideal and anti-ideal points for location site selection. Expert Syst. Appl. 2008, 35, 2041–2048. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.-Q.; Zhang, H.-Y.; Chen, X.-H. Multi-criteria decision-making based on hesitant fuzzy linguistic term sets: An outranking approach. Knowl. Based Syst. 2015, 86, 224–236. [Google Scholar] [CrossRef]
- Riera, J.V.; Massanet, S.; Herrera-Viedma, E.; Torrens, J. Some interesting properties of the fuzzy linguistic model based on discrete fuzzy numbers to manage hesitant fuzzy linguistic information. Appl. Soft Comput. 2015, 36, 383–391. [Google Scholar] [CrossRef]
- Yavuz, M.; Oztaysi, B.; Onar, S.C.; Kahraman, C. Multi-criteria evaluation of alternative-fuel vehicles via a hierarchical hesitant fuzzy linguistic model. Expert Syst. Appl. 2015, 42, 2835–2848. [Google Scholar] [CrossRef]
- Sanchez, M.A.; Castro, J.R.; Castillo, O.; Mendoza, O.; Rodriguez-Diaz, A.; Melin, P. Fuzzy higher type information granules from an uncertainty measurement. Granul. Comput. 2017, 2, 95–103. [Google Scholar] [CrossRef]
- Das, S.; Kar, S.; Pal, T. Robust decision making using intuitionistic fuzzy numbers. Granul. Comput. 2017, 2, 41–54. [Google Scholar] [CrossRef]
- Liu, P.; Mahmood, T.; Khan, Q. Multi-Attribute Decision-Making Based on Prioritized Aggregation Operator under Hesitant Intuitionistic Fuzzy Linguistic Environment. Symmetry 2017, 9, 270. [Google Scholar] [CrossRef]
- Dubois, D.J. Fuzzy Sets and Systems: Theory and Applications; Academic Press: Cambridge, MA, USA, 1980; Volume 144. [Google Scholar]
- Feng, F.; Li, Y.; Leoreanu-Fotea, V. Application of level soft sets in decision making based on interval-valued fuzzy soft sets. Comput. Math. Appl. 2010, 60, 1756–1767. [Google Scholar] [CrossRef]
- Xu, Z.; Gou, X. An overview of interval-valued intuitionistic fuzzy information aggregations and applications. Granul. Comput. 2017, 2, 13–39. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.; Shu, Y. Interval-valued intuitionistic multiplicative aggregation in group decision making. Granul. Comput. 2017, 2, 387–407. [Google Scholar] [CrossRef]
- Meng, S.; Liu, N.; He, Y. GIFIHIA operator and its application to the selection of cold chain logistics enterprises. Granul. Comput. 2017, 2, 187–197. [Google Scholar] [CrossRef]
- Wang, C.; Fu, X.; Meng, S.; He, Y. Multi-attribute decision-making based on the SPIFGIA operators. Granul. Comput. 2017, 2, 321–331. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z. The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl. Soft Comput. 2017, 60, 167–179. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Operations on type-2 fuzzy sets. Fuzzy Sets Syst. 2001, 122, 327–348. [Google Scholar] [CrossRef]
- Liu, P. A weighted aggregation operators multi-attribute group decision-making method based on interval-valued trapezoidal fuzzy numbers. Expert Syst. Appl. 2011, 38, 1053–1060. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, H. Managing multi-granularity linguistic information in qualitative group decision making: An overview. Granul. Comput. 2016, 1, 21–35. [Google Scholar] [CrossRef]
- Zhang, H. Some interval-valued 2-tuple linguistic aggregation operators and application in multiattribute group decision making. Appl. Math. Model. 2013, 37, 4269–4282. [Google Scholar] [CrossRef]
- Mendel, J.M. A comparison of three approaches for estimating (synthesizing) an interval type-2 fuzzy set model of a linguistic term for computing with words. Granul. Comput. 2016, 1, 59–69. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F. A social network analysis trust–consensus based approach to group decision-making problems with interval-valued fuzzy reciprocal preference relations. Knowl. Based Syst. 2014, 59, 97–107. [Google Scholar] [CrossRef]
- Reiser, R.H.S.; Bedregal, B.; Dos Reis, G. Interval-valued fuzzy coimplications and related dual interval-valued conjugate functions. J. Comput. Syst. Sci. 2014, 80, 410–425. [Google Scholar] [CrossRef]
- Qin, J. Interval type-2 fuzzy Hamy mean operators and their application in multiple criteria decision making. Granul. Comput. 2017, 2, 249–269. [Google Scholar] [CrossRef]
- Vahdani, B.; Hadipour, H.; Sadaghiani, J.S.; Amiri, M. Extension of VIKOR method based on interval-valued fuzzy sets. Int. J. Adv. Manuf. Technol. 2010, 47, 1231–1239. [Google Scholar] [CrossRef]
- Chatterjee, K.; Kar, S. Unified Granular-number-based AHP-VIKOR multi-criteria decision framework. Granul. Comput. 2017, 2, 199–221. [Google Scholar] [CrossRef]
- Ashtiani, B.; Haghighirad, F.; Makui, A.; ali Montazer, G. Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets. Appl. Soft Comput. 2009, 9, 457–461. [Google Scholar] [CrossRef]
- Liu, P.; You, X. Probabilistic linguistic TODIM approach for multiple attribute decision-making. Granul. Comput. 2017, 2, 333–342. [Google Scholar] [CrossRef]
- Campeol, G.; Carollo, S.; Masotto, N. Infrastructural projects and territorial development in Veneto Dolomites: Evaluation of performances through AHP. Procedia Soc. Behav. Sci. 2016, 223, 468–474. [Google Scholar] [CrossRef]
- Osmundsen, P.; Sørenes, T.; Toft, A. Offshore oil service contracts new incentive schemes to promote drilling efficiency. J. Pet. Sci. Eng. 2010, 72, 220–228. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q.; Wang, Y. Risk analysis in ultra deep scientific drilling project—A fuzzy synthetic evaluation approach. Int. J. Proj. Manag. 2013, 31, 449–458. [Google Scholar] [CrossRef]
- Ngacho, C.; Das, D. A performance evaluation framework of development projects: An empirical study of constituency development fund (CDF) construction projects in Kenya. Int. J. Proj. Manag. 2014, 32, 492–507. [Google Scholar] [CrossRef]
- Bassioni, H.A.; Price, A.D.F.; Hassan, T.M. Performance measurement in construction. J. Manag. Eng. 2004, 20, 42–50. [Google Scholar] [CrossRef]
- Hare, B.; Cameron, I.; Roy Duff, A. Exploring the integration of health and safety with pre-construction planning. Eng. Constr. Archit. Manag. 2006, 13, 438–450. [Google Scholar] [CrossRef]
- Haslam, R.A.; Hide, S.A.; Gibb, A.G.F.; Gyi, D.E.; Pavitt, T.; Atkinson, S.; Duff, A.R. Contributing factors in construction accidents. Appl. Ergon. 2005, 36, 401–415. [Google Scholar] [CrossRef] [PubMed]
- Ortega, I. Systematic prevention of construction failures: An overview. Technol. Law Insur. 2000, 5, 15–22. [Google Scholar] [CrossRef]
- Tabish, S.Z.S.; Jha, K.N. Analyses and evaluation of irregularities in public procurement in India. Constr. Manag. Econ. 2011, 29, 261–274. [Google Scholar] [CrossRef]
- Eriksson, P.E.; Westerberg, M. Effects of cooperative procurement procedures on construction project performance: A conceptual framework. Int. J. Proj. Manag. 2011, 29, 197–208. [Google Scholar] [CrossRef]
- Ali, A.S.; Rahmat, I. The performance measurement of construction projects managed by ISO-certified contractors in Malaysia. J. Retail Leis. Prop. 2010, 9, 25–35. [Google Scholar] [CrossRef]
- Chan, A.P.C. Key performance indicators for measuring construction success. Benchmarking 2004, 11, 203–221. [Google Scholar] [CrossRef]
- Fuentes, R.; Fuster, B.; Lillo-Bañuls, A. A three-stage DEA model to evaluate learning-teaching technical efficiency: Key performance indicators and contextual variables. Expert Syst. Appl. 2016, 48, 89–99. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252. [Google Scholar] [CrossRef]
- Li, K.; Lin, B. Impact of energy conservation policies on the green productivity in China’s manufacturing sector: Evidence from a three-stage DEA model. Appl. Energy 2016, 168, 351–363. [Google Scholar] [CrossRef]
- Oral, M.; Oukil, A.; Malouin, J.-L.; Kettani, O. The appreciative democratic voice of DEA: A case of faculty academic performance evaluation. Socio Econ. Plan. Sci. 2014, 48, 20–28. [Google Scholar] [CrossRef]
- Tongzon, J. Efficiency measurement of selected Australian and other international ports using data envelopment analysis. Transp. Res. Part A Policy Pract. 2001, 35, 107–122. [Google Scholar] [CrossRef]
- Menkhoff, L.; Schmidt, U.; Brozynski, T. The impact of experience on risk taking, overconfidence, and herding of fund managers: Complementary survey evidence. Eur. Econ. Rev. 2006, 50, 1753–1766. [Google Scholar] [CrossRef]
- Schmidt, F.L.; Hunter, J.E.; Outerbridge, A.N. Impact of job experience and ability on job knowledge, work sample performance, and supervisory ratings of job performance. J. Appl. Psychol. 1986, 71, 432–439. [Google Scholar] [CrossRef]
- Paquin, J.-P.; Gauthier, C.; Morin, P.-P. The downside risk of project portfolios: The impact of capital investment projects and the value of project efficiency and project risk management programmes. Int. J. Proj. Manag. 2016, 34, 1460–1470. [Google Scholar] [CrossRef]
- Jankowski, J.E. Do we need a price index for industrial R&D? Res. Policy 1993, 22, 195–205. [Google Scholar]
- McGrath, M. The R&D effectiveness index: A metric for product development performance. J. Prod. Innov. Manag. 1994, 11, 213–220. [Google Scholar]
- Meredith, J. Alternative research paradigms in operations. J. Oper. Manag. 1989, 8, 297–326. [Google Scholar] [CrossRef]
- Kardaras, D.K.; Karakostas, B.; Mamakou, X.J. Content presentation personalisation and media adaptation in tourism web sites using fuzzy Delphi method and fuzzy cognitive maps. Expert Syst. Appl. 2013, 40, 2331–2342. [Google Scholar] [CrossRef]
- Okoli, C.; Pawlowski, S.D. The Delphi method as a research tool: An example, design considerations and applications. Inf. Manag. 2004, 42, 15–29. [Google Scholar] [CrossRef]
- Kuo, Y.-F.; Chen, P.-C. Constructing performance appraisal indicators for mobility of the service industries using fuzzy Delphi method. Expert Syst. Appl. 2008, 35, 1930–1939. [Google Scholar] [CrossRef]
- Murray, T.J.; Pipino, L.L.; van Gigch, J.P. A pilot study of fuzzy set modification of Delphi. Hum. Syst. Manag. 1985, 5, 76–80. [Google Scholar]
- Hsu, T.; Yang, T. Application of fuzzy analytic hierarchy process in the selection of advertising media. J. Manag. Syst. 2000, 7, 19–39. [Google Scholar]
- Tzeng, G.H.; Teng, J.Y. Transportation investment project selection with fuzzy multiobjectives. Transp. Plan. Technol. 1993, 17, 91–112. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Aghdaie, M.H.; Derakhti, A.; Zavadskas, E.K.; Morshed Varzandeh, M.H. Decision making on business issues with foresight perspective; an application of new hybrid MCDM model in shopping mall locating. Expert Syst. Appl. 2013, 40, 7111–7121. [Google Scholar] [CrossRef]
- Keršuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (Swara). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Morshed Varzandeh, M.H. A new hybrid model using Step-Wise Weight Assessment Ratio Analysis (SWARA) technique and Adaptive Neuro-Fuzzy Inference System (ANFIS) for regional landslide hazard assessment in Iran. CATENA 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Bahrami, M. Investment prioritizing in high tech industries based on SWARA-COPRAS approach. Technol. Econ. Dev. Econ. 2014, 20, 534–553. [Google Scholar] [CrossRef]
- Chen, S.-J.; Chen, S.-M. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers. IEEE Trans. Fuzzy Syst. 2003, 11, 45–56. [Google Scholar] [CrossRef]
- Yao, J.-S.; Lin, F.-T. Constructing a fuzzy flow-shop sequencing model based on statistical data. Int. J. Approx. Reason. 2002, 29, 215–234. [Google Scholar] [CrossRef]
- Chen, S.-J.; Chen, S.-M. Fuzzy risk analysis based on measures of similarity between interval-valued fuzzy numbers. Comput. Math. Appl. 2008, 55, 1670–1685. [Google Scholar] [CrossRef]
- Chen, C.-T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Mahdavi, I.; Mahdavi-Amiri, N.; Heidarzade, A.; Nourifar, R. Designing a model of fuzzy TOPSIS in multiple criteria decision making. Appl. Math. Comput. 2008, 206, 607–617. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Elhag, T.M. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006, 31, 309–319. [Google Scholar] [CrossRef]
- Wei, S.-H.; Chen, S.-M. Fuzzy risk analysis based on interval-valued fuzzy numbers. Expert Syst. Appl. 2009, 36, 2285–2299. [Google Scholar] [CrossRef]
- Tupenaite, L.; Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Seniut, M. Multiple criteria assessment of alternatives for built and human environment renovation. J. Civ. Eng. Manag. 2010, 16, 257–266. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Zavadskas, E.; Turskis, Z.; Vilutiene, T. Multiple criteria analysis of foundation instalment alternatives by applying Additive Ratio Assessment (ARAS) method. Arch. Civ. Mech. Eng. 2010, 10, 123–141. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).