Abstract
As shown in former papers, the nonadiabatic Heisenberg model presents a mechanism of Cooper pair formation generated by the strongly correlated atomic-like motion of the electrons in narrow, roughly half-filled “superconducting bands” of special symmetry. The formation of Cooper pairs is not only the result of an attractive electron–electron interaction but is additionally the outcome of quantum mechanical constraining forces. There is theoretical and experimental evidence that only these constraining forces operating in superconducting bands may produce eigenstates in which the electrons form Cooper pairs. Here, we report evidence that also the experimentally found superconducting state in bismuth at ambient as well as at high pressure is stabilized by constraining forces.
1. Introduction
Bismuth shows sequential structure transition as a function of the applied pressure, as summarized in an illustrative form by Degtyareva et al. [1]:
At ambient pressure, Bi crystallizes in the structure Bi–I, an As-type structure with a trigonal (rhombohedral) space group and two atoms in the unit cell [2]. This structure is stable up to a pressure of 2.55 GPa. Then, with increasing pressure, Bi undergoes the monoclinic structure Bi–II and the host–guest structure Bi–III. A further structure called Bi–IV exists above the temperature of 450 K and is not relevant in this paper. Between a pressure of 7.7 and (at least) 122 GPa, the cubic Bi–V phase is stable [1].
It is interesting that all of these Bi phases become superconducting at low temperatures. The Bi–I phase is superconducting with the extremely low transition temperature mK [3]. In the Bi–II and Bi–III structures, the transition temperature increases with increasing pressure from about 4 K to 7 K. Finally, in the Bi–V phase, has the maximum value of about 8 K [4]. The different values of are evidently connected with the different crystal structures since changes discontinuously at the transitions from one structure to another [4].
This striking symmetry-dependence of the superconducting transition temperature suggests that also in bismuth superconductivity can be understood within the group-theoretical nonadiabatic Heisenberg model (NHM) [5], a model of strongly correlated atomic-like electrons in the nonadiabatic system. The NHM considers two types of narrow, roughly half-filled energy bands: The Bloch functions of the first type can be unitarily transformed into optimally localized Wannier functions adapted to the symmetry of a magnetic structure. These bands are called “magnetic bands” because they evidently stabilize the related magnetic structure [6]. The importance of magnetic bands was demonstrated in several former papers, for example also in our forgoing paper [7]. The present paper, however, does not consider magnetic bands but only the second type of roughly half-filled energy bands, called “superconducting bands”.
The Bloch functions of a superconducting band can be unitarily transformed into optimally localized spin-dependent Wannier functions adapted to the symmetry of the full space group (Definition 22 of Ref. [6]). There is both experimental and theoretical evidence that narrow, roughly half-filled superconducting bands stabilize superconductivity in any superconductor, whether it is a conventional, a high- or other superconductor. This we concluded, first, from the symmetry of the Bloch functions in the band structures of (at present 24) superconductors and non-superconductors. Under these materials, we did not find any superconductor not possessing a roughly half-filled superconducting band, and, on the other hand, we did not find a non-superconductor possessing a roughly half-filled superconducting band (see Section 1 of Ref. [6]). These findings we call above the “experimental” evidence.
The “theoretical” evidence is provided by the NHM in terms of superconducting eigenstates. The above-mentioned striking observation on 24 materials can be interpreted within the NHM defining a nonadiabatic mechanism of Cooper pair formation in narrow, roughly half-filled superconducting bands, which is characterized by constraining forces. Within this model, the formation of Cooper pairs is still mediated by boson excitations responsible, as usual, for the isotope effect. However, these boson excitations produce constraining forces as they are familiar from classical mechanics: below , they reduce the degrees of freedom of the electron system by forcing the electrons to form Cooper pairs. Indeed, there is evidence that these constraining forces operating in narrow, roughly half-filled superconducting bands are required for the Hamiltonian of the system to possess eigenstates in which the electrons form Cooper pairs [8]. A short description of the NHM and this mechanism of Cooper pair formation is given in Section 2 and Section 3, respectively, of Ref. [9]. In Section 5, we shall summarize this concept of superconductivity in the form of single statements.
The aim of the present paper is to corroborate the assertion that narrow, roughly half-filled superconducting bands stabilize superconductivity in any material: The paper provides evidence that also the experimentally established superconductivity in bismuth [3,4] is stabilized by superconducting bands.
In this context, we consider (in Section 3) only the two structures Bi–I and Bi–V at the beginning and the end of the Sequence (1). Bi–I and Bi–V possess the lowest and highest superconducting transition temperatures, respectively. Bi–II is not very informative within the NHM since it only has a low monoclinic symmetry. At this stage, it would be complicated to apply the NHM to the incommensurate host–guest structure of Bi–III. Both Bi–I and Bi–V, on the other hand, have clear symmetries with the trigonal space group (166) and the cubic space group (229), respectively [1,2]. Bi–V even has the highest possible symmetry in a solid state, which allows the NHM to make clear predictions.
2. Group-Theoretical and Computational Methods Used in the Paper
The starting point for any application of the NHM is the band structure of the considered material, in the present case, the band structures of Bi–I and Bi–V depicted in Figures 1 and 2, respectively. They are calculated by the “Fritz Haber Institute ab initio molecular simulations” (FHI-aims) computer program. The production method is the density functional theory (DFT) [10,11] to compute the total energy in the electronic ground state.
The NHM does not use the exact total energies of the electrons, but only the more qualitative run of the energy bands. It starts from the symmetry of the Bloch states in the points of symmetry in the respective Brillouin zone. Fortunately, the FHI-aims program provides the possibility of an output of the eigenvectors (thanks to Volker Blum) at any wave vector . These eigenvectors are spherical harmonics. The FHI-aims program produces typically several thousand eigenvectors. We have written a C++ computer program selecting the relevant eigenvectors at the points of symmetry and determining their symmetry using the equations given in Section 2 of Ref. [12]. The found symmetry labels are given in Figures 1 and 2, the notations of the symmetry labels are defined in Table A1 and Table A6.

Table A1.
Character tables of the single-valued irreducible representations of the trigonal space group (166) of Bi–I.

Table A6.
Character tables of the single-valued irreducible representations of the space group = of Bi–V.
Starting from the symmetry of the Bloch states in the points of symmetry, we determine the symmetry of all the optimally localized Wannier functions existing in the band structures of Bi–I and Bi–V. The basis is the group theory of Wannier functions as presented in general terms in Ref. [6]. “In general terms” means that the symmetry properties of the best localized Wannier functions are defined in any conceivable band structure in every space group. The determination of the symmetry of the optimally localized Wannier functions is a complex process, which again we solve by means of a C++ computer program. The results are given in the Tables of the Appendix A and Appendix B. The notes to the Tables give (in a very compact form) important hints about how the symmetry adapted Wannier functions are determined from the equations in Ref. [6].
3. Superconducting Bands in the Band Structure of Bismuth
3.1. Band Structure of Bi–I
The band structure of Bi–I is depicted in Figure 1. The Bloch functions of the band highlighted in red are labeled by the single-valued representations
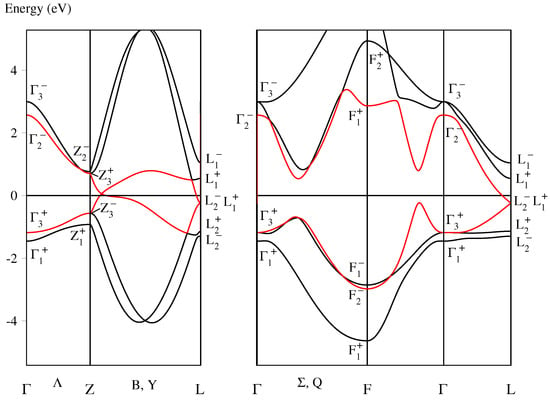
Figure 1.
Band structure of Bi–I calculated by the “Fritz Haber Institute ab initio molecular simulations” (FHI-aims) program [10,11], using the structure parameters given by Degtyareva et al. [1]. The symmetry labels are determined by the author. Bi–I has the trigonal space group [2] (international number 166), the notations of the points and lines of symmetry in the Brillouin zone for follow Figure 3.11b of Ref. [12], and the symmetry labels are defined in Table A1. denotes the Fermi level. The band highlighted in red is the superconducting band.
It is clear that this band (or any other band in the band structure) is neither identical with band 1 nor with band 2 in Table A4, meaning that we cannot unitarily transform the Bloch functions into best localized and symmetry-adapted Wannier functions situated at the Bi atoms. The situation is changed when we consider the double-valued representations of the Bloch functions:

Table A4.
Single-valued representations of all the energy bands in the space group of Bi–I with symmetry-adapted and optimally localized usual (i.e., spin-independent) Wannier functions centered at the Bi atoms.
According to Table A3, we may unitarily transform the Bloch functions (2) into Bloch functions labeled by the double-valued representations:

Table A3.
Compatibility relations between the single-valued (upper row) and double-valued (lower row) representations of the space group .
The underlined representations belong to the band listed in Table A5. Thus, we can unitarily transform the Bloch functions of this band into spin-dependent Wannier functions being best localized, centered at the Bi atoms, and symmetry-adapted to the group . Consequently, according to Definition 22 of Ref. [6], the band highlighted in red is a superconducting band.

Table A5.
Double-valued representations of the superconducting band in the space group of Bi–I.
3.2. Band Structure of Bi–V
The band structure of Bi–V is depicted in Figure 2. The Bloch functions of the band highlighted in red now are labeled by the single-valued representations
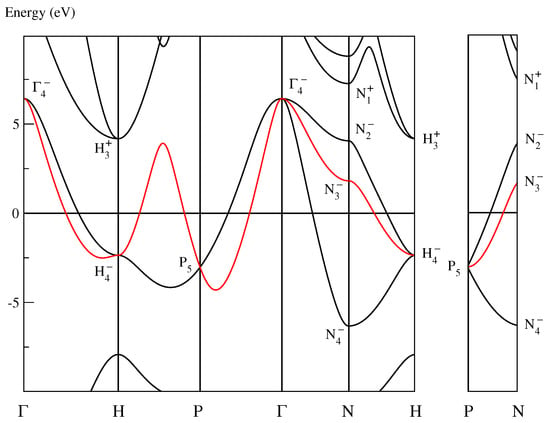
Figure 2.
Band structure of Bi–V at the pressure of 13.5 GPa calculated by the FHI-aims program [10,11], using the structure parameters at this pressure as given by Degtyareva et al. [1]. The symmetry labels are determined by the author. Bi–V has the cubic space group [1] (international number 229), the notations of the points and lines of symmetry in the Brillouin zone for follow 3.15 of Ref. [12], and the symmetry labels are defined in Table A6. denotes the Fermi level. The band highlighted in red forms the superconducting band.
Again, this band (or any other band in the band structure) has not the symmetry of any band listed in Table A8. Hence, we cannot unitarily transform the Bloch functions into best localized and symmetry-adapted Wannier functions situated at the Bi atoms. However, according to Table A7, we may unitarily transform the Bloch functions (4) into Bloch functions labeled by the double-valued representations,

Table A8.
Single-valued representations of the space group of all the energy bands of Bi–V with symmetry-adapted and optimally localized usual (i.e., spin-independent) Wannier functions centered at the Bi atoms.

Table A7.
Compatibility relations between the single-valued (upper row) and double-valued (lower row) representations of the space group .
The underlined representations belong to band 4 listed in Table A9. Thus, we can unitarily transform the Bloch functions of this band into spin-dependent Wannier functions being best localized, centered at the Bi atoms, and symmetry-adapted to the group . Consequently, according to Definition 22 of Ref. [6], the band highlighted in red is a superconducting band.

Table A9.
Double-valued representations of the space group of all the energy bands of Bi–V with symmetry-adapted and optimally localized spin-dependent Wannier functions centered at the Bi atoms.
4. Results
Both structures Bi–I and Bi–V possess a superconducting band in their band structure that
- is one of the narrowest bands in the band structure,
- is nearly half filled,
- and comprises a great part of the electrons at the Fermi level.
Consequently, the NHM predicts that both phases become superconducting. The transition temperature is calculated in the Bardeen-Cooper-Schrieffer (BCS) limit by the well-known BCS formula [13]
where still denotes the Debye temperature. However, the NHM modifies the interpretation of the other parameter in the BCS formula in that now N and V stand for the partial quantities within the superconducting band alone: N denotes the partial density of states of the electrons at the Fermi level and V denotes the partial effective electron–phonon interaction [8].
The superconducting band of Bi–I even comprises all the electrons at the Fermi level. However, the small Fermi surface and the small density of states N at the Fermi level [3] results in a extremely low superconducting transition temperature . Indeed, Prakash et al. [3] found mK.
The superconducting band of Bi–V closely resembles the superconducting band of niobium as depicted, e.g., in Figure 1 of Ref. [8]: both nearly half-filled bands have comparable widths and comprise a comparable part of the Fermi level. Thus, we may expect that the parameters in the BCS Formula (6) of both materials are also comparable. Consequently, the NHM predicts that both the Bi–V phase of bismuth and the elemental metal niobium have similar transition temperatures. Indeed, we have K and K for Bi–V and niobium, respectively. Narrow and half-filled superconducting bands rarely arise in crystals with the high bcc symmetry. Thus, the elemental bcc metals Ta, W, and Mo possess superconducting bands that are far from being half-filled and, consequently, have lower transition temperatures. In the band structures of the most elemental metals (such as Li, Na, K, Rb, Cs, Ca Cu, Ag, and Au), narrow, roughly half-filled superconducting bands cannot be found and, hence, these metals do not become superconducting [14].
In summary, the paper provides evidence that the superconducting states in both Bi–I and Bi–V are connected with the narrow and almost perfectly half-filled superconducting band in the related band structure. Thus, it provides evidence that also in bismuth the superconducting state is stabilized by constraining forces.
5. Discussion
This group-theoretical result demonstrates again [6] the significance of the concept of superconductivity defined within the NHM. In this section, we shortly summarize the main features of this concept (for a more detailed description, see Ref. [9]).
- The NHM is based on three postulates [5] concerning the atomic-like motion of the electrons in narrow, half-filled energy bands as it was already considered by Mott [15] and Hubbard [16].
- The associated localized states are not represented by (hybrid) atomic orbitals but consistently by symmetry-adapted optimally-localized Wannier states.
- The postulates of the NHM are physically evident and require the introduction of nonadiabatic localized states of well-defined symmetry emphasizing the correlated nature of any atomic-like motion.
- The atomic-like motion is determined by the conservation of the total crystal–spin angular momentum, which must be satisfied in the nonadiabatic system. In a narrow, roughly half-filled superconducting band, this conservation law plays a crucial role because the localized (Wannier) states are spin-dependent.
- The strongly correlated atomic-like motion in a narrow, roughly half-filled superconducting band produces an interaction between the electron spins and “crystal–spin-1 bosons”: at any electronic scattering process, two crystal–spin-1 bosons are excited or absorbed in order that the total crystal–spin angular momentum stays conserved.
- Crystal-spin-1 bosons are the energetically lowest localized boson excitations of the crystal that possess the crystal–spin angular momentum and are sufficiently stable to transport it (as Bloch waves) through the crystal.
- The spin–boson interaction in a narrow, roughly half-filled superconducting band leads to the formation of Cooper pairs below a transition temperature .
- The Cooper pairs arise inevitably since any electron state in which the electrons possess their full degrees of freedom violates the conservation of crystal–spin angular momentum.
- This influence of the crystal–spin angular momentum may be described in terms of constraining forces that constrain the electrons to form Cooper pairs. This feature distinguishes the present concept from the standard theory of superconductivity.
- As already mentioned in Section 1, there is evidence that only these constraining forces may produce superconducting eigenstates.
- Hence, the constraining forces are responsible for all types of superconductivity, i.e., conventional, high- and other superconductivity.
- Crystal-spin-1 bosons are coupled phonon–plasmon modes that determine the type of the superconductor.
- In the isotropic lattices of the transition elements, crystal–spin-1 bosons have dominant phonon character and confirm the electron–phonon mechanism that enters the BCS theory [13] in these materials.
- Phonon-like excitations are not able to transport crystal–spin angular-momenta within the anisotropic materials of the high- superconductors [17], often containing two-dimensional layers. Within these anisotropic materials, the crystal–spin-1 bosons are energetically higher lying excitations of dominant plasmon character leading to higher Debye temperatures and, hence, to higher superconducting transition temperatures [13].
- The theory of superconductivity as developed so far is valid without any restrictions in narrow, roughly half-filled superconducting bands because constraining forces do not alter the energy of the electron system.
- However, the standard theory may furnish inaccurate information if no narrow, roughly half-filled superconducting band exists in the band structure of the material under consideration.
It is clear that this concept of superconductivity as developed in the last 40 years should be further refined in the future.
6. Conclusions
The NHM predicts that the formation of Cooper pairs is not only the result of an attractive electron–electron interaction but is additionally the outcome of quantum mechanical constraining forces operating in narrow, roughly half-filled superconducting energy bands. As already mentioned in Section 1, this far reaching assertion is corroborated by the symmetry of the Bloch functions in the band structures of numerous superconductors and non-superconductors.
The present paper demonstrates that also the two Bi phases Bi–I and Bi–V possess a narrow and almost perfectly half-filled superconducting band in their band structures. This group-theoretical result suggests that also in bismuth the superconducting state is stabilized by constraining forces and corroborates the assertion that constraining forces stabilize superconductivity in any superconductor.
Hence, the paper provides further evidence that the superconducting band forms the “missing link” in the theory of superconductivity.
Acknowledgments
I am very indebted to Guido Schmitz for his support of my work. I thank Günter Zerweck for his valuable reference to the discovery of superconductivity in bismuth.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| NHM | Nonadiabatic Heisenberg model |
A. Appendix A. Group-Theoretical Tables for the Trigonal Space Group (166) of Bi–I
It is sometimes useful to represent trigonal (rhombohedral) systems in a hexagonal coordinate system. In this case, the unit cell contains two additional inner points, which, however, are connected to each other and to the points at the corners by the translation symmetry of the system. In the framework of the group theory of Wannier functions as presented in Ref. [6], the inner points of a unit cell must not be connected by the translation symmetry. Thus, the group theory of Wannier functions is not applicable to trigonal system represented by hexagonal axes. Therefore, in the present paper, we use exclusively the trigonal coordinate system as given in Table 3.1 of Ref. [12].
Notes to Table A1
- The symmetry elements are labeled in the Schönflies notation as illustrated, e.g., in Table 1.2 of Ref. [12].
- The character tables are determined from Table 5.7 of Ref. [12].
- The notations of the points of symmetry follow Figure 3.11b of Ref. [12].
Notes to Table A3
- The letter R stands for the letter denoting the relevant point of symmetry. For example, at point F, the representations stand for .
- Each column lists the double-valued representation below the single-valued representation , where denotes the two-dimensional double-valued representation of the three-dimensional rotation group given, e.g., in Table 6.1 of Ref. [12].
- The single-valued representations are defined in Table A1.
- The notations of double-valued representations follow strictly Table 6.13 (and Table 6.14) of Ref. [12]. In this paper, the double-valued representations are not explicitly given but are sufficiently defined by this table.
Notes to Table A4
- [1]; the exact value of z is immaterial in this table. In the hexagonal unit cell, the Bi atoms lie at the Wyckoff positions [1]. In the trigonal system, their positions in the unit cell are , where the vectors and denote the basic vectors of the trigonal lattice as given, e.g., in Table 3.1 of Ref. [12].
- The notations of the representations are defined in Table A1.
- Assume a closed band of the symmetry in one of the two rows of this table to exist in the band structure of Bi–I. Then, the Bloch functions of this band can be unitarily transformed into Wannier functions that are
- localized as well as possible,
- centered at the Bi atoms, and
- symmetry-adapted to the space group (166) [6].
The entry “OK” below the time-inversion operator K indicates that the Wannier functions may even be chosen symmetry-adapted to the magnetic groupSee Theorem 7 of Ref. [6].However, a closed band (Definition 2 of Ref. [6]) with the symmetry of band 1 or band 2 does not exist in the band structure of Bi–I (see Figure 1). - The bands are determined following Theorem 5 of Ref. [6].
- The Wannier functions at the Bi atoms listed in the upper row belong to the representation of included below the atom. These representations are defined in Table A2.
 Table A2. Character tables of the single-valued irreducible representations of the point group of the positions of the Bi atoms (Definitions 11 and 12 of Ref. [6]) in Bi–I.
Table A2. Character tables of the single-valued irreducible representations of the point group of the positions of the Bi atoms (Definitions 11 and 12 of Ref. [6]) in Bi–I. - Each row defines one band consisting of two branches because there are two Bi atoms in the unit cell.
Notes to Table A5
- [1]; the exact value of z is immaterial in this table. In the hexagonal unit cell, the Bi atoms lie at the Wyckoff positions [1]. In the trigonal system, their positions in the unit cell are , where the vectors and denote the basic vectors of the trigonal lattice as given, e.g., in Table 3.1 of Ref. [12].
- Assume an isolated band of the symmetry listed in this table to exist in the band structure of Bi–I. Then, the Bloch functions of this band can be unitarily transformed into spin-dependent Wannier functions that are
- localized as well as possible,
- centered at the Bi atoms, and
- symmetry-adapted to the space group (166) [6].
The entry “OK” below the time-inversion operator K indicates that the spin-dependent Wannier functions may even be chosen symmetry-adapted to the magnetic groupSee Theorem 10 of Ref. [6]. Hence, the listed band forms a superconducting band (see Definition 22 of Ref. [6]). - The listed band is the only superconducting band of Bi–I.
- The notations of the double-valued representations are (indirectly) defined by Table A3.
- Following Theorem 9 of Ref. [6], the superconducting band is simply determined from one of the two single-valued bands listed in Table A4 by means of Equation (97) of Ref. [6]. (According to Definition 20 of Ref. [6], both single-valued bands in Table A4 are affiliated bands of the superconducting band.)
- The superconducting band consists of two branches because there are two Bi atoms in the unit cell.
- The point group of the positions of the Bi atoms (Definitions 11 and 12 of Ref. [6]) is the group . The Wannier functions at the Bi atoms belong to the double-valued representationof , where and are defined in Table A2 and denotes the two-dimensional double-valued representation of as given, e.g., in Table 6.1 of Ref. [12]. Note that the two representations and are equivalent.
B. Appendix B. Group-Theoretical Tables for the Cubic Space Group (229) of Bi–V
Notes to Table A6
- The symmetry elements are labeled in the Schönflies notation as illustrated, e.g., in Table 1.2 of Ref. [12].
- The character tables are determined from Table 5.7 of Ref. [12].
- The notations of the points of symmetry follow Figure 3.15 of Ref. [12].
Notes to Table A7
- In the table for and H, the letter R stands for the letter denoting the point of symmetry. For example, at point H, the representations stand for .
- Each column lists the double-valued representation below the single-valued representation , where denotes the two-dimensional double-valued representation of the three-dimensional rotation group given, e.g., in Table 6.1 of Ref. [12].
- The single-valued representations are defined in Table A6.
- The notations of double-valued representations follow strictly Table 6.13 (and Table 6.14) of Ref. [12]. In this paper, the double-valued representations are not explicitly given but are sufficiently defined by this table.
Notes to Table A8
- The notations of the representations are defined in Table A6.
- Assume a closed band of the symmetry in any row of this table to exist in the band structure of Bi–V. Then, the Bloch functions of this band can be unitarily transformed into Wannier functions that are
- localized as well as possible,
- centered at the Bi atoms, and
- symmetry-adapted to the space group (229) [6].
The entry “OK” below the time-inversion operator K indicates that the Wannier functions may even be chosen symmetry-adapted to the magnetic groupSee Theorem 7 of Ref. [6].However, a closed band (Definition 2 of Ref. [6]) with the symmetry of the bands in this table does not exist in the band structure of Bi–V (see Figure 2). - The bands are determined following Theorem 5 of Ref. [6].
- The point group of the positions of the Bi atoms (Definitions 11 and 12 of Ref. [6]) is the full cubic point group . The Wannier functions at the Bi atoms belong to the representations of listed in the second column. These representations are defined in Table A6.
Notes to Table A9
- Assume an isolated band of the symmetry listed in any row of this table to exist in the band structure of Bi–V. Then, the Bloch functions of this band can be unitarily transformed into spin-dependent Wannier functions that are
- localized as well as possible,
- centered at the Bi atoms, and
- symmetry-adapted to the space group (229) [6].
The entry “OK” below the time-inversion operator K indicates that the spin-dependent Wannier functions may even be chosen symmetry-adapted to the magnetic groupSee Theorem 10 of Ref. [6]. Hence, all the listed bands forms superconducting bands, see Definition 22 of Ref. [6]. - The notations of the double-valued representations are (indirectly) defined in Table A7.
- Following Theorem 9 of Ref. [6], the superconducting bands are simply determined from the single-valued bands listed in Table A8 by means of Equation (97) of Ref. [6]. (According to Definition 20 of Ref. [6], each single-valued band in Table A8 is an affiliated band of one of the superconducting bands.)
- The superconducting bands consists of one branch each because there is one Bi atom in the unit cell.
- The point group of the positions of the Bi atoms (Definitions 11 and 12 of Ref. [6]) is the full cubic point group . The Wannier functions at the Bi atoms belong to the double-valued representations of listed in the second column, where the single-valued representations and are defined by Table A6, and denotes the two-dimensional double-valued representation of as given, e.g., in Table 6.1 of Ref. [12].
References
- Degtyareva, O.; MCMahon, M.; Nelmes, R. High-pressure structural studies of group-15 elements. High Press. Res. 2004, 24, 319–356. [Google Scholar] [CrossRef]
- Donohue, J. The Structures of Elements; Robert, E., Ed.; Krieger Publishing Company: Malabar, FL, USA, 1982. [Google Scholar]
- Prakash, O.; Kumar, A.; Thamizhavel, A.; Ramakrishnan, S. Evidence for bulk superconductivity in pure bismuth single crystals at ambient pressure. Science 2017, 355, 52–55. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, E.; Zhu, X.; Wen, H.H. Pressure-induced superconductivity in Bi single crystals. Phys. Rev. B 2017, 95, 024510. [Google Scholar] [CrossRef]
- Krüger, E. Nonadiabatic extension of the Heisenberg model. Phys. Rev. B 2001, 63, 144403. [Google Scholar] [CrossRef]
- Krüger, E.; Strunk, H.P. Group Theory of Wannier Functions Providing the Basis for a Deeper Understanding of Magnetism and Superconductivity. Symmetry 2015, 7, 561–598. [Google Scholar] [CrossRef]
- Krüger, E. Structural Distortion Stabilizing the Antiferromagnetic and Semiconducting Ground State of BaMn2As2. Symmetry 2016, 8, 99. [Google Scholar] [CrossRef]
- Krüger, E. Modified BCS Mechanism of Cooper Pair Formation in Narrow Energy Bands of Special Symmetry I. Band Structure of Niobium. J. Supercond. 2001, 14, 469–489, Please note that in this paper the term “superconducting band” was abbreviated by “σband”. [Google Scholar] [CrossRef]
- Krüger, E. Superconducting Bands Stabilizing Superconductivity in YBa2Cu3O7 and MgB2. J. Supercond. 2010, 23, 213–223. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Havu, V.; Blum, V.; Havu, P.; Scheffler, M. Efficient O(N)O(N) integration for all-electron electronic structure calculation using numeric basis functions. Comput. Phys. Commun. 2009, 228, 8367–8379. [Google Scholar] [CrossRef]
- Bradley, C.; A.P.Cracknell. The Mathematical Theory of Symmetry in Solids; Claredon: Oxford, UK, 1972. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Krüger, E. Superconductivity Originating from Quasi-Orbital Electrons II. The Superconducting Ground State of Quasi-Orbital Conduction Electrons. Phys. Status Solidi B 1978, 85, 493–503. [Google Scholar] [CrossRef]
- Mott, N.F. On the transition to metallic conduction in semiconductors. Can. J. Phys. 1956, 34, 1356–1368. [Google Scholar] [CrossRef]
- Hubbard, J. Elelectron correlations in narrow energy bands. Proc. R. Soc. London, Ser. A 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Krüger, E. One- and Two-Dimensional Sublattices as Preconditions for High–Tc Superconductivity. Phys. Status Solidi B 1989, 156, 345–354. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).