Abstract
The geodetic number of a graph is an important graph invariant. In 2002, Atici showed the geodetic set determination of a graph is an NP-Complete problem. In this paper, we compute the geodetic set and geodetic number of an important class of graphs called the k-th power of a cycle. This class of graphs has various applications in Computer Networks design and Distributed computing. The k-th power of a cycle is the graph that has the same set of vertices as the cycle and two different vertices in the k-th power of this cycle are adjacent if the distance between them is at most k.
1. Introduction
In this paper, all graphs are simple (finite, loopless, undirected, and without multiple edges), the vertex set and edge set of such graphs are denoted by and respectively. The path and cycle graphs are the graphs with and edge sets and . For a positive integer n and a set of integers , the Circulant graph is defined to be the graph with vertex set of and edge set .
For two different vertices u and v of a graph G, the distance between u and v in G (denoted by ) is defined to be the length of the shortest path between u and v. The shortest path between two vertices u and v in is called geodesic. For a vertex u of the graph G, we define the eccentricity of u in G (denoted by ) to be the maximum of the distances between u and all other vertices of G [1]. The radius of a graph G (denoted by ) is the minimum of eccentricities among all vertices of G, while the diameter of a graph G (denoted by ) is the maximum distance between any two vertices in G. Two vertices of a graph G are called antipodal in G if .
The closed interval of a graph G consists of the vertices , and all vertices lying in some geodesic in G. If the set S is a subset of then is defined to be the union of all sets where . The set S is called a geodetic set of G if . The minimum cardinality of a geodetic sets is called the geodetic number of G (denoted by ).
A graph G is called symmetric if, for every two pairs of adjacent vertices and , there is an automorphism such that and . Examples of symmetric graphs are cycles, power of cycles, and Circulant graphs [2].
The geodetic number of a graph is an important graph invariant, it was investigated for several classes of graphs by Chartrand et al. [3,4], and Chartrand and Zhang [5]. Graph theory studies have always been motivated by other fields of Science and Technology such as Computer Networks and Social Transport Network. For example, in 2017 and 2018, Paul et al. [6,7] have studied how geodetic problems are involved in Social Transport Network, Zhang and Chartrand [8] took that further and extended their study of geodetic number to oriented graphs. Furthermore, the geodetic, hull, and Steiner numbers of powers of paths were investigated by AbuGhneim et al. [9]. Additionally, for connected graphs, the closed intervals were studied extensively by Nebesky [10], as well as Mulder [11] who investigated the value of these closed intervals in studying metric properties of connected graphs. Power graphs also have applications in quantum random walks in physics and routing in networks and thus have generated interest in past and current research [12,13,14]. For example, every power of cycle is Circulant graph, and Circulant graphs play a very important and crucial role in Networks design [2].
Atici showed the geodetic set determination of a graph is an NP-Complete problem [15]. In this paper, we find the geodetic number of the k-th power of a cycle where the k-th power of a graph G is defined by the graph that has the same set of vertices as G and two different vertices in the k-th power of G are adjacent if the distance between them is at most k. Therefore, for any simple graph and positive integer k, the k-th power of G (denoted by ) is the simple graph with vertex set and edge set , obviously . The geodetic number for a wide range of classes of graphs such as cycles, paths, wheels, hypercubes, trees, and complete graphs has already been determined and its calculation is rather simple for these kinds of graphs [16].
This research starts with preliminary lemmas in Section 2. Then, in Section 3, the geodetic number of the power of cycle is determined in steps depending on the relationship of n and k, where n is the number of vertices of the cycle and k is the power of this cycle. In the first two lemmas of Section 3, we discuss all possible scenarios where the geodetic number of is 2 and 3, respectively; then, we discuss the cases when the geodetic number of is 4, and, lastly, when the geodetic number of is 5. Note that there exists no power graph with a geodetic number greater than 5. Finally, in the Conclusions Section 4, we summarize all the scenarios in one main result to find the geodetic number of .
2. Preliminary Lemmas
In this section, we prove the necessary results as tools to compute the geodetic number of power of cycles for the next section. To illustrate the idea of the following lemma, consider the graph of shown in Figure 1. Any path from vertex 0 to vertex 11 in that visits vertices or 10 has a length greater than or equal to 5, while the shortest path from vertex 0 to vertex 11 is 4. In fact, any path from vertex 0 to vertex 11 that visits the vertices or 10 will not be a shortest path. This means that the vertices or 10 are not in the closed interval . The following lemma generalizes the above example and describes the closed interval for positive integers n and k.
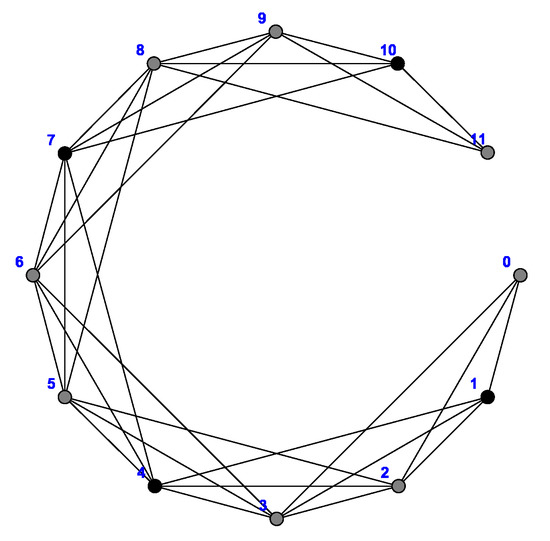
Figure 1.
Graph of .
Lemma 1.
Suppose that where r and k are positive integers and ; then, .
Proof.
Suppose that for some and for some ; then, for some positive integer q. Hence, . Since , for some positive integer m, and , we have and . Therefore, . This contradicts the fact that . □
Using the above lemma, we can characterize when a power of path has geodetic number 2:
Corollary 1.
if and only if for some positive integer q.
The following lemma clarifies when a closed interval of two vertices of intersects both sides of the vertices of the cycle (the side of and the side of ).
Lemma 2.
For positive integers n and k, if and . Then, , where .
Proof.
Suppose that . Since for some positive integer q, we have .
Since the , and , we have . Therefore, and or . Hence, . □
3. The Geodetic Number of Power of Cycles
For positive integers n and k, two different vertices and in are adjacent in if , that is,
However, when , we have
where is the complete graph with n vertices. Figure 2, Figure 3 and Figure 4 show the cycle , and , respectively.
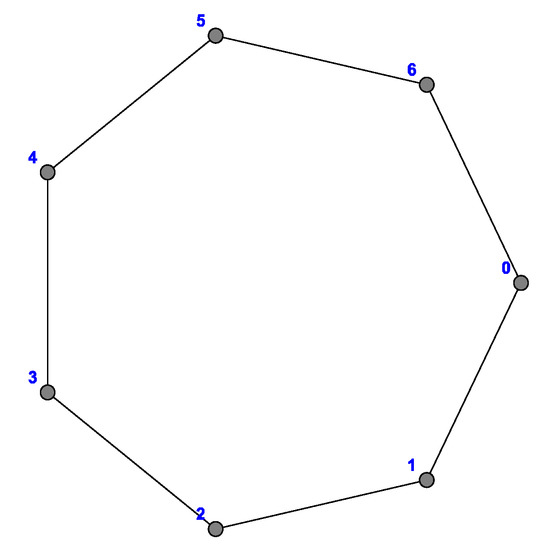
Figure 2.
.
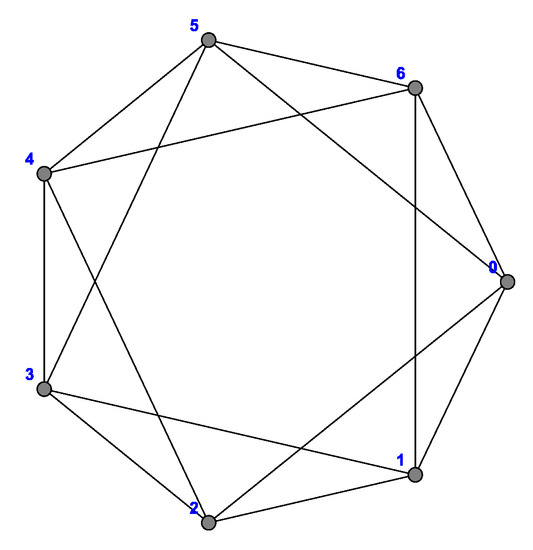
Figure 3.
.
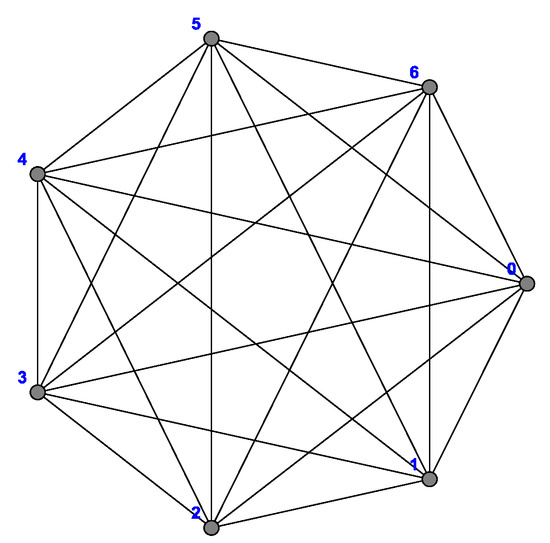
Figure 4.
.
It is obvious that the geodetic number of the complete graph with n vertices is n. In other words, if , then as shown in Figure 4 for and . Hence, we will consider the geodetic number of only when .
For any n and k positive integers, n can be written in the form , . We will consider all possible positive integer values of r and c in calculating the geodetic set and geodetic number of . It should be mentioned that we provide the geodetic set in each lemma. Then, using the symmetry of power of cycles, the geodetic set is invariant under shifting its vertices to the left or to the right.
Before we start computing the geodetic number of power of cycles, let’s consider this illustrative example to compute the geodetic number of shown in Figure 5. The distance between vertex 0 and vertex 7 in is (the length of the shortest path in from 0 to 7) while the distance between vertex 0 and vertex 7 in is . Now, the shortest paths from vertex 0 to vertex 7 in that visit the vertices are listed in Table 1.
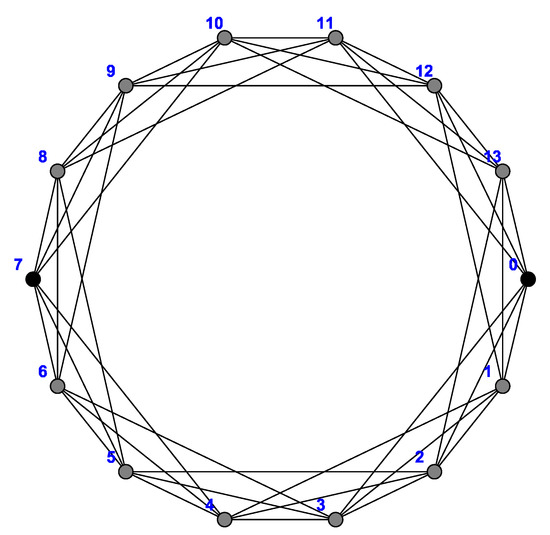
Figure 5.
Graph of .

Table 1.
Shortest paths from vertex 0 to vertex 7 in .
Using symmetry of , one can extend the paths shown in Table 1 to the paths that visit the vertices and 13. As we can see, the set of all possible shortest paths from 0 to 7 covers all vertices of and hence the geodetic number .
Lemma 3.
If for some positive integers q and r where , then if and only if .
Proof.
Suppose that , then . For each i with , the path is of length and so it is geodesic over all values of i. These paths cover the vertices . Since and are antipodal points in , we have is geodetic set of .
Now, suppose that and . Let be a minimal geodetic set of . Then, geodesic covers all vertices and
Using Corollary 1, for some positive integer m and for some positive integer j.
On the other hand, since geodesic covers all vertices and , we conclude that , so , and hence . □
In the above lemma, we found the geodetic number of when where c is an even number. The case when c is odd and will be addressed in a separate lemma later in this paper.
Lemma 4.
For the graph , suppose that for some positive integers and , then if and only if .
Proof.
Suppose that for some positive integer , then:
Case 1.
Let for some positive integer q. Consider . Using Corollary 1, S is a geodetic set.
Case 2.
Let for some positive integer q. Consider . Using Corollary 1, S is a geodetic set.
On the other hand, suppose that , where q is a positive integer and is a minimal geodetic set of . Then, using Corollary 1, and for some positive integers and c. This means that is multiple of k; therefore, and hence . □
Now, we turn our discussion to study the cases for when the geodetic number is 4. We have already addressed the case when . Next, we will discuss the case where , but . The case when will be discussed after.
Lemma 5.
For the graph , suppose that for some positive integers c and r where , and , then .
Proof.
Suppose that for some positive integer c, , and , then:
Case 1.
for for some positive integer , consider , using Corollary 1:
- (a)
- covers all vertices that lie on the shortest path from to in .
- (b)
- covers all vertices that lie on the shortest path from to in .
- (c)
- covers all vertices that lie on the shortest path from to in .
Now, since and , it is obvious that , that is, S is geodetic set of . Therefore, S is a minimal geodetic set:
Case 2.
For for some positive integer q, then, for : similar to Case1, consider . Since , we conclude that S is geodetic set of . □
Lemma 6.
If , then .
Proof.
Consider the set . Since and for all , we have and . Therefore, . Moreover, for any , is the shortest path from to in ; this means .
Using the same technique as above, we can show that and . Therefore, S is geodetic set of . □
Lemma 7.
For the graph , if for some positive integer c, where and , then .
Proof.
If , then consider the geodetic set .
If , then consider the geodetic set .
If ; then, consider the geodetic set . □
For , it is obvious that we are still missing the case when c is odd. The following lemma will address this case:
Lemma 8.
For the graph , if for some positive integer c, then .
Proof.
Consider the set . Since and for all , we have ; therefore, for every , and , the path
is shortest path from to . This means . Using the same technique, we can prove that
and
Therefore, S is geodetic set of . □
Finally, we discuss the cases for when the geodetic number is 5.
Lemma 9.
For the graph , suppose that for some positive integer r where . Then, .
Proof.
Suppose that , and that is a minimal geodetic set of .
If for all ; then, ; therefore, we may assume that where , then will either be covered by some geodesic or geodesic.
Case 1.
First, we consider the scenario where is covered by geodesic. Using Lemma 1, we have .
Now, may be covered by some geodesic or some geodesic; in the latter case, d must be equal to 2 using Lemma 1. In the former case, since , we have and , so and , if . Then, , so geodesic will only cover and , which is impossible, so .
Now, , since , then can be covered by neither geodesic nor by geodesic.
Case 2.
If is covered by some geodesic and , then, and ; this means that could not be covered by any of the geodesic, thus, will be covered by geodesic, and so, by Corollary 1; therefore, . Since is not in any of the geodesic, we have will only be covered by some geodesic, and so, . From Case1 and Case2 above, S can not be a geodesic set for , hence,
Now, it is obvious that geodesic can not cover any of the vertices , and so, can only be covered by some geodesic, , therefore, , and thus, , which is a contradiction. Hence, .
Now, take ; this is a minimal geodetic set of . □
Lemma 10.
For the graph , if , then .
Proof.
Using Lemmas 3 and 4, can not be 2 or 3. Assume that and be a geodetic set of , if for all where ; then, , without loss of generality, we may assume that for some positive integer d and . Then, can either be covered by some geodesic or geodesic.
Case 1.
If is covered by some geodesic, using Lemma 1, we conclude that . may be covered by some geodesic or some geodesic. In the former case, d must be equal to 2, in the latter case, since , we have and ; therefore, and . If . Then, ; this means that geodesic will only cover and , which is impossible since . Hence, .
Now, . Then, can be covered by neither geodesic nor by geodesic. Therefore, can not be covered by geodesic.
Case 2.
If is covered by some geodesic and , then . This means that could not be covered by any of the geodesic. Thus, will be covered by some geodesic. Using Lemma 1, we conclude that , since is not in any of the geodesic. Then, can only be covered by some geodesic and hence .
Since geodesic can not cover any of the vertices , we conclude that can only be covered by some geodesic. This gives . This contradicts the assumption . Therefore, S can not be geodetic set of . Hence, .
Now, let . Then, S is geodetic set of . □
In the above lemmas, we covered the calculation of the geodetic number of for all the scenarios of . We summarize our calculations in Theorem 1 in the Conclusions section.
4. Conclusions
Even though the determination of the geodetic number of graphs is an NP-Complete problem, in this paper, we were able to compute the geodetic number of power of cycles and we summarize our calculations in the following main theorem.
Theorem 1.
For positive integers n and k, we have:
As previously mentioned in the Introduction, geodetic number of a graphs has many applications in Computer Networks, Social Networks and Social Transport Networks. Steiner number and hull number are two other important graph theoretic parameters that have important applications in network theory. It would be interesting for further research to calculate those numbers for power of cycles as well as calculating the geodetic number of Circulant graphs.
Author Contributions
The authors contributed equally.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, B.K. The geodetic number of a graph. J. Appl. Math. Comput. 2004, 16, 525–532. [Google Scholar]
- Meijer, P.T. Connectivities and Diameters of Circulant Graphs. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 1991. [Google Scholar]
- Chartrand, G.; Harary, F.; Zhang, P. Extremal problems in geodetic graph theory. In Proceedings of the Twenty-ninth Southeastern International Conference on Combinatorics, Graph Theory and Computing, Boca Raton, FL, USA, 9–13 March 1998; pp. 157–168. [Google Scholar]
- Chartrand, G.; Harary, F.; Zhang, P. On the geodetic number of a graph. Netw. Int. J. 2002, 39, 1–6. [Google Scholar] [CrossRef]
- Chartrand, G.; Zhang, P. Realizable ratios in graph theory: Geodesic parameters. Bull. Inst. Comb. Appl. 1999, 27, 69–80. [Google Scholar]
- Manuel, P.; Klavžar, S.; Xavier, A.; Arokiaraj, A.; Thomas, E. Strong geodetic problem in networks. Discuss. Math. Graph Theory 2018. [Google Scholar] [CrossRef]
- Manuel, P.; Klavžar, S.; Xavier, A.; Arokiaraj, A.; Thomas, E. Strong edge geodetic problem in networks. Open Math. 2017, 15, 1225–1235. [Google Scholar] [CrossRef]
- Chartrand, G.; Zhang, P. The geodetic number of an oriented graph. Eur. J. Comb. 2000, 21, 181–189. [Google Scholar] [CrossRef]
- AbuGhneim, O.A.; Al-Khamaiseh, B.; Al-Ezeh, H. The geodetic, hull, and Steiner numbers of powers of paths. Util. Math. 2014, 95, 289–294. [Google Scholar]
- Nebeskỳ, L. A characterization of the interval function of a connected graph. Czech. Math. J. 1994, 44, 173–178. [Google Scholar]
- Mulder, H.M. The Interval Function of a Graph; Centrum Voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Agnarsson, G.; Halldórsson, M.M. Coloring powers of planar graphs. SIAM J. Discret. Math. 2003, 16, 651–662. [Google Scholar] [CrossRef]
- Brandstädt, A.; Chepoi, V.D.; Dragan, F.F. Perfect elimination orderings of chordal powers of graphs. Discret. Math. 1996, 158, 273–278. [Google Scholar] [CrossRef]
- Effantin, B.; Kheddouci, H. The b-chromatic number of some power graphs. Discret. Math. Theor. Comput. Sci. 2003, 6, 45–54. [Google Scholar]
- Atici, M. Computational complexity of geodetic set. Int. J. Comput. Math. 2002, 79, 587–591. [Google Scholar] [CrossRef]
- Hernando, C.; Jiang, T.; Mora, M.; Pelayo, I.M.; Seara, C. On the Steiner, geodetic and hull numbers of graphs. Discret. Math. 2005, 293, 139–154. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).