Some Picture Fuzzy Dombi Heronian Mean Operators with Their Application to Multi-Attribute Decision-Making
Abstract
1. Introduction
2. Preliminaries
2.1. Picture Fuzzy Sets
- 1
- ,
- 2
- ,
- 3
- ,
- 4
- .
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
2.2. Heronian Mean
3. The Picture Fuzzy Dombi Heronian Mean Operators
3.1. The Picture Fuzzy Dombi Heronian Mean (PFDHM) Operator
3.2. The Picture Fuzzy Dombi Weighted Heronian Mean (PFDWHM) Operator
3.3. The Picture Fuzzy Dombi Geometric Heronian Mean (PFDGHM) Operator
3.4. The Picture Fuzzy Dombi Weighted Geometric Heronian Mean (PFDWGHM) Operator
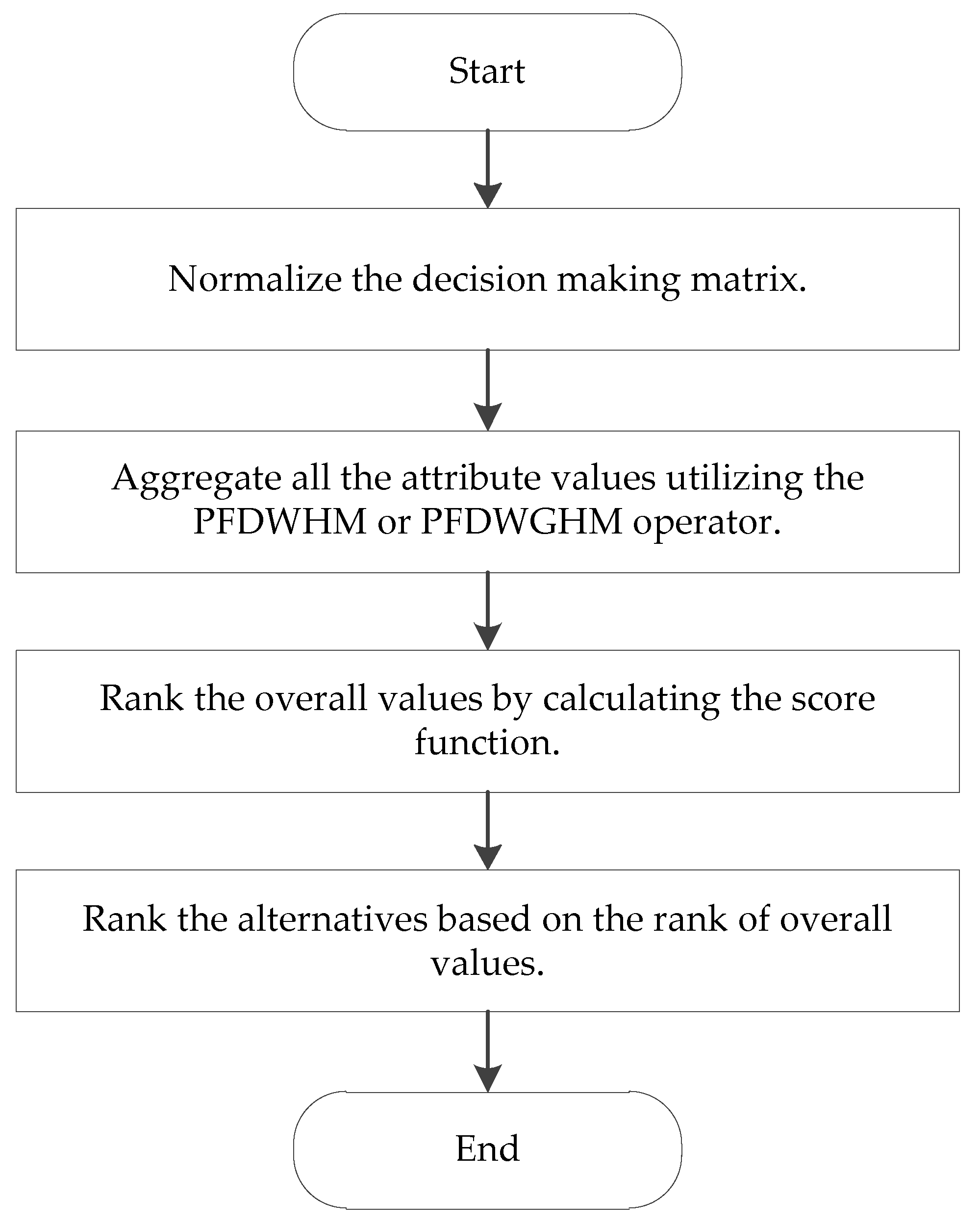
4. A Novel Approach to Multi-Attribute Decision-Making (MADM) Based on the Proposed Operators
4.1. Description of Atypical MADM Problem with Picture Fuzzy Information
4.2. An Algorithm for the Picture Fuzzy MADM Problem
5. Application Instance
5.1. The Decision-Making Process
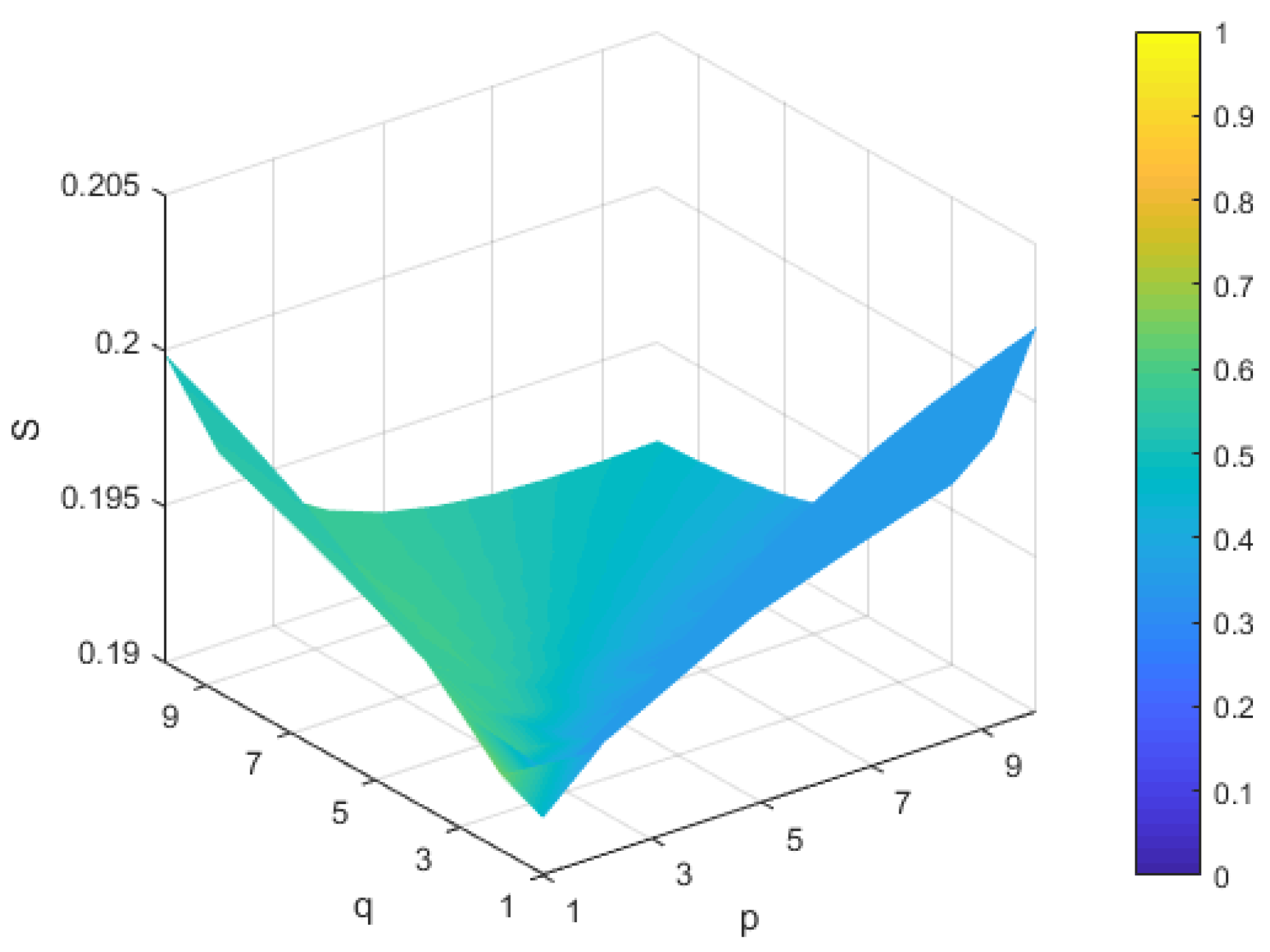
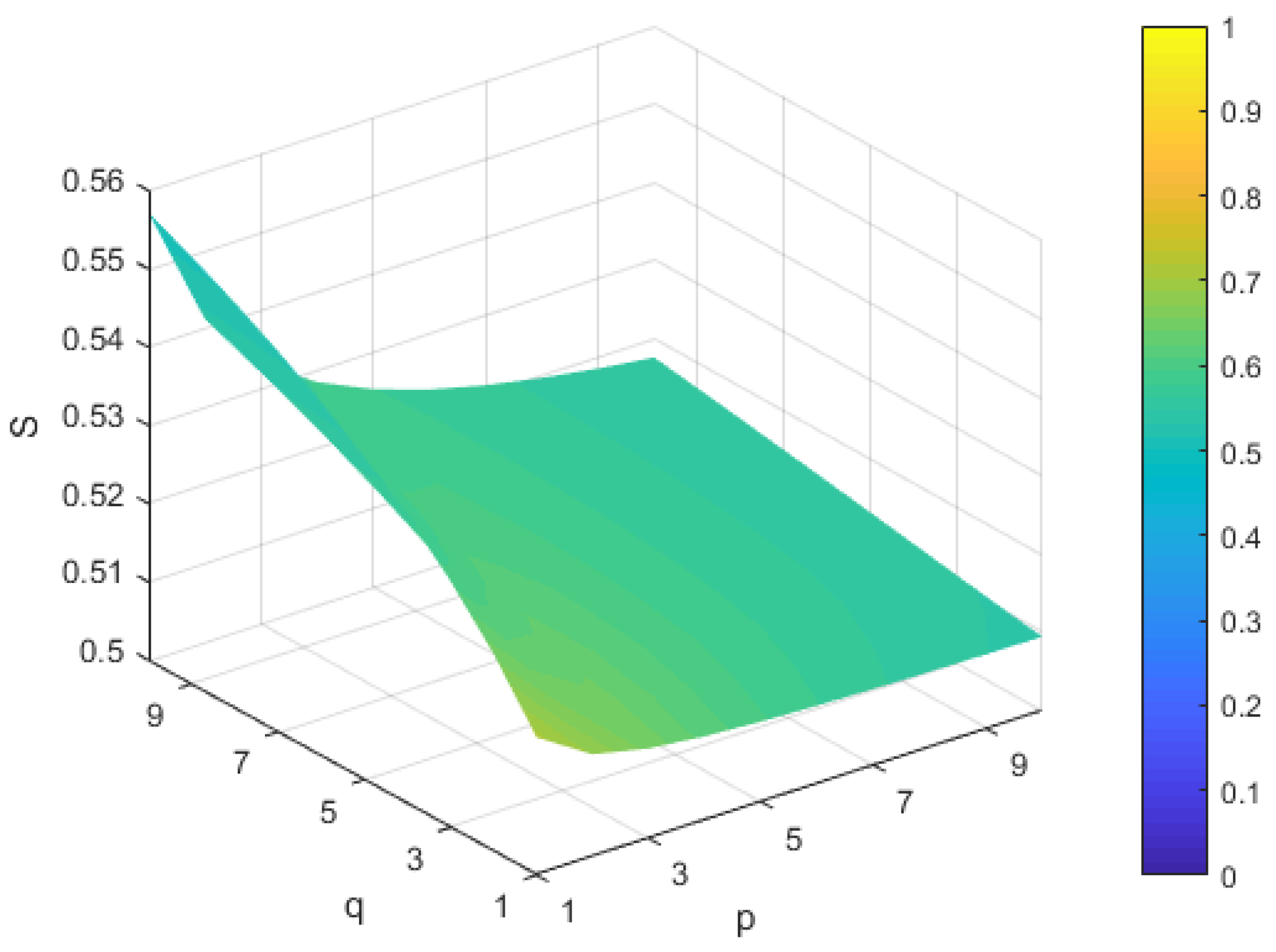
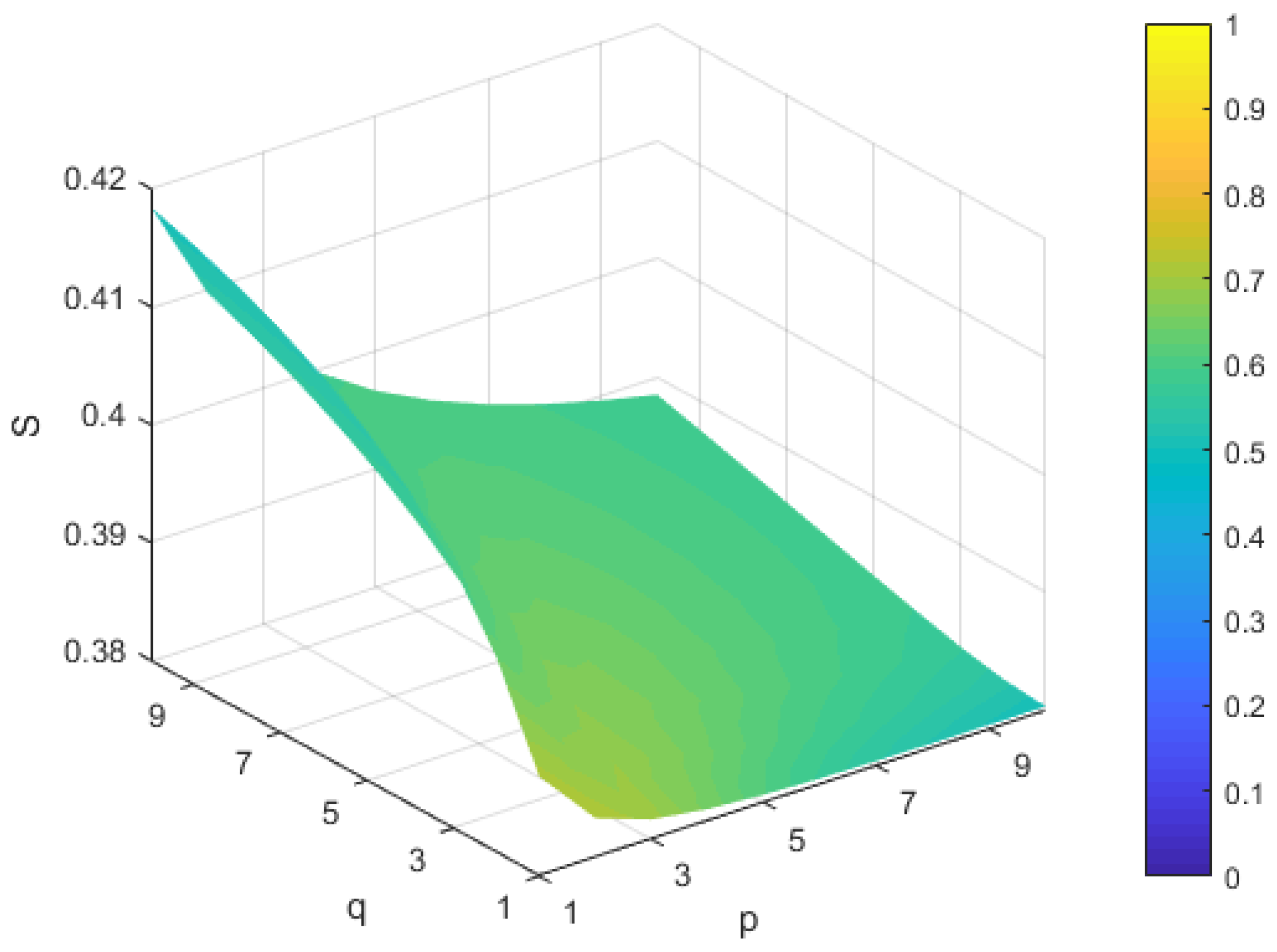
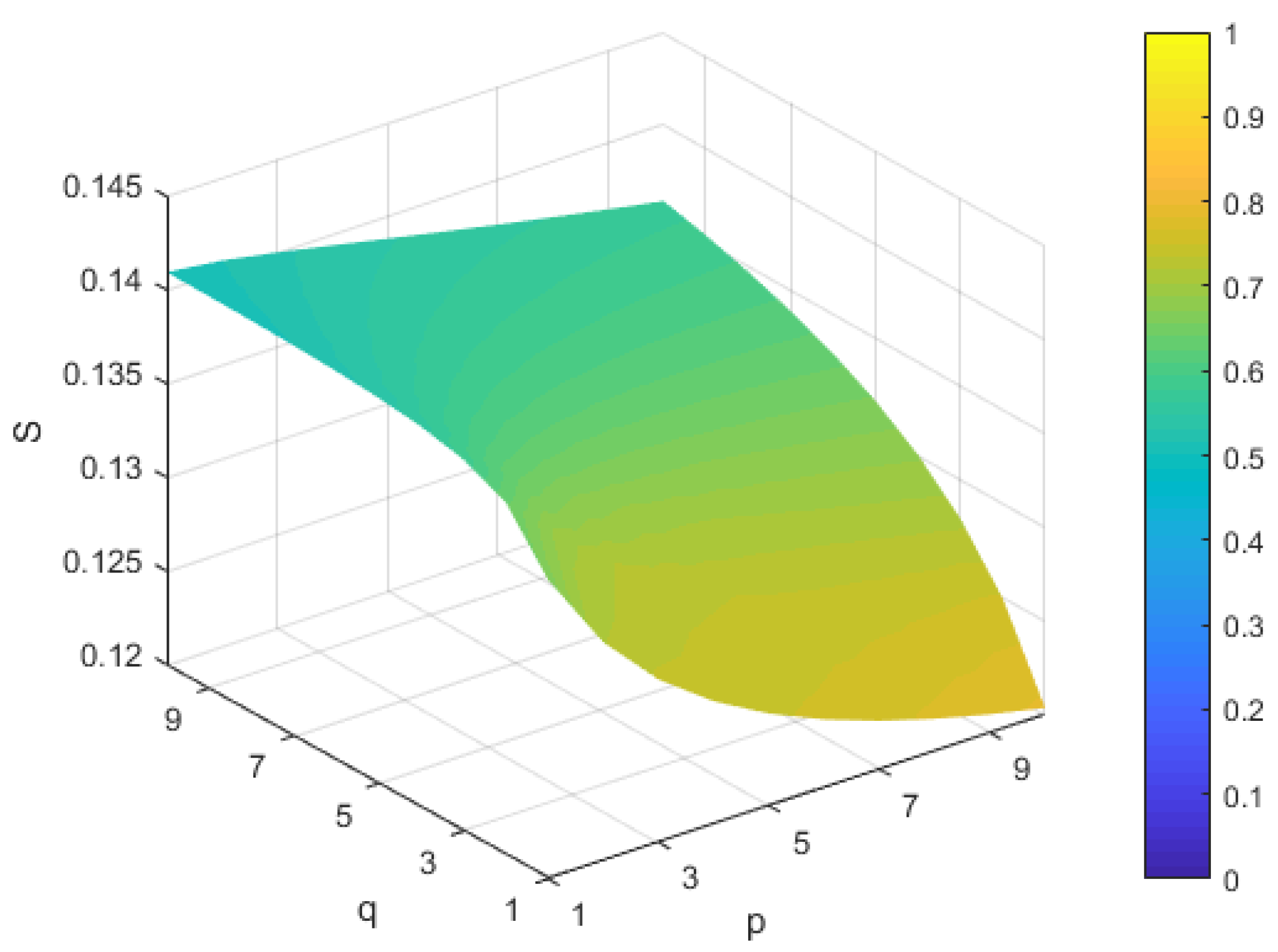
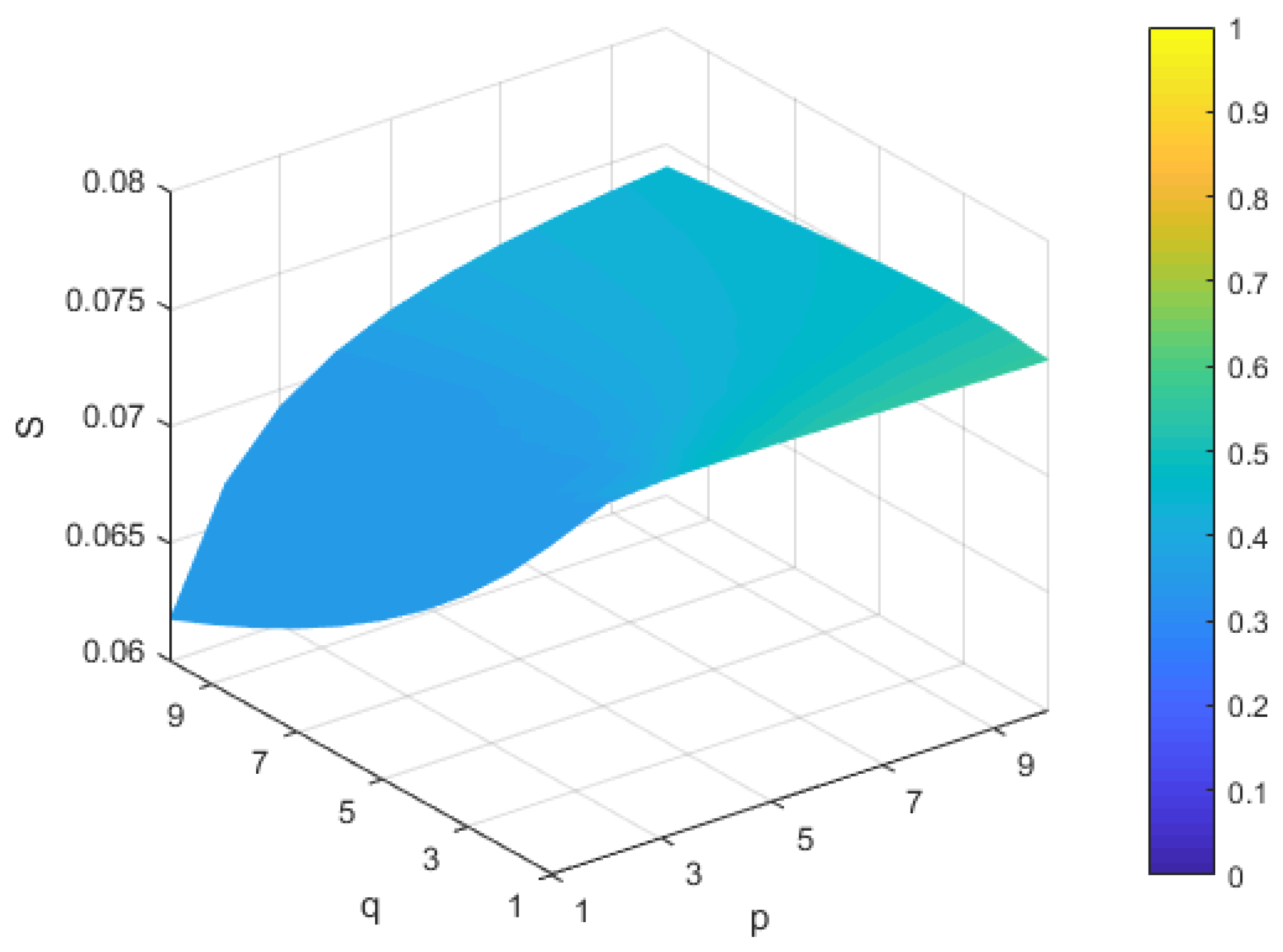
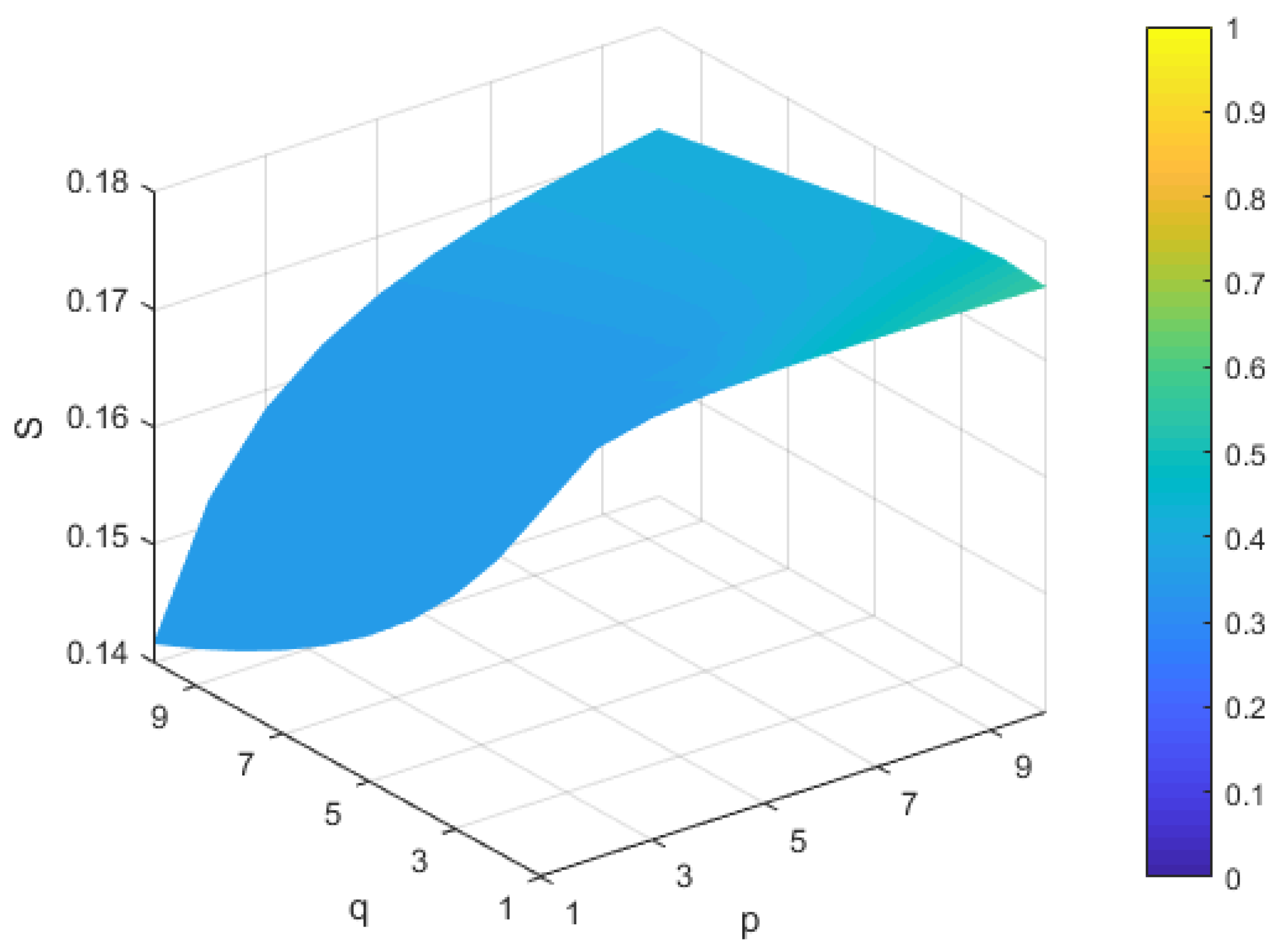
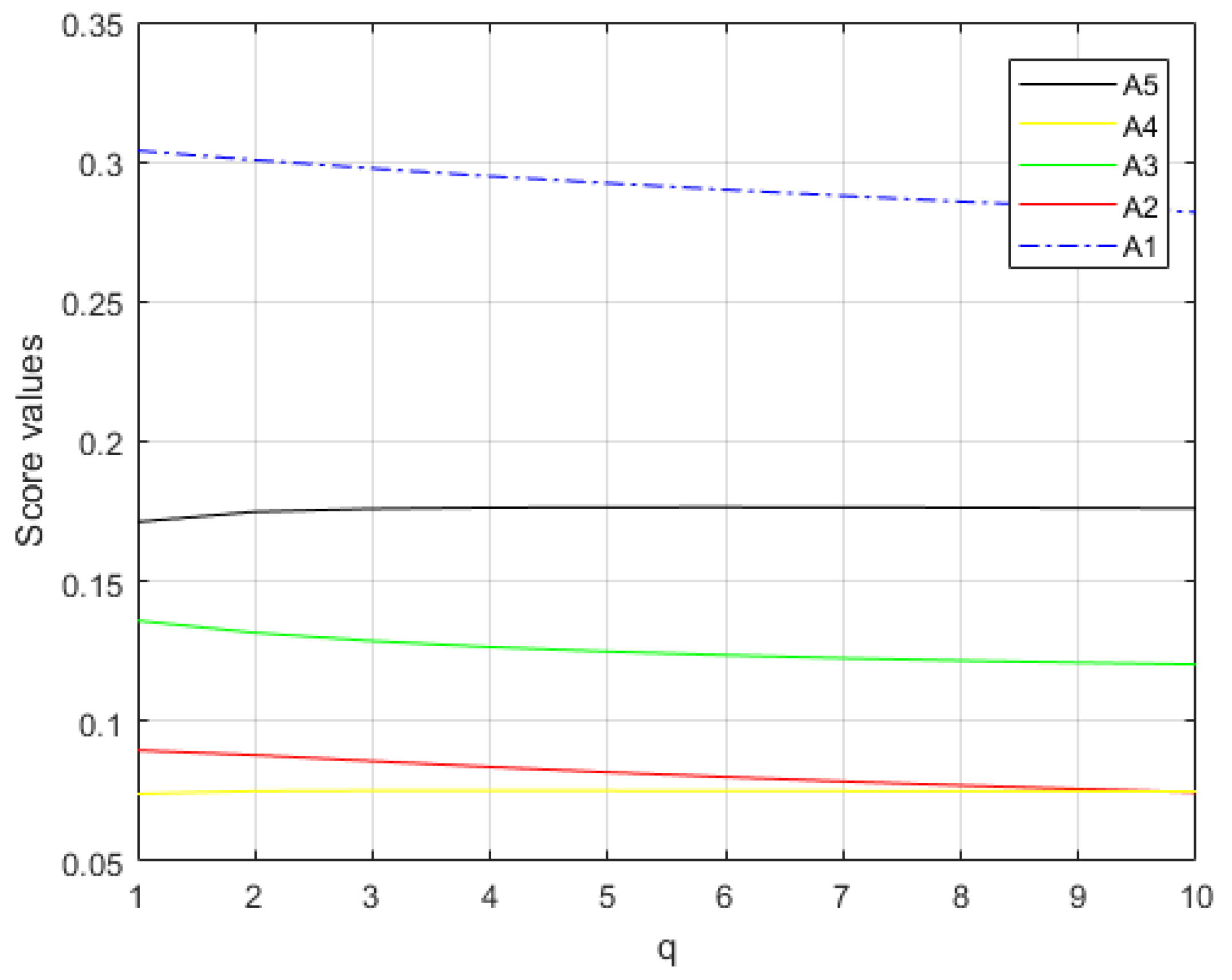
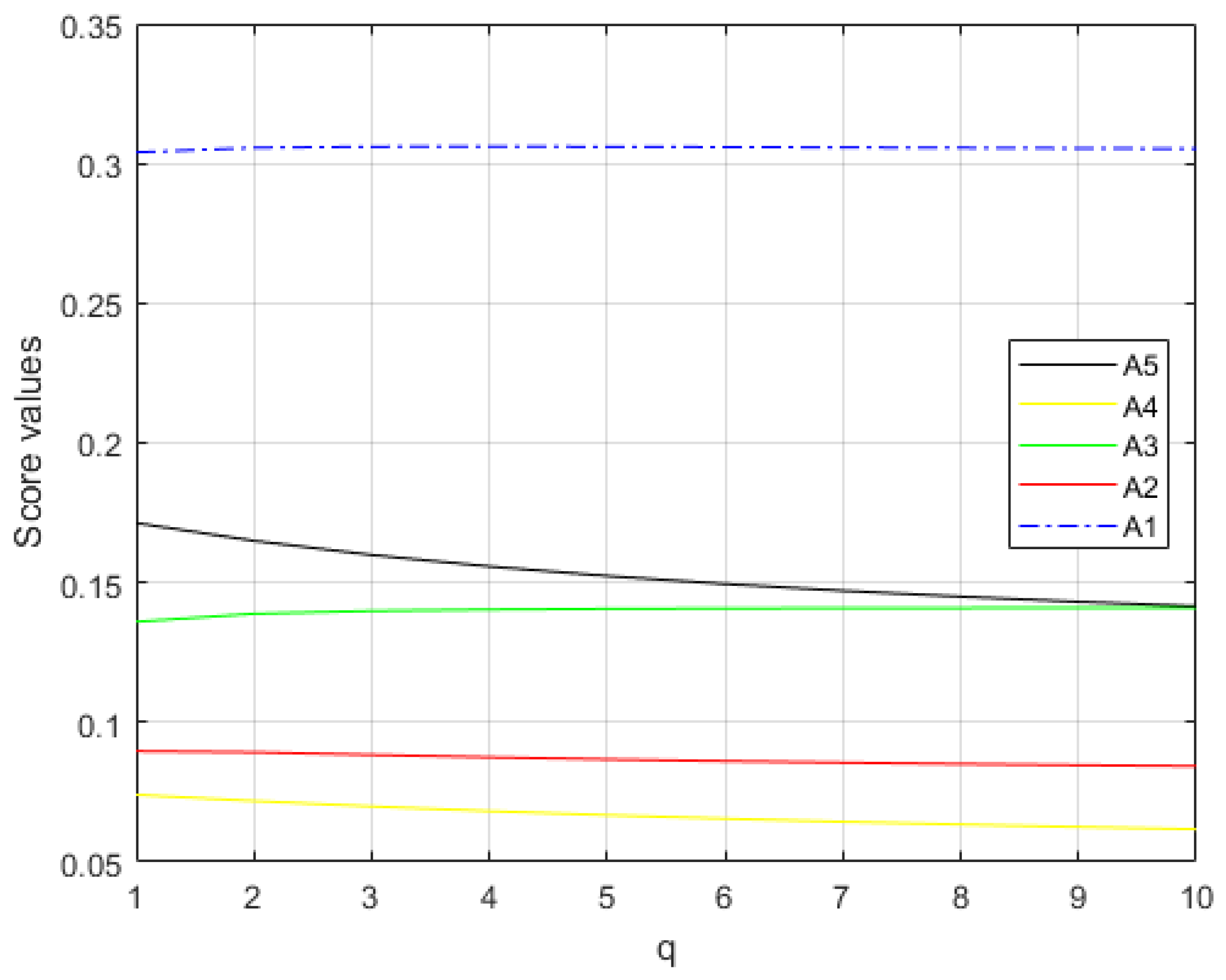
5.2. Sensitivity Analysis
5.3. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Medina, J.; Ojeda-Aciego, M. Multi-adjoint t-concept lattices. Inf. Sci. 2010, 180, 712–725. [Google Scholar] [CrossRef]
- Pozna, C.; Minculete, N.; Precup, R.E.; Kóczy, L.T.; Ballagi, Á. Signatures: Definitions, operators and applications to fuzzy modelling. Fuzzy Sets Syst. 2012, 201, 86–104. [Google Scholar] [CrossRef]
- Jankowski, J.; Kazienko, P.; Wątróbski, J.; Lewandowska, A.; Ziemba, P.; Ziolo, M. Fuzzy multi-objective modeling of effectiveness and user experience in online advertising. Expert Syst. Appl. 2016, 65, 315–331. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, D.; Jarial, S.K. A hybrid clustering method based on improved artificial bee colony and fuzzy C-means algorithm. Int. J. Artif. Intell. 2017, 15, 40–60. [Google Scholar]
- Blanco-Mesa, F.; Gil-Lafuente, A.M.; Merigo, J.M. Fuzzy decision making: A bibliometric-based review. J. Intell. Fuzzy Syst. 2017, 32, 2033–2050. [Google Scholar] [CrossRef]
- Merigó, J.M.; Gil-Lafuente, A.M.; Yager, R.R. An overview of fuzzy research with bibliometric indicators. Appl. Soft Comput. 2015, 27, 420–433. [Google Scholar] [CrossRef]
- Shi, Z.J.; Wang, X.Q.; Palomares, I.; Guo, S.J.; Ding, R.X. A novel consensus model for multi-attribute large-scale group decision making based on comprehensive behavior classification and adaptive weight updating. Knowl.-Based Syst. 2018, 158, 196–208. [Google Scholar] [CrossRef]
- Xing, Y.P.; Zhang, R.T.; Wang, J.; Zhu, X.M. Some new Pythagorean fuzzy Choquet–Frank aggregation operators for multi-attribute decision making. Int. J. Fuzzy Syst. 2018, 33, 2189–2215. [Google Scholar] [CrossRef]
- Xu, Y.; Shang, X.P.; Wang, J.; Wu, W.; Huang, H.Q. Some q-rung dual hesitant fuzzy Heronian mean operators with their application to multiple attribute group decision-making. Symmetry 2018, 10, 472. [Google Scholar] [CrossRef]
- Mao, X.B.; Hu, S.S.; Dong, J.Y.; Wan, S.P.; Xu, G.L. Multi-attribute group decision making based on cloud aggregation operators under interval-valued hesitant fuzzy linguistic environment. Int. J. Fuzzy Syst. 2018, 20, 2273–2300. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.T.; Zhu, X.M.; Xing, Y.P.; Buchmeister, B. Some hesitant fuzzy linguistic Muirhead means with their application to multiattribute group decision-making. Complexity 2018, 2018, 5087851. [Google Scholar] [CrossRef]
- Yu, G.F.; Li, D.F.; Fei, W. A novel method for heterogeneous multi-attribute group decision making with preference deviation. Comput. Ind. Eng. 2018, 124, 58–64. [Google Scholar] [CrossRef]
- Zhang, R.T.; Wang, J.; Zhu, X.M.; Xia, M.M.; Yu, M. Some generalized Pythagorean fuzzy Bonferroni mean aggregation operators with their application to multiattribute group decision-making. Complexity 2017, 2017, 5937376. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.T.; Wang, J.; Zhu, X.M.; Xing, Y.P. Pythagorean fuzzy power Muirhead mean operators with their application to multi-attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 2035–2050. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.T.; Wang, J.; Shang, X.P.; Bai, K.Y. A novel approach to multi-attribute group decision-making with q-rung picture linguistic information. Symmetry. 2018, 10, 172. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Wang, W.Z.; Liu, X.F. Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Trans. Fuzzy Syst. 2012, 20, 923–938. [Google Scholar] [CrossRef]
- Zhang, Z.M. Multi-criteria group decision-making methods based on new intuitionistic fuzzy Einstein hybrid weighted aggregation operators. Neural Comput. Appl. 2017, 28, 3781–3800. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Intuitionistic fuzzy Bonferroni means. IEEE Trans. Syst. Man Cybern. B Cybern. 2011, 41, 568–578. [Google Scholar] [PubMed]
- Xia, M.M.; Xu, Z.S.; Zhu, B. Geometric Bonferroni means with their application in multi-criteria decision making. Knowl.-Based Syst. 2013, 40, 88–100. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W. An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J. Intell. Fuzzy Syst. 2014, 27, 2177–2190. [Google Scholar]
- Yu, D.J. Intuitionistic fuzzy geometric Heronian mean aggregation operators. Appl. Soft Comput. 2013, 13, 1235–1246. [Google Scholar] [CrossRef]
- Liu, P.D.; Li, D.F. Some Muirhead mean operators for intuitionistic fuzzy numbers and their applications to group decision making. PLoS ONE 2017, 12, e0168767. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.P.; Chen, H.H.; Fei, W.; Li, D.F. A MAGDM method considering the amount and reliability information of interval-valued intuitionistic fuzzy sets. Int. J. Fuzzy Syst. 2017, 19, 715–725. [Google Scholar] [CrossRef]
- Afful-Dadzie, E.; Oplatkova, Z.K.; Prieto, L.A.B. Comparative state-of-the-art survey of classical fuzzy set and intuitionistic fuzzy sets in multi-criteria decision making. Int. J. Fuzzy Syst. 2017, 19, 726–738. [Google Scholar] [CrossRef]
- Tao, Z.F.; Liu, X.; Chen, H.Y.; Zhou, L.G. Ranking interval-valued fuzzy numbers with intuitionistic fuzzy possibility degree and its application to fuzzy multi-attribute decision making. Int. J. Fuzzy Syst. 2017, 19, 646–658. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Tian, C. Hesitant intuitionistic fuzzy aggregation operators based on the Archimedean t-norms and t-conorms. Int. J. Fuzzy Syst. 2017, 19, 702–714. [Google Scholar] [CrossRef]
- Yuan, J.H.; Li, C.B. A new method for multi-attribute decision making with intuitionistic trapezoidal fuzzy random variable. Int. J. Fuzzy Syst. 2017, 19, 5–26. [Google Scholar] [CrossRef]
- Zhang, Z.M. Several new interval-valued intuitionistic fuzzy Hamacher hybrid operators and their application to multi-criteria group decision making. Int. J. Fuzzy Syst. 2016, 18, 829–848. [Google Scholar] [CrossRef]
- He, Y.D.; He, Z.; Shi, L.X. Multiple attributes decision making based on scaled prioritized intuitionistic fuzzy interaction aggregation operators. Int. J. Fuzzy Syst. 2016, 18, 924–938. [Google Scholar] [CrossRef]
- Wei, G. Approaches to interval intuitionistic trapezoidal fuzzy multiple attribute decision making with incomplete weight information. Int. J. Fuzzy Syst. 2015, 17, 484–489. [Google Scholar] [CrossRef]
- Cuong, B. Picture fuzzy sets-first results. Part 1. Semin. Neuro Fuzzy Syst Appl. 2013. [CrossRef]
- Le, H.S.; Viet, P.V.; Hai, P.V. Picture inference system: A new fuzzy inference system on picture fuzzy set. Appl. Intell. 2017, 46, 652–669. [Google Scholar]
- Son, L.H. Generalized picture distance measure and applications to picture fuzzy clustering. Appl. Soft Comput. 2016, 46, 284–295. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, C.C.; Ji, S.W.; Liu, T. Adjustable soft discernibility matrix based on picture fuzzy soft sets and its applications in decision making. J. Intell. Fuzzy Syst. 2015, 29, 1711–1722. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy cross-entropy for multiple attribute decision making problems. J. Bus. Econ. Manag. 2016, 17, 491–502. [Google Scholar] [CrossRef]
- Bo, C.; Zhang, X. New operations of picture fuzzy relations and fuzzy comprehensive evaluation. Symmetry 2017, 9, 268. [Google Scholar] [CrossRef]
- Peng, X.D.; Dai, J.G. Algorithm for picture fuzzy multiple attribute decision-making based on new distance measure. Int. J. Uncertain. Quantif. 2017, 7, 2. [Google Scholar] [CrossRef]
- Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Picture 2-tuple linguistic aggregation operators in multiple attribute decision making. Soft Comput. 2018, 22, 989–1002. [Google Scholar] [CrossRef]
- Wei, G.W. Picture 2-tuple linguistic Bonferroni mean operators and their application to multiple attribute decision making. Int. J. Fuzzy Syst. 2017, 19, 997–1010. [Google Scholar] [CrossRef]
- Wei, G.W. Some cosine similarity measures for picture fuzzy sets and their applications to strategic decision making. Informatica 2017, 28, 547–564. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Li, D.X.; Dong, H.; Jin, X. Model for evaluating the enterprise marketing capability with picture fuzzy information. J. Intell. Fuzzy Syst. 2017, 33, 3255–3263. [Google Scholar] [CrossRef]
- Peng, S.M. Study on enterprise risk management assessment based on picture fuzzy multiple attribute decision-making method. J. Intell. Fuzzy Syst. 2017, 33, 3451–3458. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fund. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- Dombi, J. A general class of fuzzy operators, the De-Morgan class of fuzzy operators and fuzziness induced by fuzzy operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, J.L.; Chen, S.M. Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 2018, 69, 1–24. [Google Scholar] [CrossRef]
- He, X.R. Typhoon disaster assessment based on Dombi hesitant fuzzy information aggregation operators. Nat. Hazards 2018, 90, 1153–1175. [Google Scholar] [CrossRef]
- Chen, J.Q.; Ye, J. Some single-valued neutrosophic Dombi weighted aggregation operators for multiple attribute decision-making. Symmetry 2017, 9, 82. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. Unione Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Sykora, S. Mathematical means and averages: Generalized Heronian means. Stans Lib. 2009. [Google Scholar] [CrossRef]
- Yu, D.J.; Wu, Y.Y. Interval-valued intuitionistic fuzzy Heronian mean operators and their application in multi-criteria decision making. Afr. J. Bus. Manag. 2012, 6, 4158–4168. [Google Scholar] [CrossRef]

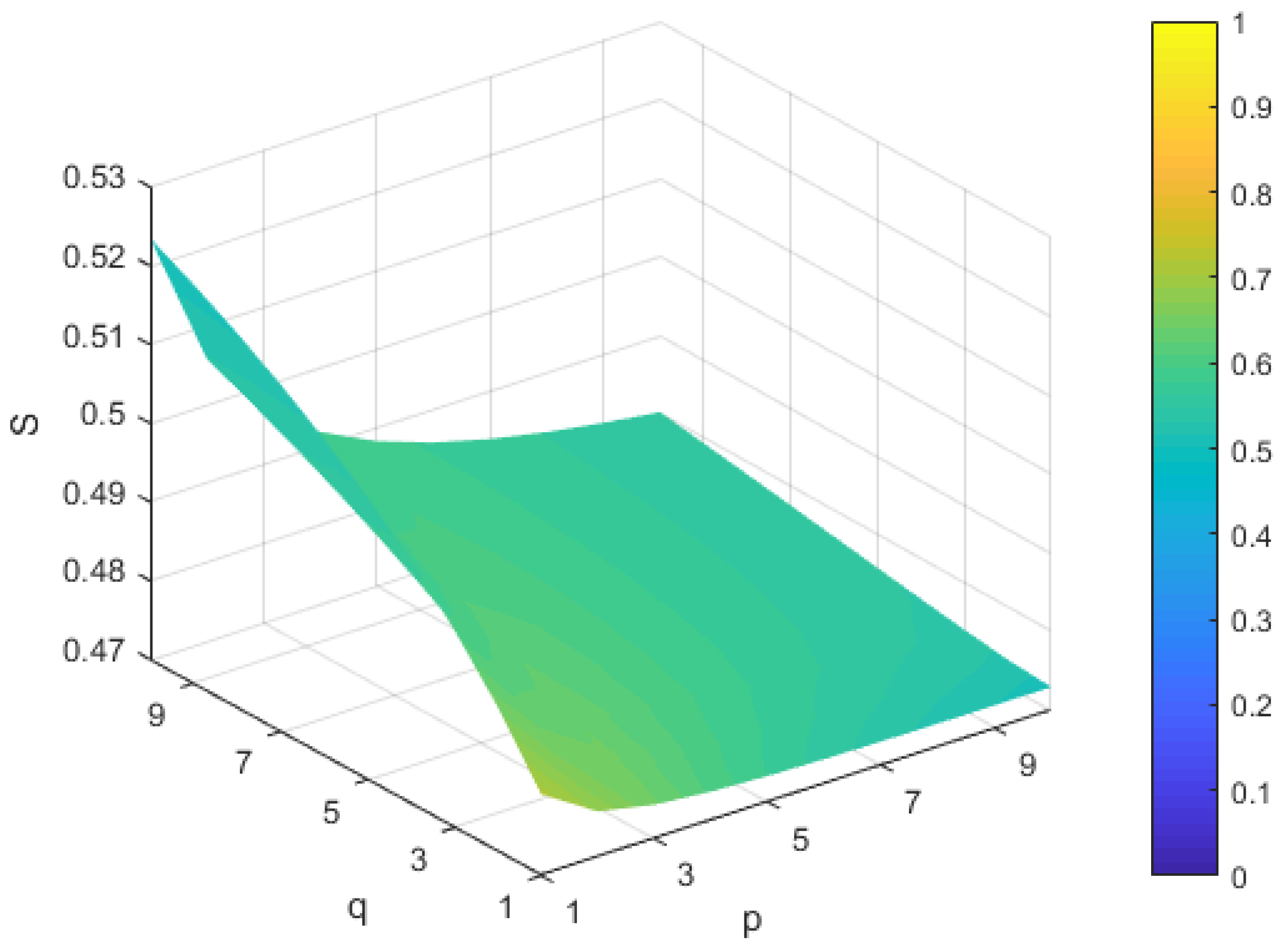
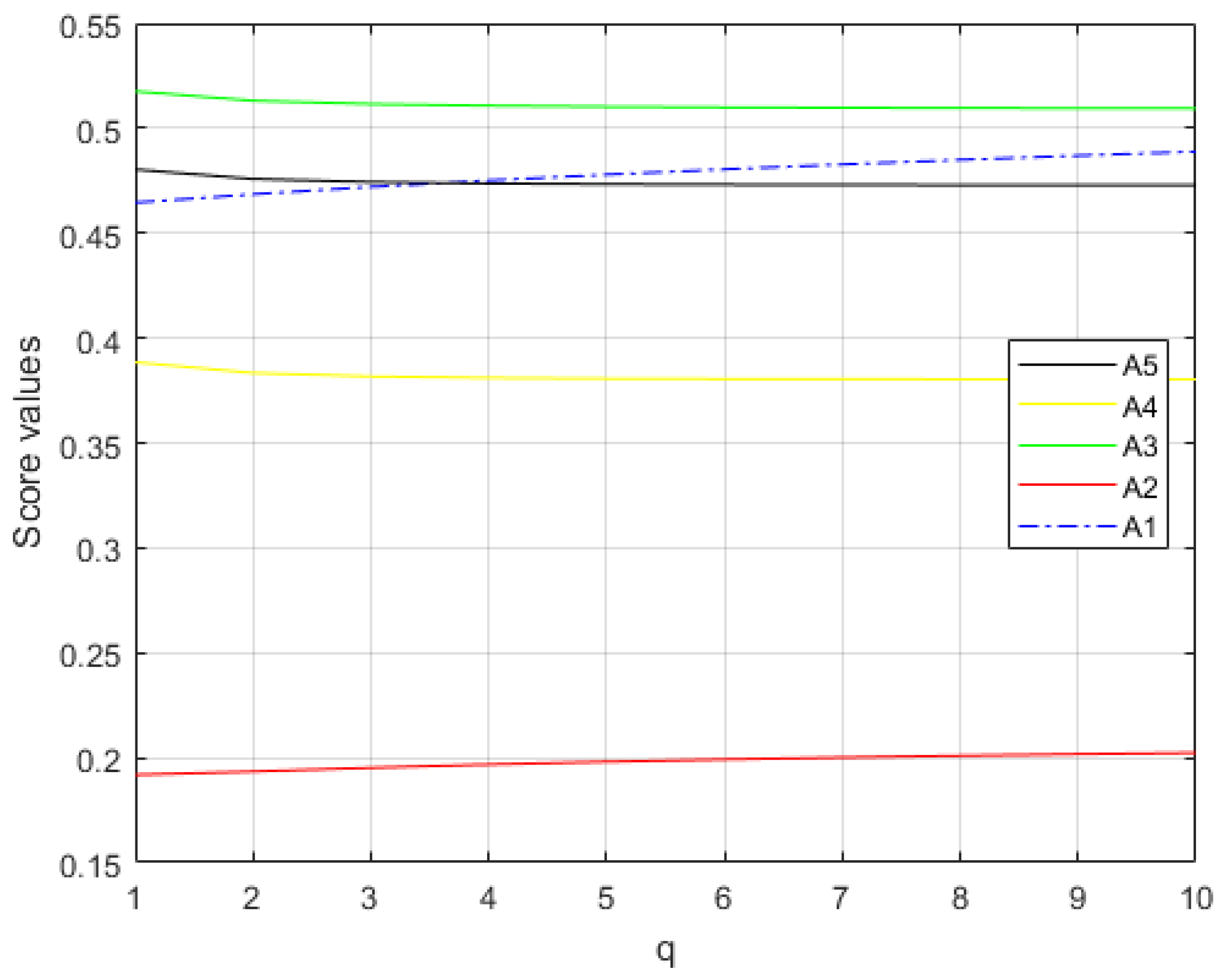

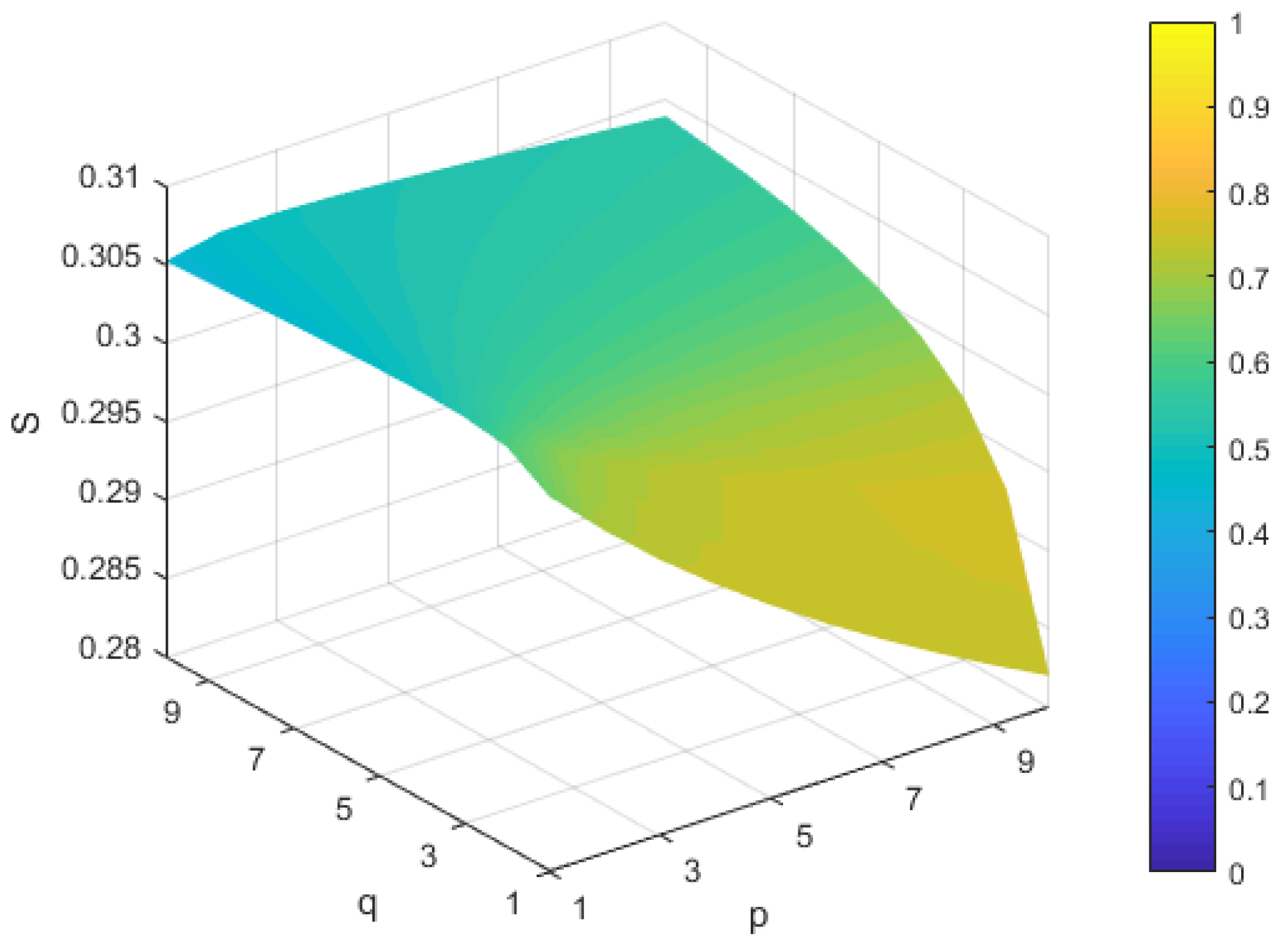
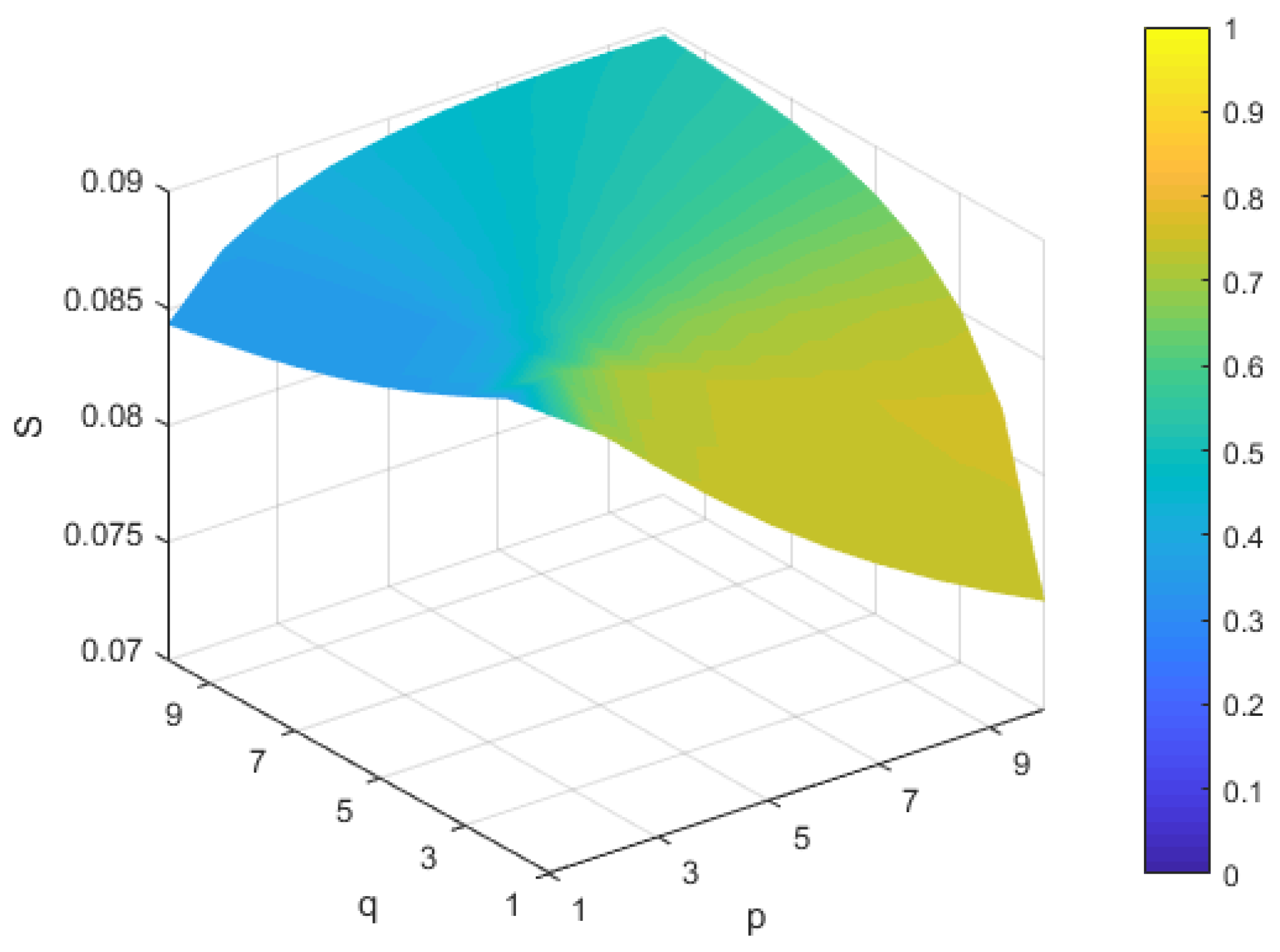
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | (0.53,0.33,0.09) | (0.89,0.08,0.03) | (0.42,0.35,0.18) | (0.08,0.89,0.02) |
| A2 | (0.73,0.12,0.08) | (0.13,0.64,0.21) | (0.03,0.82,0.13) | (0.73,0.15,0.08) |
| A3 | (0.91,0.03,0.02) | (0.07,0.09,0.05) | (0.04,0.85,0.10) | (0.68,0.26,0.06) |
| A4 | (0.85,0.09,0.05) | (0.74,0.16,0.10) | (0.02,0.89,0.05) | (0.08,0.84,0.06) |
| A5 | (0.90,0.05,0.02) | (0.68,0.08,0.21) | (0.05,0.87,0.06) | (0.13,0.75,0.09) |
| Method | Ranking Results | |
|---|---|---|
| Wei’s [45] method based on picture fuzzy weighted average (PFWA) operator | ||
| Wei’s [49] method based on picture fuzzy Hamacher weighted average operator (PFHWA) operator () | ||
| The proposed method based on PFDWHM operator ) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, R.; Huang, H.; Wang, J. Some Picture Fuzzy Dombi Heronian Mean Operators with Their Application to Multi-Attribute Decision-Making. Symmetry 2018, 10, 593. https://doi.org/10.3390/sym10110593
Zhang H, Zhang R, Huang H, Wang J. Some Picture Fuzzy Dombi Heronian Mean Operators with Their Application to Multi-Attribute Decision-Making. Symmetry. 2018; 10(11):593. https://doi.org/10.3390/sym10110593
Chicago/Turabian StyleZhang, Hongran, Runtong Zhang, Huiqun Huang, and Jun Wang. 2018. "Some Picture Fuzzy Dombi Heronian Mean Operators with Their Application to Multi-Attribute Decision-Making" Symmetry 10, no. 11: 593. https://doi.org/10.3390/sym10110593
APA StyleZhang, H., Zhang, R., Huang, H., & Wang, J. (2018). Some Picture Fuzzy Dombi Heronian Mean Operators with Their Application to Multi-Attribute Decision-Making. Symmetry, 10(11), 593. https://doi.org/10.3390/sym10110593





